Comprehensive Fracture Model of Reservoir Ice Layers in the Northeastern Cold Region of China
Abstract
1. Introduction
2. Experimental Methods and Details
2.1. Long-Term Monitoring
2.1.1. Meteorological Monitoring
2.1.2. Hydrological Monitoring
2.1.3. Ice Monitoring
2.2. Experimental Materials
2.2.1. Selection of Ice Material
2.2.2. Ice Specimen Preparation
2.2.3. Specimen Preparation for the Cracking Test
2.3. Experimental Methods
2.3.1. Mechanical Tests
2.3.2. Ice Crystal Tests
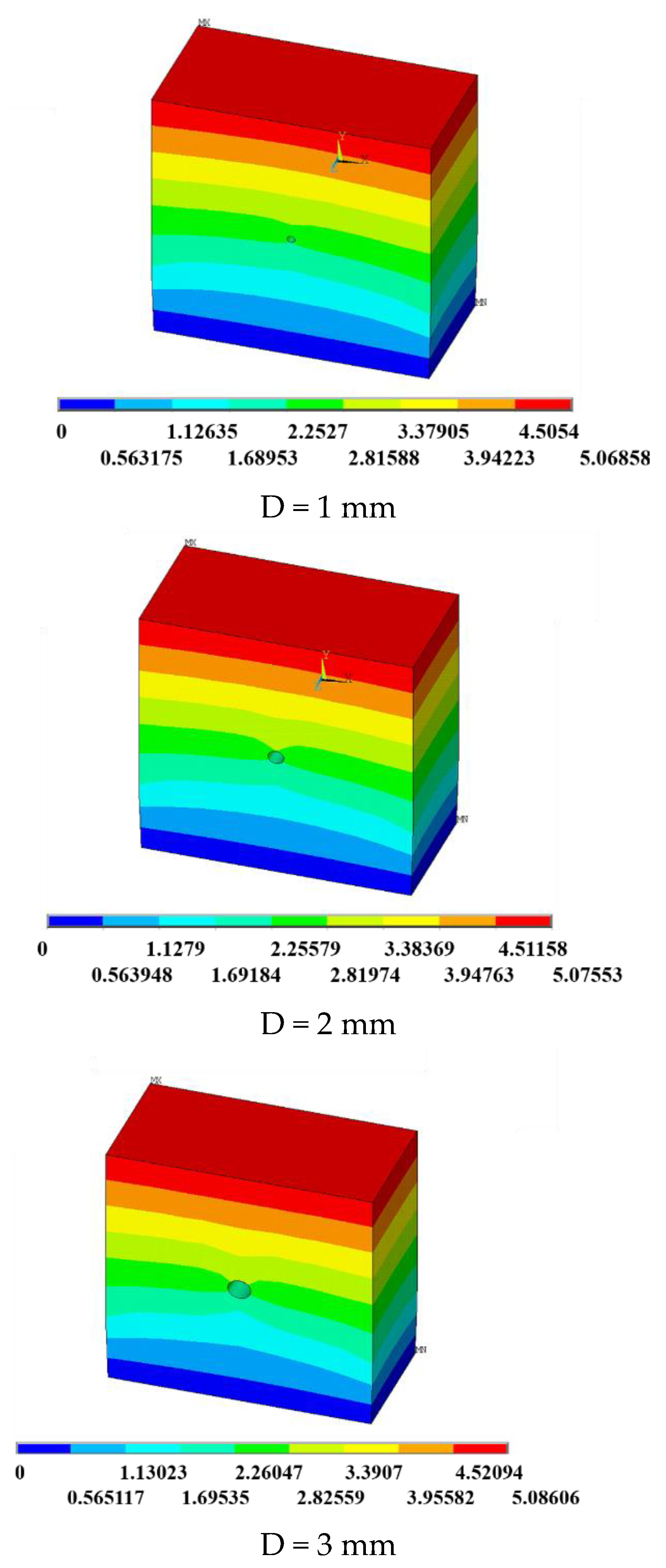
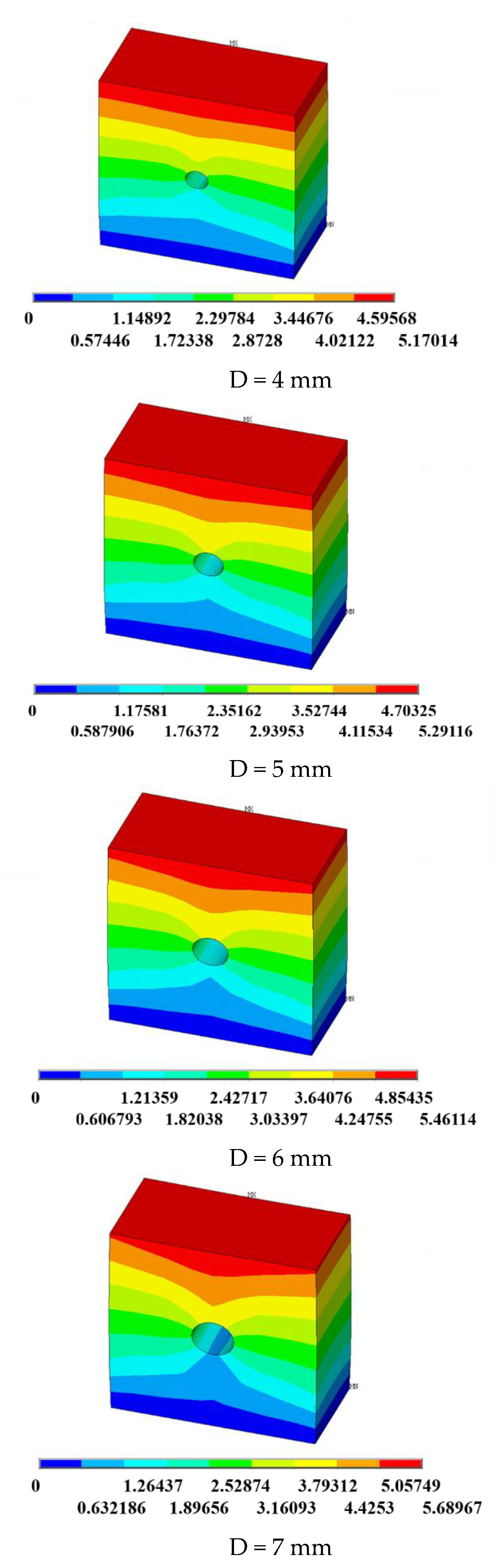
2.3.3. Ice Fracture Simulation
3. Results and Discussion
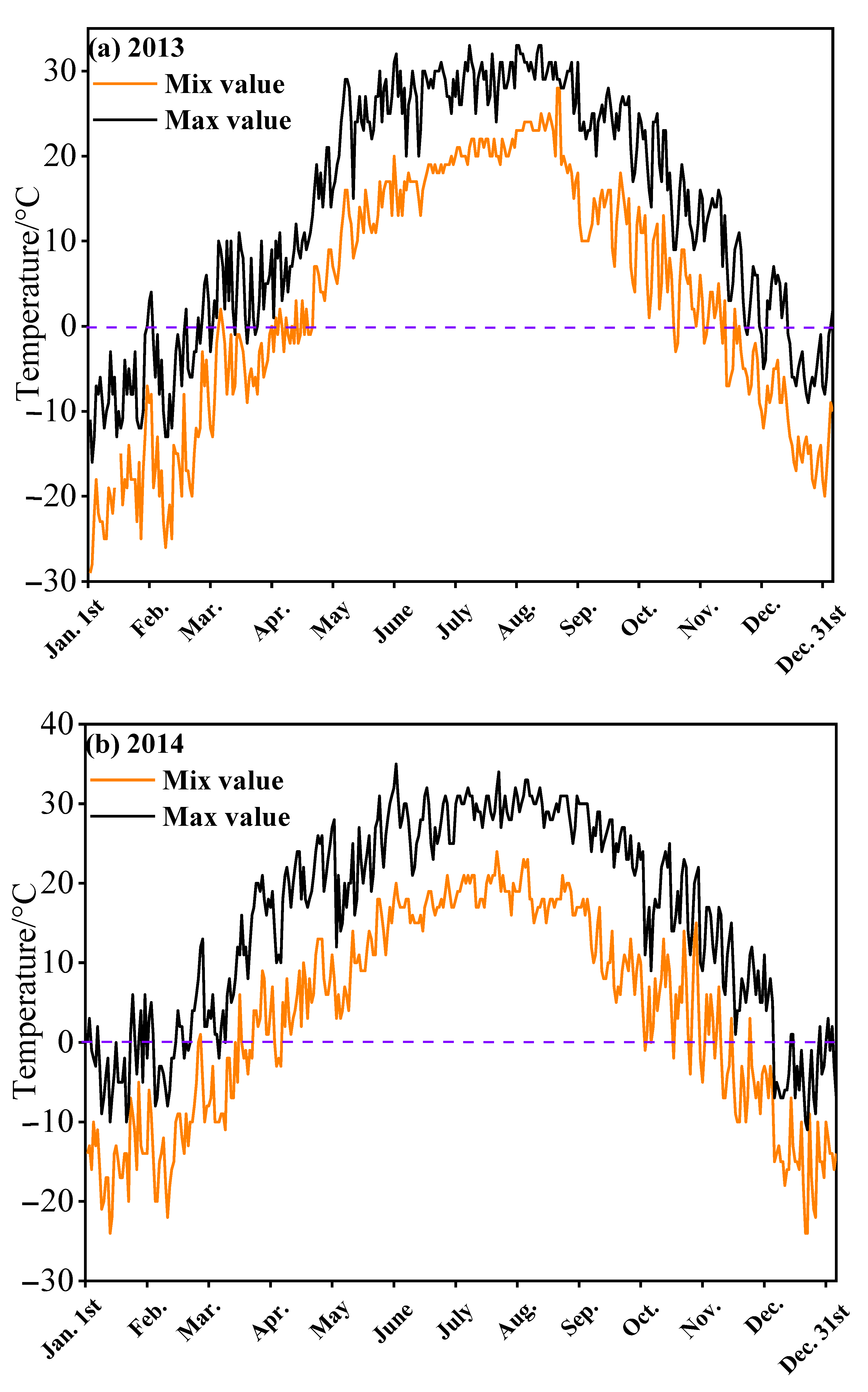
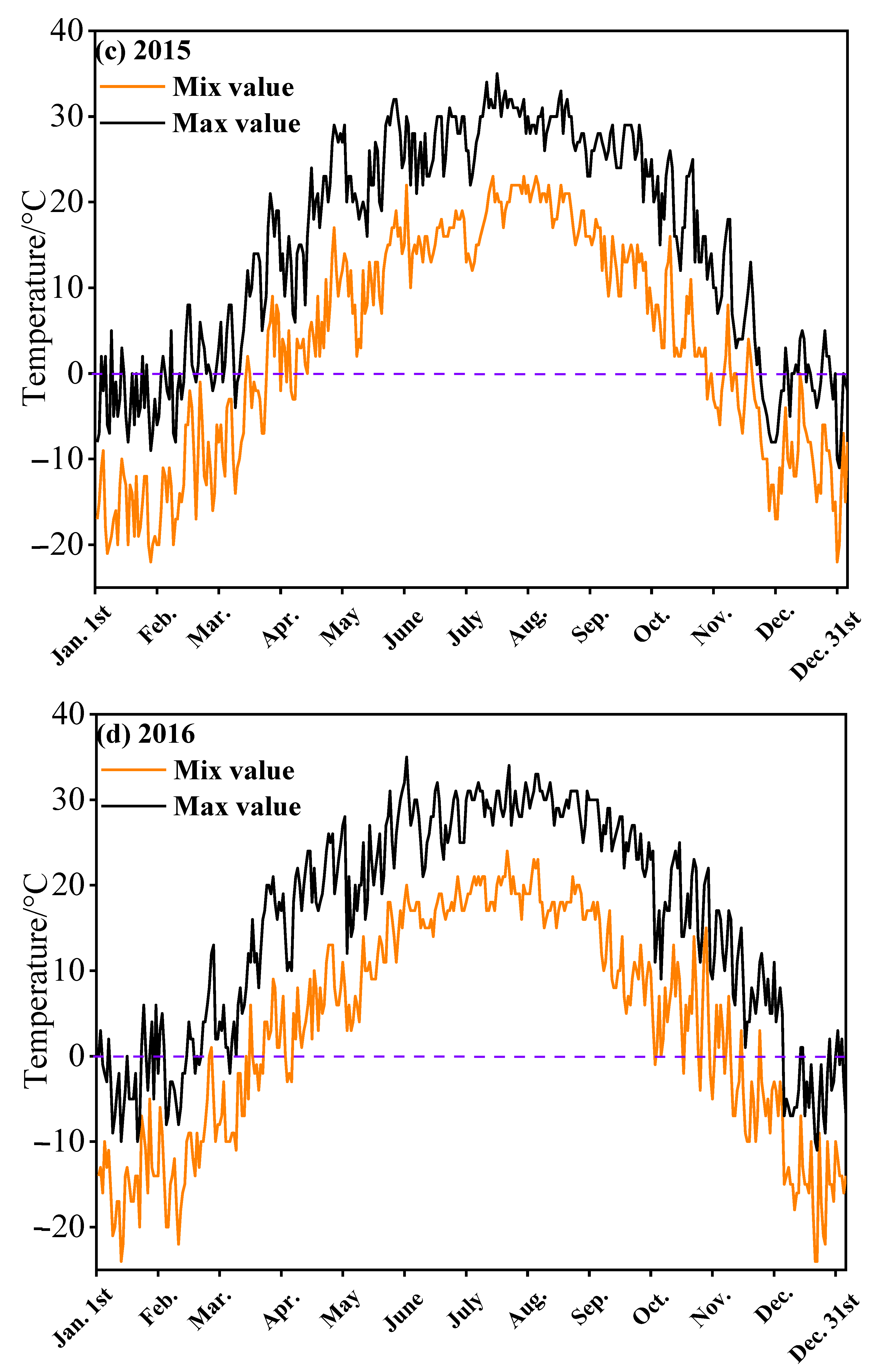
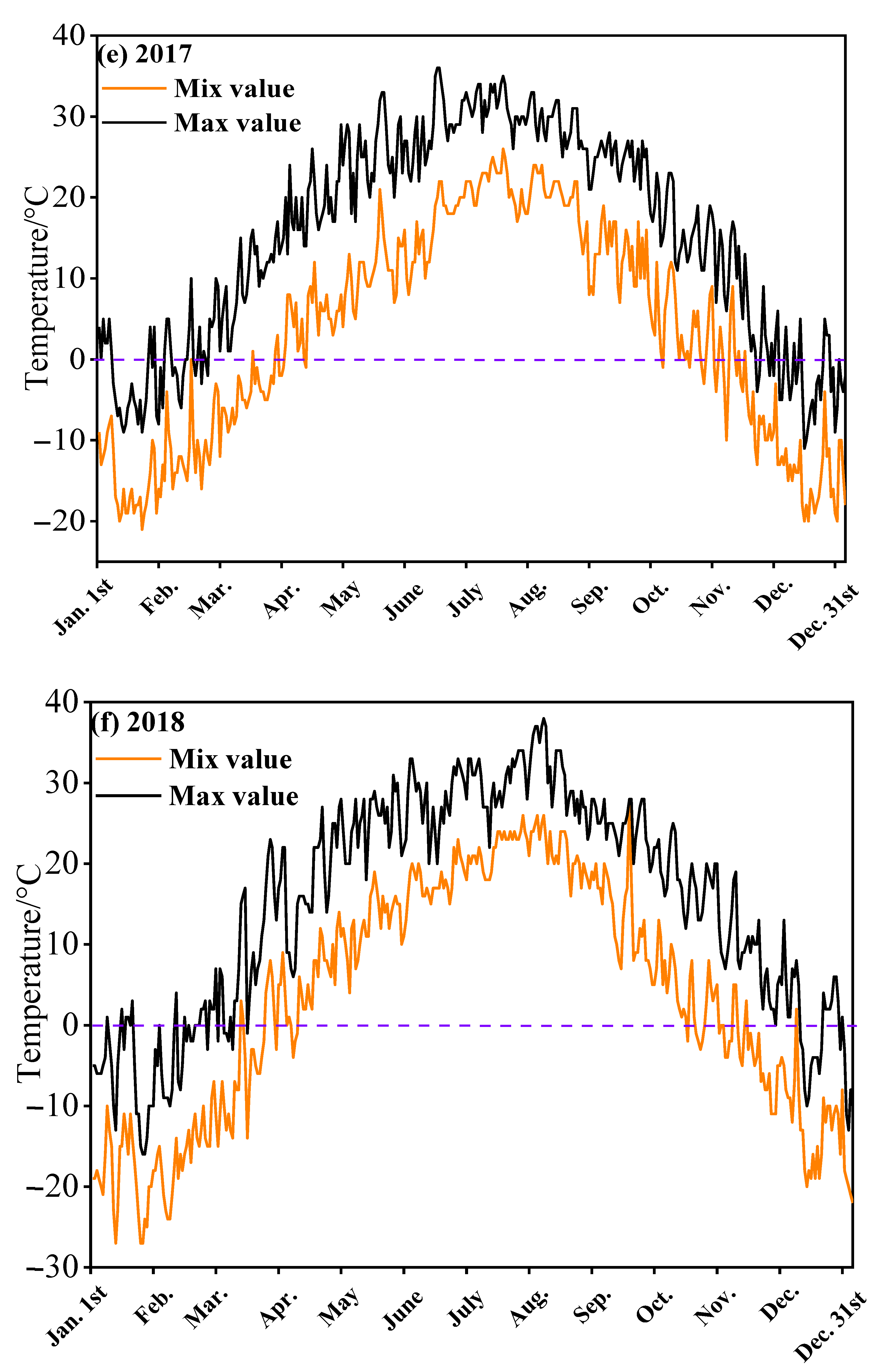
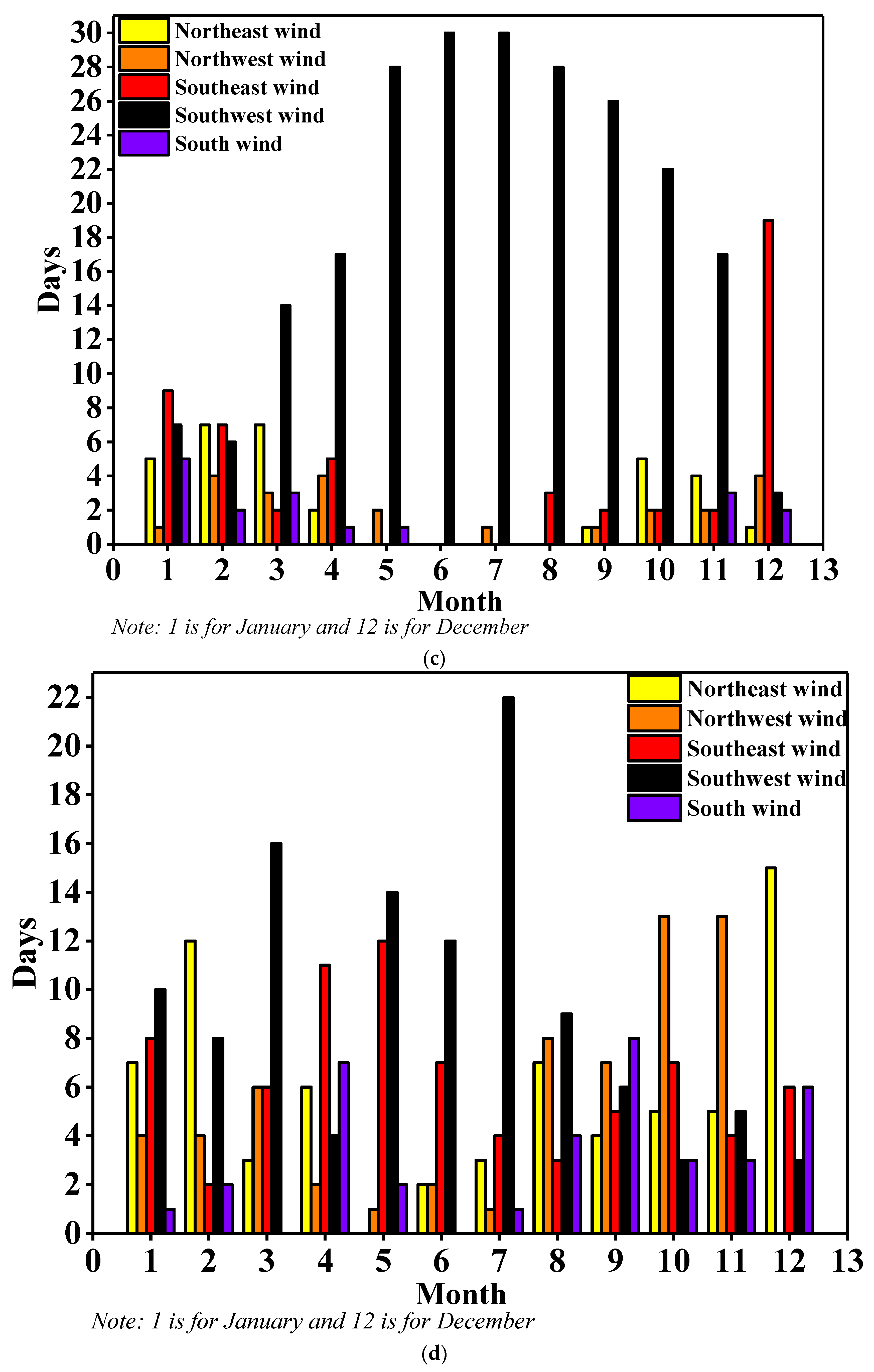
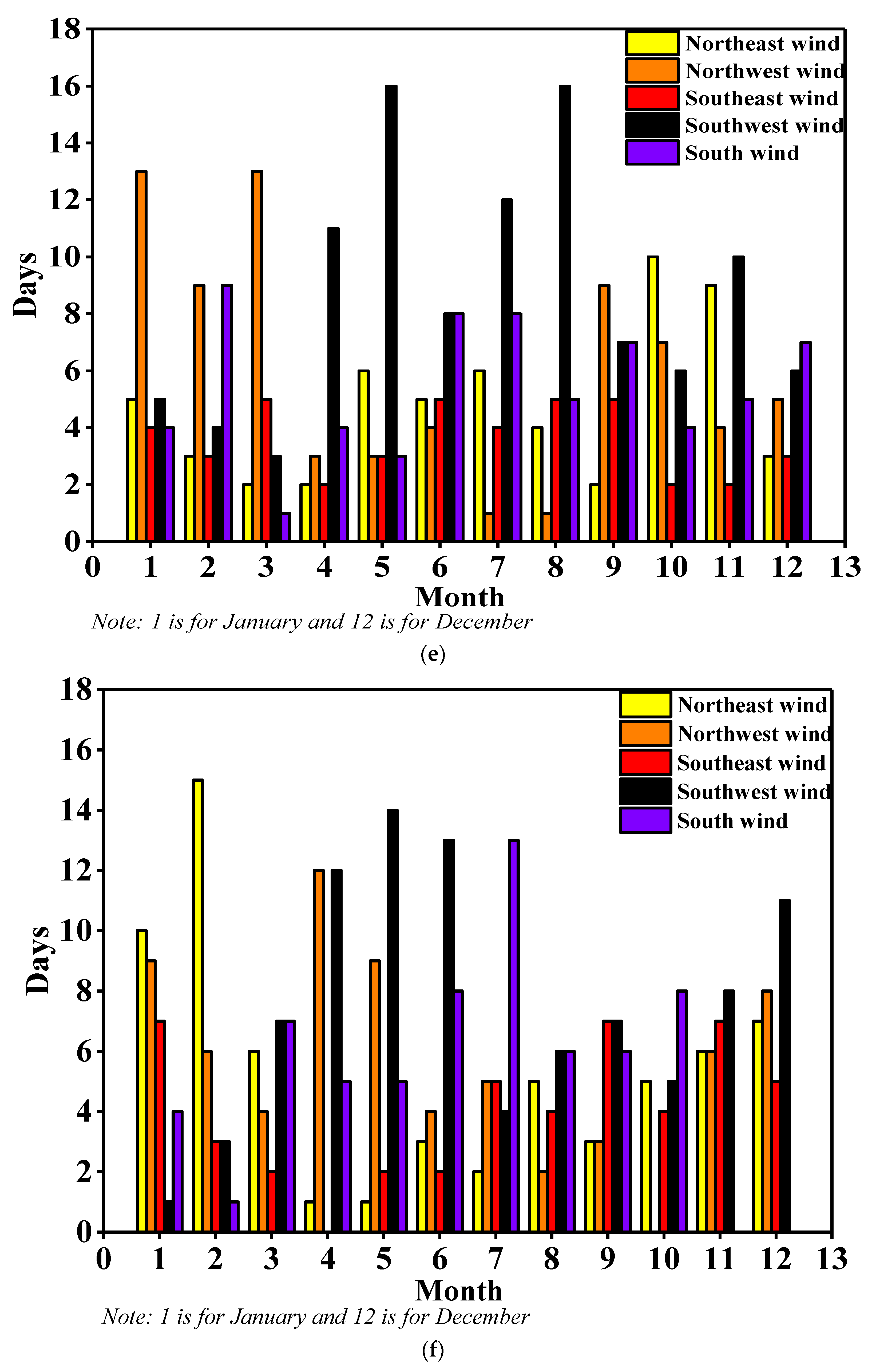
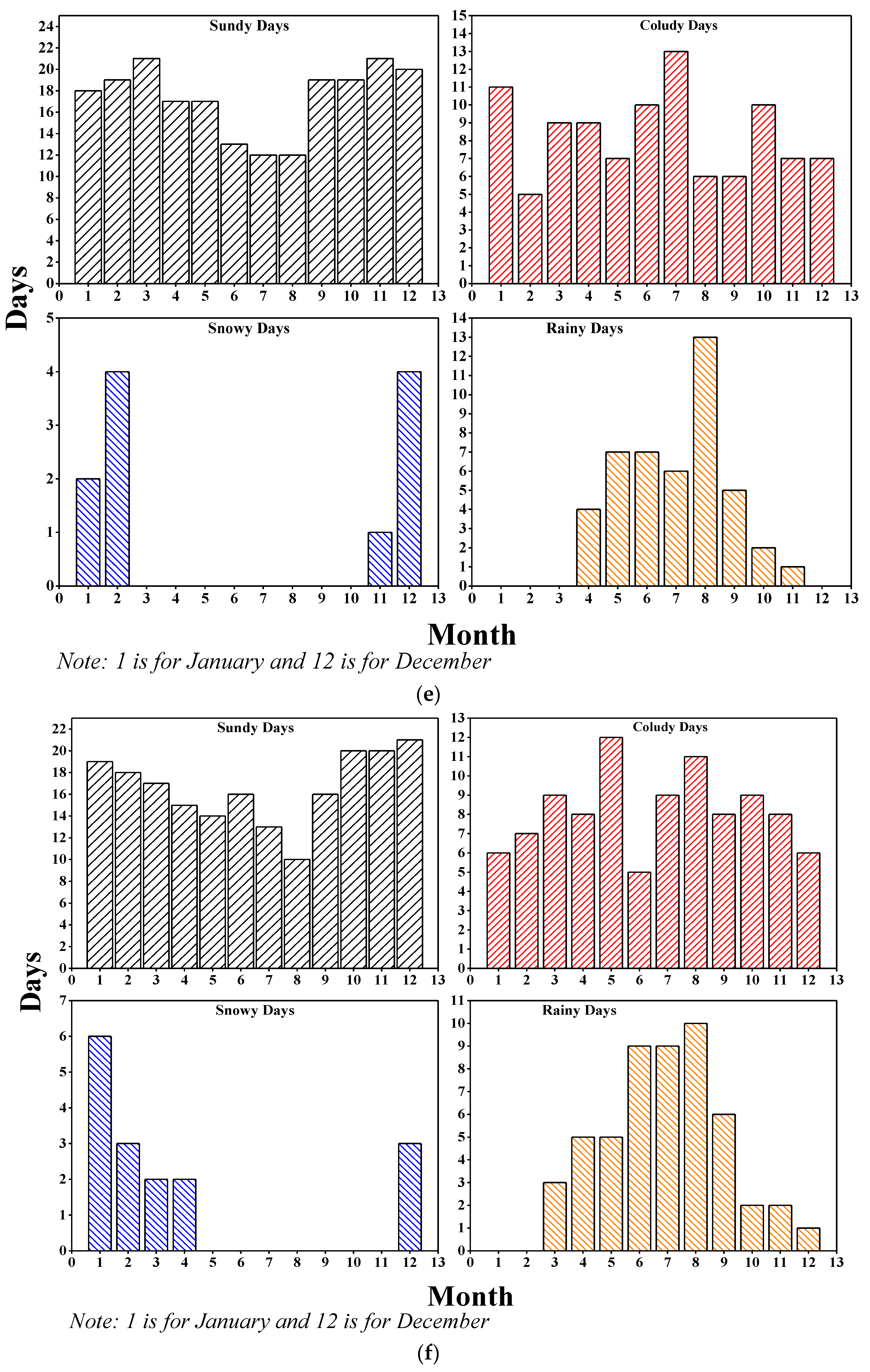
3.1. Analysis of Meteorological Changes
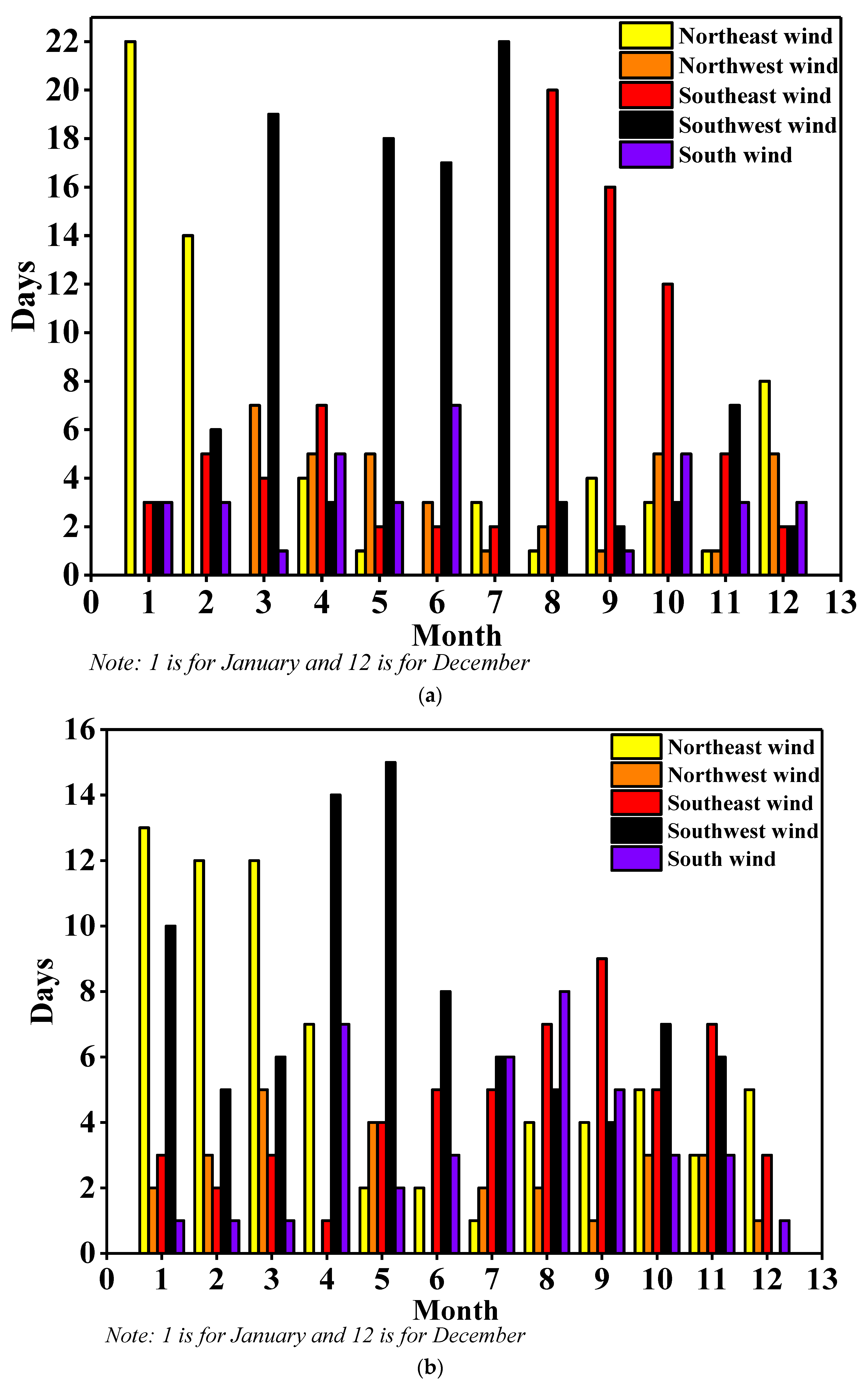
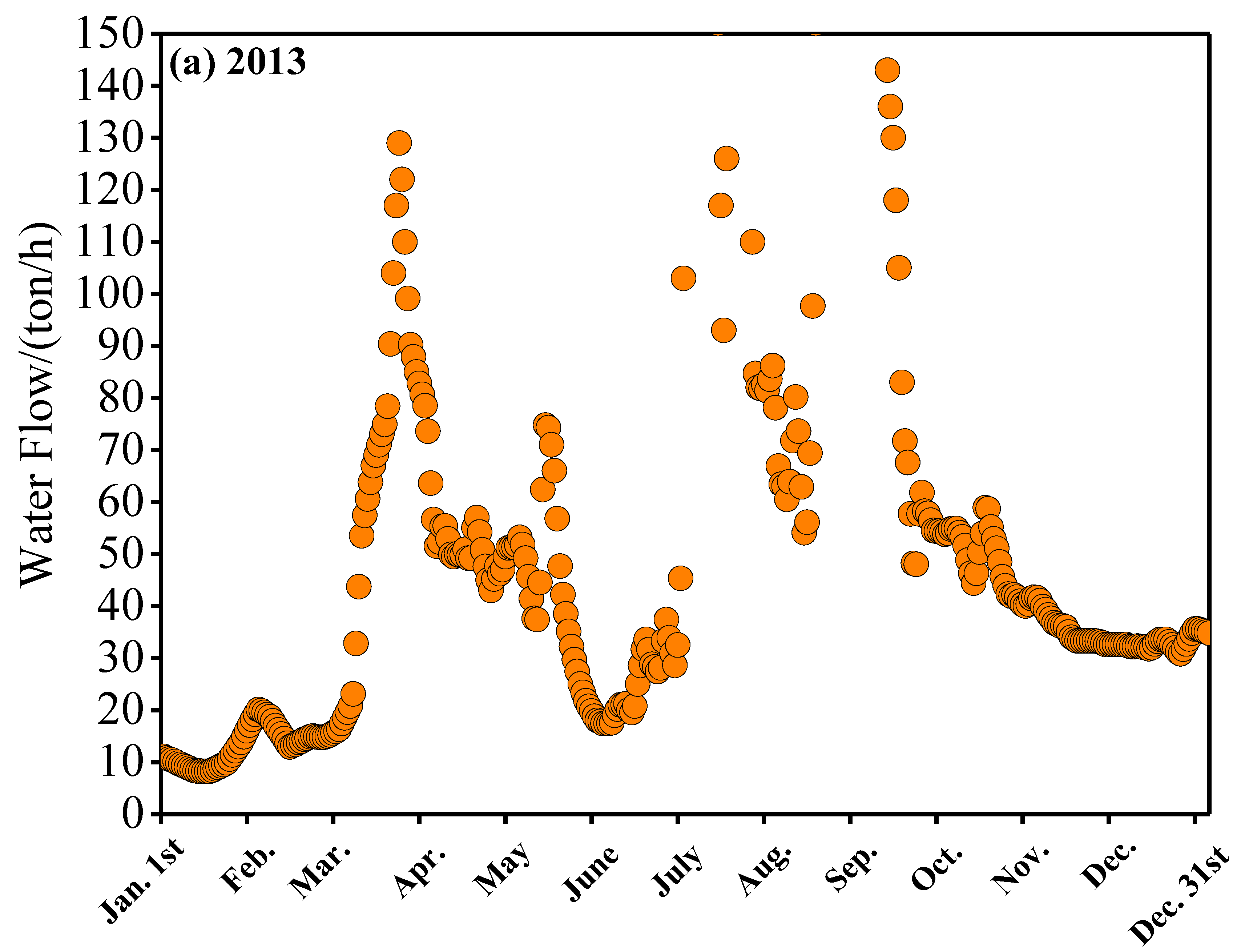
3.2. Analysis of the Hydrological Environment
3.3. Analysis of the Internal Structure of Ice Materials
3.3.1. Analysis of the Ice Crystal Structure
3.3.2. Bubble Density of the Ice Structure
3.3.3. Density and Clay Content of Ice Structure
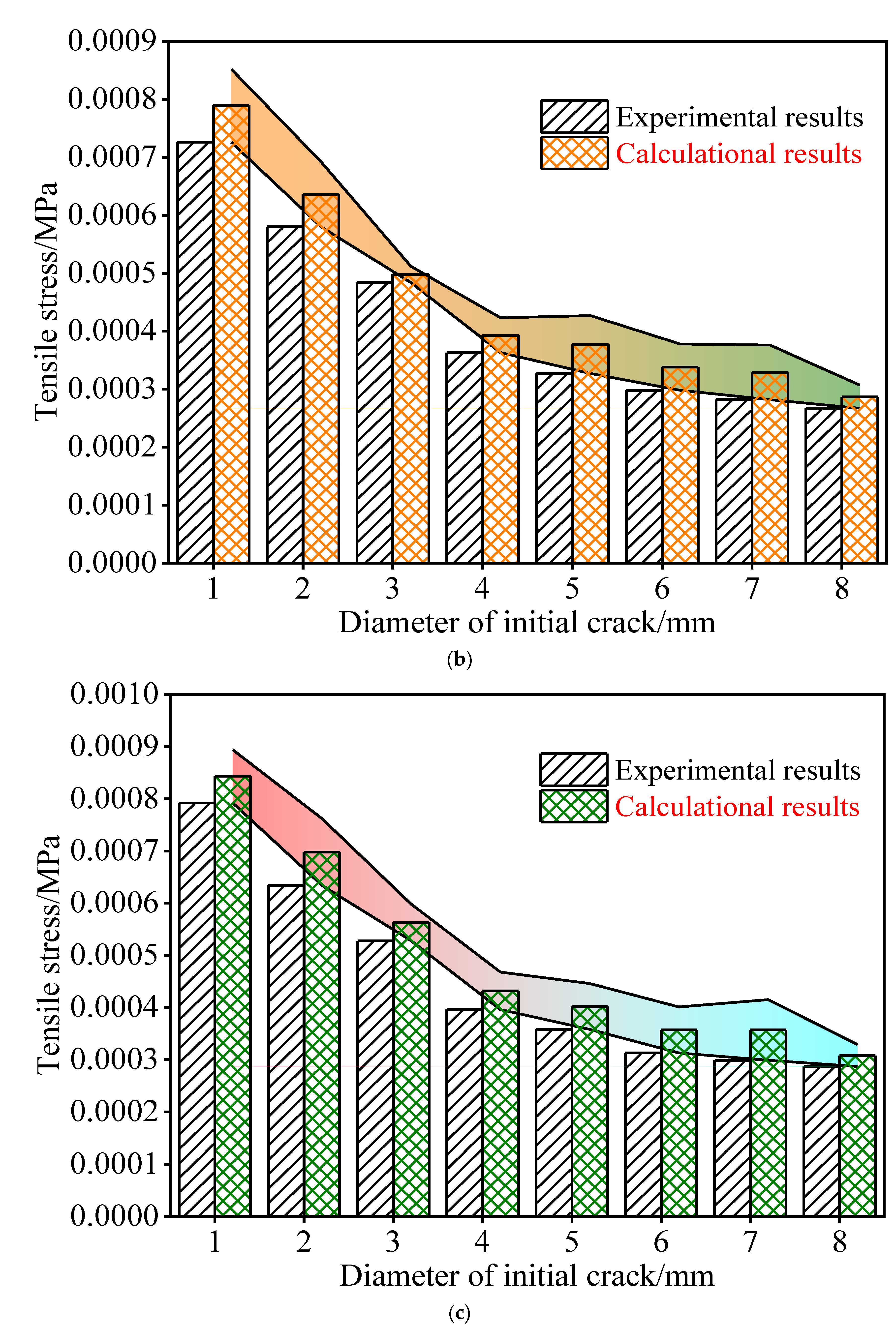
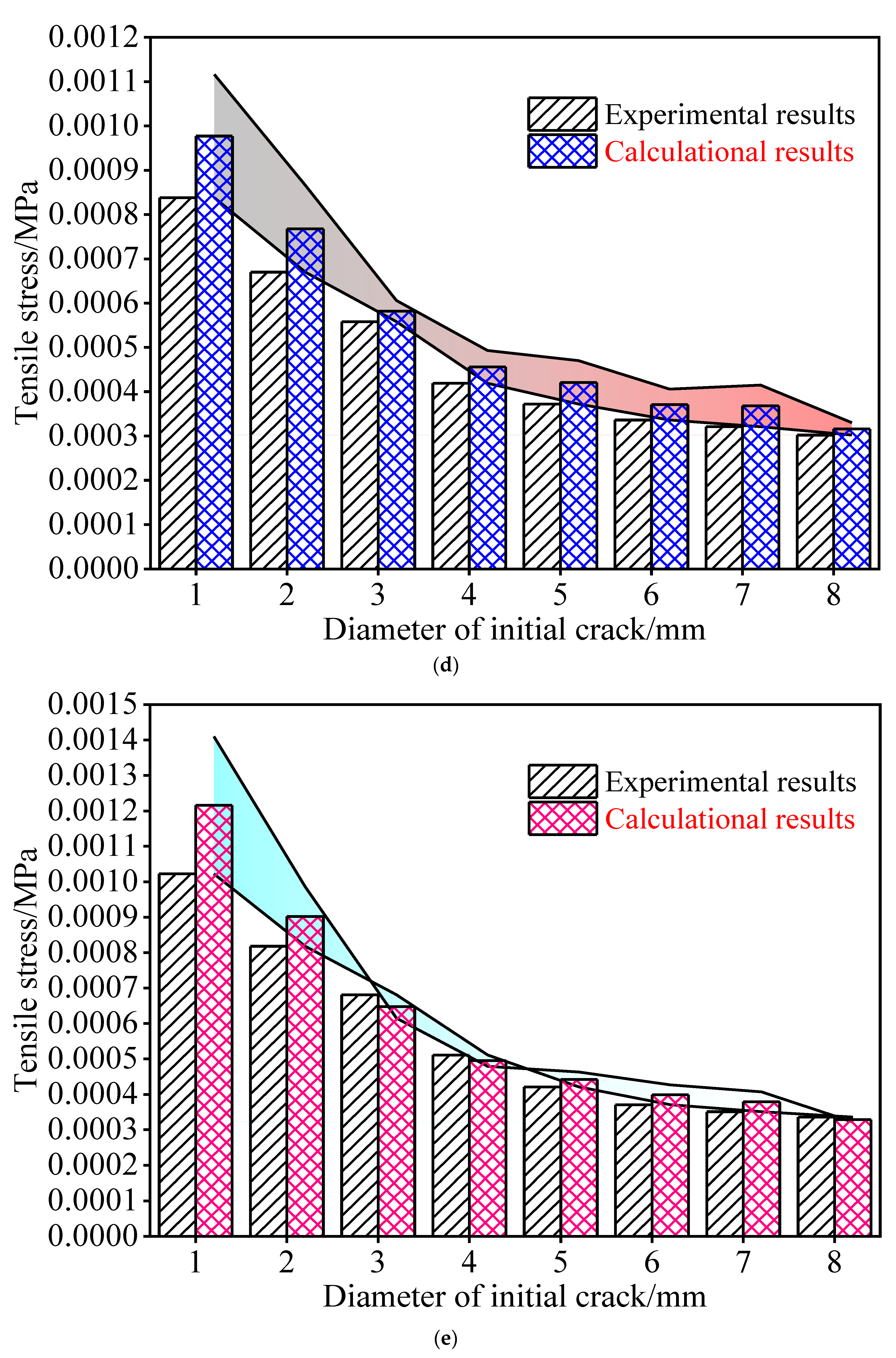
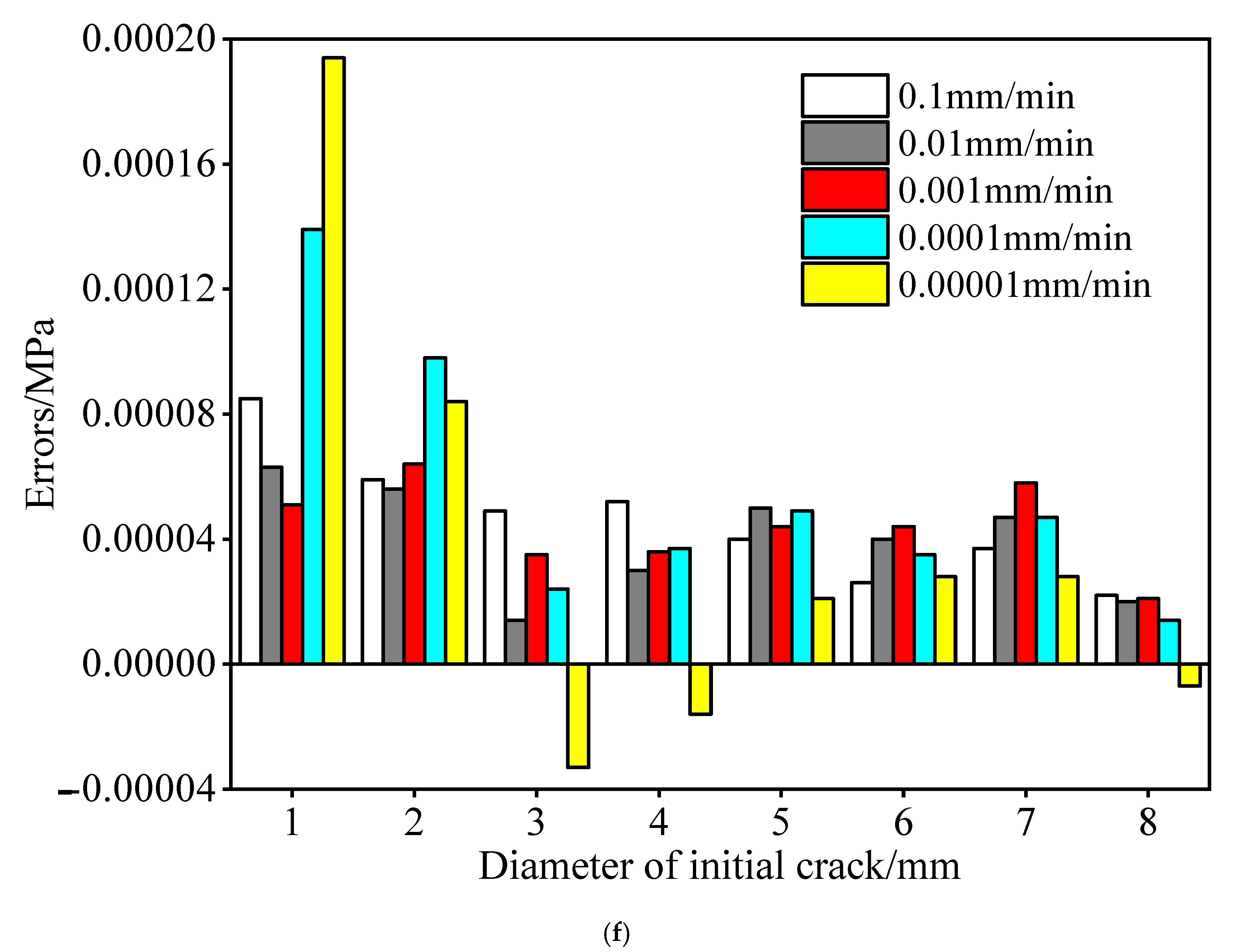
3.4. Comprehensive Fracture Model of the Ice Material
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, F.; Ma, H.Y. Application of Fracture Mechanics to Ice Engineering. J. Glaciol. Geocryol. 2010, 32, 139–150. [Google Scholar]
- Li, H.S.; Zhu, Y.L. Frozen Soil Fracture Mechanics and Application; Ocean Book Publishing: Beijing, China, 2002. [Google Scholar]
- Carter, D.; Sodhi, D.; Stander, E. Ice Thrust in Reservoirs. J. Cold Reg. Eng. 1998, 12, 169–183. [Google Scholar] [CrossRef]
- Karimidastenaei, Z.; Klöve, B.; Sadegh, M.; Haghighi, A.T. Polar Ice as an Unconventional Water Resource: Opportunities and Challenges. Water 2021, 13, 3220. [Google Scholar] [CrossRef]
- Cox, G.F.N.; Abdelnour, R. A Preliminary Investigation of Thermal Ice Pressure. Cold Reg. Sci. Technol. 1984, 9, 221–229. [Google Scholar] [CrossRef]
- Li, H.S. Calculation of Static Ice Pressure onto Slope in Plain Reservoir. Mech. Eng. 1991, 14, 29–32. [Google Scholar]
- Liu, X.Z.; Liu, P. Testing Research on the Compressive Fracture Toughness of Slab Fracture of Frozen Soil. Cold Reg. Sci. Technol. 2011, 165, 421–428. [Google Scholar] [CrossRef]
- Liu, X.Z.; Li, H.S. Experimental Study on The Plane Strain Fracture Toughness for Undisturbed Frozen Soils. Recent Dev. Res. Permafr. Eng. Cold Reg. 2009, 28, 611–625. [Google Scholar]
- Barry, N.W.; Raghu, N.S.; Sun, G. Rock Fracture Mechanics Principles Design and Applications; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Liu, X.Z.; Wu, Y. Research on Test of Model Nonlinear Fracture Toughness of Undisturbed Frozen Soils Based on Energy Balance Method. Rock Soil Mech. 2009, 30, 83–87. [Google Scholar]
- Li, X.L. Damage and Fracture Analysis on Concrete with an Oblique Crack. J. Nanchang Univ. (Eng. Technol.) 2004, 26, 56–58. [Google Scholar]
- Guo, S.H.; Sun, Z.Q.; Xie, X.Q. Research on Mode and Criterion of Rock Fracture under Compressive Loading. Chin. J. Geotech. Eng. 2004, 24, 304–308. [Google Scholar]
- Cai, Z.; Sun, B.T.; Guo, S.R. Experimental Research on Ice Load qnd Its Calculation Method. Earthq. Eng. Eng. Vib. 1997, 17, 49–56. [Google Scholar]
- Wang, J.F.; Yu, T.L.; Huang, M.L. Experimental Research on Uniaxial and Unconfined Compressive Strength of River Ice. Low Temp. Archit. Technol. 2007, 1, 11–13. [Google Scholar]
- Lu, Q.; Tang, A.; Zhong, N.P. Calculating Method of River Ice Loads on Piers the Mechanical Behavior Test of River Ice. J. Nat. Disasters 2002, 11, 75–79. [Google Scholar]
- Yu, T.; Yuan, Z.G.; Huang, M.L. Experimental Study on Mechanical Behavior of River Ice. J. Liaoning Tech. Univ. (Nat. Sci.) 2009, 28, 937–940. [Google Scholar]
- Zhang, L.M.; Li, Z.J.; Jia, Q. Experimental Study on Uniaxial Compressive Strengths of Artificial Freshwater Ice. J. Hydraul. Eng. 2009, 140, 1392–1396. [Google Scholar]
- Yue, Q.J.; Ren, X.H.; Chen, J.B. The Test and Mechanism Investigation on Ductile Brittle Transition of Sea Ice. J. Basic Sci. Eng. 2005, 13, 35–42. [Google Scholar]
- Liu, X.Z.; Liu, P. The Laboratorial Study of Fracture Energy Release Rate of the Reservoir Ice Layer. Archit. Build. Mater. 2011, 22, 3802–3807. [Google Scholar] [CrossRef]
- Ji, S.Y.; Liu, H.L.; Xu, N.; Ma, H.Y. Experiments on sea ice fracture toughness in the Bohai Sea. Adv. Water Sci. 2013, 24, 386–391. [Google Scholar]
- Goetze, C.G. A Study of Brittle Fracture as Applied to Ice; Technical Note; U.S. Army Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1965; p. 63. [Google Scholar]
- Hellgren, R.; Enzell, J.; Ansell, A.; Nordström, E.; Malm, R. Estimating the Ice Loads on Concrete Dams Based on Their Structural Response. Water 2022, 14, 597. [Google Scholar] [CrossRef]
- Hamza, H.; Muggeridge, D.B. Plane strain fracture toughness (KIC) of fresh water ice. In Proceedings of the 5th International POAC Conference, Trondheim, Norway, 13–18 August 1979; Volume 1, pp. 697–707. [Google Scholar]
- Urabe, N.; Yoshitake, A. Strain rate dependent fracture toughness (KIC) of pure ice and sea ice. In Proceedings of the 6th International IAHR Symposium on Ice, Quebec City, QC, Canada, 11 August 1981; Volume 2, pp. 551–563. [Google Scholar]
- Timco, G.W.; Frederking, R.M.W. Comparative strengths of fresh water ice. Gold Reg. Sci. Technol. 1982, 6, 21–27. [Google Scholar] [CrossRef][Green Version]
- Timco, G.W.; Frederking, R.M.W. The effects of anisotropy and microcracks on the fracture toughness KIC of freshwater ice. In Proceedings of the 5th International OMAE Conference, Tokyo, Japan, 13 April 1986; pp. 341–348. [Google Scholar]
- Liu, H.W.; Miller, K.J. Fracture toughness of fresh-water ice. J. Glaciol. 1979, 22, 135–143. [Google Scholar] [CrossRef][Green Version]
- Parsons, B.L.; Snellen, J.B. Fracture toughness of freshwater prototype ice and carbamide model ice. In Proceedings of the 8th International POAC Conference, Narssarssuaq, Greenland, 7–14 September 1985; Volume 1, pp. 128–137. [Google Scholar]
- Dempsey, J.P. The fracture toughness of ice. In Ice-Structure Interaction; Springer: Berlin/Heidelberg, Germany, 1991; pp. 109–145. [Google Scholar]
- Dempsey, J.P.; Jochmann, P.; Fransson, L.; Mu, Z.; Weiss, J.; Palmer, A.C. Cleavage fracture of warm brackish ice. In Proceedings of the 22nd International Conference on Port and Ocean Engineering under Arctic Conditions, Espoo, Finland, 9–13 June 2013; p. 6. [Google Scholar]
- Prasanna, M.; Wei, M.; Polojärvi, A.; Cole, D.M. Laboratory experiments on floating saline ice block breakage in ice-to-ice contact. Cold Reg. Sci. Technol. 2021, 189, 103315. [Google Scholar] [CrossRef]
- Wells, J.; Jordaan, I.; Derradji-Aouat, A.; Taylor, R. Small-scale laboratory experiments on the indentation failure of polycrystalline ice in compression: Main results and pressure distribution. Cold Reg. Sci. Technol. 2011, 65, 314–325. [Google Scholar] [CrossRef]
- Liu, X.Z.; Li, B.; Li, Z.J.; Shen, W.G. A new fracture model for reservoir ice layers in the northeast cold region of China. Constr. Build. Mater. 2018, 191, 795–811. [Google Scholar] [CrossRef]
- Kusumoto, S.; Kimura, N.; Uchida, T.; Takase, T. Study of fracture toughness of coarse grained ice and the effect of specimen size (a). J. Soc. Mater. Sci. 1986, 35, 659–663. (In Japanese) [Google Scholar] [CrossRef]
- Kusumoto, S.; Kimura, N.; Takase, T.; Kidera, T. Study of fracture toughness of columnar grained ice using large specimens (b). J. Soc. Mater. Sci. 1986, 35, 887–891. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Wang, T.; Yang, K.; Guo, Y.; Huo, S. Application of artificial neural networks to forecasting of river ice condition. J. Hydraul. Eng. 2005, 36, 1204–1208. (In Chinese) [Google Scholar]
- Li, Z.J.; Zhang, L.M.; Lu, P. Experimental study on the effect of porosity on the uniaxial compressive strength of sea ice in Bohai Sea. Sci. China Technol. Sci. 2011, 54, 2429–2436. (In Chinese) [Google Scholar] [CrossRef]
- Li, Z.J.; Huang, W.F.; Jia, Q.; Leppäranta, M. Characteristics of crystals, bubbles and density of freshwater ice in reservoirs. J. Hydraul. Eng. 2009, 40, 1333–1338. (In Chinese) [Google Scholar]
- Zhang, Y.D.; Li, Z.J.; Guo, W.D.; Yu, H.H.; Liang, W.W. Methods and equipment for three-point bending strength test of ice. Water Resour. Sci. Cold Reg. Eng. 2008, 1, 63–68. (In Chinese) [Google Scholar]
- Wei, M.; Polojärvi, A.; Cole, D.M.; Prasanna, M. Strain response and energy dissipation of floating saline ice under cyclic compressive stress. Cryosphere 2020, 14, 2849–2867. [Google Scholar] [CrossRef]
- Wei, M.; Dai, F. Laboratory-scale mixed-mode I/II fracture tests on columnar saline ice. Theor. Appl. Fract. Mech. 2021, 114, 102982. [Google Scholar] [CrossRef]
- Water Resources of PRC. Specification for Rock Test of Water Resources and Hydropower Develop; Water Power Press: Beijing, China, 2001; pp. 32–33. [Google Scholar]
- Langway, C.C. Ice Fabrics and the Universal Stage; Department of Defense, Department of the Army, Corps of Engineers, Snow Ice and Permafrost Research Establishment: Wilmette, IL, USA, 1959; pp. 468–492. Available online: https://usace.contentdm.oclc.org/digital/collection/p266001coll1/id/2291/ (accessed on 29 April 2022).
- Langway, C.C. Ice Fabrics and the Universal Stage; U.S. Army Snow Ice and Permafermafrost Resesrch Establishment, Corps of Engineers: Wilmette, IL, USA, 1958; pp. 551–573. [Google Scholar]
- Cho, H.; Shepson, P.B.; Barrie, L.A. NMR investigation of the quasi-brine layer in ice/brine mixtures. J. Phys. Chem. B 2002, 106, 11226–11232. [Google Scholar] [CrossRef]
- Coa, G.F.N.; Weeks, W.F. Profile properties of undeformed first-year sea ice. CRREL Rep. 1988, 13, 1–66. [Google Scholar]
- Durand, G.; Gagliardini, O.; Thorsteinsson, T. Ice microstructure and fabric: An up-to-date approach for measuring textures. J. Glaciol. 2006, 52, 619–630. [Google Scholar] [CrossRef]
- Eicken, H.; Bock, C. Magnetic resonance imaging of sea-ice pore fluids: Methods and thermal evolution of pore microstructure. Cold Reg. Sci. Technol. 2000, 31, 207–225. [Google Scholar] [CrossRef][Green Version]
- Frost, H.J. Mechanims of Crack Nucleation in lce. Eng. Fract. Mech. 2001, 68, 1823–1837. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Y.P.; Chai, L. Glacier change and response to climate in the northern slope of the middle Nyainqêntanglha Mountains during 1990–2020. Prog. Geogr. 2021, 40, 2073–2085. [Google Scholar] [CrossRef]
- Tian, H.Z.; Yang, T.B.; Liu, Q.P. Relationship between climate change and glacier retreat over the last 40 years in Lenglongling range of eastern Qilian Mountains. Res. Soil Water Conserv. 2012, 19, 34–38. [Google Scholar]
- Radić, V.; Hock, R. Regional and global volumes of glaciers derived from statistical upscaling of glacier inventory data. J. Geophys. Res. Earth Surf. 2010, 115, F01010. [Google Scholar] [CrossRef]
- Golden, K.M.; Eicken, H.; Heaton, A.L. Thermal evolution of permeability and microstructure in sea ice. Geophys. Res. Lett. 2007, 34, 1–6. [Google Scholar] [CrossRef]
- Miyamoto, A.; Weikusat, I.; Hondoh, T. Complete determination of ice crystal orientation using Laue X-ray diffraction method. J. Glaciol. 2011, 57, 103–110. [Google Scholar] [CrossRef]
- Timco, G.W.; Weeks, W.F. A review of the engineering properties of sea ice. Cold Reg. Sci. Technol. 2010, 60, 107–129. [Google Scholar] [CrossRef]





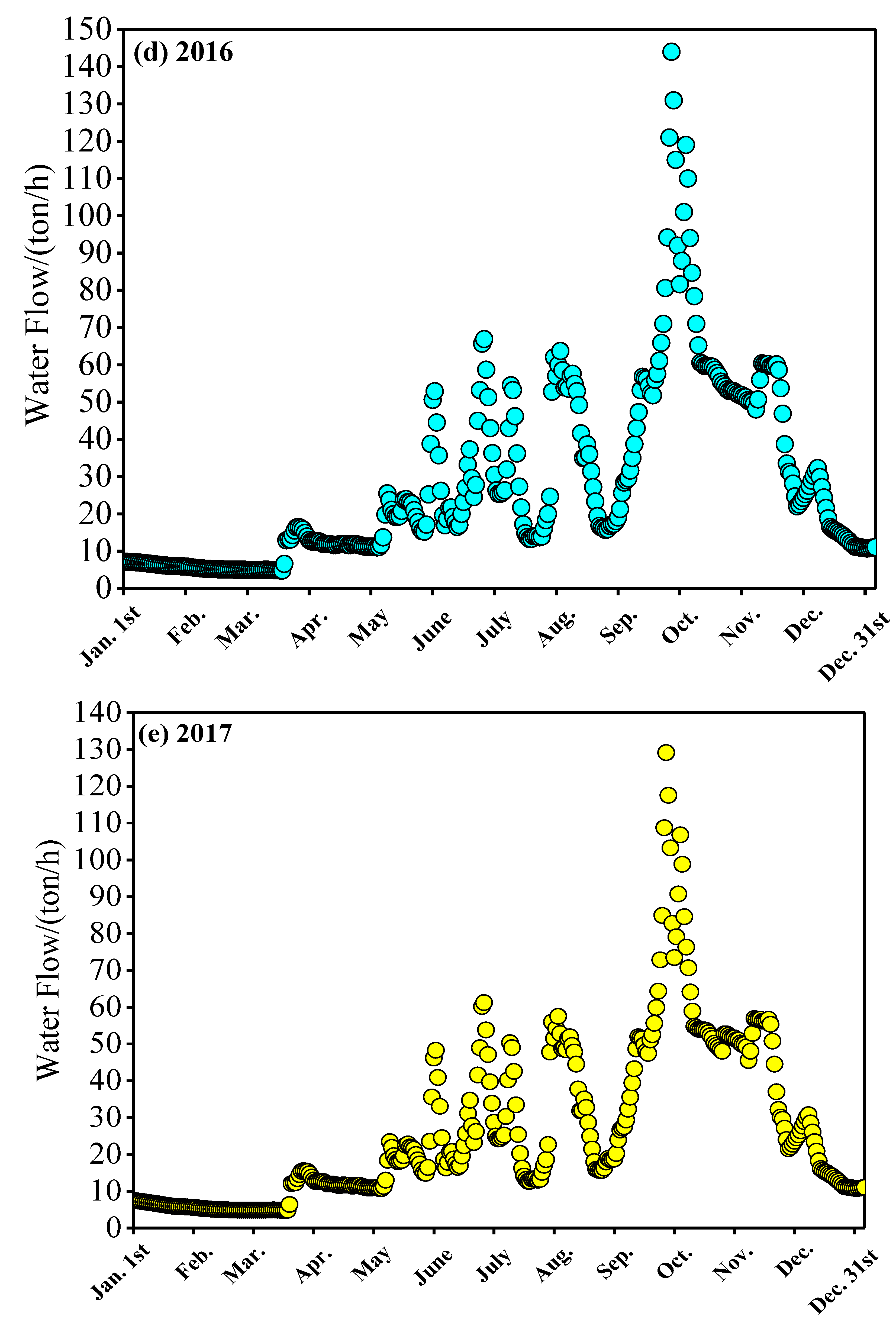
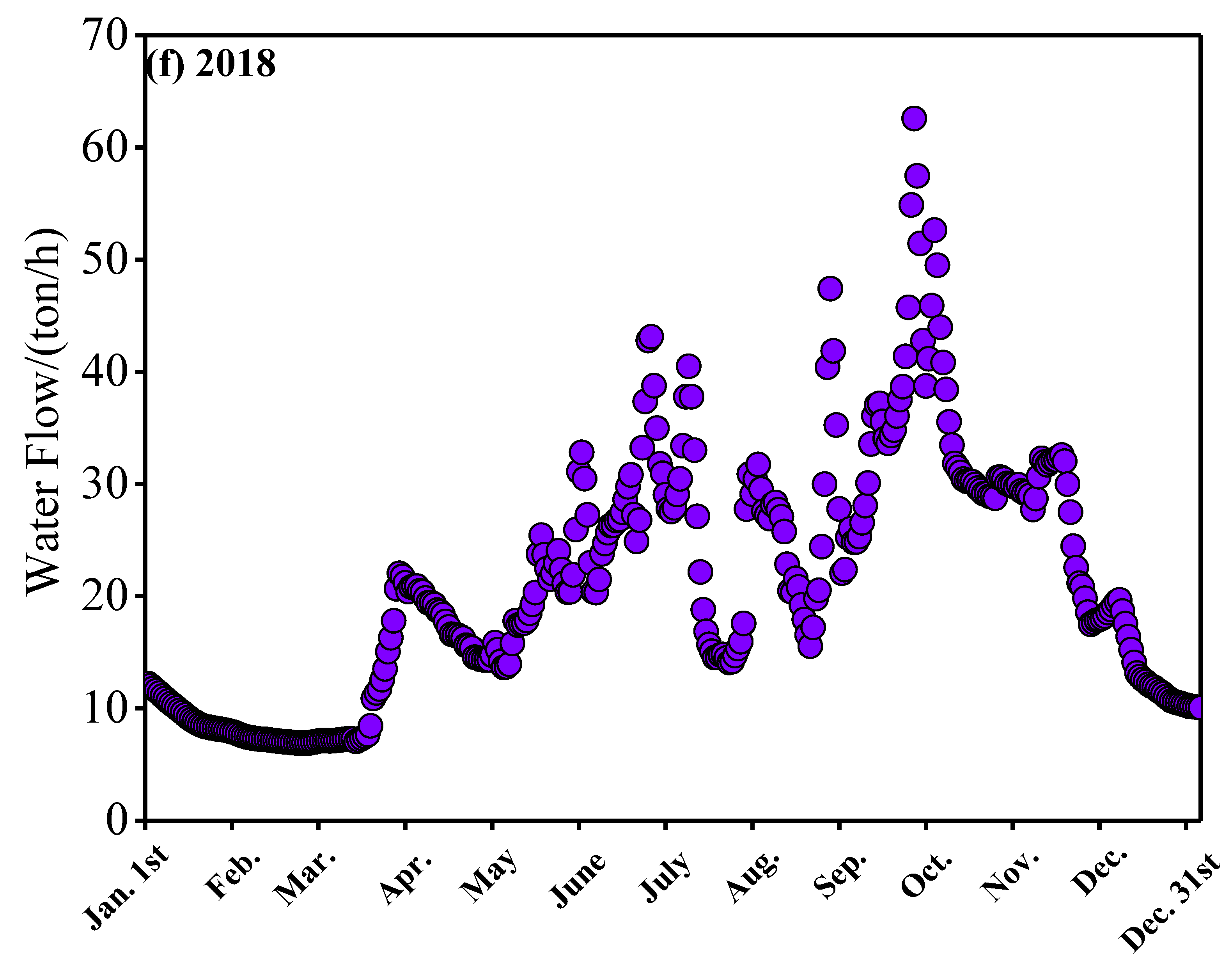
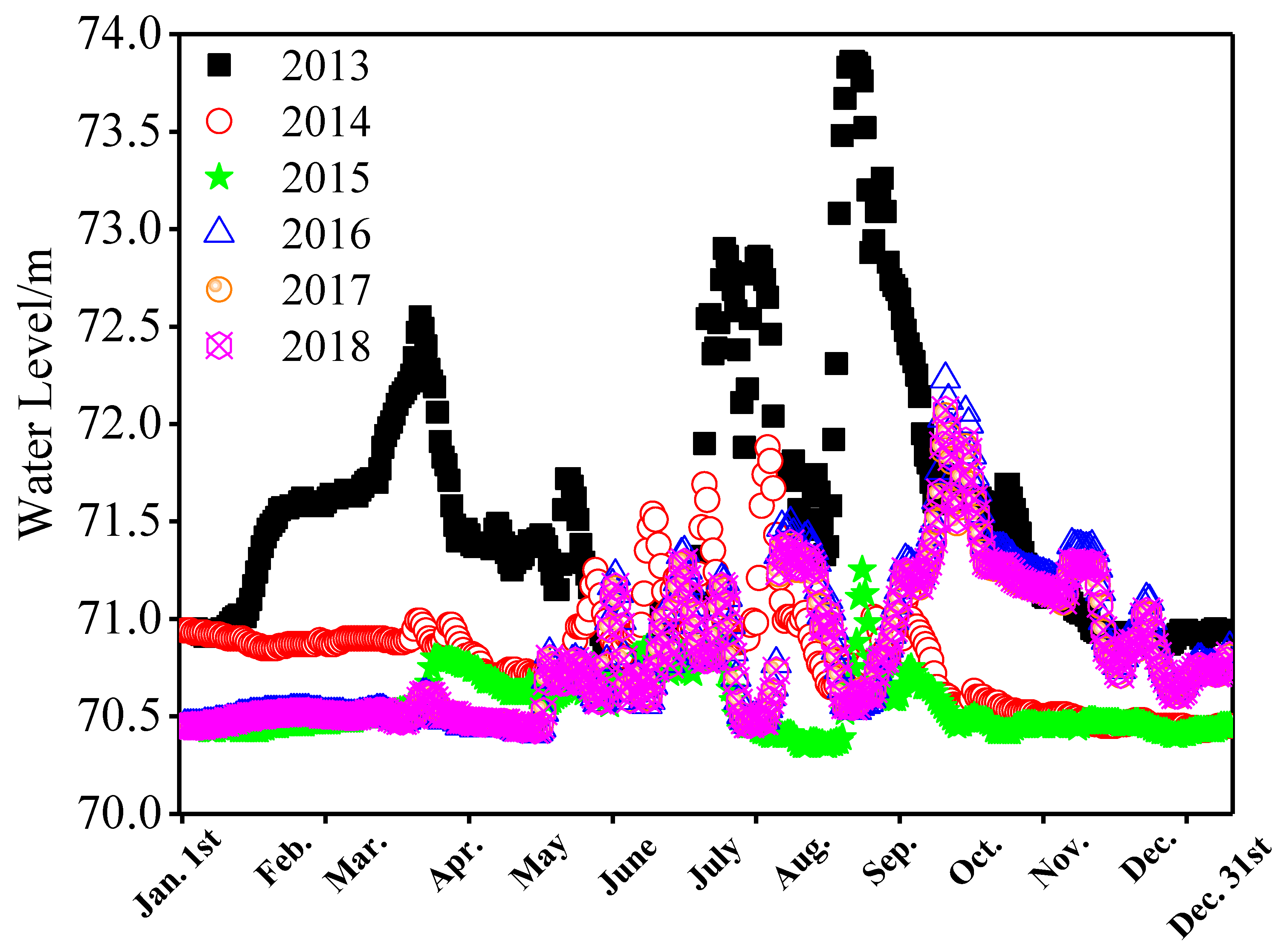
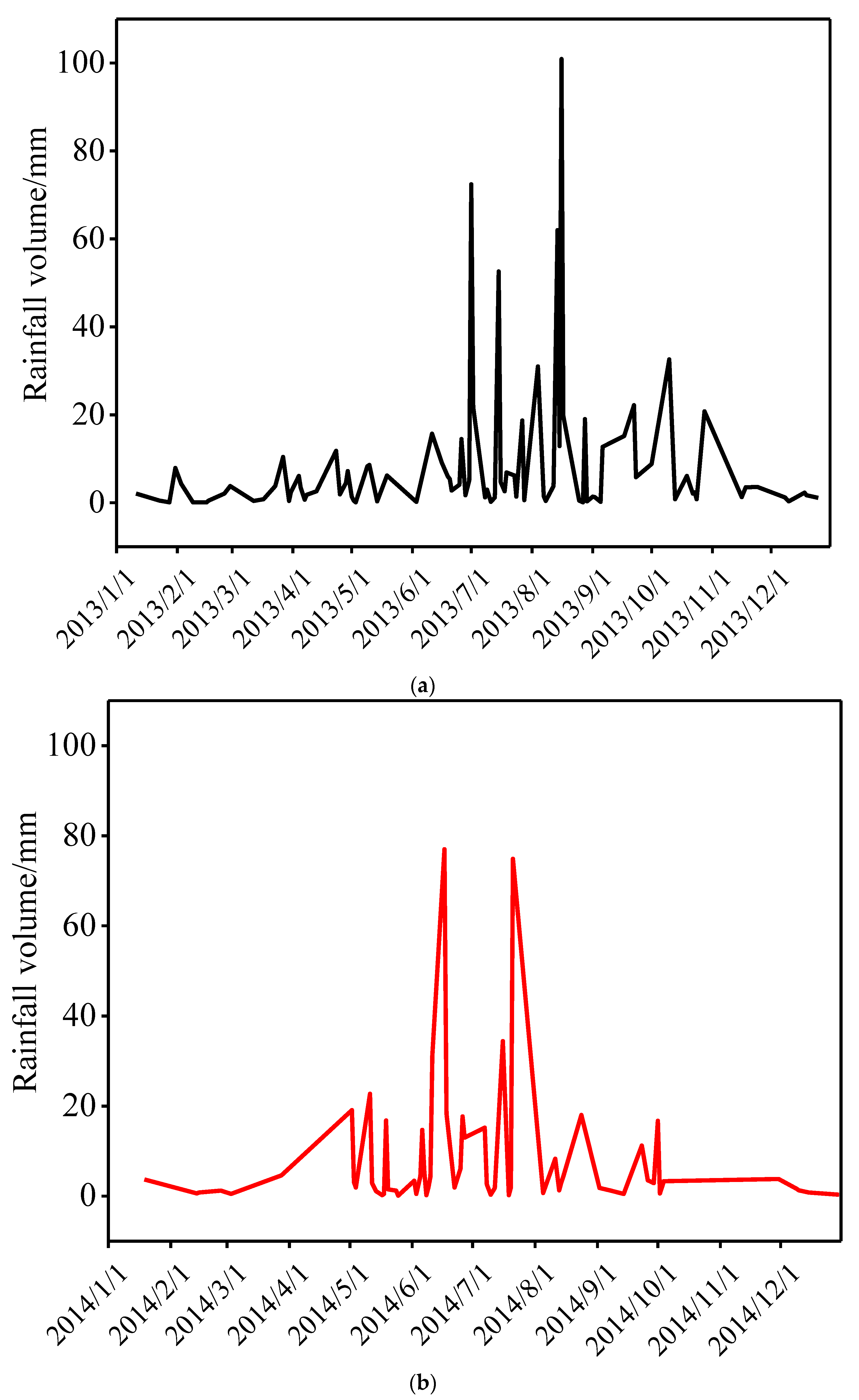
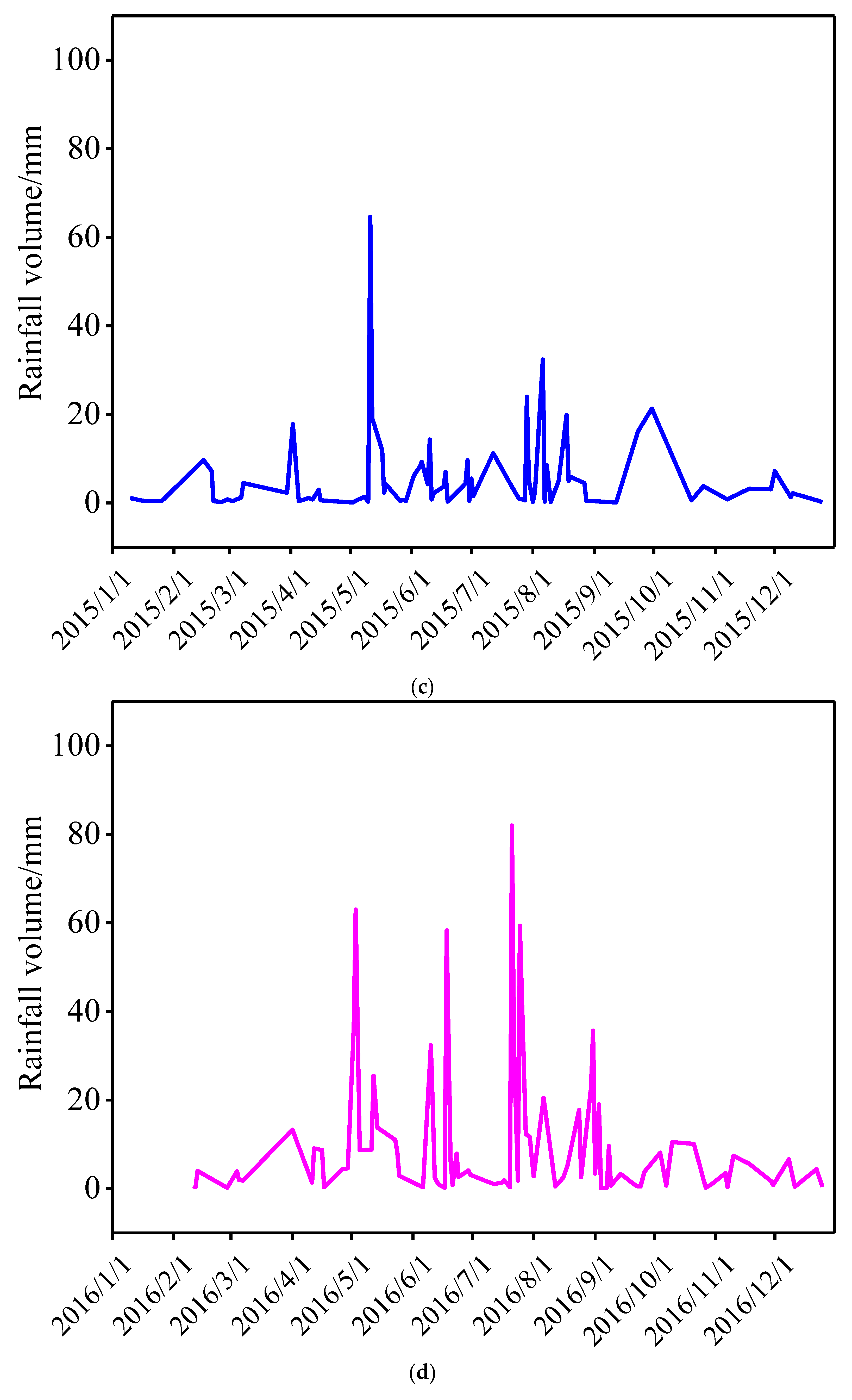
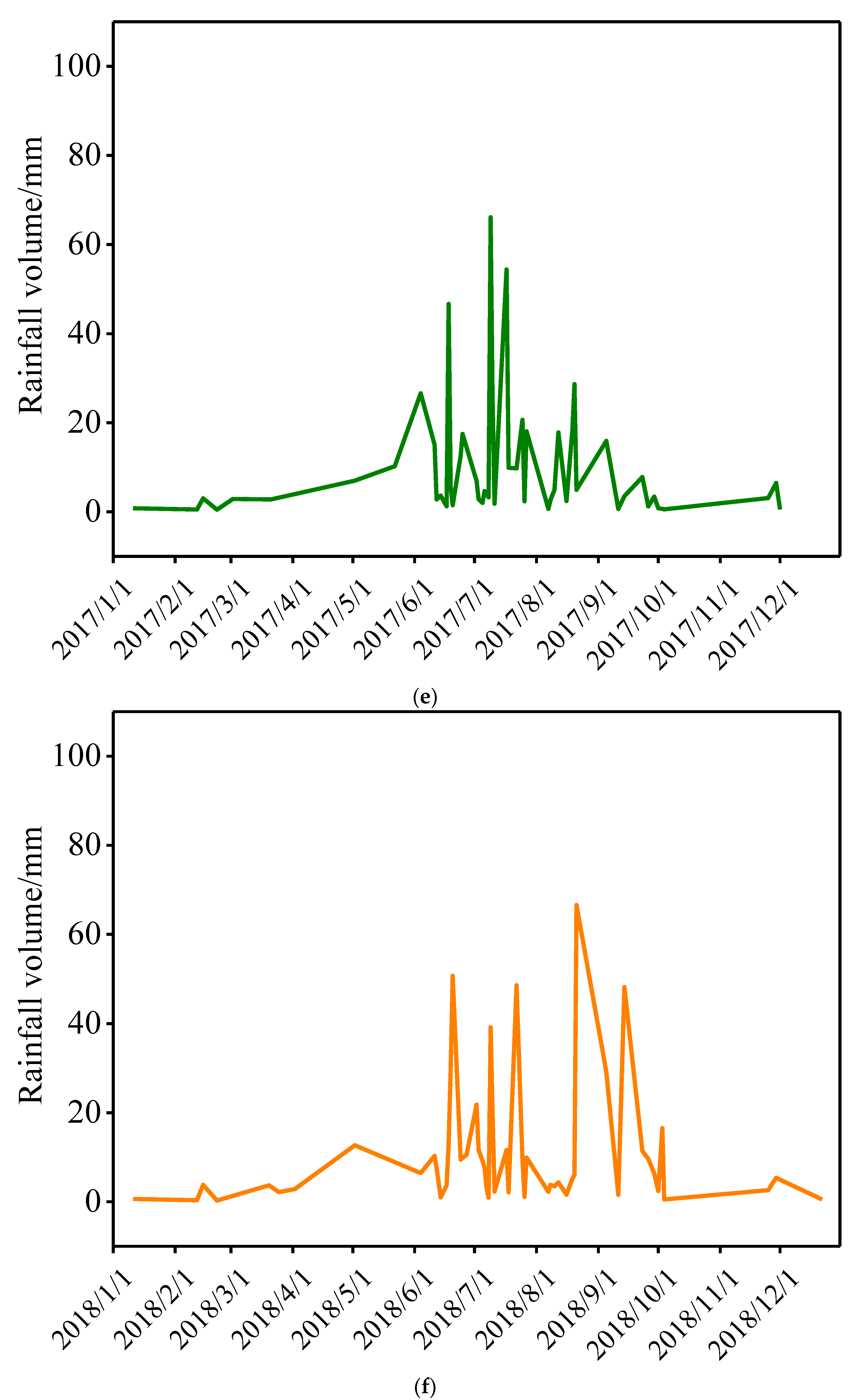








| Reservoir Name | Reservoir Location | Annual Average Temperature | Freeze Period/Year | Test Temperature |
|---|---|---|---|---|
| ShifoSi | Shenyang, LiaoNing | 8.1 °C | December to March | −9.6 °C |
| Aperture Value | 1 mm | 2 mm | 3 mm | 4 mm | 5 mm | 6 mm | 7 mm | 8 mm |
|---|---|---|---|---|---|---|---|---|
| Number of pieces | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 |
| Loading Speed | 0.1 mm/s | 0.01 mm/s | 0.001 mm/s | 0.0001 mm/s | 0.00001 mm/s |
|---|---|---|---|---|---|
| Number of pieces | 150 | 150 | 150 | 150 | 150 |
| Simulation Calculation Settings | Software | Unit Type | Modelling Size | Elastic Modulus | Poisson’s Stress | Loading Stress | Loading Method | Boundary Conditions |
|---|---|---|---|---|---|---|---|---|
| Parameters/Details | Ansys | Solid 45 | 10 mm × 10 mm × 10 mm (Hexahedral) | 56 MPa | 0.3 | 8.16 MPa | Symmetrical loading on both sides | Fixed constraints on both sides |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Li, B.; Zhang, Y.; Zhang, C. Comprehensive Fracture Model of Reservoir Ice Layers in the Northeastern Cold Region of China. Sustainability 2022, 14, 7326. https://doi.org/10.3390/su14127326
Liu X, Li B, Zhang Y, Zhang C. Comprehensive Fracture Model of Reservoir Ice Layers in the Northeastern Cold Region of China. Sustainability. 2022; 14(12):7326. https://doi.org/10.3390/su14127326
Chicago/Turabian StyleLiu, Xiaozhou, Ben Li, Yaodan Zhang, and Chen Zhang. 2022. "Comprehensive Fracture Model of Reservoir Ice Layers in the Northeastern Cold Region of China" Sustainability 14, no. 12: 7326. https://doi.org/10.3390/su14127326
APA StyleLiu, X., Li, B., Zhang, Y., & Zhang, C. (2022). Comprehensive Fracture Model of Reservoir Ice Layers in the Northeastern Cold Region of China. Sustainability, 14(12), 7326. https://doi.org/10.3390/su14127326





