Abstract
In the development of traditional supply-chain finance, the information asymmetry of all parties in the supply chain has become the primary problem hindering its development. Blockchain technology is an effective method to solve the problem of information silos. Based on differential game theory, this paper constructs a game model of supply-chain financial information-sharing behavior based on blockchain technology. Three scenarios of independent decision, the cost-subsidy mechanism of financial institutions, and dealers and collaborative decisions are studied, and the theoretical model is verified through a simulation algorithm. The results show that information sharing in supply-chain finance based on blockchain technology is much higher than that of traditional supply-chain finance, and the use of blockchain technology can promote more sustainable development of supply chains. Blockchain technology can effectively solve the information-silo effect, and the information sharing cost-subsidy mechanism can effectively relieve the cost pressure of information sharing and optimize the supply-chain structure. In addition, the amount of information and benefits shared among the three parties of supply-chain finance based on blockchain technology and the overall benefits show an increasing and stabilized trend over time. This study provides a reference for supply-chain finance members to reasonably choose the optimal strategic behavior.
1. Introduction
Since 2016, Chinese ministries and commissions have repeatedly mentioned the construction of innovative supply-chain finance. In 2021, the chip crisis occurred in the United States, and the U.S. Secretary of Commerce and the director of the National Economic Council hosted a chip industry summit to discuss the lack of cores that have brought U.S. auto production to a standstill. Although the ministry had called on companies in different industrial sectors to submit commercial data on their supply chains, many companies refused. They fear that the ministry might request confidential pricing information and fail to improve supply transparency, resulting in the shutdown of car production. Because of the complexity of the supply-chain system and the concern of commercial disclosure among enterprises, the information-silo effect is inevitable. Therefore, in order to promote effective communication among supply-chain members and improve the transparency of the supply chain, it is urgent to reform the traditional model of supply-chain finance.
Supply-chain finance mainly relies on the credit endorsement of core enterprises to obtain more financing opportunities for small and medium-sized enterprises (SMEs). It can effectively solve the problems of difficult and expensive financing for small and medium-sized enterprises. However, with the development of technology such as logistics, the supply-chain finance system has developed into a more diversified and complex cross-regional financial system. Globalization, diversification of regulatory policy, and different cultures and human behavior in supply-chain networks make the evaluation and risk management in the complex network information nearly impossible [1]. The information-sharing problem of supply-chain finance has become more prominent. The traditional supply-chain financing model cannot adapt to the rapid development of the market, and a highly complex supply chain, resulting in further deterioration of the original information-sharing problem [2]. As a result, the following two problems have emerged.
The first problem is the information-silo effect of the supply chain. The supply-chain system involves many enterprises, and the transaction information is scattered among many enterprises. The complexity of the system requires rigorous auditing for information access, and the emergence of a multi-layered supply chain leads to the further extension of audit time. Therefore, core enterprises cannot quickly access the information of each enterprise. The high cost of information transmission also seriously hinders the flow rate of information, resulting in the fragmentation of supply-chain financial information. The costs of reliability and transparency design complicate the traceability management in supply-chain finance, causing further issues such as reputational competition [3].
The second problem is information asymmetry. As an open economy, supply-chain finance performs less well than cluster enterprises [4]. Product manufacturers have a natural advantage in controlling and hiding the quantity, accuracy, and type of products. The conflict of interest among supply-chain members causes manufacturers to hide information from other members. This highly controlled information flow also hinders the efficiency of information sharing and supply-chain finance [5,6]. In order to solve the problems caused by information silo and information asymmetry, supply-chain finance has to focus on core functions and develop toward cooperation such as outsourcing, advanced value chain, and open innovation [4].
With the emergence and development of blockchain technology, its decentralization and high transparent characteristics have attracted the attention of many scholars. Blockchain technology is a decentralized distributed ledger technology based on computer programs [7]. Its essence is to jointly maintain the reliability of the database through decentralization and distrust, with the advantages of good credit and high security. Many experts and scholars have studied the development of blockchain technology. They analyze the advantages of blockchain technology and the limitations of the current development of supply-chain finance, making them closely associated. Blockchain technology combines the characteristics of decentralized “untrusted” databases. It ensures the immutability of data and the public accessibility of data flows, allowing transactions on a global scale, disintermediation of processes, and multi-party decentralization. In this way, the problem of information silo in supply-chain finance can be effectively solved. Furthermore, the new decentralized tracking capability system of blockchain technology can support the visibility of products at the logistics stage through appropriate real-time information sharing under product security. The information asymmetry can be reduced, and the efficiency, reliability, and transparency of the entire supply chain can be improved [8,9,10,11,12,13,14,15,16]. Blockchain technology also reduces the risk of information sharing and data systems, bringing more security to the flow of information between all supply-chain finance participants.
In the context of global sustainability, the selection of suppliers has become more multidimensional and complex to ensure a green and efficient supply chain [17,18]. In addition to solving the problem of information silos within the supply chain financial system, blockchain technology can also promote the sustainable development of the supply-chain system in the natural, social, and economic fields [11,19]. First, blockchain technology can select appropriate supply-chain participants according to the green performance of companies. The green and safe driving behavior of logistics drivers, ecological design, and environmental performance of the whole supply chain are systematically monitored. Alongside the improved transparency of carbon credit through the trust mechanism, carbon-emission trading mechanisms within the supply chain can be promoted [20,21,22], thus enhancing the circularity of the supply-chain system [23,24,25,26]. Second, the supply chain provides credit loans to many SMEs that cannot be financed by banks to solve their financial problems, providing a large number of jobs for society and reducing the unemployment rate. The application of blockchain technology further improves the work efficiency, security, and health of the supply chain and avoids corruption among participants with high transparency [27]. Third, blockchain technology can quickly and accurately track the transaction of the supply chain in the first place. It improves the transparency and efficiency of the supply chain and the accessibility and quality of information, effectively preventing commercial corruption. A healthy and transparent enterprise can increase the brand reputation and profits, leading to improved supply-chain economics [28,29,30].
At present, most studies on blockchain technology in supply-chain finance adopt various analytical methods such as literature analysis, qualitative analysis, and evolutionary game [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. These studies analyze the application of blockchain technology in the supply-chain finance models, development situations, and the benefit distribution of supply-chain members. Regarding the ecosystems and costs of the supply chain, these studies have ignored the importance of information sharing in supply-chain finance and the mechanism of blockchain technology in the game process. The decentralized characteristics and open thinking of blockchain technology can effectively improve the accuracy of financial information sharing in the supply chain and the benefit of each member of the supply chain [31,32,33,34,35,36,37,38]. However, the advantages of blockchain technology in sharing financial information in the supply chain and the mechanism of blockchain technology are not analyzed with intuitive data. Differential game theory is usually applied to fields such as dynamics and environmental problems [39,40,41,42].
This paper analyzes the information-sharing problem using differential game theory in the context of the traditional supply chain and blockchain-based supply chain. The mechanism of blockchain technology is analyzed based on the non-cooperative game, Stackelberg master-slave game, and Nash game. Furthermore, this study discusses the technology to solve the information-sharing problem and explores the optimal decision of the three parties of supply chain finances, thus ensuring the adequacy, security, and efficiency of information sharing. The findings of this study can improve the transparency of the supply chain, optimize the structure of the supply-chain system, improve the endogeneity of the supply-chain financial system, and promote its sustainable development.
The rest of this paper is organized as follows. Section 2 introduces a supply chain financing model based on blockchain technology; Section 3 establishes the differential game model of information sharing behavior; Section 4 is the numerical simulation and sensitivity analysis; Section 5 presents the discussion and conclusions.
2. Supply Chain Financing Model Based on Blockchain Technology
For the convenience of study, this paper only considers the supply chain finance system with one supplier, one distributor, and one financial institution. The supplier is a small and medium-sized enterprise, and the distributor is the core enterprise. The core of the supply-chain financing model embedded with blockchain technology is the supply-chain system. With the natural distributed characteristics of blockchain, it effectively integrates logistics, business flow, and capital flow into the system. The problem of financing credit investigation for SMEs can be solved, thus realizing an efficient and transparent supply chain. Its basic framework is shown in Figure 1. Core enterprises and financial institutions register and input information into the blockchain and obtain electronic signatures. They can check the transaction process, repayment situation, and other information through electronic signatures. Technical support parties insert pre-defined terms into the blockchain to form smart contracts that fully automate the transaction process and reduce the risk of human intervention. Core enterprises issue digital payment promises to SMEs (suppliers) on the blockchain, and suppliers can split the promises and transfer some promises to the next level of suppliers, enabling the decentralized financing method. When the target amount of financing is fully completed, the smart contract can automatically transfer the raised funds to the SMEs. After each transaction is completed by SMEs, the information is transferred to the blockchain to realize the bookkeeping by core enterprises, financial institutions, and SMEs, ensuring the timeliness of the information.
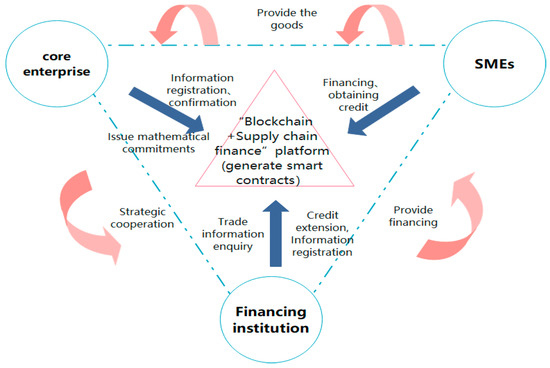
Figure 1.
Supply-chain finance system embedded with blockchain technology.
3. A Differential Game Model of Information Sharing Behavior
3.1. Parameter Description
This study investigates the behavioral selection strategy for the amount of information shared by parties in the supply-chain finance system embedded with blockchain technology. The variables used in the model are described in Table 1.

Table 1.
Description of variables and parameters.
3.2. The Revenues Model of Supply Chain Members
1. The total amount of information shared throughout the supply-chain finance is a dynamic process that changes over time. The change in the amount of shared information is mainly determined by the number of participants in the supply-chain information sharing at the time . Therefore, the change in the total amount of shared information can be expressed by the differential equation below:
where is the initial amount of shared information.
2. Traditional supply-chain finance
In addition to the basic income, each member of the traditional supply-chain finance system also needs to pay high credit-investigation fees. Therefore, the income function of enterprise participants in supply chain finance can be expressed as:
Suppliers:
Distributors:
Financing institutions:
3. The application of blockchain technology in supply-chain finance is to realize the efficiency and transparency of supply chain finance by uploading information to the block by users and using the distributed characteristics of blockchain. Under the premise of ensuring information security, increasing the amount of information sharing can guarantee the efficient operation of the supply chain and maximize the benefits of the whole supply chain. In addition, the high cost of information sharing is considered. Therefore, the revenues function of enterprise participants in supply chain finance can be expressed as:
Suppliers:
Distributors:
Financing institutions:
3.3. Different Decision-Making Situations of Traditional Supply-Chain Finance Members
3.3.1. Independent Decision-Making of Supply-Chain Finance Members
When each participant in supply-chain finance makes independent decisions, suppliers, distributors, and financial institutions will decide to share information to maximize their interests. The equilibrium decision combination obtained after the three-party game is the static feedback Nash equilibrium.
The objective functions of suppliers, distributors, and financial institutions are:
Theorem 1.
When the three-party enterprises in the supply chain are in a non-cooperative state, the information shared by each party are , the Nash equilibrium revenues function of all parties are and the overall revenues are as follows:
Proof.
Based on the optimal control theory, the Hamilton–Jacobi–Bellman (HJB) equations satisfied by suppliers, distributors, and financial institutions are as follows:
The maximum values for suppliers, distributors, and financial institutions are obtained. Afterward, setting the partial derivative of the right end of the HJB equation to, the following equation can be obtained:
When it is substituted into the HJB equation, the following equation can be obtained after simplification:
Set , obtain:
when the above equations are substituted into and optimal linear functions , the following equation can be obtained:
Thus, the overall equilibrium revenues of the supply-chain financial system are:
End. □
Corollary 1.
The amount of information shared by the supply chain finance system at the time is , where . When time tends to infinity, the stable value of the overall shared information sharing amount of the supply chain financial system is .
3.3.2. Stackelberg Game Under Financial Institutions and Distributors Information Sharing Cost Subsidies
In the supply chain system, SMEs (suppliers) should be encouraged to actively participate in information sharing. Core enterprises (distributors) and financial institutions should provide incentives for SMEs, thus enhancing the probability of information sharing to reduce the probability of default. In this study, this incentive mechanism is formulated as an information-sharing cost subsidy from strong enterprises (core enterprises and financial institutions) to weak enterprises (SMEs). In this case, financial institutions play a leading role by providing financing and subsidies. Financial institutions first decide the amount of information sharing and subsidy coefficient , and core enterprises decide the amount of information sharing and subsidy coefficient based on the decisions made by financial institutions. Finally, SMEs make decisions based on the decisions of financial institutions and core enterprises, thus maximizing their interests. The equilibrium decision combination obtained by the three parties after the game is a dynamic feedback Stackelberg equilibrium.
The objective function of suppliers, distributors, and financial institutions is:
Theorem 2.
In the case of enterprise information-sharing cost-subsidy mechanism, the dynamic feedback Stackelberg equilibrium information sharing quality of all financial parties in the supply chain, the subsidy coefficients of core enterprises and financial institutions, the revenues functions of all parties, and the overall revenues of the supply chain are as follows:
Proof.
With the inclusion of incentives, the objective function for suppliers, distributors, and financial institutions is:
Therefore, the HJB equation obtained by the optimal control theory is:
Firstly, the information sharing quality of SMEs (suppliers) is solved by retroduction, and the maximum value of the HJB equation for suppliers is obtained. When the partial derivative of the right end of the HJB equation is set to 0, the following equation can be obtained:
And it is simplified by substituting it into the HJB equation of the core enterprise (distributors):
By setting the partial derivatives of the right ends of the HJB equation with respect to and , respectively, and setting them to 0, the following equation can be obtained:
After the substitution of and into the HJB equation of financial institutions, the equation can be simplified as follows:
When the partial derivatives of the right ends of the HJB equation with respect to and , respectively, are set to 0, the following equation can be obtained:
The and are substituted into the HJB equation of suppliers, distributors, and financial institutions. The solution of the HJB equation is the linear minimum value function of. By setting , it can be obtained that:
After the substitution of the above equations into and the optimal linear functions , the following equation can be obtained:
Thus, the overall equilibrium revenues of the supply-chain financial system is:
The subsidy coefficient and are as follows:
End. □
Corollary 2.
The information shared by the supply chain system at time is , where . When time tends to infinity, the stable value of the overall information sharing amount of the supply chain system is obtained.
3.3.3. The Collaborative Decision-Making Situation of All Participants in Supply-Chain Finance
When each participant in the supply-chain system only considers the overall benefits, the three parties make collaborative decisions. The overall objective function is as follows:
Theorem 3.
In the case of collaborative decision-making by all participants, the information shared by all parties under static feedback Nash equilibrium and the overall revenues of the supply chain are as follows:
Proof.
At this point, the objective function is the overall revenues of the supply chain:
According to the optimal control theory, the HJB equation for its overall revenues is:
After obtaining the maximum value of the HJB equation, the partial derivative of the right end of the HJB equation with respect to , and are set to 0, and the following equation can be obtained:
Substituting it into the HJB equation allows it to be simplified as:
Since the solution of the HJB equation is the minimum linear function of, the following equation can be obtained after setting , it can be obtained:
After the substitution of the above equations into and linear optimal function , the following equation can be obtained:
End. □
Corollary 3.
The information shared by the supply-chain system at time is , where . When time tends to infinity, the stable value of the overall information sharing amount of the supply-chain system is obtained.
3.4. Different Decision-Making Scenarios of Blockchain-Based Supply-Chain Finance System Participants
According to the hypothesis, after the introduction of blockchain technology, the cost of maintaining the blockchain platform replaces the cost of information sharing among supply-chain participants. Therefore, the following theorems and corollaries are obtained according to the differences of the three game scenarios.
Theorem 4.
When the three parties of the supply chain are not cooperating, the amount of information shared is , , and , the Nash equilibrium return functions are , and , and the overall revenue is as follows:
Corollary 4.
The amount of information shared by the supply-chain financial system at time is , where . When time tends to infinity, the stable overall amount of information sharing in the supply chain system is obtained.
Theorem 5.
In the case of enterprise information sharing cost subsidy mechanism, dynamic feedback Stackelberg balanced information sharing quality , and of all financial parties in the supply chain, the subsidy coefficients and of core enterprises and financial institutions, the revenues functions , and of all parties, and the overall revenues of the supply chain are as follows:
Corollary 5.
The information shared by the supply chain system at time is , where . When time tends to infinity, the stable overall amount of information sharing in the supply chain system is obtained.
Theorem 6.
In the case of collaborative decision-making by all participants, the information shared under static feedback Nash equilibrium , and , and the overall revenues of the supply chain are as follows:
Corollary 6.
The information shared by the supply chain system at time is ,where . When time tends to infinity, the stable overall amount of information sharing in the supply chain system is obtained.
3.5. Comparison
Corollary 7.
, , , , , .
The above inference shows that when blockchain technology is integrated into the traditional supply-chain financial system, the amount of information provided by all parties in the supply chain will increase significantly as the cost of blockchain maintenance is much lower than that of information sharing.
Corollary 8.
, , , When , .
Corollary 8 shows that when the supply chain system collaborates, the amount of information sharing by suppliers, distributors, and financial institutions is higher than that in the case of independent decision-making and the Stackelberg game with the subsidy mechanism of distributors and financial institutions. In the case that distributors and financial institutions subsidize suppliers’ information-sharing costs, the amount of information sharing between distributors and financial institutions is the same as that in the case of independent decision-making. However, when , i.e., when the revenues to suppliers per unit of information shared by blockchain are less than twice that to financial institutions, the supplier’s amount of information sharing in the case that distributors and financial institutions subsidize suppliers’ information sharing costs is higher than that under independent decision-making. When , i.e., when the revenues of blockchain sharing per unit of information to financial institutions are greater than the sum of those to suppliers and distributors, the amount of information shared by suppliers in the case that distributors and financial institutions subsidize suppliers’ information sharing costs is higher than that under supply-chain cooperation, which is often not the case.
Corollary 9.
and . When , .
Corollary 9 indicates that when the supply-chain system operates cooperatively, the overall benefit of the system could be maximized if the collaboration among supply chain participants is optimal. When , each unit of information on blockchain brings small benefits to suppliers. To encourage information sharing by the suppliers, financial institutions and distributors will subsidize the cost. The overall revenues of the system under the subsidy mechanism are greater than those under independent decision-making. Therefore, from the perspective of information sharing, the cooperation of the three parties in the supply chain system is the Pareto optimality, the financial institutions and distributors subsidizing the cost of supplier’s information sharing is the secondary Pareto optimality, and the efficiency of independent decision-making in the supply chain system is the lowest.
Corollary 10.
In the Stackelberg game with the subsidy mechanism of distributors and financial institutions, when , .
Corollary 10 suggests that when the revenue to financial institutions per unit of information shared by blockchain is greater than that to suppliers, the overall revenue of the suppliers under the subsidy mechanism increases compared with that under independent decision-making. When , . The large subsidy coefficient in the two cases above indicates that financial institutions receieving high income from information sharing tend to relieve suppliers of the information sharing costs and reduce the subsidy pressure from distributors to suppliers. Thus, suppliers and distributors can obtain higher income under the subsidy mechanism. When ,, i.e., when each unit of information shared by blockchain brings twice the revenues to distributors as it does to suppliers, the revenues of financial institutions under the subsidy mechanism increase compared with that under independent decision-making. The higher subsidy coefficient of distributors to suppliers suggests that distributors receiving high revenues from information sharing tend to ease suppliers’ pressure of information sharing costs and reduce the subsidy pressure from financial institutions to suppliers. Thus, financial institutions can receive higher revenues under the subsidy mechanism.
To sum up, whether from the perspective of information-sharing amount or economic interests, supply-chain system collaboration pushes the overall revenue to Pareto equilibrium and prevents the risk of some enterprises becoming “free riders”. In the meantime, sharing the whole information cost of the supply-chain system can improve the amount of information sharing and maximize the revenues of the system.
4. Numerical Simulation and Sensitivity Analysis
A numerical analysis of the above optimal decision was performed in Python. Given the few blockchain-based supply-chain financial institutions at present, only the “One Enterprise Chain” platform of Ping An Bank was studied, considering the operation mechanism of supply-chain finance, the characteristics of model variables, and the actual situations. To rationalize the fitting image, the benchmark parameter is set as follows:. Finally, the following numerical analysis results were obtained.
4.1. Comparison of Information Sharing between Traditional and Blockchain-Based Supply Chain Finance
In this section, the amount of information sharing was compared between traditional and blockchain-based supply chain finance under three game situations of feedback Nash equilibrium.
Figure 2, Figure 3 and Figure 4 show that when blockchain technology is integrated into the traditional supply chain finance system, the amount of information provided by the supply chain increases significantly as the blockchain maintenance cost is far lower than that of information sharing.
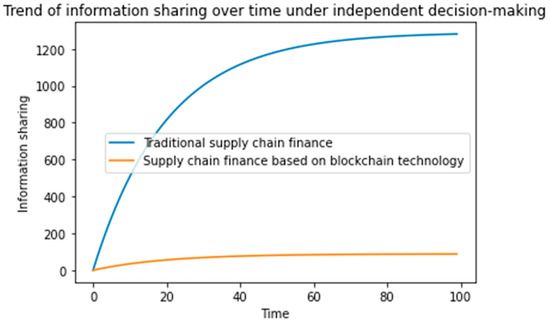
Figure 2.
Comparison of the amount of information sharing between traditional and blockchain-based supply-chain finance systems under independent decision-making.
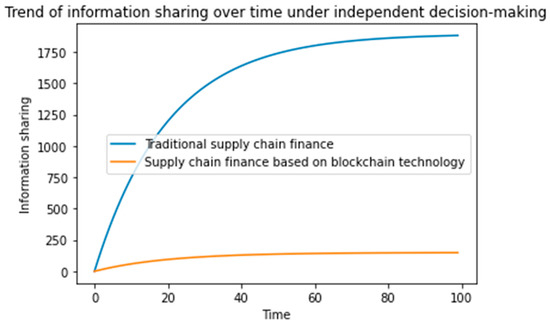
Figure 3.
Comparison of the amount of information sharing in traditional and blockchain-based supply-chain finance systems under the subsidy policy.
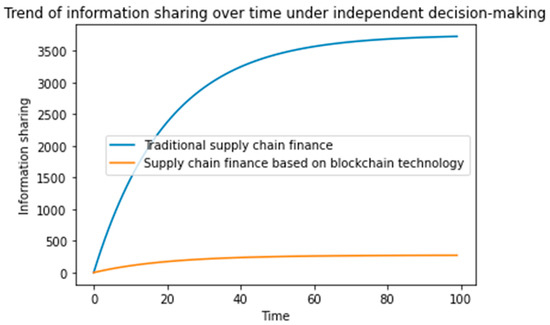
Figure 4.
Comparison of the amount of information sharing between traditional and blockchain-based supply-chain finance systems under collaborative cooperation.
4.2. Optimal Information Sharing Amount and Instantaneous Revenues Analysis
The evolutionary trajectory of the total amount of information and the total revenue of the supply-chain system was studied under three game situations of feedback Nash equilibrium, and the changes in the revenue of all supply-chain parties were analyzed under independent decision-making and subsidy mechanisms.
Figure 5 illustrates the evolutionary trajectory of the total amount of information sharing in the supply-chain system under three game situations of feedback Nash equilibrium. When the initial amount of information sharing is 0, it increases gradually and converges to a stable value with time. However, the total amount of information sharing in the supply-chain system under the collaborative game is far greater than under independent decision-making or with information cost subsidies from financial institutions and distributors. When the revenues of suppliers, distributors, and financial institutions from each unit of information on blockchain satisfy , the information sharing cost subsidies from financial institutions and distributors incentivize more information sharing, and the amount of information sharing of the whole system exceeds that under independent decision-making, conforming to the Pareto improvement. The results of theoretical derivation are verified.
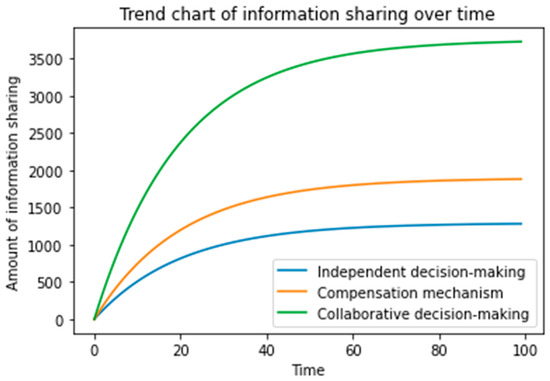
Figure 5.
Variation in system information sharing under three conditions.
Figure 6 illustrates the evolutionary trajectory of the total revenue of the supply chain system under three game scenarios of feedback Nash equilibrium, where the total revenue gradually increases and converges to a stable value with time. When the revenues of suppliers, distributors, and financial institutions from each unit of information on blockchain satisfy , the amount of information sharing in the whole supply chain system increases significantly due to information sharing cost subsidies from financial institutions and distributors, which promotes the efficient and transparent operation and, in turn, the overall revenues of the system. The supply-chain system with collaborative cooperation has the highest degree of transparency, i.e., information sharing. In this case, the overall revenue of the supply-chain system is much higher than that of the other two cases, which conforms to the Pareto equilibrium and verifies the results of theoretical deduction.
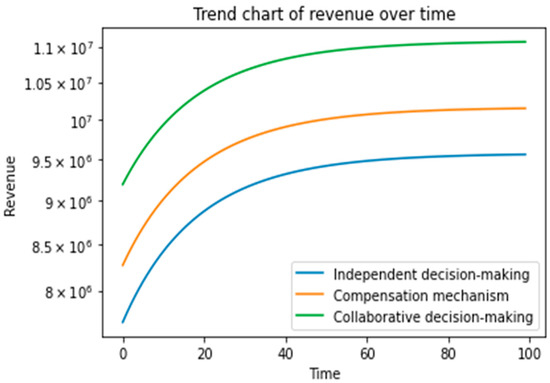
Figure 6.
Changes in system overall revenues under the three conditions.
Figure 7 illustrates the evolutionary trajectory of suppliers’ revenues under independent decision-making of feedback Nash equilibrium and subsidies from distributors and financial institutions, where suppliers’ revenues gradually increase and converge to stable values with time.
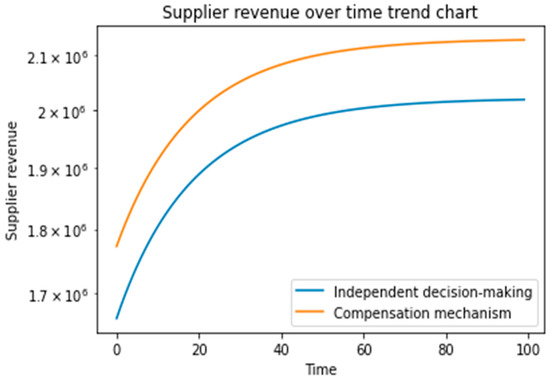
Figure 7.
The suppliers’ revenue over time under independent decision and subsidy policies.
Figure 8 illustrates the evolutionary trajectory of distributors’ revenues under independent decision-making of feedback Nash equilibrium and subsidies from distributors and financial institutions, where the distributors’ revenues gradually increase and converge to stable values with time.
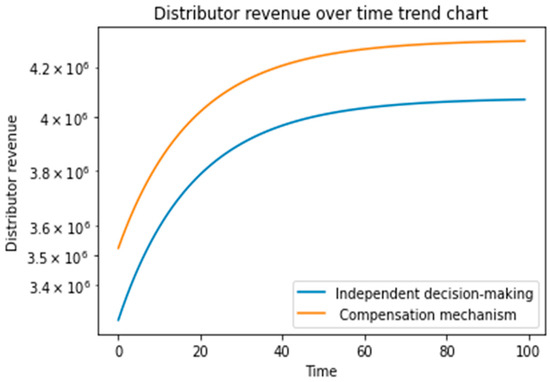
Figure 8.
Distributors’ revenue under independent decision-making and subsidy policies.
Figure 9 illustrates the evolutionary trajectory of financial institutions’ revenues under independent decision-making of feedback Nash equilibrium and subsidies from distributors and financial institutions, where the revenues of financial institutions gradually increase and converge to stable values with time.
Figure 9.
Financial institutions’ revenues under independent decision-making and subsidy policies.
According to the figure descriptions above, the overall revenue and amount of information sharing in the supply-chain system increase first and gradually stabilize with time. With increasingly intensive cooperation, the participants of the supply-chain system tend to share more information to obtain higher revenues. As the system cooperation stabilizes, the information sharing and revenues also tend to stabilize.
4.3. Numerical Simulation and Sensitivity Analysis
This study also analyzed the effect of changes in the information discount rate on the information sharing degree and the overall revenues of the system when the information discount rate tends to stabilize.
Figure 10 shows the evolutionary trajectory of the amount of information sharing with the information discount rate under three game situations as the total amount of information sharing in the system tends to stabilize. As the information discount rate increases, the amount of information sharing decreases gradually. When the information discount rate gradually approaches 1, the amount of information sharing also approaches 0. Therefore, the higher information discount rate discourages the parties of the supply chain from sharing information, while the lower information discount rate encourages them to share information and improve their revenues.
Figure 10.
Variation of the amount of information sharing as the information discount rate stabilizes.
Figure 11 illustrates the evolutionary trajectory of the system’s overall revenues as functions of the stabilizing information discount rate under three game scenarios. With the gradual increase of the information discount rate, the overall revenue of the system and the amount of information sharing gradually decreased. Thus, the higher information discount rate disinclined the parties in the supply chain to share information, and the reduced information sharing seriously damaged the overall revenues of the system. In contrast, the active circulation of information effectively improved the overall revenues of the system.
Figure 11.
Changes in overall system revenue as the information discount rate stabilizes.
Figure 12 illustrates the evolutionary trajectory of the system’s overall revenues as a function of the stabilizing discount rate under three game scenarios. As the discount rate gradually increases, the overall revenues of the system gradually decrease, indicating that the higher discount rate leads to smaller revenues for the whole system, which conforms to the economic patterns.
Figure 12.
Changes in the system’s overall revenue as the discount rate stabilizes.
5. Conclusions
Based on the dynamic changes in the amount of information sharing over time, this study considered the independent decisions in the supply-chain system, the cost subsidy of information sharing by financial institutions and distributors to suppliers, and the cooperative supply-chain system. A differential game model was established to obtain the feedback Nash equilibrium solution. The findings showed that the amount of information sharing in blockchain-based supply chain finance was much higher than that of traditional supply chain finance. When the per-unit-information benefits brought by blockchain to the suppliers were small, the information sharing cost-subsidy mechanism can achieve Pareto improvement of information sharing degree and economy. However, the supply-chain system cooperation was optimal both in information sharing degree and overall economic revenues. Information discount rate had a certain impact on information sharing degree and the overall revenue of the supply-chain system, indicating the importance of information-sharing efficiency. The increase in the discount rate also decreased the present overall revenue of the supply-chain system, indicating that the model conformed to the economic patterns. Based on the game analysis of information sharing behaviors of all parties in the supply chain system, this study effectively evaluated the practicability of blockchain to solve the supply-chain financial information-sharing problem and described the influence of information-sharing degree on the revenues of the supply chain system and all the parties. Too little information sharing led to information asymmetry among all parties in the supply chain and affected their revenues. Excessive information sharing did not increase the revenues of all parties in the supply chain but led to the risk of confidential information theft. In the meantime, the information shared within the supply-chain system and the revenues of all parties tended to stabilize as the cooperation time increased, which was consistent with the long-term economic stability of the market.
Due to space limitations and simplified calculation, the model in this paper was not ideal as it simply divided the whole supply chain system into suppliers, distributors, and financial institutions. Some descriptions of the complex supply chain system may have deviated. In the meantime, although the actual situation was considered in the numerical analysis data, some deviations remained. Changes in the amount of information sharing within the supply chain system not only related to time, the amount of information sharing among all parties, and the information discount rate but also deviated in the discussion of information sharing behavior of all parties. Therefore, the game model for the amount of information shared among all parties in the supply chain system still needs further study.
Author Contributions
Conceptualization, G.W. and S.M.; methodology, S.M.; software, M.X.; validation, M.X., S.M. and G.W.; formal analysis, M.X.; investigation, M.X.; resources, G.W.; data curation, M.X.; writing—original draft preparation, M.X.; writing—review and editing, S.M.; visualization, G.W.; supervision, G.W.; project administration, S.M.; funding acquisition, S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Social Science Foundation of China grant number [No. 20BGL009].
Acknowledgments
This research has been funded by the National Social Science Foundation of China (No. 20BGL009). Comments and suggestions of an anonymous referee were very helpful in improving the paper and all individuals included in this section have consented to the acknowledgement.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sam, S. Traceability and supply chain complexity: Confronting the issues and concerns. Eur. Bus. Rev. 2014, 26, 271–284. [Google Scholar]
- Wan, P.K.; Huang, L.; Holtskog, H. Blockchain-enabled Information Sharing within a Supply Chain: A Systematic Literature Review. IEEE Access 2020, 99, 1. [Google Scholar] [CrossRef]
- Sara, S. Sustainable, multiperiod supply chain network model with freight carrier through reduction in pollution stock. Transp. Res. Part E 2018, 118, 421–444. [Google Scholar]
- Tejpal, G.; Garg, R.; Sachdeva, A. Trust among supply chain partners: A review. Meas. Bus. Excel. 2013, 17, 51–71. [Google Scholar] [CrossRef]
- Nestle, V.; Tube, F.A.; Heidenreich, S.; Bogers, M. Establishing open innovation culture in cluster initia-tives: The role of trust and information asymmetry. Technol. Forecast. Soc. Change 2018, 146, 563–572. [Google Scholar] [CrossRef]
- Nakasumi, M. Information Sharing for Supply Chain Management Based on Block Chain Technology. In Proceedings of the IEEE 19th Conference on Business Informatics (CBI), Dubai, United Arab Emirates, 24 July 2017. [Google Scholar]
- Scott, B.; Loonam, J.; Kumar, V. Exploring the rise of blockchain technology: Towards distributed collaborative organizations. Strateg. Change 2017, 26, 423–428. [Google Scholar] [CrossRef]
- Swan, M. Blockchain: Blueprint for a New Economy; O’Reilly: Sebastopol, CA, USA, 2015. [Google Scholar]
- Kristoffer, F.; David, S. The Supply Chain Has No Clothes: Technology Adoption of Blockchain for Supply Chain Transparency. Logistics 2018, 2, 2. [Google Scholar]
- Zheng, Z.; Xie, S.; Dai, H.; Chen, X.; Wang, H. An Overview of Blockchain Technology: Architecture, Consensus, and Future Trends. In Proceedings of the 2017 IEEE International Congress on Big Data (BigData Congress), Honolulu, HI, USA, 25–30 June 2017. [Google Scholar]
- Park, A.; Li, H. The Effect of Blockchain Technology on Supply Chain Sustainability Performances. Sustainability 2021, 13, 1726. [Google Scholar] [CrossRef]
- Medhi, P.K. Blockchain-Enabled Supply Chain Transparency, Supply Chain Structural Dynamics, and Sustainability of Complex Global Supply Chains—A Text Mining Analysis. World Sci. Book Chapters 2020, 273–372. [Google Scholar] [CrossRef]
- Sfw, A.; Mmq, B.; Lt, C. Dynamics between blockchain adoption determinants and supply chain performance: An empirical investigation-ScienceDirect. Int. J. Prod. Econ. 2020, 229, 107791. [Google Scholar]
- Kopyto, M.; Lechler, S.; von der Gracht Heiko, A.; Hartmann, E. Potentials of blockchain technology in supply chain management: Long-term judgments of an international expert panel. Technol. Forecast. Soc. Change 2020, 161, 120330. [Google Scholar] [CrossRef]
- Perboli, G.; Musso, S.; Rosano, M. Blockchain in Logistics and Supply Chain: A Lean Approach for Designing Real-World Use Cases. IEEE Access 2018, 6, 62018–62028. [Google Scholar]
- Chen, J.; Cai, T.; He, W.; Chen, L.; Zhao, G.; Zou, W.; Guo, L. A Blockchain-Driven Supply Chain Finance Application for Auto Retail Industry. Entropy 2020, 22, 95. [Google Scholar] [CrossRef] [PubMed]
- Govindan, K.; Rajendran, S.; Sarkis, J.; Murugesan, P. Multi criteria decision making approaches for green supplier evaluation and selection: A literature review. J. Clean. Prod. 2013, 98, 66–83. [Google Scholar] [CrossRef]
- Kshetri, N. Blockchain and sustainable supply chain management in developing countries. Int. J. Inf. Manag. 2021, 60, 102376. [Google Scholar] [CrossRef]
- Saberi, S.; Kouhizadeh, M.; Sarkis, J. Blockchain technology and its relationships to sustainable supply chain management. Int. J. Prod. Res. 2019, 57, 2117–2135. [Google Scholar] [CrossRef]
- Kouhizadeh, M.; Sarkis, J. Blockchain Practices, Potentials, and Perspectives in Greening Supply Chains. Sustainability 2018, 10, 3652. [Google Scholar] [CrossRef]
- Rejeb, A.; Rejeb, K. Blockchain and supply chain sustainability. Logforum 2020, 16, 363–372. [Google Scholar] [CrossRef]
- Mukherjee, A.A.; Singh, R.K.; Mishra, R.; Bag, S. Application of blockchain technology for sustainability development in agricultural supply chain: Justification framework. Oper. Manag. Res. 2021, 1–17. [Google Scholar] [CrossRef]
- Rane, S.B.; Thakker, S.V.; Kant, R. Stakeholders’ involvement in green supply chain: A perspective of blockchain IoT-integrated architecture. Manag. Environ. Qual. Int. J. 2020, 32, 1166–1191. [Google Scholar] [CrossRef]
- Tian, F. A supply chain traceability system for food safety based on HACCP, blockchain & Internet of things. In Proceedings of the 2017 International Conference on Service Systems and Service Management, Dalian, China, 16–18 June 2017; pp. 1–6. [Google Scholar]
- Varavallo, G.; Caragnano, G.; Bertone, F. Traceability Platform Based on Green Blockchain: An Application Case Study in Dairy Supply Chain. Sustainability 2022, 14, 3321. [Google Scholar] [CrossRef]
- Di Vaio, A.; Varriale, L. Blockchain technology in supply chain management for sustainable performance: Evidence from the airport industry. Int. J. Inf. Manag. 2020, 52, 102014. [Google Scholar] [CrossRef]
- Li, Z.; Guo, H.; Barenji, A.V. A sustainable production capability evaluation mechanism based on blockchain, LSTM, analytic hierarchy process for supply chain network. Int. J. Prod. Res. 2020, 28, 7399–7419. [Google Scholar] [CrossRef]
- Tan, B.Q.; Wang, F.; Liu, J.; Kang, K.; Costa, F. A Blockchain-Based Framework for Green Logistics in Supply Chains. Sustainability 2020, 12, 4656. [Google Scholar] [CrossRef]
- Esmaeilian, B.; Sarkis, J.; Lewis, K.; Behdad, S. Blockchain for the future of sustainable supply chain management in Industry 4.0. Resour. Conserv. Recycl. 2020, 163, 105064. [Google Scholar] [CrossRef]
- Kouhizadeh, M.; Saberi, S.; Sarkis, J. Blockchain technology and the sustainable supply chain: Theoretically exploring adoption barriers. Int. J. Prod. Econ. 2021, 231, 107831. [Google Scholar] [CrossRef]
- Moosavi, J.; Naeni, L.M.; Fathollahi-Fard, A.M. Blockchain in supply chain management: A review, bibliometric, and network analysis. Environ. Sci. Pollut. Res. 2021, 1–15. [Google Scholar] [CrossRef]
- Hayrutdinov, S.; Saeed, M.; Rajapov, A. Coordination of Supply Chain under Blockchain System-Based Product Lifecycle Information Sharing Effort. J. Adv. Transp. 2020, 2020, 5635404. [Google Scholar] [CrossRef]
- Schmidt, C.G.; Wagner, S.M. Blockchain and supply chain relations: A transaction cost theory perspective. J. Purch. Supply Manag. 2019, 25, 100552. [Google Scholar] [CrossRef]
- Yang, J.; Wen, J.; Jiang, B.; Wang, H. Blockchain-Based Sharing and Tamper-Proof Framework of Big Data Networking. IEEE Netw. 2020, 34, 62–67. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, T.; Hu, H.; Gong, J.; Ren, X.; Xiao, Q. Blockchain-based framework for improving supply chain traceability and information sharing in precast construction. Autom. Constr. 2020, 111, 103063.1–103063.13. [Google Scholar] [CrossRef]
- Nandi, M.L.; Nandi, S.; Moya, H.; Kaynak, H. Blockchain technology-enabled supply chain systems and supply chain performance: A resource-based view. Supply Chain Manag. Int. J. 2020, 25, 841–862. [Google Scholar] [CrossRef]
- Abidi, M.H.; Alkhalefah, H.; Umer, U.; Mohammed, M.K. Blockchain-based secure information sharing for supply chain management: Optimization assisted data sanitization process. Int. J. Intell. Syst. 2020, 36, 260–290. [Google Scholar] [CrossRef]
- Ali, M.H.; Chung, L.; Kumar, A.; Zailani, S.; Tan, K.H. A sustainable Blockchain framework for the halal food supply chain: Lessons from Malaysia. Technol. Forecast. Soc. Chang. 2021, 170, 120870. [Google Scholar] [CrossRef]
- Caputo, M.R.; Ling, C. How to do comparative dynamics on the back of an envelope for open-loop Nash equilibria in differential game theory. Optim. Control Appl. Methods 2016, 38, 443–458. [Google Scholar] [CrossRef]
- Chai, R.; Savvaris, A.; Tsourdos, A.; Chai, S. Multi-objective trajectory optimization of Space Manoeuvre Vehicle using adaptive differential evolution and modified game theory. Acta Astronaut. 2017, 136, 273–280. [Google Scholar] [CrossRef]
- Steffen, J.; Georges, Z. Developments in differential game theory and numerical methods: Economic and management applications. Comput. Manag. Sci. 2007, 4, 159–181. [Google Scholar]
- Yang, J.; Long, R.; Chen, H.; Sun, Q. A comparative analysis of express packaging waste recycling models based on the differential game theory. Resour. Conserv. Recycl. 2021, 168, 105449. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).