Abstract
Electrical power networks are expanded regularly to meet growing energy requirements. Reactive power dispatch (RPD) optimization is a powerful tool to enhance a system’s efficiency, reliability, and security. RPD optimization is classified as a non-linear and non-convex problem. In this paper, the RPD optimization problem is solved based on novel hybrid genetic algorithms—equilibrium optimizer (GAEO) optimization algorithms. The control variables are determined in such a way that optimizes RPD and minimizes power losses. The efficiency of the proposed optimization algorithms is compared to other techniques that have been used recently to solve the RPD problem. The proposed algorithm has been tested for optimization RPD for three test systems, IEEE14-bus, IEEE-30bus, and IEEE57-bus. The obtained results show the superiority of GAEO over other techniques for small test systems, IEEE14-bus and IEEE-30bus. GAEO shows good results for large system, IEEE 57-bus.
1. Introduction
Energy resources are scarce and deficit; as a result, the optimization of available resources is necessary. Research in electrical power systems is a developing field. An electric power system’s operation, economy, and quality are tightly linked to reactive power compensation. Consumer loads include both active and reactive demand. Active demand is for useful energy. Reactive demand must be managed efficiently to deliver active power efficiently, improve power quality, release system capacity, improve system stability, reduce system losses, reduce voltage deviation, and improve the system power factor [1,2]. Reactive power management is always a main concern for utilities in order to improve system security and operation; hence, optimum reactive power dispatch (ORPD) has appeared as an important solution [3].
RPD optimization is defined as a mixed-integer, non-linear problem used to adjust the electric power system control parameters subjected to equality and inequality constraints to enhance the stability, security, and efficiency of the power network to provide the best economic operations. These parameters may be discreet, such as reactive power compensation and transformer tap settings, or continuous, such as generator bus voltages [4,5]. ORPD has been solved using different algorithms such as traditional methods and meta-heuristics optimization algorithms. Traditional methods such as linear and nonlinear programming, quadratic programming method, and the gradient method fail to obtain accurate results, especially for discrete variable problems. Meta-heuristics optimization algorithms, which improve calculation accuracy and increase convergence speed, include particle swarm optimization (PSO), flower pollination algorithm (FPA), sine cosine algorithm (SCA), water wave optimization (WWO), bat algorithm (BA), and many others [6]. Meta-heuristics algorithms are used to approximate solutions to complicated optimization problems without having complete information about the problem. They have been applied in many fields of life. Meta-heuristics include the exploration and exploitation phases. The balance between these two phases determines the efficiency of the algorithm [7].
Optimization algorithms have been provided as a magical solution in order to achieve the most beneficial results of any system. They have been applied not only in engineering, but also in many other applications, such as statistical, social, agricultural, and medical. Optimization techniques have been applied in power systems to improve system performance, decrease power losses, and reduce voltage flickers. They have been applied in a variety of electrical network parts, generation, transmission, and distribution. For instance, they have been used to optimize power flow [8,9,10], size, and location of a DG connected to a grid [11,12,13,14,15,16].
RPD has been optimized according to a variety of objective functions such as power loss minimization, enhanced voltage profile, maximized voltage stability index, and cost optimization. Single- and multi-objective functions have been applied with the aim of enhanced system stability and security. Different optimization techniques have been tested for different types of test systems. Small and large test systems with differing numbers of control variables have been tested in optimizing RPD. ORPD has been widely tested for an IEEE 30 bus system with 19 variables as in [17,18,19,20,21,22,23,24,25,26,27,28,29,30]. ORPD has been tested for an IEEE 118 bus system with 77 control variables as in [17,18,21,22,24,29,30]. ORPD has been tested for an IEEE 57 bus system with 25 control variables as in [17,20,22,25,29]. ORPD has been tested for an IEEE 300 bus system with 190 control variables as in [5,18,21]. ORPD has been tested for an IEEE 14 bus system with 9 variables as in [3,5,24,31]. ORPD has been tested for an IEEE 30 bus system with 13 variables as in [17,23,25,27,28,31].
A hybrid optimization technique is a combination of two or more optimization algorithms. It aims to enhance the performance of the original algorithm. This could be executed by achieving a balance between exploration and exploitation, which prevents the original algorithm from being trapped into local optima [12]. GAEO is a new hybrid technique created by the authors of [32]. GAEO is a combination of two algorithms, a genetic algorithm (GA) and an equilibrium optimizer (EO). It has been successfully applied to optimize the size and location of distributed generators (DG) based on single and multi-objective functions [32].
The RPD problem has been studied for many years; however, this topic still gathers the attention of the power system industry and researchers. The RPD problem derives its importance from the need to secure the operation of power systems by decreasing power losses and increasing system efficiency. The main contributions of this paper can be summarized as follows:
- Solving the RPD problem using a new algorithm, GAEO, for the first time as far as the authors know based on literature review.
- The validity of the GAEO algorithm for minimizing power loss is investigated and compared with results of other techniques.
- GAEO is applied to optimize the RPD problem for the first time on three test systems: IEEE14-bus, IEEE-30bus, and IEEE57-bus.
This paper is organized as follows: a literature review is provided as an introduction for this research, the second section introduces GAEO, the third section introduces a detailed model of the operating system, the fourth section introduces the mathematical model and procedure of the proposed algorithm, results and discussions are then introduced, and finally, the conclusion and references are provided.
2. Hybrid Genetic Algorithm Equilibrium Optimizer (GAEO)
Evolutionary algorithms have been applied to optimize complicated problems for many years. GA is one of these widespread evolutionary algorithms. GA gained its popularity due to the simplicity of implementation and its efficiency. It is a local search technique inspired from Darwinian evolutionary theory using selection, crossover, and mutation techniques. These three techniques can be explained briefly as follows: Selection means that the best generation (solution) will move on to the next step. Crossover means generating improved and new generations, referred to as parents. Mutations allow a new generation to have different characteristics compared to their parents [32,33].
The equilibrium optimizer (EO) was introduced by Farmarzi in 2020. EO is inspired by the estimation of dynamic and equilibrium states determined through controlling volume mass balance models. Each particle works as a search agent; i.e., particles represent solutions and particles’ concentrations represent position. Each particle updates its concentration according to the best solution so far (equilibrium candidates) until it reaches optimal results (equilibrium state). To apply the EO algorithm, it requires three main steps. First is initialization, which means the initial concentration vector is randomly created using a large number of particles. Second, candidates are selected for an equilibrium pool. An EO is used to observe the equilibrium state through determining four best particles so far (to improve exploration) plus the arithmetic mean of them (to improve exploitation). These five particles make up what is called the equilibrium pool. Third, adjusting the concentration level enables EO to make balance between both exploration and exploitation [32,34].
The main question here is why to hybridize GA and EO. In order to understand things correctly, we must be aware of two aspects, exploitation and exploration. Exploitation requires that the algorithm search for better solutions by browsing the bounding region. On the other hand, exploration requires scanning the whole search space efficiently. In order to obtain a better solution, both exploration and exploitation must be balanced. An EO algorithm can be easily trapped into local optima, which means that EO is more exploitive. On the other hand, GA is more explorative. Therefore, hybridization between these two algorithms would provide a new and powerful algorithm [32].
3. Modelling of Power System
ORPD aims to optimize a nonlinear fitness function while keeping control variables within their limits. Two distinct functions need to be optimized, power losses and voltage deviation of all buses. This problem is expressed in a mathematical form as follows [31]:
where the fitness function is represented by F for, the decision variables represented by u and x. the independent control parameters may be represented by
The dependent variables may be represented by
3.1. Objective Function
Minimization of power loss, which is the main objective function, can be represented by Equation (6).
where stand for the voltage magnitude of buses i and j, the mutual conductance between buses i and j is represented by Gk, and the difference in angle between i and j is represented by . The second objective function, which is the minimization of voltage deviation, can be represented by Equation (7).
where stands for the reference voltage of the buses, and stands for number of load buses in the proposed network.
3.2. System Constraints
The fitness functions have been optimized according to number of constraints.
3.2.1. Equality Constraints
3.2.2. Inequality Constraints
The inequality constraints must be within the pre-determined limits.
where , , , and stand for PV bus numbers, on-load tap changing a transformer’s number, number of capacitors, and number of branches, respectively. and stands for lower and upper limits for slack bus. The apparent power along the transmission line is represented by .
4. Modeling and Implementation of GAEO Algorithm
The hybrid GAEO algorithm has been applied to improve the performance of electrical networks by optimizing RPD. The working mechanism for GAEO can be introduced briefly in a few lines. Firstly, power system data and operating parameters of GAEO are provided. Then, the initial population is randomly created by EO, which is passed to GA (crossover and mutation) to select the best half of the population and update the location of the other half of the population. Then, EO is applied to determine the best candidate solution. Finally, the best solution of each cycle is updated. The flow chart and procedures of the GAEO algorithm are illustrated by Figure 1 [32].
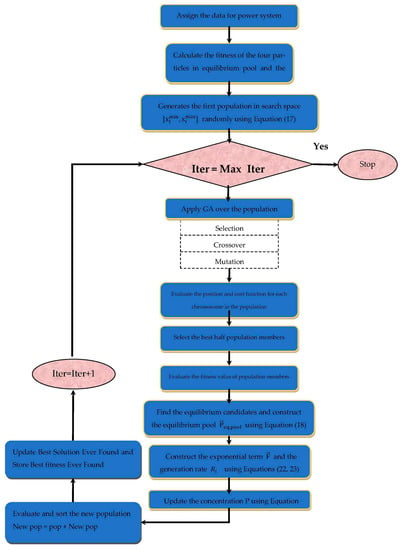
Figure 1.
Flow chart of GAEO.
To provide the optimum solution, GAEO requires some steps that can mainly be categorized into two parts, initialization and main loop, each of which consists of many steps. A complete discussion of the GAEO algorithm mechanism can be explained by twelve steps as follows.
4.1. Initialization
Step 1: Provide data for a power system including, bus data, lines data, generators, tap transformers, compensation capacitors, and the network configuration.
Step 2: Provide the control parameters of EO and GA.
Step 3: Adjust the iteration counter to zero as illustrated by Equation (16) and then randomly creating the initial population by the EO algorithm in search space [. Then, the initial best solution is selected according to the sorting position and the fitness of each particle as expressed by Equation (17).
where is the concentration of i particles at starting, and , are upper and lower limits respectively. , is a uniform random value lies between 0 and 1 ().
4.2. Main Loop
The main loop includes three phases, which illustrate the main operation of both algorithms and the role of each one of them in optimizing RPD.
4.2.1. Using GA (Crossover and Mutations)
Step 4: Choose the first half of the population obtained from step 3 and passing to the GA algorithm. The performance of the GA algorithm mainly depends on the size of the population (fitness) to reduce the complexity of the EO algorithm.
Step 5: Use the GA algorithm after performing pairing and mating through single point crossover, once the new population has been modified or mutated.
Step 6: Calculate the positions and fitness of each chromosome using the GA algorithm.
Step 7: Select the best half of the population members of EO and then update the location of the other half using GA crossover.
4.2.2. Using EO on the Best Half Population Members
Step 8: Use EO to evaluate the fitness function of the particles. Then, determine the equilibrium candidates through sorting as illustrated by Equation (18).
where the equilibrium state vector is denoted by , the four best particles so far, identified through the whole optimization process, are denoted by , and the first four candidate solutions’ mean value is denoted by .
These solutions are assumed to be approximate equilibrium states.
4.2.3. Balancing of Both Exploration and Exploitation
Exploitation and exploration are balanced through the exponential term vector, which is represented by Equation (19).
where the turnover rate is denoted by , and t is the time which defined as a function of iteration (Iter) expressed by Equation (20).
where and are is the current iterations and is the maximum number of iterations and a2 is the exploitation ability control variables. The value of the is expressed by Equation (21).
where r is a uniform random vector [0, 1], a1 is the exploration ability control variables, and the direction of exploration and exploitation is affected by .
Substitute from Equation (18) into Equation (16), so the exponential term can be expressed by Equation (22).
EO using generation rate factor to improve the exploitation phase as expressed by Equation (23).
where is a constant and is the initial value which can be calculated using Equation (24).
The generation rate is controlled using which is the generation possibility to contribute during the position update process. The concentration (P) can by defined as follows using Equation (26).
where V is the control volume and considered as unit.
Step 9: Evaluate the fitness of an old population and the new population every cycle.
Step 10: Sort the new and old population according to the fitness function and then create the new population.
Step 11: Update the iteration number.
Step 12: Check for stop condition, else go to step 5.
4.3. Adjusting Operating Parameters
GAEO, like many other hybrid optimization algorithms, has a lot of parameters. In order to achieve good results and reach the best value, these parameters have to be adjusted accurately. The operating parameters of the GAEO algorithm are illustrated as follows:
- The exploration ability of control variables (a1).
- The exploitation ability of control variables (a2).
- Mutrate.
- Selection and participation probability of concentration updating by the generation rate control variable (GP).
Trial and error is the main technique to obtain the operating parameters properly. From observation, it can be concluded that parameters from one to three are best adjusted at the original values of the creator (2, 1, 0.09, 0.5), which provide the best benefits so far. The generation rate is expected to be the key parameter (as it has a substantial effect on the results) and must be adjusted according to the problem. The generation rate can also be determined by trial and error method.
5. Simulation and Results
In this section, the proposed algorithm (hybrid GAEO) is implemented to optimize RPD. The proposed algorithm was tested upon three types of test systems, IEEE 14-bus, IEEE 30-bus, and IEEE 57 bus. The minimization of power losses over the whole network is chosen to be the objective function. The system simulation was executed using MATLAB R2016a software.
GAEO has been used to optimize power losses for all three test systems as follows:
Case I, IEEE 14-bus system.
Case II, Modified IEEE 30-bus system.
Case III, IEEE 57-bus system.
The data for these test systems are illustrated by Table 1 and include the number of buses, the number of variables, the number of generators, the number of tape transformers, and the number of compensators [35,36].

Table 1.
Test systems description and details.
The upper and lower limits of control variables, generating units, transformer tap changing, and reactive compensators are illustrated by Table 2.

Table 2.
Control parameters limits.
5.1. Case I IEEE 14-Bus System
GAEO was used to achieve ORPD upon IEEE 14-bus system based on minimum power losses in the system. The tuning parameters of GAEO have been adjusted according to Table 3.

Table 3.
Adjusting parameters of GAEO for IEEE 14-bus system.
Table 4 illustrates the control parameters and optimum values obtained by GAEO, sine cosine algorithm (SCA), chaotic bat algorithm (CBA), and improved slap swarm algorithm (ISSA) algorithms. The obtained results were compared to the best obtained solution so far based on recent articles [5,35,37]. GAEO successfully reduced the power loss to 12.2694 MW which is very close to the minimum value obtained by sine-cosine algorithm (SCA) proposed in [35], but still the best value obtained.

Table 4.
Control variables and optimum values obtained for IEEE 14-bus system.
Figure 2 clarifies the comparison of GAEO against other algorithms. GAEO algorithm comes first, with minimum power loss 12.2694 MW followed by SCA 12.27 MW. ISSA and CBA-IV come last, with the largest power losses, 12.834 and 12.2923, respectively.
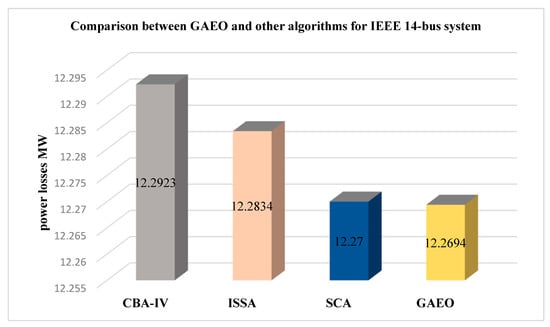
Figure 2.
Comparison between GAEO and other algorithms for the IEEE 14-bus system.
Figure 3 illustrates the convergence curve of GAEO for IEEE 14-bus system while minimizing power losses of all system lines. The convergence curve is not fast but, it is almost quite smooth. GAEO reaches the optimum value after one hundred iterations.
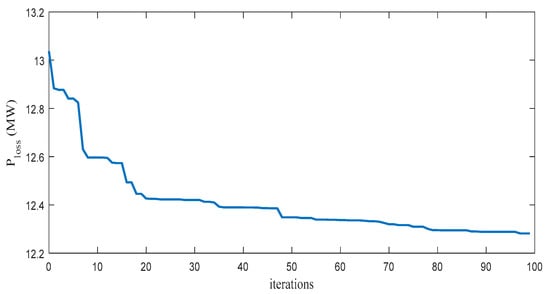
Figure 3.
Convergence curve of GAEO for IEEE 14-bus system power loss minimization.
5.2. Modified IEEE 30-Bus System
Another challenge for the proposed algorithm (GAEO) is how to minimize power losses of the modified IEEE 30-bus system in order to achieve ORPD while keeping control variables within their predefined limits. The tuning parameters of GAEO were adjusted according to Table 5.

Table 5.
Adjusting parameters of GAEO for IEEE 30-bus system.
Table 6 provides the obtained results by GAEO compared to two algorithms, diversity-enhanced particle swarm optimization (DEPSO) and classification and Pareto domination-based multi-objective evolutionary algorithm (CPSMOEA). GAEO greatly reduces the system losses compared to other techniques. The losses were decreased to 16.0428 MW, which is much lower than 16.17 MW and 17.52 MW obtained by CPSMOEA and DEPSO, respectively.

Table 6.
Control variables and optimum value obtained for the IEEE 30-bus system.
Figure 4 illustrates a comparison between GAEO and other algorithms for the IEEE 30-bus system. As shown, GAEO has obtained the minimum value, 16.0428 MW, which is significantly more than CPSMOEA, which minimized power loss to 16.17. Finally, DEPSO comes last, with power loss equal to 17.52 MW.
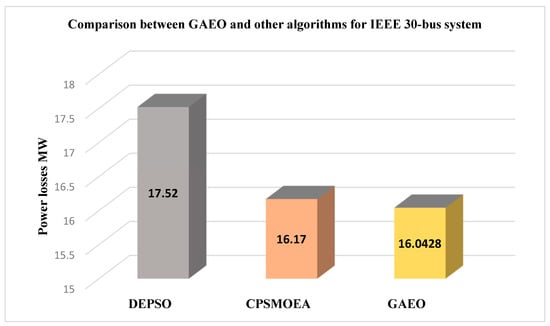
Figure 4.
Comparison between GAEO and other algorithms for IEEE 30-bus system.
The convergence curve of GAEO is fast; i.e., it reaches its optimum value quickly and is smooth, as illustrated by Figure 5.
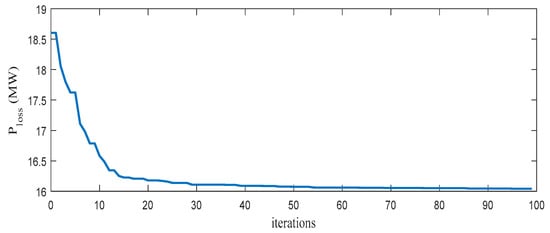
Figure 5.
GAEO convergence curve for IEEE 30-bus.
5.3. Case III IEEE 57-bus System
IEEE 57-bus is a large system. It consists of seven generators, fifteen transformer tap changers, three reactive compensator units, fifty-seven buses, and eighty lines. The tuning parameters of GAEO were adjusted according to Table 7.

Table 7.
Adjusting the parameters of GAEO for IEEE 57-bus system.
Applying GAEO to obtain ORPD while minimizing power losses is expected to be a milestone in judging our algorithm. As illustrated in Table 8, the chaotic bat algorithm (CBA) provided the best result so far at 21.9627 MW.

Table 8.
Control variables and optimum values for the IEEE 57-bus system.
Figure 6 illustrates a comparison between GAEO and other algorithms based on power loss for IEEE57-bus system. Chaotic bat algorithm (CBA-IV) comes first with the minimum power loss, i.e., 21.9627 MW. GAEO comes second with active power losses of 23.2514 MW. Sine-cosine algorithm (SCA) comes last at 24.05 MW. GAEO has provided good results, but they were not superior CBA. This case shows that GAEO has a shortage when dealing with larger systems such as many other algorithms.
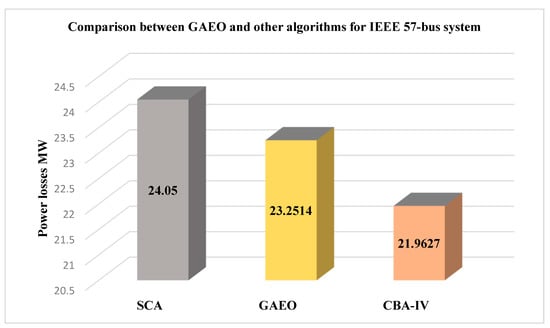
Figure 6.
Comparison between GAEO and other algorithms for IEEE 57-bus system.
The GAEO convergence curve is illustrated in Figure 7. Due to its random nature, GAEO has started below its optimum value 1.299 × 109 but reached the best value so far within 200 iterations.
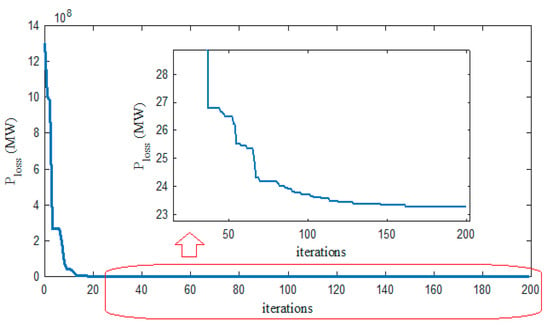
Figure 7.
Convergence curve of GAEO for the IEEE 57-bus system power loss minimization.
6. Conclusions and Future Work
Electrical networks become much more complicated due to regular expansion. This comes from increasing power demand due to industrial development and population increases. Power system utilities should provide efficient, reliable, and secure operation of electrical networks to meet power demands. This can be achieved by improving old methods or creating new ones. RPD optimization has been used in the past to enhance system performance, but it is still an efficient and applicable method. In this paper, a new hybrid optimization technique, namely genetic algorithm-equilibrium optimizer (GAEO), has been successfully applied to minimize system power losses by optimizing RPD. Three test systems were used to evaluate the proposed algorithm, IEEE 14-bus, IEEE 30-bus, and IEEE 57-bus systems. The obtained results of GAEO were compared to results obtained by recent powerful algorithms, sine cosine algorithm (SCA), improved slap swarm algorithm (ISSA), chaotic bat algorithm (CBA-IV), classification and Pareto domination based multi-objective evolutionary algorithm (CPSMOEA), and diversity-enhanced particle swarm optimization (DEPSO). According to the results obtained, we can say that GAEO has succeeded in two cases showing fast convergence and good performance. In the first case, the minimum power loss has been obtained by GAEO at 12.2694 MW, followed by SCA at 12.27 MW. In the second case (IEEE 30-bus system), GAEO succeeded in minimizing power loss to 16.0428, which is much better than CPSMOEA at 16.17 MW. As expected for all algorithms, it passed partially in the third case by obtaining a good result, but not an optimal result. In the third case (IEEE 57-bus system), CBA-IV achieved the best result compared to GAEO and SCA. GAEO, like any other hybrid technique, requires many parameter adjustments, which is an expected disadvantage. Another disadvantage is that GAEO could not provide the best result in 57-bus system, which contains 25 control parameters. It can be concluded that GAEO is a good optimization technique that may be very useful in small systems. GAEO needs to be modified in order to cope with large systems. Exploration characteristics need to be enhanced.
Author Contributions
Conceptualization, M.H., T.S. and D.O.; methodology, M.H., A.F. and S.A.; software, M.H. and D.O.; validation, M.A., S.A. and D.O.; formal analysis, M.H. and A.F.; investigation, M.H., S.A. and D.O.; resources, M.A. and T.S.; data curation, M.A., M.H. and A.F.; writing—original draft preparation, M.H. and D.O.; writing—review and editing, T.S. and S.A.; visualization, M.H. and D.O.; supervision, T.S.; project administration, T.S. and M.A.; funding acquisition, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Taif University Researchers Supporting Project Number (TURSP-2020/146), Taif University, Taif, Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to acknowledge the financial support received from Taif University Researchers Supporting Project Number (TURSP-2020/146), Taif University, Taif, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mobarak, Y.; Hemeida, A.; El-Bahnasawy, A.; Hamada, M. Reactive power compensation on Egypt Electricity Network for optimal energy saving. Eng. Technol. Appl. Sci. Res. 2019, 9, 3699–3704. [Google Scholar] [CrossRef]
- Hemeida, A.M.; Hamada, M.M.; Mobarak, Y.A.; El-Bahnasawy, A.; Ashmawy, M.G.; Senjyu, T. TCSC with auxiliary controls based voltage and reactive power controls on grid power system. Ain Shams Eng. J. 2020, 11, 587–609. [Google Scholar] [CrossRef]
- Ben oualid Medani, K.; Sayah, S.; Bekrar, A. Whale optimization algorithm based optimal reactive power dispatch: A case study of the Algerian power system. Electr. Power Syst. Res. 2018, 163, 696–705. [Google Scholar] [CrossRef]
- Gilvaei, M.N.; Jafari, H.; Ghadi, M.J.; Li, L. A novel hybrid optimization approach for reactive power dispatch problem considering voltage stability index. Eng. Appl. Artif. Intell. 2020, 96, 103963. [Google Scholar] [CrossRef]
- Mugemanyi, S.; Qu, Z.; Rugema, F.X.; Dong, Y.; Bananeza, C.; Wang, L. Optimal reactive power dispatch using chaotic bat algorithm. IEEE Access 2020, 8, 65830–65867. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, J.; Yang, X.; Ling, Y. Optimal reactive power dispatch using water wave optimization algorithm. Oper. Res. 2020, 20, 2537–2553. [Google Scholar] [CrossRef]
- Hemeida, A.M.; Hassan, S.A.; Mohamed, A.-A.A.; Alkhalaf, S.; Mahmoud, M.M.; Senjyu, T.; El-Din, A.B. Nature-inspired algorithms for feed-forward neural network classifiers: A survey of one decade of research. Ain Shams Eng. J. 2020, 11, 659–675. [Google Scholar] [CrossRef]
- Mohamed, A.-A.A.; Mohamed, Y.S.; El-Gaafary, A.A.; Hemeida, A.M. Optimal power flow using moth swarm algorithm. Electr. Power Syst. Res. 2017, 142, 190–206. [Google Scholar] [CrossRef]
- Mohamed, A.-A.A.; El-Gaafary, A.A.; Mohamed, Y.S.; Hemeida, A.M. Multi-objective modified grey wolf optimizer for optimal power flow. In Proceedings of the 2016 Eighteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27–29 December 2016; pp. 982–990. [Google Scholar] [CrossRef]
- El-Gaafary, A.A.; Mohamed, Y.S.; Hemeida, A.M.; Mohamed, A.-A.A. Grey wolf optimization for multi input multi output system. Univers. J. Commun. Netw. 2015, 3, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Saleh, A.A.; Mohamed, A.-A.A.; Hemeida, A.M.; Ibrahim, A.A. Comparison of different optimization techniques for optimal allocation of multiple distribution generation. In Proceedings of the 2018 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 19–21 February 2018; pp. 317–323. [Google Scholar] [CrossRef]
- Hemeida, A.M.; Bakry, O.M.; Mohamed, A.A.A.; Mahmoud, E.A. Genetic Algorithms and Satin Bowerbird Optimization for optimal allocation of distributed generators in radial system. Appl. Soft Comput. 2021, 111, 107727. [Google Scholar] [CrossRef]
- Saleh, A.A.; Mohamed, A.-A.A.; Hemeida, A.M.; Ibrahim, A.A. Multi-objective whale optimization algorithm for optimal allocation of distributed generation and capacitor bank. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 459–465. [Google Scholar] [CrossRef]
- Saleh, A.A.; Senjyu, T.; Alkhalaf, S.; Alotaibi, M.A.; Hemeida, A.M. Water cycle algorithm for probabilistic planning of renewable energy resource, considering different load models. Energies 2020, 13, 5800. [Google Scholar] [CrossRef]
- Saleh, A.A.; Mohamed, A.-A.A.; Hemeida, A.M. Optimal allocation of distributed generations and capacitor using multi-objective different optimization techniques. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 377–383. [Google Scholar] [CrossRef]
- Alkhalaf, S.; Senjyu, T.; Saleh, A.A.; Hemeida, A.M.; Mohamed, A.-A.A. A MODA and MODE comparison for optimal allocation of distributed generations with different load levels. Sustainability 2019, 11, 5323. [Google Scholar] [CrossRef] [Green Version]
- Mei, R.N.S.; Sulaiman, M.H.; Mustaffa, Z.; Daniyal, H. Optimal reactive power dispatch solution by loss minimization using moth-flame optimization technique. Appl. Soft Comput. 2017, 59, 210–222. [Google Scholar] [CrossRef] [Green Version]
- Abaza, A.; Fawzy, A.; El-Sehiemy, R.A.; Alghamdi, A.S.; Kamel, S. Sensitive reactive power dispatch solution accomplished with renewable energy allocation using an enhanced coyote optimization algorithm. Ain Shams Eng. J. 2021, 12, 1723–1739. [Google Scholar] [CrossRef]
- Saddique, M.S.; Bhatti, A.R.; Haroon, S.S.; Sattar, M.K.; Amin, S.; Sajjad, I.A.; ul Haq, S.S.; Awan, A.B.; Rasheed, N. Solution to optimal reactive power dispatch in transmission system using meta-heuristic techniques―Status and technological review. Electr. Power Syst. Res. 2020, 178, 106031. [Google Scholar] [CrossRef]
- Ettappan, M.; Vimala, V.; Ramesh, S.; Kesavan, V.T. Optimal reactive power dispatch for real power loss minimization and voltage stability enhancement using artificial bee colony algorithm. Microprocess. Microsyst. 2020, 76, 103085. [Google Scholar] [CrossRef]
- Mouassa, S.; Bouktir, T.; Salhi, A. Ant lion optimizer for solving optimal reactive power dispatch problem in power systems. Eng. Sci. Technol. Int. J. 2017, 20, 885–895. [Google Scholar] [CrossRef]
- Heidari, A.A.; Abbaspour, R.A.; Jordehi, A.R. Gaussian bare-bones water cycle algorithm for optimal reactive power dispatch in electrical power systems. Appl. Soft Comput. 2017, 57, 657–671. [Google Scholar] [CrossRef]
- Jamal, R.; Men, B.; Khan, N.H. A novel nature inspired meta-heuristic optimization approach of GWO optimizer for optimal reactive power dispatch problems. IEEE Access 2020, 8, 202596–202610. [Google Scholar] [CrossRef]
- Barakat, A.F.; El-Sehiemy, R.; Elsaid, M.; Osman, E. Solving reactive power dispatch problem by using JAYA optimization algorithm. In International Journal of Engineering Research in Africa; Trans Tech Publications Ltd.: Bäch SZ, Switzerland, 2018; Volume 36, pp. 12–24. [Google Scholar] [CrossRef]
- Khan, N.H.; Wang, Y.; Tian, D.; Raja, M.A.Z.; Jamal, R.; Muhammad, Y. Design of fractional particle swarm optimization gravitational search algorithm for optimal reactive power dispatch problems. IEEE Access 2020, 8, 146785–146806. [Google Scholar] [CrossRef]
- Abdel-Fatah, S.; Ebeed, M.; Kamel, S. Optimal reactive power dispatch using modified sine cosine algorithm. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 510–514. [Google Scholar] [CrossRef]
- Muhammad, Y.; Khan, R.; Ullah, F.; Aslam, M.S.; Raja, M.A.Z. Design of fractional swarming strategy for solution of optimal reactive power dispatch. Neural Comput. Appl. 2020, 32, 10501–10518. [Google Scholar] [CrossRef]
- Sahli, Z.; Hamouda, A.; Bekrar, A.; Trentesaux, D. Reactive power dispatch optimization with voltage profile improvement using an efficient hybrid algorithm. Energies 2018, 11, 2134. [Google Scholar] [CrossRef] [Green Version]
- Aljohani, T.M.; Ebrahim, A.F.; Mohammed, O. Single and multiobjective optimal reactive power dispatch based on hybrid artificial physics–particle swarm optimization. Energies 2019, 12, 2333. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.T.; Vo, D.N. Improved social spider optimization algorithm for optimal reactive power dispatch problem with different objectives. Neural Comput. Appl. 2020, 32, 5919–5950. [Google Scholar] [CrossRef]
- Shaheen, M.A.; Hasanien, H.M.; Alkuhayli, A. A novel hybrid GWO-PSO optimization technique for optimal reactive power dispatch problem solution. Ain Shams Eng. J. 2021, 12, 621–630. [Google Scholar] [CrossRef]
- Bakry, O.; Dardeer, M.; Senjyu, T.; Alkhalaf, S. Multi-Objective Hybrid Genetic Algorithms and Equilibrium Optimizer GAEO to Integrate Renewable Energy Sources with Distribution Networks. Aswan Univ. J. Sci. Technol. 2021, 1, 34–69. [Google Scholar]
- Albadr, M.A.; Tiun, S.; Ayob, M.; Al-Dhief, F. Genetic algorithm based on natural selection theory for optimization problems. Symmetry 2020, 12, 1758. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Saddique, M.S.; Habib, S.; Haroon, S.S.; Bhatti, A.R.; Amin, S.; Ahmed, E.M. Optimal Solution of Reactive Power Dispatch in Transmission System to Minimize Power Losses using Sine-Cosine Algorithm. IEEE Access 2022, 10, 20223–20239. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Y. Multi-Objective Optimal Reactive Power Dispatch of Power Systems by Combining Classification-Based Multi-Objective Evolutionary Algorithm and Integrated Decision Making. IEEE Access 2020, 8, 38198–38209. [Google Scholar] [CrossRef]
- Tudose, A.M.; Picioroaga, I.I.; Sidea, D.O.; Bulac, C. Solving single-and multi-objective optimal reactive power dispatch problems using an improved salp swarm algorithm. Energies 2021, 14, 1222. [Google Scholar] [CrossRef]
- Vishnu, M.; TK, S.K. An improved solution for reactive power dispatch problem using diversity-enhanced particle swarm optimization. Energies 2020, 13, 2862. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).