1. Introduction
The growing need to employ composite materials in several sectors has driven increasingly important advancements toward the improvement of structural maintenance techniques [
1,
2] that will allow the rapid and cost-saving integrity assessment of crucial components. For these reasons, structural health monitoring (SHM) systems have been intensively studied during the past few decades. The SHM paradigm is to monitor the integrity of a structure and detect both the location and severity of possible damage. Among the diverse ways to perform SHM, the guided wave (GW) propagation technique using permanently installed piezoelectric transmitter/receiver transducers (PTRTs) is one of the most popular. The greatest advantage of this solution is that these elastic waves can travel along thin-walled structures with low attenuation and high sensitivity to reveal several types of damage. Moreover, monitoring is also guaranteed for areas that are difficult to inspect, and with very low economic and energy costs [
3,
4]. By comparing the signal datasets from two different states of the structure, i.e., the baseline (known and supposed to be damage-free) and actual (unknown) ones, the damage-related features can be extracted and used to properly characterize the faulty areas of the components. However, the complexity of GW analysis can hinder such key features.
One of the main problems with GW is related to the existence of different propagating modes (symmetric,
S, and antisymmetric,
A) of different orders (
with
) traveling at different speeds according to frequency (dispersion behavior), laminate thickness, and fiber direction (slowness phenomenon) [
5]. Unlike slowness, the dispersion is also present in isotropic and homogeneous materials. Other factors that make the prediction of the propagation of GWs more complex concern the geometric characteristics of the structure, such as surface curvatures, and the environmental and operational conditions. In relation to geometrical discontinuities (for example, stiffeners), different approaches based on the baseline subtraction scheme have been used by several authors to determine the GW characteristics and to identify the reflected/scattered/converted modes [
6,
7,
8]. The curvature effect on GW propagation has been analyzed by several authors. Paul David Wilcox [
9] studied a series of aluminum plates with different radius to thickness ratios. After tracing the dispersion curves for each panel, he concluded that the effect of plate curvature on the phase and group velocities is negligible only if the radius/thickness ratio is greater than around 10:1. Nevertheless, the effect of curvature was found to become significant, even at this radius/thickness ratio. A more in-depth study was done by Ka Lok Jimmy Fong [
10], who examined the curvature effect of aluminum strips by comparing the phase velocity and the displacement mode shapes of fundamental symmetric and antisymmetric modes at different curvature radii. It was noticed that the effect of the curvature ceased to be negligible only for small radii of curvature. In addition, “optimal frequencies” were identified for each mode, at which, even for high curvatures, the differences in phase velocity were minimal. The authors Santana et al. [
11] presented the effect of high curvature to thickness ratios on the characteristics of Lamb waves that were propagating over the skins of composite structures. For the curved portion, the
wave mode velocity increased asymptotically with an increase in radius, whereas the
wave mode exhibited an opposite behavior. It was also observed that for the
mode, the group velocity changed even before and after the curved region of the panel, while the
group velocity was found to be practically unchanged. The authors, however, did not elucidate the reasons for this phenomenon.
Finite element analysis (FEA), from this point of view, can represent a valid alternative that broadens the understanding of GW mechanisms in curved panels, as well as in more complex components [
12,
13], with the aim of reducing the time and costs related to an experimental test campaign. There are two main approaches to performing GW propagation analysis: the explicit and the implicit formulation schemes. However, since the propagation of GWs is a dynamic phenomenon, the explicit method is mostly used. On the other side, using the Abaqus
® CAE environment (Dassault Systems, Simulia Corp., Providence, RI, USA), the implicit method foresees a procedure available for piezoelectric analysis allowing using C3D8E finite elements for the modeling of the piezoelectric sensors, which are not available for dynamic explicit FEA. One limitation of this approach is that the Abaqus
® code does not account for piezoelectric effects in the total energy balance equation, which can lead to an apparent imbalance of the total energy of the model in some situations.
The author Tianwei Wang [
14] checked the effectiveness of three different analysis methods: explicit dynamic analysis (EDA), implicit dynamic analysis (IDA), and combined implicit-explicit dynamic analysis (CIEDA). The most significant difference found was that the results from the Abaqus/Implicit code have a short time delay. Secondly, the magnitude of the signals predicted by the explicit scheme was smaller. This is because, in this case, the actuator input voltage to the predicted sensors’ displacement ratios were found to be smaller than to the real ones. However, the general trend of implicit results was similar to the co-simulation one, which can be used to illustrate the characteristics of wave propagation in a plate. Leckey et al. [
15] compared group velocity and wavenumber domain using three different simulation tools for implicit modeling (Comsol, Abaqus/Implicit, and Ansys) and two explicit approaches (a custom code executing the elastodynamic finite integration technique and Abaqus/Explicit) for simple composite specimens. The comparisons showed that the results predicted by all simulation tools matched well with the theory, and agreed well with the experimental observations (laser Doppler vibrometry data). Marković et al. [
16] recommended the explicit FEA implemented in the Abaqus software for wave propagation modeling and considered it to be one of the most effective methods currently available. Despite the potential of the co-simulation procedure, for more complex structures the explicit method is more useful and powerful since it is much faster. One drawback is that the explicit FEA formulation requires particular attention when an operational load condition has to be defined before the simulation of GW propagation. In fact, considering a quasi-static load, the simulation requires the standard/implicit formulation. Therefore, to overcome the issues related to the combination of two different solution schemes, the efficiency of the implicit FEA must be proved against experimental data.
Recent works in the published literature propose the advanced FE approach for the prediction of GW in composites, focusing also on crack propagation and impact detection methodologies [
17,
18,
19]. Other authors have already investigated the GW propagation mechanisms of flat plates using the explicit FEA [
20], extracting the dispersion curves for an aluminum panel, and using the numerical data for the training of an artificial neural network for damage detection intent.
In this work, the propagation mechanisms of GWs in flat and curved panels that are both made of CFRP material were investigated numerically, under both the explicit and implicit formulation schemes. In other authors’ works, the emphasis was on the modeling of a piezoelectric GW-based SHM system on a composite glass-fiber-reinforced polymeric (FRP) structure. The shell and solid finite element modeling approaches were investigated, and the results of the explicit FE analyses were validated against the experimental results [
13]. Attention was also paid to the prediction of GW behavior when the same GFRP structure was subjected to a bending load [
21]. However, all analyses were developed under the explicit scheme.
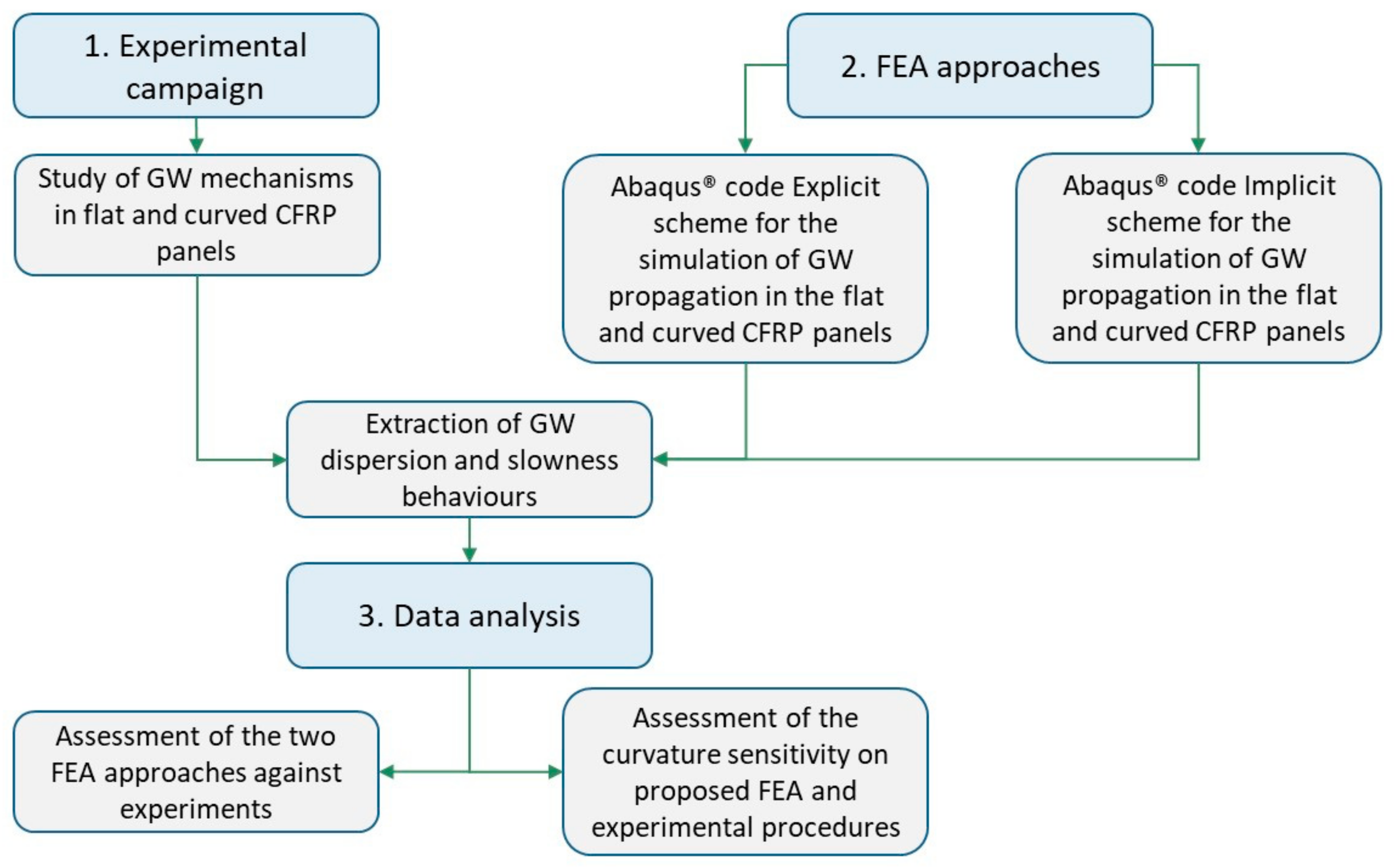
Hence, this paper aims to understand the different levels of accuracy provided by both schemes, in terms of GW propagation mechanisms and dispersion curve calculation, for cases that study a different aspect from the flat panels usually investigated in the literature. To accomplish this goal, the Abaqus/Explicit and Abaqus/Implicit software packages were used. Afterward, the predicted signals and dispersion curves extracted from the two approaches were compared with the results of an experimental campaign. Such a comparison allowed to investigate the reliability and efficiency of the numerical procedures in simulating GWs propagation. In all cases, a frequency range of from 100 kHz to 300 kHz and four different propagation directions (0°, 45°, −45°, and 90°) were investigated to highlight dispersive behavior and the slowness phenomenon, respectively. A flowchart of the research activities proposed herein is presented in
Figure 1.
The remainder of the paper is organized as follows. The descriptions of the case studies and of the experimental campaign are presented in
Section 2, while the modeling aspects of both numerical approaches are detailed in
Section 3.
Section 4 reports and discusses the results; finally,
Section 5 concludes the paper.
3. Numerical Approach
Concerning numerical modeling, two different approaches have been used to model the plate and the PTRTs: the explicit (Abaqus/Explicit) and the implicit (Abaqus/Implicit) formulation schemes.
The aim of this work is to compare the explicit and implicit FEA results for the simulation of GWs. As mentioned in
Section 1, although the explicit procedure is well established in the literature for simulating GWs for the unloaded configurations of the component, several problems arise when dealing with actual operating scenarios. A quasi-static load, for example, can be modeled in both schemes, although the explicit scheme hides several numerical issues that are linked to the rising internal energy of the model and to possible load-induced numerical vibrations [
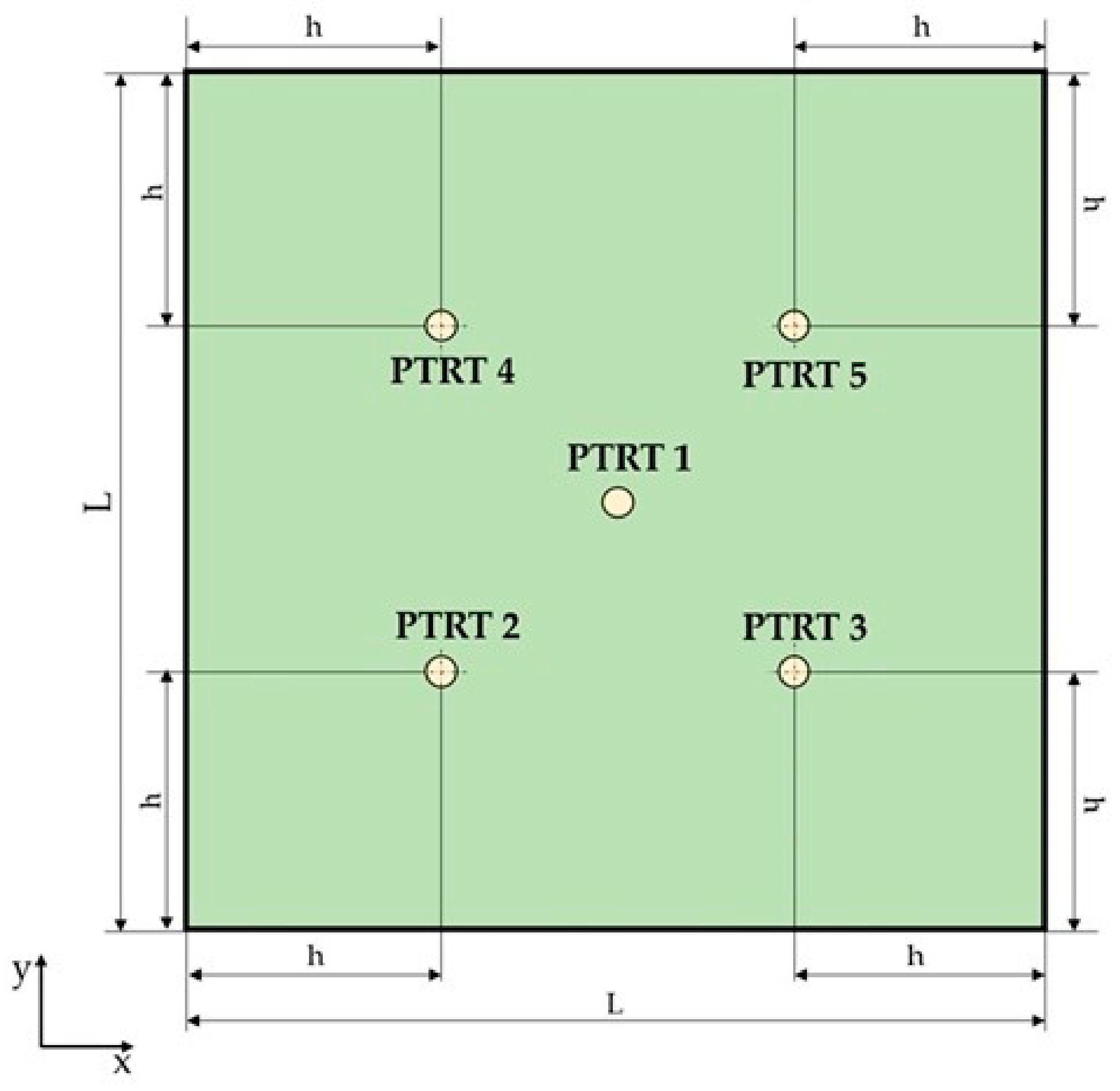
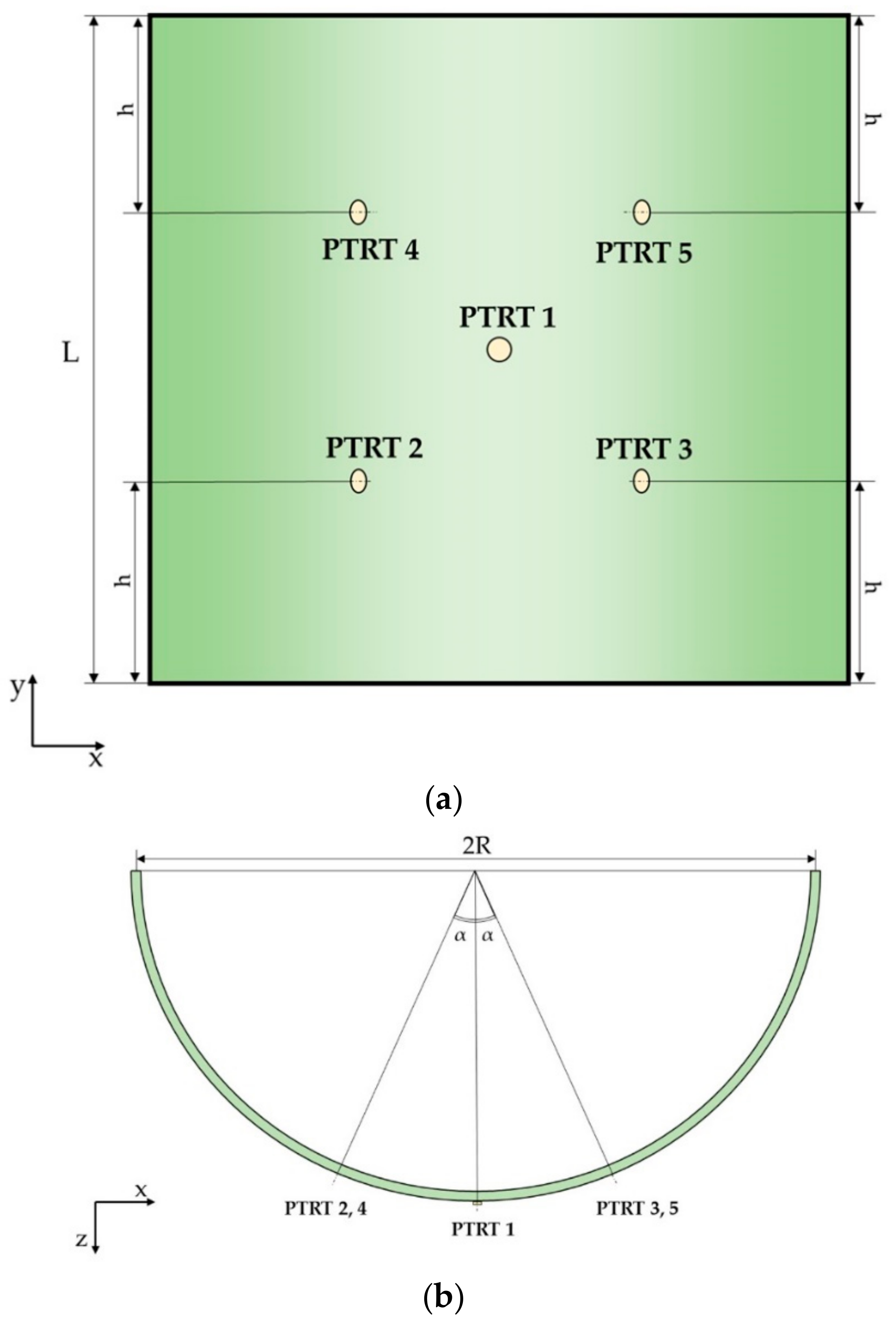
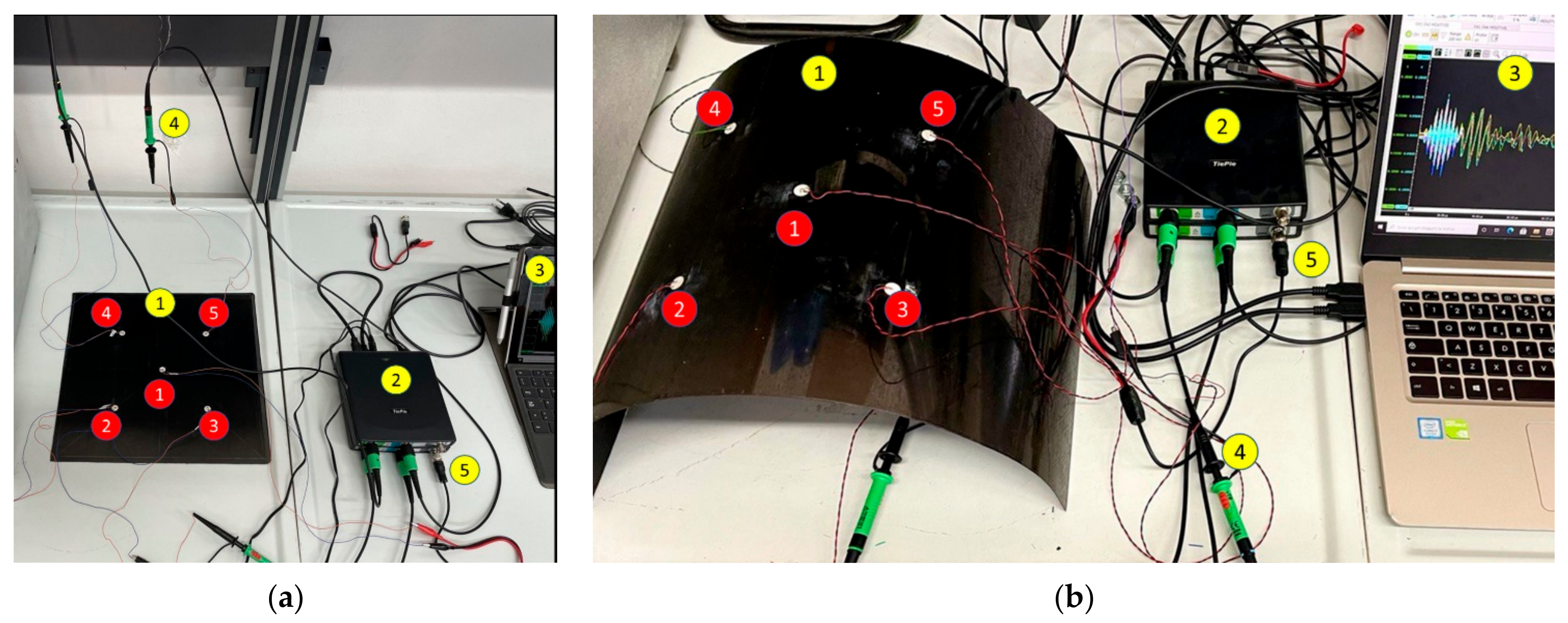
26]. Thus, the implicit formulation can be adopted to simulate and study the load effect on GWs with reduced effort, compared to the explicit FEA. However, before proceeding with load effects modeling on GWs, the implicit scheme must be verified and assessed for simple components under laboratory conditions (i.e., flat panels, and undamaged and unloaded configurations). To accomplish this goal, different FEAs have been developed and studied herein, as listed in
Table 2.
For both modeling procedures, to reduce the number of simulations, a chirp excitation signal [
7] has been used to study the dispersive behavior of GWs in the frequency band investigated in the experiments (100–300 kHz). This signal, shown in
Figure 7, has an initial frequency of 80 kHz, a final frequency of 320 kHz, and a time window of
s. A wider range is mandatory to properly reconstruct data at the boundary frequencies. All simulations have been performed with an Intel
® Xeon
® Gold 6248R CPU with a total of 24 cores and 48 threads.
Explicit vs. Implicit FEA
The main differences between the explicit and implicit FEA formulations for the test cases that are analyzed herein can be detailed as follows.
In the case of the explicit FEA formulation, S4R conventional two-dimensional shell elements (having 6 degrees of freedom (DOFs) for each node) with an average element size of 2 mm were chosen for the plate, while C3D8R solid elements (characterized by 3 DOFs for each node) with an average element size of 0.5 mm were chosen for the sensors. These values allowed discretizing 8 NPW (nodes per wavelength) under 300 kHz carrier frequency. This method is conditionally stable; the time step, equal to , was chosen by considering the wave speed and the minimum element length.
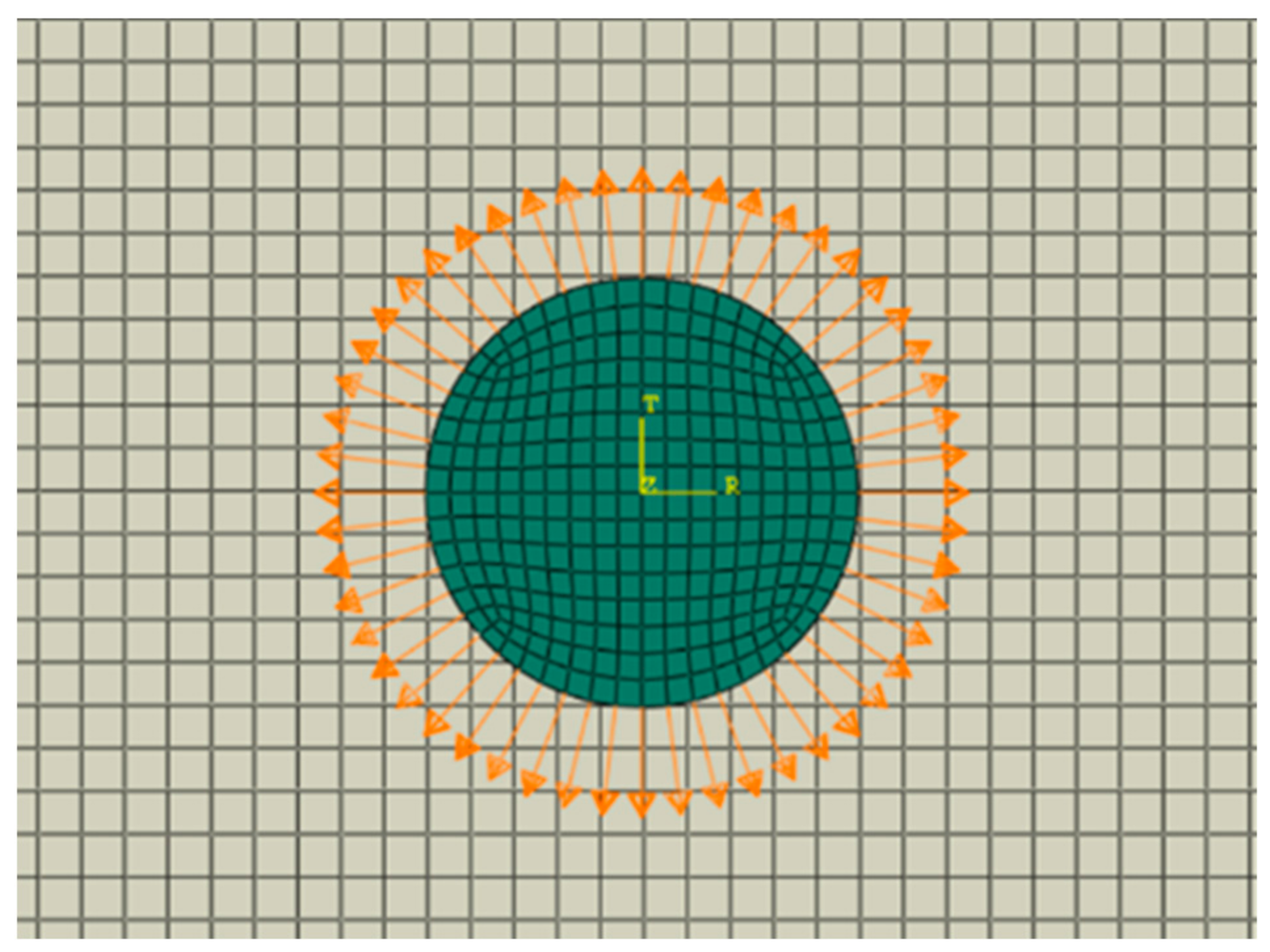
Regarding the GW propagation, radial displacements that were equivalent to the input voltage, represented by the orange-colored line in
Figure 7, were calculated according to the piezoelectric relationships (the mathematical details can be found in [
7]), depending on PTRT, and the plate material and geometrical properties. As shown in
Figure 8, this effective radial displacement was applied to the circumference of the upper surface of the actuator, after having defined a proper polar coordinate system at its center. In terms of the computational costs, each analysis took about 10 min.
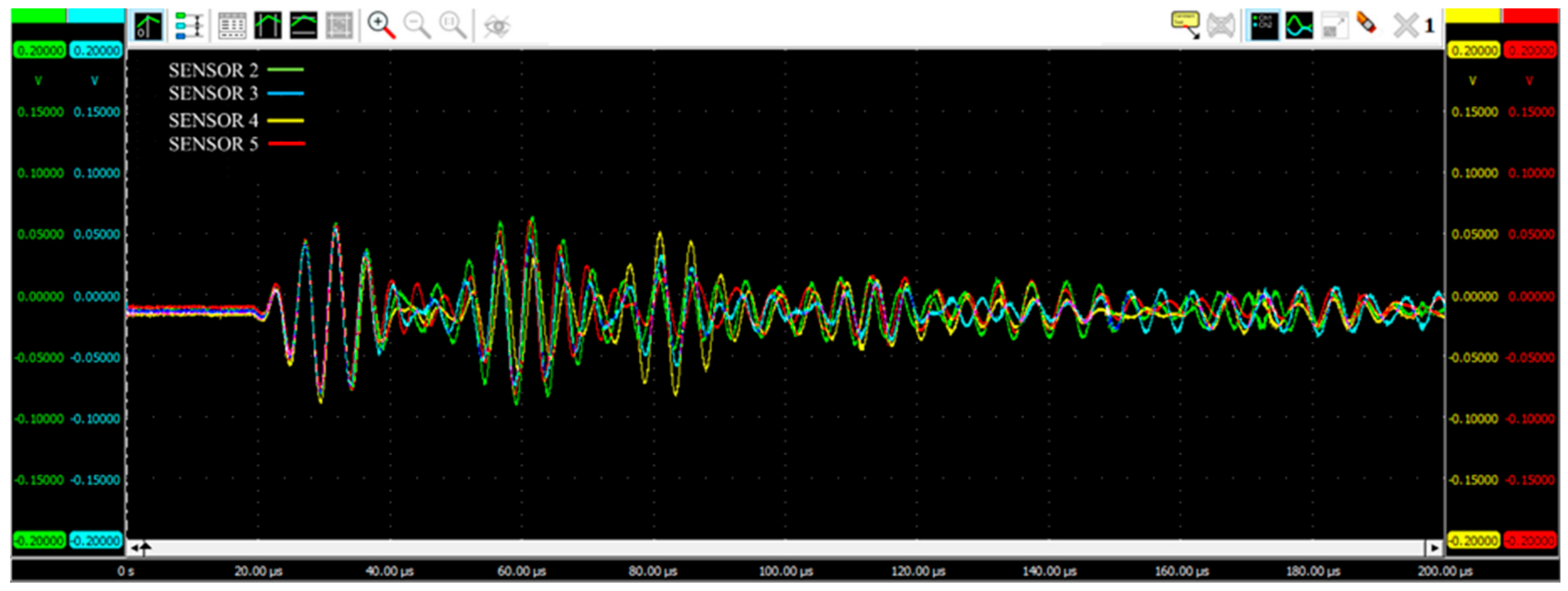
The predicted signals, recorded at the various sensor locations, were calculated as the average of the in-plane strains reads by all the nodes defining each sensor. According to the piezoelectric relationships, the voltage in PTRTs can be calculated via strain measurements, using a conversion constant for the sensing (further mathematical details can be found in [
2,
20]).
For the implicit formulation, C3D8I solid elements (characterized by 3 DOFs for each node) with an average element size of 2 mm were chosen for the plate, while the C3D8E solid elements (having an additional DOF related to the electrical potential with respect to the C3D8I element type, one that was not available for the explicit procedure) with an average element size of 0.5 mm were chosen for the sensors. Again, these values allowed discretizing 8 NPW, which is the minimum number required, according to the literature [
13,
27], at a 300 kHz carrier frequency. The C3D8E elements included the piezoelectric coupling by defining the piezoelectric coefficient and the dielectric matrices, according to the properties listed in
Table 3.
The main advantage of this approach is that, differently from the explicit procedure, the diagnostic signal expressed in voltage can be directly applied to the terminals of the transducers, and the corresponding voltage response in the sensors can be directly acquired without any conversion. In detail, for the GW excitation and sensing, the signal, shown in voltage (the blue line in
Figure 6), was applied at the upper surface of the actuator, while the electrical potential was imposed at 0 on the lower surface as the initial conditions (with the voltage applied along the polarization direction) [
28]. For the receivers, the electrical potential had to be considered as 0 at the lower surfaces in terms of initial conditions as well, while the predicted signals in terms of voltage could be measured directly at the upper surfaces.
Although the implicit method is not as conditionally stable as the explicit one, the same maximum increment of the explicit formulation was chosen. Regarding the computational costs, each analysis took about 7 h for the implicit formulation, while only roughly 10 min of computational time was necessary for the explicit approach.
In both cases, details about the discretization of the model (
Figure 9) are listed in
Table 4 in terms of the number of nodes, number of elements, and characteristic element dimensions.
The adhesive bonding of the sensor array on the plates was modeled herein through the use of a node-to-surface contact formulation, employing “tie” interfaces at the contact surfaces. Finally, the four corners of the plates were constrained.
Then, signals were processed by means of the developed code. In particular, recorded data were reconstructed in n-cycles, using sinusoidal tone-burst Hanning-windowed signals from 100 kHz to 300 kHz, with a step of 50 kHz, using the reconstruction procedure described in [
29]. The reconstruction phase in the tone-burst response is fundamental to enabling the representation of the signals in the time domain (because of the dispersive nature of GWs [
25]), and the GW group velocities extraction for each carrier frequency.
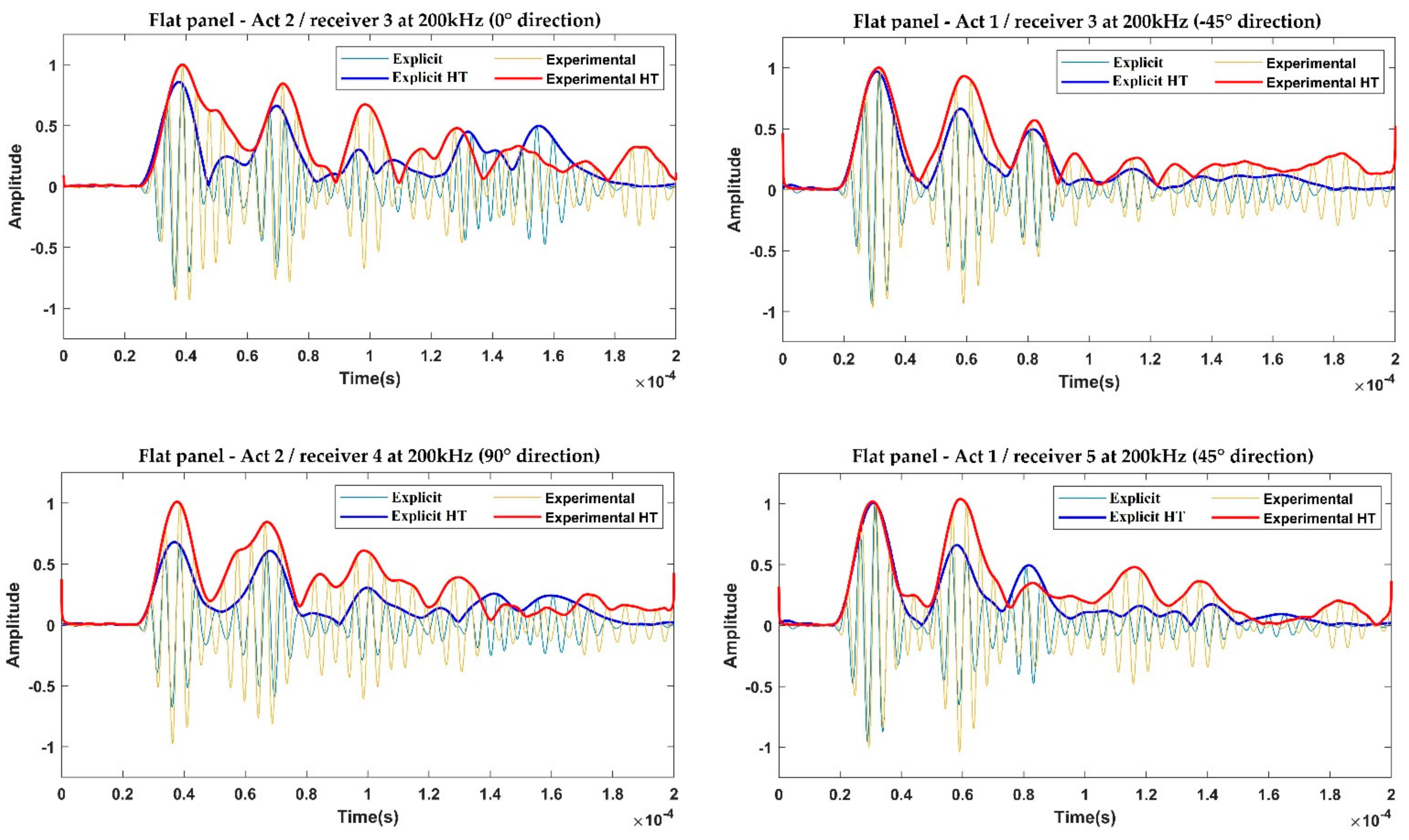
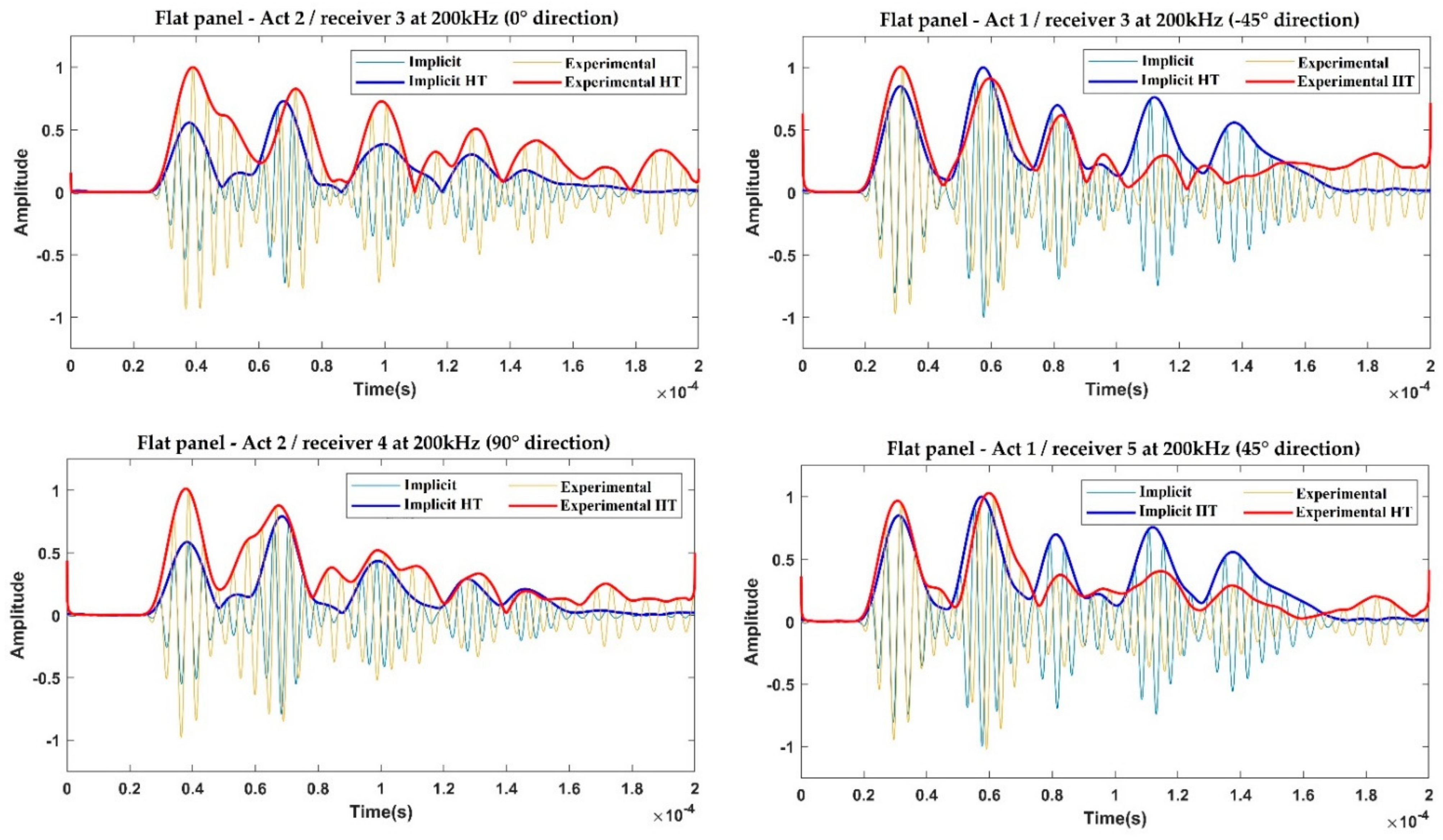
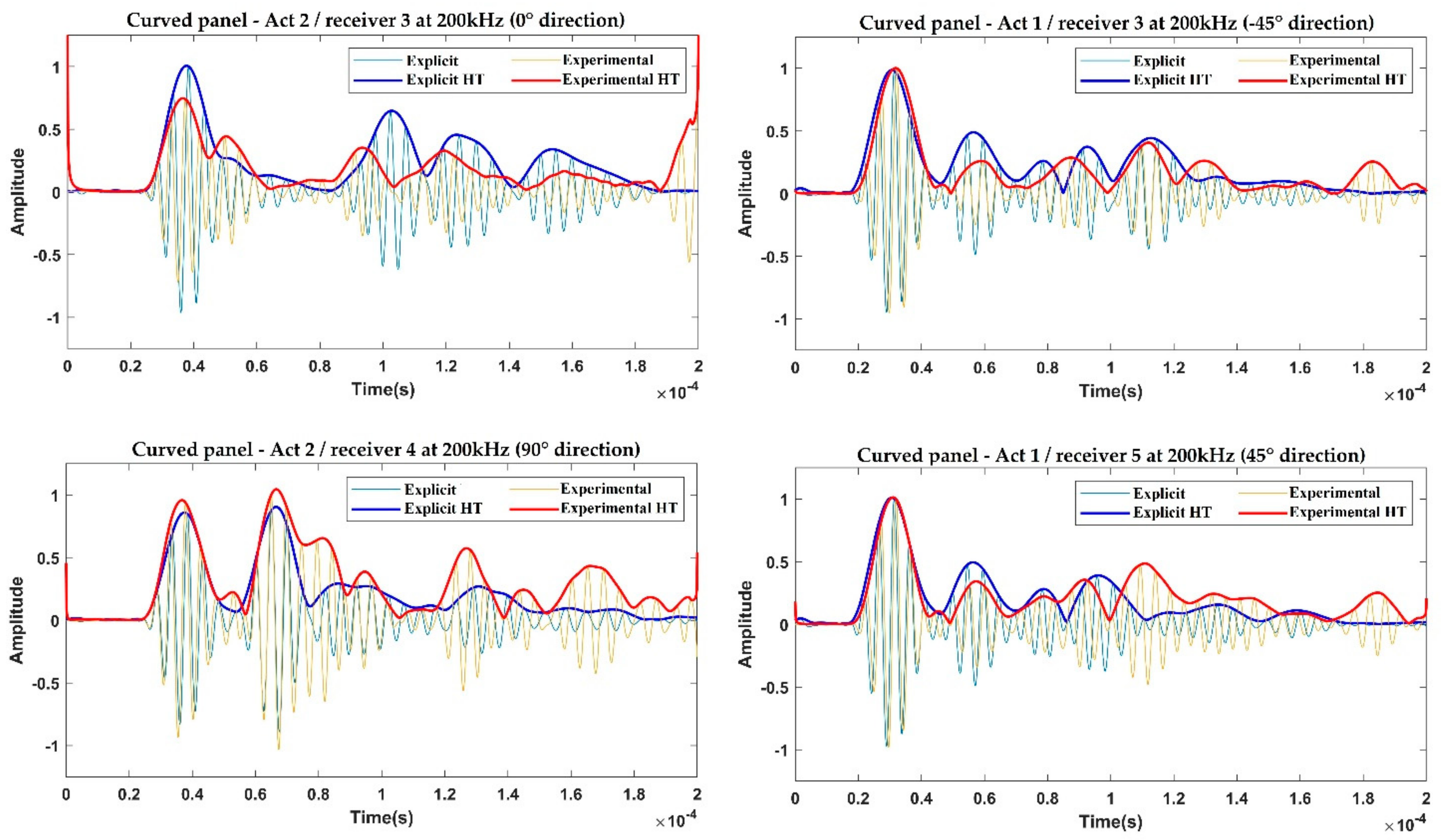
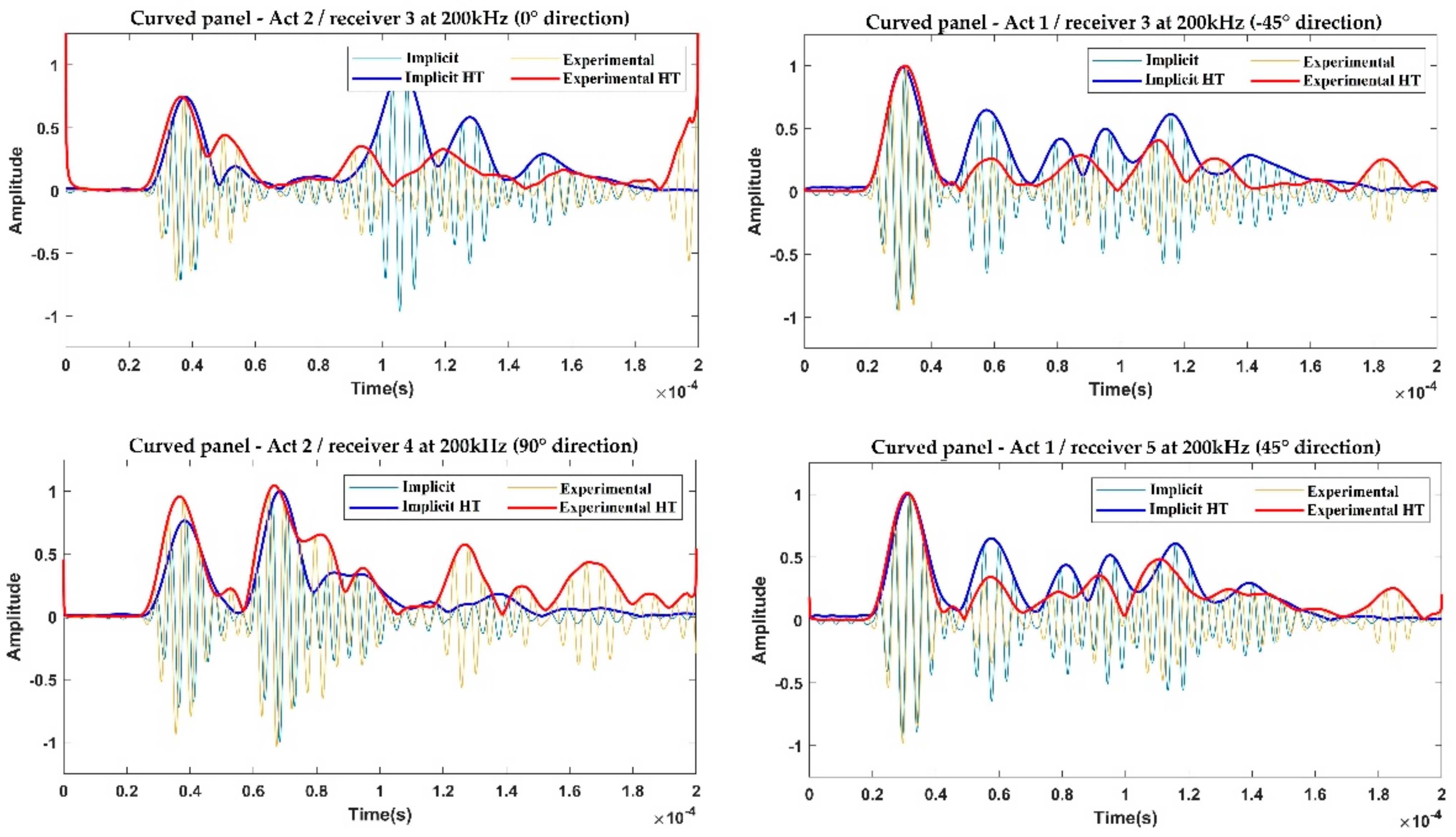
Thus, the numerical results and experimental data are compared, in terms of amplitudes and dispersion curves.
5. Conclusions
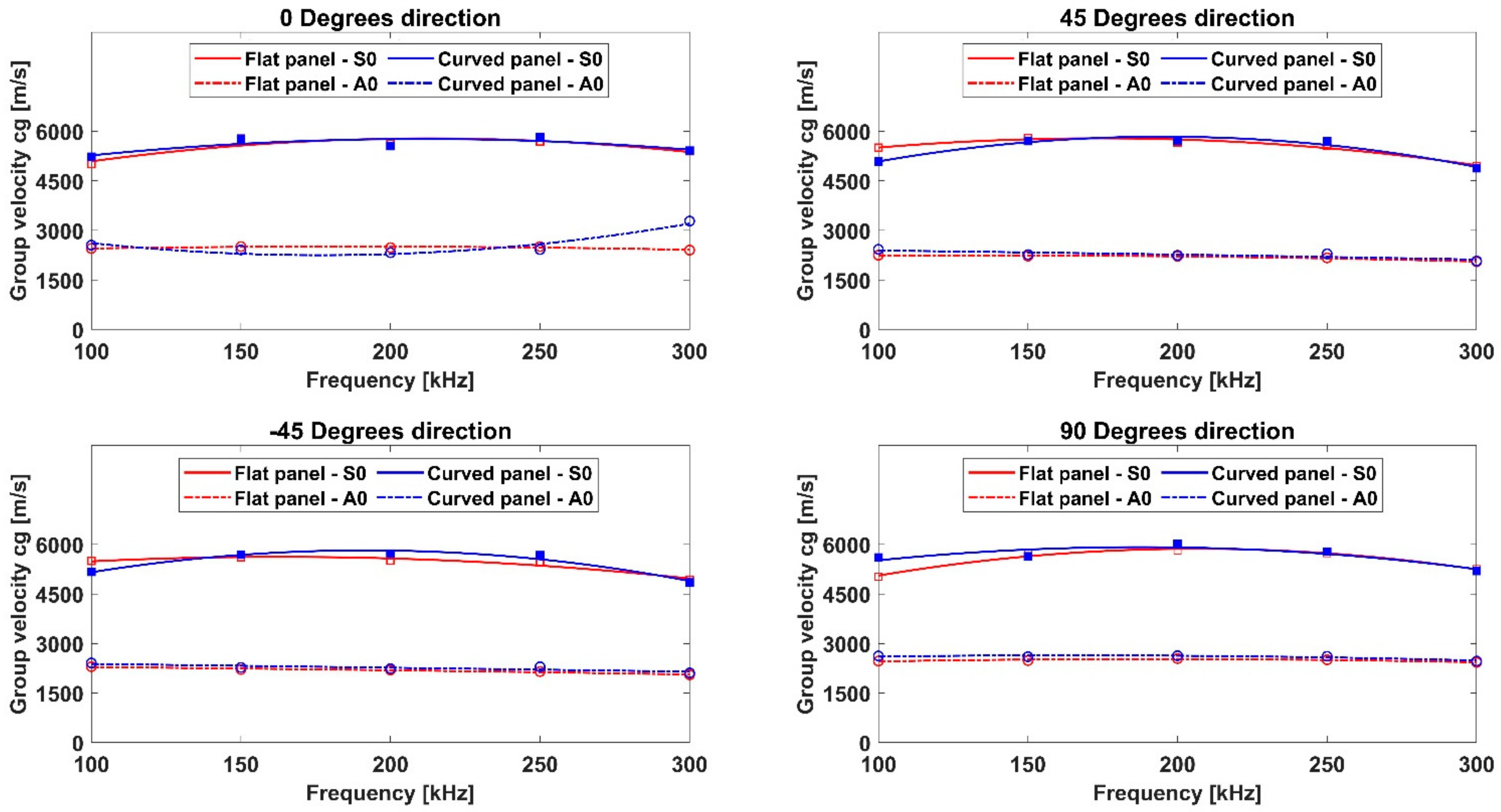
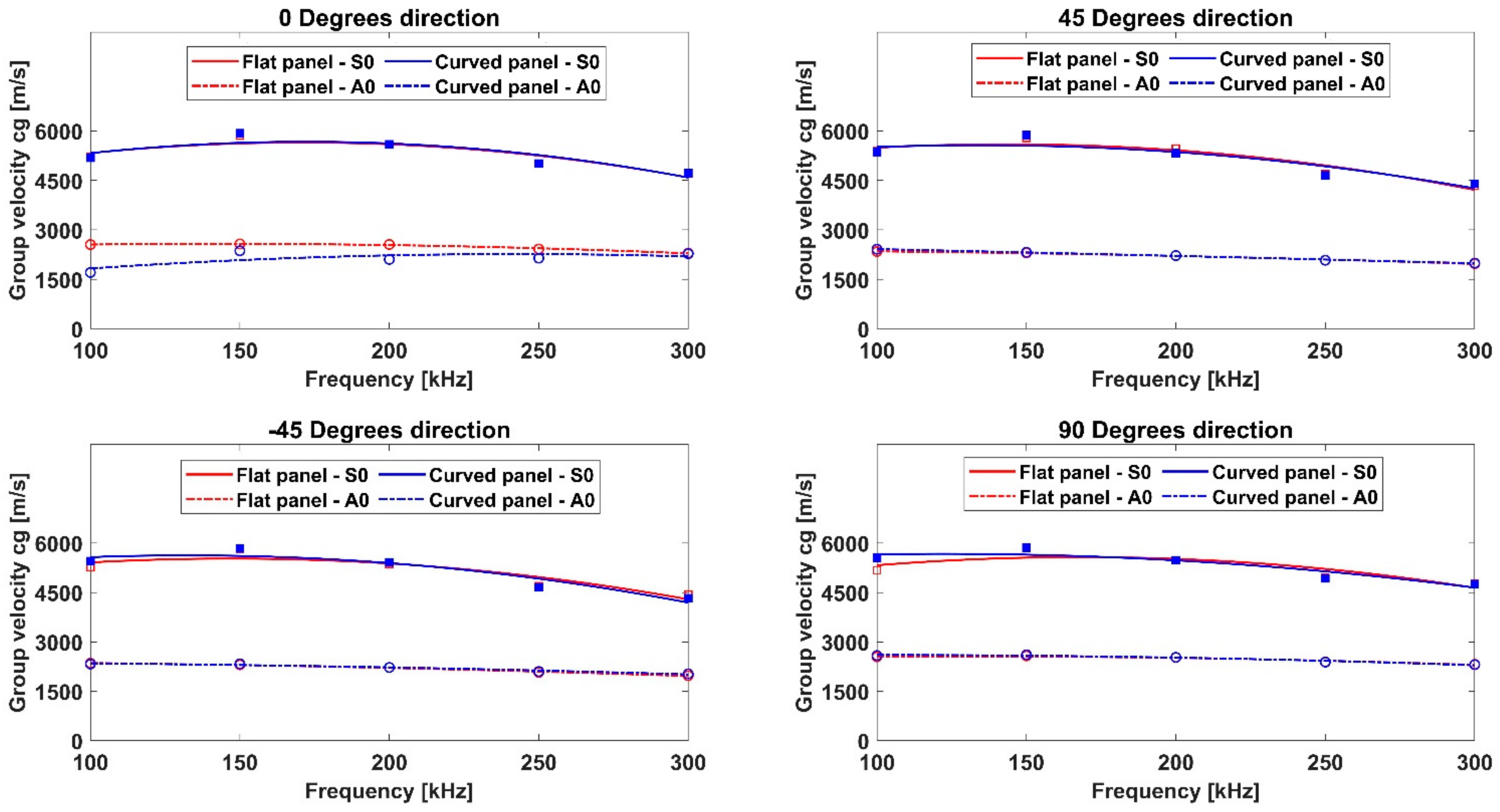
In this paper, numerical and experimental investigations into two CFRP composite components, a flat and a curved panel, were carried out to study the GW propagation mechanisms.
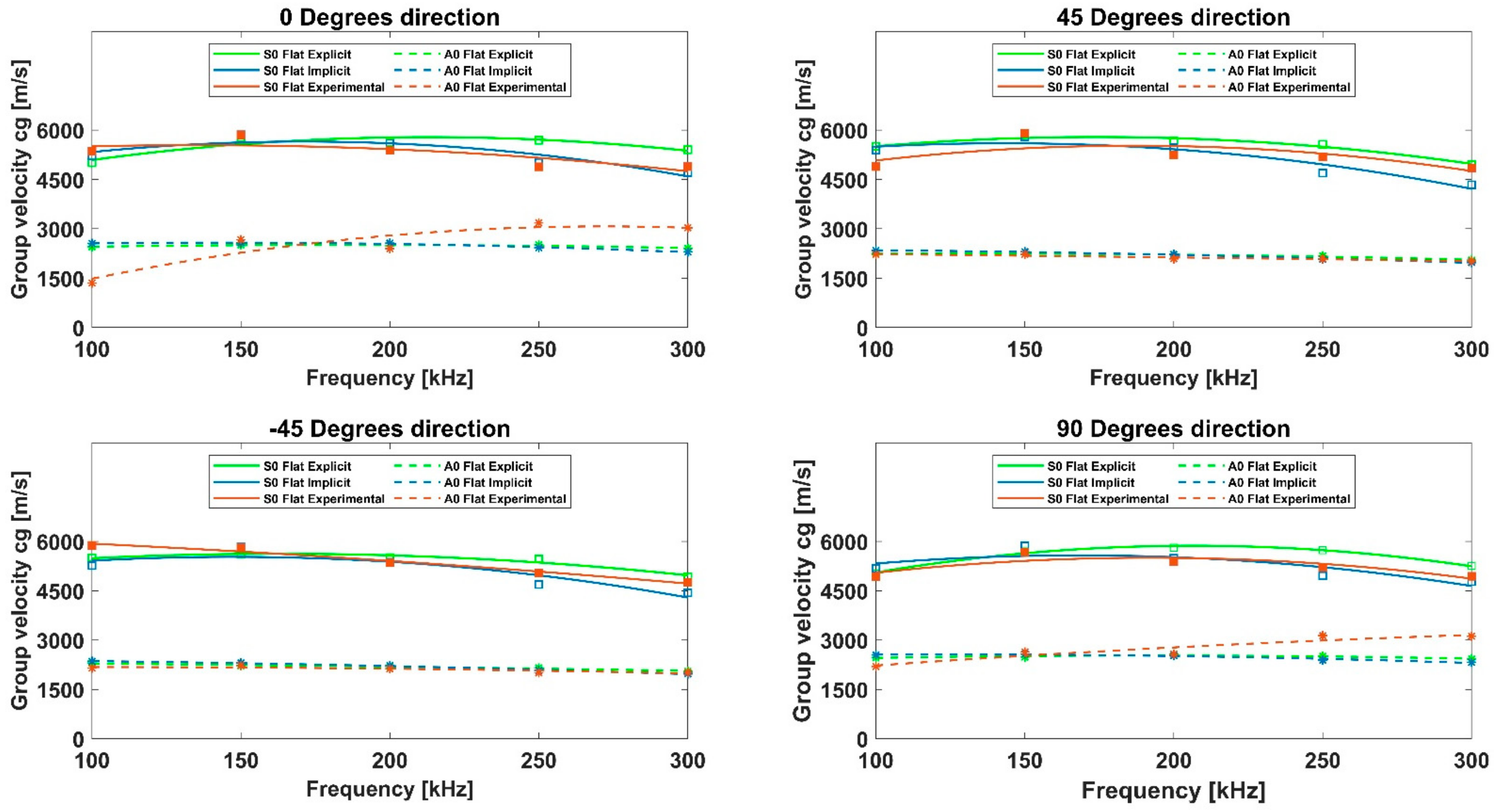
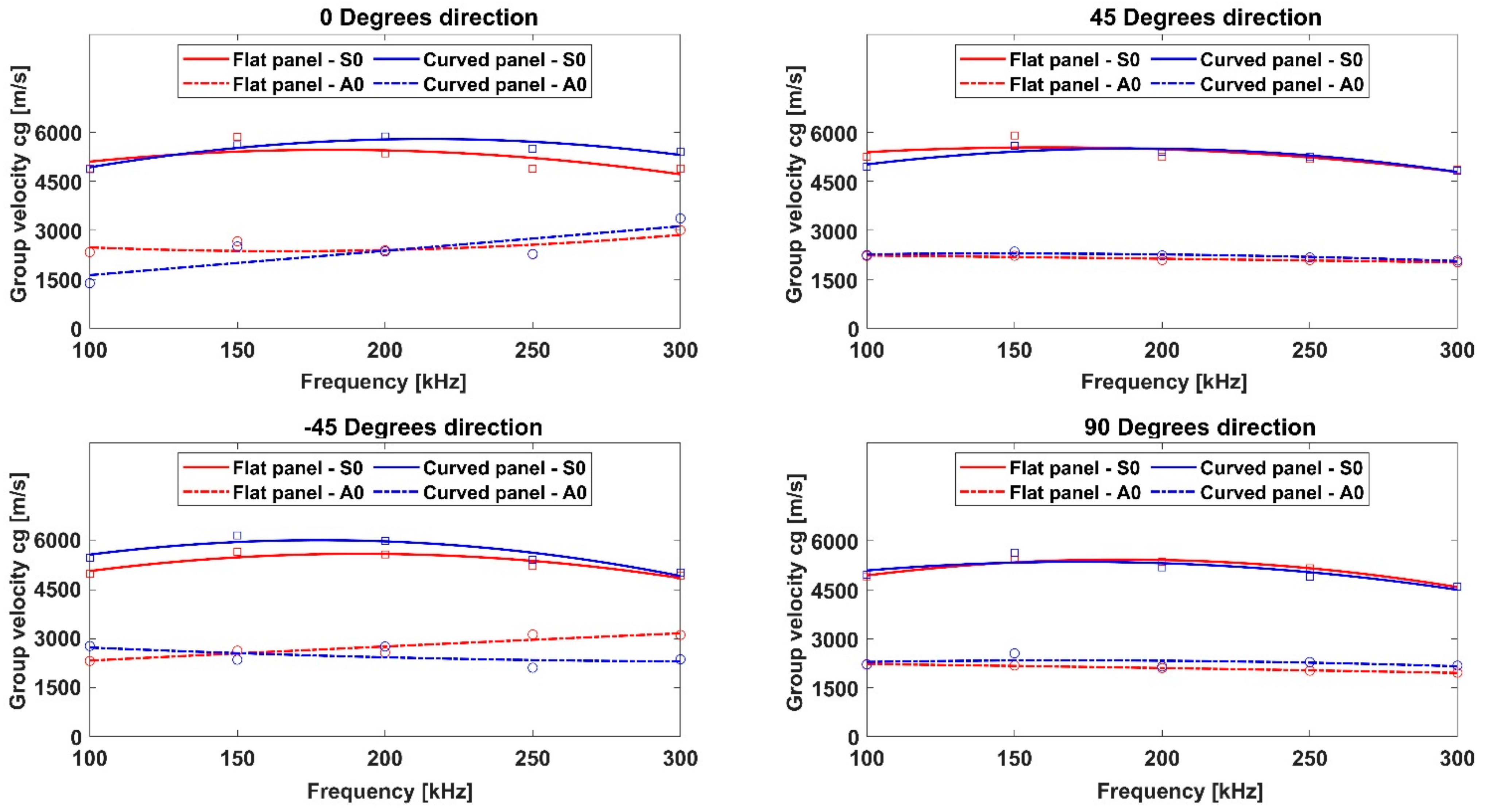
Two finite element modeling approaches, based on implicit and explicit formulations, respectively, were investigated. An experimental campaign was also carried out. The predicted measures, in terms of the recorded signals and GW dispersion curves, were compared against the experimental dataset in order to assess and validate the numerical procedures, also comparing those for curved panels. The results were extracted for both geometrical configurations in a specific frequency range, 100–300 kHz, which is characteristic of non-destructive testing techniques. The numerical and experimental dispersion curves were extracted to highlight and compare the performance of the two numerical approaches. Moreover, the dispersion curves for both flat and curved panels, extracted by the experiments as well as by both implicit and explicit schemes, were respectively compared to highlight the different curvature sensitivity of the three approaches. The results comparison allowed to assess the reliability of the different modeling approaches when modeling GW propagation phenomena (dispersion and slowness). Specifically, it was proved that even if both numerical formulation schemes can provide accurate results with respect to the experimental data for both panel configurations, the explicit FEA model is in fact preferable, due to the considerably reduced computational costs. This aspect is fundamental for properly modeling GW propagation in real in-service scenarios, for example, under quasi-static loading conditions, for which an implicit FEA should be instead preferred despite the higher computational costs.
Furthermore, for the curved panel, which was characterized by a thickness-to-curvature radius of 1:111.67, the propagation speeds (for varying propagation paths) of the and modes are quite similar to those registered in the flat configuration of the panel. This result agrees with the literature. A better match between the dispersion curve trends for the numerical approaches was found for the investigated configurations, while the experimental data showed a slight mismatch. This result could, however, be justified due to the slight mismatch in the positioning of the transducers on the curved panel, in terms of both location and adhesion.
This work represents the basis for the next research activity steps, which will involve a study of the load effect on GW propagation mechanisms in curved FRP composite engineering structures, for the assessment of SHM system damage sensitivity.