Prediction of Bidirectional Shear Strength of Rectangular RC Columns Subjected to Multidirectional Earthquake Actions for Collapse Prevention
Abstract
:1. Introduction
1.1. MEP
1.2. ANFIS
2. Methodology
2.1. Fitting Parameters
2.1.1. MEP Parameters
2.1.2. ANFIS Parameters
2.2. Performance Evaluation of Models
2.3. Modelling
3. Results Analysis and Discussion
3.1. ANFIS Modeling Results
3.2. MEP Modeling Results
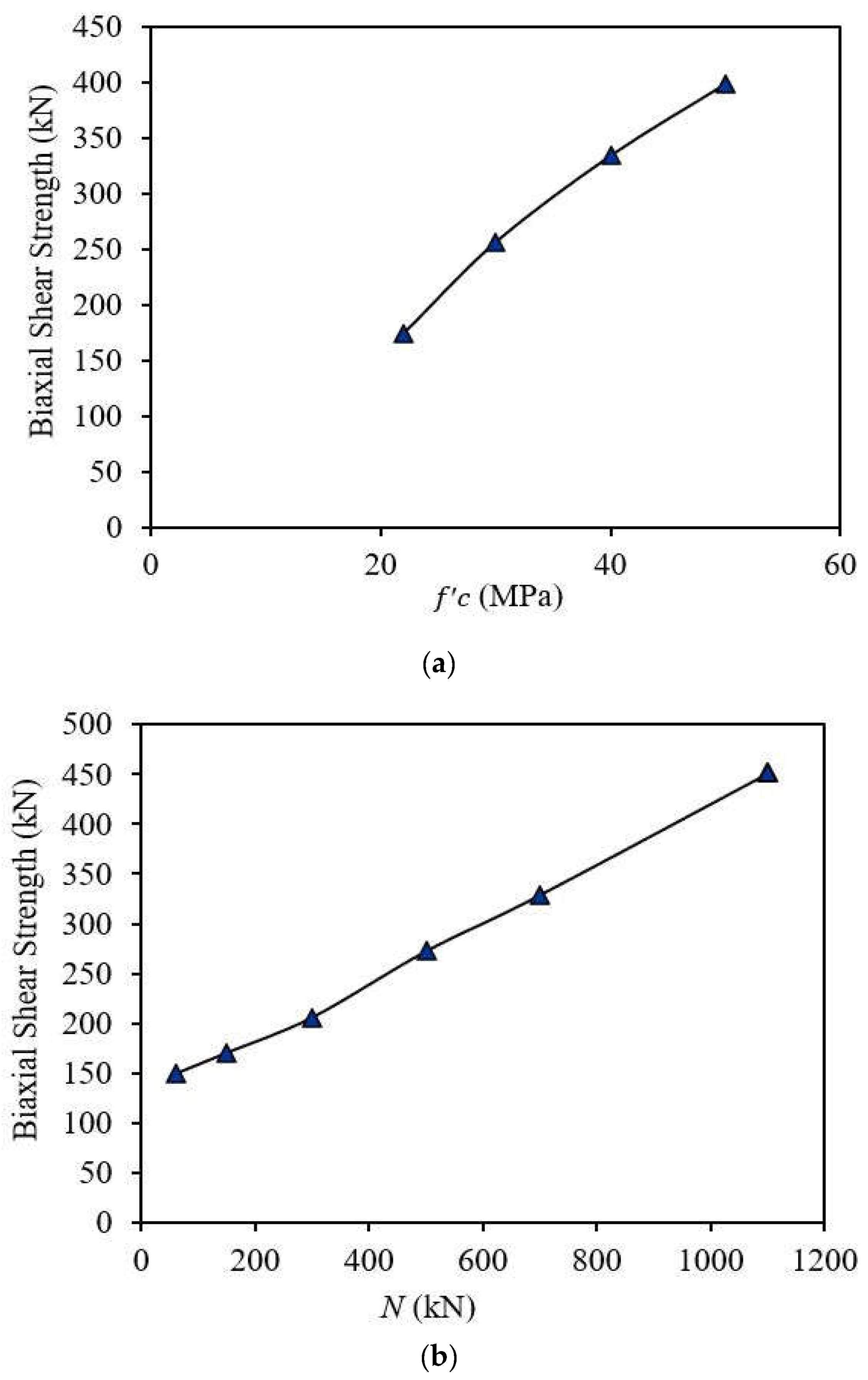
4. Parametric Analysis of MEP-Based Models
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| RC | Reinforced Concrete |
| MEP | Multi Expression Programming |
| V | Biaxial Shear Strength |
| GEP | Gene Expression Programming |
| GA | Genetic Algorithm |
| GP | Genetic Programming |
| G2 | Gene 2 |
| G4 | Gene 4 |
| G6 | Gene 6 |
| x1 & x2 | Sample inputs in ANFIS |
| μAi & μBi−2 | Weights obtained while connecting fuzzy membership functions |
| Firing strength | |
| fi | Linear function |
| pk, qk & rk | Linear function parameters for particular rule ‘k’ |
| OF | Objective Function |
| ρ | Performance Index |
| ith Experimental | |
| ith Predicted | |
| ith Mean Experimental | |
| ith Mean Predicted | |
| Number of learning (training and validation) data | |
| Number of testing dataset | |
| Performance index of learning dataset | |
| Performance index of testing dataset | |
| R | Correlation coefficient |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
| RRMSE | Relative Root Mean Square Error |
| Concrete Compressive Strength | |
| Gross Sectional Area of Column | |
| Longitudinal Reinforcement Percentage | |
| Shear Reinforcement Percentage | |
| Yield Strength of Longitudinal Reinforcement | |
| Axial Load Of Column | |
| Width Of Column Web | |
| Depth Of Column | |
| Column Height |
References
- Azim, I.; Yang, J.; Bhatta, S.; Wang, F.; Liu, Q.-F. Factors influencing the progressive collapse resistance of RC frame structures. J. Build. Eng. 2020, 27, 100986. [Google Scholar] [CrossRef]
- Shi, Q.; Ma, L.; Wang, Q.; Wang, B.; Yang, K. Seismic performance of square concrete columns reinforced with grade 600 MPa longitudinal and transverse reinforcement steel under high axial load. Structures 2021, 32, 1955–1970. [Google Scholar] [CrossRef]
- Lee, C.S.; Han, S.W. Cyclic behaviour of lightly-reinforced concrete columns with short lap splices subjected to unidi-rectional and bidirectional loadings. Eng. Struct. 2019, 189, 373–384. [Google Scholar] [CrossRef]
- Pham, T.P.; Li, B. Seismic Behavior of Reinforced Concrete Columns with Light Transverse Reinforcement under Different Lateral Loading Directions. ACI Struct. J. 2013, 110, 833. [Google Scholar] [CrossRef]
- Rodrigues, H.; Furtado, A.; Arêde, A. Behavior of Rectangular Reinforced-Concrete Columns under Biaxial Cyclic Loading and Variable Axial Loads. J. Struct. Eng. 2016, 142, 04015085. [Google Scholar] [CrossRef]
- Bonet, J.L.; Barros, M.H.F.M.; Romero, M.L. Comparative study of analytical and numerical algorithms for designing rein-forced concrete sections under biaxial bending. Comput. Struct. 2006, 84, 2184–2193. [Google Scholar] [CrossRef] [Green Version]
- Mark, P. Shear-resistant design of biaxially loaded RC beams. Mag. Concr. Res. 2007, 59, 21–28. [Google Scholar] [CrossRef]
- Galal, K.; Ghobarah, A. Flexural and shear hysteretic behaviour of reinforced concrete columns with variable axial load. Eng. Struct. 2003, 25, 1353–1367. [Google Scholar] [CrossRef]
- Okamura, H.; Higai, T. Proposed design equation for shear strength of reinforced concrete beams without web rein-forcement. In Proceedings of the Japan Society of Civil Engineers; Japan Society of Civil Engineers: Tokyo, Japan, 1980; pp. 131–141. [Google Scholar]
- Hansapinyo, C.; Chaisomphob, T.; Maekawa, K.; Pimanmas, A. Experimental Investigation on Rectangular Reinforced Concrete Beam subjected to Bi-axial Shear. In Proceedings of the Eight Asia-Pacific on Structural Engineering and Construction; Nanyang Technological University: Singapore, 2001. [Google Scholar]
- Tinini, A.; Minelli, F.; Belletti, B.; Scolari, M. Biaxial shear in RC square beams: Experimental, numerical and analytical program. Eng. Struct. 2016, 126, 469–480. [Google Scholar] [CrossRef]
- Murad, Y.Z. Predictive model for bidirectional shear strength of reinforced concrete columns subjected to biaxial cyclic loading. Eng. Struct. 2021, 244, 112781. [Google Scholar] [CrossRef]
- Iqbal, M.F.; Liu, Q.-F.; Azim, I.; Zhu, X.; Yang, J.; Javed, M.F.; Rauf, M. Prediction of mechanical properties of green concrete incorporating waste foundry sand based on gene expression programming. J. Hazard. Mater. 2020, 384, 121322. [Google Scholar] [CrossRef] [PubMed]
- Oltean, M.; Grosan, C. A comparison of several linear genetic programming techniques. Complex Syst. 2003, 14, 285–314. [Google Scholar]
- Arabshahi, A.; Gharaei-Moghaddam, N.; Tavakkolizadeh, M. Development of applicable design models for concrete columns confined with aramid fiber reinforced polymer using Multi-Expression Programming. Structures 2020, 23, 225–244. [Google Scholar] [CrossRef]
- Iqbal, M.F.; Javed, M.F.; Rauf, M.; Azim, I.; Ashraf, M.; Yang, J.; Liu, Q.-F. Sustainable utilization of foundry waste: Forecasting mechanical properties of foundry sand based concrete using multi-expression programming. Sci. Total Environ. 2021, 780, 146524. [Google Scholar] [CrossRef] [PubMed]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; The MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Jalal, F.E.; Xu, Y.; Iqbal, M.; Jamhiri, B.; Javed, M.F. Predicting the compaction characteristics of expansive soils using two genetic programming-based algorithms. Transp. Geotech. 2021, 30, 100608. [Google Scholar] [CrossRef]
- Oltean, M.; Dumitrescu, D. Multi Expression Programming. 2002. Available online: https://www.researchgate.net/publication/2918165_Multi_Expression_Programming (accessed on 5 October 2021).
- Alavi, A.H.; Gandomi, A.H.; Sahab, M.G.; Gandomi, M. Multi expression programming: A new approach to formulation of soil classification. Eng. Comput. 2010, 26, 111–118. [Google Scholar] [CrossRef]
- Aho Alfred, V.; Ravi, S.; Ullman Jeffrey, D. Compilers, Principles, Techniques; Addison Wesley: Boston, MA, USA, 1986; Volume 7, p. 9. [Google Scholar]
- Sharifi, S.; Abrishami, S.; Gandomi, A.H. Consolidation assessment using Multi Expression Programming. Appl. Soft Comput. 2020, 86, 105842. [Google Scholar] [CrossRef]
- Khan, M.A.; Aslam, F.; Javed, M.F.; Alabduljabbar, H.; Deifalla, A.F. New prediction models for the compressive strength and dry-thermal conductivity of bio-composites using novel machine learning algorithms. J. Clean. Prod. 2022, 350, 131364. [Google Scholar] [CrossRef]
- Sayyaadi, H. Modeling, Assessment, and Optimization of Energy Systems; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Azim, I.; Yang, J.; Javed, M.F.; Iqbal, M.F.; Mahmood, Z.; Wang, F.; Liu, Q.-F. Prediction model for compressive arch action capacity of RC frame structures under column removal scenario using gene expression programming. Structures 2020, 25, 212–228. [Google Scholar] [CrossRef]
- Azim, I.; Yang, J.; Iqbal, M.F.; Mahmood, Z.; Javed, M.F.; Wang, F.; Liu, Q.-F. Prediction of Catenary Action Capacity of RC Beam-Column Substructures under a Missing Column Scenario Using Evolutionary Algorithm. KSCE J. Civ. Eng. 2021, 25, 891–905. [Google Scholar] [CrossRef]
- Azim, I.; Yang, J.; Iqbal, M.F.; Javed, M.F.; Nazar, S.; Wang, F.; Liu, Q.-F. Semi-analytical model for compressive arch action capacity of RC frame structures. Structures 2020, 27, 1231–1245. [Google Scholar] [CrossRef]
- Liu, Q.-F.; Iqbal, M.F.; Yang, J.; Lu, X.-Y.; Zhang, P.; Rauf, M. Prediction of chloride diffusivity in concrete using artificial neural network: Modelling and performance evaluation. Constr. Build. Mater. 2021, 268, 121082. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Behnood, A.; Arashpour, M. Predicting the compressive strength of normal and High-Performance Concretes using ANN and ANFIS hybridized with Grey Wolf Optimizer. Constr. Build. Mater. 2020, 232, 117266. [Google Scholar] [CrossRef]
- Morcous, G.; Lounis, Z. Prediction of Onset of Corrosion in Concrete Bridge Decks Using Neural Networks and Case-Based Reasoning. Comput. Aided Civ. Infrastruct. Eng. 2005, 20, 108–117. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.I. Mix proportions for HPC incorporating multi-cementitious composites using artificial neural networks. Constr. Build. Mater. 2012, 28, 14–20. [Google Scholar] [CrossRef]
- Bilim, C.; Atis, C.; Tanyildizi, H.; Karahan, O. Predicting the compressive strength of ground granulated blast furnace slag concrete using artificial neural network. Adv. Eng. Softw. 2009, 40, 334–340. [Google Scholar] [CrossRef]
- Murad, Y.; Imam, R.; Abu Hajar, H.; Habeh, D.; Hammad, A.; Shawash, Z. Predictive compressive strength models for green concrete. Int. J. Struct. Integr. 2019, 11, 169–184. [Google Scholar] [CrossRef]
- Gandomi, A.; Faramarzifar, A.; Rezaee, P.G.; Asghari, A.; Talatahari, S. New design equations for elastic modulus of concrete using multi expression programming. J. Civ. Eng. Manag. 2015, 21, 761–774. [Google Scholar] [CrossRef] [Green Version]
- Gandomi, A.H.; Alavi, A.H.; Yun, G.J. Formulation of uplift capacity of suction caissons using multi expression programming. KSCE J. Civ. Eng. 2011, 15, 363–373. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Güllü, H.; Canakci, H.; Özbakır, L. Prediction of compressive and tensile strength of limestone via genetic programming. Expert Syst. Appl. 2008, 35, 111–123. [Google Scholar] [CrossRef]
- Alavi, A.H.; Mollahasani, A.; Gandomi, A.H.; Bazaz, J.B. Formulation of secant and reloading soil deformation moduli using multi expression programming. Eng. Comput. 2012, 29, 173–197. [Google Scholar] [CrossRef]
- Jalal, F.E.; Xu, Y.; Iqbal, M.; Javed, M.F.; Jamhiri, B. Predictive modeling of swell-strength of expansive soils using artificial intelligence approaches: ANN, ANFIS and GEP. J. Environ. Manag. 2021, 289, 112420. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, M.; Onyelowe, K.C.; Jalal, F.E. Smart computing models of California bearing ratio, unconfined compressive strength, and resistance value of activated ash-modified soft clay soil with adaptive neuro-fuzzy inference system and ensemble random forest regression techniques. Multiscale Multidiscip. Model. Exp. Des. 2021, 4, 207–225. [Google Scholar] [CrossRef]
- Gandomi, A.; Tabatabaei, S.M.; Moradian, M.H.; Radfar, A.; Alavi, A.H. A new prediction model for the load capacity of castellated steel beams. J. Constr. Steel Res. 2011, 67, 1096–1105. [Google Scholar] [CrossRef]
- Iqbal, M.; Zhao, Q.; Zhang, D.; Jalal, F.E.; Jamal, A. Evaluation of tensile strength degradation of GFRP rebars in harsh alkaline conditions using non-linear genetic-based models. Mater. Struct. 2021, 54, 190. [Google Scholar] [CrossRef]
- Despotovic, M.; Nedić, V.; Despotović, D.; Cvetanović, S. Evaluation of empirical models for predicting monthly mean horizontal diffuse solar radiation. Renew. Sustain. Energy Rev. 2016, 56, 246–260. [Google Scholar] [CrossRef]
- Frank, I.; Todeschini, R. The Data Analysis Handbook; Elsevier: Amsterdam, The Netherlands, 1994; Volume 14. [Google Scholar]
- ACI 318-11. Building Code Requirements for Structural Concrete and Commentary, PCA Notes on ACI 318-11; with Design Applications; ACI International: Farmington Hills, MI, USA, 2011. [Google Scholar]
- Zhang, Q.; Barri, K.; Jiao, P.; Salehi, H.; Alavi, A.H. Genetic programming in civil engineering: Advent, applications and future trends. Artif. Intell. Rev. 2021, 54, 1863–1885. [Google Scholar] [CrossRef]
- Yazoghli-Marzouk, O.; Vulcano-Greullet, N.; Cantegrit, L.; Friteyre, L.; Jullien, A. Recycling foundry sand in road construction–field assessment. Constr. Build. Mater. 2014, 61, 69–78. [Google Scholar] [CrossRef]
- Haitham, A.-T. Effect of Transverse Reinforcement on the Axial Compressive Strength of Reinforced Concrete Columns. Al Qadisiyah J. Eng. Sci. 2016, 9, 119–134. [Google Scholar]
- Woods, C.; Matamoros, A.B. Effect of longitudinal reinforcement ratio on the failure mechanism of R/C columns most vulnerable to collapse. In Proceedings of the 9th US National and 10th Canadian Conference on Earthquake Engineering, Toronto, ON, Canada, 25–29 July 2010. [Google Scholar]

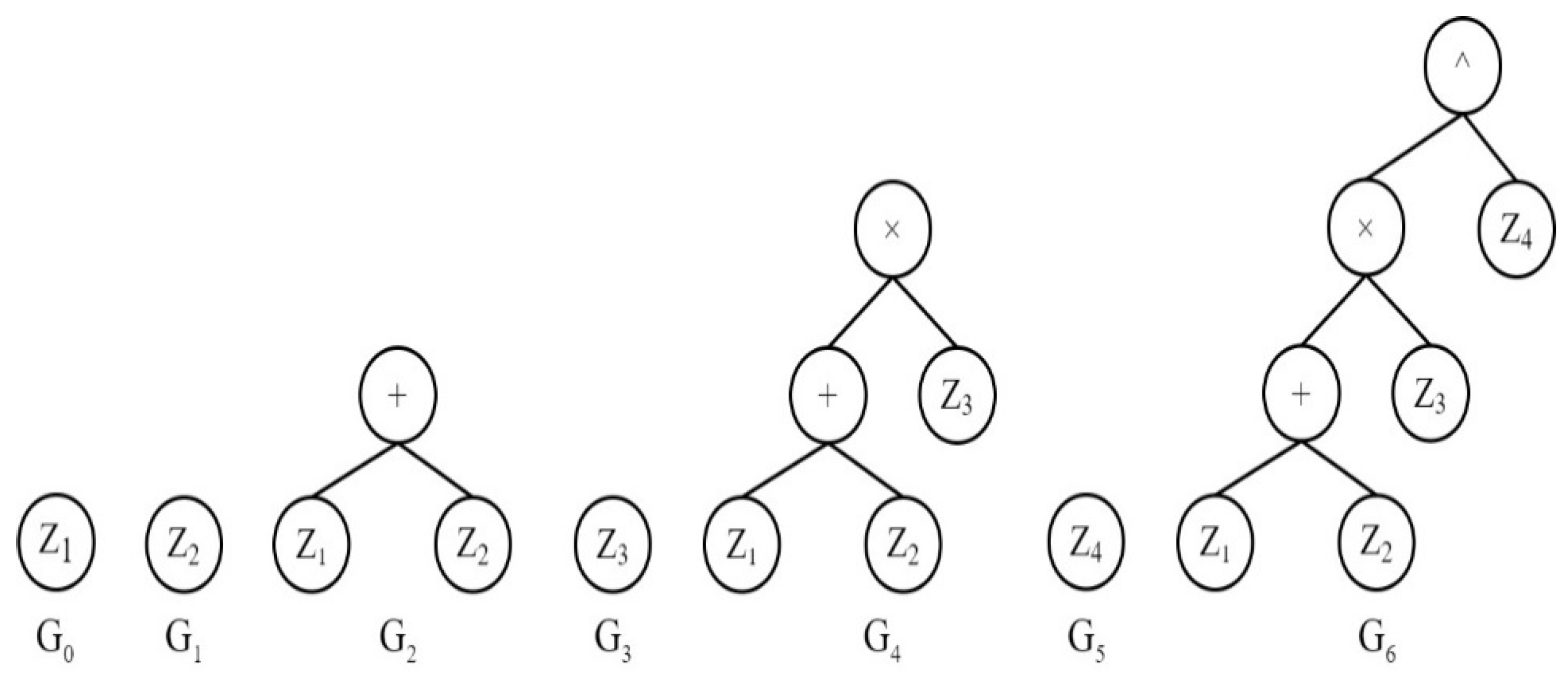
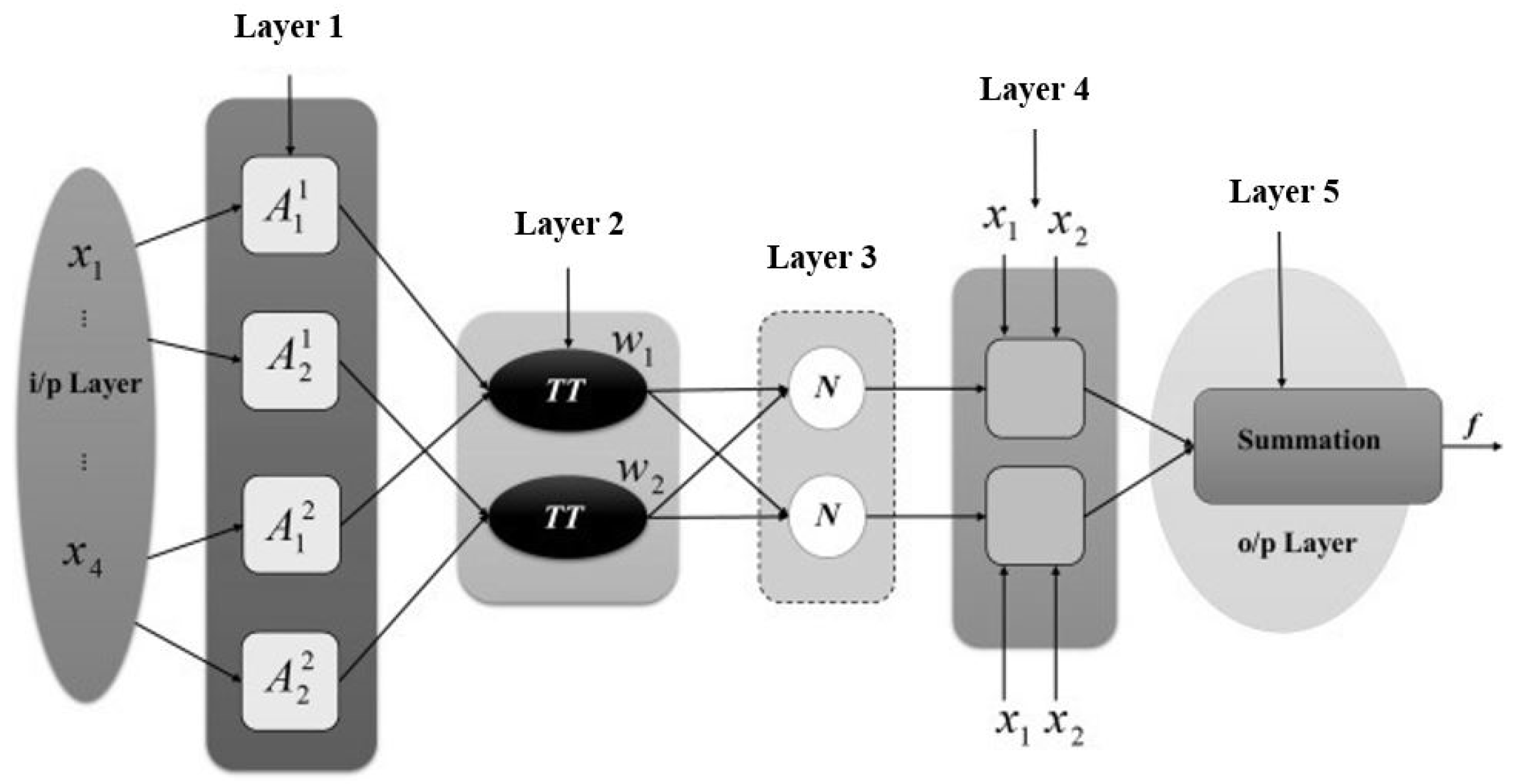
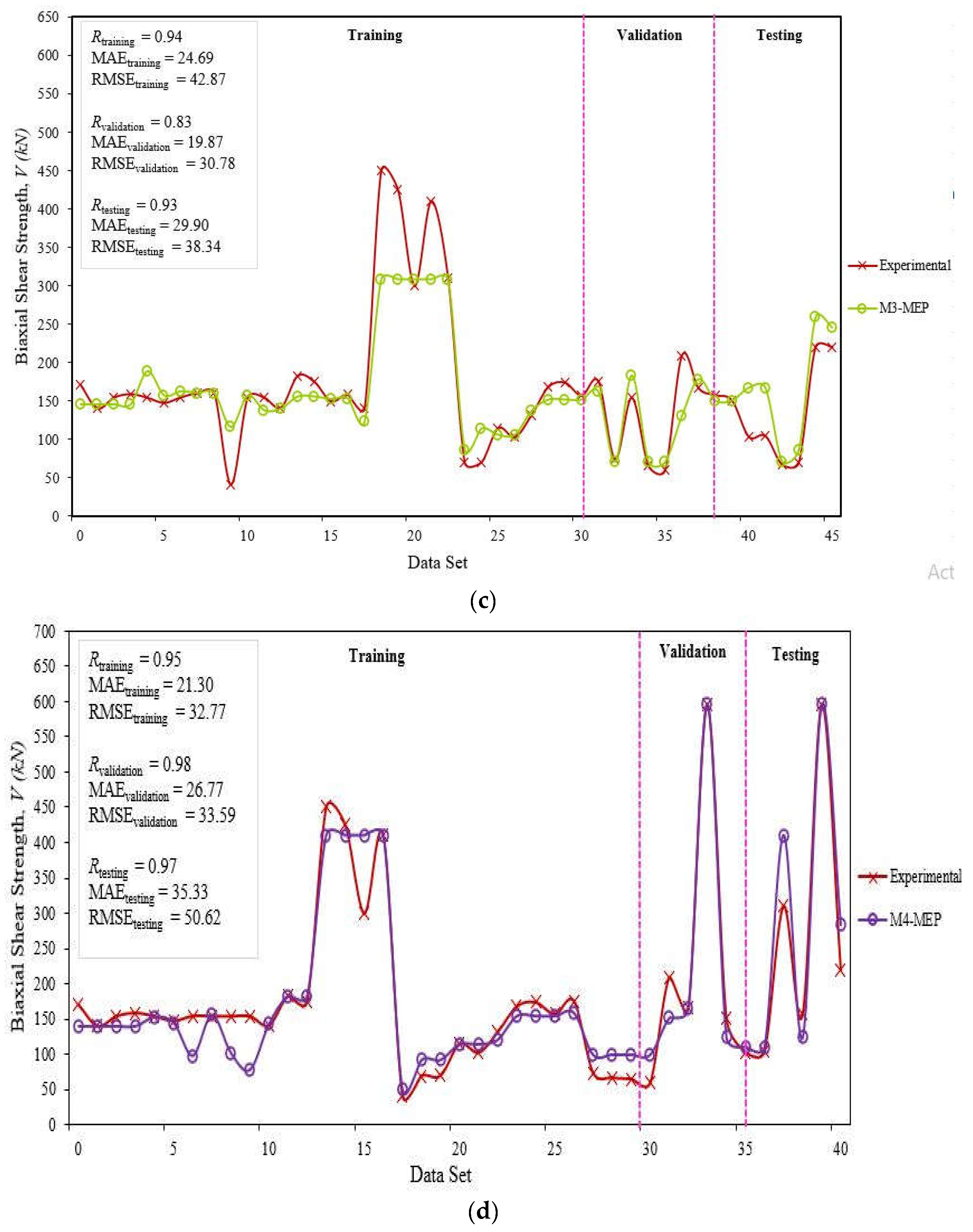



| Parameters | Settings | |||
|---|---|---|---|---|
| M1-MEP | M2-MEP | M3-MEP | M4-MEP | |
| Number of sub-population | 30 | 30 | 30 | 30 |
| Size of subpopulation | 200 | 200 | 200 | 200 |
| Code length | 45 | 35 | 30 | 35 |
| Crossover probability | 0.9 | 0.9 | 0.9 | 0.9 |
| Mathematical operators | +, −, ×, ÷, √ | +, −, ×, ÷, √ | +, −, ×, ÷, √ | +, −, ×, ÷, √ |
| Mutation probability | 0.01 | 0.01 | 0.01 | 0.01 |
| Tournament size | 4 | 4 | 2 | 2 |
| Operators | 0.5 | 0.5 | 0.5 | 0.5 |
| Mutation probability | 0.5 | 0.5 | 0.5 | 0.5 |
| Number of generations | 1000 | 2000 | 5000 | 3000 |
| Parameters | Settings | |||
|---|---|---|---|---|
| M1-ANFIS | M2-ANFIS | M3-ANFIS | M4-ANFIS | |
| Linear parameters | 729 | 243 | 243 | 729 |
| Non-linear parameters | 54 | 45 | 45 | 54 |
| Fuzzy rules | 729 | 243 | 243 | 729 |
| Nodes | 1503 | 524 | 524 | 1503 |
| Epochs | 50 | 50 | 50 | 50 |
| Error goal | 0 | 0 | 0 | 0 |
| Type of MF | Trimf | Trimf | Trimf | Trimf |
| Structure of fuzzy | Sugeno | Sugeno | Sugeno | Sugeno |
| Type of FIS | Grid Partition | Grid Partition | Grid Partition | Grid Partition |
| Optimization technique | Backpropagation and least square | Backpropagation and least square | Backpropagation and least square | Backpropagation and least square |
| Type of output function | Linear | Linear | Linear | Linear |
| Parameter | Expression | Criteria |
|---|---|---|
| Correlation coefficient (R) | >0.8 [40] | |
| Mean absolute error (MAE) | Minimum [41] | |
| Root mean square error (RMSE) | Minimum | |
| Relative root mean square error (RRMSE) | 0–0.1 (Excellent) or 0.11–0.2 (Good) [42] | |
| <0.2 [34] | ||
| Objective function (OF) | Close to zero [25] |
| Parameter | (kN) | (mm) | (mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | 19.23 | 8.44 × 105 | 1.85 | 28.05 | 1.16 × 105 | 1.568 | 440.93 | 0.25 | 1493.86 |
| Standard Error | 0.694 | 8.02 × 104 | 0.070 | 0.693 | 6.77 × 103 | 0.115 | 10.82 | 0.03 | 79.38 |
| Median | 23 | 1.00 × 106 | 1.755 | 27 | 1.20 × 105 | 1.056 | 400.00 | 0.13 | 1700.00 |
| Mode | 23 | 1.00 × 106 | 2.06 | 38.2 | 9.00 × 104 | 2.547 | 400.00 | 0.11 | 1700.00 |
| Standard Deviation | 6.13 | 7.08 × 105 | 0.615 | 6.12 | 4.34 × 104 | 0.739 | 69.30 | 0.18 | 508.28 |
| Sample Variance | 37.60 | 5.02 × 1011 | 0.378 | 37.51 | 1.88 × 109 | 0.546 | 4801.83 | 0.03 | 258,343.76 |
| Kurtosis | −1.1036 | 1.30 × 101 | −0.556 | −0.572 | 5.57 | −1.312 | 0.45 | −0.58 | −0.69 |
| Skewness | −0.710 | 2.83 | 0.379 | 0.120 | 1.37 | 0.724 | 0.08 | 0.94 | −0.62 |
| Minimum | 8.85 | 1.00 × 105 | 0.7 | 15.92 | 4.00 × 104 | 0.848 | 276.00 | 0.09 | 570.00 |
| Maximum | 25.7 | 4.29 × 106 | 3.35 | 38.2 | 2.92 × 105 | 2.777 | 575.60 | 0.63 | 2438.40 |
| Parameter | (kN) | (mm) | (mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (MPa) | 1.00 | 0.22 | −0.32 | 0.21 | −0.11 | −0.30 | −0.07 | −0.20 | 0.03 |
| (kN) | 0.22 | 1.00 | 0.10 | 0.17 | 0.14 | 0.24 | 0.29 | −0.04 | 0.49 |
| (mm) | −0.32 | 0.10 | 1.00 | 0.16 | 0.76 | 0.05 | 0.51 | −0.28 | 0.36 |
| (mm) | 0.21 | 0.17 | 0.16 | 1.00 | 0.73 | −0.26 | −0.32 | −0.52 | 0.49 |
| (mm2) | −0.11 | 0.14 | 0.76 | 0.73 | 1.00 | −0.11 | 0.11 | −0.43 | 0.51 |
| (%) | −0.30 | 0.24 | 0.05 | −0.26 | −0.11 | 1.00 | 0.34 | 0.67 | −0.22 |
| (MPa) | −0.07 | 0.29 | 0.51 | −0.32 | 0.11 | 0.34 | 1.00 | 0.14 | 0.25 |
| (%) | −0.20 | −0.04 | −0.28 | −0.52 | −0.43 | 0.67 | 0.14 | 1.00 | −0.47 |
| (mm) | 0.03 | 0.49 | 0.36 | 0.49 | 0.51 | −0.22 | 0.25 | −0.47 | 1.00 |
| Model | Dataset | R | MAE | RMSE | RSE | RRMSE | ρ | OF |
|---|---|---|---|---|---|---|---|---|
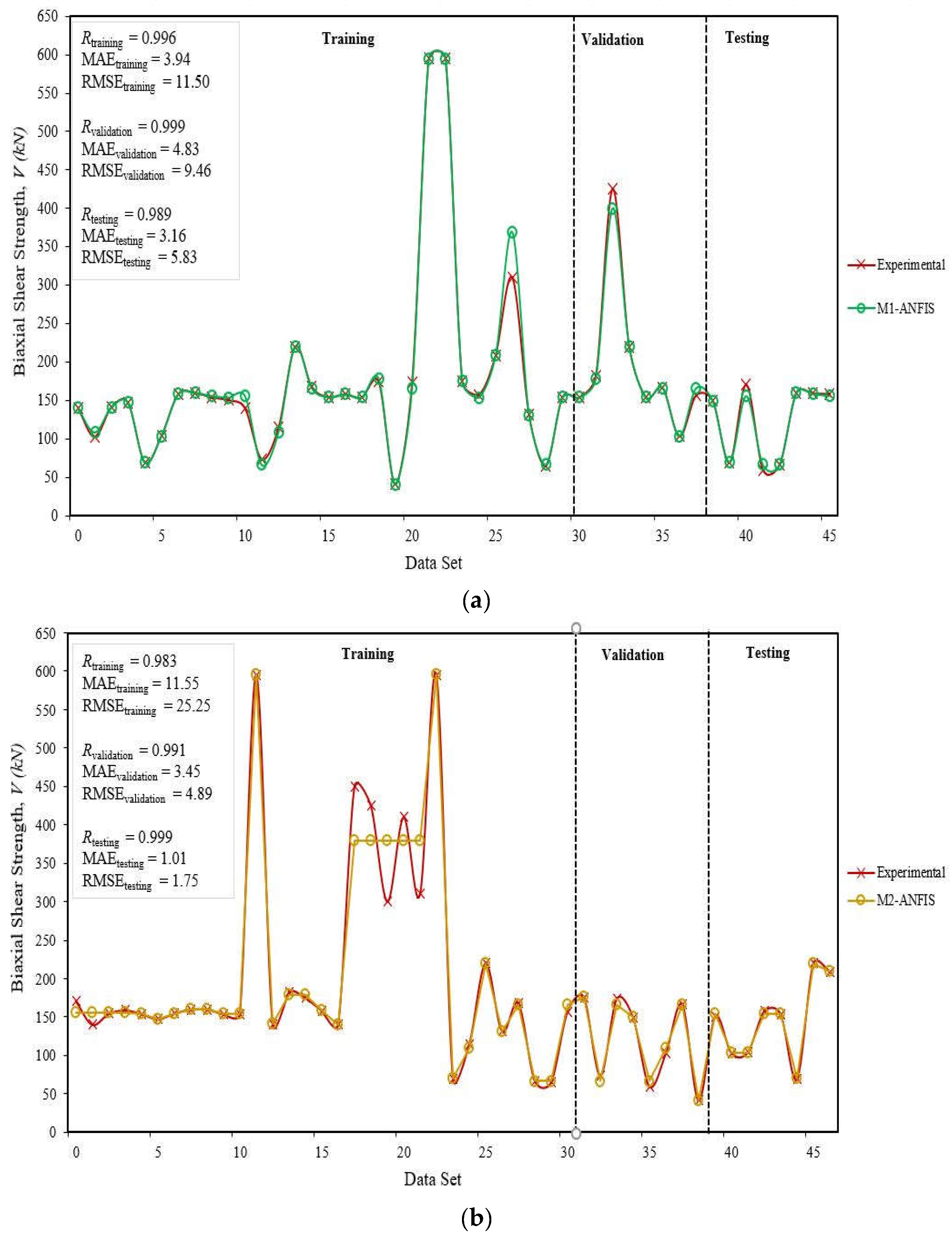
| M1-ANFIS | Training | 0.992 | 3.94 | 11.50 | 0.01 | 0.07 | 0.03 | 0.026 |
| Validation | 0.999 | 4.83 | 9.46 | 0.011 | 0.05 | 0.02 | ||
| Testing | 0.994 | 3.16 | 5.83 | 0.016 | 0.05 | 0.02 | ||
| M2-ANFIS | Training | 0.983 | 11.55 | 25.25 | 0.03 | 0.12 | 0.06 | 0.015 |
| Validation | 0.996 | 3.45 | 4.89 | 0.009 | 0.04 | 0.02 | ||
| Testing | 0.999 | 1.01 | 1.75 | 0.001 | 0.01 | 0.01 | ||
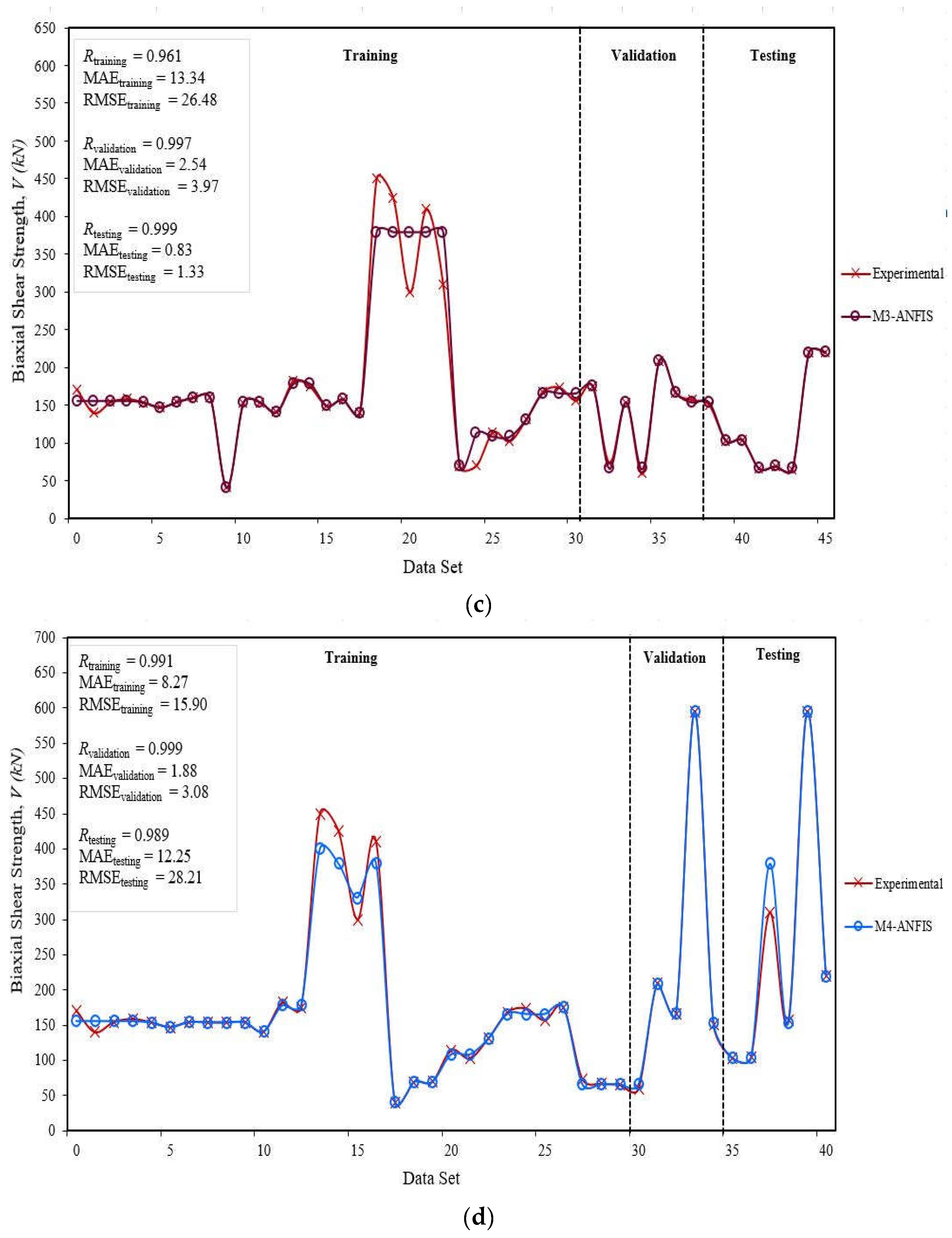
| M3-ANFIS | Training | 0.961 | 13.34 | 26.48 | 0.08 | 0.15 | 0.08 | 0.03 |
| Validation | 0.997 | 2.54 | 3.97 | 0.006 | 0.03 | 0.01 | ||
| Testing | 0.999 | 0.83 | 1.33 | 0.0005 | 0.01 | 0.01 | ||
| M4-ANFIS | Training | 0.991 | 8.27 | 15.90 | 0.03 | 0.09 | 0.05 | 0.04 |
| Validation | 0.999 | 1.88 | 3.08 | 0.0003 | 0.01 | 0.01 | ||
| Testing | 0.989 | 12.25 | 28.21 | 0.027 | 0.11 | 0.06 |
| Model | Dataset | R | MAE | RMSE | RSE | RRMSE | ρ | OF |
|---|---|---|---|---|---|---|---|---|
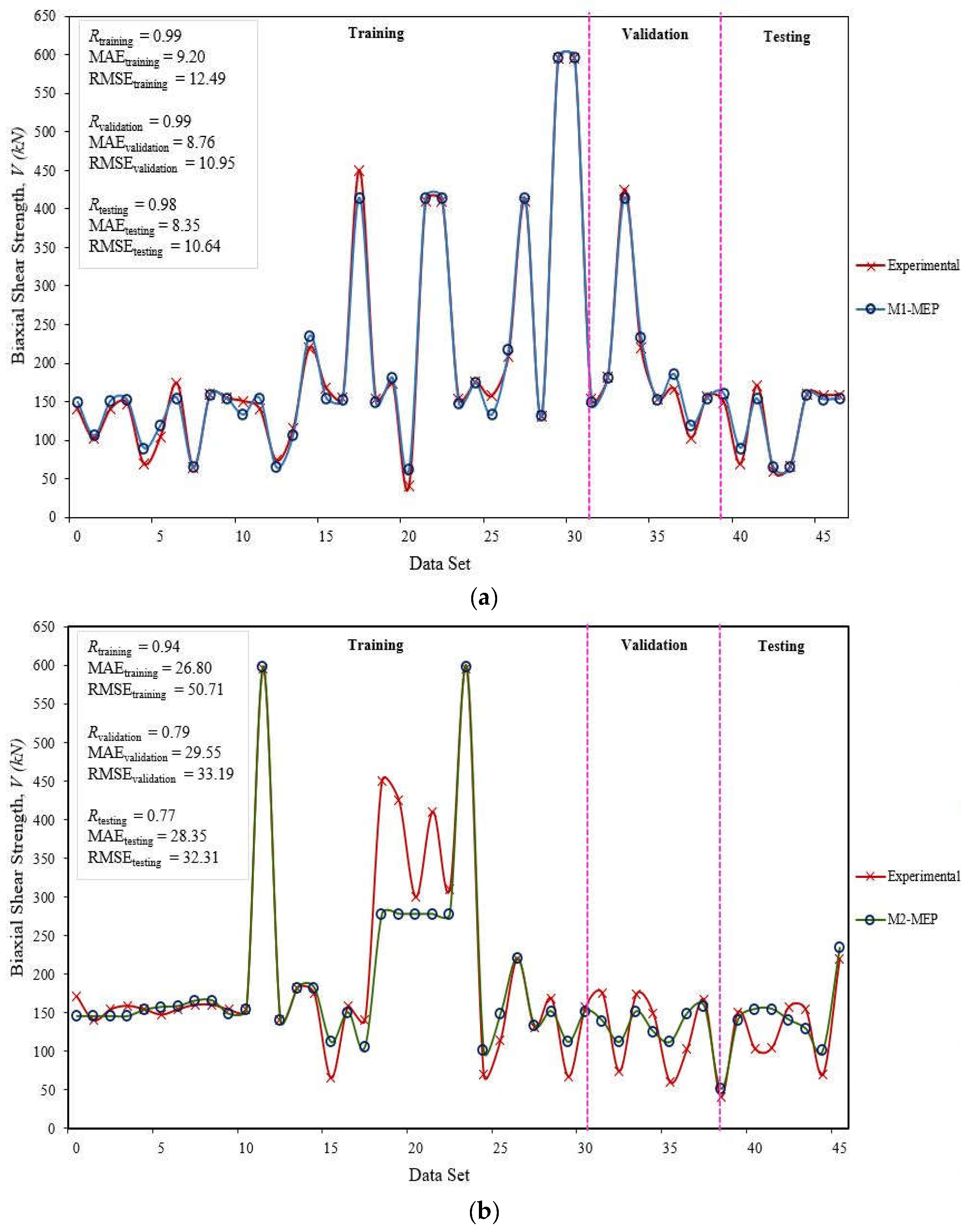
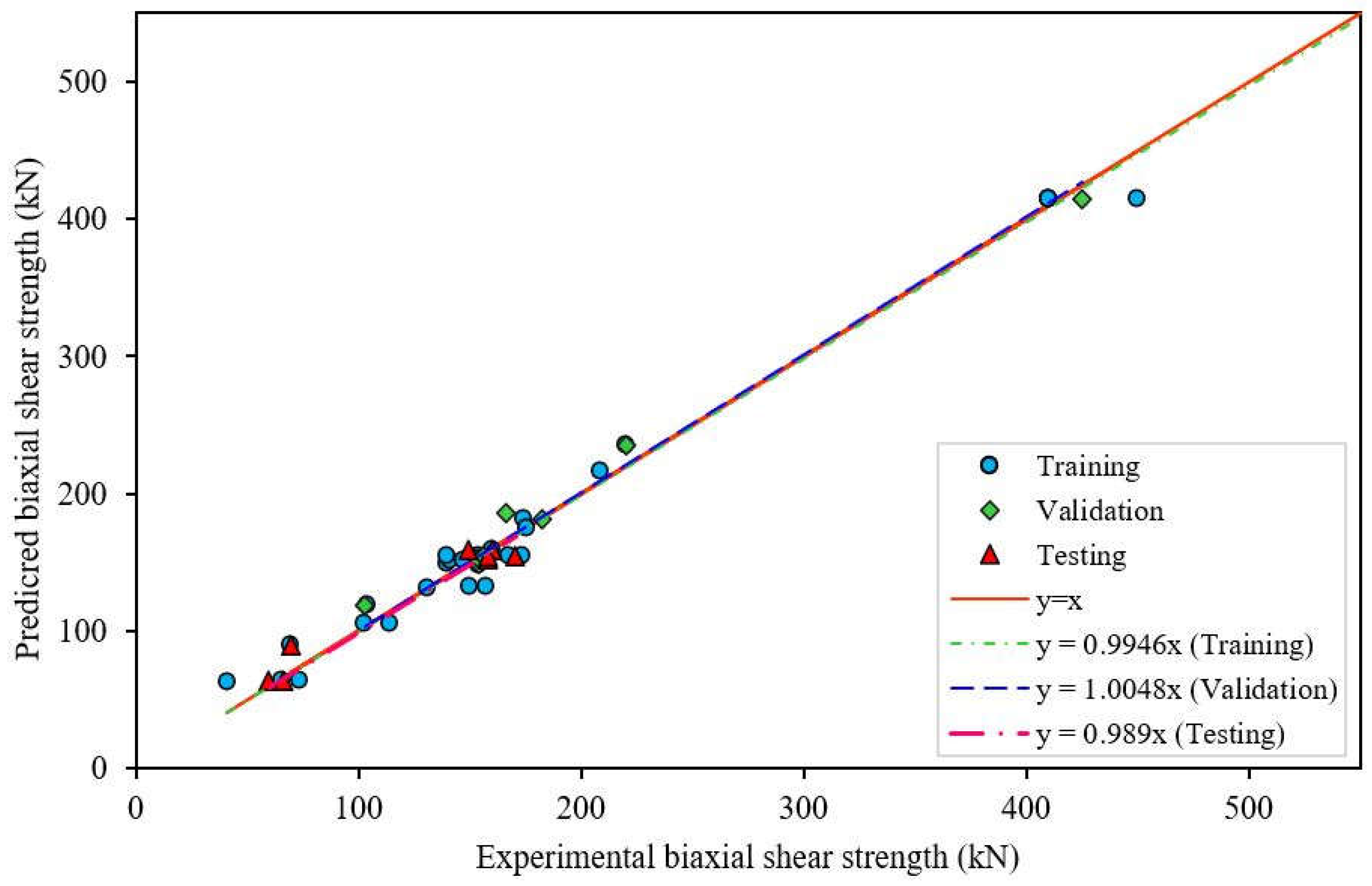
| Biaxial shear strength | Training | 0.993 | 9.20 | 12.49 | 0.01 | 0.06 | 0.03 | 0.059 |
| Validation | 0.995 | 8.76 | 10.95 | 0.014 | 0.06 | 0.03 | ||
| Testing | 0.977 | 8.35 | 10.64 | 0.054 | 0.09 | 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, Y.; Azim, I.; Rauf, M.; Iqbal, M.F.; Ge, X.; Ashraf, M.; Tariq, M.A.U.R.; Ng, A.W.M. Prediction of Bidirectional Shear Strength of Rectangular RC Columns Subjected to Multidirectional Earthquake Actions for Collapse Prevention. Sustainability 2022, 14, 6801. https://doi.org/10.3390/su14116801
Pang Y, Azim I, Rauf M, Iqbal MF, Ge X, Ashraf M, Tariq MAUR, Ng AWM. Prediction of Bidirectional Shear Strength of Rectangular RC Columns Subjected to Multidirectional Earthquake Actions for Collapse Prevention. Sustainability. 2022; 14(11):6801. https://doi.org/10.3390/su14116801
Chicago/Turabian StylePang, Yingbo, Iftikhar Azim, Momina Rauf, Muhammad Farjad Iqbal, Xinguang Ge, Muhammad Ashraf, Muhammad Atiq Ur Rahman Tariq, and Anne W. M. Ng. 2022. "Prediction of Bidirectional Shear Strength of Rectangular RC Columns Subjected to Multidirectional Earthquake Actions for Collapse Prevention" Sustainability 14, no. 11: 6801. https://doi.org/10.3390/su14116801
APA StylePang, Y., Azim, I., Rauf, M., Iqbal, M. F., Ge, X., Ashraf, M., Tariq, M. A. U. R., & Ng, A. W. M. (2022). Prediction of Bidirectional Shear Strength of Rectangular RC Columns Subjected to Multidirectional Earthquake Actions for Collapse Prevention. Sustainability, 14(11), 6801. https://doi.org/10.3390/su14116801









