Abstract
The paper presents a method of application of an ANN (Artificial Neural Network) to predict the permeability coefficient k in sandy soils: FSa, MSa, CSa. To develop an ANN the results of permeability coefficients from pumping and consolidation tests were applied. The proposed ANN with an architecture 6-8-1 predicts the value of permeability coefficient k based on the following parameters: soil type, relative density ID, void ratio e and effective soil diameter d10. The mean relative error and single maximum value of the relative error for the proposed ANN are following: Mean RE = ±4%, Max RE = 7.59%. The use of the ANN to predict the soil permeability coefficient allows the reduction of the costs and time needed to conduct laboratory or field tests to determine this parameter.
1. Introduction
Due to the intensive development of the construction industry, areas with difficult subsoil conditions or high groundwater levels are more and more often built on. Therefore, before starting the preparation of an investment project, it is necessary to thoroughly identify the subsoil, i.e., to determine, apart from subsoil strength parameters, the permeability coefficient k. The parameter k describes the soil’s hydraulic permeability, i.e., the filtration ability of water through the subsoil. The permeability coefficient k in the subsoil depends on the following properties: type of soil, grain size and shape, porosity, soil structure and water viscosity [1]. Typical values of the parameter k in mineral soils are in the range 1 × 10−2 ÷ 1 × 10−10 m·s−1.
The permeability coefficient k is determined using many methods, ranging from estimations based on uncomplicated calculations to complex laboratory and field tests. Choosing the method of determining the parameter k depends mainly on the type of soil. Eurocode 7 distinguishes four methods of the evaluation of the parameter k: laboratory tests, field tests, estimation based on oedometer test and empirical correlations. Selection of the method for determining the parameter k should be preceded by a thorough analysis of the properties and homogeneity of the tested soil, as well as of the factors that may affect the tested parameter [2,3].
Permeability coefficient k in soils is often estimated based on empirical correlations, in which the content of grain size (most often the effective soil diameter d10), porosity and specific surface area are used [4,5]. However, existing empirical formulas ignore the impact of soil structure, permeability anisotropy and the soil grain shape. Research indicates that the parameter k of the same material may differs significantly if it is estimated based on different empirical formulas [6,7]. Therefore, it is crucial to determine the exact empirical formulas and the correctness of the values of the parameters used, which may affect the calculation results. It is also important that the empirical formulas depend on a greater number of parameters of the analysed soil and the exact determination of the parameters used in empirical formulas.
The most accurate way to evaluate the permeability coefficient k are field tests. In field tests the heterogeneity of the subsoil structure and hydraulic permeability anisotropy are best reflected. Obviously, the accuracy of the determined parameter depends on the correctness of the performed tests. The most common field test is pumping test. The main goal of the pumping test is to obtain, by pumping water from the well (piezometer), a hydrodynamic reaction of the subsoil, which enables the identification of the filtration parameters of the soil and the conditions of its supply [8,9,10]. The pumping test is most often used to estimate the parameter k in well-permeable soils, mainly sands. In soils with less permeability (k < 10−6 m·s−1), the BAT probe test is used. This test involves the connection of a piezometer to the probe measuring part with a glass water container in which pressure changes are registered. Parameter k is determined on the basis of pressure changes in a function of time. Depending on the degree of filling the pores with water in the soil, the test may be performed under the conditions of water supply (inflow) or outflow from the probe tip. In the laboratory, parameter k is determined using constant or variable gradient methods. Constant-gradient methods, including the Rowe chamber and Trautwein system and ZW-K2 apparatus, are most often used to evaluate the parameter k in well-permeable soils [11]. Variable-gradient methods, including the flow-pump method, Kamienski tube method and modified oedometer with a burette, are used to evaluate the parameter k in low-permeable soils. Of the above-mentioned variable-gradient methods, the flow-pump method is the most commonly used. In this method, the differences in pressure at the top and bottom of the soil sample are measured after establishing a constant water flow velocity in the test sample. The test is continued until the pressure stabilizes in the soil sample.
ANNs (Artificial Neural Networks) are a tool used in science for modelling complex phenomena [12,13,14,15]. In recent years, they have gained more and more popularity and are widely used for statistical analysis [16]. In recent years they have been successfully applied in civil engineering [17,18,19,20]. Waszczyszyn [21,22] used neural networks in the analysis of hybrid computational systems, regression problems, development of Recurent Cascade Neural Networks (RCNNs), Binarized Neural Networks (BNNs) and Principal Component Analysis. Rafiq et al. [23] applied three types of neural networks in engineering: multi-layer perceptron (MLP), normalized RBF (NRBF) and radial basis network (RBF). Research on the use of ANNs in construction, in particular in relation to the subsoil, was presented inter alia by: Shahin et al. [24,25], Dihoru et al. [26], Pichler et al. [27], Sulewska [28], Tian et al. [29], Zhou et al. [30], Ellis et al. [31], Sidarta and Ghaboussi [32], Penumadu and Zhao [33], Basheer [34], Najjar and Huang [35], Fu et al. [36], Lee et al. [37], Das and Basudhar [38], Byeon et al. [39], Wrzesinski [40], Wrzesinski et al. [41], Lin et al. [42,43], Liu et al. [44]. So far, many applications of ANNs in construction have been reported in the literature; however, there are no reports on the using of ANNs to evaluate the parameter k in non-cohesive soils.
The paper presents the using ANN (Artificial Neural Network) to predict the permeability coefficient k in sandy soils. In order to propose an ANN, a series of laboratory and field tests to determine parameter k were carried out and the basic index properties of tested soils were determined.
2. Materials and Methods
Research was performed on sands characterized by different grain size. The study started with the selection of 50 test sites in the field. The criterion for selecting the test sites was the subsoil with homogeneous permeable sandy soils and the possibility of performing field tests and collecting samples for laboratory tests. The conducted research to determine permeability coefficients was divided into field and laboratory tests. The field studies included pumping tests, while the laboratory studies included consolidometer tests and tests to determine basic index properties. A total of 50 field tests and 120 laboratory tests were performed, in which the permeability coefficients k were determined.
Pumping tests to determine permeability coefficients k were performed in accordance with the standard method [45,46,47]. In carried research 1 well and 2 piezometers were installed for each test. The pumping test started with the installation of a well in the subsoil. The diameters of all installed wells were 400 mm and they were installed at a depth of 1.10 ÷ 2.00 m. The installation depth depended on the test site. Then, 2 piezometers were installed in the subsoil. The first piezometer was installed at a distance of 2.0 m, the second at a distance of 4 or 5 m from the edge of the well. PVC wells and piezometers were used. The pumping tests were carried out by pumping water and simultaneous measurements of changes in the water level inside installed piezometers. The tests were repeated two or three times, at the test sites in particular, to verify the results. Differences in the permeability coefficients k did not exceed 5% (at the same test site). The water level in the piezometers was measured 28–30 days after the end of the studies. Parameters k in pumping tests were determined in accordance with the following formula:
where Q—water flow, z2—water level in piezometer 2, z1—water level in piezometer 1, x2—distance between well and piezometer 2 and x1—distance between well and piezometer 1.
A typical scheme of the performed pumping tests is presented in Figure 1.
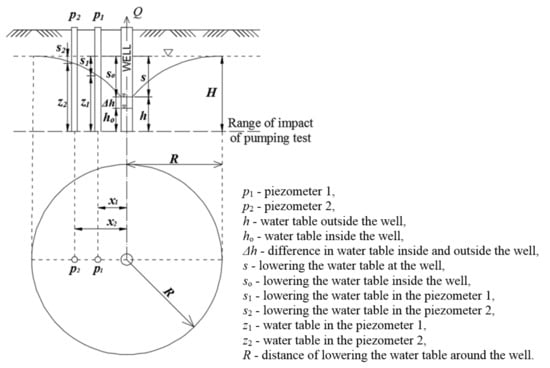
Figure 1.
Pumping test system scheme.
Additionally, cone penetrometer tests (CPT) and electrical resistivity measurements were performed before pumping tests. Laboratory tests were performed on soil samples collected from the test sites. In laboratory the following tests were performed: tests on grain size distribution of soil, on the permeability coefficient in consolidometer and tests using a scanning electron microscope.
Grain size distribution of tested soils were carried out in accordance with EN ISO 14688-1: 2002 and EN ISO 14688-2: 2004 [48,49]. Based on these tests, the effective soil diameter d10 was evaluated. The results of the grain size distribution tests indicate that the analysed soils, according to EN ISO 14688-2: 2006 and EN ISO 14688-2: 2006-Ap2: 2012, are FSa-Fine Sand, MSa-Middle Sand and CSa-Coarse Sand. According to the EN ISO 14688-2: 2006 standard, the tested sands were characterized by a gravel fraction of 0 ÷ 19%, sand fraction of 80 ÷ 98%, silt fraction of 0 ÷ 12% and clay fraction of 0 ÷ 2%.
Relative densities ID of tested soils were determined using cone penetrometer tests (CPT). Void ratios e were determined using electrical resistivity measurement. After connecting the electrodes to the power source and the gauge, several dozen measurements were made with a frequency of 12 s for the same place. The arithmetic mean of the measurement results was taken as the final result of the electrical resistance.
For the analysed soils, tests of the structure and chemical composition were carried out using a scanning electron microscope (XL Series, FEG Quanta 250 model) equipped with a chemical composition analysis system based on EDS X-ray energy dispersion.
Permeability coefficient tests to determine parameters k were performed in a laboratory with the use of consolidometer (Figure 2). The tests started with the compaction of soil in the Proctor apparatus. The diameters of compacted samples were 150 mm and their heights were 60 mm. Soil samples were compacted until the values of the relative density ID determined in the field studies using the cone penetrometer tests (CPT) were reached [50,51]. The determination of the permeability coefficient was based on the analysis of the consolidation process in the uniaxial state of strain. For this purpose, consolidometer tests were performed using the flow pump method for soil saturation. Tests were performed with a continuous inflow of water at constant gradients of 0.50. Based on the obtained characteristics, the permeability coefficients k were determined by the Taylor method. The values of the parameter k for particular soils obtained with the same gradients did not differ from each other by more than 5%.

Figure 2.
Consolidometer used in tests.
The grain size distribution, relative density ID, void ratio e and effective soil diameter d10 of tested soils can be seen in Table 1.

Table 1.
Grain size distribution, relative densities, void ratios and effective soil diameters d10 of soils.
3. Results
Performed research allowed the determination of the parameters k of tested soils using two methods: the pumping test and the consolidometer test. The parameters k, evaluated based on performed tests, are presented in Table 2.

Table 2.
Permeability coefficients k, evaluated based on pumping and consolidometer tests.
On the basis of the conducted research, it can be stated that similar values of the permeability coefficient k were obtained in field and laboratory tests for soils from the same test site. The influence of the relative density ID on the permeability coefficients k is significant in the tested soils. Higher values of permeability coefficients k were in soils characterized by a lower relative density ID, higher void ratio e and lower value of effective soil diameter d10.
The tests carried out using the scanning electron microscope showed that the tested non-cohesive soils have different grain shapes, even if the sieve analysis shows a similar content of individual fractions and chemical composition. Sample SEM photos showing the structure and chemical composition spectra for selected sample of fine sand (FSa), characterized by similar relative density ID from two test sites (wells no. 1 and 6), are presented in Figure 3.
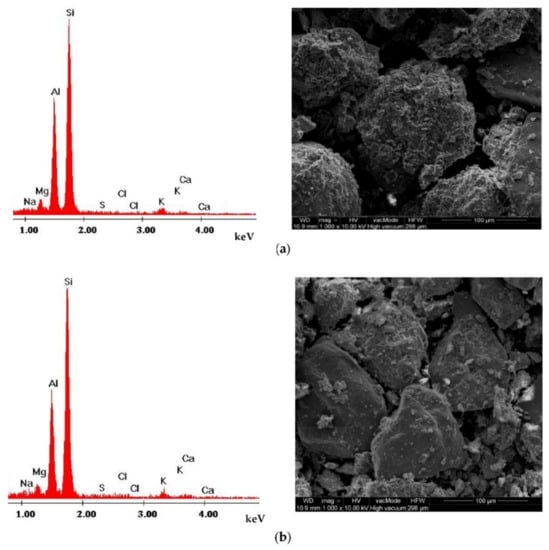
Figure 3.
Chemical composition spectra and sample SEM photos showing the structure for FSa, characterized by similar relative density ID from two test sites (wells no. 1 and 6): (a) FSa from well no. 1, (b) FSa from well no. 6.
The conducted research shows that the shape of the soil grains and arrangement of grains has an impact on the parameter k. The performed tests confirmed that irregularly shaped soil grains hold more water in the micro-cavities in comparison with grains with more regular shapes. The differences in parameter k are significant for the same sand characterized by similar relative density ID, void ratio e and the effective soil diameter d10. For instance, the difference in parameter k is two-fold in FSa between wells no. 1 and 6. The impact of the analysed parameters on the parameter k is the highest in fine sands (FSa).
4. ANN (Artificial Neural Network) Analysis
4.1. Architecture of ANN
The class of ANNs used in the presented research is that of multilayer perceptrons (MLPs) with one hidden layer. The architecture of the ANNs N-H-M type is defined by: N—number of nodes in the input layer X1–XN, H—number of nodes in the hidden layer, M = Y—number of nodes in the output layer.
ANNs were developed in accordance with the criterion of minimization of the error function. The criterion was the sum of squares of differences (SOS) evaluated using the equation:
where P—number of cases of set P, di—known values of the tests, yi—predicted values using ANN.
Errors measures were separately calculated for subsets: training Tr, testing T and validation V. The assessment of the ANN’s predictive quality took into account the value of the error measures in the test subset T. The selected error measures for ANNs were determined using the following formulas:
- -
- Relative error for individual cases:
- -
- Determination coefficient R2:
- -
- Mean absolute error:
- -
- Root mean squared error:
where di—measured value, yi—predicted value by ANN, —measured mean value in subset.
4.2. Data Sets, Training and Testing the ANN
In the performed ANN analysis, two data sets were used: set A and set B. Set A was obtained in field and laboratory tests and consisted of nA = 50 cases. Set A was described by five variables: X1 = soil type Є {FSa; MSa, CSa}; X2 = relative density ID Є {0.22 ÷ 0.92}; X3 = void ratio e Є {0.405 ÷ 0.728%}; and X4 = effective soil diameter d10 Є {0.04 ÷ 0.63} as well as Y = permeability coefficient k (Table 1). Variable X1 was treated as quality variable “one from N” type and required the use of many input neurons because three soil types were used. Set B consisted of data obtained in consolidometer tests and included nB = 120 cases. Set B was described by independent variables X1–X4, and dependent variable Y = k. The development and training of the ANN was carried out with the use of set B. The selected ANN was used to predict permeability coefficient k on the basis of new data from field tests (set A).
Set B was randomly assigned to 60, 30 and 30 laboratory test results of the subsets: training Tr, testing T, and validation V, respectively. Subset testing T was used to periodically check the generalizability acquired by the ANN, while subset validation V was used for the final evaluation of the trained ANN.
Predictive quality of the neural regression model was estimated based on performed error analysis. Errors were determined in subset training Tr, testing T and validation V. ANNs were optimized in terms of the training method, the number of neurons in the hidden layer, the activation function of neurons in the hidden layer and the output layer. A Conjugate gradient (CG) and early stopping methods were used to train the network. The Conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-definite, while the early stopping method is a form of regularization used to avoid overfitting when training a learner with an iterative method, such as gradient descent. Such methods update the learner so as to make it better fit the training data with each iteration. The training was finished after 28 training cycles. ANNs with the best predictive quality were evaluated on the basis of the lowest values of root mean squared errors RMS, the highest values of determination coefficient R2 and the lowest mean values of relative errors RE [52].
The performed neural network analysis allows the selection of ANN 6-8-1 (6 input neurons, 8 neurons in one hidden layer, 1 output neuron), which best predicts the parameter k. The selected ANN is presented in Figure 4. Activation functions were identified. For the hidden neurons, this was a tanh sigmoid curve, and for the output neuron, this was a logistic function. The errors measures (RMS, MAE, R2) for the developed ANN 6-8-1, in particular, and the subsets training Tr, testing T and validation V of set B are shown in Table 3. Prediction mean relative error Mean RE of the selected ANN 6-8-1 was a maximum of about ±4% in all subsets of data set B.
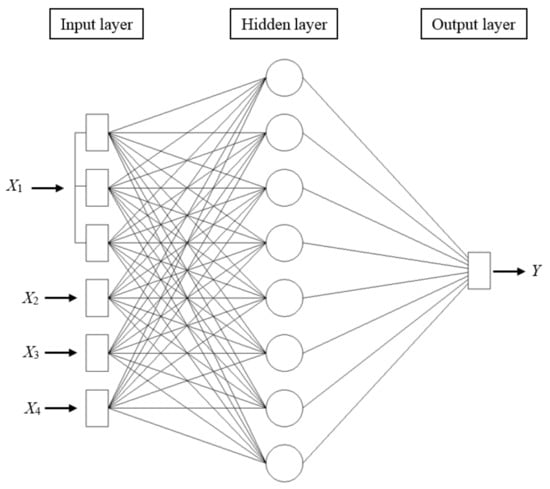
Figure 4.
Architecture of the developed ANN 6-8-1.

Table 3.
Errors measures for ANN 6-8-1 in the subsets training Tr, testing T, validation V of set B.
4.3. ANN Estimation
The proposed ANN 6-8-1 was tested by applying it to predict the permeability coefficient k on the basis of field data from set A. Variables X1, X2, X3 and X4 (Table 1) were introduced and Y = k values were estimated using the proposed ANN. Measured values of parameter k determined in pumping tests and values of parameter k predicted using developed ANN 6-8-1 are presented in Table 4. The value of the maximum single relative error Max RE was equal to 7.59%.

Table 4.
Measured values of permeability coefficient k from field tests and predicted values of k using developed ANN 6-8-1.
5. Conclusions
The paper concerns the determination of the permeability coefficient k using an ANN (Artificial Neural Network). In order to develop an ANN, field and laboratory tests of the parameter k were performed and index properties of the tested soils were determined. The research was performed in following soils: FSa, MSa and CSa. On the basis of the conducted research, it can be stated that similar values of the permeability coefficient k were obtained in field and laboratory tests from soils from the same test site. The influence of the relative density ID on the permeability coefficients k is significant in the tested soils. Higher values of permeability coefficients k were found in soils characterized by a lower relative density ID, higher void ratio e and lower value of effective soil diameter d10.
The proposed ANN with the 6-8-1 architecture predicts the real value of the permeability coefficient k based on the following data: soil type, relative density ID, void ratio e and effective soil diameter d10. The presented ANN estimates the permeability coefficients k with values of determination coefficient R2 = 0.97, mean relative error RE = ±4% and single maximum relative error Max RE = 7.59%.
The presented research frames the work as an experimental campaign and characterization of sandy soils. Further field and laboratory tests of the permeability coefficient k and the consideration of additional factors influencing the value of the tested parameter should be performed because the conclusions of the analysis refer only to the tested soils. The presented ANN model may be upgraded, new functions can be entered, including other types of soil, and can thus be extended to more types of non-cohesive and cohesive soils. The development of an ANN for the prediction of the soil permeability coefficient allows the reduction of the costs and time needed to conduct laboratory or field tests to determine this parameter.
Author Contributions
G.W. and A.M. prepared the research program, performed laboratory and field tests, developed an ANN and prepared the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated and analyzed during the current study are available from the authors upon reasonable request.
Conflicts of Interest
Authors declare no conflict of interest.
References
- Todd, D. Groundwater Hydrology, 2nd ed.; John Wiley & Sons: Chichester, UK, 1980. [Google Scholar]
- Wrzesiński, G. Anisotropy of soil shear strength parameters caused by the principal stress rotation. Arch. Civ. Eng. 2021, 67, 163–187. [Google Scholar] [CrossRef]
- Wrzesiński, G.; Lechowicz, Z. Testing of undrained shear strength in a Hollow Cylinder Apparatus. Studia Geotech. Mech. 2015, 37, 69–73. [Google Scholar] [CrossRef]
- Szymkiewicz, A.; Kryczałło, A. Calculation of permeability coefficient of sands and gravel based on grain size distribution curve: Review of empirical relations. Inżynieria Morska Geotech. 2011, 2, 110–121. [Google Scholar]
- Twardowski, K.; Drożdżak, R. Pośrednie metody oceny właściwości filtracyjnych gruntów. Wiertnictwo Nafta Gaz 2006, 23, 477–486. [Google Scholar]
- Parylak, K.; Zięba, Z.; Bułdys, A.; Witek, K. The verification of determining a permeability coefficient of non-cohesive soil based on empirical formulas including its microstructure. Acta Sci. Pol. Archit. 2013, 12, 43–51. [Google Scholar]
- Wrzesiński, G. Permeability coefficient tests in non-cohesive soils. Sci. Rev. Eng. Environ. Sci. 2020, 29, 72–80. [Google Scholar] [CrossRef][Green Version]
- MacDonald, A.; Barker, J.; Davies, J. The bailer test: A simple effective pumping test for assessing borehole success. Hydrogeol. J. 2008, 16, 1065–1075. [Google Scholar] [CrossRef]
- Pawluk, K.; Połoński, M.; Lendo-Siwicka, M.; Wrzesiński, G. Two-objective optimization for optimal design of the multi-layered permeable reactive barriers. IOP Conference Series: Materials Science and Engineering. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 1–11. [Google Scholar] [CrossRef]
- Polak, K.; Kaznowska-Opala, K.; Pawlecka, K.; Klich, J. Interpretation of pumping tests results on the basis of examination of AGH-1 well. Przegląd górniczy 2014, 10, 106–111. [Google Scholar]
- Head, K.; Epps, R. Manual of Soil Laboratory Testing. Vol. 2. Permeability, Shear Strength and Compressibility Test; Whittles Publishing: Scotland, UK, 2011. [Google Scholar]
- Jang, D.; Park, H.; Choi, G. Estimation of Leakage Ratio Using Principal Component Analysis and Artificial Neural Network in Water Distribution Systems. Sustainability 2018, 10, 750. [Google Scholar] [CrossRef]
- Kang, P.-S.; Lim, J.-S.; Huh, C. Artificial Neural Network Model to Estimate the Viscosity of Polymer Solutions for Enhanced Oil Recovery. Appl. Sci. 2016, 6, 188. [Google Scholar] [CrossRef]
- Li, W.; Cui, L.; Zhang, Y.; Cai, Z.; Zhang, M.; Xu, W.; Zhao, X.; Lei, Y.; Pan, X.; Li, J.; et al. Using a Backpropagation Artificial Neural Network to Predict Nutrient Removal in Tidal Flow Constructed Wetlands. Water 2018, 10, 83. [Google Scholar] [CrossRef]
- Zhu, X.; Fan, Y.; Zhang, F.; Ye, X.; Chen, C.; Yue, H. Multiple-Factor Based Sparse Urban Travel Time Prediction. Appl. Sci. 2018, 8, 279. [Google Scholar] [CrossRef]
- Paez, T.L. Neural networks in mechanical systems simulation, identification and assessment. Shock. Vib. 1993, 1, 177–199. [Google Scholar] [CrossRef][Green Version]
- Adeli, H. Neural Networks in Civil Engineering: 1989–2000. Comput.-Aided Civ. Inf. 2001, 16, 126–142. [Google Scholar] [CrossRef]
- Ghaboussi, J. Biologically inspired soft computing methods in structural mechanics and engineering. Struct. Eng. Mech. 2001, 11, 485–502. [Google Scholar] [CrossRef]
- Rojas, R. Neural Networks: A Systematic Introduction; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Wrzesiński, G.; Sulewska, M.J.; Lechowicz, Z. Evaluation of the Change in Undrained Shear Strength in Cohesive Soils due to Principal Stress Rotation Using an Artificial Neural Network. Appl. Sci. 2018, 8, 781. [Google Scholar] [CrossRef]
- Waszczyszyn, Z. Advances of Soft Computing in Engineering CISM Courses and Lectures; Springer: Vienna, Austria, 2010. [Google Scholar]
- Waszczyszyn, Z. Artificial neural networks in civil engineering: Another five years of research in Poland. Comp. Assist. Mech. Eng. Sci. 2011, 18, 131–146. [Google Scholar]
- Rafiq, M.Y.; Bugmann, G.; Easterbrook, D.J. Neural network design for engineering applications. Comput. Struct. 2001, 79, 1541–1552. [Google Scholar] [CrossRef]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. Artificial Neural Network Applications in Geotechnical Engineering. Aust. Geomech. 2001, 36, 49–62. [Google Scholar]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. State of the Art of Artificial Neural Networks in Geotechnical Engineering. Elect. J. Geotech. Eng. 2008, 8, 1–26. [Google Scholar]
- Dihoru, L.; Muir Wood, D.; Sadek, T.; Lings, M. A neural network for error prediction in a true triaxial apparatus with flexible boundaries. Comput. Geotech. 2005, 32, 59–71. [Google Scholar] [CrossRef]
- Pichler, B.; Lackner, R.; Mang, H.A. Back analysis of model parameters in geotechnical engineering by means of soft computing. Int. J. Numer. Meth. Eng. 2003, 57, 1943–1978. [Google Scholar] [CrossRef]
- Sulewska, M.J. Applying artificial neural networks for analysis of geotechnical problems. Comp. Assist. Mech. Eng. Sci. 2011, 18, 231–241. [Google Scholar]
- Tian, J.; Li, C.; Liu, J.; Yu, F.; Cheng, S.; Zhao, N.; Wan Jaafar, W.Z. Groundwater Depth Prediction Using Data-Driven Models with the Assistance of Gamma Test. Sustainability 2016, 8, 1076. [Google Scholar] [CrossRef]
- Zhou, T.; Wang, F.; Yang, Z. Comparative Analysis of ANN and SVM Models Combined with Wavelet Preprocess for Groundwater Depth Prediction. Water 2017, 9, 781. [Google Scholar] [CrossRef]
- Ellis, G.W.; Yao, C.; Zhao, R.; Penumadu, D. Stress-strain modeling of sands using artificial neural network. J. Geotech. Eng. 1995, 121, 429–435. [Google Scholar] [CrossRef]
- Sidarta, D.E.; Ghaboussi, J. Constitutive modeling of geomaterials from non-uniform material test. Comput. Geotech. 1998, 22, 53–71. [Google Scholar] [CrossRef]
- Penumadu, D.; Zhao, R. Triaxial compression behavior of sand and gravel using artificial neural networks (ANN). Comput. Geot. 1999, 24, 207–230. [Google Scholar] [CrossRef]
- Basheer, I.A. Selection of methodology for neural network modeling of constitutive hysteresis behavior of soils. Comput.-Aided Civ. Inf. 2000, 15, 440–458. [Google Scholar] [CrossRef]
- Najjar, Y.M.; Huang, C. Simulating the stress-strain behavior of Georgia kaolin via recurrent neuronet approach. Comput. Geot. 2007, 34, 346–361. [Google Scholar] [CrossRef]
- Fu, Q.; Hashash, Y.M.A.; Hung, S.; Ghaboussi, J. Integration of laboratory testing and constitutive modeling of soils. Comput. Geotech. 2007, 34, 330–345. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, S.R.; Kim, Y.S. An approach to estimate unsaturated shear strength using artificial neural network and hyperbolic formulation. Comput. Geotech. 2003, 30, 489–503. [Google Scholar] [CrossRef]
- Das, S.K.; Basudhar, P.K. Undrained lateral load capacity of piles in clay using artificial neural network. Comput. Geotech. 2006, 33, 454–459. [Google Scholar] [CrossRef]
- Byeon, W.Y.; Lee, S.R.; Kim, Y.S. Application of flat DMT and ANN to Korean soft clay deposits for reliable estimation of undrained shear strength. Int. J. Offshore Polar Eng. 2006, 16, 73–80. [Google Scholar]
- Wrzesiński, G. Stability Analysis of an Embankment with Influence of the Principal Stress Rotation on the Shear Strength of Subsoil. Ph.D. Thesis, Warsaw University of Life Sciences–SGGW, Warsaw, Poland, 2016. [Google Scholar]
- Wrzesiński, G.; Kowalski, J.; Miszkowska, A. Numerical analysis of dewatering process of deep excavation. In Proceedings of the 18th International Multidisciplinary Scientific Geoconference SGEM 2018: Hydrogeology, Engineering Geology and Geotechnics, Albena, Bulgaria, 30 June 2018; Issue 1.2, Science and Technologies in Geology, Exploration and Mining. Volume 18, pp. 497–504. [Google Scholar]
- Lin, P.Y.; Ni, P.P.; Guo, C.C.; Mei, G.X. Mapping Soil Nail Loads Using FHWA Simplified Models and Artificial Neural Network Technique. Can. Geotech. J. 2020, 57, 1453–1471. [Google Scholar] [CrossRef]
- Lin, P.Y.; Chen, X.Y.; Jiang, M.J.; Song, X.G.; Xu, M.J.; Huang, S. Mapping shear strength and compressibility of soft soils with artificial neural networks. Eng. Geol. 2022, 300, 106585. [Google Scholar] [CrossRef]
- Liu, D.; Lin, P.Y.; Zhao, C.Y.; Qiu, J.J. Mapping horizontal displacement of soil nail walls using machine learning approaches. Acta Geotech. 2021, 16, 4027–4044. [Google Scholar] [CrossRef]
- Driscoll, F. Groundwater and Wells, 2nd ed.; Johnson Filtration Systems Inc.: St Paul, MN, USA, 1986. [Google Scholar]
- ICRC. Technical Review: Practical Guidelines for Test Pumping in Water Wells; International Committee of the Red Cross: Geneva, The Switzerland, 2011. [Google Scholar]
- Kruseman, G.P.; de Ridder, N.A. Analysis and Evaluation of Pumping Test Data, 2nd ed.; Publication 47; International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1994. [Google Scholar]
- EN ISO 14688-1; Geotechnical Investigation and Testing-Identification and Classification of Soil-Part 1: Identification and Description. International Organization for Standardization: Geneva, Switzerland, 2002.
- EN ISO 14688-2; Geotechnical Investigation and Testing-Identification and Classification of Soil-Part 2: Principles for a Classification. International Organization for Standardization: Geneva, Switzerland, 2004.
- Head, K. Manual of Soil Laboratory Testing. Vol. 1. Soil Classification and Compaction Test; Pentech Press: London, UK, 1996. [Google Scholar]
- Tymosiak, D.; Sulewska, M.J. The study of compactibility parameters in non-cohesive soils by Proctor compaction test. Acta Sci. Pol. Archit. 2016, 15, 43–54. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).