Abstract
The fleet operation model in which electric vehicles coexist with traditional vehicles is becoming increasingly popular. Because electric vehicles have certain disadvantages and usage limitations, the multi-center management of the distribution of mixed fleets is very complex. There is no research on the multi-center mixed vehicle routing problem based on the integration of reverse logistics and dynamic energy consumption. In response to this challenge, this study proposes a solution to the multi-center mixed vehicle routing problem considering dynamic energy consumption and integrated reverse logistics. Specifically, three studies were carried out: (1) Considering the influencing factors of the operating cost system of the mixed fleet, a system dynamics model was constructed. (2) On the basis of considering delaying the aging of electric vehicle batteries, a new charging station insertion strategy was designed. (3) Based on a novel charging station insertion strategy, a fast non-dominated sorting multi-objective genetic algorithm with an elite strategy was designed to solve this problem. We designed 15 groups of examples to prove the effectiveness of the model and algorithm. The experimental results show that 46.67% of the cases have more than 60% customer satisfaction. The average expenditure cost of 15 groups of cases is CNY 2018.33, which can improve the average customer satisfaction by 22.94%. This method helps companies to formulate transportation plans according to the actual situation, including providing a cost model that considers multiple influencing factors and improving the average customer satisfaction while reducing the total cost expenditure. We believe that the results of this research can provide methods and ideas for logistics companies with multiple distribution centers to formulate large-scale distribution plans.
1. Introduction
The problems of environmental pollution and decarbonization of transportation have become the focus of attention. The transport industry produces about a quarter of global CO2 emissions each year, and this amount is predicted to double by 2050 [1]. With the rapid development of logistics and e-commerce, the pressure of freight transportation in various cities is also increasing. In 2021, 39.14 billion tons of goods were transported by road transport in China, an increase of 14.25 percent over the previous year [2]. Electric vehicles are widely used in the cargo transportation industry because they are powered by renewable energy, emit less pollution, consume less energy, and generate less noise [3]. In 2021, China’s production of new energy vehicles reached 3.677 million units, up 152.5 percent from the previous year [2]. Islamic research results show that when the fleet consists of only conventional vehicles, the average CO2 emission increases by 13.58% compared to the mixed-fleet vehicle model [4]. In the “China Logistics Industry Investment Promotion Report 2015–2016”, jointly released by the Ministry of Commerce and Deloitte, it is pointed out that China’s reverse logistics market will exceed CNY 2 trillion in market capacity from 2016 to 2020, and the proportion of the entire social logistics system will be more than 20% [5].
However, electric cars also have their drawbacks. Its technology is not perfect, and the acquisition cost and battery cost are relatively high [6]. The important energy storage component of electric vehicles is lithium-ion batteries, but the abnormal decline of their lifespans has made the logistics industry unable to choose electric vehicles as the main force of logistics transportation [7]. Wang et al. found that the depth of battery charge and discharge and the number of charge and discharge cycles affect battery life [8]. When assigning delivery tasks to electric vehicles, delivery tasks that consume too much energy will cause the battery to be charged and discharged frequently, affecting battery life. Epding et al. demonstrate the effect of rest time during charge and discharge cycles on battery capacity recovery and battery life, with the fastest decline in capacity without rest time [9]. The study by Zang et al. showed that due to the high cost of battery replacement, the impact of delivery tasks on battery life and battery depreciation should be considered [10].
In order to overcome the current limitations of electric vehicles, combining electric vehicles with traditional vehicles to form a logistics transportation fleet is more suitable for the current logistics situation. Due to the limited use of electric vehicles, the management of multi-distribution centers using mixed fleets to plan distribution tasks is very complex. The most fundamental difference between electric vehicles and fuel vehicles is that electric vehicles will enter the charging station for charging during the driving process, resulting in charging costs [11]. In order to avoid the energy shortage of electric vehicles during the driving process, it is necessary to calculate the energy consumption of electric vehicles more accurately according to information such as vehicle load, speed, actual road conditions and other influencing factors in different road sections. Ferro et al. took into account the total mass of the vehicle, the gradient of the terrain, the travel speed that affects the rolling and aerodynamic resistance, and other factors to establish a detailed models of electric vehicle dynamic energy consumption [12]. Hou et al. established a traditional vehicle fuel consumption model considering the weight of fuel vehicles loaded with cargo [13]. Li et al. considered factors such as different speeds, loads, and distances in different road sections to build a dynamic energy consumption model for electric vehicles [14]. Based on real-time road conditions, a traditional vehicle energy dissipation model has been established that takes into account road slope, traffic flow and road congestion [15]. Based on these studies, this paper establishes a dynamic energy consumption estimation model for mixed fleets from the perspective of work carried out during vehicle driving.
The independent operation of forward and reverse logistics in the logistics network inevitably increases the energy consumption and transportation cost of enterprises [16]. Splitting services for customers with both positive and negative needs can also affect customer satisfaction and customers’ visual impression of the company, which in turn affects the company’s reputation and customer loyalty. It is necessary to integrate the forward and reverse logistics in the logistics network to reduce the waste of resources [17]. Foroutan et al. studied the green vehicle routing and scheduling problem with a heterogeneous fleet, including reverse logistics in the form of collecting returned goods [18]. According to the author’s understanding, most scholars ignore the impact of forward and reverse logistics coordinated distribution on the distribution network in the research on mixed-fleet routes, and there is no research on the optimization of mixed-fleet routes considering forward and reverse logistics.
On the basis of considering that electric vehicles will enter the charging station in the case of insufficient power, how to reasonably configure the number of electric vehicles and fuel vehicles in the mixed fleet is an important factor affecting the cost of enterprises [19]. Al-dal’ain et al. proposed a novel integrated model to consider both routing and fleet composition decisions for using electric vehicles in urban freight distribution, minimizing the operational cost for different fleet compositions of electric and conventional vehicles. This article assumes that the vehicle is recharged to maximum capacity when it arrives at the parking lot and does not consider the effect of overcharging the battery on lifespan [20]. Malladi et al. established an objective function to minimize the total fleet operation cost, which is composed of variable energy and maintenance costs and fixed usage costs that can account for acquisition, insurance, maintenance, driver salaries, and penalties for not serving customers. This article takes a robust optimization approach to electric vehicles: planning for worst-case scenarios minimizes the risk of an electric vehicle draining its battery during operation [21]. Yu et al. studied the green mixed fleet vehicle routing problem to minimize the total cost comprising the distance traveled cost by all utilized fleets and the total emitted pollution cost from the utilized fleet of ICVs. This article assumes that the electric vehicle operates after a fully charged charging station and does not consider the effects of overcharging and overdischarging on the battery [22]. Hou et al. comprehensively considered the influence of factors such as the opening of multi-distribution centers, the joint distribution of fuel vehicles and electric vehicles, and the continuous change of vehicle speed. The optimization model had the goal of minimizing the sum of operating cost and time window penalty cost. This article sets a minimum state of charge for electric batteries to avoid overdischarging [23]. Li et al. proposed a hybrid fleet configuration and path optimization model. The model considers the difference in fixed cost, variable cost, and cruising range of the two types of vehicles and obtains the optimal configuration and routing results of the mixed fleet, while considering the impact of charging facilities. This article assumes that the electric vehicles are fully charged at the distribution center and known charging stations [24]. Wang et al. established a multi-objective programming model. The upper-layer model minimizes the operation cost and economic cost of carbon emission to optimize the vehicle and charging scheme, while the lower-layer model tries to optimize the crew-scheduling scheme. This article assumes that the parking lot is available and charged. In order to prevent the battery from being damaged by overcharging and overdischarging, the upper and lower limits of the battery state of charge are set [25]. Shojaei et al. developed a cost model to minimize freight company costs, including fleet purchase and maintenance fees, fuel costs (electricity and gas), carbon dioxide and noise emissions taxes, and labor costs associated with fleet drivers. This article assumes that charging or refueling only happens at depot locations [26]. Rinaldi et al. assume that vehicles in a mixed fleet are only charged or refueled at night, and the optimization goal is to minimize the total operating cost. This article introduces a minimum value of the battery charge at trip completion, which must be usually kept above a certain threshold to guarantee normal operating conditions and to prolong battery life. [27]. Lu et al. proposed a joint optimization model for hybrid bus fleet scheduling under micro-driving conditions, which minimizes the total cost including vehicle acquisition costs, charging station costs, energy costs, empty driving costs, scheduling costs, etc., [28]. Zhao et al. proposed a vehicle routing problem with a mixed fleet of conventional and electric vehicles and soft time windows. A bi-objective programming model is established to minimize the total operational cost and time penalty cost. Total operating costs include vehicle fixed costs, vehicle energy costs, charging costs, and carbon emissions costs. This article assumes that the electric vehicle is fully charged when it leaves the distribution center [29]. Ren et al. established a dual-objective optimization model, considering both environment benefit and customer satisfaction. There are two objectives in the model: minimizing pollutant emissions and minimizing the total delay time. This article does not take into account the charging time and charging costs generated by the charging behavior of electric vehicles at the charging station [30]. Li et al. studied the vehicle routing problem of a hybrid electric vehicle and a fuel vehicle with a time window, constructing an integer programming model of the problem to minimize transportation costs for mixed fleets. The electric vehicle continues on the delivery mission after being fully charged at a charging station [31].
However, most studies aim to minimize costs such as fixed use costs, carbon emission costs, penalty costs, and vehicle operating costs. They do not take into account the depreciation cost of electric vehicle batteries and ignore customer satisfaction, which is not conducive to the long-term future of logistics companies. Most studies make certain assumptions about the charging process, such as setting the maximum battery charge and maximum discharge limits, but ignore the impact of deep battery charging and discharging and frequent charging and discharging on battery life. Many scholars have fixed the starting point of vehicles and closed distribution in their studies on the route of the mixed fleet, ignoring the overall cooperation between distribution centers. Few studies have involved route optimization of multiple distribution centers, unlimited starting points of vehicles and open distribution.
Existing research does not realize the importance of the dynamic energy consumption during driving, the depreciation of electric vehicle batteries, and the integrated reverse logistics for the distribution path planning of the mixed fleet. There is no research on the multi-center mixed vehicle routing problem based on the integration of reverse logistics and dynamic energy consumption.
On the basis of the above research, this paper considers the dynamic energy consumption of vehicles, integrates reverse logistics, and studies the path optimization problem of hybrid fleet with an open collaborative distribution of multiple distribution centers.
First, we establish a multi-center distribution model for mixed fleets after in-depth research by analyzing the influencing factors of the operating cost of the hybrid fleet: the energy consumption cost, the fixed cost, the penalty cost, the opportunity cost, the charging cost, the battery depreciation cost, and the carbon emission cost. The battery depreciation cost model is established considering the impact of battery depth charge and discharge and the number of charge and discharge times on the battery depreciation cost. Vensim software was used to establish the causal loop diagram of the operating cost system of the hybrid fleet, and the system dynamics model was established: fuzzy time window, vehicle load, maximum energy consumption of electric vehicles, maximum charge–discharge cycle time of electric vehicles, and other soft and hard constraints are used as constraints to minimize operating costs and maximize average customer satisfaction.
Second, to further refine the charging assumption, based on the charging and discharging cycle time of electric vehicles, in order to delay battery aging, a novel plug-in strategy for charging stations is proposed, which allows each electric vehicle to be charged and discharged at any charging station, and the electric vehicle can be charged multiple times at the same time. The method was applied to large-scale numerical examples.
Finally, based on a novel charging station insertion strategy, a fast non-dominated sorting multi-objective genetic algorithm (CSPS-NSGA II) with an elite strategy was designed to solve this problem. This algorithm was verified by numerical examples.
The remainder of the paper is organized as follows. In Section 2, building a system dynamics model for a mixed-fleet operating cost system is described, along with the detailed steps of the charging station plug-in strategy, including detailed steps for CSPS-NSGA II. Section 3 presents the data and parameters used in our study as well as the computational results and related conclusions. The impact of important parameter changes on the model is discussed in Section 4, and Section 5 concludes with concluding remarks and a possible future outlook.
2. Materials and Methods
2.1. System Dynamics Model
The logistics distribution network scenario is described as follows: In a certain cycle, a logistics distribution network is formed by multiple distribution centers. The distribution vehicle starts from the distribution center to meet the different pickup and delivery needs of each customer that does not exceed the vehicle load. When the vehicle load is exceeded, it returns to any distribution center. The dynamic energy consumption of the vehicle is calculated by considering factors such as the vehicle’s load capacity, driving distance, average driving speed, and road conditions in different road sections.
Under the constraints of vehicle load and fuzzy time window, the delivery and receipt of goods at different customer points in the logistics network are integrated. Vehicle load ratings are known, combined cargo weight determines mixed-fleet size, and the ratio of the number of fuel vehicles to the number of electric vehicles in the mixed fleet is optimized. Electric vehicles can enter the same charging station multiple times for partial charging and discharging. Based on the known location of the charging station and the energy consumption before the electric vehicle enters the charging station, the charging time and charging cost of the electric vehicle at the charging station can be determined. On the basis of considering the charging and discharging cycle time of electric vehicles and the maximum energy consumption of electric vehicles, this paper solves the optimization problem of hybrid fleet path for open collaborative distribution of multi-distribution centers. The solution goal is to minimize the sum of vehicle energy consumption cost, charging cost, penalty cost, opportunity cost, battery depreciation cost, and carbon emission cost and maximize average customer satisfaction on the basis of satisfying all customer needs.
The schematic diagram of mixed-fleet logistics distribution is shown in Figure 1.
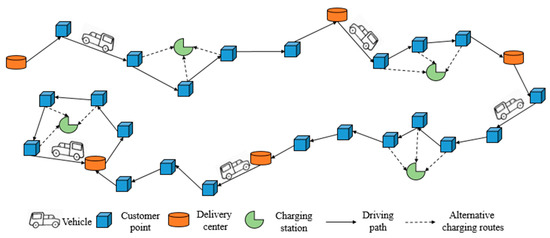
Figure 1.
Schematic diagram of mixed-fleet logistics distribution.
The system boundary is the basis of system dynamics modeling and simulation. The hybrid fleet operating cost system includes seven subsystems: energy consumption subsystem, vehicle fixed-use cost subsystem, time cost subsystem, charging cost subsystem, battery depreciation cost subsystem, carbon emission cost subsystem, and customer satisfaction system. The system boundary includes a collection of main influencing elements within the seven major subsystems. Only the internal state of the system is considered when setting initial conditions. As an important analytical tool to study system structure and system behavior, system dynamics has been applied in the research of new energy fleets, but there are few studies on the operating cost of mixed fleets.
A theoretical model of the operating cost of a mixed fleet is established based on system dynamics. The model mainly has the following assumptions: The distribution center has a sufficient number of vehicles; the reverse demand of customers and coordinate distribution is integrated; the loading and unloading time of the distribution center is not considered; each electric vehicle leaves after the charging station reaches the correct degree of charge; all charging stations can handle an unlimited number of electric vehicles at the same time; the electric vehicle rests after the charge–discharge cycle time reaches the set sum of the vehicle working time and the charging time (the battery ages slowly during the rest period, which is beneficial to prolong the service life); if the delivery time exceeds the charge–discharge cycle time, the delivery task will be carried out by a fuel truck; the process of refueling fuel vehicles is not considered.
The mathematical description is as follows: In a certain period of logistics network, there are N departure nodes and H customer nodes. The distribution vehicles in each distribution center have different maximum loads. The logistics task from the supply node to the customer node or the logistics task from the customer node to the next customer node has the distribution demand and the recycling demand at the customer point h. The needs of the customers are divided into different vehicles, and each vehicle visits the distribution center and customers in a certain order for pickup and delivery. Return to either distribution center occurs when customer demand cannot be met. The vehicles departing from the distribution center have less than the maximum vehicle load . The vehicle loading and unloading of goods at the customer point is less than the maximum vehicle load . During this process, if the energy consumption of the delivery vehicle exceeds the maximum energy consumption , the electric vehicle enters the charging station for charging and calculates the charging time to reach the charging depth. Fuel vehicles have a short energy replenishment time, and the process of replenishing fuel is ignored. To improve the profit of operating a mixed fleet, we calculate the total cost incurred in operating a mixed fleet. In order to improve the service quality of the fleet to customers, the satisfaction of each customer is calculated, and the satisfaction is normalized: 1 represents the maximum satisfaction, and 0 represents the minimum satisfaction. The structure diagram of the operating cost system of the mixed fleet is shown in Figure 2.
Figure 2.
Structure diagram of mixed-fleet operating cost system.
The influencing factors of the seven subsystems included in the mixed fleet operating cost system are analyzed as follows:
Energy consumption subsystem: The vehicle work process is affected by factors such as rolling resistance coefficient, air resistance coefficient, vehicle windward area, gravitational acceleration, road slope, air density, road elevation between nodes, and energy consumption conversion coefficient. The vehicle does work during transportation, and different road sections have different slopes, as shown in Figure 3. The energy consumption subsystem is affected by four key factors: the proportion of fuel vehicles and electric vehicles in the fleet, unit energy consumption cost, energy consumption conversion coefficient, and vehicle work.

Figure 3.
Work conducted during vehicle driving.
Vehicle fixed-use cost subsystem: The vehicle fixed-use cost subsystem is affected by four key factors: labor cost, vehicle depreciation cost, vehicle use cost, and the proportion of fuel vehicles, and electric vehicles in the fleet.
Time cost subsystem: The time cost of the vehicle includes two parts: the opportunity cost of arriving earlier than the time window expected by the customer and the penalty cost of arriving later than the time window expected by the customer. Opportunity cost is incurred when the vehicle arrives at the designated location earlier than the time window requested by the customer, and penalty cost is incurred when the vehicle arrives at the designated location later than the time window requested by the customer. The time cost subsystem is affected by four key factors: the time for the vehicle to arrive at the location specified by the customer, the time window the customer specifies for the arrival of the vehicle, the unit penalty cost, and the unit opportunity cost.
Charging cost subsystem: The charging cost subsystem is affected by four key factors: unit charging cost, energy consumption conversion factor, charging rate, and work performed during the driving distance of the vehicle. In order to avoid the shortened lifespan of electric vehicles caused by overcharging and over discharging, the electric vehicles are arranged to enter the charging station when the remaining power of the electric vehicle is less than 20% and leave the charging station when the charging depth reaches 100%, and then go to the next customer point. Electric vehicles take up delivery time during the charging process, resulting in charging costs.
Depreciation cost system: The battery depreciation cost subsystem is affected by seven key factors: the maximum energy consumption of the electric vehicle, the unit energy consumption cost of the vehicle, the number of charges, the number of battery charge and discharge cycles, the depth of battery discharge, the battery type, and minimum charge state of electric vehicle battery.
Carbon emission cost system: The carbon emission cost subsystem is affected by four key factors: the carbon emission per unit energy consumption of fuel vehicles, the carbon emission per unit energy consumption of electric vehicles, the carbon emission tax levied by the government, and the fleet size.
Customer satisfaction system: The customer satisfaction system is affected by three key factors: the vehicle arrival time, the customer’s expected vehicle arrival time window, and the customer’s specified vehicle arrival time window.
The causal diagram of the hybrid-fleet operating system model is shown in Figure 4. In Figure 4, “+” represents a promoting effect between variables, and “−” represents a reducing effect between variables.
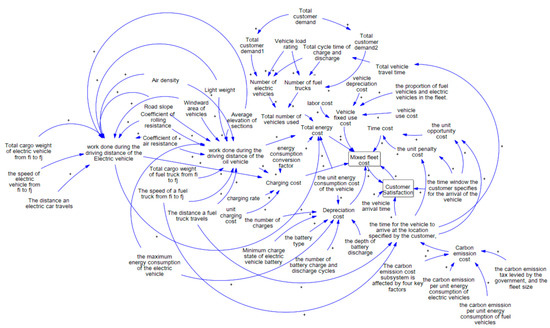
Figure 4.
Causal loop diagram of mixed-fleet operating cost system.
The equation parameters are defined as Table 1.

Table 1.
Algorithm parameters.
We seek to improve the vehicle energy consumption estimation model proposed by Rafael et al. [32]. The energy consumption estimation model of the mixed-vehicle fleet is established considering factors such as vehicle parameters, road parameters, and vehicle loads. The work conducted in the driving distance of the vehicle mainly includes the resistance work of the external environment to the vehicle and the gravitational work formed by the vehicle and the load of the vehicle. The energy cost calculation equation is:
The equation for calculating the energy consumption cost of fuel vehicles is:
The equation for calculating the energy consumption cost of electric vehicles is:
The equation for calculating the energy consumption cost of the mixed fleet is:
The fixed cost of a vehicle is the fixed-use cost of each vehicle, including the sum of labor costs and vehicle depreciation costs. The equation for calculating the fixed cost of a vehicle is:
The time cost of the vehicle includes the opportunity cost of arriving earlier than the time window and the penalty cost is later than the time window. The time for the vehicle to arrive at each customer point is:
Penalty cost occurs when the vehicle arrives later than the time window required by the customer. The equation for calculating the penalty cost is:
Opportunity cost occurs when the vehicle arrives earlier than the time window required by the customer. The equation for calculating the opportunity cost is:
The equation for calculating the charging cost is:
The depreciation cost of the battery is determined by the number of battery charge–discharge cycles and the battery charge–discharge depth. The depreciation cost model of the battery cycle times and the battery discharge depth depreciation cost model are established. The equation is:
The equation for calculating the battery depreciation cost is:
The carbon emissions mainly come from fuel vehicles, as electric vehicles can be regarded as having zero emissions. The equation for calculating the carbon emission cost is:
Constructing the relationship between time window and customer satisfaction based on trapezoidal fuzzy membership function is performed. The equation is:
On the basis of considering the dynamic energy consumption of vehicles and integrating reverse logistics, the problem of hybrid fleet path optimization for open collaborative distribution of multi-distribution centers is studied. We establish a cost–customer average satisfaction dual-objective optimization model. Objective function 1 includes energy consumption cost, vehicle fixed-use cost, opportunity cost caused by an earlier time window, penalty cost caused by a later time window, charging cost, battery depreciation cost, and carbon emission cost. Objective function 2 considers the impact of fuzzy time window on customer satisfaction, solves the average customer satisfaction, and transforms the maximization of average customer satisfaction into a minimization problem. The hybrid fleet operating cost minimization model is:
The model for maximizing average customer satisfaction for mixed fleets is:
s.t.
Equation (19) indicates that each vehicle is delivered once at most. Equation (20) indicates that all tasks are planned to be completed. Equation (21) indicates the vehicle load limit when the distribution center departs. Equation (22) indicates that the vehicle loads and unloads the load at the customer point less than the vehicle load limit. Equation (23) indicates that the vehicle departs from a certain distribution center and returns to any distribution center. Equation (24) indicates that the remaining power of the electric vehicle from node i to node j is not lower than the maximum discharge depth. Equation (25) indicates that the electric vehicle is in a fully charged state when it leaves the distribution center. Equation (26) indicates the travel time of the electric vehicle less than the charge–discharge cycle time.
2.2. Problem Analysis
Advanced optimization algorithms (e.g., heuristics, meta-heuristics) have been shown to be effective solutions in many different domains, such as online learning, scheduling, multi-objective optimization, transportation, medicine, data classification, etc. Zhao et al. proposed a learning-based algorithm, aimed to enhance the generalization ability. On the basis of a decomposition-based multi-objective optimization framework, a learning automaton (LA) is included in the algorithm. The results of the experiment indicate that the proposed algorithm obtains satisfactory performance in determining the convergence and the approximation of the PF [33]. Pasha et al. presented a decomposition-based heuristic algorithm to solve the model proposed and efficiently tackle large-size problem instances, demonstrating the effectiveness of the proposed methodology [34]. Dulebenets et al. proposed four multi-objective heuristic algorithms to solve large-scale emergency evacuation problems [35]. Dulebenets et al. proposed a novel delayed start parallel evolutionary algorithm to solve the truck scheduling problem. The algorithm executes separate evolutionary algorithms on its islands in a sequential manner and exchanges the promising solutions among the active islands based on an adaptive migration criterion [36]. Li et al. studied the ambulance routing problem considering variable patient conditions, where the non-dominated sorting genetic algorithm II (NSGA-II) and multi-objective particle swarm optimization (MOPSO) are used to find high-quality solutions over a short time [37]. Verma et al. provides an extensive review of the popular multi-objective optimization algorithm NSGA-II for selected combinatorial optimization problems, viz., assignment problem, allocation problem, travelling salesman problem, vehicle routing problem, scheduling problem, and knapsack problem [38].
Path planning problems are large-scale complex problems. Most studies solve the path problem based on heuristic algorithms. Based on the heuristic algorithm and a novel charging station insertion strategy, this paper designs an improved fast non-dominated sorting multi-objective genetic algorithm with an elite strategy.
In the solution of multi-objective problems, the multi-objective problem is transformed into a single-objective problem through the method of assigning weights, which has strong subjectivity. Electric vehicles in mixed fleets are charged at charging stations due to their limited capacity. In this paper, a charging station plug-in strategy is proposed to update the route, taking into account the battery life of the electric vehicle, and distinguishing the fuel vehicle and the electric vehicle type by the charge–discharge cycle time. When the energy consumption of the electric vehicle is about to exceed its maximum energy consumption value, the electric vehicle will drive to the charging station closest to the customer point for charging, re-insert the location of the charging station in the route, and update the route. The electric vehicle route is updated as shown in Figure 5. The multi-objective optimization algorithm can solve the optimal solution of the two objectives at the same time. This paper uses the multi-objective algorithm to solve the problem. Multi-objective genetic algorithm (NSGA II) shows good performance in solving path planning problems, but it will fall into local optimal solution. To sum up, this paper designs a fast non-dominated sorting genetic algorithm based on charging station plug-in strategy and elite strategy: CSPS-NSGA II, which jumps out of the local optimum, improves the quality of the solution, and obtains a more uniformly distributed non-inferior solution.
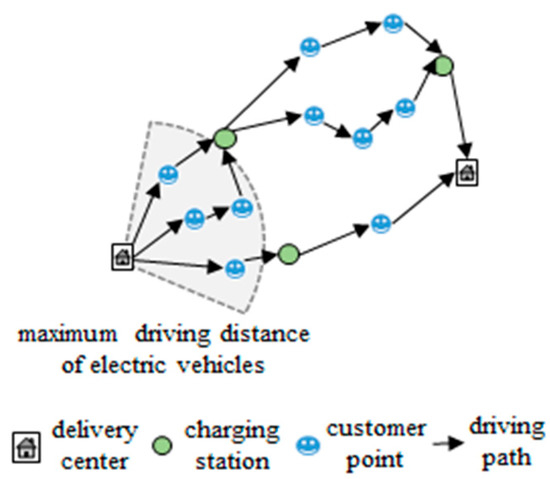
Figure 5.
Electric vehicle routing update.
The detailed steps of the charging station plug-in strategy are as follows:
- Select the distribution center from which the vehicle departs and the distribution center where the vehicle returns. The vehicle returns to any distribution center after serving all customers. Two distribution centers (or possibly the same distribution center) are combined with the customer points that satisfy the load of the vehicle to form an initial route;
- Assuming that the vehicle performing the route distribution task is an electric vehicle, it is determined whether the vehicle travel time in the route exceeds the charging and discharging cycle time. If it exceeds, go to step 3, otherwise go to step 4;
- Route is the driving route of the oil truck. If the total weight of the cargo exceeds the maximum load of the vehicle, delete this route; otherwise, store the feasible solution set. If the time to reach the customer point exceeds the time constraint, calculate the penalty cost and opportunity cost;
- The route is the driving path of the electric vehicle. If the total weight of the goods exceeds the maximum load of the vehicle, delete this route; otherwise, store the feasible solution set. If the time to reach the customer point exceeds the time constraint, calculate the penalty cost and opportunity cost. If the driving distance does not exceed the maximum driving distance of the electric vehicle, store the feasible solution set; otherwise, add a charging station closest to the customer point that exceeds the maximum driving distance of the electric vehicle and go to step 5;
- If the nearest charging station is added to the customer point that exceeds the maximum driving distance of the electric vehicle and the distance still exceeds the maximum driving distance of the electric vehicle, subtract one customer point and then add the nearest charging station for the new customer Determine whether the distance exceeds the maximum travel distance of the electric vehicle. If it exceeds, go to step 6; otherwise, insert the location index of the charging station between the new customer point and the subtracted customer point, calculate the charging time to reach the charging depth, and go to step 7;
- Subtract one customer point again, add a charging station closest to the new customer, and judge whether the distance exceeds the maximum travel distance of the electric vehicle at this time. If it exceeds, go back to step 5; otherwise, insert the location index of the charging station between the new customer point and the subtracted customer point, calculate the charging time to reach the charging depth, and go to step 7;
- After adding a charging station, determine whether the remaining distance of the path exceeds the maximum travel distance of the electric vehicle. If it exceeds, continue to join the charging station and go to step 4; otherwise, go to step 8;
- Store the feasible solution set.
The pseudo-code for the above charging station plug-in strategy is shown in Algorithm 1. The flow of CSPS-NSGA II algorithm is shown in Figure 6.
| Algorithm 1. Pseudo code of charging station plug-in strategy. |
| begin |
| maxenergy = = 50 kWh // maximum energy consumption of electric vehicles |
| = = 10 h // maximum charge–discharge cycle time for electric vehicles |
| calculate drivingtime // calculate vehicle travel time |
| calculate energymatrix // calculate the energy consumption matrix between adjacent nodes of the vehicle |
| calculate minenergy // calculate the energy consumption of driving to the charging station closest to the customer point |
| calculate charge // calculate the number of charges |
| if drivingtime < // determine the type of vehicle, if it is an electric vehicle |
| find((energymatrix (j) + minenergy (j) > ii* maxenergy)&&(energymatrix(j) + minenergy (j) < (ii + 1)* maxenergy)) // find the location of the customer point j that is insufficient for the ii-th charge |
| if energymatrix (j − k) + minenergy (j) < ii* maxenergy // need to be plugged into the charging station after subtracting k customers |
| INDEX = j − k; // calculate index of the location where the charging station needs to be plugged in |
| index = minenergy (j); // calculate the distance to the nearest charging station to j customer point |
| ret = [ret(:,1: INDEX) index ret(:,(INDEX + 1):end)];// form new chromosomes |
| end |
| end |
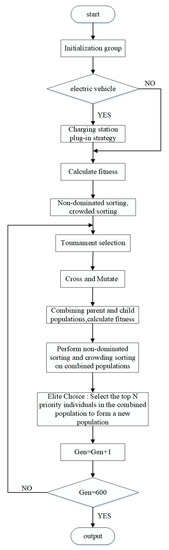
Figure 6.
Flow chart of CSPS-NSGA II.
The specific steps of CSPS-NSGA II proposed in this paper are as follows:
- For input parameters, input objective function and constraints, select various parameters (population size, crossover rate, mutation rate, etc.,) according to the actual problem;
- Initialize the population, encode each node in the logistics distribution network through integer coding, and the individual composed of all nodes represents the vehicle travel path, as shown in Figure 7. When the cargo weight exceeds the vehicle load, return to any distribution center. The chromosome consists of the vehicle departure node, the customer node served by the vehicle, the vehicle return node, and the number of vehicles. For example, the driving route of a vehicle is 3→9→7→6→10→12→1. Randomly generate chromosome combinations to become the initial population.
 Figure 7. Population initialization.
Figure 7. Population initialization. - The charging station set includes all charging stations, and the same charging station can be repeatedly selected to be inserted into the chromosome; that is, the charging station can be visited multiple times by different routes. According to the charging station plug-in strategy, the routes that need to be inserted into the charging station nodes are re-coded, and the initial population is re-formed, as shown in Figure 8.
 Figure 8. Charging station insertion strategy.
Figure 8. Charging station insertion strategy. - Calculate the fitness of the initialized population;
- For non-dominated quick sort, calculate the non-dominated value (Rank value) and crowding degree, as shown in Figure 9. After the non-dominant sorting is completed, the better individuals such as grade 1 and grade 2 are selected as the next-generation parent population. In order to keep the same number as the original parent population in the new-generation parent population, grade 3 cannot all be put into the new generation parent population. Then, the individuals of grade 3 are sorted by crowding degree, and the one with higher crowding degree is selected as the next-generation parent population.
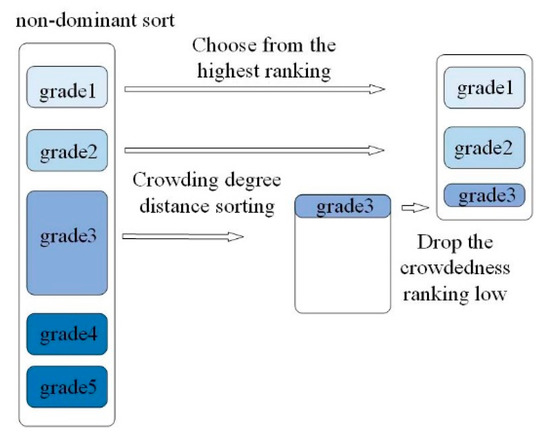 Figure 9. Fast non-dominated sorting.
Figure 9. Fast non-dominated sorting. - The tournament selects parents suitable for breeding. Each child needs to have two parents (Parent1 and Parent2), and the parents are selected through a competition in the parent population. Two individuals are randomly selected from the parent population and then compared. First, compare according to rank. If the rank is different, take the individual with better rank. If the rank is the same, compare the crowding degree (Crowding), and take the individual with better crowding distance. Finally, Parent1 is filtered out. The same method filters out Parent2;
- Genetic operation, crossover, and mutation operation. The crossover process is to extract the genes of the selected individuals and mix them. The crossover operation is realized by partial matching crossover (PMX). During the mutation process, a random gene is selected and modified. The specific operation process is shown in Figure 10 and Figure 11. The gene points for genetic manipulation are customer points and charging stations; select and delete charging stations that do not conform to the charging station insertion strategy, and finally form a solution set.
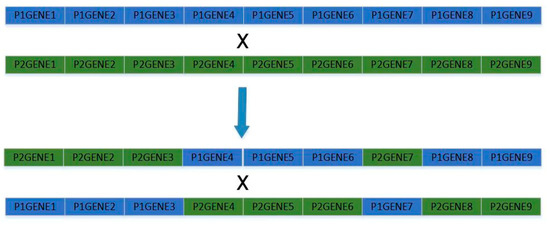 Figure 10. PXM crossover operation.
Figure 10. PXM crossover operation.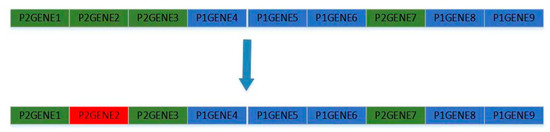 Figure 11. Mutation operation.
Figure 11. Mutation operation. - Form the progeny population, combine the parent and progeny populations and calculate the fitness of the combined population;
- For non-dominated quick sort, calculate the non-dominated value rank value and crowding degree of the combined population;
- For elite selection, select the top N individuals in the combined population to form a new population. The parent population and the progeny population are synthesized into a population according to the following rules to generate a new parent population from the population. According to the order of Pareto level from low to high, put the population of the same level into the parent population until a certain level of individuals of this level cannot be put into the parent population, arrange the individuals in this layer from large to small according to the degree of crowding, and put them in turn. Enter the parent population until it reaches the parent population;
- End the iteration if the set maximum number of iterations is reached; otherwise, return to Step 6.
3. Results
3.1. Parameter Settings
There are no standard test examples for MDMFVRPSPD. Montoya et al. studied the electric vehicle problems (EVRP) [39]. In the experiment, examples in the research content were selected to verify the algorithm designed in this paper, and the EVRP example was modified to generate a test example of MDMFVRPSPD for experimental verification. The algorithm programming adoption is MATLAB R2019b, the operating system is Windows10, the computer memory is 16 G, CPU is Inteli7-11800H, and the computer frequency is 2.3 GHz.
The data provided in [39] are: single distribution center coordinate, customer coordinate, charging station coordinate, customer service time, electric vehicle battery capacity etc. On this basis, fuzzy time window information, multi-distribution center coordinates, vehicle load of mixed fleet, average speed of each section and other variables are added.
According to the research conclusion put forward by Zhang [40],. The tax on CO2 emissions is 50 CNY/t. The following parameters refer to [8] literature assumptions:, . According to the research conclusion put forward by Wang [25], we arrange the vehicle to enter the charging station when 20% power is left, , .
Gasoline for motor vehicles (standard number: GB 17930-2016) stipulates that the density of gasoline should be between 0.72 and 0.775 g per milliliter at 20 °C [41]. The calorific value of gasoline is about 44000 kJ/kg; if the density is 0.73 g/mL, then 1 L gasoline can produce 3.212 × 104 kJ energy. ξ = 1/3.212 × 104. A value of 1 kWh can provide 3600 kJ energy. ξ′ = 1/3.6 × 103.
The purchase of different models of electric vehicles by different companies results in different and d. The values of and d can be determined according to the actual situation of different companies. This paper assumes that the total number of charge and discharge cycles q of the electric vehicle d is 2000 times. This paper assumes that the charging and discharging cycle time before the electric vehicle is = 10 h; when the electric vehicle operates for 10 h, the operation is stopped and the battery is put on hold for a period of time to rest.
The following parameters refer to [42] literature assumptions: = 1 CNY/kWh. The following parameters refer to [23] literature assumptions: , = 2.5 t, fleet load for 20 customer examples = 7 t, fleet load for 40 customer examples = 5 t, fleet load for 80 customer examples = 6 t, = 15 CNY/h, = 8 CNY/h. The fixed cost of a vehicle is the fixed use cost of each vehicle, including the sum of labor costs and vehicle depreciation costs. When the arrangement of vehicles for fuel vehicles, = CNY 600, = 6.26 CNY/L. When the arrangement of vehicles for electric vehicles, = CNY 400, = 0.6226 CNY/kWh. On this basis, the algorithm and model are verified.

Table 2.
Data parameters.

Table 3.
Algorithm parameters.
3.2. Example Test
In this paper, 20 customers’, 40 customers’, and 80 customers’ arithmetic examples are selected to verify the validity of the model and algorithm. We use the following convention to name the examples [39]: tcAcBsCcDE. Among them: A is the method used to place customers (0: Uniform random, 1: gather,2: the combination); B is the number of customers; C is the number of charging stations; CD stands for “T” if the charging station is not randomly located. If it is randomly positioned, it is “F”; E is the number of instances of each parameter combination.
We assume that the total weight of the goods that need to be picked up and delivered by 20 customers is exactly two vehicles, the total weight of the goods that need to be picked up and delivered by 40 customers is exactly five vehicles, and the total weight of the goods that need to be picked up and delivered by 80 customers is exactly six vehicles. During initial testing, the charging station plug-in strategy allowed only one charge and was found to be able to handle only small instances, not some large ones. A new charging station insertion strategy allows electric vehicles to enter the same charging station repeatedly, allowing for unlimited charging of electric vehicles.
CSPS-NSGA II is used to solve the multi-site vehicle routing problem of simultaneous delivery and pickup under dynamic energy consumption as shown in Table 4. Among them: is the average number of the Pareto optimal solution set entering the charging station. The number 1/2 refers to the number of times an electric vehicle enters a charging station. Max(), Min(), and Average() are the maximum, minimum, and average values of objective function 1 (total customer cost) in Pareto optimal frontier, respectively, Max(), Min(), and Average() are the maximum, minimum, and average values, respectively, of objective function 2 (1-average customer satisfaction) in Pareto optimal frontier, and V is vehicle usage. In o1 and o2, o1 refers to the number of fuel vehicles and o2 refers to the number of electric vehicles. The number 1–1/0–2 indicates the ratio of the number of fuel vehicles to electric vehicles in the fleet. There are two cases. The first scenario is a mixed fleet of one fuel vehicle and one electric vehicle. The second scenario is a mixed fleet of zero fuel vehicles and two electric vehicles.

Table 4.
Example test results.
Three examples, namely tc2c20s3cf0, tc2c40s5ct2, and tc2c80s8cf4, are randomly selected from the examples with 20, 40, and 80 customers, respectively. The Pareto non-inferior solution set distribution of the mixed fleet is shown in Figure 12, Figure 13 and Figure 14. Each point of Pareto optimal frontier corresponds to a different Pareto optimal solution. The abscissa axis represents the value of the objective function , and the ordinate axis represents the value of the objective function .
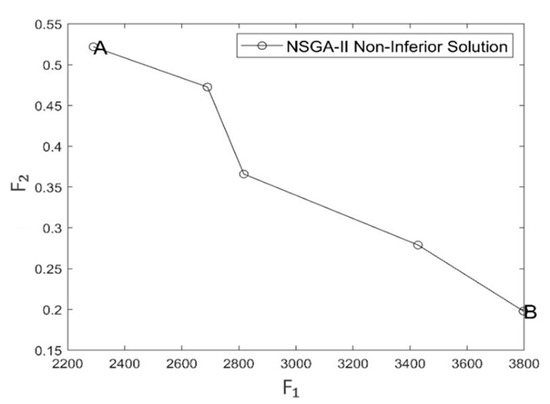
Figure 12.
Distribution of Pareto set for the example of 20 customers.
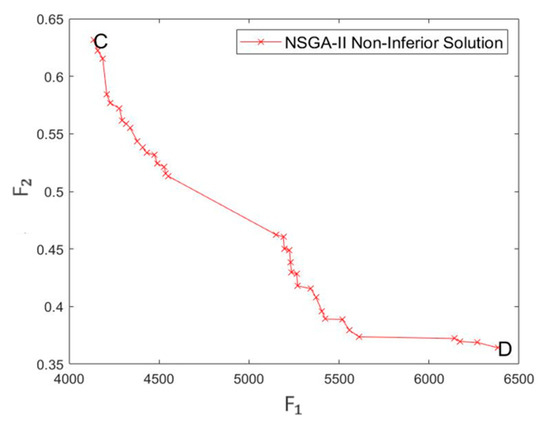
Figure 13.
Distribution of Pareto set for the example of 40 customers.
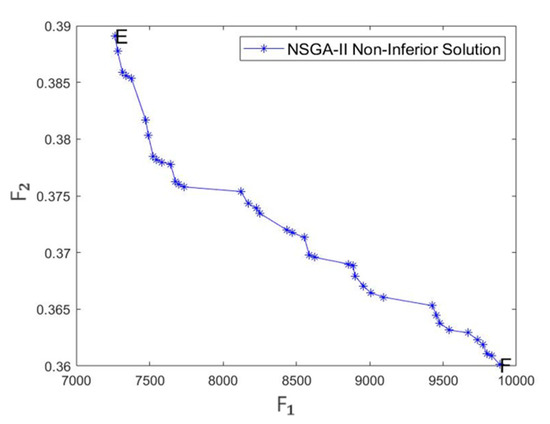
Figure 14.
Distribution of Pareto set for the example of 80 customers.
- It can be concluded from the test table of calculation example results in Table 4 and Figure 12, Figure 13 and Figure 14 that there is a contradiction between customer satisfaction and distribution enterprise cost. Random generation of 20, 40, or 80 customer points of each pick and delivery volume occurs. When the goods carried by the vehicles meet the vehicle load, the vehicles return to any distribution center. In order to compare the impact of the number of vehicles on the objective function, the number of vehicles in the fleet is assumed to be 2, 5, and 6. In the 20-customer example, each car needs to satisfy 10 customers on average. In the case of 40 customers, each car needs to satisfy 8 customers on average, and in the case of 80 customers, each car needs to satisfy 13 customers on average. In the CSPS-NSGA II solution results, 46.67% of the examples have customer satisfaction of more than 60%, 46.67% of the examples have customer satisfaction of more than 50%, and 6.67% of the examples have customer satisfaction of more than 40%. The average cost of each calculation case of 15 calculation cases is CNY 2018.33, which can improve the average customer satisfaction by 22.94%.
- It can be seen from the comparison of 20 customer examples, 40 customer examples, and 80 customer examples in Table 4 that with the increase in customer points, the distribution distance will increase. The distribution path with too long a distance will lead to the frequent charging and discharging of electric vehicles in charging stations, resulting in redundant formal costs and charging costs. Therefore, the number of fuel vehicles will gradually increase, while the number of electric vehicles will gradually decrease.
- This can be seen from the comparison of 20 customer examples and 40 customer examples as well as 20 customer examples and 80 customer examples in Table 4. The number of distribution vehicles increases with the number of customer points, and the total cost of distribution increases with the number of customer points and the number of distribution vehicles. The more customer points in the driving path of each vehicle, the more difficult the time window of customer demand is to meet and the lower the customer satisfaction is. The greater the number of customers, the greater the cost of enterprise distribution.
- From the 40-customer example in Table 4 and the 80-customer examples: when the distribution task for the number of electric vehicles in the mixed team uses more fuel, then average customer satisfaction is low, because the electric car in the process of long-distance distribution frequently enters into the charging station, and charging time influences the customer satisfaction.
Points A, B, C, D, E, F are shown in Figure 12, Figure 13 and Figure 14 above. The optimization path results of solutions A, C, and E with the minimum total cost in the non-inferior Pareto solution set and solutions B, D, and F with the maximum total cost are shown in Table 5. and are the solutions of objective function 1 and objective function 2, respectively.

Table 5.
CSPS-NSGAII optimization path results.
As can be seen from Table 4, the total cost of point A is CNY 2290.20, with an average customer satisfaction of 47.8%; the total cost of point B is CNY 3797.38, with an average customer satisfaction of 80.21%; the cost of CNY 1507.18 increases customer satisfaction by 32.41%; the total cost of point C is CNY 4134.77, with an average customer satisfaction of 36.85%; the total cost of point D is CNY 6381.82, with an average customer satisfaction of 63.59%, with a 26.74% increase in customer satisfaction at a cost of CNY 2247.05. The total cost of point E is CNY 7263.14, with an average customer satisfaction of 61.09%; the total cost of point F is CNY 9886.94, with an average customer satisfaction of 63.99%; the cost of CNY 2623.8 increases customer satisfaction by 2.9%. The experimental results show that the model and algorithm designed in this paper are effective and can solve small and large calculation examples.
3.3. Economic Benefits
To further demonstrate the benefits of hybrid fleets to businesses, a comparative analysis of the total cost and average customer satisfaction of fuel and hybrid fleets is presented in Table 6. Average() is the average of the total customer cost of the mixed fleet at the Pareto optimal frontier, while Average() is the average of the 1-average customer satisfaction of the mixed fleet at the Pareto optimal frontier. Average() is the average of the total customer cost of the fuel fleet at the Pareto optimal frontier, while Average() is 1-average customer satisfaction of the fuel fleet at the Pareto optimal frontier.

Table 6.
Cost comparison of fuel and hybrid fleets.
A comparison of the total cost and average customer satisfaction between the fuel fleet and the hybrid fleet is shown in Figure 15.
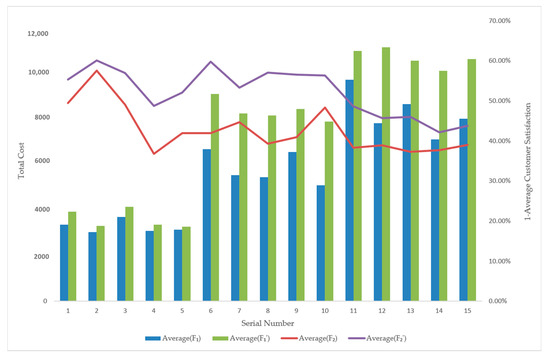
Figure 15.
A comparison of the total cost and average customer satisfaction between the fuel fleet and the hybrid fleet.
As can be seen from Table 6 and Figure 15, the cost and average customer satisfaction of using the hybrid fleet are much lower than the cost of using the oil fleet. When companies face large-scale logistics and distribution orders, mixed fleets can be prioritized to complete distribution tasks, which will reduce enterprise distribution costs and improve customer satisfaction.
4. Discussion
4.1. Electric Vehicle Charge and Discharge Cycle Time
In the process of path optimization of hybrid fleet, different charging and discharging cycle times of electric vehicles have certain influence on the optimization results. A group of examples were randomly selected to compare the optimization results under different charge–discharge cycle time constraints, as shown in Figure 16. Among them, the abscis-sa represents the charging and discharging cycle time, the left ordinate represents the total cost, and the right ordinate represents the average customer satisfaction.
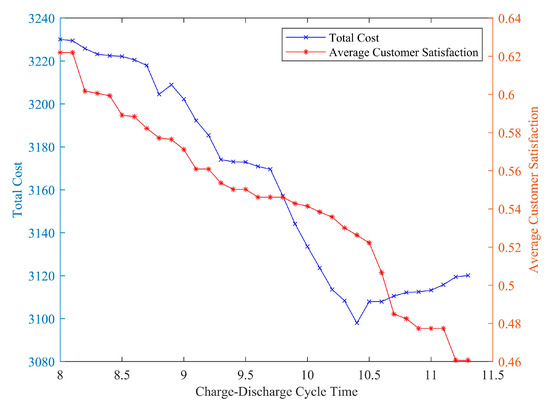
Figure 16.
Sensitivity analysis of electric vehicle charging and discharging cycle time.
The experimental results show that the total distribution cost decreases with the increase in the maximum charge–discharge cycle time of electric vehicles, but when it increases to a certain extent, the total distribution cost decreases slowly until it no longer decreases and presents an increasing trend. This is because with the increase in the maximum charge–discharge cycle time of electric vehicles and the increase in the available number of electric vehicles, the distribution cost of the system gradually decreases. When the number of electric vehicles increases to fully serve all customers, the increase in electric vehicles can no longer reduce the distribution cost. The average customer satisfaction decreases with an increase in the maximum charge–discharge cycle time of electric vehicles. This is because, with the increase in the available number of electric vehicles, electric vehicles frequently enter charging stations during delivery tasks, resulting in charging costs and battery depreciation costs, which violate customer time windows and reduce customer satisfaction. Thus, logistics enterprise can choose according to the residual life of electric vehicles flexible electric vehicle maximum charge and discharge cycle time, but the electric vehicle charging and discharging cycle time is not the bigger the better and can vary according to the different battery life of each electric car, customer demand factors such as scale and demand distribution, and reasonable electric vehicle maximum charge and discharge cycle time.
4.2. Battery Capacity and Charging Rate
A group of hybrid motorcades was randomly selected as an example. Given the battery capacity and charging rate of the electric vehicle, the battery capacity and charging rate gradually increased. The influence of battery capacity on total distribution cost and customer satisfaction is shown in Figure 17 when the remaining electric power of electric vehicles is lower than 20% and the charging depth is 100%. The ordinate represents the average customer satisfaction in Figure 17a, and the ordinate represents the total cost in Figure 17b.
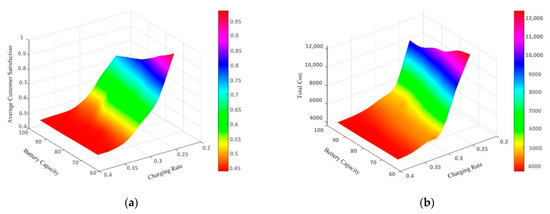
Figure 17.
Sensitivity analysis of electric vehicle battery capacity and charging rate: (a) Impact of battery capacity and charge rate on total cost; (b) impact of battery capacity and charge rate on average customer satisfaction.
The total distribution cost and average customer satisfaction decrease with the increase in battery capacity, because the driving distance of vehicles increases with the increase in battery capacity. More customer points can be included in the vehicle travel schedule to reduce the number of vehicles used. However, when the battery capacity increases to a certain extent, the total cost gradually decreases with the increase in battery capacity until it no longer changes, because the electric vehicle with the increase in battery capacity can serve all customers of the existing customer base without entering the charging station. The total distribution cost and average customer satisfaction decrease with the increase in charging rate because the increase in charging rate reduces the charging time, and electric vehicles can reach more customer points to provide services within the customer time window. However, when the battery capacity increases to a certain extent, the trend of the total cost decreasing with the increase in charging rate is no longer obvious until it no longer decreases; that is, the electric vehicle can serve all customers without visiting the charging station. Battery capacity and charging rate have great influence on total cost and customer satisfaction for logistics enterprises in the purchase of vehicles when combining different charging rates of charging stations in the area of city and purchasing different battery capacities of electric vehicle resources rationally. The distribution area with a low charging rate of the charging station arranges the larger battery capacity for electric vehicles, while the distribution area with a high charge rate of charging stations arranges the battery capacity of small electric vehicles.
5. Conclusions
This paper studies the multi-center hybrid vehicle routing problem integrating re-verse logistics.
According to the principle of system dynamics, the operating cost system of the mixed fleet is analyzed, which mainly includes seven subsystems: energy consumption subsystem, vehicle fixed-use cost subsystem, time cost subsystem, charging cost subsystem, depreciation cost system, carbon emission cost system, and customer satisfaction degree system. A two-layer optimization model is established, and the upper-layer optimization objective is to minimize the total cost. The total cost consists of energy cost, fixed cost, penalty cost, opportunity cost, charging cost, battery depreciation cost, and carbon emission cost. The lower-level optimization goal is to maximize the average customer satisfaction.
On the basis of considering delaying the aging of electric vehicle batteries, a novel charging station insertion strategy is designed. A fast non-dominated sorting multi-objective genetic algorithm based on charging station insertion strategy and elite strategy was designed. The effectiveness of the model and algorithm is verified by numerical examples, and the results show that 46.67% of the examples have customer satisfaction over 60%, 46.67% of the examples have customer satisfaction over 50%, and 6.67% of the examples have customer satisfaction over 40%. The average cost of each calculation case of 15 calculation cases is CNY 2018.33, which can improve the average customer satisfaction by 22.94%. The model and algorithm proposed in this paper can obtain satisfactory solution in an acceptable time for both small and large cases.
Sensitivity analysis was conducted on key factors of charging and discharging cycle time, battery capacity and charging rate of electric vehicles; the influence of their changes on total cost and customer satisfaction was studied, and corresponding management suggestions were put forward.
This study enriches the theoretical research on vehicle routing problems in mixed fleets. This method helps companies to formulate transportation plans according to the actual situation, including providing a cost model that considers multiple influencing factors and improving the average customer satisfaction while reducing the total cost expenditure. Logistics enterprises with multiple distribution centers can give priority to this idea when developing high-precision distribution schemes for large-scale distribution tasks.
In daily life, the needs of customers are dynamically changing. The limitation of this paper is that it does not consider the dynamic changes of customer needs. Considering the dynamic demands of customers, the multi-center mixed-vehicle routing problem based on dynamic energy consumption and integrated reverse logistics will be the focus of future research.
Author Contributions
Conceptualization, M.L. and Y.S.; methodology, B.Z.; software, M.L.; validation, M.L., Y.S. and B.Z.; formal analysis, M.L.; investigation, M.L.; resources, M.L.; data curation, M.L.; writing—original draft preparation, M.L. and B.Z.; writing—review and editing, Y.S.; visualization, M.L.; supervision, Y.S.; project administration, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
Thanks to each member of the team, it is the mutual encouragement and joint efforts of each member of the team that enabled us to successfully complete this study. As the saying goes, the fire is high when everyone adds wood, and the contribution of every member of the team is indispensable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bruglieri, M.; Mancini, S.; Pezzella, F.; Pisacane, O. A path-based solution approach for the green vehicle routing problem. Comput. Oper. Res. 2019, 103, 109–122. [Google Scholar] [CrossRef]
- National Bureau of Statistics. Statistical Bulletin of the People′s Republic of China on National Economic and Social Development in 2021. 2021. Available online: http://www.stats.gov.cn/tjsj/zxfb/202202/t20220227_1827960.html (accessed on 19 March 2022).
- Teoh, T.; Kunze, O.; Teo, C.C.; Wong, Y.D. Decarbonisation of urban freight transport using electric vehicles and opportunity charging. Sustainability 2018, 10, 3258. [Google Scholar] [CrossRef] [Green Version]
- Islam, M.A.; Gajpal, Y.; ElMekkawy, T.Y. Mixed fleet based green clustered logistics problem under carbon emission cap. Sustain. Cities Soc. 2021, 72, 103074. [Google Scholar] [CrossRef]
- Xv, X.; Jiang, M.; Deng, Y. Dynamic vehicle routing problem with simultaneous pickup and delivery in collaborative distributi-on under demand concurrent. J. Manag. Sci. China 2021, 24, 106–126. [Google Scholar]
- Rahman, I.; Vasant, P.M.; Singh, B.S.M.; Abdullah-Al-Wadud, M.; Adnan, N. Review of recent trends in optimization techniques for plug-in hybrid, and electric vehicle charging infrastructures. Renew. Sust. Energ. Rev. 2016, 58, 1039–1047. [Google Scholar] [CrossRef]
- Luo, L.; He, P.; Zhou, S.; Lou, G.; Fang, B.; Wang, P. Optimal scheduling strategy of EVs considering the limitation of battery state switching times. Energy Rep. 2022, 8, 918–927. [Google Scholar] [CrossRef]
- Wang, M. The Electric Vehicle Routing Problem considering Nonlinear Battery Depreciation; Tsinghua University: Beijing, China, 2018. [Google Scholar]
- Epding, B.; Ramberg, B.; Jahnke, H.; Stradtmann, I.; Kwade, A. Investigation of significant capacity recovery effects due to long rest periods during high current cyclic aging tests in automotive lithium ion cells and their influence on lifetime. J. Energy Storage 2019, 22, 249–256. [Google Scholar] [CrossRef]
- Zang, Y.; Wang, M.; Qi, M. A column generation tailored to electric vehicle routing problem with nonlinear battery depreciation. Comput. Oper. Res. 2022, 137, 105527. [Google Scholar] [CrossRef]
- Pelletier, S.; Jabali, O.; Laporte, G. The electric vehicle routing problem with energy consumption uncertainty. Transp. Res. B-Meth. 2019, 12, 225–255. [Google Scholar] [CrossRef]
- Ferro, G.; Paolucci, M.; Robba, M. Optimal Charging and Routing of Electric Vehicles with Power Constraints and Time-of-Use Energy Prices. IEEE Trans. Veh. Technol. 2020, 69, 14436–14447. [Google Scholar] [CrossRef]
- Hou, D.; Fan, H.; Ren, X. Multi-Depot Joint Distribution Vehicle Routing Problem Considering Energy Consumption with Time-Dependent Networks. Symmetry 2021, 13, 2082. [Google Scholar] [CrossRef]
- Li, J.; Wang, F.; He, Y. Electric Vehicle Routing Problem with Battery Swapping Considering Energy Consumption and Carbon Emissions. Sustainability 2020, 12, 10537. [Google Scholar] [CrossRef]
- You, G. Sustainable vehicle routing problem on real-time roads: The restrictive inheritance-based heuristic algorithm. Sustain. Cities Soc. 2022, 79, 103682. [Google Scholar] [CrossRef]
- Gan, J.; Zhan, X.; Li, J. Electric refrigerate vehicle routing optimization with time windows and energy consumption. Ind. Eng. Manag. 2022, 27, 204–210. [Google Scholar]
- Hornstra, R.P.; Silva, A.; Roodbergen, K.J.; Coelho, L.C. The vehicle routing problem with simultaneous pickup and delivery and handling costs. Comput. Oper. Res. 2020, 115, 10485. [Google Scholar] [CrossRef]
- Foroutan, R.A.; Rezaeian, J.; Mahdavi, I. Green vehicle routing and scheduling problem with heterogeneous fleet including reverse logistics in the form of collecting returned goods. Appl. Soft Comput. 2020, 94, 106462. [Google Scholar] [CrossRef]
- Jia, Y.; Zeng, W.; Xing, Y.; Yang, D.; Li, J. The Bike-Sharing Rebalancing Problem Considering Multi-Energy Mixed Fleets and Traffic Restrictions. Sustainability 2021, 13, 270. [Google Scholar] [CrossRef]
- Al-dal’ain, R.; Celebi, D. Planning a mixed fleet of electric and conventional vehicles for urban freight with routing and replacement considerations. Sustain. Cities Soc. 2021, 73, 103105. [Google Scholar] [CrossRef]
- Malladi, S.S.; Christensen, J.M.; Ramirez, D.; Larsen, A.; Pacino, D. Stochastic fleet mix optimization: Evaluating electromobility in urban logistics. Transp. Res. E-Log 2022, 158, 102554. [Google Scholar] [CrossRef]
- Yu, V.F.; Jodiawan, P.; Gunawan, A. An Adaptive Large Neighborhood Search for the green mixed fleet vehicle routing problem with realistic energy consumption and partial recharges. Appl. Soft Comput. 2021, 105, 107251. [Google Scholar] [CrossRef]
- Hou, K.; Fan, H.; Ren, X. Vehicle routing optimization of multi-center hybrid fleet joint distrubution under time-varying road network. J. Dalian Marit. Univ. 2022, 48, 11–22. [Google Scholar]
- Li, Y.; Zhang, P.; Wu, Y. Vehicle routing problem with mixed fleet of conventional and electric vehicles. J. Syst. Manag. 2020, 29, 522–531. [Google Scholar]
- Wang, J.; Wang, H.; Chang, A.; Song, C. Collaborative Optimization of Vehicle and Crew Scheduling for a Mixed Fleet with Electric and Conventional Buses. Sustainability 2022, 14, 3627. [Google Scholar] [CrossRef]
- Shojaei, M.; Fakhrmoosavi, F.; Zockaie, A.; Ghamami, M.; Mittal, A.; Fishelson, J. Sustainable Transportation Networks Incorporating Green Modes for Urban Freight Delivery. J. Transp. Eng. A-Syst. 2022, 148, 04022028. [Google Scholar] [CrossRef]
- Rinaldi, M.; Picarelli, E.; D′Ariano, A.; Viti, F. Mixed-fleet single-terminal bus scheduling problem: Modelling, solution scheme and potential applications. Omega 2020, 96, 102070. [Google Scholar] [CrossRef]
- Lu, T.; Yao, E.; Zhang, Y.; Yang, Y. Joint Optimal Scheduling for a Mixed Bus Fleet Under Micro Driving Conditions. IEEE Trans. Intell. Transp. Syst. 2021, 22, 2464–2475. [Google Scholar] [CrossRef]
- Zhao, P.; Liu, F.; Guo, Y.; Duan, X.; Zhang, Y. Bi-Objective Optimization for Vehicle Routing Problems with a Mixed Fleet of Conventional and Electric Vehicles and Soft Time Windows. J. Adv. Transp. 2021, 2021, 9086229. [Google Scholar] [CrossRef]
- Ren, X.; Huang, H.; Feng, S.; Liang, G. An improved variable neighborhood search for bi-objective mixed-energy fleet vehicle routing problem. J. Clean. Prod. 2020, 275, 124155. [Google Scholar] [CrossRef]
- LI, D.; Chen, Y.; Zhang, Z. A branch-and price algorithm for electric vehicle routing problem with time windows and mixed fleet. Syst. Eng.-Theory Pract. 2021, 41, 995–1009. [Google Scholar]
- Rafael, B.; Balazs, K.; Bo, E. Energy consumption estimation integrated into the electric vehicle routing problem. Transp. Res. D Transp. Environ. 2019, 69, 141–167. [Google Scholar]
- Zhao, H.; Zhang, C. An online-learning-based evolutionary many-objective algorithm. Inf. Sci. 2020, 509, 1–21. [Google Scholar] [CrossRef]
- Pasha, J.; Dulebenets, M.A.; Fathollahi-Fard, A.M.; Tian, G.D.; Lau, Y.Y.; Singh, P.; Liang, B.B. An integrated optimization method for tactical-level planning in liner shipping with heterogeneous ship fleet and environmental considerations. Adv. Eng. Inform. 2021, 48, 101299. [Google Scholar] [CrossRef]
- Dulebenets, M.A.; Pasha, J.; Kavoosi, M.; Abioye, O.F.; Ozguven, E.E.; Moses, R.; Boot, W.R.; Sando, T. Multiobjective optimization model for emergency evacuation planning in geographical locations with vulnerable population groups. J. Manag. Eng. 2020, 36, 04019043. [Google Scholar] [CrossRef]
- Dulebenets, M.A. A Delayed Start Parallel Evolutionary Algorithm for just-in-time truck scheduling at a cross-docking facility. Int. J. Prod. Econ. 2019, 212, 236–258. [Google Scholar] [CrossRef]
- Rabbani, M.; Oladzad-Abbasabady, N.; Akbarian-Saravi, N. Ambulance routing in disaster response considering variable patient condition: NSGA-II and MOPSO algorithms. J. Ind. Manag. Optim. 2022, 18, 1035. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V.A. Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Montoya, A.; Gueret, C.; Mendoza, J.E.; Villegas, J.G. The electric vehicle routing problem with nonlinear charging function. Transp. Res. B-Meth. 2017, 103, 87–110. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Qiao, X.; Xiao, B.; Wang, R.; Mao, C. Multi-objective vehicle routing optimization based on low carbon perspective and random demand. J. Railw. Sci. Eng. 2021, 18, 2165–2174. [Google Scholar]
- National Energy Administration, Gasoline for Motor Vehicles, GB 17930-2016. 2016. Available online: http://openstd.samr.gov.cn/bzgk/gb/newGbInfo?hcno=C45A3554980A86E41F5AA4C6F3D48DC1 (accessed on 19 March 2022).
- Zheng, Y.; Li, F.; Dong, J.; Luo, J.; Zhang, M.; Yang, X. Optimal Dispatch Strategy of Spatio-temporal Flexibility for Electric Vehicle Charging and Discharging under “EVs-traffic-distribution” Model. Autom. Electr. Power Syst. 2022, 1–27. Available online: http://kns.cnki.net/kcms/detail/32.1180.TP.20220430.0926.002.html (accessed on 27 April 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).