Analysis of M/M/1/N Stochastic Queueing—Inventory System with Discretionary Priority Service and Retrial Facility
Abstract
:1. Introduction
Literature Review
2. Model Description
2.1. Definitions
2.1.1. Non-Preemptive Priority (Head-of-The-Line Priority Discipline)
2.1.2. Preemptive Priority Discipline
2.1.3. Mixed-Priority Discipline
2.1.4. Discretionary Priority Discipline
2.2. Notations
2.3. Explanation of the Model
- The HP customer is at service;
- The LP customer is receiving stage-II service;
- The LP customer is at stage-I service, when the inventory is greater than L;
- The HP customer decides to wait with probability ;
- With zero inventory level.
- When the inventory is zero;
- On interruption from an HP customer at stage-I;
- If the server is busy with HP or LP customers.
3. Analysis
3.1. Steady-State Analysis
3.2. Computation of R-Matrix
3.3. System Performance Measures
- Expected inventory level:
- Expected perishable rate:
- Expected reorder rate:
- Expected number of HP customers in the waiting hall:
- Expectation of HP customer entering into the waiting hall:
- Expected waiting time of an HP:
- Expected number of LP customers in the orbit:
- Expected number of LP customers lost:
- Expected number of HP customers lost:
- Expected number of times an HP customer interrupts an LP customer:
- Probability of server being idle:
- Probability of server being busy:
- Expected number of times a server carries out the orbital search:
- Overall rate of retrial:
- Successful rate of retrial:
- Fraction of successful rate of retrial:
3.4. Cost Analysis
4. Numerical Discussions
- Mixed priority: At , the optimum value is obtained similarly at , and as shown in Table 2. This shows the impact of interruption, based on the discretionary priority. On comparing with case (i), as we expected, the discretionary priority service process gives the minimum optimal total cost rather than the usual priority service patterns.
- Preemptive priority discipline: At , the optimum total cost is obtained at , , and , as shown in Table 3. Even though the of this case is minimum than that of the case (i), we conclude that case (ii) provides the best service discipline. This is because, when a company allows preemptive priority, it may lose its LP customers. The growth of the company obviously depends upon all types of customers. So, the company must satisfy them by providing their best service. In such a way, discretionary priority discipline is considered the best one.
- Mixed priority: At r = 0.5, the total cost follows the same pattern of increment and decrement as in case (i), for all the parameters considered in Table 4, respectively. The optimum total cost obtained is at and . Thus, the optimum value obtained in discretionary priority is less than that of non-preemptive priority.
- Preemptive priority discipline: At , for the same value of the parameter as in case (i), we obtain the optimum total cost to be , which is less than those of non-preemptive and discretionary priority disciplines. However, depending on this , we cannot make the inference that preemptive priority discipline is economical. Although it seems like preemptive priority discipline is more profitable than the other priority discipline, it leads to the loss of new patrons for the business. A new LP customer who is ignored or made to wait for a long duration may leave the system before trying the product even once. Hence, discretionary priority is best suited to increase the customer base.
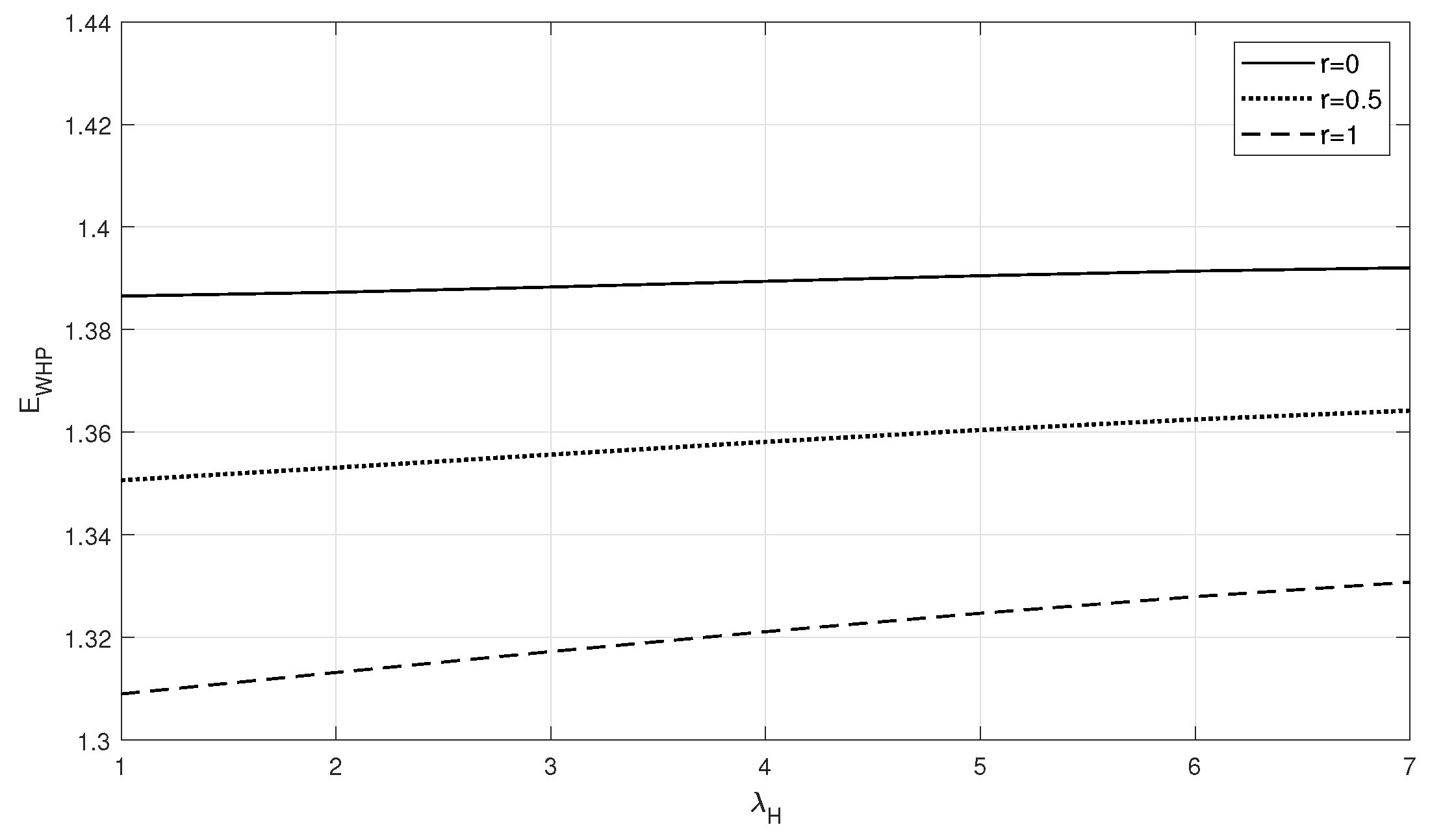
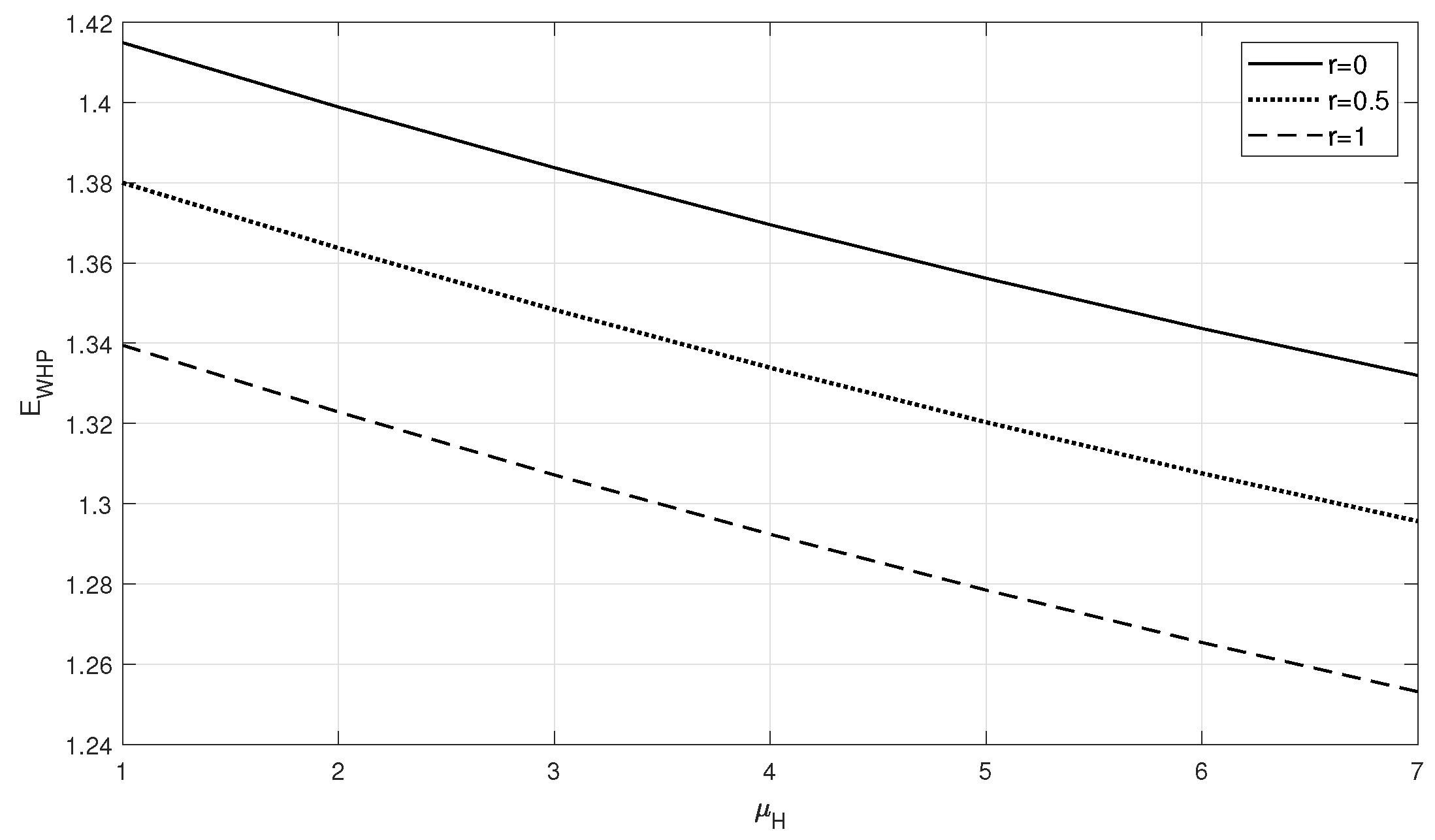
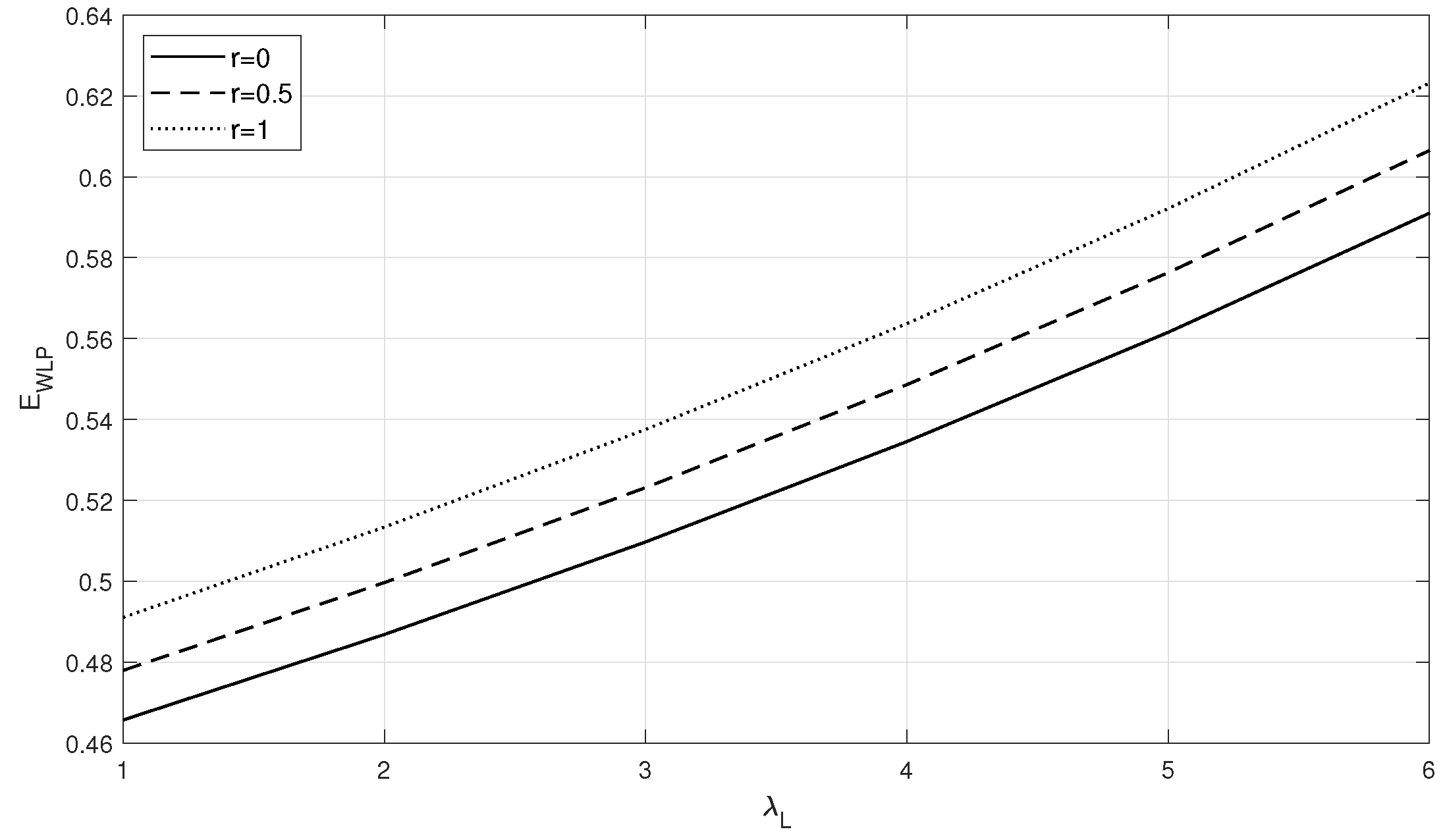
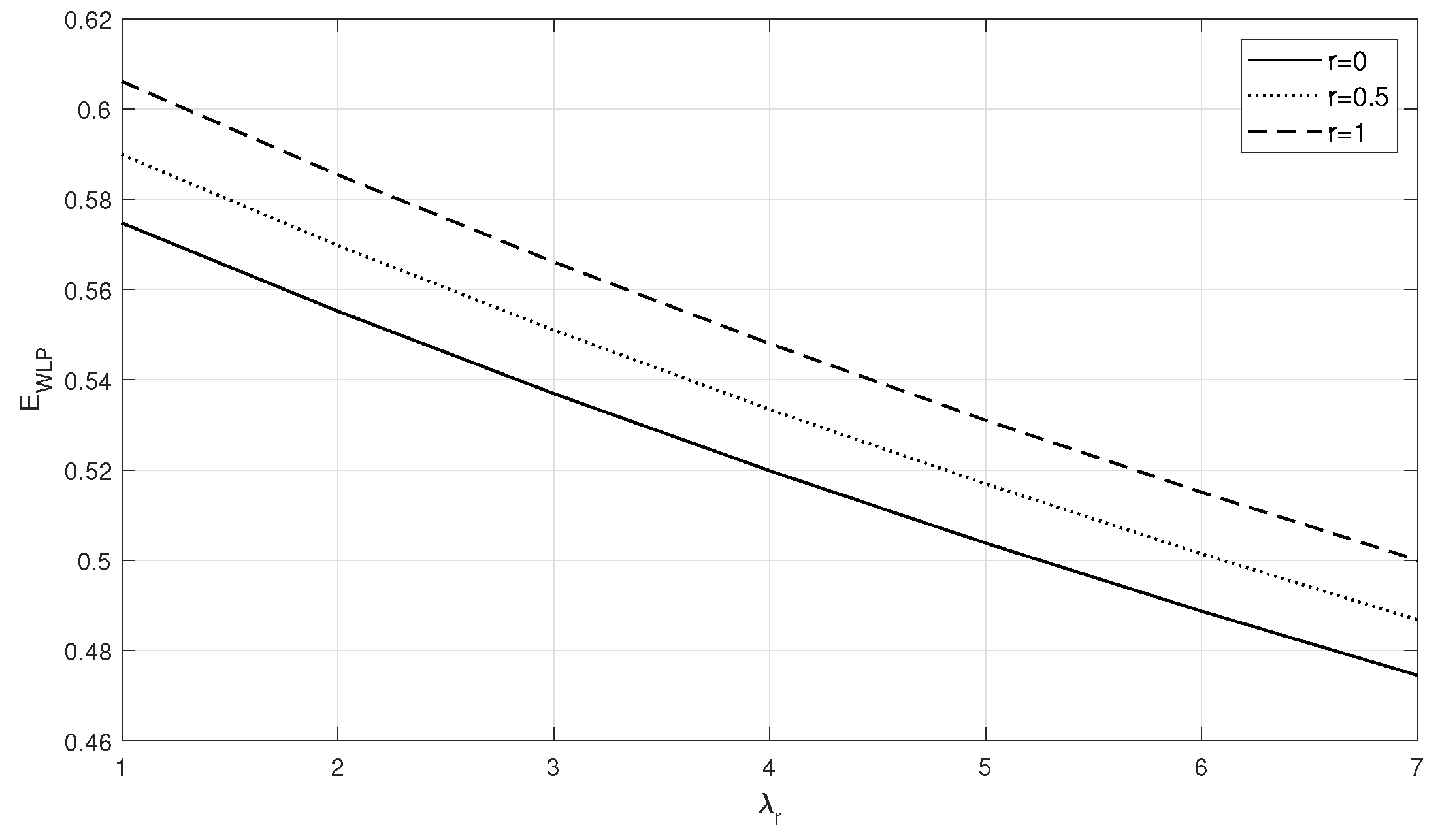
- Mixed priority: At , the measures and show the same variations as in case (i) for the respective parameters, but the difference is that the waiting time of HP customers is less, and the waiting time of LP customers is higher, compared with those in case (i).
- Preemptive Priority discipline: At , similar to case (i), the waiting times remain with the same variation with respect to the parameters considered in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, and the measure is considerably less and is much higher compared with those in case (i).
- Mixed priority: At , the loss of HP customers encountered by following discretionary priority is less compared with non-preemptive priority. In the same way, the loss of LP customers by following discretionary priority is greater compared with non-preemptive priority.
- Preemptive Priority: As seen previously, the measure is a little less compared with case (i), and is slightly greater than mixed priority. Thus, the loss of an HP customer heightens with non-discretionary priority, and an LP customer rises with preemptive priority. However, the intensified loss of any one type of customer will affect the reputation of the organization, which in turn decreases the growth of the business. Hence, to maintain an admissible loss of any type of customer, the following discretionary priority is advisable.
- The increases with despite the increment in on positive interruption.Since an increase in service rates allows the server to serve all customers in less time, the measure decreases with an increase in service rate and increases with arrival rate.
- It is clear from the table that, as the service rate, , increases, the server may complete the service to all HP customers, and the LP customers obtain a successful chance of retrial.
- Mixed priority: In contrast to case (i), we obtain the same increment and reduction in the case for the parameters, respectively. However, with discretionary priority, decreases and increases.
- Preemptive priority discipline: As discussed in case (i), the changes with respect to other parameters at are in the same order, but decreases, and increases slightly higher compared with case (i). With this, we conclude that the waiting hall accumulates non-preemptive priority, and the customers in orbit increase with preemptive priority. This also affects the business environment and once again shows the importance of discretionary priority discipline.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Melikov, A.Z.; Molchanov, A.A. Stock optimization in transport/storage. Cybern. Syst. Anal. 1992, 28, 484–487. [Google Scholar] [CrossRef]
- Sigman, K.; Simichi-Levi, D. Light traffic heuristic for an M/G/1 queue with limited inventory. Ann. Oper. Res. 1992, 40, 371–380. [Google Scholar] [CrossRef]
- Berman, O.; Kim, E. Stochastic models for inventory management at service facility. Commun. Stat. Stoch. Model. 1999, 15, 695–718. [Google Scholar] [CrossRef]
- Berman, O.; Sapna, K.P. Inventory Management for service facility for systems with arbitrarily distributed service time. Commun. Stat. Stoch. Model. 2000, 16, 343–360. [Google Scholar] [CrossRef]
- Sangeetha, N.; Sivakumar, B. Optimal service rates of a perishable inventory system with service facility. Int. J. Math. Oper. Res. 2020, 16, 515–550. [Google Scholar] [CrossRef]
- Jeganathan, K.; Selvakumar, S.; Anbazhagan, N.; Amutha, S.; Porpattama, H. Stochastic modeling on M/M/1/N inventory system with queue-dependent service rate and retrial facility. Aims Math. 2021, 6, 7386–7420. [Google Scholar] [CrossRef]
- Jacob, J.; Shajin, D.; Krishnamoorthy, A.; Vishnevsky, V.; Kozyrev, D. Queueing-Inventory with One Essential and m Optional Items with Environment Change Process Forming Correlated Renewal Process (MEP). Mathematics 2022, 10, 104. [Google Scholar] [CrossRef]
- Sugapriya, C.; Nithya, M.; Jeganathan, K.; Anbazhagan, N.; Joshi, G.P.; Yang, E.; Seo, S. Analysis of Stock-Dependent Arrival Process in a Retrial Stochastic Inventory System with Server Vacation. Processes 2022, 10, 176. [Google Scholar] [CrossRef]
- Klimenok, V.I.; Dudin, A.N.; Vishnevsky, V.M.; Semenova, O.V. Retrial BMAP/PH/N Queueing System with a Threshold-Dependent Inter-Retrial Time Distribution. Mathematics 2022, 10, 269. [Google Scholar] [CrossRef]
- Amirthakodi, M.; Sivakumar, B. An inventory system with service facility and feedback customers. Int. J. Ind. Syst. Eng. 2019, 33, 374–411. [Google Scholar]
- Jeganathan, K.; Anbazhagan, N.; Amutha, S.; Vinitha, V. A queueing inventory system with threshold based priority service and a flexible server. J. Stat. Manag. Syst. 2020, 24, 663–684. [Google Scholar] [CrossRef]
- Jeganathan, K.; Selvakumar, S.; Saravanan, S.; Anbazhagan, N.; Amutha, S.; Cho, W.; Joshi, G.P.; Ryoo, J. Performance of Stochastic Inventory System with a Fresh Item, Returned Item, Refurbished Item, and Multi-Class Customers. Mathematics 2022, 10, 1137. [Google Scholar] [CrossRef]
- Jeganathan, K.; Reiyas, M.A.; Selvakumar, S.; Anbazhagan, N. Analysis of Retrial Queueing-Inventory System with Stock Dependent Demand Rate: (s,S) Versus (s,Q) Ordering Policies. Int. J. Appl. Comput. Math. 2020, 5, 1–27. [Google Scholar] [CrossRef]
- Wang, J.; Qiu, Q.; Wang, H. Joint optimization of condition-based and age-based replacement policy and inventory policy for a two-unit series system. Reliab. Eng. Syst. Saf. 2021, 205, 107251. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, X.; Song, Y.; Qiu, Q. Joint optimization of condition-based maintenance and spares inventory for a series–parallel system with two failure modes. Comput. Ind. Eng. 2022, 168, 108094. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Joshua, A.N.; Kozyrev, D. Analysis of a Batch Arrival, Batch Service Queuing-Inventory System with Processing of Inventory While on Vacation. Mathematics 2021, 9, 419. [Google Scholar] [CrossRef]
- Maqbali, K.A.K.A.; Joshua, V.C.; Krishnamoorthy, A. On a Single Server Queueing Inventory System with Common Life Time for Inventoried Items. Commun. Comput. Inf. Sci. 2021, 1391, 186–197. [Google Scholar]
- Reshmi, P.S.; Jose, K.P. A queueing–inventory system with perishable items and retrial of customers. Malaya J. Math. 2019, 7, 165–170. [Google Scholar] [CrossRef] [Green Version]
- Sivakumar, B.; Arivarignan, A. A modified lost sales inventory system with two types of customers. Qual. Technol. Quant. Manag. 2008, 5, 339–349. [Google Scholar] [CrossRef]
- Uzunoglu Kocer, U.; Yalçin, B. Continuous review (s, Q) inventory system with random lifetime and two demand classes. Opsearch 2019, 57, 104–118. [Google Scholar] [CrossRef]
- Yadavalli, V.S.S.; Anbazhagan, N.; Jeganathan, K. A retrial inventory system with impatient customers. Int. J. Appl. Math. Inf. Sci. 2015, 9, 637–650. [Google Scholar]
- Zhang, J.; Zhao, X.; Song, Y.; Qiu, Q. Joint optimization of maintenance and spares ordering policy for a use-oriented product-service system with multiple failure modes. Appl. Stoch. Model. Bus Ind. 2021, 37, 1123–1142. [Google Scholar] [CrossRef]
- Falin, G.I.; Artalejo, J.R.; Martin, M. On the single server retrial queue with priority customers. Queueing Syst. 1993, 14, 439–455. [Google Scholar] [CrossRef]
- Jeganathan, K.; Anbazhagan, N.; Kathiresan, J. A Retrial Inventory System with Non-preemptive Priority Service. Int. J. Inf. Manag. Sci. 2013, 24, 57–77. [Google Scholar]
- Chakravarthy, S.R. A Dynamic Non-preemptive Priority Queueing Model with Two Types of Customers. In Proceedings of the Mathematics and Computing, ICMC, Varanasi, India, 9–11 January 2018; Springer: Singapore, 2018; Volume 253, pp. 23–42. [Google Scholar]
- Korenevskaya, M.; Zayats, O.; Ilyashenko, A.; Muliukha, V. Retrial Queuing System with Randomized Push-Out Mechanism and Non-Preemptive Priority. Procedia Comput. Sci. 2019, 150, 716–725. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Divya, V. (M, MAP)/(PH, PH)/1 Queue with Non-preemptive Priority and Working Vacation under N-Policy. J. Indian Soc. Probab. Stat. 2020, 21, 69–122. [Google Scholar] [CrossRef]
- Kumar, B.K.; Madheswari, S.P.; Arivudainambi, D. 2005. On the Busy Period of an M/G/1 Retrial Queueing System with Two-Phase Service and Preemptive Resume. Stoch. Model. Appl. 2005, 8, 18–34. [Google Scholar]
- Tarabia, A.M.K. Analysis of M/M/1 Queueing System with two Priority Classes. OPSEARCH 2007, 44, 346–365. [Google Scholar] [CrossRef]
- Jeganathan, K.; Kathiresan, J.; Anbazhagan, N. A retrial inventory system with priority customers and second optional service. Opsearch 2016, 53, 808–834. [Google Scholar] [CrossRef]
- Gao, S.; Wang, J. Stochastic analysis of a preemptive retrial queue with orbital search and multiple vacations. Rairo-Oper. Res. 2018, 54, 231–249. [Google Scholar] [CrossRef] [Green Version]
- Adiri, I.; Domb, I. A Single Server Queueing System Working under Mixed Priority Discipline. Oper. Res. 1982, 30, 97–115. [Google Scholar] [CrossRef]
- Cho, Y.; Un, C. Analysis of the M/G/1 Queue under a combined Preemptive/Nonpreemptive Priority Discipline. IEEE Trans. Commun. 1993, 41, 132–141. [Google Scholar] [CrossRef]
- Fajardo, V.A.; Drekic, S. On a General Mixed Priority Queue with Server Discretion. Stoch. Model. 2016, 32, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Avi-Itzhak, B.; Brosh, I.; Naor, P. On discretionary priority queueing. Zamm-J. Appl. Math. Mech. Fiir Angew. Math. Mech. 1964, 44, 235–242. [Google Scholar] [CrossRef] [Green Version]
- Melkonian, V.; Kaiser, M. Discretionary Priority Discipline: A Reasonable Compromise between Preemptive and Nonpreemtive Disciplines. Appl. Math. Lett. 1996, 9, 91–94. [Google Scholar] [CrossRef]
- Lian, Z.; Zhao, N. A two-stage M/G/1 queue with discretionary priority. In Proceedings of the 2011 IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 6–9 December 2011; pp. 1402–1406. [Google Scholar]
- Zhao, N.; Guo, Y.; Lian, Z.; Wang, M. Analysis of a MAP/PH/1 queue with discretionary priority. In Proceedings of the 2015 Winter Simulation Conference (WSC), Huntington Beach, CA, USA, 6–9 December 2015; pp. 2872–2883. [Google Scholar]
- Lian, Z.; Zhao, N. A Two-Stage Discretionary Priority Service System with Markovian Arrival Inputs. In Proceedings of the 2010 IEEE International Conference on Industrial Engineering and Engineering Management, Macao, China, 7–10 December 2010; pp. 438–442. [Google Scholar]
- Zhao, N.; Lian, Z.; Wu, K. Analysis of a MAP/PH/1 Queue with Discretionary Priority Based on Service Stages. Asia-Pac. J. Oper. Res. 2015, 32, 1550042. [Google Scholar] [CrossRef]
- Neuts, M. Matrix Geometric Solutions in Stochastic Models: An Algorithmic Approach; John Hopkins University Press: Baltimore, MD, USA, 1981. [Google Scholar]


| S|s | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 28 | 3.187610 | 3.132378 | 3.114067 | 3.102593 | 3.110016 | 3.132837 | 3.164871 |
| 29 | 3.170042 | 3.116397 | 3.108295 | 3.093581 | 3.099043 | 3.120513 | 3.151056 |
| 30 | 3.157677 | 3.103865 | 3.097418 | 3.088793 | 3.092117 | 3.111897 | 3.140980 |
| 31 | 3.153721 | 3.101571 | 3.095904 | 3.089001 | 3.095888 | 3.114345 | 3.142301 |
| 32 | 3.162313 | 3.113600 | 3.111644 | 3.106273 | 3.114821 | 3.135832 | 3.163509 |
| S|s | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 28 | 3.156901 | 3.107505 | 3.094919 | 3.087682 | 3.098520 | 3.119306 | 3.155629 |
| 29 | 3.140263 | 3.092402 | 3.089834 | 3.079195 | 3.088026 | 3.107578 | 3.142287 |
| 30 | 3.128573 | 3.080375 | 3.079441 | 3.074810 | 3.081410 | 3.099400 | 3.132570 |
| 31 | 3.125040 | 3.078352 | 3.078033 | 3.075131 | 3.085328 | 3.102140 | 3.134130 |
| 32 | 3.133964 | 3.090639 | 3.094001 | 3.092575 | 3.104508 | 3.124117 | 3.155706 |
| S|s | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 28 | 3.027256 | 3.005787 | 3.018169 | 3.027169 | 3.050287 | 3.068396 | 3.120758 |
| 29 | 3.014473 | 2.994246 | 3.015881 | 3.020835 | 3.041772 | 3.058894 | 3.109163 |
| 30 | 3.005563 | 2.984233 | 3.007418 | 3.018146 | 3.036500 | 3.052381 | 3.100798 |
| 31 | 3.003744 | 2.983274 | 3.006425 | 3.018997 | 3.041181 | 3.056248 | 3.103275 |
| 32 | 3.013988 | 2.996584 | 3.023343 | 3.037225 | 3.061479 | 3.080069 | 3.126179 |
| 33 | 3.022344 | 3.005740 | 3.032852 | 3.047970 | 3.072497 | 3.092072 | 3.138950 |
| 0.05 | 0.85 | 0.60 | 2.75 | 2.979013 | 2.973860 | 2.942602 | 2.938585 | 2.899332 | 2.896864 |
| 2.80 | 2.954551 | 2.948898 | 2.918055 | 2.913559 | 2.874628 | 2.871711 | |||
| 2.85 | 2.931692 | 2.925533 | 2.895107 | 2.890126 | 2.851522 | 2.848149 | |||
| 0.70 | 2.75 | 2.990586 | 2.985467 | 2.954113 | 2.950135 | 2.910731 | 2.908310 | ||
| 2.80 | 2.966412 | 2.960791 | 2.929858 | 2.925397 | 2.886322 | 2.883448 | |||
| 2.85 | 2.943827 | 2.937697 | 2.907188 | 2.902239 | 2.863496 | 2.860163 | |||
| 0.95 | 0.60 | 2.75 | 2.991737 | 2.987089 | 2.957554 | 2.953994 | 2.916601 | 2.914532 | |
| 2.80 | 2.966064 | 2.960974 | 2.931800 | 2.927819 | 2.890698 | 2.888237 | |||
| 2.85 | 2.941959 | 2.936423 | 2.907617 | 2.903210 | 2.866367 | 2.863511 | |||
| 0.70 | 2.75 | 2.991737 | 2.996258 | 2.957554 | 2.963084 | 2.916601 | 2.923494 | ||
| 2.80 | 2.966064 | 2.970501 | 2.931800 | 2.937274 | 2.890698 | 2.897572 | |||
| 2.85 | 2.941959 | 2.946289 | 2.907617 | 2.913009 | 2.866367 | 2.873197 | |||
| 0.1 | 0.85 | 0.60 | 2.75 | 3.106973 | 3.099336 | 3.064676 | 3.058380 | 3.014288 | 3.009778 |
| 2.80 | 3.083714 | 3.075479 | 3.041333 | 3.034460 | 2.990770 | 2.985716 | |||
| 2.85 | 3.062043 | 3.053205 | 3.019577 | 3.012126 | 2.968839 | 2.963238 | |||
| 0.70 | 2.75 | 3.118530 | 3.110927 | 3.076163 | 3.069904 | 3.025633 | 3.021167 | ||
| 2.80 | 3.095568 | 3.087364 | 3.053121 | 3.046281 | 3.002421 | 2.997407 | |||
| 2.85 | 3.074181 | 3.065369 | 3.031652 | 3.024231 | 2.980781 | 2.975217 | |||
| 0.95 | 0.60 | 2.75 | 3.118081 | 3.111224 | 3.078620 | 3.073032 | 3.031223 | 3.027343 | |
| 2.80 | 3.093557 | 3.086174 | 3.054006 | 3.047916 | 3.006432 | 3.002082 | |||
| 2.85 | 3.070585 | 3.062675 | 3.030949 | 3.024355 | 2.983203 | 2.978382 | |||
| 0.70 | 2.75 | 3.127136 | 3.120334 | 3.087575 | 3.082047 | 3.040010 | 3.036197 | ||
| 2.80 | 3.102982 | 3.095650 | 3.063340 | 3.057305 | 3.015606 | 3.011320 | |||
| 2.85 | 3.080360 | 3.072498 | 3.040641 | 3.034099 | 2.992743 | 2.987982 | |||
| 0.15 | 0.85 | 0.60 | 2.75 | 3.227871 | 3.124522 | 3.180782 | 3.172613 | 3.124522 | 3.118335 |
| 2.80 | 3.205585 | 3.101958 | 3.158412 | 3.149586 | 3.101958 | 3.095151 | |||
| 2.85 | 3.184858 | 3.080966 | 3.137602 | 3.128126 | 3.080966 | 3.073538 | |||
| 0.70 | 2.75 | 3.239407 | 3.229767 | 3.239407 | 3.184112 | 3.135819 | 3.129678 | ||
| 2.80 | 3.217425 | 3.207099 | 3.217425 | 3.161390 | 3.113568 | 3.106804 | |||
| 2.85 | 3.196987 | 3.185980 | 3.196987 | 3.140222 | 3.092876 | 3.085485 | |||
| 0.95 | 0.60 | 2.75 | 3.237823 | 3.229153 | 3.194032 | 3.186784 | 3.141275 | 3.135916 | |
| 2.80 | 3.214209 | 3.204947 | 3.170322 | 3.162508 | 3.117363 | 3.111471 | |||
| 2.85 | 3.192134 | 3.182281 | 3.148160 | 3.139778 | 3.095006 | 3.088582 | |||
| 0.70 | 2.75 | 3.246812 | 3.238204 | 3.202911 | 3.195730 | 3.149959 | 3.144675 | ||
| 2.80 | 3.223575 | 3.214372 | 3.179589 | 3.171837 | 3.126443 | 3.120623 | |||
| 2.85 | 3.201857 | 3.192058 | 3.157792 | 3.149469 | 3.104462 | 3.098105 | |||
| N | ||||||||
|---|---|---|---|---|---|---|---|---|
| 7 | 1.6 | 2.75 | 0.003336 | 0.005413 | 0.003179 | 0.005173 | 0.002990 | 0.004882 |
| 2.80 | 0.003239 | 0.005245 | 0.003083 | 0.005006 | 0.002894 | 0.004717 | ||
| 2.85 | 0.003156 | 0.005097 | 0.002999 | 0.004859 | 0.002811 | 0.004570 | ||
| 1.7 | 2.75 | 0.003173 | 0.005191 | 0.003024 | 0.004963 | 0.002845 | 0.004687 | |
| 2.80 | 0.003068 | 0.005012 | 0.002920 | 0.004786 | 0.002742 | 0.004511 | ||
| 2.85 | 0.002977 | 0.004854 | 0.002829 | 0.004628 | 0.002652 | 0.004355 | ||
| 1.8 | 2.75 | 0.003054 | 0.005025 | 0.002911 | 0.004806 | 0.002741 | 0.004542 | |
| 2.80 | 0.002943 | 0.004839 | 0.002802 | 0.004622 | 0.002633 | 0.004360 | ||
| 2.85 | 0.002846 | 0.004673 | 0.002706 | 0.004457 | 0.002537 | 0.004197 | ||
| 8 | 1.6 | 2.75 | 0.001648 | 0.002828 | 0.001570 | 0.002702 | 0.001476 | 0.002549 |
| 2.80 | 0.001591 | 0.002723 | 0.001514 | 0.002598 | 0.001421 | 0.002447 | ||
| 2.85 | 0.001543 | 0.002631 | 0.001466 | 0.002507 | 0.001373 | 0.002358 | ||
| 1.7 | 2.75 | 0.001547 | 0.002683 | 0.001474 | 0.002565 | 0.001387 | 0.002422 | |
| 2.80 | 0.001486 | 0.002572 | 0.001414 | 0.002456 | 0.001327 | 0.002314 | ||
| 2.85 | 0.001432 | 0.002474 | 0.001361 | 0.002359 | 0.001275 | 0.002219 | ||
| 1.8 | 2.75 | 0.001474 | 0.002576 | 0.001405 | 0.002464 | 0.001323 | 0.002328 | |
| 2.80 | 0.001409 | 0.002461 | 0.001341 | 0.002350 | 0.001260 | 0.002217 | ||
| 2.85 | 0.001353 | 0.002358 | 0.001286 | 0.002249 | 0.001205 | 0.002117 | ||
| 9 | 1.6 | 2.75 | 0.000821 | 0.001491 | 0.000782 | 0.001424 | 0.000735 | 0.001344 |
| 2.80 | 0.000789 | 0.001426 | 0.000750 | 0.001361 | 0.000704 | 0.001282 | ||
| 2.85 | 0.000761 | 0.001371 | 0.000723 | 0.001306 | 0.000677 | 0.001228 | ||
| 1.7 | 2.75 | 0.000760 | 0.001399 | 0.000724 | 0.001337 | 0.000681 | 0.001262 | |
| 2.80 | 0.000725 | 0.001331 | 0.000690 | 0.001271 | 0.000647 | 0.001197 | ||
| 2.85 | 0.000695 | 0.001272 | 0.000660 | 0.001212 | 0.000618 | 0.001140 | ||
| 1.8 | 2.75 | 0.000716 | 0.001331 | 0.000683 | 0.001273 | 0.000642 | 0.001203 | |
| 2.80 | 0.000679 | 0.001261 | 0.000646 | 0.001205 | 0.000607 | 0.001136 | ||
| 2.85 | 0.000647 | 0.001199 | 0.000615 | 0.001144 | 0.000576 | 0.001076 | ||
| 2.75 | 2.60 | 2.40 | 0.223480 | 0.223851 | 0.223730 | 0.224161 | 0.224073 | 0.224585 |
| 2.45 | 0.223453 | 0.223827 | 0.223700 | 0.224133 | 0.224038 | 0.224551 | ||
| 2.50 | 0.223427 | 0.223803 | 0.223671 | 0.224107 | 0.224004 | 0.224519 | ||
| 2.65 | 2.40 | 0.223458 | 0.223831 | 0.223708 | 0.224141 | 0.224051 | 0.224566 | |
| 2.45 | 0.223431 | 0.223807 | 0.223678 | 0.224113 | 0.224016 | 0.224532 | ||
| 2.50 | 0.223405 | 0.223783 | 0.223649 | 0.224087 | 0.223983 | 0.224500 | ||
| 2.70 | 2.40 | 0.223436 | 0.223812 | 0.223686 | 0.224122 | 0.224030 | 0.224547 | |
| 2.45 | 0.223409 | 0.223787 | 0.223656 | 0.224094 | 0.223995 | 0.224513 | ||
| 2.50 | 0.223383 | 0.223764 | 0.223628 | 0.224068 | 0.223962 | 0.224481 | ||
| 2.80 | 2.60 | 2.40 | 0.223403 | 0.223775 | 0.223653 | 0.224086 | 0.223998 | 0.224514 |
| 2.45 | 0.223374 | 0.223750 | 0.223622 | 0.224057 | 0.223962 | 0.224479 | ||
| 2.50 | 0.223347 | 0.223726 | 0.223592 | 0.224030 | 0.223927 | 0.224445 | ||
| 2.65 | 2.40 | 0.223379 | 0.223754 | 0.223630 | 0.224065 | 0.223975 | 0.224493 | |
| 2.45 | 0.223351 | 0.223729 | 0.223598 | 0.224037 | 0.223939 | 0.224458 | ||
| 2.50 | 0.223324 | 0.223705 | 0.223569 | 0.224009 | 0.223904 | 0.224425 | ||
| 2.70 | 2.40 | 0.223357 | 0.223734 | 0.223608 | 0.224046 | 0.223953 | 0.224474 | |
| 2.45 | 0.223329 | 0.223709 | 0.223576 | 0.224017 | 0.223917 | 0.224439 | ||
| 2.50 | 0.223302 | 0.223685 | 0.223547 | 0.223989 | 0.223883 | 0.224406 | ||
| 2.85 | 2.60 | 2.40 | 0.223327 | 0.223701 | 0.223577 | 0.224013 | 0.223924 | 0.224443 |
| 2.45 | 0.223297 | 0.223674 | 0.223545 | 0.223983 | 0.223887 | 0.224407 | ||
| 2.50 | 0.223269 | 0.223649 | 0.223514 | 0.223954 | 0.223851 | 0.224373 | ||
| 2.65 | 2.40 | 0.223302 | 0.223679 | 0.223553 | 0.223991 | 0.223900 | 0.224422 | |
| 2.45 | 0.223273 | 0.223653 | 0.223521 | 0.223961 | 0.223863 | 0.224386 | ||
| 2.50 | 0.223245 | 0.223628 | 0.223490 | 0.223933 | 0.223827 | 0.224351 | ||
| 2.70 | 2.40 | 0.223279 | 0.223658 | 0.223530 | 0.223970 | 0.223878 | 0.224402 | |
| 2.45 | 0.223250 | 0.223632 | 0.223498 | 0.223941 | 0.223840 | 0.224366 | ||
| 2.50 | 0.223222 | 0.223607 | 0.223467 | 0.223912 | 0.223804 | 0.224331 | ||
| r | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.5 | 2.75 | 2.40 | 0.001919 | 0.002247 | 0.971408 | 0.972786 | 0.015359 | 0.014580 |
| 2.45 | 0.001921 | 0.002249 | 0.971198 | 0.972595 | 0.015423 | 0.014632 | ||
| 2.50 | 0.001923 | 0.002251 | 0.970997 | 0.972412 | 0.015484 | 0.014682 | ||
| 2.80 | 2.40 | 0.001921 | 0.002251 | 0.970795 | 0.972169 | 0.015546 | 0.014750 | |
| 2.45 | 0.001923 | 0.002253 | 0.970575 | 0.971969 | 0.015615 | 0.014806 | ||
| 2.50 | 0.001925 | 0.002255 | 0.970364 | 0.971778 | 0.015679 | 0.014859 | ||
| 2.85 | 2.40 | 0.001922 | 0.002255 | 0.970186 | 0.971555 | 0.015732 | 0.015732 | |
| 2.45 | 0.001923 | 0.002257 | 0.969956 | 0.971346 | 0.015804 | 0.015804 | ||
| 2.50 | 0.001925 | 0.002259 | 0.969736 | 0.971146 | 0.015873 | 0.015873 | ||
| 1 | 2.75 | 2.40 | 0.003858 | 0.004527 | 0.970324 | 0.971718 | 0.015939 | 0.015181 |
| 2.45 | 0.003863 | 0.004532 | 0.970121 | 0.971534 | 0.015995 | 0.015224 | ||
| 2.50 | 0.003868 | 0.004536 | 0.969926 | 0.971358 | 0.016048 | 0.015266 | ||
| 2.80 | 2.40 | 0.003860 | 0.004536 | 0.969673 | 0.971062 | 0.016135 | 0.015358 | |
| 2.45 | 0.003865 | 0.004540 | 0.969460 | 0.970869 | 0.016196 | 0.015406 | ||
| 2.50 | 0.003870 | 0.004544 | 0.969255 | 0.970684 | 0.016252 | 0.015451 | ||
| 2.85 | 2.40 | 0.003860 | 0.004543 | 0.969027 | 0.970408 | 0.016329 | 0.015536 | |
| 2.45 | 0.003865 | 0.004547 | 0.968804 | 0.970206 | 0.016394 | 0.015588 | ||
| 2.50 | 0.003870 | 0.004551 | 0.968589 | 0.970012 | 0.016454 | 0.015636 | ||
| N | ||||||||
|---|---|---|---|---|---|---|---|---|
| 7 | 0.05 | 2.75 | 1.166812 | 1.294542 | 1.133508 | 1.259561 | 1.092839 | 1.216619 |
| 2.80 | 1.155714 | 1.281839 | 1.122121 | 1.246556 | 1.081005 | 1.203148 | ||
| 2.85 | 1.145370 | 1.269916 | 1.111490 | 1.234334 | 1.069927 | 1.190461 | ||
| 0.1 | 2.75 | 1.176179 | 1.304286 | 1.138123 | 1.264415 | 1.092326 | 1.216121 | |
| 2.80 | 1.165538 | 1.292048 | 1.127166 | 1.251849 | 1.080899 | 1.203065 | ||
| 2.85 | 1.155644 | 1.280587 | 1.116958 | 1.240061 | 1.070223 | 1.190789 | ||
| 0.15 | 2.75 | 1.185531 | 1.314007 | 1.143894 | 1.270412 | 1.094334 | 1.218132 | |
| 2.80 | 1.175302 | 1.302194 | 1.133339 | 1.258259 | 1.083308 | 1.205488 | ||
| 2.85 | 1.165815 | 1.291153 | 1.123528 | 1.246881 | 1.073028 | 1.193620 | ||
| 8 | 0.05 | 2.75 | 1.196611 | 1.333320 | 1.162571 | 1.297436 | 1.120983 | 1.253362 |
| 2.80 | 1.184390 | 1.319239 | 1.150062 | 1.283055 | 1.108028 | 1.238515 | ||
| 2.85 | 1.173006 | 1.306032 | 1.138391 | 1.269550 | 1.095910 | 1.224544 | ||
| 0.1 | 2.75 | 1.207098 | 1.344284 | 1.168216 | 1.303401 | 1.121370 | 1.253814 | |
| 2.80 | 1.195381 | 1.330726 | 1.156191 | 1.289522 | 1.108882 | 1.239453 | ||
| 2.85 | 1.184499 | 1.318037 | 1.145001 | 1.276513 | 1.097230 | 1.225963 | ||
| 0.15 | 2.75 | 1.217523 | 1.355182 | 1.174969 | 1.310463 | 1.124237 | 1.256745 | |
| 2.80 | 1.206273 | 1.342103 | 1.163403 | 1.297056 | 1.112209 | 1.242855 | ||
| 2.85 | 1.195845 | 1.329887 | 1.152660 | 1.284515 | 1.101009 | 1.229833 | ||
| 9 | 0.05 | 2.75 | 1.217496 | 1.361326 | 1.182931 | 1.324789 | 1.140678 | 1.279882 |
| 2.80 | 1.204370 | 1.346108 | 1.169522 | 1.309276 | 1.126827 | 1.263907 | ||
| 2.85 | 1.192158 | 1.331848 | 1.157027 | 1.294722 | 1.113888 | 1.248891 | ||
| 0.1 | 2.75 | 1.228956 | 1.373376 | 1.189474 | 1.331744 | 1.141857 | 1.281196 | |
| 2.80 | 1.216383 | 1.358733 | 1.176600 | 1.316790 | 1.128530 | 1.265767 | ||
| 2.85 | 1.204714 | 1.345043 | 1.164633 | 1.302789 | 1.116108 | 1.251293 | ||
| 0.15 | 2.75 | 1.240316 | 1.385311 | 1.197085 | 1.339751 | 1.145488 | 1.284957 | |
| 2.80 | 1.228252 | 1.371198 | 1.184714 | 1.325320 | 1.132663 | 1.270051 | ||
| 2.85 | 1.217078 | 1.358028 | 1.173237 | 1.311835 | 1.120736 | 1.256093 | ||
| 2.75 | 2.60 | 2.40 | 0.168374 | 0.205167 | 0.172715 | 0.210847 | 0.177406 | 0.217027 |
| 2.45 | 0.166878 | 0.203129 | 0.171119 | 0.208675 | 0.175696 | 0.214703 | ||
| 2.50 | 0.165467 | 0.201211 | 0.169613 | 0.206630 | 0.174082 | 0.212513 | ||
| 2.65 | 2.40 | 0.167100 | 0.203432 | 0.171412 | 0.209068 | 0.176071 | 0.215202 | |
| 2.45 | 0.165626 | 0.201427 | 0.169838 | 0.206931 | 0.174385 | 0.212914 | ||
| 2.50 | 0.164236 | 0.199539 | 0.168354 | 0.204918 | 0.172793 | 0.210758 | ||
| 2.70 | 2.40 | 0.165892 | 0.201789 | 0.170176 | 0.207385 | 0.174805 | 0.213474 | |
| 2.45 | 0.164439 | 0.199815 | 0.168624 | 0.205280 | 0.173141 | 0.211219 | ||
| 2.50 | 0.163068 | 0.197957 | 0.167160 | 0.203297 | 0.171571 | 0.209095 | ||
| 2.80 | 2.60 | 2.40 | 0.162540 | 0.197251 | 0.166733 | 0.202716 | 0.171263 | 0.208663 |
| 2.45 | 0.161115 | 0.195324 | 0.165212 | 0.200662 | 0.169633 | 0.206463 | ||
| 2.50 | 0.159772 | 0.193510 | 0.163777 | 0.198726 | 0.168094 | 0.204388 | ||
| 2.65 | 2.40 | 0.161327 | 0.195611 | 0.165492 | 0.201035 | 0.169992 | 0.206938 | |
| 2.45 | 0.159923 | 0.193714 | 0.163992 | 0.199012 | 0.168384 | 0.204770 | ||
| 2.50 | 0.158599 | 0.191929 | 0.162577 | 0.197107 | 0.166866 | 0.202727 | ||
| 2.70 | 2.40 | 0.160177 | 0.194057 | 0.164315 | 0.199443 | 0.168786 | 0.205303 | |
| 2.45 | 0.158792 | 0.192190 | 0.162836 | 0.197450 | 0.167199 | 0.203167 | ||
| 2.50 | 0.157487 | 0.190431 | 0.161440 | 0.195573 | 0.165701 | 0.201154 | ||
| 2.85 | 2.60 | 2.40 | 0.157094 | 0.189915 | 0.161148 | 0.195181 | 0.165528 | 0.200911 |
| 2.45 | 0.155734 | 0.188089 | 0.159696 | 0.193232 | 0.163970 | 0.198822 | ||
| 2.50 | 0.154452 | 0.186369 | 0.158325 | 0.191396 | 0.162500 | 0.196853 | ||
| 2.65 | 2.40 | 0.155937 | 0.188360 | 0.159964 | 0.193587 | 0.164315 | 0.199275 | |
| 2.45 | 0.154597 | 0.186563 | 0.158532 | 0.191669 | 0.162779 | 0.197218 | ||
| 2.50 | 0.153333 | 0.184870 | 0.157181 | 0.189861 | 0.161329 | 0.195278 | ||
| 2.70 | 2.40 | 0.154839 | 0.186888 | 0.158841 | 0.192078 | 0.163164 | 0.197726 | |
| 2.45 | 0.153518 | 0.185118 | 0.157428 | 0.190188 | 0.161648 | 0.195698 | ||
| 2.50 | 0.152272 | 0.183450 | 0.156095 | 0.188406 | 0.160217 | 0.193786 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeganathan, K.; Vidhya, S.; Hemavathy, R.; Anbazhagan, N.; Joshi, G.P.; Kang, C.; Seo, C. Analysis of M/M/1/N Stochastic Queueing—Inventory System with Discretionary Priority Service and Retrial Facility. Sustainability 2022, 14, 6370. https://doi.org/10.3390/su14106370
Jeganathan K, Vidhya S, Hemavathy R, Anbazhagan N, Joshi GP, Kang C, Seo C. Analysis of M/M/1/N Stochastic Queueing—Inventory System with Discretionary Priority Service and Retrial Facility. Sustainability. 2022; 14(10):6370. https://doi.org/10.3390/su14106370
Chicago/Turabian StyleJeganathan, K., S. Vidhya, R. Hemavathy, N. Anbazhagan, Gyanendra Prasad Joshi, Chanku Kang, and Changho Seo. 2022. "Analysis of M/M/1/N Stochastic Queueing—Inventory System with Discretionary Priority Service and Retrial Facility" Sustainability 14, no. 10: 6370. https://doi.org/10.3390/su14106370
APA StyleJeganathan, K., Vidhya, S., Hemavathy, R., Anbazhagan, N., Joshi, G. P., Kang, C., & Seo, C. (2022). Analysis of M/M/1/N Stochastic Queueing—Inventory System with Discretionary Priority Service and Retrial Facility. Sustainability, 14(10), 6370. https://doi.org/10.3390/su14106370








