Development and Application of Intelligent Assessment System for Metacognition in Learning Mathematics among Junior High School Students
Abstract
:1. Introduction
2. Literature Review
2.1. Metacognition
2.2. Relationships between Metacognition and Mathematics Performance
2.3. Assessment of Mathematical Metacognition
2.4. Research Questions
- How to construct a metacognitive intelligence assessment system for junior secondary school students in mathematics?
- How to apply the system in Hexi District, Tianjin City, China, and test the effectiveness of its application?
3. Method
3.1. Design and Participants
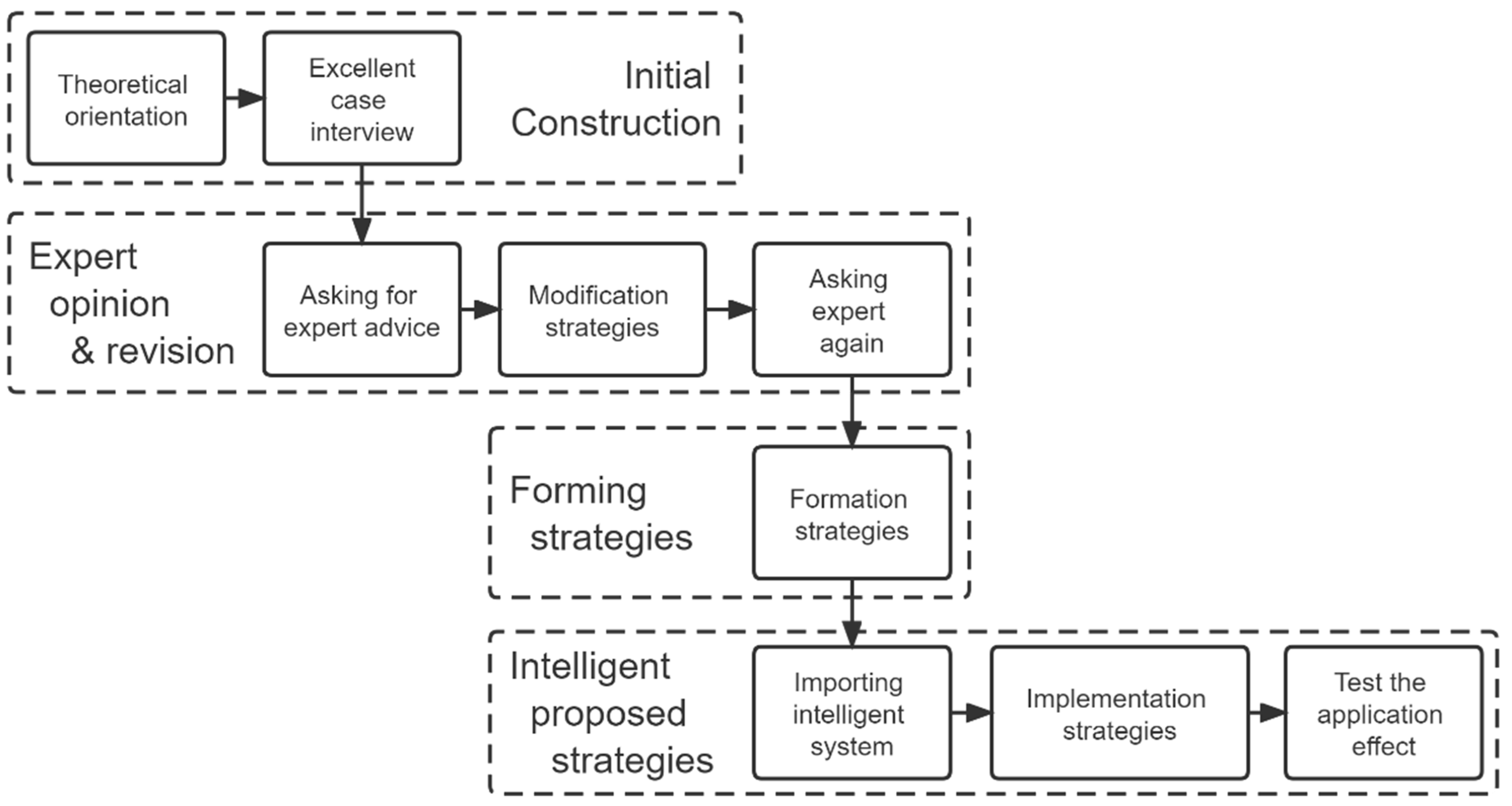
3.1.1. Designing the Research of the Intelligent Assessment and Strategy Implementation System for Students’ Metacognition in Junior High School Mathematics
- (1)
- A strategic framework was preliminarily constructed according to the existing metacognition-related research and theoretical foundations;
- (2)
- Greater details were added into the strategies via case-by-case analysis, interviews, etc., after taking into account the aforementioned research on metacognitive characteristics of highly productive middle school students;
- (3)
- The improvement strategies were revised and perfected via expert consultation;
- (4)
- The experts were re-consulted to confirm the strategies;
- (5)
- These expert-approved strategies were embedded into the intelligent strategy implementation module;
- (6)
- The metacognitive improvement strategies were implemented; and lastly,
- (7)
- The strategies’ effectiveness was tested.
3.1.2. Designing the Application Effectiveness Testing and Research of the Intelligent Assessment and Strategy Implementation System
3.2. Instruments
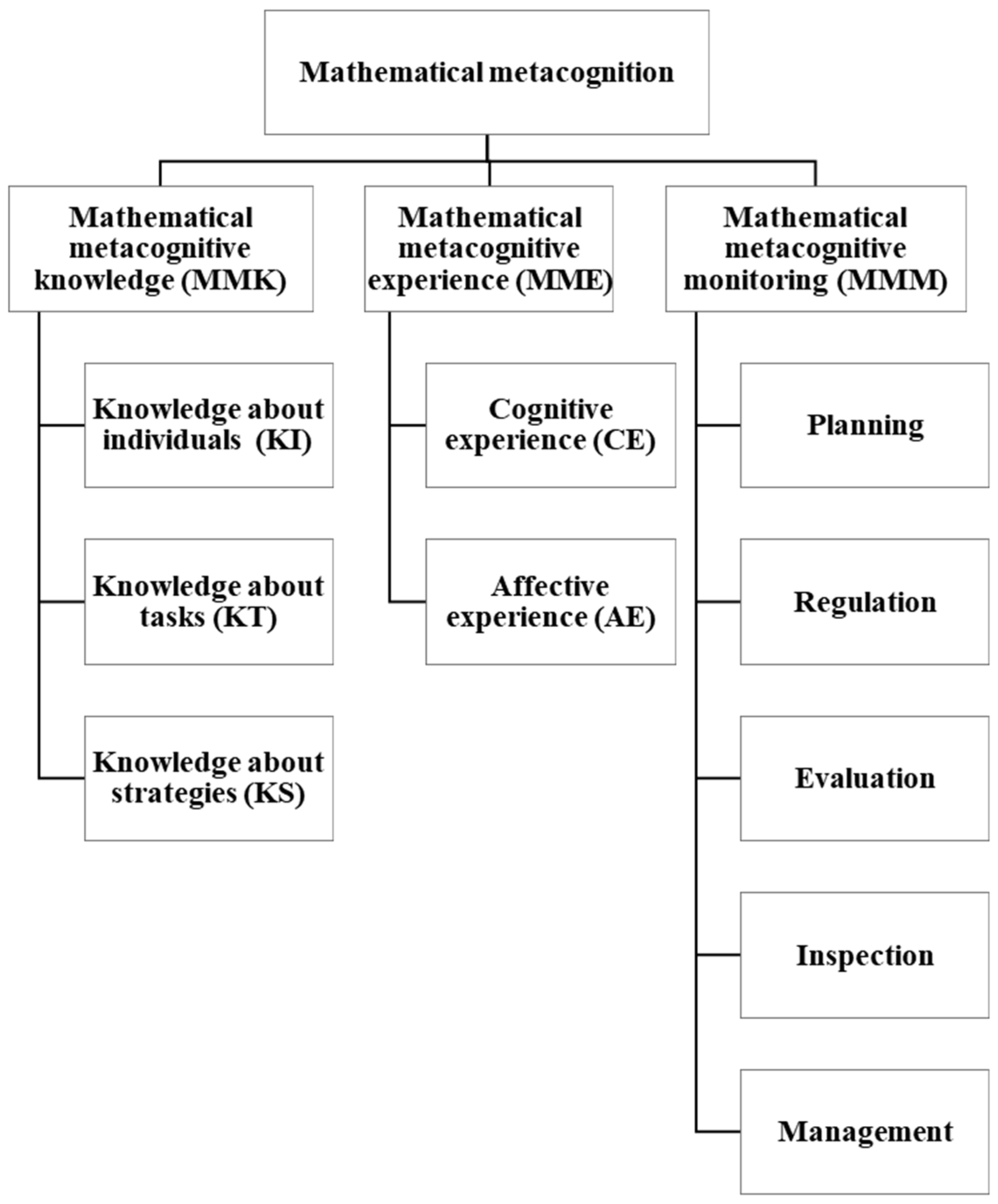
3.2.1. Questionnaire on Metacognition in Learning Mathematics
3.2.2. Test of Academic Performance in Mathematics
3.2.3. Intelligent Assessment System
4. Results
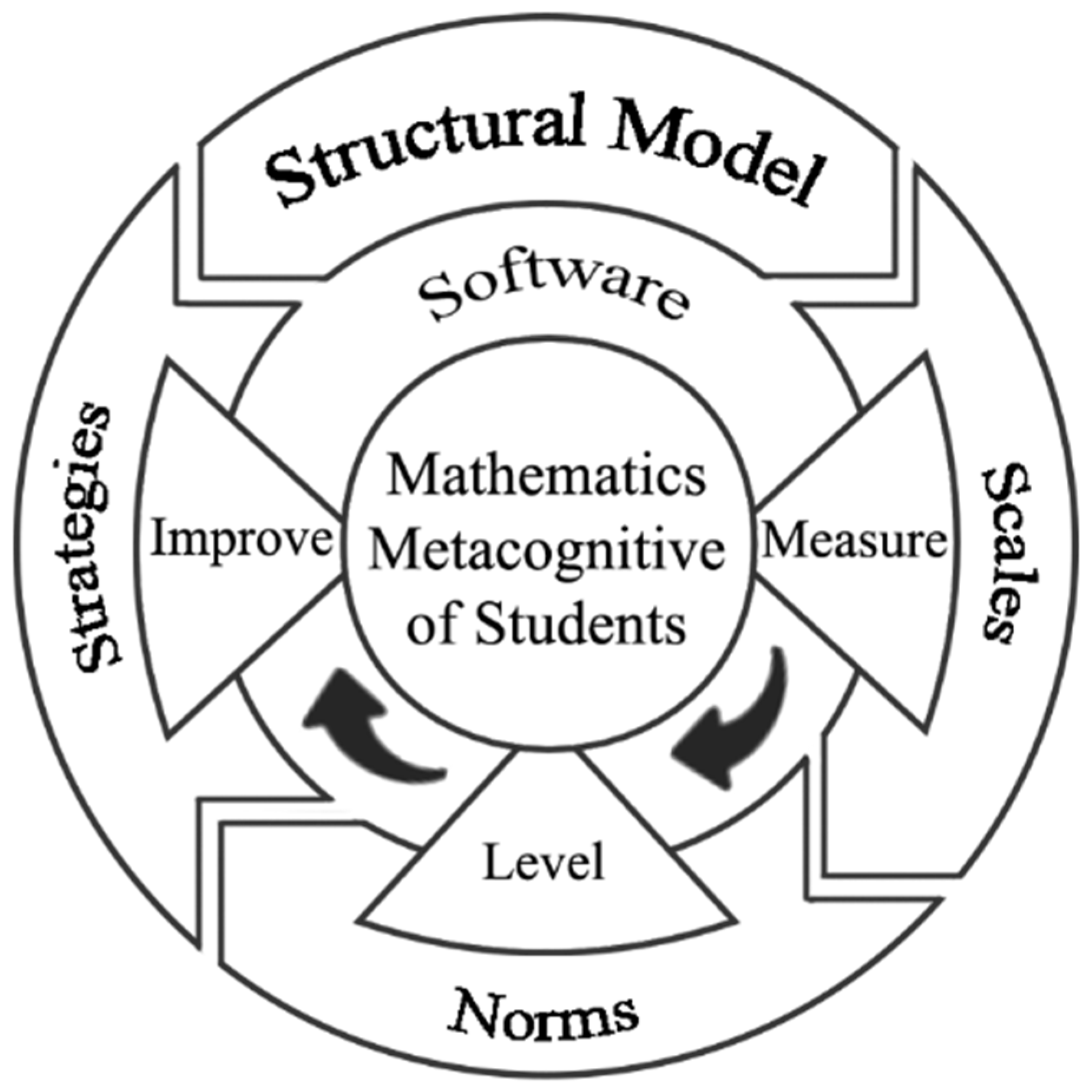
4.1. Development of Intelligent Assessment System
4.1.1. Assessment Theoretical Framework and Assessment Scale
4.1.2. Regional Norms
4.1.3. Development of Improvement Strategy
Initial Construction of Improvement Strategy
- (1)
- Based on theoretical orientation construction of the strategic framework
- (2)
- Based on excellent case interviews enrichment of specific content of strategy
- Metacognitive knowledge dimension. Excellent students had a strong sense of reflection and would summarize the mastery of mathematical knowledge and the success or failure of problem-solving results and correctly attribute them. They were good at self-questioning in the problem-solving process and able to extract and transform information in text, graphics and symbols.
- Metacognitive experience dimension. Excellent students had the habit of previewing knowledge in advance and summarizing the knowledge framework independently. They had a more positive emotional experience during mathematical learning and could overcome or transform negative experience.
- Metacognitive monitoring dimension. Excellent students would formulate reasonable learning, problem-solving or examination plans, timely adjust their learning mentality and regularly test and evaluate their mathematical learning results.
Revision of Improvement Strategy
- There were repeats in suggestions of each sub-dimension and problems in orientated dimensions. For example, experts pointed out that “both knowledge and regulation dimensions of the strategy paid attention to the application of metacognitive cues, and the strategic orientation dimensions needed to be further considered”, “the examination-oriented mentality did not belong to the learning mentality, so whether it should be considered in the dimension of regulation”, and “checking writing errors did not belong to the planning dimension”.
- The logicality between the recommendations still needed to be strengthened. For instance, the logicality of “first judge whether it conforms to their own situation, and then actively improve their own mathematical learning” should be strengthened. The logical relationship between “paying attention to group honor” and “comparing your past mathematical learning state and achievement with the present” is unclear.
- The language was not refined and accurate enough. Experts suggested that the language should be refined in many parts of the full text. For example, “Facing the praise of teachers and classmates or the progress in achievements” could be changed to “when making progress or being praised”. “Pay attention to problem-solving dexterity” is inaccurate and difficult for students to understand and implement. The overall modification suggestions for the mathematical metacognitive improvement strategy are displayed in Table 2.
Determination of Improvement Strategy
4.1.4. Intelligent Assessment Software
4.2. Intelligence Assessment Diagnosis and Norm-Referenced Analysis
4.2.1. Results of Mathematics Metacognitive Diagnosis of Junior High School Students of Hexi District and Norm-Referenced Analysis
- (1)
- Results of mathematics metacognitive diagnosis of junior high school students of Hexi District
- (2)
- Norm-referenced analysis of the levels of students in Hexi District against the norm of Tianjin
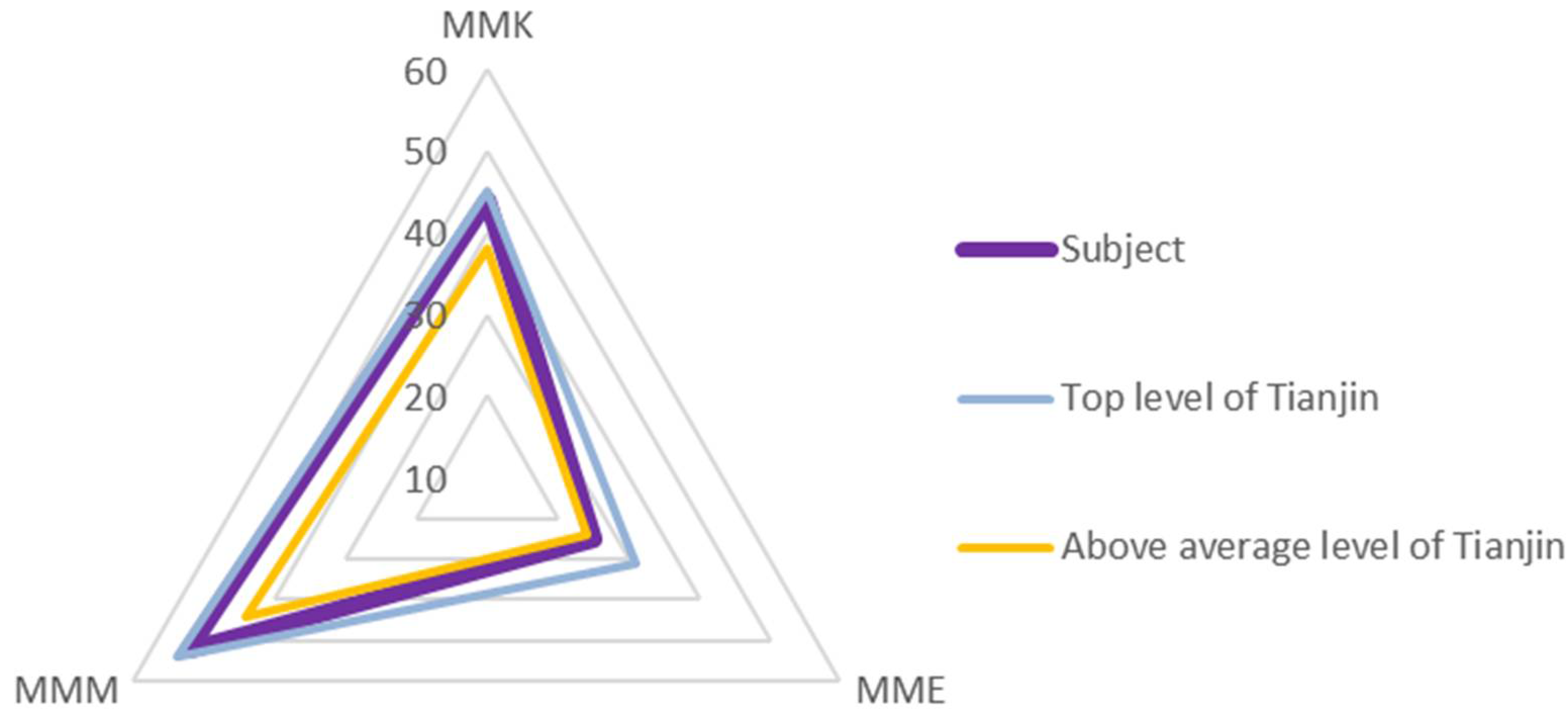
4.2.2. Results of Mathematics Metacognitive Diagnosis of Students Participating in the Case Study and Norm-Reference Analysis
4.3. Test of Applicative Efficacy of the Intelligence Assessment and Strategy Implementation System
4.3.1. Analysis of the Overall Applicative Efficacy in the Region
4.3.2. Analysis of Applicative Efficacy on Students Participating in the Case Study
- (1)
- Analysis of applicative efficacy on student A who had weak MMK
- (2)
- Analysis of applicative efficacy on student B who had weak MME
- (3)
- Analysis of applicative efficacy on student C who had weak MMM
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Questionnaire of Junior High School Students’ Mathematics Metacognition Level
| 1 | Mathematical Metacognitive Knowledge | Score | ||||
|---|---|---|---|---|---|---|
| 1.1 | I am aware of my mathematical learning ability and confident that I can solve various mathematical questions on my own. | 5 | 4 | 3 | 2 | 1 |
| 1.2 | I have a relatively clear understanding of common solving or demonstration approaches to mathematical problems. | 5 | 4 | 3 | 2 | 1 |
| 1.3 | I am aware of the goals or tasks of my mathematical learning. | 5 | 4 | 3 | 2 | 1 |
| 1.4 | I know what knowledge is examined in mathematical homework assigned by my teacher. | 5 | 4 | 3 | 2 | 1 |
| 1.5 | I am able to grasp mathematical knowledge (e.g., concept, equation and theorem) taught in classroom. | 5 | 4 | 3 | 2 | 1 |
| 1.6 | I am able to discern the level of my understanding about some issues. | 5 | 4 | 3 | 2 | 1 |
| 1.7 | I know whether I have understood the mathematical content I learned. | 5 | 4 | 3 | 2 | 1 |
| 1.8 | I have a clear understanding of the types of mathematical learning tasks (e.g., autonomous learning and group discussion). | 5 | 4 | 3 | 2 | 1 |
| 1.9 | I often adopt a variety of methods to solve mathematical problems. | 5 | 4 | 3 | 2 | 1 |
| 1.10 | I find that I have actively used effective learning strategies. | 5 | 4 | 3 | 2 | 1 |
| 1.11 | I adopt different learning approaches for different mathematical content. | 5 | 4 | 3 | 2 | 1 |
| 2 | Mathematical Metacognitive Experience | Score | ||||
| 2.1 * | I cannot connect newly learned mathematical concepts or theorems with similar knowledge (e.g., cannot connect linear equations in one unknown with linear inequalities in one unknown). * | 5 | 4 | 3 | 2 | 1 |
| 2.2 | I try to find out central ideas behind mathematical problems (e.g., overall substitution). | 5 | 4 | 3 | 2 | 1 |
| 2.3 | In mathematical learning, the times I make mistakes will be fewer if I noticed such mistakes many times. | 5 | 4 | 3 | 2 | 1 |
| 2.4 | I realize that I have to plan the goals of my mathematical learning. | 5 | 4 | 3 | 2 | 1 |
| 2.5 | Successfully solving mathematical problems makes me happy. | 5 | 4 | 3 | 2 | 1 |
| 2.6 | I have a sense of accomplishment after completing mathematical homework. | 5 | 4 | 3 | 2 | 1 |
| 2.7 * | I am always confident about myself before learning new mathematical knowledge. * | 5 | 4 | 3 | 2 | 1 |
| 3 | Mathematical Metacognitive Monitoring | Score | ||||
| 3.1 | After solving a problem, I would carefully summarize the inherent connections between different knowledge points to deepen my understanding. | 5 | 4 | 3 | 2 | 1 |
| 3.2 | Before taking a mathematics test, I would review relevant content in a planned manner (e.g., knowledge points where errors can easily occur or content that has not been adequately acquired). | 5 | 4 | 3 | 2 | 1 |
| 3.3 | When a mathematical problem cannot be solved by one method, I would timely turn to other problem-solving strategies. | 5 | 4 | 3 | 2 | 1 |
| 3.4 | When solving problems, I frequently remind myself of the necessity to pay attention to the given conditions or conclusions. | 5 | 4 | 3 | 2 | 1 |
| 3.5 | When I meet difficulties, I would try to re-find the solutions. | 5 | 4 | 3 | 2 | 1 |
| 3.6 | If I do not understand a mathematical concept, I would analyze an actual example related to the concept. | 5 | 4 | 3 | 2 | 1 |
| 3.7 | In mathematical learning, I would reflect over areas I have not fully grasped. | 5 | 4 | 3 | 2 | 1 |
| 3.8 | After a certain period of mathematical learning, I would evaluate the effectiveness of my learning in various ways. | 5 | 4 | 3 | 2 | 1 |
| 3.9 | After solving a problem, I would check whether my method is correct. | 5 | 4 | 3 | 2 | 1 |
| 3.10 | When solving a mathematical problem, I would think of whether I have solved its key questions. | 5 | 4 | 3 | 2 | 1 |
| 3.11 | When I have finished my mathematical homework, I would repeat some of the key parts to ensure that I have fully understood them. | 5 | 4 | 3 | 2 | 1 |
| 3.12 | I would memorize some problem-solving techniques (e.g., when doing an operation, start with involution, followed by multiplication and division and finally addition and subtraction). | 5 | 4 | 3 | 2 | 1 |
| 3.13 | I can better understand a problem when I take notes of its knowledge points. | 5 | 4 | 3 | 2 | 1 |
| 4 | Lie Detection Questions | Score | ||||
| 4.1 | In mathematical learning, I would reflect over areas I have not fully grasped. | 5 | 4 | 3 | 2 | 1 |
| 4.2 | I am aware of the goals or tasks of my mathematical learning. | 5 | 4 | 3 | 2 | 1 |
| 4.3 | When solving a mathematical problem, I would think of whether I have solved its key questions. | 5 | 4 | 3 | 2 | 1 |
| 4.4 | Successfully solving mathematical problems makes me happy. | 5 | 4 | 3 | 2 | 1 |
| 4.5 | I never erroneously solve a mathematical problem. | 5 | 4 | 3 | 2 | 1 |
Appendix B
| Performance | Improvement Strategy |
|---|---|
| Dimension: Mathematical metacognitive knowledge (55 points) | |
| Sub-dimension: Knowledge about individuals (25 points) | |
Middle-level students (13 ≤ X < 17):
|
|
| Sub-dimension: Knowledge about tasks (15 points) | |
Middle-level students (8 ≤ X < 10):
|
|
| Sub-dimension: Knowledge about strategies (15 points) | |
Middle-level students (8 ≤ X < 10):
|
|
| Dimension: Mathematical metacognitive experience (35 points) | |
| Sub-dimension: Cognitive experience (20 points) | |
Middle-level students (11 ≤ X < 14):
|
|
| Sub-dimension: Affective experience (15 points) | |
Middle-level students (8 ≤ X < 10):
|
|
| Dimension: Mathematical metacognitive monitoring (65 points) | |
| Sub-dimension: Planning (10 points) | |
| Middle-level students (5 ≤ X < 7): There is room for improvement in working out mathematical learning plans. Low-level students (X < 5): Are weak in working out mathematical learning plans. |
|
| Sub-dimension: Regulation (20 points) | |
Middle-level students (11 ≤ X < 14):
|
|
| Sub-dimension: Evaluation (10 points) | |
Middle-level students (5 ≤ X < 7):
|
|
| Sub-dimension: Inspection (15 points) | |
Middle-level students (8 ≤ X < 11):
|
|
| Sub-dimension: Management (10 points) | |
Middle-level students (5 ≤ X < 7):
|
|
References
- OECD. PISA 2018 Results (Volume I); PISA, OECD Publishing: Paris, France, 2019. [Google Scholar]
- Flavell, J.H. Metacognition and cognitive monitoring: A new area of cognitive–developmental inquiry. Am. Psychol. 1979, 34, 906–911. [Google Scholar] [CrossRef]
- Grinstein, L.; Lipsey, S.I. Encyclopedia of Mathematics Education; Routledge: New York, NY, USA, 2001. [Google Scholar]
- De Boer, H.; Donker, A.S.; Kostons, D.D.N.M.; van der Werf, G.P.C. Long-term effects of metacognitive strategy instruction on student academic performance: A meta-analysis. Educ. Res. Rev. 2018, 24, 98–115. [Google Scholar] [CrossRef] [Green Version]
- Desoete, A.; De Craene, B. Metacognition and mathematics education: An overview. ZDM Math. Educ. 2019, 51, 565–575. [Google Scholar] [CrossRef]
- Ohtani, K.; Hisasaka, T. Beyond intelligence: A meta-analytic review of the relationship among metacognition, intelligence, and academic performance. Metacogn. Learn. 2018, 13, 179–212. [Google Scholar] [CrossRef]
- Ader, E. What would you demand beyond mathematics? Teachers’ promotion of students’ self-regulated learning and metacognition. ZDM Math. Educ. 2019, 51, 613–624. [Google Scholar] [CrossRef]
- Lingel, K.; Lenhart, J.; Schneider, W. Metacognition in mathematics: Do different metacognitive monitoring measures make a difference? ZDM Math. Educ. 2019, 51, 587–600. [Google Scholar] [CrossRef]
- Shilo, A.; Kramarski, B. Mathematical-metacognitive discourse: How can it be developed among teachers and their students? Empirical evidence from a videotaped lesson and two case studies. ZDM Math. Educ. 2019, 51, 625–640. [Google Scholar] [CrossRef]
- Zhao, N.; Teng, X.; Li, W.; Li, Y.; Wang, S.; Wen, H.; Yi, M. A path model for metacognition and its relation to problem-solving strategies and achievement for different tasks. ZDM Math. Educ. 2019, 51, 641–653. [Google Scholar] [CrossRef]
- Verschaffel, L.; Van Dooren, W.; Star, J. Applying cognitive psychology based instructional design principles in mathematics teaching and learning: Introduction. ZDM Math. Educ. 2017, 49, 491–496. [Google Scholar] [CrossRef]
- Veenman, M.V.J.; van Cleef, D. Measuring metacognitive skills for mathematics: Students’ self-reports versus on-line assessment methods. ZDM Math. Educ. 2019, 51, 691–701. [Google Scholar] [CrossRef]
- Flavell, J.H. The nature of intelligence. In Metacognitive Aspects of Problem-Solving; Resnick, L.B., Ed.; Erlbaum: Hillsdale, NJ, USA, 1976; pp. 231–236. [Google Scholar]
- Flavell, J.H. Speculations about the nature and development of metacognition. In Metacognition, Motivation, and Understanding; Weinert, F.E., Kluwe, R.H., Eds.; Erlbaum: Hillsdale, NJ, USA, 1987; pp. 20–29. [Google Scholar]
- Brown, A.L. Knowing When, Where, and How to Remember: A Problem of Metacognition. In Advances in Instructional Psychology; Glaser, R., Ed.; Erlbaum: Hillsdale, NJ, USA, 1977; Volume 1, pp. 77–165. [Google Scholar]
- Brown, A.L. Metacognition, executive control, self-regulation, and other more mysterious mechanisms. In Metacognition, Motivation, and Understanding; Kluwe, F.R.R., Ed.; Lawrence Erlbaum: Hillsdale, NJ, USA, 1987; pp. 65–116. [Google Scholar]
- Kuzle, A. Assessing metacognition of grade 2 and grade 4 students using an adaptation of multi-method interview approach during mathematics problem-solving. Math. Educ. Res. J. 2018, 30, 185–207. [Google Scholar] [CrossRef]
- Veenman, M.V. The role of intellectual and metacognitive skills in math problem solving. In Metacognition in Mathematics Education; Desoete, A., Veenman, M., Eds.; Haupauge Digital: Haupauge, NY, USA, 2006; pp. 35–50. [Google Scholar]
- Hidayat, R.; Zulnaidi, H.; Syed Zamri, S.N.A. Roles of metacognition and achievement goals in mathematical modeling competency: A structural equation modeling analysis. PLoS ONE 2018, 13, e0206211. [Google Scholar] [CrossRef] [PubMed]
- Zohar, A. Explicit Teaching of Metastrategic Knowledge: Definitions, Students’ Learning, and Teachers’ Professional Development. In Metacognition in Science Education: Trends in Current Research; Zohar, A., Dori, Y.J., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 197–223. [Google Scholar]
- Gascoine, L.; Higgins, S.; Wall, K. The assessment of metacognition in children aged 4–16 years: A systematic review. Rev. Educ. 2017, 5, 3–57. [Google Scholar] [CrossRef]
- Schneider, W.; Artelt, C. Metacognition and mathematics education. ZDM Math. Educ. 2010, 42, 149–161. [Google Scholar] [CrossRef]
- Desoete, A.; Baten, E.; Vercaemst, V.; De Busschere, A.; Baudonck, M.; Vanhaeke, J. Metacognition and motivation as predictors for mathematics performance of Belgian elementary school children. ZDM Math. Educ. 2019, 51, 667–677. [Google Scholar] [CrossRef]
- Dennis, M.S.; Sharp, E.; Chovanes, J.; Thomas, A.; Burns, R.M.; Custer, B.; Park, J. A Meta-Analysis of Empirical Research on Teaching Students with Mathematics Learning Difficulties. Learn. Disabil. Res. Pract. 2016, 31, 156–168. [Google Scholar] [CrossRef]
- Chytrý, V.; Říčan, J.; Eisenmann, P.; Medová, J. Metacognitive Knowledge and Mathematical Intelligence—Two Significant Factors Influencing School Performance. Mathematics 2020, 8, 969. [Google Scholar] [CrossRef]
- Baten, E.; Desoete, A. Metacognition and motivation in school-aged children with and without mathematical learning disabilities in Flanders. ZDM Math. Educ. 2019, 51, 679–689. [Google Scholar] [CrossRef]
- Hacker, D.J.; Plumb, C.; Marra, R.M.; Bossaller, S. Board 63: How Problem Solving Skills Develop: Studying Metacognition in a PBL Engineering Curriculum. In Proceedings of the 2019 ASEE Annual Conference & Exposition, Tampa, FL, USA, 15–19 June 2019. [Google Scholar]
- Cui, B.; Li, J.; Wang, G. Design and development of a questionnaire on the metacognitive level of mathematics for junior high school students. J. Math. Educ. 2018, 27, 45–51. (In Chinese) [Google Scholar]
- Wang, G.; Li, J.; Mi, Y. The Establishment and Application of the Norm of Mathematics Metacognition Level of Junior Middle School Students—A Case Study of Tianjin. J. Tianjin Norm. Univ. (Elem. Educ. Ed.) 2020, 21, 12–17. (In Chinese) [Google Scholar]
- Dong, Q. Discussion of metacognition. J. Beijing Norm. Univ. (Soc. Sci.) 1989, 1, 68–72. (In Chinese) [Google Scholar]
- Sperling, R.A.; Howard, B.C.; Miller, L.A.; Murphy, C. Measures of Children’s Knowledge and Regulation of Cognition. Contemp. Educ. Psychol. 2002, 27, 51–79. [Google Scholar] [CrossRef] [Green Version]
- Tang, F.; Liang, Y. Study on Cultivating the Primary School Students’ (Grade 4–6) Math Metacognitive Monitoring Study Strategy. J. Math. Educ. 2008, 1, 47–50. (In Chinese) [Google Scholar]
- Liu, J.; Meng, S. The occurrence conditions and teaching training strategies of students’ self-regulated learning ability. J. Tianjin Acad. Educ. Sci. 2007, 5, 62–64. (In Chinese) [Google Scholar]
- Stanton, J.D.; Sebesta, A.J.; Dunlosky, J. Fostering Metacognition to Support Student Learning and Performance. CBE—Life Sci. Educ. 2021, 20, 3. [Google Scholar] [CrossRef]


| Level | T-Score | Raw Score (X) | Percentage Rating (PR) | |
|---|---|---|---|---|
| Mathematical metacognition | Top | T ≥ 68 | X ≤ 120 | PR ≤ 96.58 |
| Above Average | 56 ≤ T < 68 | 102 ≤ X < 120 | 73.88 ≤ PR < 96.58 | |
| Average | 44 ≤ T < 56 | 83 ≤ X < 102 | 29.08 ≤ PR < 73.88 | |
| Below Average | 32 ≤ T < 44 | 61 ≤ X < 83 | 3.80 ≤ PR < 29.08 | |
| Low | T < 32 | X < 61 | PR < 3.80 | |
| MMK | Top | T ≥ 68 | X ≥ 45 | PR ≥ 96.43 |
| Above Average | 56 ≤ T < 68 | 38 ≤ X < 45 | 75.25 ≤ PR < 96.43 | |
| Average | 44 ≤ T < 56 | 29 ≤ X <38 | 31.97 ≤ PR < 75.25 | |
| Below Average | 32 ≤ T < 44 | 19 ≤ X < 29 | 4.02 ≤ PR < 31.97 | |
| Low | T < 32 | X < 19 | PR < 4.02 | |
| MME | Top | T ≥ 68 | X ≥ 31 | PR ≥ 97.04 |
| Above Average | 56 ≤ T < 68 | 24 ≤ X < 31 | 71.83 ≤ PR < 97.04 | |
| Average | 44 ≤ T < 56 | 19 ≤ X < 24 | 32.05 ≤ PR < 71.83 | |
| Below Average | 32 ≤ T < 44 | 14 ≤ X < 19 | 5.85 ≤ PR < 32.50 | |
| Low | T < 32 | X < 14 | PR < 5.85 | |
| MMM | Top | T ≥ 68 | X ≥ 54 | PR ≥ 96.51 |
| Above Average | 56 ≤ T < 68 | 44 ≤ X < 54 | 76.16 ≤ PR < 96.51 | |
| Average | 44 ≤ T < 56 | 34 ≤ X < 44 | 28.63 ≤ PR < 76.16 | |
| Below Average | 32 ≤ T < 44 | 24 ≤ X < 34 | 3.64 ≤ PR < 28.63 | |
| Low | T < 32 | X < 24 | PR < 3.64 |
| Dimension | Sub-Dimension | Modification Suggestion |
|---|---|---|
| MMK | KI | No change is needed |
| KT | Strengthen logicality and check for typos | |
| KS | Give some examples to help students understand | |
| MME | CE | The preview part should focus on the study of algebraic knowledge rather than the solution of algebraic problems |
| AE | Consider the overall logical structure and adjust the language to highlight the positive function of homework | |
| MMM | Planning | Some recommendations do not fall into this category, and refine language |
| Regulation | When giving advice to students, do not use words that are not easy to understand, such as “dexterity” | |
| Inspection | Deleting part is not a recommendation for test dimension | |
| Evaluation | Do not focus too much on solving problems. Solving problems is not the totality of mathematics | |
| Management | Carefully study the definition of this dimension in scale papers and highlight “management” |
| Performance | Improvement Strategy |
|---|---|
| Dimension: Mathematical metacognitive knowledge (55 points) | |
| Sub-dimension: Knowledge about individuals (25 points) | |
Middle-level students (13 ≤ X < 17):
|
|
| Sub-dimension: Knowledge about tasks (15 points) | |
Middle-level students (8 ≤ X < 10):
|
|
| Sub-dimension: Knowledge about strategies (15 points) | |
Middle-level students (8 ≤ X < 10):
|
|
| Dimension: Mathematical metacognitive experience (35 points) | |
| Sub-dimension: Cognitive experience (20 points) | |
Middle-level students (11 ≤ X < 14):
|
|
| Sub-dimension: Affective experience (15 points) | |
Middle-level students (8 ≤ X < 10):
|
|
| Dimension: Mathematical metacognitive monitoring (65 points) | |
| Sub-dimension: Planning (10 points) | |
| Middle-level students (5 ≤ X < 7): There is room for improvement in working out math learning plans. Low-level students (X < 5): Are weak in working out math learning plans. |
|
| Sub-dimension: Regulation (20 points) | |
Middle-level students (11 ≤ X < 14):
|
|
| Sub-dimension: Evaluation (10 points) | |
Middle-level students (5 ≤ X < 7):
|
|
| Sub-dimension: Inspection (15 points) | |
Middle-level students (8 ≤ X < 11):
|
|
| Sub-dimension: Management (10 points) | |
Middle-level students (5 ≤ X < 7):
|
|
| N | Min | Max | Mean (M) | Standard Deviation | Dimension Full Score | Scoring Rate (S) | |
|---|---|---|---|---|---|---|---|
| Mathematical metacognition | 2100 | 31 | 155 | 121.3605 | 18.59534 | 155 | 78.30% |
| MMK | 2100 | 11 | 63 | 44.1105 | 7.56249 | 55 | 80.20% |
| MME | 2100 | 7 | 35 | 25.0095 | 3.49106 | 35 | 71.46% |
| MMM | 2100 | 13 | 75 | 52.2405 | 8.99428 | 65 | 80.37% |
| N | Min | Max | Mean (M) | Standard Deviation | Dimension Full Score | Scoring Rate (S) | |
|---|---|---|---|---|---|---|---|
| KI | 2100 | 5.00 | 25.00 | 20.5338 | 3.53100 | 25 | 82.14% |
| KT | 2100 | 3.00 | 39.00 | 12.2988 | 2.23434 | 15 | 81.99% |
| KS | 2100 | 3.00 | 39.00 | 11.2780 | 2.64080 | 15 | 75.19% |
| CE | 2100 | 4.00 | 20.00 | 14.3033 | 2.28116 | 20 | 71.52% |
| AE | 2100 | 3.00 | 15.00 | 10.7062 | 1.89552 | 15 | 71.37% |
| Planning | 2100 | 2.00 | 36.00 | 7.6064 | 1.92350 | 10 | 76.06% |
| Regulation | 2100 | 4.00 | 20.00 | 16.6011 | 2.80477 | 20 | 83.01% |
| Evaluation | 2100 | 2.00 | 10.00 | 7.8237 | 1.69608 | 10 | 78.24% |
| Inspection | 2100 | 3.00 | 15.00 | 11.6604 | 2.53955 | 15 | 77.74% |
| Management | 2100 | 2.00 | 10.00 | 8.5488 | 1.41231 | 10 | 85.49% |
| Student | Raw Score | T-Score | Norm Level | Scoring Rate (S) |
|---|---|---|---|---|
| A | 108 | 59.9 | Average | 69.67% |
| B | 111 | 61.3 | Average | 71.61% |
| C | 110 | 60.9 | Average | 70.97% |
| D | 108 | 59.9 | Average | 69.67% |
| E | 110 | 60.9 | Average | 70.97% |
| F | 108 | 59.9 | Average | 69.67% |
| Dimension | Student | Raw Score | T-Score | Norm Level | Scoring Rate (S) |
|---|---|---|---|---|---|
| MMK | A | 34 | 51.9 | Average ) | 61.82% |
| B | 42 | 61.9 | Above average ) | 76.36% | |
| C | 43 | 63.5 | Above average ) | 78.18% | |
| D | 36 | 54.4 | Average ) | 65.45% | |
| E | 40 | 59.5 | Above average | 72.73% | |
| F | 43 | 62.82 | Above average ) | 78.18% | |
| MME | A | 21 | 49.2 | Average ) | 60.00% |
| B | 16 | 39.3 | Below average ) | 45.71% | |
| C | 24 | 56.1 | Above average ) | 68.57% | |
| D | 23 | 54.0 | Average | 65.71% | |
| E | 18 | 43.3 | Below average ) | 51.43% | |
| F | 23 | 54.0 | Average ) | 65.71% | |
| MMM | A | 53 | 67.1 | Above average ) | 81.54% |
| B | 53 | 67.1 | Above average ) | 81.54% | |
| C | 43 | 55.9 | Average ) | 66.15% | |
| D | 49 | 62.7 | Above average ) | 75.38% | |
| E | 52 | 65.8 | Above average ) | 80.00% | |
| F | 42 | 54.1 | Average ) | 64.62% |
| Mean | N | Standard Deviation | t | df | p | |
|---|---|---|---|---|---|---|
| Result 1 | 80.870 | 568 | 15.593 | −1.154 | 567 | 0.249 |
| Result 2 | 81.324 | 568 | 17.827 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Kang, Y.; Jiao, Z.; Chen, X.; Zhen, Y.; Zhang, D.; Su, M. Development and Application of Intelligent Assessment System for Metacognition in Learning Mathematics among Junior High School Students. Sustainability 2022, 14, 6278. https://doi.org/10.3390/su14106278
Wang G, Kang Y, Jiao Z, Chen X, Zhen Y, Zhang D, Su M. Development and Application of Intelligent Assessment System for Metacognition in Learning Mathematics among Junior High School Students. Sustainability. 2022; 14(10):6278. https://doi.org/10.3390/su14106278
Chicago/Turabian StyleWang, Guangming, Yueyuan Kang, Zicong Jiao, Xia Chen, Yiming Zhen, Dongli Zhang, and Mingyu Su. 2022. "Development and Application of Intelligent Assessment System for Metacognition in Learning Mathematics among Junior High School Students" Sustainability 14, no. 10: 6278. https://doi.org/10.3390/su14106278
APA StyleWang, G., Kang, Y., Jiao, Z., Chen, X., Zhen, Y., Zhang, D., & Su, M. (2022). Development and Application of Intelligent Assessment System for Metacognition in Learning Mathematics among Junior High School Students. Sustainability, 14(10), 6278. https://doi.org/10.3390/su14106278






