Specifying Spatial Dependence for Teak Stands Specific to Solomon Island-Derived Clones in Tawau, Sabah, Malaysia: A Preliminary Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Analysis Structure
2.3. Defining Spatial Dependence Methods
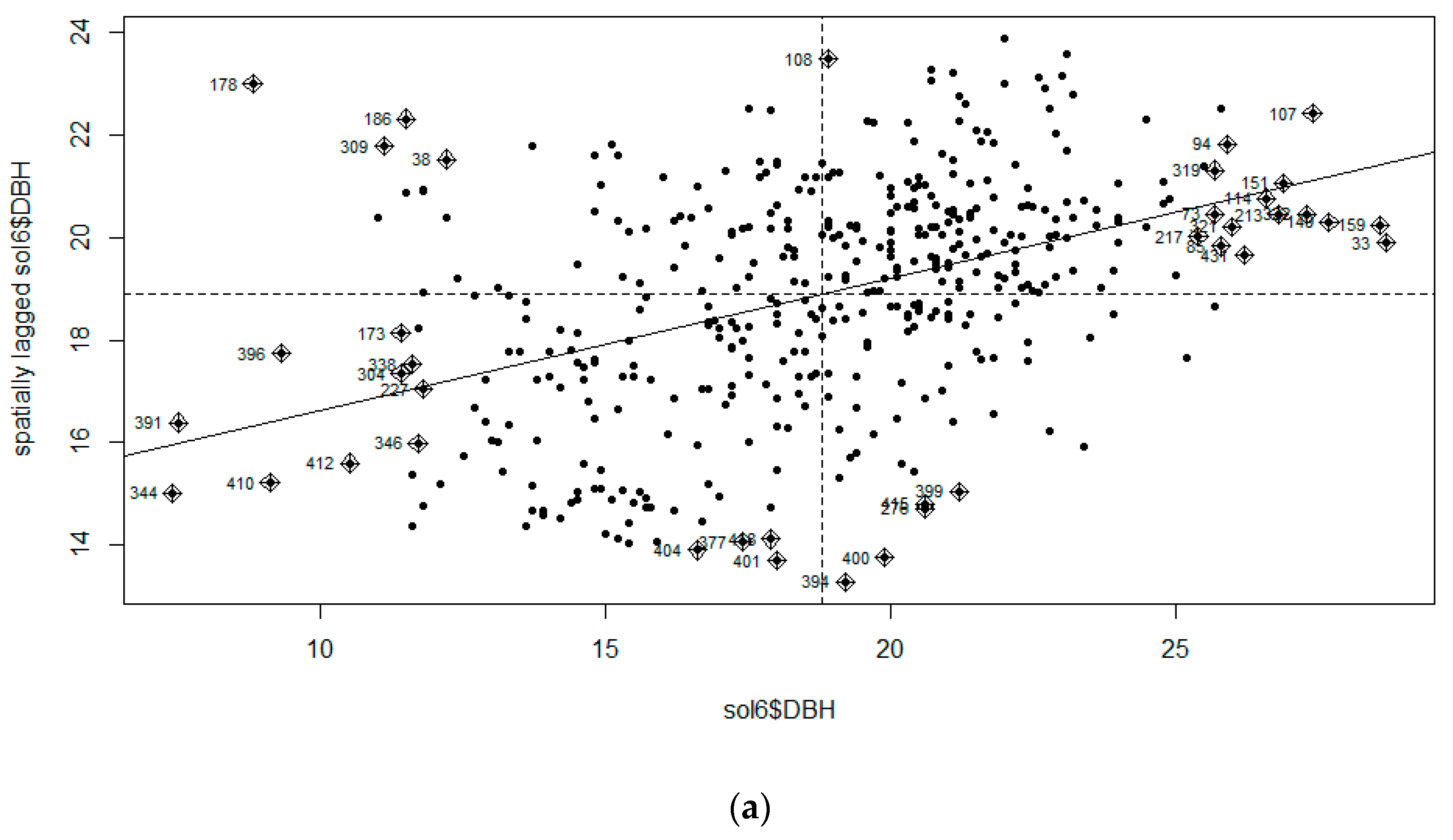
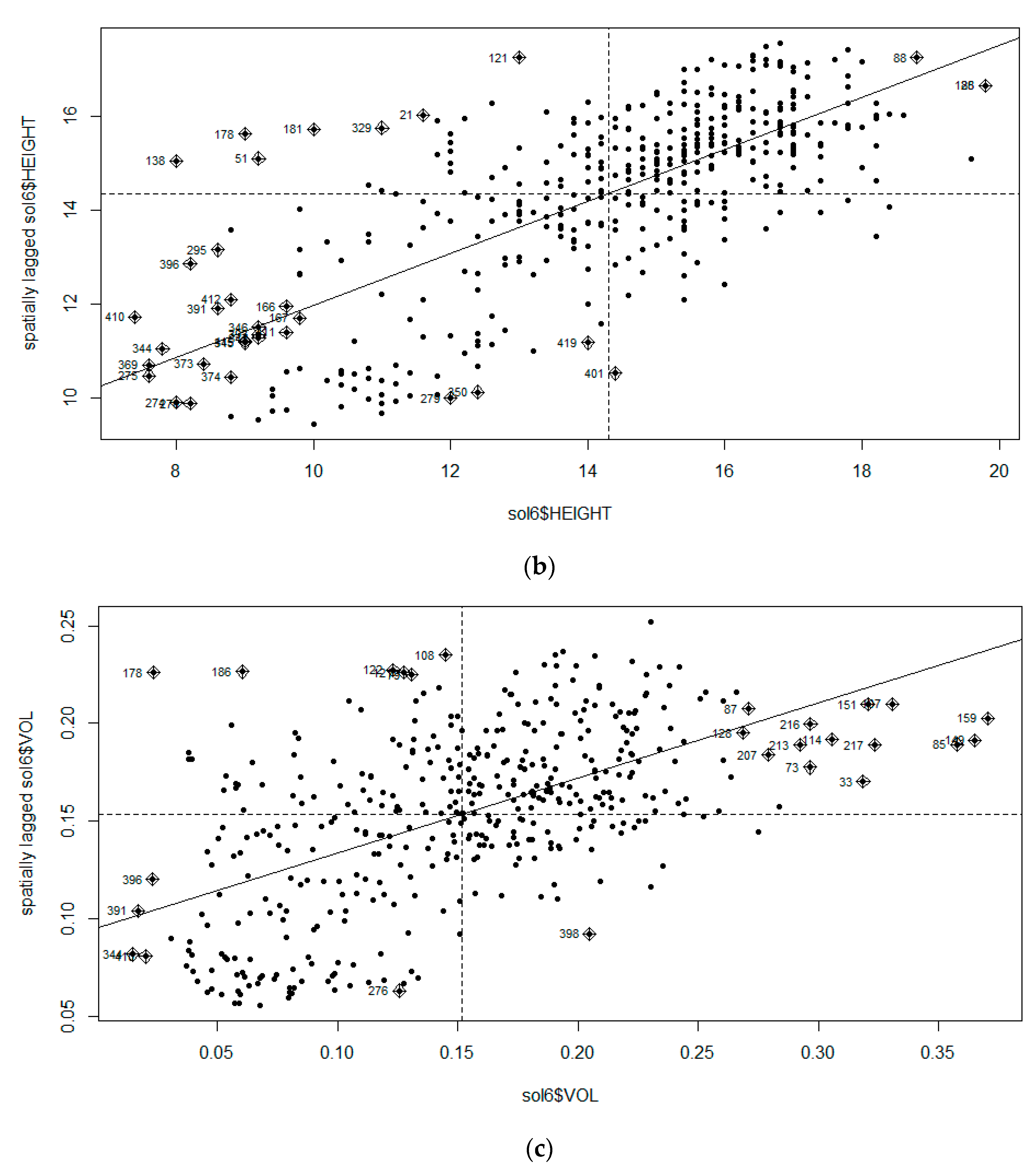
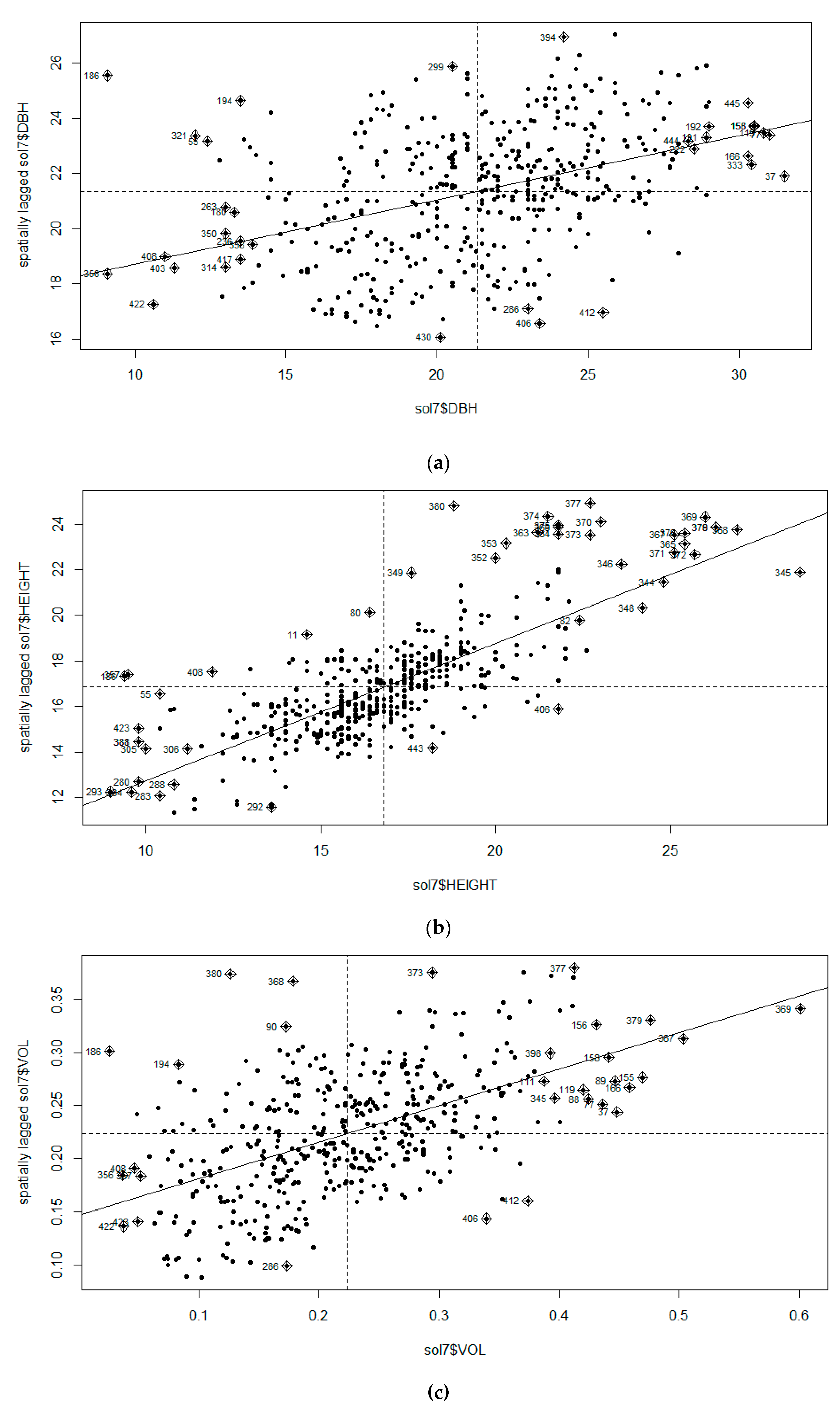
2.3.1. Moran’s I
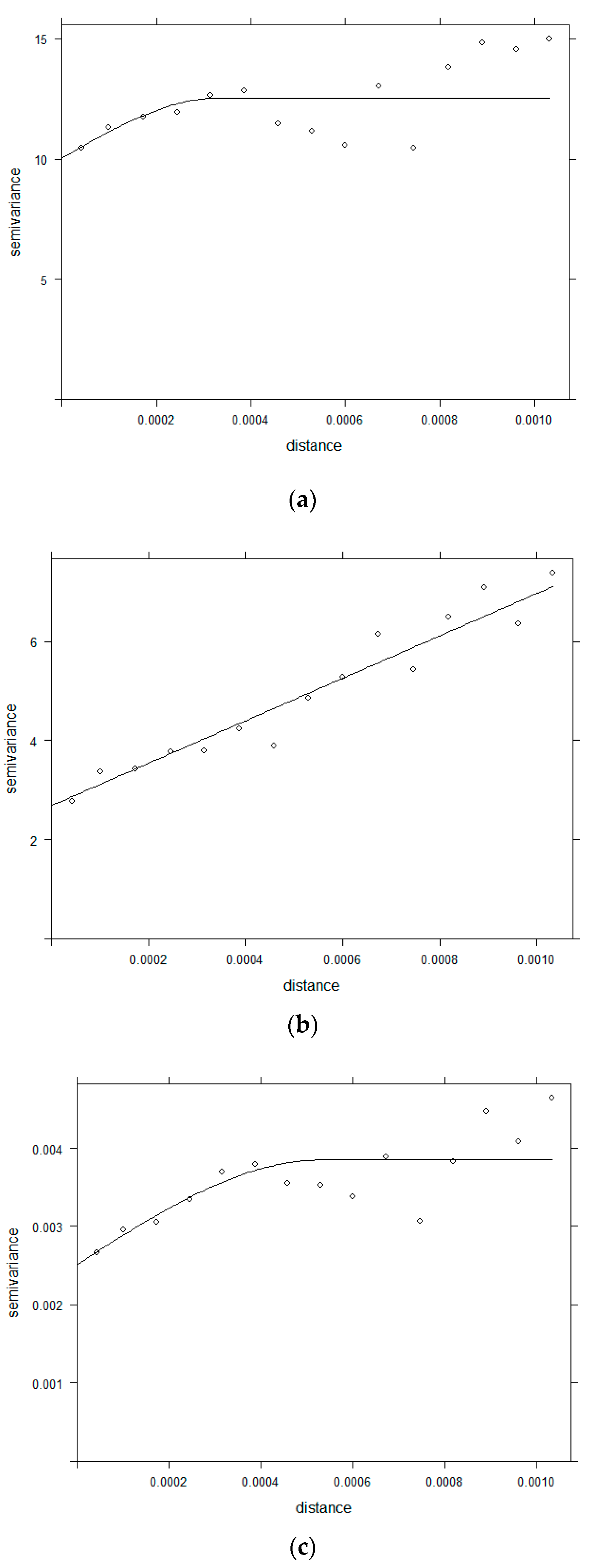
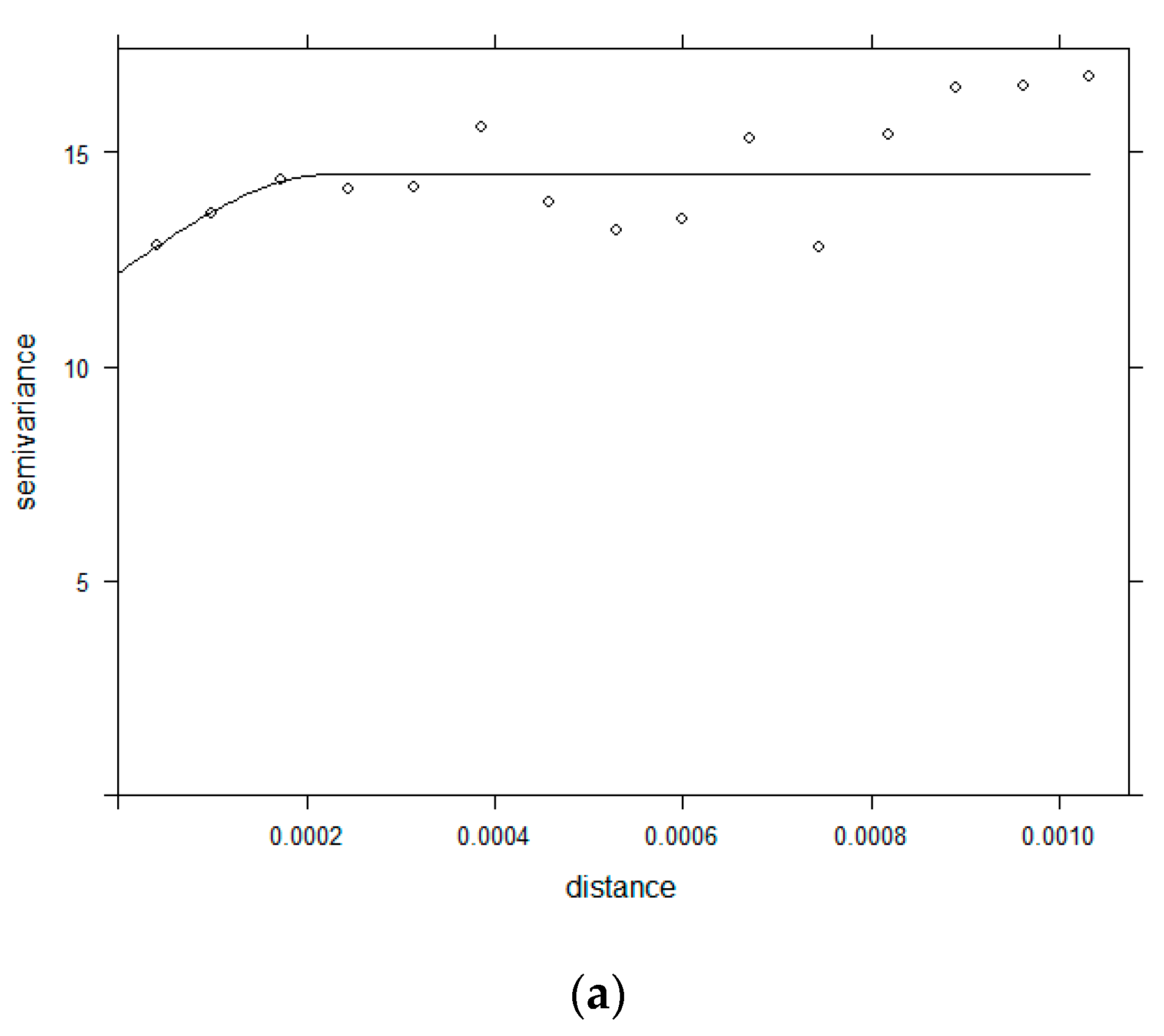
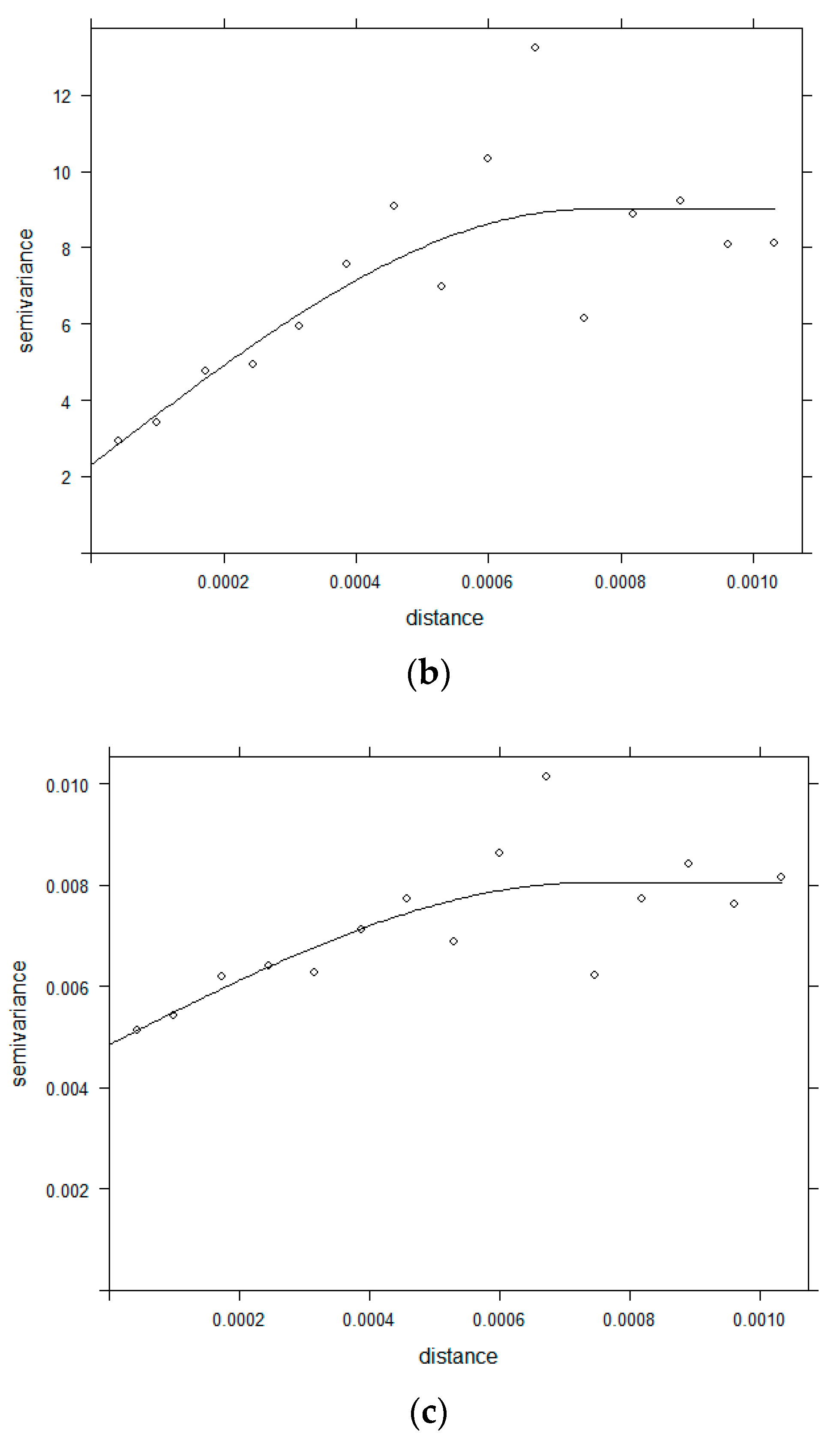
2.3.2. Semivariogram
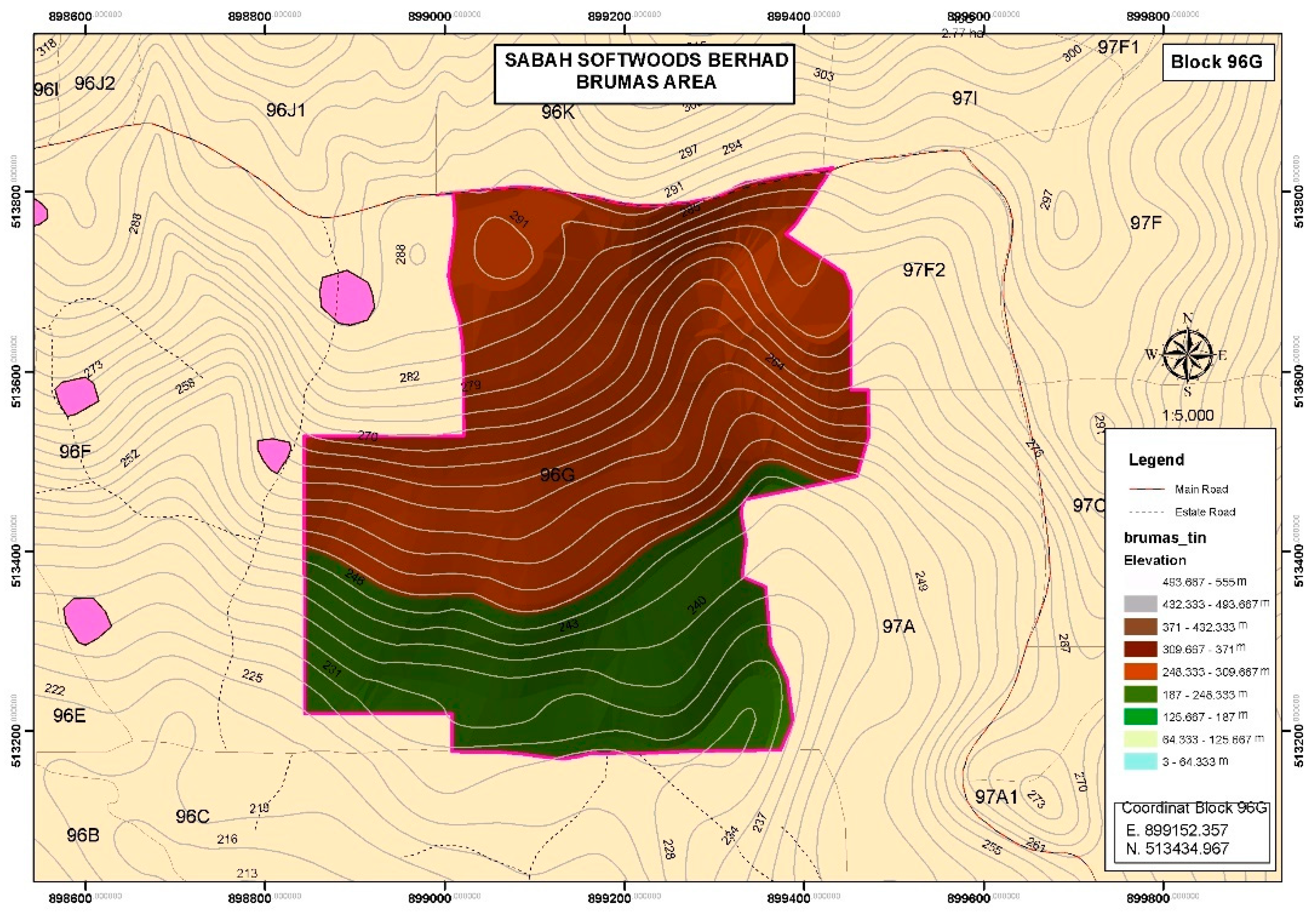
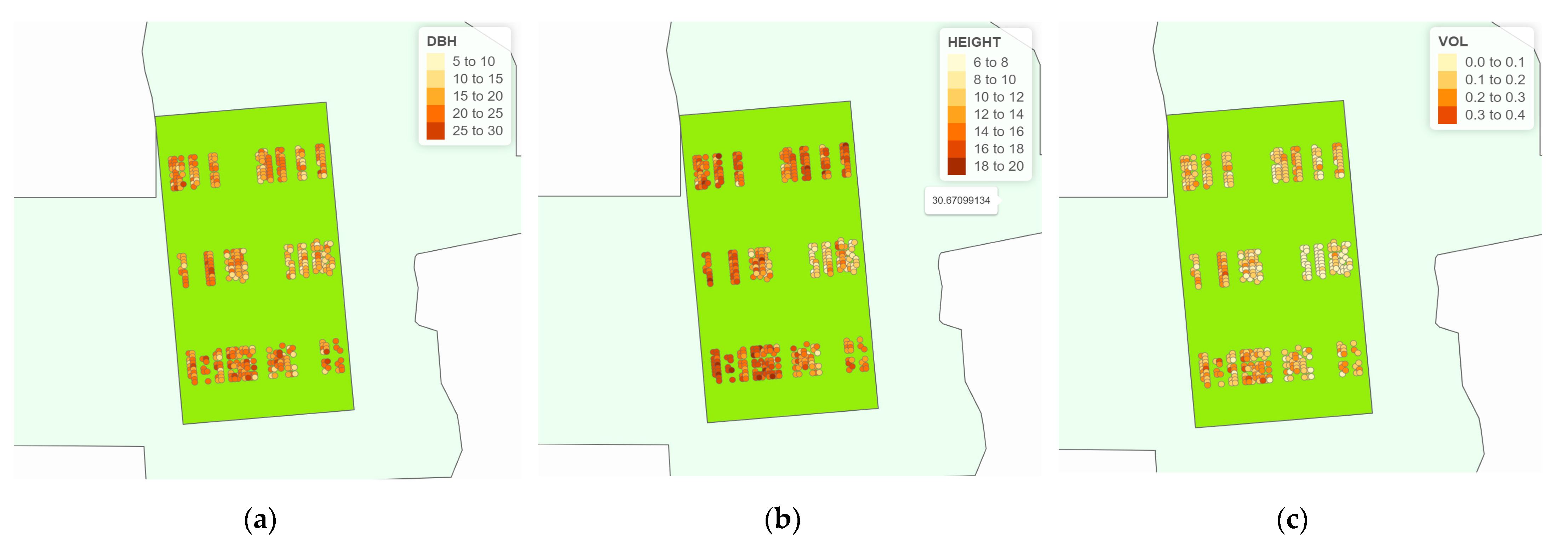
2.3.3. Thematic Map
3. Results
3.1. Moran’s I Analysis
3.2. Semivariogram Analysis for Spatial Dependence
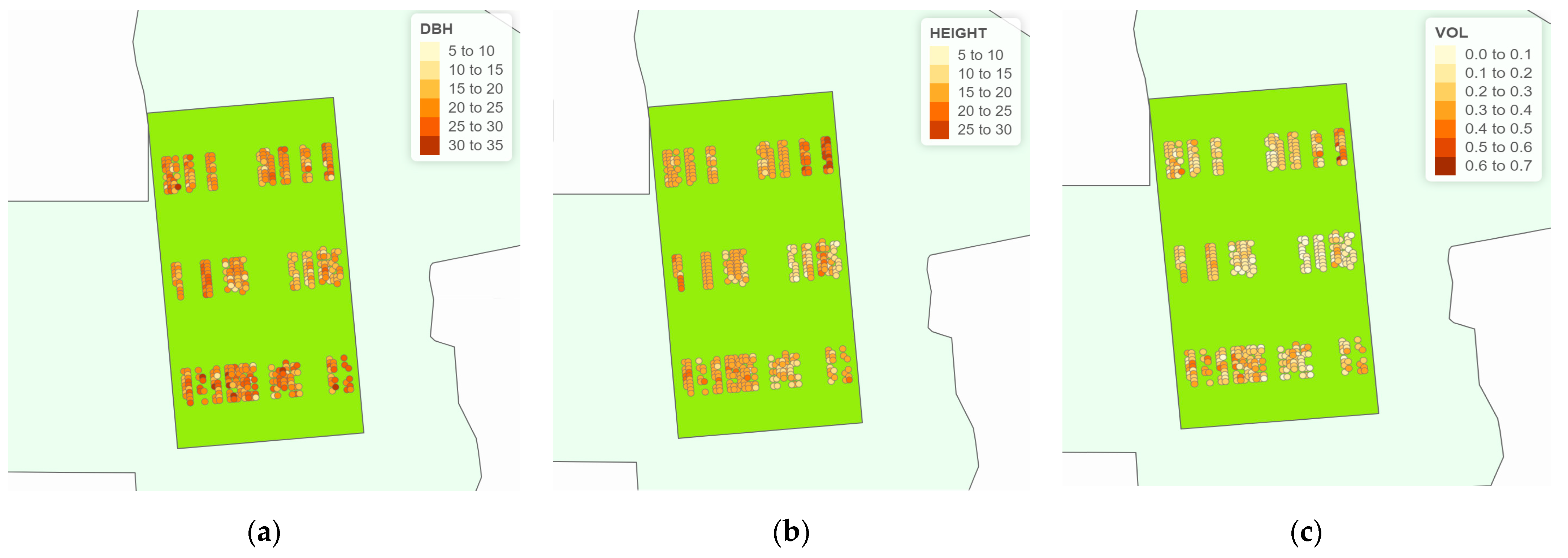
3.3. The Graphical Analysis of Thematic Maps
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crawford, T.W. Scale Analytical. In International Encyclopedia of Human Geography; Elsevier: Amsterdam, The Netherlands, 2009; pp. 29–36. ISBN 978-0-08-044910-4. [Google Scholar]
- Legendre, P. Spatial autocorrelation: Trouble or new paradigm? Ecology 1993, 74, 1659–1673. [Google Scholar] [CrossRef]
- Legendre, P.; Legendre, L. Numerical Ecology; Elsevier: Amsterdam, The Netherlands, 2012; ISBN 0-444-53869-0. [Google Scholar]
- Anselin, L.; Bera, A.K. Introduction to spatial econometrics. In Handbook of Applied Economic Statistics; Marcel Dekker: New York, NY, USA, 1998; p. 237. [Google Scholar]
- Fox, J.C.; Bi, H.; Ades, P.K. Spatial dependence and individual-tree growth models: I. Characterising spatial dependence. For. Ecol. Manag. 2007, 245, 10–19. [Google Scholar] [CrossRef]
- Tewari, V.P.; Singh, B. Total wood volume equations for Tectona grandis Linn F. stands in Gujarat, India. J. For. Environ. Sci. 2018, 34, 313–320. [Google Scholar]
- Koirala, A.; Montes, C.R.; Bullock, B.P.; Wagle, B.H. Developing taper equations for planted teak (Tectona grandis L.f.) trees of central lowland Nepal. Trees For. People 2021, 5, 100103. [Google Scholar] [CrossRef]
- Kenzo, T.; Himmapan, W.; Yoneda, R.; Tedsorn, N.; Vacharangkura, T.; Hitsuma, G.; Noda, I. General estimation models for above-and below-ground biomass of teak (Tectona grandis) plantations in Thailand. For. Ecol. Manag. 2020, 457, 117701. [Google Scholar] [CrossRef]
- Pelissari, A.L.; Roveda, M.; Caldeira, S.F.; Sanquetta, C.R.; Corte, A.P.D.; Rodrigues, C.K. Geostatistical modeling of timber volume spatial variability for Tectona grandis LF precision forestry. Cerne 2017, 23, 115–122. [Google Scholar] [CrossRef]
- Ghosh, S.; Nandy, S.; Mohanty, S.; Subba, R.; Kushwaha, S.P.S. Are phenological variations in natural teak (Tectona grandis) forests of India governed by rainfall? A remote sensing based investigation. Environ. Monit. Assess. 2019, 191, 786. [Google Scholar] [CrossRef]
- Gil, R.L.; Lanssanova, L.R.; Chig, L.A.; de Almeida Garrett, A.T.; de Oliveira, R.V.; de Oliveira, F.P.; Ferreira, K.R. Modelling spatial variability of soil chemical attributes in Tectona grandis stands in central-west Brazil. J. Trop. For. Sci. 2018, 30, 376–383. [Google Scholar]
- Popoola, F.S.; Adesoye, P.O. Crown ratio models for Tectona grandis (Linn. f) stands in Osho Forest reserve, Oyo State, Nigeria. J. For. Environ. Sci. 2012, 28, 63–67. [Google Scholar] [CrossRef]
- Zahabu, E.; Mugasha, W.M.; Katani, J.Z.; Malimbwi, R.E.; Mwangi, J.R.; Chamshama, S.A.O. Allometric biomass and volume models for Tectona grandis plantations. In Allometric Tree Biomass and Volume Models in Tanzania; E&D Vision Publishing Ltd: Dar es Salaam, Tansania, 2018. [Google Scholar]
- Dantani, A.; Shamaki, S.; Gupa, M.; Sa’idu, M.; Mukhtar, R.; Umar, M.; Abubakar, A.; Abubakar, A. Allometric Models for Estimating Site Index of Teak (Tectona grandis Linn F.) in Kanya Forest Plantation, Kebbi State, Nigeria. Asian J. Environ. Y Ecol. 2019, 10, 1–7. [Google Scholar] [CrossRef]
- de Almeida Garrett, A.T.; Bonete, I.P.; do Amaral Machado, S.; Pelissari, A.L.; da Silva, F.A.; Filho, A.F.; Lanssanova, L.R.; Ciarnoschi, D. Mixed-effect non-linear modelling for diameter estimation along the stem of Tectona grandis in mid-western Brazil. South. For. J. For. Sci. 2019, 81, 167–173. [Google Scholar]
- de Souza Maria, L.; Litter, F.A.; de Almeida Carneiro, M.; da Silva, F.R.; Garcia, M.L.; de Carvalho, M.A.C. Dendrometric evaluation of a clonal population of Tectona grandis in forest-livestock system. Ciência Rural 2019, 49. [Google Scholar]
- Neto, A.A.L.M.; Farias, P.R.S.; de Matos, G.S.B.; Rodrigues, G.R.; da Silva, J.O.; da Costa, L.S.L.; Anhê, B.B. Nutritional diagnosis and spatial variability of leaf nutrients in teak field in the Eastern Amazon. J. Plant Nutr. 2021, 1–10. [Google Scholar] [CrossRef]
- Adams, E.A. World forest area still on the decline. Europe 2012, 989, 1–5. [Google Scholar]
- Bennett, L. Deforestation and Climate Change; Climate Institute: Washington, DC, USA, 2017. [Google Scholar]
- Clark, D.A.; Clark, D.B. Assessing the growth of tropical rain forest trees: Issues for forest modeling and management. Ecol. Appl. 1999, 9, 981–997. [Google Scholar] [CrossRef]
- Goh, D.K.; Galiana, A. Vegetative Propagation of Teak; JIRCAS: Ibaraki, Japan, 2000. [Google Scholar]
- Goh, D.K.; Monteuuis, O. Rationale for developing intensive teak clonal plantations, with special reference to Sabah. Bois For. Trop. 2005, 285, 5–15. [Google Scholar]
- Goh, D.K.S.; Japarudin, Y.; Alwi, A.; Lapammu, M.; Flori, A.; Monteuuis, O. Growth differences and genetic parameter estimates of 15 teak (Tectona grandis L.f.) genotypes of various ages clonally propagated by microcuttings and planted under humid tropical conditions. Silvae Genet. 2013, 62, 196–206. [Google Scholar] [CrossRef] [Green Version]
- Monteuuis, O.; Goh, D.K.S. Field growth performances of teak genotypes of different ages clonally produced by rooted cuttings, in vitro microcuttings, and meristem culture. Can. J. For. Res. 2015, 45, 9–14. [Google Scholar] [CrossRef]
- Monteuuis, O.; Goh, D.K.S.; Garcia, C.; Alloysius, D.; Gidiman, J.; Bacilieri, R.; Chaix, G. Genetic variation of growth and tree quality traits among 42 diverse genetic origins of Tectona grandis planted under humid tropical conditions in Sabah, East Malaysia. Tree Genet. Genomes 2011, 7, 1263–1275. [Google Scholar] [CrossRef]
- Karahan, G.; Erşahin, S. Geostatistical analysis of spatial variation in forest ecosystems. Eurasian J. For. Sci. 2018, 6, 9–22. [Google Scholar]
- Gatrell, A.C. Autocorrelation in Spaces. Environ. Plan. A Econ. Space 1979, 11, 507–516. [Google Scholar] [CrossRef]
- Olea, R.A. A six-step practical approach to semivariogram modeling. Stoch. Environ. Res. Risk Assess. 2006, 20, 307–318. [Google Scholar] [CrossRef]
- Arlinghaus, S.L.; Griffith, D.A.; Arlinghaus, W.C.; Drake, W.D.; Nystuen, J.D. (Eds.) Practical Handbook of Spatial Statistics, 1st ed.; CRC Press: Boca Raton, FL, USA, 2020; ISBN 978-1-00-306768-9. [Google Scholar]
- Reed, D.D.; Burkhart, H.E. Spatial Autocorrelation of Individual Tree Characteristics in Loblolly Pine Stands. For. Sci. 1985, 31, 575–587. [Google Scholar]
- Musin, O.R. Properties of the Delaunay triangulation. In Proceedings of the Thirteenth Annual Symposium on Computational Geometry—SCG ’97, Nice, France, 4–6 June 1997; ACM Press: Nice, France, 1997; pp. 424–426. [Google Scholar]
- Anselin, L. Global Spatial Autocorrelation (1), Moran Scatter Plot and Spatial Correlogram. In GeoDa: An Introduction to Spatial Data Analysis; The University of Chicago: Chicago, IL, USA, 2018. [Google Scholar]
- Olea, R.A. The Semivariogram. In Geostatistics for Engineers and Earth Scientists; Springer US: Boston, MA, USA, 1999; pp. 67–90. ISBN 978-1-4613-7271-4. [Google Scholar]
- Bachmaier, M.; Backes, M. Variogram or semivariogram? Understanding the variances in a variogram. Precis. Agric. 2008, 9, 173–175. [Google Scholar] [CrossRef]
- Camana, F.; Deutsch, C.V. The Nugget Effect. Geostatistics Lessons. Available online: http://www.geostatisticslessons.com/lessons/nuggeteffect (accessed on 16 March 2019).
- Anselin, L.; Syabri, I.; Kho, Y. GeoDa: An Introduction to Spatial Data Analysis. In Handbook of Applied Spatial Analysis; Fischer, M.M., Getis, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 73–89. ISBN 978-3-642-03646-0. [Google Scholar]
- Sakai, A.K.; Oden, N.L. Spatial pattern of sex expression in silver maple (Acer saccharinum L.): Morisita’s index and spatial autocorrelation. Am. Nat. 1983, 122, 489–508. [Google Scholar] [CrossRef]
- Duncan, R.P.; Stewart, G.H. The temporal and spatial analysis of tree age distributions. Can. J. For. Res. 1991, 21, 1703–1710. [Google Scholar] [CrossRef]
- Kuuluvainen, T.; Penttinen, A.; Leinonen, K.; Nygren, M. Statistical opportunities for comparing stand structural heterogeneity in managed and primeval forests: An example from boreal spruce forest in southern Finland. Silva Fenn. 1996, 30, 315–328. [Google Scholar] [CrossRef] [Green Version]
- Magnussen, S. A method to adjust simultaneously for spatial microsite and competition effects. Can. J. For. Res. 1994, 24, 985–995. [Google Scholar] [CrossRef]
- Kenkel, N.C.; Hendrie, M.L.; Bella, I.E. A long-term study of Pinus banksiana population dynamics. J. Veg. Sci. 1997, 8, 241–254. [Google Scholar] [CrossRef]
- García, O. The state-space approach in growth modelling. Can. J. For. Res. 1994, 24, 1894–1903. [Google Scholar] [CrossRef]
- Cressie, N. Geostatistical analysis of spatial data. In Spatial Statistics and Digital Image Analysis; The National Academies Press: Washington, DC, USA, 1991; pp. 87–108. [Google Scholar]

| 6th Year | 7th Year | |||||
|---|---|---|---|---|---|---|
| Moran’s I | p-Value | Monte Carlo | Moran’s I | p-Value | Monte Carlo | |
| DBH | 0.2568735864 | <0.0001 | 0.001 | 0.2321702692 | <0.0001 | 0.001 |
| Height | 0.5525857451 | <0.0001 | 0.001 | 0.6033771319 | <0.0001 | 0.001 |
| Volume | 0.3853519365 | <0.0001 | 0.001 | 0.3452859439 | <0.0001 | 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiram, J.J.; Mohamad Yunus, R.; Japarudin, Y.; Lapammu, M. Specifying Spatial Dependence for Teak Stands Specific to Solomon Island-Derived Clones in Tawau, Sabah, Malaysia: A Preliminary Study. Sustainability 2022, 14, 6005. https://doi.org/10.3390/su14106005
Kiram JJ, Mohamad Yunus R, Japarudin Y, Lapammu M. Specifying Spatial Dependence for Teak Stands Specific to Solomon Island-Derived Clones in Tawau, Sabah, Malaysia: A Preliminary Study. Sustainability. 2022; 14(10):6005. https://doi.org/10.3390/su14106005
Chicago/Turabian StyleKiram, Johannah Jamalul, Rossita Mohamad Yunus, Yani Japarudin, and Mahadir Lapammu. 2022. "Specifying Spatial Dependence for Teak Stands Specific to Solomon Island-Derived Clones in Tawau, Sabah, Malaysia: A Preliminary Study" Sustainability 14, no. 10: 6005. https://doi.org/10.3390/su14106005
APA StyleKiram, J. J., Mohamad Yunus, R., Japarudin, Y., & Lapammu, M. (2022). Specifying Spatial Dependence for Teak Stands Specific to Solomon Island-Derived Clones in Tawau, Sabah, Malaysia: A Preliminary Study. Sustainability, 14(10), 6005. https://doi.org/10.3390/su14106005






