A Comparative Analysis of Homogenous Groups’ Preferences by Using AIP and AIJ Group AHP-PROMETHEE Model
Abstract
:1. Introduction
2. Literature Review
- Elaborate on a new model, AIJ–Group AHP–PROMETHEE, to evaluate urban public transport.
- Comparative analysis with the conventional AIP approach to testing the applicability of the new model.
- Sensitivity analysis for the PROMETHEE outputs is possible for the AIJ approach and is not applicable in the case of the AIP approach because of the final aggregation.
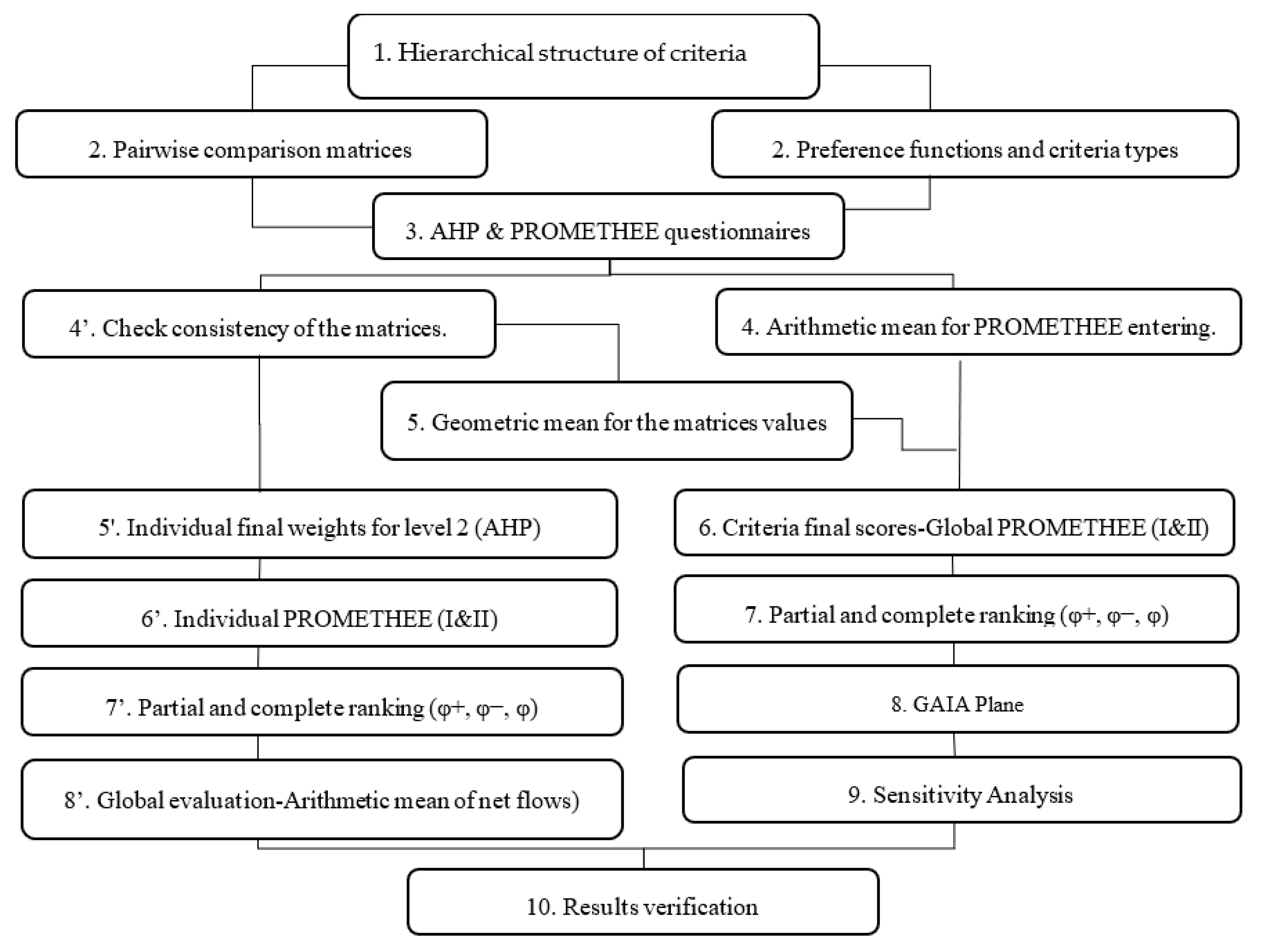
3. Materials and Methods
3.1. AHP Method
3.2. PROMETHEE Method
3.2.1. PROMETHEE I
3.2.2. PROMETHEE II
3.3. Aggregation of Individual Priorities
3.4. Aggregation of Individual Judgements
4. Results
4.1. The Aggregation of Individual Priorities
4.2. The Aggregation of Individual Judgements
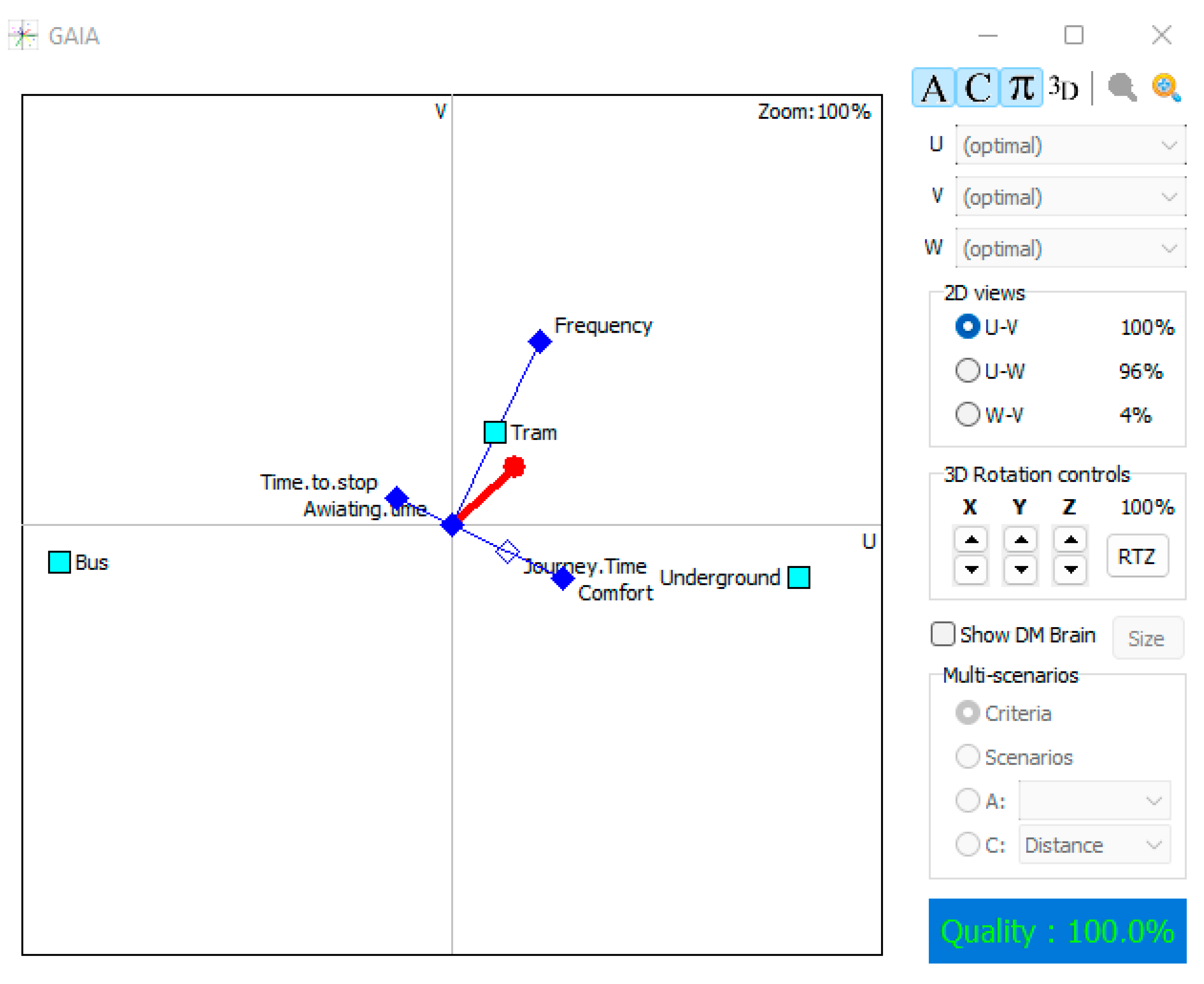
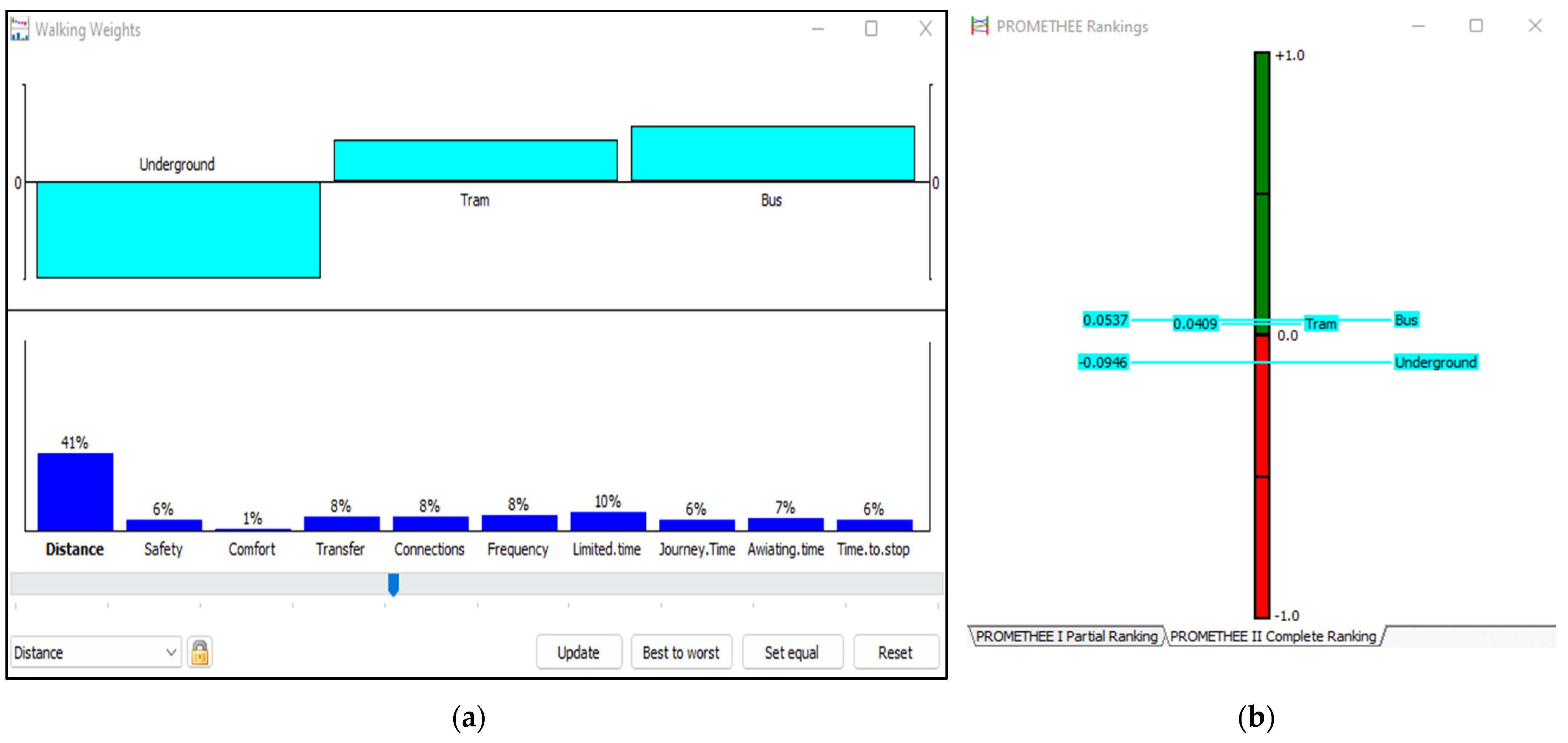
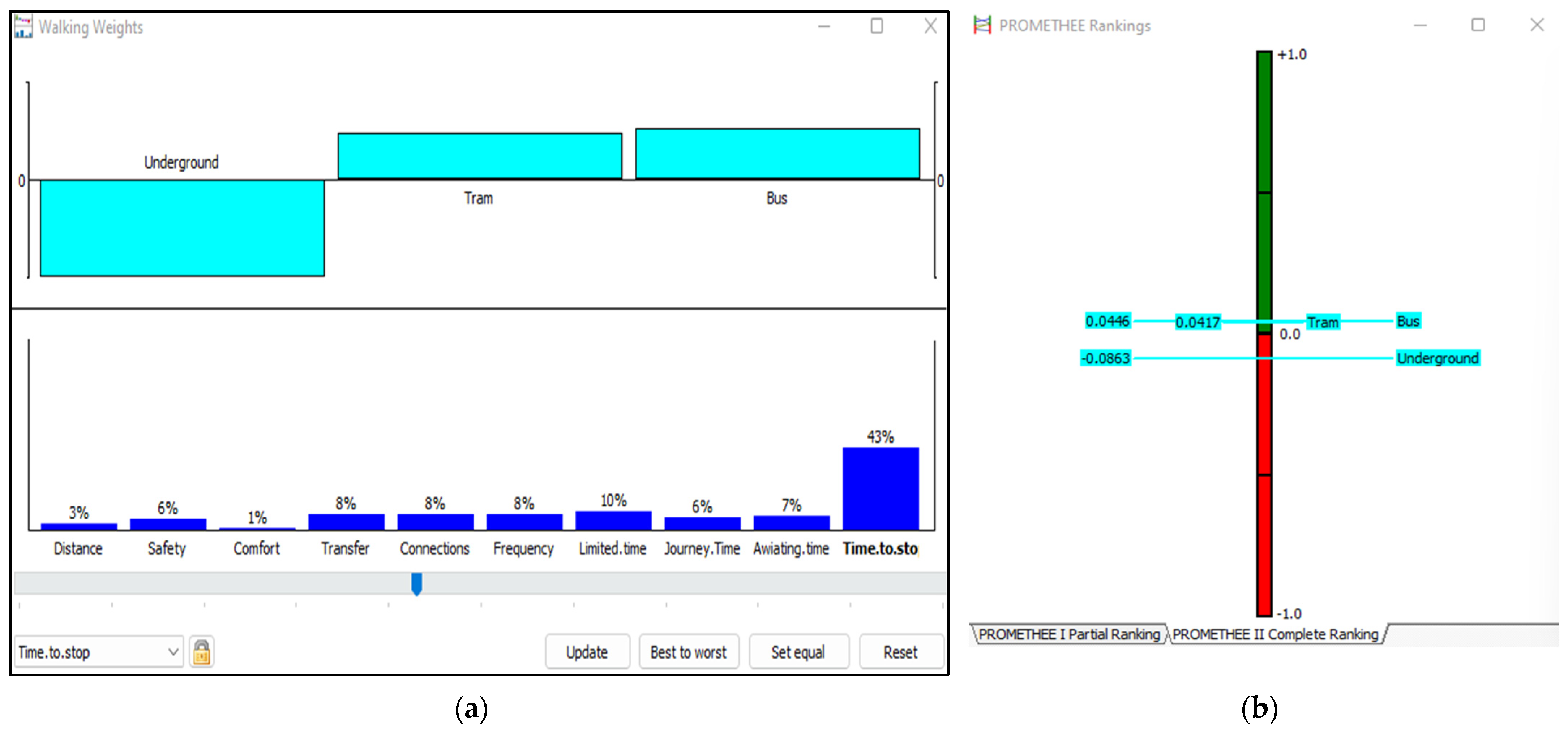
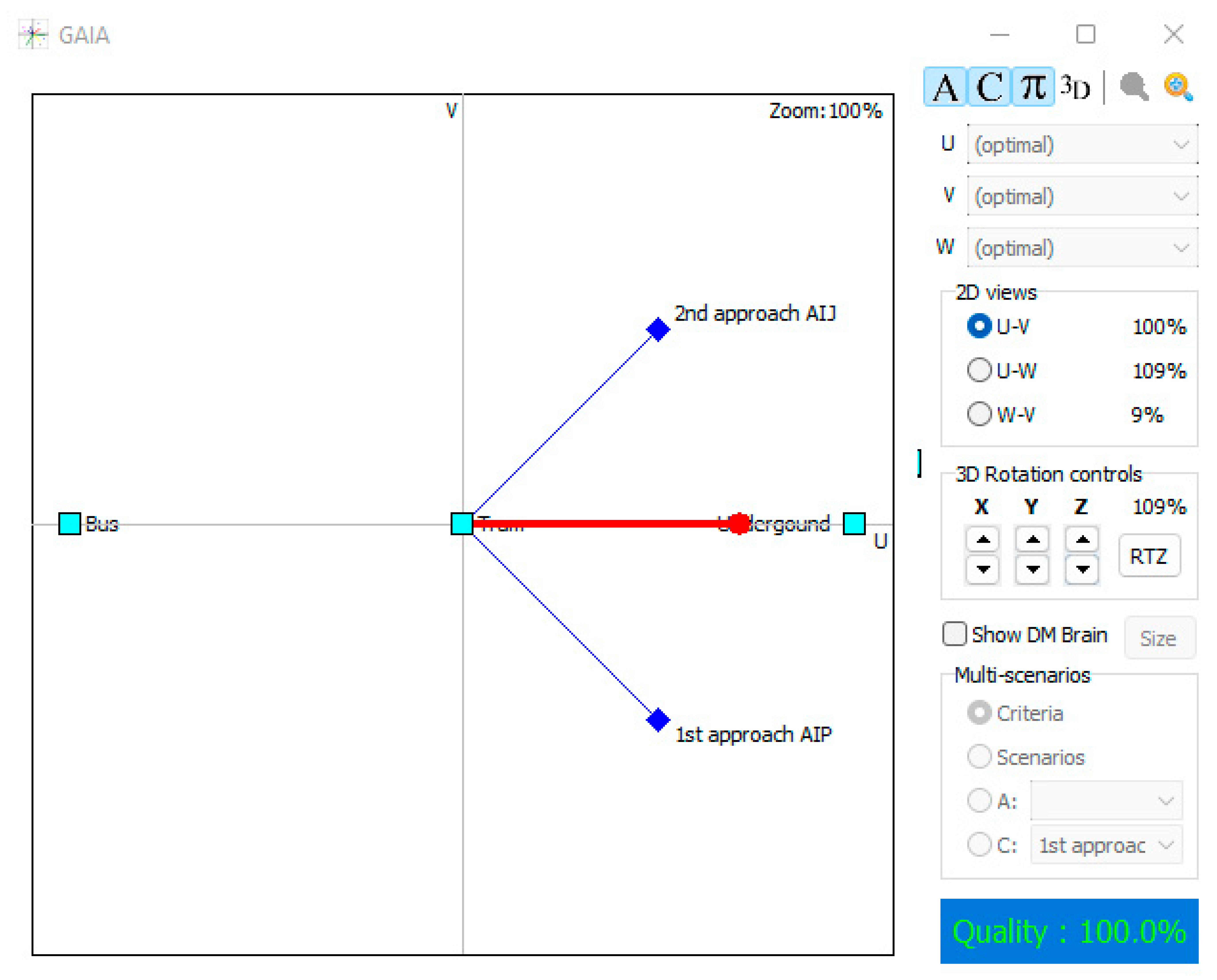
4.3. GAIA Plane and Sensitivity Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Briand, A.S.; Côme, E.; Trépanier, M.; Oukhellou, L. Analyzing year-to-year changes in public transport passenger behaviour using smart card data. Transp. Res. Part C Emerg. Technol. 2017, 79, 274–289. [Google Scholar] [CrossRef]
- Bonnel, P.; Munizaga, M.A. Transport survey methods—In the era of big data facing new and old challenges. Transp. Res. Procedia 2018, 32, 1–15. [Google Scholar] [CrossRef]
- Milne, D.; Watling, D. Big data and understanding change in the context of planning transport systems. J. Transp. Geogr. 2019, 76, 235–244. [Google Scholar] [CrossRef]
- Jain, S.; Ronald, N.; Thompson, R.; Winter, S. Predicting susceptibility to use demand responsive transport using demographic and trip characteristics of the population. Travel Behav. Soc. 2017, 6, 44–56. [Google Scholar] [CrossRef]
- Coll, J.E.; Zalaquett, C. The Relationship of Worldviews of Advisors and Students and Satisfaction with Advising: A Case of Homogenous Group Impact. J. Coll. Student Retent. Res. Theory Pract. 2007, 9, 273–281. [Google Scholar] [CrossRef]
- Yeung, J.; Wearing, S.; Hills, A.P. Child transport practices and perceived barriers in active commuting to school. Transp. Res. Part A Policy Pract. 2008, 42, 895–900. [Google Scholar] [CrossRef]
- Behzadian, M.; Hosseini-Motlagh, S.M.; Ignatius, J.; Goh, M.; Sepehri, M.M. PROMETHEE Group Decision Support System and the House of Quality. Gr. Decis. Negot. 2013, 22, 189–205. [Google Scholar] [CrossRef]
- Forman, E.; Peniwati, K. Aggregating individual judgments and priorities with the Analytic Hierarchy Process. Eur. J. Oper. Res. 1998, 108, 165–169. [Google Scholar] [CrossRef]
- Bernasconi, M.; Choirat, C.; Seri, R. Empirical properties of group preference aggregation methods employed in AHP: Theory and evidence. Eur. J. Oper. Res. 2014, 232, 584–592. [Google Scholar] [CrossRef] [Green Version]
- Qureshi, M.N.; Kumar, P.; Kumar, D. Framework for benchmarking logistics performance using fuzzy AHP. Int. J. Bus. Perform. Supply Chain Model. 2009, 1, 82–98. [Google Scholar] [CrossRef]
- Ransikarbum, K.; Khamhong, P. Integrated Fuzzy Analytic Hierarchy Process and Technique for Order of Preference by Similarity to Ideal Solution for Additive Manufacturing Printer Selection. J. Mater. Eng. Perform. 2021, 30, 6481–6492. [Google Scholar] [CrossRef]
- Ransikarbum, K.; Pitakaso, R.; Kim, N.; Ma, J. Multicriteria decision analysis framework for part orientation analysis in additive manufacturing. J. Comput. Des. Eng. 2021, 8, 1141–1157. [Google Scholar] [CrossRef]
- Alkharabsheh, A.; Moslem, S.; Oubahman, L.; Duleba, S. An integrated approach of multi-criteria decision-making and grey theory for evaluating urban public transportation systems. Sustainability 2021, 13, 2740. [Google Scholar] [CrossRef]
- Çelikbilek, Y.; Moslem, S.; Duleba, S. A combined grey multi criteria decision making model to evaluate public transportation systems. Evol. Syst. 2022, in press. [Google Scholar] [CrossRef]
- De Luca, S. Public engagement in strategic transportation planning: An analytic hierarchy process based approach. Transp. Policy 2014, 33, 110–124. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Brans, J.P.; Vincke, P.; Mareschal, B. How to select and how to rank projects: The PROMETHEE method. Eur. J. Oper. Res. 1986, 24, 228–238. [Google Scholar] [CrossRef]
- Macharis, C.; Brans, J.; Mareschal, B.; Bertrand, M.; Jean Pierre, B.; Cathy, M. The GDSS PROMETHEE procedure—A PROMETHEE-GAIA based procedure for group decision support. J. Decis. Syst. 1998, 7, 283–307. [Google Scholar]
- Tian, X.; Xu, Z.; Gu, J. Group decision-making models for venture capitalists: The promethee with hesitant fuzzy linguistic information. Technol. Econ. Dev. Econ. 2019, 25, 743–773. [Google Scholar] [CrossRef]
- Oubahman, L.; Duleba, S. Evaluation of urban public transport by using PROMETHEE method. In Proceedings of the XI International Conference on Transport Sciences Győr Online, Online, 10 June 2021; pp. 291–297. [Google Scholar]
- Duleba, S.; Alkharabsheh, A.; Gündoğdu, F.K. Creating a common priority vector in intuitionistic fuzzy AHP: A comparison of entropy-based and distance-based models. Ann. Oper. Res. 2021, in press. [Google Scholar] [CrossRef]
- Duleba, S. An Ahp-Ism Approach for Considering Public Preferences in a public transport development decision. Transport 2019, 34, 662–671. [Google Scholar] [CrossRef] [Green Version]
- Ossadnik, W.; Schinke, S.; Kaspar, R.H. Group Aggregation Techniques for Analytic Hierarchy Process and Analytic Network Process: A Comparative Analysis. Gr. Decis. Negot. 2016, 25, 421–457. [Google Scholar] [CrossRef] [Green Version]
- De Oña, J.; De Oña, R.; Eboli, L.; Mazzulla, G. Perceived service quality in bus transit service: A structural equation approach. Transp. Policy 2013, 29, 219–226. [Google Scholar] [CrossRef]
- Redman, L.; Friman, M.; Gärling, T.; Hartig, T. Quality attributes of public transport that attract car users: A research review. Transp. Policy 2013, 25, 119–127. [Google Scholar] [CrossRef]
- Wang, J.J.; Yang, D.L. Using a hybrid multi-criteria decision aid method for information systems outsourcing. Comput. Oper. Res. 2006, 34, 3691–3700. [Google Scholar] [CrossRef]
- Mahdi, A.; Esztergár-Kiss, D. Modelling the Accommodation Preferences of Tourists by Combining Fuzzy-AHP and GIS Methods. J. Adv. Transp. 2021, 2021, 9913513. [Google Scholar] [CrossRef]
- Turcksin, L.; Bernardini, A.; Macharis, C. A combined AHP-PROMETHEE approach for selecting the most appropriate policy scenario to stimulate a clean vehicle fleet. Procedia-Soc. Behav. Sci. 2011, 20, 954–965. [Google Scholar] [CrossRef] [Green Version]
- Ghasemi, P.; Talebi, E. An Integrated FAHP-PROMETHEE Approach for Selecting the Best Flexible Manufacturing System. Eur. Online J. Nat. Soc. Sci. 2014, 3, 1137–1150. [Google Scholar]
- Wudhikarn, R.; Chakpitak, N.; Neubert, G. Improving the strategic benchmarking of intellectual capital management in logistics service providers. Sustainability 2020, 12, 10174. [Google Scholar] [CrossRef]
- Wudhikarn, R. Improving the intellectual capital management approach using the hybrid decision method. J. Intellect. Cap. 2018, 19, 670–691. [Google Scholar] [CrossRef]
- Zha, S.; Guo, Y.; Huang, S.; Tang, P. A Hybrid MCDM Approach Based on ANP and TOPSIS for Facility Layout Selection. Trans. Nanjing Univ. Aeronaut. Astronaut. 2018, 35, 1027–1037. [Google Scholar] [CrossRef]
- Escobar, M.T.; Moreno-Jiménez, J.M. Aggregation of individual preference structures in AHP-group decision making. Gr. Decis. Negot. 2007, 16, 287–301. [Google Scholar] [CrossRef]
- Blagojevic, B.; Srdjevic, B.; Srdjevic, Z.; Zoranovic, T. Heuristic aggregation of individual judgments in AHP group decision making using simulated annealing algorithm. Inf. Sci. 2016, 330, 260–273. [Google Scholar] [CrossRef]
- Coffey, L.; Claudio, D. In defense of group fuzzy AHP: A comparison of group fuzzy AHP and group AHP with confidence intervals. Expert Syst. Appl. 2021, 178, 114970. [Google Scholar] [CrossRef]
- Abel, E.; Mikhailov, L.; Keane, J. Group aggregation of pairwise comparisons using multi-objective optimization. Inf. Sci. 2015, 322, 257–275. [Google Scholar] [CrossRef]
- Lolli, F.; Ishizaka, A.; Gamberini, R.; Rimini, B.; Ferrari, A.M.; Marinelli, S.; Savazza, R. Waste treatment: An environmental, economic and social analysis with a new group fuzzy PROMETHEE approach. Clean Technol. Environ. Policy 2016, 18, 1317–1332. [Google Scholar] [CrossRef] [Green Version]
- Christian, A.V.; Zhang, Y.; Salifou, C. Application of PROMETHEE-GAIA Method in the Entry Mode Selection Process in International Market Expansion. Open J. Bus. Manag. 2016, 04, 238–250. [Google Scholar] [CrossRef] [Green Version]
- Moslem, S.; Ghorbanzadeh, O.; Blaschke, T.; Duleba, S. Analysing Stakeholder Consensus for a Sustainable Transport Development Decision by the Fuzzy AHP and Interval AHP. Sustainability 2019, 11, 3271. [Google Scholar] [CrossRef] [Green Version]
- Nayum, A.; Nordfjærn, T. Predictors of public transport use among university students during the winter: A MIMIC modelling approach. Travel Behav. Soc. 2021, 22, 236–243. [Google Scholar] [CrossRef]
- Hensher, D.A.; Ho, C.Q.; Reck, D.J. Mobility as a service and private car use: Evidence from the Sydney MaaS trial. Transp. Res. Part A Policy Pract. 2021, 145, 17–33. [Google Scholar] [CrossRef]
- Duleba, S.; Moslem, S. Sustainable Urban Transport Development with Stakeholder Participation, an sustainability Sustainable Urban Transport Development with Stakeholder Participation, an AHP-Kendall Model: A Case Study for Mersin. Sustainability 2018, 10, 3647. [Google Scholar] [CrossRef] [Green Version]
- Nalmpantis, D.; Roukouni, A.; Genitsaris, E.; Stamelou, A.; Naniopoulos, A. Evaluation of innovative ideas for Public Transport proposed by citizens using Multi-Criteria Decision Analysis (MCDA). Eur. Transp. Res. Rev. 2019, 11, 22. [Google Scholar] [CrossRef] [Green Version]
- Yagmahan, B.; Yılmaz, H. An integrated ranking approach based on group multi-criteria decision making and sensitivity analysis to evaluate charging stations under sustainability. Environ. Dev. Sustain. 2022, in press. [Google Scholar] [CrossRef]
- Wu, S.; Wu, M.; Zhao, S.; Wan, S.; Dong, Y. Deriving 2-ranks from multiplicative preference relations in a group context: An investigation with axiomatic design. Comput. Ind. Eng. 2022, 168, 108106. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, F.; Huang, Y.; Xu, C.; Zhang, B.; Ke, Y.; Jia, W. A two-stage decision framework for inland nuclear power plant site selection based on GIS and type-2 fuzzy PROMETHEE II: Case study in China. Energy Sci. Eng. 2020, 8, 1941–1961. [Google Scholar] [CrossRef]
- Ozsahin, I. Identifying a personalized anesthetic with fuzzy promethee. Healthc. Inform. Res. 2020, 26, 201–211. [Google Scholar] [CrossRef]
- Wang, J.J.; Wang, M.M.; Liu, F.; Chen, H. Multistakeholder strategic third-party logistics provider selection: A real case in China. Transp. J. 2015, 54, 312–338. [Google Scholar] [CrossRef]
- Oubahman, L.; Duleba, S. Review of PROMETHEE method in transportation. Prod. Eng. Arch. 2021, 27, 69–74. [Google Scholar] [CrossRef]
- Stanković, J.J.; Janković-Milić, V.; Marjanović, I.; Janjić, J. An integrated approach of PCA and PROMETHEE in spatial assessment of circular economy indicators. Waste Manag. 2021, 128, 154–166. [Google Scholar] [CrossRef]
- de Oña, J.; Estévez, E.; de Oña, R. Public transport users versus private vehicle users: Differences about quality of service, satisfaction and attitudes toward public transport in Madrid (Spain). Travel Behav. Soc. 2021, 23, 76–85. [Google Scholar] [CrossRef]
- Díez-Mesa, F.; de Oña, R.; de Oña, J. Bayesian networks and structural equation modelling to develop service quality models: Metro of Seville case study. Transp. Res. Part A Policy Pract. 2018, 118, 1–13. [Google Scholar] [CrossRef]
- Amenta, P.; Lucadamo, A.; Marcarelli, G. On the choice of weights for aggregating judgments in non-negotiable AHP group decision making. Eur. J. Oper. Res. 2021, 288, 294–301. [Google Scholar] [CrossRef]
- Alkharabsheh, A.; Moslem, S.; Duleba, S. Evaluating passenger demand for development of the urban transport system by an AHP model with the real-world application of Amman. Appl. Sci. 2019, 9, 4759. [Google Scholar] [CrossRef] [Green Version]
- Shih, H.S. Threshold-Enhanced PROMETHEE Group Decision Support under Uncertainties. Math. Probl. Eng. 2021, 2021, 5594074. [Google Scholar] [CrossRef]
- Aczel, J.; Saaty, T.L. Procedures for Synthesizing. J. Math. Psychol. 1983, 27, 93–102. [Google Scholar] [CrossRef]
- Mareschal, B. Promethee Methods. In Multiple Criteria Decision Analysis: State of the Art Surveys; Springer: New York, NY, USA, 2005. [Google Scholar]
- Duleba, S.; Mishina, T.; Shimazaki, Y. A dynamic analysis on public bus transport’s supply quality by using AHP. Transport 2012, 27, 268–275. [Google Scholar] [CrossRef]
- Nguyen-Phuoc, D.Q.; Currie, G.; De Gruyter, C.; Kim, I.; Young, W. Modelling the net traffic congestion impact of bus operations in Melbourne. Transp. Res. Part A Policy Pract. 2018, 117, 1–12. [Google Scholar] [CrossRef]
- Jenelius, E. Public transport experienced service reliability: Integrating travel time and travel conditions. Transp. Res. Part A Policy Pract. 2018, 117, 275–291. [Google Scholar] [CrossRef] [Green Version]
- Alkharabsheh, A.; Duleba, S. Public Transportation Service Quality Evaluation during the COVID-19 Pandemic in Amman City Using Integrated Approach Fuzzy AHP-Kendall Model. Vehicles 2021, 3, 20. [Google Scholar] [CrossRef]
- Zheng, Y.; Kong, H.; Petzhold, G.; Barcelos, M.M.; Zegras, C.P.; Zhao, J.; Brasil, W.R.I.; Independ, A. Gender differences in the user satisfaction and service quality improvement priority of public transit bus system in Porto Alegre and Fortaleza, Brazil. Travel Behav. Soc. 2022, 28, 22–37. [Google Scholar] [CrossRef]
- Brans, J.P.; Mareschal, B. The PROMCALC & GAIA decision support system for multicriteria decision aid. Decis. Support Syst. 1994, 12, 297–310. [Google Scholar] [CrossRef]
| Reference | Model | Methodology |
|---|---|---|
| F. Lolli, et al. [37] | Group Fuzzy PROMETHEE | The AIP approach to select the optimum waste treatment |
| Jelena J. Stankovic, et al. [50] | PCA–PROMETHEE | Principal component analysis and PROMETHEE method to evaluate the development of the circular economy |
| Juan de Ona, et al. [51] | Statistical analysis | A statistical approach to analyze public and private service quality |
| Díez–Mesa, et al. [52] | Structural Equation Modelling | Evaluation of Underground mode service quality by using Structural equation modelling approach |
| P. Amenta, et al. [53] | Group AHP | The AIJ approach to aggregate decision makers evaluations into a common group preference matrix |
| M. Escobar, et al. [33] | Group AHP | The AIP approach for group AHP method |
| L. Turcksin, et al. [28] | AHP–PROMETHEE | Combination of two MCDA methods and the exploit of GAIA plane to promote clean fleet factors |
| A. Alkharabsheh, et al. [54] | Group AHP | The AIJ group AHP for the evaluation of passenger demand for public transport |
| L. Oubahman, et al. [20] | Group PROMETHEE | AIP approach to aggregate the final scores of PROMETHEE method computed for every decision maker |
| Hsu–Shih Shih [55] | Group PROMETHEE | The enhancement of threshold determination for a group of decision makers in PROMETHEE I, II and III |
| Proposed model | Group AHP–Group PROMETHEE | The AIP approach for the model Group AHP-PROMETHEE The AIJ approach for the model Group AHP-PROMETHEE Comparative analysis between both approaches Cardinal outputs and sensitivity analysis of the AIJ Group AHP-PROMETHEE model, GAIA plane Application of the new model to evaluate urban public transport service quality |
| Numerical Values | Verbal Description |
|---|---|
| 1 | Equal importance of both elements |
| 3 | Moderate importance of one element over another |
| 5 | Strong importance of one element over another |
| 7 | Very Strong importance of one element over another |
| 9 | Absolute importance of one element over another |
| 2,4,6,8 | Intermediate values |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.58 | 0.9 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
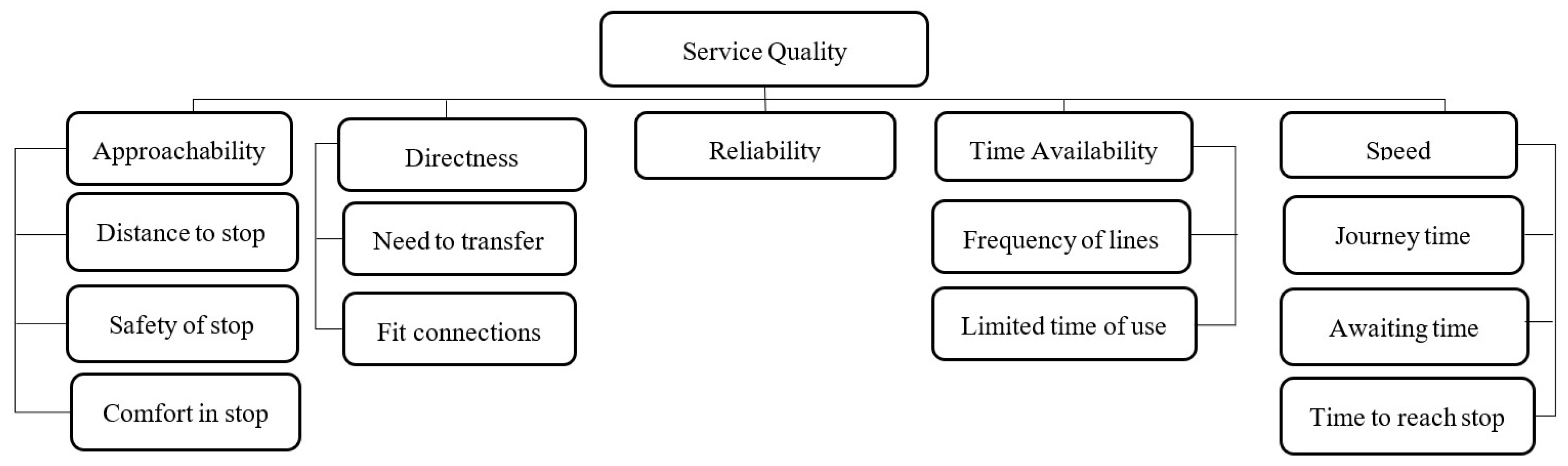
| Criteria | Adopted Nomination in Figures | Interpretation |
|---|---|---|
| Service quality | - | All provided services except on-vehicle and information services |
| Approachability | - | Line access |
| Directness | - | Ability to reach the destination without shifting vehicles |
| Reliability | - | Respecting planned schedules |
| Time availability | - | Time frame of line operation |
| Speed | - | The speed of travelling process |
| Distance to stop | Distance | Proximity of origin stations |
| Safety of stop | Safety | Subjective feeling |
| Comfort in stop | Comfort | Seats, cooling system, heating system |
| Need to transfer | Transfer | Need to change the vehicle to reach the destination |
| Fit connections | Connections | Time connection between lines to reach the destination |
| Frequency of lines | Frequency | Frequency of buses, Trams and Underground modes |
| Limited time of use | Limited.time | Time between the first and the last line of a day |
| Journey time | Journey.time | The time between on-board and getting off the vehicle |
| Awaiting time | Awaiting.time | Waiting time in the station for the line |
| Time to reach stop | Time.to.stop | Time to reach the origin station |
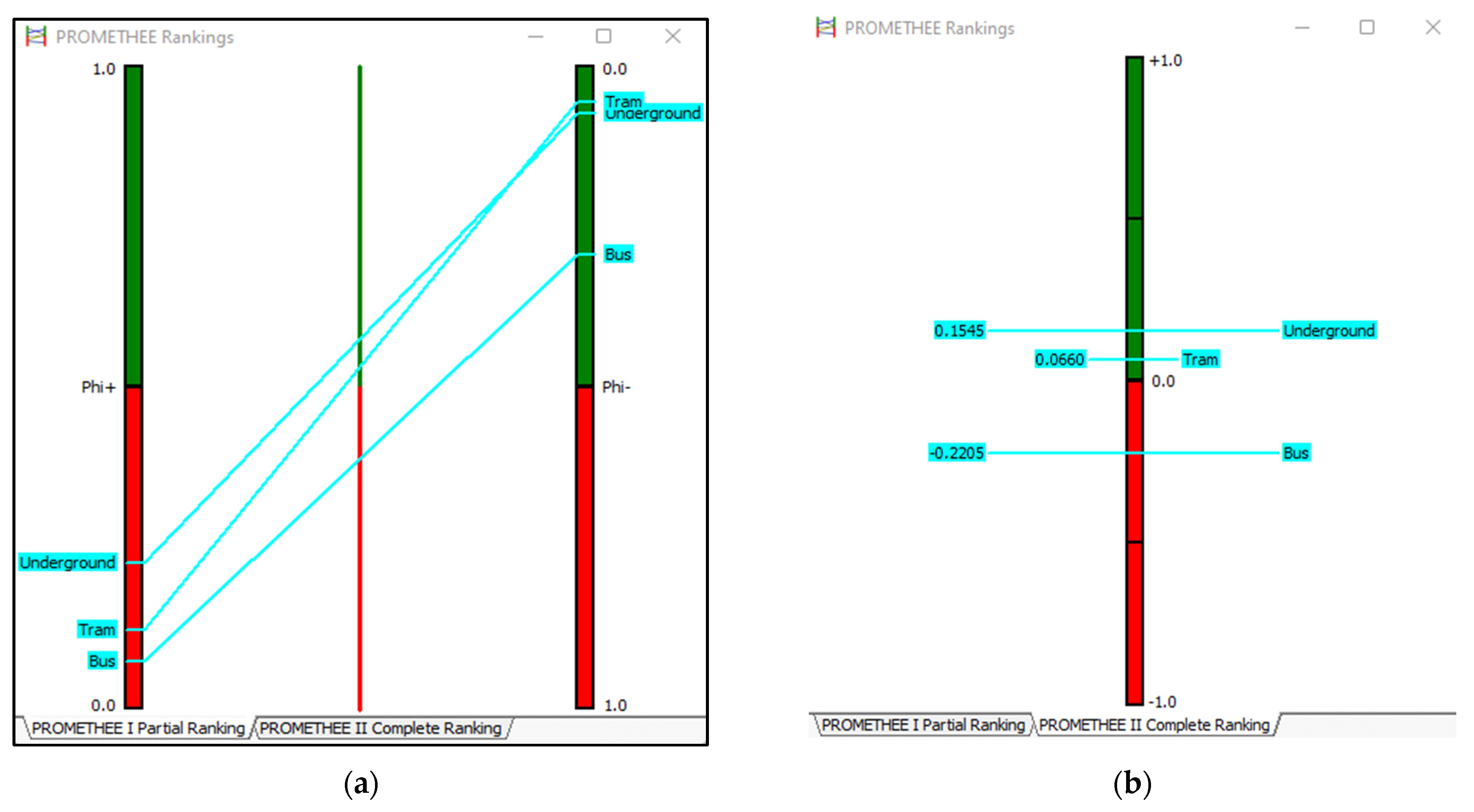
| AIP | Ranking | |||
|---|---|---|---|---|
| Bus | 0.085018 | 0.252672 | −0.16765 | 3 |
| Tram | 0.148229 | 0.130923 | 0.017306 | 2 |
| Underground | 0.231249 | 0.080907 | 0.150339 | 1 |
| First Level Criteria | Weight | Ranking | Second Level Criteria | Local Weight | Local Ranking | Final Weight | New Ranking |
|---|---|---|---|---|---|---|---|
| Approachability | 0.13695723 | 5 | Distance to stop | 0.30313998 | 9 | 0.04151721 | 9 |
| Safety of stop | 0.58742974 | 1 | 0.08045275 | 7 | |||
| Comfort in stop | 0.10943029 | 10 | 0.01498727 | 10 | |||
| Directness | 0.20093286 | 3 | Need to transfer | 0.49852044 | 4 | 0.10016914 | 4 |
| Fit connections | 0.50147956 | 3 | 0.10076372 | 3 | |||
| Time availability | 0.23720442 | 2 | Frequency of lines | 0.45573878 | 5 | 0.10810325 | 2 |
| Limited time of use | 0.54426122 | 2 | 0.12910117 | 1 | |||
| Speed | 0.25002706 | 1 | Journey time | 0.31907272 | 8 | 0.07977681 | 8 |
| Awaiting time | 0.35912068 | 6 | 0.08978989 | 5 | |||
| Time to reach stop | 0.3218066 | 7 | 0.08046036 | 6 | |||
| Reliability | 0.13981934 | 4 |
| AIJ | Ranking | |||
|---|---|---|---|---|
| Bus | 0.0729 | 0.2934 | −0.2205 | 3 |
| Tram | 0.1223 | 0.0563 | 0.066 | 2 |
| Underground | 0.2274 | 0.0729 | 0.1545 | 1 |
| Criteria | Weight Stability Interval | Criteria | Weight Stability Interval |
|---|---|---|---|
| Distance to stop | [0.00%, 19.08%] | Frequency of lines | [0%, 100%] |
| Safety of stop | [0.65%, 100%] | Limited time of use | [0%, 100%] |
| Comfort in stop | [0%, 100%] | Journey time | [0%, 100%] |
| Need to transfer | [0%, 100%] | Awaiting time | [0%, 100%] |
| Fit connections | [0%, 100%] | Time to reach stop | [0%, 23%] |
| AIP Approach | AIJ Approach | Net Flow Ratio | |
|---|---|---|---|
| Bus | −0.16765 | −0.2205 | 0.760317 |
| Tram | 0.017306 | 0.066 | 0.262212 |
| Underground | 0.150339 | 0.1545 | 0.973068 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oubahman, L.; Duleba, S. A Comparative Analysis of Homogenous Groups’ Preferences by Using AIP and AIJ Group AHP-PROMETHEE Model. Sustainability 2022, 14, 5980. https://doi.org/10.3390/su14105980
Oubahman L, Duleba S. A Comparative Analysis of Homogenous Groups’ Preferences by Using AIP and AIJ Group AHP-PROMETHEE Model. Sustainability. 2022; 14(10):5980. https://doi.org/10.3390/su14105980
Chicago/Turabian StyleOubahman, Laila, and Szabolcs Duleba. 2022. "A Comparative Analysis of Homogenous Groups’ Preferences by Using AIP and AIJ Group AHP-PROMETHEE Model" Sustainability 14, no. 10: 5980. https://doi.org/10.3390/su14105980
APA StyleOubahman, L., & Duleba, S. (2022). A Comparative Analysis of Homogenous Groups’ Preferences by Using AIP and AIJ Group AHP-PROMETHEE Model. Sustainability, 14(10), 5980. https://doi.org/10.3390/su14105980






