Abstract
During the last decade, with the rapid development of information technology, the immense volume of data poses a challenge to decision-makers. We use a combined dynamic decision-making approach based on the analytic hierarchy process (AHP) to select the best supplier. In this paper, we discuss the interaction between criteria that can lead to expanding our proposed dynamic framework to consider the inner dependencies among criteria. The main contributions are: (1) identifying the most important criteria of supplier selection in a steel bar manufacturer in Taiwan; (2) proposing a simple and rapid analysis of the appropriate supplier selection evaluation framework; and (3) using the AHP and transformation matrix to present the inner dependence among the criteria.
1. Introduction
The analytic hierarchy process (AHP) originally developed by Professor Thomas L. Saaty in the 1970s has been widely used to solve multicriteria decision-making problems [1,2,3,4]. These problems consist of supply chain management [5], evaluating the best supplier [6], and assessing the risk of infectious diseases [7]. The AHP uses a reciprocal decision matrix obtained by pair-wise comparisons so that the information is given in a linguistic form [8,9]. It assumes independency among criteria, and the alternatives are considered to be independent of the decision criteria and of each other. However, in many real-world cases, there is interdependence among the criteria and the alternatives. Therefore, AHP has been criticized for allowing the introduction of new criteria/alternatives to cause rank reversals among existing alternatives [1,8,10,11]. Under rank reversals, the linkage between alternatives is caused by normalization of the eigenvectors. Hence, the addition of an alternative or the removal of an alternative leads to a change in the weights of the other alternatives [8].
Although much research has been done on supplier selection processes in other industries [12,13,14], decision-making problems pose many challenges when technologies are applied to supplier selections. First, decision makers rely on experience to set a weight rating for each criterion, but they do not apply a consistent method for analyzing the pair-wise structural comparison of a criterion that might be preferred by decision makers. Second, the AHP cannot handle uncertainty decisions in comparison of the criteria. Finally, the number of comparisons is sometimes difficult and tedious. Karlsson et al. [15] pointed out that “the manual pair-wise comparison matrix is time-consuming, and the decision model is not agile enough for fast changing environment”. Uncertainty is a common phenomenon in a business environment and further inconsistency arises due to cognitive limitations. To address these issues, we argue that event-condition-action (ECA) rules are well suited for identifying inconsistencies which were caused by the cooperative data access. The system behavior is achieved through the definition of ECA rules as a part of the system. When an event is detected, then one or more rules may be triggered. If the condition is evaluated to be true, then the action is executed. Our solution takes advantage of the framework that has been developed for decision-making process modelling and execution and applies it to the dynamic data management domain. The purpose of this study is to improve the capability of the ECA rule-based framework based on the inner dependencies among criteria that exist in the decision problem. We employ a dynamic AHP algorithm to determine the inner dependence and independence status of a set of interval vectors; we use a qualitative method to support the decision makers’ reasoning.
The remainder of this paper is organized as follows: Section 2 reviews pair-wise comparison literature and related studies regarding the proposed methodology. In Section 3, we analyze the AHP decision model and propose a new ECA rule-based framework for dynamic AHP decision-making. Section 4 provides the analyses of the change impact of the inner dependence and independence criteria in the comparison matrix. A numerical illustration of the evaluation of the best supplier of a steel bar manufacturer located in Taiwan is provided in Section 5. Section 6 is to interpret and describe the significance of our findings. Finally, conclusions are summarized in Section 7.
2. Related Work
The AHP is a flexible decision-making process [1] that enables managers to set priorities and make the most appropriate decision when both qualitative and quantitative aspects of a decision require consideration. A vital benefit of the AHP is its formal approach for achieving a consensus on various evaluation factors and their influence on a final ranking decision, thereby enabling committee members to reach an agreement with substantially less effort [16].
Yu and Li [17] stated that the AHP is based on expert judgments or experiences from historical data, and evaluates weights by pair-wise comparison matrices. It was used for pair-wise comparison to derive priority scales [1,2,8]. Given a pair-wise comparison matrix , as shown in Equation (1), where the number in the row and column gives the relative importance of as compared with . The diagonal elements of the matrix are always 1 and we only need to fill up the upper triangular matrix. If is the element of row i column j of the matrix, then the lower diagonal is filled using this formula . All of the elements in the comparison matrix are positive, i.e., = 1 [2,3]. A consistent pair-wise comparison matrix has the transitivity property that for all i, j, and k [2,18]. Saaty suggests the use of a nine-point scale to transform the verbal judgments into numerical quantities representing the values of [1,2].
Matrix A has been multiplied on the right by the transposing of the vector of weights . The result of this multiplication is nW, as shown in Equation (2) [1,2].The AHP assumes independency among all criteria, but many decision problems are dependent on partial criteria, even dependent among all criteria [19]. There are several types of dependencies. The dependency types are: inner dependence and outer dependence [19]. Sometimes it is difficult to satisfy decision-making requirements due to influencing criteria. In AHP, the consistency of Matrix A is measured by the consistency index (C.I.), as shown in Equation (3). is the maximum eigenvalue and n is the number of criteria used in the pair-wise comparison matrix [1]. Equation (4) is used to compute weight priorities [1].
There are many decision problems which cannot be structured in an AHP hierarchy because these decision problems involve the interaction and dependence of higher-level elements in an AHP hierarchy on lower-level elements. Many methods have been proposed to revise or modify the extensions of the AHP. For example, Saaty [20] proposed the analytic network process (ANP) to deal with the effects of outer dependence, inner dependence and feedback. The ANP is considered as an extension of the AHP. Mao et al. [21] proposed a DEMATEL method to deal with inner dependence and outer dependence. Liu et al. [22] also extended the AHP to consider the correlation between criteria in the AHP.
Additionally, many researchers have investigated dynamic decision-making-related topics. Due to the complexity of dynamic decision-making problems, the AHP is typically combined with multiple criteria decision-making or other methods. For example, Improta et al. [23] and Gonzalez-Prida et al. [24] proposed a dynamic framework for the AHP to improve the static model. Yu et al. [25] also addressed the static AHP problems using the Delphi and the AHP methods. Benítez et al. [26] developed a framework for dealing with partial and/or incomplete preference data at multiple times. Duleba et al. [27] proposed an algorithm for scoring the missing data of the matrices problem. Soni and Vaishnavi [28] developed a hybrid fuzzy AHP model of risk analysis in the supply chain. Each piece of research gives some insights into the types of problems studied by AHP method practitioners.
Most real-world situations and decisions made by organizations are complex and occur in real-time. This study is different from previous approaches. In contrast, we use only inner dependencies between criteria to evaluate the AHP decision-making process with the degree of automation and consistency.
3. Model Formulation
Liu and Wu [29,30,31] examined the priority and importance of the criteria, sub-criteria and alternatives to set up the hierarchy architecture. These studies focused on constructing and applying the ECA rule-based on specific problems and by extracting knowledge from one or more human experts. Finally, the traditional AHP based on ECA rules concepts was developed to evaluate and select the best alternative (shown in Figure 1).
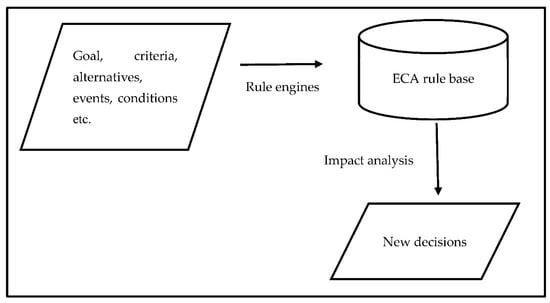
Figure 1.
Dynamic AHP decision-making process.
The studies conducted by Liu and Wu [29,30,31] only focused on one-pair variables. However, many real-world applications involve independencies and inner dependencies between criteria, which are insufficiently flexible for solving most decision-making issues. Therefore, we extended the rule-based dynamic decision-making framework to include inner dependencies among criteria, thereby enabling effective solving of complex situations.
3.1. A Dynamic Decision Framework
We propose a new dynamic AHP decision-making framework to solve the problem of a fast-changing environment. The framework includes a theorem for analyzing the change impact of the correlation among criteria and a new AHP decision model with ECA rules.
The general structure of the framework consists of mainly two components: (1) the AHP component helps to capture the decision-making criteria, sub-criteria and alternatives from all decision makers and form the pair-wise comparison matrix of the criteria and sub-criteria by using the nine-point scale. By calculating the eigenvalue of the matrix and consistency, the alternatives can be checked using the rule-based AHP model; and (2) the rule-based component first learns handling knowledge acquired from experts and represented in the form of ECA rules, and uses the impact analysis module to compute the priority weights of AHP for partial and all inner dependence among criteria. The ECA rule-based system is an automation system and is designed to perform a function with minimal or no human intervention. The decision makers only need to think about whether the analysis results are what they want. The solutions can be developed faster than by human expert(s).
We focus on the requirements’ criteria inner dependency in the decision-making process by acquiring knowledge from one or more decision makers (Figure 2). Then the AHP model can be converted into the ECA rule. The ECA rule base is responsible for event detection and assists the decision maker in the automatic discovery of pair-wise matrix element changes. It can also help the decision maker(s) to identify the prioritization criteria in specific context. We extend the basic general decision-making AHP to include the ECA rules. The first step involves identifying the change criteria, impact of events, and trends. The second step involves determining the criteria employed by the decision maker and how many criteria would be changed if changes are within the matrix or the input data.
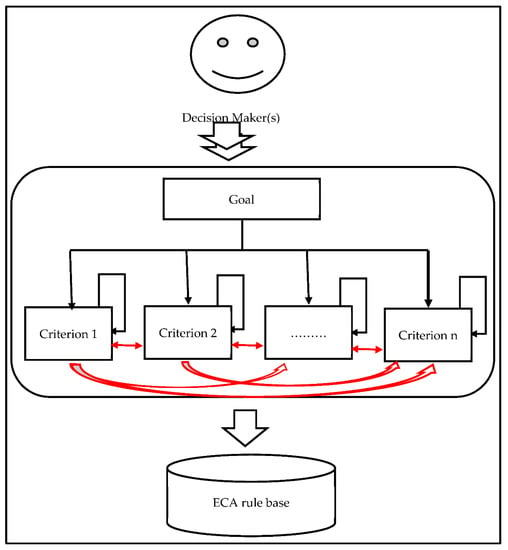
Figure 2.
Inner dependency-based decision making process.
3.2. Inner Dependence in a Pair-Wise Comparison Matrix
As mentioned previously, the original AHP assumes that criteria/alternatives are independent of one another. However, the criteria/alternatives’ dependencies often have a direct impact on the quality of the decision-making problems. There are several types of dependencies including partial/all inner dependence among criteria/alternatives and partial/all outer dependence among criteria/alternatives [16]. Depending on the conditions of the criteria, we consider the following three cases: (1) the AHP with an independent hierarchy; (2) the AHP with a partial inner dependent hierarchy; and (3) the AHP with an all inner dependent hierarchy.
4. Case Illustration
The formulation of the AHP method is presented in this section. Depending on the conditions of criteria, we consider the three cases: (1) the independence AHP; (2) the all inner dependence AHP; and (3) the partial inner dependence AHP. Mathematical formulations of the AHP method are carried out as follows [32]: (1) constructing a pair-wise comparison matrix; (2) estimating the relative weights; (3) checking the consistency; and (4) obtaining the overall rating. In the following subsections, we describe the criteria employed in our analysis.
4.1. Case 1: The Independence AHP
Given a pair-wise comparison matrix , as shown in Equation (5).
where the number in the row and column gives the relative importance of as compared with . The original AHP assumes that criteria are independent of one another. When , for , the matrix is consistent and its principal eigenvalue is equal to n. Matrix A has been multiplied on the right by the transpose of the vector of weights . The result of this multiplication is nW. As an example, we formed a 3 × 3 matrix (Table 1). The eigenvector is equal to .

Table 1.
Paired comparison analysis.
4.2. Case 2: The All Inner Dependence AHP
If all matrix elements are to be dependent on each other, then it is called the all inner dependence AHP. The matrix is used to calculate the new coordinates of the transformed criteria. By changing the values of a decision matrix, it is possible to apply transformations to criteria. In inner dependence AHP, we assume the dependency matrix , as shown in Equation (6).
where the number in the row and column gives the relative importance of as compared with . is consistent and its principal eigenvalue is equal to n. Matrix F has been multiplied on the right by the transpose of the vector of weights . The result of this multiplication is nW, as shown in Equation (7).
As an example, Table 2 is the original evaluation matrix and criteria ranking. There are three criteria: criterion 1, criterion 2, and criterion 3. Due to the fast changes of the business environment, a decision maker is typically asked to evaluate again for the original pair-wise comparison. If criterion 1 is dependent on criterion 2 and criterion 3, the decision maker needs to change the relative weight of criterion 1 and criterion 2. For instance, the relative weight of criterion 1 and criterion 2 is adjusted from 3 to 5. In addition, the relative weight of criterion 1 and criterion 3 is adjusted from 5 to 7 as shown in Table 3. We can observe that the ranking of criterion 1, criterion 2, and criterion 3 remains the same.

Table 2.
Independent paired comparison analysis.

Table 3.
Criterion 1 inner-dependent paired comparison analysis.
If criterion 2 is dependent on criterion 1 and criterion 3, the decision maker needs to change the pair-wise comparisons. For instance, the decision maker adjusts the relative weight of criterion 1 and criterion 2 from 3 to 1/3 and adjusts the relative weight of criterion 1 and criterion 3 from 5 to 2. In addition, the relative weight of criterion 2 and criterion 3 is adjusted from 2 to 5 as shown in Table 4. We can observe changes in the ranking of criteria 1 and criterion 2.

Table 4.
Criterion 2 inner-dependent paired comparison analysis.
Finally, if criterion 3 is dependent on criterion 1 and criterion 2, the decision maker needs to change the pair-wise comparisons. For instance, the decision maker adjusts the relative weight of criterion 1 and criterion 2 from 3 to 2 and adjusts the relative weight of criterion 1 and criterion 3 from 5 to 1/2. In addition, the relative weight of criterion 2 and criterion 3 is adjusted simultaneously from 2 to 1/4 as shown in Table 5. Criteria 3 becomes the most important criterion followed by criterion 1.

Table 5.
Criterion 3 inner-dependent paired comparison analysis.
Subordinate matrix is as follows:
All criteria dependent on each other become
4.3. Case 3: The Partial Inner Dependence AHP
As an example, we first form a 5 × 5 matrix, as shown in Table 6. The column names of C1, C2, C3, C4, and C5 represent criterion 1, criterion 2, criterion 3, criterion 4 and criterion 5, respectively. The independent paired comparison analysis eigenvectors are equal to . Table 7 and Table 8 represent the dependencies among the criteria for each other, respectively. Finally, we calculate the partial inner dependence by .

Table 6.
Independent paired comparison analysis.

Table 7.
Criterion 1 partial-dependent paired comparison analysis.

Table 8.
Criterion 3 and Criterion 4 partial-dependent paired comparison analysis.
Subordinate matrix M2 is as follows:
Partial criteria dependent on each other become
5. A Numerical Illustration
A real numerical illustration [31] of a decision-making analysis based on inner dependence AHP associated with a transformation matrix in a steel bar manufacturer in Taiwan is presented. The investigation was conducted by using categorizing and connecting strategies to analyze the decision maker interview results and determine the criteria that were most likely to support the effective decision-making process.
The normal AHP assumes independence among criteria and alternatives, however, a real decision-making process often involves the interaction and dependence of criteria. The dependency and interaction indicates some kind of interactions among the elements. The proposed inner dependence AHP framework had the following steps:
- We first interviewed decision maker(s) to estimate rankings of alternatives. The rankings are shown in Table 9. A good assessment of the alternatives relies on the criteria that should influence the selection of alternatives for responding to the goal. The weights of alternatives are estimated by the holistic judgments of the decision maker(s).
 Table 9. Original matrix and criteria ranking.
Table 9. Original matrix and criteria ranking. - Inter-dependencies among criteria expressed by a pair-wise matrix must also be examined; and the influence of each criterion on each of other criteria can be represented by an eigenvector. Like normal AHP, the pair-wise comparison in inner dependence AHP is performed in a matrix, and a local priority vector can be derived as an estimate of the relative importance associated with the criteria being compared by using Equation (7).
- Relationship (FW = nW)
Note: C.I. = 0.02 and C.R. = 0.018- b.
- Price (FW = nW)
Note: C.I. = 0 and C.R. = 0- c.
- Location (FW = nW)
Note: C.I. = 0 and C.R. = 0 - In Equation (7), where W is the equivalent priority vector of F. is the transformation matrix of W. verifying the condition The consistency condition is given by . If is the maximum eigenvalue of F and F is consistent then , where n is the number of criteria used in the pair-wise comparison matrix. The transformation matrix is used to present the inner dependency among criteria. If the values of the eigenvalue make two matrices equal, the inner dependency exists among criteria, e.g., the dependence conditions in a and the independence conditions in b.
- The dependence condition is expressed below.
- The independence condition is expressed below.
In this study, we used the AHP and transformation matrix to present the inner dependence among criteria/matrices. Both methods have their own advantages. The advantages of the both methods are:
- (1)
- The AHP evaluates the criteria for decision-making quantitatively;
- (2)
- The AHP is easy to analyze the inner dependence;
- (3)
- The inner dependence reflects the better relationship among criteria; and
- (4)
- The transformation matrix uses one or more numbers, or coordinates, to uniquely determine the position of the points. We used it to present the inner dependence among criteria/matrices.
In contrast, the traditional methods only consider or assume independency among criteria and alternatives. In our study, the proposed inner dependency AHP associated with a matrix method to deal with interactions among criteria and matrices is a more general framework by further considering the inner dependency relationships instead of only considering or assuming independency among the criteria and alternatives’ relationships.
6. Discussions
Our aim is to help decision maker(s) make better decisions but the authors are not domain experts. The main problem was to obtain domain knowledge from decision maker(s). Our key idea in addressing this problem lies in providing organizations with a methodology and a platform based on mapping decision makers’ requirements into dynamic AHP decision-making processes (shown in Figure 3). We used a quantitative method to support the decision maker(s) reasoning. The role of ECA is to provide flexible solutions to assist decision makers based on the regular function of a supplier selection system when criteria have inner dependences.
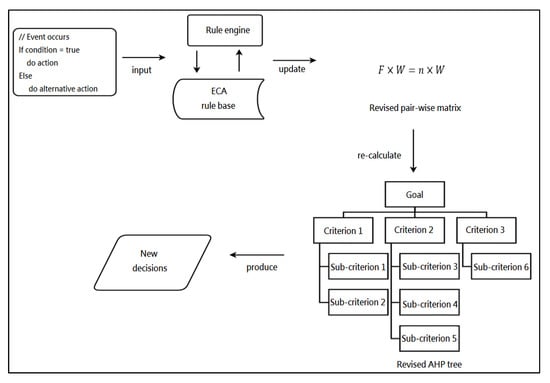
Figure 3.
An inner dependence analysis dynamic decision-making framework scenario.
The main contributions of this study are: (1) the main criteria and issues of supplier selection are identified. (2) The ECA rule-based system is considered as a promising solution to support dynamic and flexible decision-making in a competitive environment. (3) This study is pioneering research to study the relationship between AHP and the transformation matrix.
The original AHP assumed that the criteria are independent, which is commonly used and widely accepted, but its limitation is that, in some cases, the independence assumption does not hold among the criteria. The ignorance of interaction among criteria may lead to unreasonable results. Our method considers the inner dependence between the criteria of the hierarchy. We proposed a new methodology to help companies make better decisions more quickly.
In order to show the rationality and effectiveness of the proposed approach, we compared it with the following methods: (1) Tahriri et al.’s method [12] is on the basis of AHP, which can be applied to improve and assist decision-making processes to resolve the supplier selection problem. They used Expert Choice software to determine the weights of the decision criteria in AHP. Their future research emphasizes the problems relating to ambiguous, subjective, and imprecise judgments by suggesting the use of fuzzy theory to tackle this challenge; (2) Azimifard et al.’s method [13] is based on AHP and TOPSIS, which can be applied to choose the best supplier. Their study used a software package to perform sensitivity analysis. Their future research focuses on considering the uncertainty of a human’s subjective judgments and recommends the use of grey system theory or fuzzy theory to tackle this challenge; and (3) Wang and Chen’s method [14] is based on a bi-objective analytic hierarchy process (AHP)—mixed integer nonlinear programming (MINLP)—genetic algorithm (GA) approach. Their method can be applied to choose the best supplier. However, the proposed methodology may be a bit complicated and difficult to be applied in practice. The superiorities of our explored method are summarized as follows: (1) it can offer a more flexible method to manage the changes in dynamic environments; and (2) it can reflect the interactive influence among criteria in the decision-making process.
7. Conclusions
This paper is a major extension of a preliminary conference paper [26] in the direction of evaluating supplier’s selection criteria with the following contributions: (1) this research is used to deal with problems which have dependent criteria; (2) the novel method is more suitable than the traditional AHP to solve problems with different degrees of effects among criteria; and (3) we demonstrate a numerical illustration to illustrate feasibility of the proposed method to suit real-world applications.
This research is the first effort in exploring AHP and rule base in the decision theory domain to improve the quality of the decision-making process. We proposed an inner dependence analysis dynamic decision-making framework to assist decision makers based on the regular function of a supplier selection system when criteria have inner dependences. However, the proposed methodology has the following limitations. First, as the size of the judgment matrix increases, it becomes more and more difficult to find the optimal decomposition result. Second, in order to have a more reliable result, future research can focus on considering the uncertainty of a human’s subjective judgments and use fuzzy theory to improve the quality of decision-making. This method does not consider the uncertainty of a human’s subjective judgments in the decision-making process. It is the nature of human beings to make decisions under uncertain circumstances [12,13,14]. Future research can investigate different methods for decomposing a judgment matrix, such as fuzzy AHP [28], Pythagorean fuzzy interactive weighted averaging [33,34,35,36], or Pythagorean fuzzy interactive weighted geometry [33,35,36], and the likelihood of them being more practical to use under uncertain circumstances.
Author Contributions
Conceptualization, Y.-N.L. and H.-H.W.; formal analysis, Y.-N.L. and H.-H.W.; investigation, Y.-N.L. and H.-H.W.; methodology, Y.-N.L. and H.-H.W.; writing—original draft, Y.-N.L.; writing—review and editing, H.-H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to the anonymous referee for constructive criticism.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saaty, T.L. How to Make a Decision: The Analytic Hierarchy Process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision-making with the AHP: Why is the Principal Eigen-vector Necessary. Eur. J. Oper. Res. 2003, 145, 85–91. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making with the Analytic Hierarchy Process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef] [Green Version]
- Tramarico, C.L.; Mizuno, D.; Salomon, V.A.P.; Marins, F.A.S. Analytic Hierarchy Process and Supply Chain Management: A bibliometric study. Procedia Comput. Sci. 2015, 55, 441–450. [Google Scholar] [CrossRef] [Green Version]
- Fallahpour, A.; Olugu, E.U.; Musa, S.N. A hybrid model for supplier selection: Integration of AHP and multi expression programming (MEP). J. Neural Comput. Appl. 2017, 28, 499–504. [Google Scholar] [CrossRef]
- Suner, A.; Oruç, O.E.; Buke, C.; Ozkaya, H.D.; Kitapcioglu, G. Evaluation of Infectious Diseases and Clinical Microbiology Specialists’ Preferences for Hand Hygiene: Analysis Using the Multi-Attribute Utility Theory and the Analytic Hierarchy Process Methods. BMC Med. Inform. Decis. Mak. 2017, 17, 129. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Chakraborty, C.; Ouyang, H. The Analytic Hierarchy Process: Structuring, Measurement, and Synthesis; Decision Making and Decision Support Technologies; IGI Global: Harrisburg, PA, USA, 2008. [Google Scholar] [CrossRef]
- Lai, W.H. Corporate Firm-Level Knowledge Accumulation and Engineering Manpower Outsourcing. Int. J. Ind. Eng.-Theory 2011, 18, 191–202. Available online: https://journals.sfu.ca/ijietap/index.php/ijie/article/view/309 (accessed on 6 July 2011).
- Dyer, R.F.; Forman, E.H. Group Decision Support with the Analytic Hierarch Process. Decis. Support Syst. 1992, 8, 99–124. [Google Scholar] [CrossRef]
- Harker, P.T.; Vargas, L.G. Reply to “Remarks on the Analytic Hierarchy Process” by J. S. Dyer. Manag. Sci. 1990, 36, 269–273. [Google Scholar] [CrossRef] [Green Version]
- Tahriri, F.; Osman, M.R.; Ali AYusuff, R.M.; Esfandiary, A. AHP Approach for Supplier Evaluation and Selection in A Steel Manufacturing Company. J. Ind. Eng. Manag. 2008, 1, 54–76. [Google Scholar] [CrossRef]
- Azimifard, A.; Moosavirad, S.H.; Ariafar, S. Selecting Sustainable Supplier Countries for Iran’s Steel Industry at Three Levels by Using AHP And TOPSIS Methods. Resour. Policy 2018, 57, 30–44. [Google Scholar] [CrossRef]
- Wang, Y.C.; Chen, T. A Bi-Objective AHP-MINLP-GA Approach for Flexible Alternative Supplier Selection Amid the COVID-19 Pandemic. Soft Comput. Lett. 2021, 3, 100016. [Google Scholar] [CrossRef]
- Karlsson, L.; Thelin, T.; Regnell, B.; Berander, P.; Wohlin, C. Pairwise Comparisons Versus Planning Game Partitioning-Experiments on Requirements Prioritisation Techniques. J. Empir. Softw. Eng. 2007, 12, 3–33. [Google Scholar] [CrossRef]
- Bahurmoz, A. The Analytic Hierarchy Process: A Methodology for Win-Win Management. J. Egypt Comput. Sci. 2006, 26, 3–16. [Google Scholar] [CrossRef]
- Yu, L.; Li, M. Interval-Valued AHP Method for Early Warning System Under Uncertainty. In IEIS2019; Li, M., Dresner, M., Zhang, R., Hua, G., Shang, X., Eds.; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Holder, R.D. Some Comments on the Analytic Hierarchy Process. J. Oper. Res. Soc. 1990, 41, 1073–1076. [Google Scholar] [CrossRef]
- Ohnishi, S.I.; Yamanoi, T. A new weight representation using fuzzy set for partial inner dependence AHP. In Proceedings of the IEEE Xplore 2016 International Conference on Fuzzy Theory and Its Applications (iFuzzy), Leipzig, Germany, 23–26 August 2017. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy and Analytic Network Measurement Processes: Applications to Decisions under Risk. Eur. J. Pure Appl. Math. 2008, 1, 122–196. [Google Scholar] [CrossRef]
- Mao, S.; Han, Y.; Deng, Y.; Pelusi, D. A hybrid DEMATEL-FRACTAL method of handling dependent evidences. J. Eng. Appl. Artif. Intell. 2020, 91, 103543. [Google Scholar] [CrossRef]
- Liu, H.H.; Yeh, Y.Y.; Huang, J.J. Correlated Analytic Hierarchy Process. Math. Probl. Eng. 2014, 3, 1–7. [Google Scholar] [CrossRef]
- Improta, G.; Converso, G.; Murino, T.; Gallo MPerrone, A.; Romano, M. Analytic Hierarchy Process (AHP) in Dynamic Configuration as a Tool for Health Technology Assessment (HTA): The Case of Biosensing Optoelectronics in Oncology. Int. J. Inf. Technol. Decis. Mak. 2019, 18, 1533–1550. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Prida, V.; Barberá, L.; Viveros, P.; Crespo Marquez, A. Dynamic analytic hierarchy process: AHP method adapted to a changing environment. IFAC Proc. Vol. 2012, 45, 25–29. [Google Scholar] [CrossRef]
- Yu, A.; Jia, Z.; Zhang, W.; Deng, K.; Herrera, F. A Dynamic Credit Index System for TSMEs in China Using the Delphi and Analytic Hierarchy Process (AHP) Methods. J. Sustain. 2020, 12, 1715. [Google Scholar] [CrossRef] [Green Version]
- Benítez, J.; Delgado-Galván, X.; Izquierdo, J.; Pérez-García, R. An Approach to AHP Decision in a Dynamic Context. J. Decis. Support Syst. 2012, 53, 499–506. [Google Scholar] [CrossRef]
- Duleba, S.; Mishina, T.; Shimazaki, Y. A Dynamic Analysis on Public Bus Transport’s Supply Quality by Using AHP. J. Transp. 2012, 27, 268–275. [Google Scholar] [CrossRef]
- Vaishnavi, S.U. Analyzing Risk in Dynamic Supply Chains Using Hybrid Fuzzy AHP Model. Appl. Artif. Intell. Tech. Eng. 2019, 697, 411–420. [Google Scholar] [CrossRef]
- Liu, Y.N.; Wu, S.-Y. Using Normalization and AHP for improving supplier selection process in steel bars industry. In Proceedings of the e-CASE & e-Tech 2013: International Conference on e-Commerce, e-Administration, e-Society, e-Education, and e-Technology, Kitakyushu, Japan, 3–5 April 2013. [Google Scholar]
- Liu, Y.N.; Wu, S.-Y. Elasticity decision-making structure in integrating ECA and AHP. In Proceedings of the e-CASE & e-Tech 2014: International Conference on e-Commerce, e-Administration, e-Society, e-Education, and e-Technology, Nogoya, Japan, 2–4 April 2014. [Google Scholar]
- Liu, Y.N.; Wu, S.-Y. A rule-based approach for dynamic analytic hierarchy process decision-making. Int. J. Manag. Inf. Decis. Sci. 2020, 12, 36–74. [Google Scholar] [CrossRef]
- Hasnain, S.; Ali, M.K.; Akhter Javed Ahmed, B.; Abbas, N. Selection of an industrial boiler for a soda-ash production plant using analytical hierarchy process and TOPSIS approaches. J. Case Stud. Therm. Eng. 2020, 19, 100636. [Google Scholar] [CrossRef]
- Wang, L.; Garg, H. Algorithm for Multiple Attribute Decision-Making with Interactive Archimedean Norm Operations under Pythagorean Fuzzy Uncertainty. Int. J. Comput. Intell. Syst. 2021, 14, 503–527. [Google Scholar] [CrossRef]
- Ma, Z.M.; Xu, Z.S. Symmetric Pythagorean Fuzzy Weighted Geometric/Averaging Operators and Their Application in Multicriteria Decision-Making Problems. Int. J. Intell. Syst. 2016, 31, 1198–1219. [Google Scholar] [CrossRef]
- Garg, H. A New Generalized Pythagorean Fuzzy Information Aggregation Using Einstein Operations and Its Application to Decision Making. Int. J. Intell. Syst. 2016, 31, 886–920. [Google Scholar] [CrossRef]
- Wu, S.J.; Wei, G.W. Pythagorean Fuzzy Hamacher Aggregation Operators and Their Application to Multiple Attribute Decision Making. Int. J. Knowl.-Based Intell. Eng. Syst. 2017, 21, 189–201. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).