Abstract
The past decade has seen impressive developments in financial technology (FinTech) in China. As a new technology and innovative method that competes with, and also supplements, traditional financial methods, fintech has had a significant impact on traditional financial businesses and has thus challenged the role of commercial banks as credit intermediaries in the financial sector. This paper examines the potential risks that fintech brings to commercial banks in China, and collects data from 19 systemically important banks from 2011–2020 to analyze the effect of fintech development on commercial banks’ financial risks in order to achieve sustainable development in the financial sector. Using the Z value and non-performing loan ratio as the criterion variables, this study shows that the impact of fintech on the financial risks of systemically important banks demonstrates an inverted U-shaped pattern, with the financial risk increasing first and then decreasing alongside the further development of fintech. The results also show that commercial banks’ responses to fintech development has been comparatively slow. Managerial suggestions are then discussed on risk supervision for commercial banks and the financial sector in China and other emerging markets.
1. Introduction
Information technology has been widely adopted in the era of information age and many studies have focused on technological development in the financial sector and its impact on the financial market [1,2,3,4,5,6,7]. Consequently, financial technology (Fintech) has become an attractive topic both in practice and in academic research [1,8]. Fintech was first proposed by Citibank in 1993 to refer to the idea of bringing financial innovation through technology, including changing traditional financial services and generating new business models, applications, processes, and products [8].
Fintech has brought dramatic changes to the financial sector [1,9,10]. The deep integration of finance and technology can stimulate change in the traditional financial field, promote the innovation in financial services, improve the efficiency of resource allocation, increase the diversification of financial products, optimize the traditional financial operation and management modes, and further enable the digitalization of financial industry [9,11,12]. The fintech innovation occurs across every aspect of financing services, such as payment and settlement, deposit and loan business, capital investment and financing, and market financial facilities [13]. The innovative practices brought by fintech have been in competition with traditional financing services on the one hand and have complemented the core functions of banking, insurance, payment, and other services on the other. In particular, the development of fintech in big data, blockchain, cloud computing, and artificial intelligence has profoundly influenced traditional financial institutions and financial market systems [11,12,14,15].
Commercial banks, as one of the most important foundations of the financial sector, are among the first to face the challenges and opportunities brought about by fintech. Fintech has impacted the operation and business model of commercial banks and has changed their competitive positions and management methods. In response to these challenges, commercial banks also use fintech to diversify their financial services, optimize service platforms, expand customer groups and business boundaries, as well as transform and upgrade to new business models. For instance, the Chinese banking industry has invested RMB207.8 billion (around US$35 billion) in the field of financial information technology in 2020, and 11 commercial banks have established fintech banking subsidiaries [16,17].
While fintech has promoted innovation in the financial sector, it has changed traditional financial market models and has also blurred the boundaries between financial industry and other industries, leading to new financial risks. For example, using fintech as an innovative financing method, the largest P2P online lending platform, Lending Club, has sold illegal loans since 2018 in the United States; the Bitcoin exchange company Bitfinex was hacked, resulting in the loss of nearly 120,000 units of Bitcoin. Other illegal fundraising practices have also frequently occurred in many fintech-based companies [18,19]. Therefore, it has become increasingly urgent for the financial industry to examine and further manage potential risks associated with the advancement of fintech in order to implement an effective supervision mechanism to achieve sustainable growth in the financial sector.
The objective of this study is to explore fintech-related financial risks for China’s systemically important commercial banks in order to better understand the impact of fintech advancement on the financial sector and its sustainable development in China. This study will focus on the Chinese market in order to explore potential risks associated with fintech in systemically important commercial banks because China is one of the most important emerging markets, and has attracted scholars from a variety of disciplines to explore its economic expansion [4,20,21,22,23,24,25,26,27,28]. This study is new in that it is one of a few that have examined all 19 systemically important commercial banks in China and the potential financial risks fintech may bring to the financial sector. China has also become a pioneer in fintech development and financial innovation, wherein both commercial banks and non-banking companies have created many fintech-based, innovative financial services [4,20,29,30,31,32]. It is thus very important to examine the impact of fintech advancement on the financial risks associated with Chinese commercial banks in order to better develop and manage financial markets in China and other emerging markets, which also helps balance the need for developing fintech and for reducing the financial risks it brings to the financial industry [20].
The rest of the article will be organized as follows. We will first review the relevant literature on fintech, examine the relationship between fintech and financial risks to construct a theoretical framework, and then analyze the mechanism through which fintech affects commercial banks’ risks. We will collect data from 19 systemically important commercial banks in China and construct a fintech development index to empirically analyze the direction and extent of fintech’s impact on the financial risks of these systemically important commercial banks. In the end, practical implications will be discussed alongside possible future research directions.
2. Literature Review and Conceptual Framework
The concept of fintech originates in the United States and it is the combination of the words of finance and technology [8]. It is literally understood as the application of technology in the financial field. The Financial Stability Board (FSB) defines fintech as financial innovation brought by technology. It can change traditional financial markets, financial institutions and financial services, and create emerging business models, applications, processes and products [33].
The study of fintech in China began with research on internet finance [32,33,34,35,36]. Internet finance can simplify the operating process of financial services and reduce labor and transaction costs [33,37], having a positive effect on traditional banks. Allen et al. [9] pointed out that Internet finance can resolve the weakness of traditional banks and improve the quality of bank credit and loan services. Wu and colleagues contended that the development of internet finance can be grouped into two categories [32]: one is that technology companies provide financial services through their own technology; the second type of internet finance is that traditional commercial banks cooperated with technology companies to overcome the deficiencies of traditional financial business by adopting technology from technology companies. This type of cooperation can reduce the cost of traditional financial businesses, promote technological innovation, and improve business efficiency to reduce financial risks for traditional commercial banks. With the second type of internet finance, commercial banks can improve their credit and loan quality by adopting advanced fintech skills, such as using big data mining to analyze in-depth customer information, increase information transparency, and reduce credit default rates [24]. Studies also recognize possible negative impacts of internet finance, such as weakening commercial banks’ deposit business, which can force banks to increase the cost of their deposit business or force commercial banks to enter high risk markets, increasing the risk of insolvency for commercial banks [16]. Dai and Fang [38] also believed that the competition between internet finance companies and commercial banks reduces commercial banks’ profitability and increases their probability of bankruptcy.
Fintech has developed rapidly in China since 2015 [16,17], from the financial informatization to the optimization of financial processes and capital diversification, and to the recent wide adoption of leading financial technology, including big data, cloud computing, blockchain, and artificial intelligence, which have fundamentally changed the traditional financial industry in many aspects, such as operating costs, operating efficiency, media transmission, data collection and analysis, etc. [16,17]
Researchers have different views on the impact of fintech on the traditional financial sector [5]. Some believe that the development of fintech will aggravate the risks of commercial banks, others argue that fintech will mitigate the risks of commercial banks, while a mixed view believes that fintech can aggravate and mitigate the risks of commercial banks through a non-linear relationship [5]. Due to the excessive use of leverage tools and the excessive pursuit of innovation in the financial market, fintech products and transaction processes have become more complicated, leading to an incapability to defuse crisis events in the financial system. Scholars have also argued that financial innovation could have both positive and negative effects on the development of the financial market, and the key is to balance the benefits and risks of the financial innovation process [30]. Wang [12] believed that financial innovation can be divided into system innovation and tool-based innovation. System innovation is linked with global financial risks, and tool-based innovation is a trigger of systemic financial risks [12]. In addition, as fintech companies introduce new forms of financial products and services with lower credit and loan requirements, both technical and financial risks will increase for traditional banks. Li found that fintech companies are faced with different types of risks, such as business risks and technology dependence risks [17].
Other studies on fintech supported a dynamic relationship between fintech and commercial banks’ financial risks, and there exists a path to aggravate the financial risk, as well as a path to mitigate the financial risks [39,40,41]. Guo and Shen [34] found that fintech reduces risks by improving technology in the early stage but increases risks along with the rise of innovation costs in the middle and late stages, a U-shaped relationship [34]. Wang et al. [36] pointed out that, in the short term, fintech can help commercial banks absorb deposits and improve liquidity [36]. However, with the participation of external institutions, traditional commercial banks will be negatively impacted by an increased cost, such as more bad loans. Gu and Yang [33] argued that commercial banks’ financial risks caused by fintech are higher than the benefits brought by fintech, thus showing the net result of increased financial risks [33]. The inconclusive findings in the field thus merit further exploration in this direction.
2.1. Fintech Advancement and Financial Risk
Financial risk is a term used to describe possible exposure to monetary loss in financial transactions and further financial institutions’ failure to pay off debts [24,33,36]. Financial risk has four types, including market risk, operational risk, liquidity risk, and credit risk. Market risk occurs when the company encounters an unpredictable loss of equity market, commodity prices, interest rates, and credit spreads [33]. Operational risk is caused by mistakes, damages, or interruptions to the operating process [34]. Liquidity risk is the inability of banks to access cash for funding obligations [33,34]. Credit risk occurs when borrowers and counterparties fail to meet contractual obligations [34]. Possible risks in the banking system include systematic risk and unsystematic risk [34,42]. The systematic risk is inherent to the overall market, reflecting the effect of economic, financial, and geopolitical factors, such as interest rate risk, governance risk, market risk, macroeconomic risk, etc., that cannot be avoided [33,34], whereas the unsystematic risk is associated with specific entities or sectors, such as operational risk, credit risk, liquidity risk, regulatory risk, etc., which can be mitigated by diversification [42].
Early research on fintech suggests that fintech innovation will exacerbate the original information asymmetry problem [43], thereby increasing the probability of financial risks in the market [34]. As fintech is introduced into the financial field, the structure of financial industry becomes highly complex, with traditional banking system, stocks market, and insurance, plus various financial technology companies providing digital currencies, online payment systems, investments, online loans, etc. [34]. Bats and Houben [44] stated that the financial structure can affect financial risk. The emergence of fintech has allowed many technology companies to enter the financial market, thus introducing competition to the financial market [42]. The newly added competitors can, on the one hand, help increase financial stability by encouraging innovations, diversifying products, and increasing efficiency [45]. On the other hand, they can also cause more fragility in the market and increase profits for traditional commercial banks [15].
The growing innovation of fintech companies without proper regulations also amplifies the volatility, contagion, and procyclicality of the financial market. For example, the use of fintech for algorithmic trading in the stock market can magnify the negative consequences, produce information asymmetry, and possibly become a source of contagion in the financial system [46]. The online trading platform with fintech can amplify swings in asset prices and increase the procyclicality in the market [47]. The third-party payment platform provides an optimized funds transfer process which increases the volatility of the banking system as its cost of capitals are influenced. Without proper regulatory body or supervision, the technology company using fintech to conduct financial activities may not be able or may not be willing to price default risk accurately, resulting in high-risk decisions and excessive financial risks [42]. Third-party service providers of fintech have sometimes bypassed the market regulations, posing additional risks to the financial system [42].
In addition, the insurance sector uses fintech to collect a huge amount of personal information and calculate the risk more precisely with an algorithm model [42]. The insurance services provided to the clients are designed and adjusted according to the best of company and personal interest. While the enhanced monitoring program innovated by fintech can provide updated information about clients for insurance companies, fintech also has negative effects in the insurance sector, such as the privacy risk, emerging technological risk, etc. [34] The investment sector, such as foreign exchange trading, may also be affected by fintech through decentralization and digitalization. The stock market or trading system can be affected by fintech through high-frequency trading and e-trading [42]. Fintech has eased the traditional trading complexity, increased the transparency of transactions, and reduced the services fees, which improve trading efficiency and reduce the potential operational risk, but if the use of cryptocurrency in foreign exchange has been widely accepted, it will influence the currency rate in the market, affecting commerce business and generating systemic risks [34]; the high-frequency trading in the stock market may also result in new technological risk and monopoly risk [34]; decentralization in the trading system with fintech may induce money laundering behaviors, resulting in regulatory and compliance risks [34,42].
2.2. Systemically Important Banks
A systemically important commercial bank is a financial institution that, due to its size, complexity and interconnectedness, would cause significant disruption to the financial system and economy if it encountered a financial crisis [48]. The regulatory requirements of systemically important commercial banks were brought up by the financial crisis in 2008. In order to solve the problem of “too big to fail” for such institutions, the regulatory policy of systemically important banks is proposed with international regulatory bodies.
The Financial Stability Board released the regulatory framework for Global Systemically Important Financial Institutions (G-SIFI) in 2011. Based on this, the People’s Bank of China and the China Banking and Insurance Regulatory Commission jointly developed and released the “Systemically Important Bank Evaluation Method” and “Additional Regulatory Provisions” in 2020 [34]. According to these regulations, there are 19 systemically important banks in China, all of which are large commercial banks.
The systemically important banks are highly intercorrelated with other financial institutions, so their stable operation is associated with the stability of the entire financial system [48]. Being a systemically important bank means that the institution has a higher market influence and more responsibility for preventing potential financial risks. Therefore, higher capital and leverage ratio requirements are conducive to improving loss-absorbing capacity. Reasonable risk defense, recovery, and manageable plans are conducive to solving and preventing potential problems during operation [34]. These requirements are useful in promoting the stable operation and development of systemically important banks, and the increasing adoption of fintech in the systemically important banks will affect these requirements. Therefore, examining the impact of fintech development on these systemically important commercial banks are thus crucial for a nation’s economic growth and stability [49,50].
2.3. Financial Risk of Commercial Banks in the Early Stage of Fintech Development
In the early stage of fintech development, when the financial regulatory environment is relatively loose, the emerging of various deposit and loan platforms has weakened the intermediary role of traditional commercial banks, diverted commercial banks’ deposit and loan business, and intensified the market competition [34]. The advantages of online financial business are that they have a low entry threshold, a simplified approval process, a fast loan speed, and a low transaction cost [33]. Online financial business has created a new channel of market financing, and its disintermediation characteristic is often favored by original retail loan customers, so it often leads to more competition in the banking industry [33].
In payment and settlement services, previous businesses are dominated by commercial banks. Fintech companies have launched third-party payment platforms based on their technological advantages to provide customers with a faster, lower cost and diversified payment systems, including mobile wallets, peer-to-peer payments, remittance, and foreign exchange transactions [34]. The payment system transcends the limitations of space and time and exempts payment fees, transfer fees, and other transaction fees. User experiences have been greatly improved and the convenience is well received and favored by the public. Thus, fintech-based businesses have challenged the long-term dominant role of commercial banks in the deposit business [33,34]. In the field of wealth management, traditional commercial banks have considerable experience and high security, but also have huge limitations [34]. For example, commercial banks prefer to serve clients with a high value of wealth, and clients with a low value of wealth have been largely neglected. The traditional commercial banks also have restrictions in terms of product benefits, flexibility, and convenience, but fintech companies are capable of launching wealth management products that meet all clients’ individual needs using data collections and big data analysis [33,34].
Overall, fintech has penetrated the traditional territories that are often dominated by commercial banks [51]. Traditional commercial banks will have to employ high-risk services or behaviors to re-attract clients [42]. Considering the huge loss in business profits caused by fintech-based companies, commercial banks will also have to increase their risk tolerance and choose higher risk behaviors in order to maintain a reasonable profit level, such as lowering loan requirements and increasing loan services to high-risk clients like small enterprises and individuals [33]. In addition, as the credit market of traditional commercial banks is also facing the competition from fintech companies, they will have to apply new technology to expand business boundaries, which will bring up hidden financial risks. Although commercial banks may achieve a comparable interest income through expanded services, the potential risks of commercial banks have often been greatly increased [34].
2.4. Financial Risks in the Middle and Late Stages of Fintech Development
Along with the fast development of fintech, more advanced technologies have appeared. The innovation and adoption of fintech in commercial banks are also significantly improved [33]. The scope of involved businesses is expanding, such as fintech-based consumer finance, robot-advisory, risk control, etc. Furthermore, the highly risky P2P online lending platform has been regulated due to concerns about crisis and supervision issues, which has alleviated the impact of fintech on commercial banks and brought positive changes to the financial sector [33].
The first benefit associated with fintech advancement is reduced customer acquisition costs [33,35]. Traditional commercial banks have been acquiring customers and operating at relatively high costs for a long time, while the emerging of fintech has reduced customer acquisition and operational costs, increased profit margins for commercial banks, and reduced the high-risk preference decisions. Moreover, brick and mortar branch services often require a lot of human resources with uneven qualities of customer service, which affects the efficiency of business process and is not favorable for banks to explore potential customers [33]. With the deep integration of fintech, commercial banks have transformed branches into digital, intelligent, and mobile services. Technology such as big data and artificial intelligence have been widely used to develop financial platforms and products, including mobile banking, online banking, flexible wealth management, funds transfers and transactions, utility payment, salary services, smart community, and other high-quality services. Customers do not need to spend a lot of time queuing for services as the quality and efficiency of financial services are improved [35,36]. Fintech can also facilitate scenario-based customer acquisition channels. Additionally, commercial banks can use fintech to achieve precise market delivery with big data to analyze customer needs, design targeted products and services, and deliver them to the target customer groups at a relatively low cost, which helps achieve quantitative customer acquisition and improve commercial banks’ operational efficiency [35].
The second benefit associated with fintech advancement is reduced operating costs. Using fintech like blockchain technology can establish standardized and intelligent business operation processes, simplify traditional complicated procedures, create a standardized business model, and reduce the cost of each node in the entire operation line [35]. Promoting product innovation based on big data can reduce the costs of human resources and the time required for user surveys, can efficiently analyze and explain product features and match services with the targets, and reduce collection costs, information query costs, and business innovation costs [33]. Using AI technology can promote smart offline branches and basic services such as bank card applications, funds transfer and remittance, deposits and withdrawals [52]. At the same time, AI customer service and robot advisors can replace branch staff to reduce the human resource costs. In addition, fintech can be applied to capital management, budget management, and pricing management to reduce the operational costs of commercial banks [35].
The third benefit associated with fintech advancement is improved risk management [33,34,35,42]. Commercial banks with fintech can use big data and cloud computing to deeply explore customer information and analyze the value of potential customers, and then use artificial intelligence and other technologies to build intelligent analysis models for risk management [35]. Consequently, commercial banks are able to evaluate the credit status of each customer, predict their risk levels, alleviate the effect of information asymmetry between the borrower and the lender, and reduce banks’ financial risks [34]. Fintech can also build a more reliable risk monitoring and warning system for commercial banks to greatly reduce data acquisition and process time, instantly monitor risk changes, promote data sharing and inter-departmental collaboration, and conduct comprehensive and timely risk assessment [33] (please see Figure 1 for the illustrated impact of fintech at different stages).
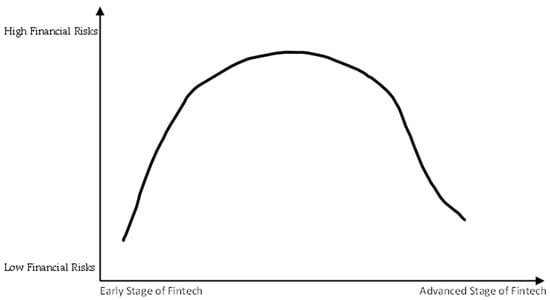
Figure 1.
The Proposed Impact of Fintech Advancement on Financial Risks.
Based on the above discussions, we propose that the impact of fintech on the financial risks of commercial banks is an inverted U shape: commercial banks’ financial risk will be aggravated in the early stage of fintech development and then mitigated in the middle and late stages of fintech advancement.
3. Methodology
3.1. Measure of Financial Risks
There are three common methods to assess financial risks in the literature: the first is the empirical method or the signal method, which often analyzes the countries that have experienced financial crises in history, explores the commonalities during the crisis, analyzes the economic situation, and searches for similarities of target countries to predict financial crises. The second is the modeling method, which uses the GARCH model or neural network model to construct a corresponding evaluation system to calculate the probability of the occurrence of financial crisis [53]. The third is the stress index method, which uses the financial stress level in the selected time period as the basis for assessing financial risks.
The signal method has lower frequency requirements on data identification and is often used in countries that have experienced financial crises. It is not applicable for the situation in China. The modeling method analyzes the systemic risk generation mechanism with many complicated built-in parameters, and it is difficult to collect enough sample indicators, and thus this method is theoretically strong but requires a large sample. We choose the stress index method in this study to measure the financial risk of Chinese commercial banks. Research literature shows that the measuring indicator used in financial risk studies are different, including capital asset ratio, expected default rate, capital adequacy ratio, stock volatility, non-performing loan ratio, and Z value.
Since most Chinese banks are not publicly listed, it is difficult to obtain data on their stock price volatility or stock return. The expected default rate recommended by Altunbaş et al. [54] is difficult to obtain in China because there is no established database on this type of data. We choose to use the Z value in this study as a measure of commercial banks’ risk. The Z value was proposed by Laeven and Levine [55] to measure the probability of bank bankruptcy (inversely related) and it is a valid measure of commercial banks’ financial risk. The calculation formula is as follows:
Among them, ROA represents the return on assets, and CAR represents the capital asset ratio. When these two indicators are larger, the financial risk of the bank is smaller. σ(ROA) represents the standard deviation of asset returns and the volatility of returns. The smaller the volatility, the higher the stability of the bank. Therefore, the Z value is an inverse indicator. The higher its value, the lower the bank bankruptcy rate, the stronger the stability, and the smaller the financial risk. Empirical studies often consider the peak and thick tail of the Z value. Considering the fact that the Z value may be zero, it is recommended to perform not just logarithmic regression on the Z value, but also process the data in the format of ln(1 + Z).
In addition, since non-performing loans can be another indicator to measure the financial risk of commercial banks, it is appropriate to add the non-performing loan ratio as a substitute risk variable in order to ensure the robustness of the results. Empirical analysis using the non-performing loans can be used to test the robustness of the Z value. The higher the non-performing loan ratio, the greater the financial risk of commercial banks. Therefore, we use two indicators of financial risk of commercial banks in this study—the Z value and the non-performing loan ratio.
3.2. Fintech Advancement
This study follows previous research to adopt a text mining method to measure the advancement of fintech [32,56]. First, we constructed a list of functional keywords from the four dimensions of fintech, based on fintech applications in the commercial banking business, as shown in Table 1.

Table 1.
Fintech Index Keywords.
Second, data are obtained by using python crawlers to collect these keywords’ annual search frequency provided by Baidu Search Index from 2011 to 2020. Baidu is the largest search engine with the most comprehensive websites and the highest usage rate in China. The Baidu Index can be used to analyze data traces left by people on the search engine and reflect their attention to the searched keywords recorded by Baidu. Baidu data are considered an important basis for data reference by many enterprises. The keyword frequency in the Baidu Search Index is a good indicator to assess the development of fintech [32].
The data obtained by python crawlers cannot be used directly for empirical analysis, and the fintech index has to be constructed by principal component analysis. First, the Kaiser-Meyer-Olkin (KMO) test and Bartlett spherical tests are performed on the data of the four dimensions of fintech keywords. When the KMO value is greater than 0.5 and the p value is less than 0.05, it satisfies the conditions of factor analysis, and the factor analysis method is then used to process the data to calculate the fintech index, and the formula for the standardized fintech index is as follows:
Among them, represents the Baidu search index value of the keyword, represents the maximum value of the search index value, and represents the minimum value of the search index value.
3.3. Control Variables
In order to ensure the robustness and validity of statistical results, we need to control for the impact of a set of control variables by considering monetary policy, economic development level, bank profitability, operating efficiency, growth ability, liquidity level, and financial deepening degree—both at the macro level and at the micro level. The macro level control variables include the GDP growth rate to represent the level of economic development, the M2 growth frequency to represent the impact of monetary market policies, and the stock market value and GDP ratio to represent the financial deepening level. At the micro level, the bank’s return on assets is chosen to reflect the bank’s profitability. The cost-to-income ratio is used to represent operating efficiency, the growth rate of asset scale is used to represent the bank’s growth capability, and the bank’s loan-to-deposit ratio is used to reflect the bank’s liquidity. In addition, because the impact of fintech on financial risk is heterogeneous, a dummy variable is introduced to represent a bank’s ownership. When the sample is one of the five state-owned banks, the variable is set as 1, and 0 for other cases (please see Table 2).

Table 2.
Variable List.
3.4. Model Construction
This study uses a dynamic panel data model. Because previous financial risk may have an impact on current risk, so the lag term of the explained variable is added to the regression. The inclusion of the lag term of the outcome variable may cause endogeneity problems, so a generalized method of moments (GMM) model is used as the statistical method for estimation, as in previous research [32]. This model does not need to assume variable distribution, nor does it need to consider the distribution of random variable information, so it can overcome the endogeneity problem. The regression Equation (1) designed in this paper is as follows:
Among them, is the bankruptcy probability of bank i in year t, which reflects the bank’s financial risk; is the bankruptcy probability of bank i during in the t − 1 period, representing the financial risk in previous period; F is the fintech index that represents the advancement of fintech. The fintech index is the main independent variable; GDP, M2, FD, ROA, CT, AG, LDR are control variables; is the individual fixed effect; is the random disturbance term.
Based on the above equation, the interaction term between fintech index and the bank type dummy variable is introduced to verify the effect of heterogeneity, and the regression Equation (2) is designed as follows:
4. Analysis of Empirical Results
4.1. Sample Selection and Descriptive Statistics
We select 19 systemically important commercial banks (SIBs) in China as our sample, including 5 state-owned commercial banks, 10 joint-stock commercial banks, and 4 city-based commercial banks: Ping An Bank, China Everbright Bank, Huaxia Bank, China Guangfa Bank, Ningbo Bank, Bank of Shanghai, Bank of Jiangsu, Bank of Beijing, Shanghai Pudong Development Bank, China CITIC Bank, Minsheng Bank, Postal Savings Bank, Bank of Communications, China Merchants Bank, Industrial Bank, Industrial and Commercial Bank of China, Bank of China, China Construction Bank, and Agricultural Bank. Their total assets account for 60% of the total assets of the entire Chinese banking industry. Relevant bank data are obtained from the Cathay Pacific database, the Financial Statistics Yearbook, and the annual reports of commercial banks. The descriptive statistics results are shown in Table 3.

Table 3.
Descriptive statistics of SIBs.
It can be seen from the above table that the standard deviation of the bankruptcy risk (Z value) of systemically important commercial banks is 0.19782, the maximum value is 2.38326, the minimum value is 1.44615, and the average value is 1.96874, because the Z value is a reverse indicator, indicating that the differences between systemically important banks’ risk pressure is not big and the probability of bankruptcy risk is low. For the non-performing loan ratio, the standard deviation of non-performing loan ratios of systemically important commercial banks is 0.39725, which is relatively small, indicating that the difference in non-performing loans of systemically important banks is not obvious, and it is considerably stable compared with other types of banks [16,17]. The maximum value of profitability is 0.46354 and the minimum value is 0.16526. The standard deviation is 0.06717, indicating that the asset returns of systemically important commercial banks are not significantly different, and the returns are stable with no significant loss. The maximum value of growth capability is 0.44096, the minimum value is −0.04271, and the standard deviation is 0.07945, indicating that there is a gap in growth capability among systemically important commercial banks.
The data of fintech advancement are from the Baidu Search Index. The research window of the sample is set for the past ten years from 2011 to 2020. This study uses STATA statistical software for analysis. The data of other control variables are from the China Statistical Yearbook. Descriptive statistics are as follows (please see Table 4).

Table 4.
Descriptive statistics of fintech and control variables.
This study adopts the text mining method to construct the fintech index with the search frequency rate of 18 keywords from the four dimensions including basic technology, payment settlement, resource allocation, and information transmission. The standardized fintech index from the Baidu Search Index data for the past ten years (2011–2020) are shown in Table 5.

Table 5.
Standardized fintech keyword data.
The fintech index keyword data constructed from four dimensions need to pass the KMO and Bartlett spherical tests, and the test results are reported in Table 6. For the fintech keyword test in Table 6, the KMO value representing the basic technology dimension is 0.510, and the p-value is 0.000; the KMO value representing the payment settlement dimension is 0.509, and the p-value is 0.001; the KMO value representing the resource allocation dimension is 0.638, and the p-value is 0.000; the KMO value representing the dimension of information transmission is 0.623, and the p-value is 0.000. The KMO values of all four dimensions are greater than 0.5 and the p-values are all significant at the 0.001 level. Therefore, the principal component analysis method can be used to process the data analysis method. After principal component factor analysis, the scores of each dimension are shown in Table 7.

Table 6.
Fintech keywords KMO and Bartlett sphericity test results.

Table 7.
Factor scores in the four dimensions of fintech.
The scores of each dimension and each factor obtained in the above table are used as weights. The principal component analysis method in the factor analysis method is used to propose the common factors, and the load matrix is selected and rotated by the maximum variance method to obtain the score coefficient matrix to construct the factor score formula. Suppose is each dimension (where i = 1,2,3,4), is the original keyword of each dimension, and is the original keyword score, the formula is:
The formula for scoring the basic technology is:
Among them, represents the basic technology dimension, represents artificial intelligence, represents big data, represents cloud computing, represents the Internet of Things, and represents blockchain.
The formula for scoring payment and settlement is:
Among them, represents payment and settlement dimension, represents online payment, represents mobile payment, represents network payment, and represents third-party payment.
The formula for scoring resource allocation is:
Among them, represents the dimension of resource allocation, represents online loans, represents network security, represents online lending, represents Internet insurance, and represents online wealth management.
The formula for scoring information transmission is:
Among them, represents the dimension of information transmission, represents online banking, represents mobile banking, represents e-banking, and represents online banking; the results obtained from these formulas are standardized to obtain the four-dimensional fintech index, as shown in Table 8.

Table 8.
Results of fintech index.
The standardized fintech composite indexes reflect the development trend of fintech in China from 2011 to 2020. The development of fintech in China was relatively slow from 2011 to 2013, while the development trend of fintech in China from 2013 to 2015 was fast. From 2015 to 2018, the development of fintech fluctuated slightly but showed an overall upward trend. There is a slight drop for 2019–2020, which is probably affected by other factors such as the curb of P2P loan platforms and then the epidemic occurred in 2020, but overall, fintech still attracts widespread attention and has been a growing trend for the past ten years.
4.2. Stationarity Test
Panel data are used in this study for empirical analysis, and the unit root test on the panel data is first conducted to ensure the stability of the data. There were several commonly used panel unit root tests, including the ADF-Fisher test, the Im-Pesaran-Shin (IPS) method, the Levin-Lin-Chu (LLC) method, the Breitung test, the HadriLM test, and the HT test. Since the bank data used in this study are unbalanced panel data, the ADF-Fisher test is preferred and is performed at the bank level. The results of the stationarity test for each variable are shown in Table 9, all of which have passed the four transformation methods and all the corresponding p values are 0.0000, indicating that the null hypothesis of the panel unit root is strongly rejected. That is, the variables at the bank level have passed the stationarity test. The pseudo-regression phenomenon that might appear in the panel model is less possible [32].

Table 9.
Stationarity test results.
4.3. Analysis Results
The panel data of 19 systemically important commercial banks in China were analyzed. After passing the stationarity test, the system generalized moment estimation is used to analyze the impact of fintech advancement on the financial risk of these systemically important banks. The results are reported in Table 10.

Table 10.
Analysis results of the impact of fintech on SIBs’ financial risk.
Model 1 and Model 2 in Table 10 are the empirical results of the regression Equation (1) and the regression Equation (2) developed in our model construction. The Z value is the measurement of the ability of systemically important banks to deal with the risk of bankruptcy with Ln(1 + Z) used in calculation. The AR(1) test results are 0.006 and 0.001, respectively, which are less than 0.1. The AR(2) test results are 0.189 and 0.214 respectively, which are greater than 0.1. The Hansen test results are 0.352 and 0.455, which are greater than 0.1. These results show that the models are valid, and the selected variables are reasonable with no phenomenon of second-order sequence autocorrelation or over-identification.
Model 1 and Model 2 both show that the coefficients of the lagged Z value (L.Z) are significantly positive at p < 0.01, indicating a positive relationship between commercial banks’ previous financial risks and current financial risks. This implies that there are persistent financial risks for commercial banks, and previously accumulated financial risks could increase current financial risk, leading to possible financial crises if not addressed.
The coefficients of the fintech index are significantly negative in the primary regression (−0.058 and −0.0362), and significantly positive in the quadratic term (0.0397 and 0.0232). This shows that the development of fintech has an inverted U-shaped impact on systemically important banks’ financial risks. In the early stages of fintech, the advancement of fintech increases commercial banks’ financial risks (a negative relationship with the reversed probability of bankruptcy). However, alongside the further development of fintech to a late stage, the advancement of fintech can enable commercial banks to expand customer groups, improve operational efficiency, and achieve fintech innovations to effectively control financial risks and reduce possible bankruptcy risks for systemically important banks (a positive relationship with the reversed probability of bankruptcy for the quadratic term of fintech). These results support our proposed relationship in this study. In addition, the coefficient value of the fintech index is generally small. Therefore, when these selected systemically important banks are affected by fintech advancement, their responses tend to be stable and not very sensitive, which means that they are more conservative in the face of innovations and changes brought about by fintech.
The regression results of the control variables are also shown in the table. From the macroeconomic point of view, the coefficient for GDP growth rate is significantly positive at p < 0.01, indicating that as the overall economy gets better, it will reduce commercial banks’ financial risks with a low probability of bankruptcy. The coefficient for monetary policy (M2) growth rate is significantly negative at p < 0.01, indicating that systemically important banks will have higher financial risks under loose monetary policy. The coefficient for financial deepening index (FD) is also significantly positive, meaning that commercial banks’ financial risks as measured as probability of bankruptcy are reduced as financial markets expand and financial structures become mature.
For microeconomic variables, the banks’ profitability impact is reflected in the regression coefficient of the return on assets, and it is significantly positive at p < 0.01, which shows that the banks will not pursue high risk businesses that may cause damage to these banks when their revenues are high. The liquidity level of commercial banks (LDR) is significantly and positively related to the Z value (p < 0.01), indicating that the banks’ ability to raise cash when in need could reduce the financial risks of banks. The impact of growth ability (AG) and operating efficiency (CT) on commercial banks’ financial risk is less clear, as no significant coefficients were found.
4.4. Robustness Test
In order to test whether the results were robust, we conducted a robustness test. Three robustness testing methods can be used to validate our model, such as replacing research variables, adjusting measurement methods, and replacing variable data. In this study, we use replacement of the key outcome variables to test the robustness. The bankruptcy probability (Z value) is replaced with the non-performing loan ratio (NPLR). Normally, commercial banks with higher non-performing loan ratios have a higher probability of bankruptcy, i.e., high financial risks, so using this indicator as the outcome variable is consistent with our analysis.
Since the Z value is a negative indicator, and the non-performing loan ratio is a positive indicator, the expected coefficients of explanatory variables in the regression should be opposite those in the Z value regression when the non-performing loan ratio is used as an outcome variable. The regression Equations (3) and (4) of the NPLR are designed as follows:
Using the same regression method and with the above equations, we obtain empirical results for the non-performing loan ration as the outcome variable (as in Table 11). The AR(2) tests of the model are 0.496 and 0.877, and the Hansen tests are 0.555 and 0.734, all of which are greater than 0.1, indicating that there are no autocorrelation problems or over-identifying restrictions, and the models are acceptable. In the original model, as shown in Table 10, the banks have a lower probability of bankruptcy as the Z value gets higher. The non-performing loan ratio as a replaced variable is opposite to the Z value. The higher the non-performing loan ratio, the greater the potential financial risk faced by these banks. The lag term of the non-performing loan ratio (L.NPLR) in Table 11 is significantly positive, at p < 0.01, which reveals the persistence of financial risks over the time. In the robust regression results, the coefficients of the first power of the key independent variable (Fintech) are significantly positive and the coefficients of the second power of the key independent variable are significantly negative, exactly the opposite to those in the Z-value models in Table 10, which is also true for those control variables with significant coefficients, such as GDP, M2, ROA, and LDR. The result of this test is consistent with the conclusion of our original model, in support of the robustness of our research findings.

Table 11.
Robustness test of the impact of fintech on SIBs’ financial risk.
5. Discussions and Conclusions
The past decade has seen an unprecedented growth in research into fintech, the integration between information technology and financial services [5,56]. The non-intermediated P2P lending, smart online financing and cryptocurrencies are just parts of this emerging new landscape of fintech-assisted and customized financial services. Research into fintech has argued that the development of fintech guides the transformation and upgrade of the traditional financial industry, and that the advancement of fintech can reduce the effect of information asymmetry, thereby reducing the probability of financial risks [3]. Li [17] further showed that fintech can improve the efficiency of resource allocation and reduce the financial risks of banks, and its innovation can contribute to the development of financial industry [29].
However, technological innovations such as fintech can also bring negative effects [57,58,59,60]. Berger and Udell [61] showed that fintech can increase the risk for commercial banks. Xia and Chunsom [28] found that the emergence of third-party payments weakened the bank sector’s role as the intermediary, making commercial banks less profitable. Li and Jiang [56] pointed out that fintech will affect the pattern of the traditional financial industry and bring competitors to traditional commercial banks. Puro et al. [52] also found that fintech has greatly reduced the profit and income of commercial banks and eventually will weaken commercial banks’ customer groups.
This study is intended to explore the impact of fintech advancement on China’s systemically important commercial banks’ financial risks, using the Z value and non-performing loan ratio as outcome variables and aggregated search indexes are generated by a search engine as fintech development. This study collect data from 19 systemically important banks in China from 2011 to 2020 to empirically explore the influence of fintech development on commercial banks’ risks. This study is one of a few that have examined all 19 systemically important commercial banks in China and the potential financial risks that fintech may bring to the financial sector.
The results show that the effect of fintech on the financial risks of commercial banks appears to be an inverted U-shaped trend. This is in part due to the slow response of these systemically important commercial banks when fintech-assisted companies have partially taken over the traditional financial market in the early stage of the development of fintech. During this period, fintech influences the deposit and loan business and payment services of commercial banks, and thus increases the competition pressure on commercial banks, which often leads to riskier behaviors on the bank side and thus higher financial risks. Along with the development of fintech in the middle and late stage of fintech development, commercial banks are forced to actively pursue fintech applications, in actions such as transforming into new digital service models and through using technology to optimize risk control to expand business boundaries, improve risk management, and alleviate information asymmetry. At this stage, the impact of fintech on commercial banks’ financial risks tends to be positive. In other words, the development of fintech is a facilitator for commercial banks to improve efficiency and reduce risks.
The findings of this study have valuable implications. The inverted U-shaped relationship identified in this study can help enrich the research on fintech and related issues in the financial sector. It can also expand the research horizon on fintech advancement by pointing out a more complex impact of fintech on traditional commercial banks and thus adds values to the literature. Based on the results, especially the positive impact of fintech on the financial sector in the more advanced stage of fintech development, commercial banks should pursue the innovation and application of fintech more actively, along with the development of fintech. They should rely on fintech to innovate financial products, optimize the financial environments, and promote the transformation and upgrade of financial services for more sustainable growth. Meanwhile, commercial banks should also focus on the maintenance and upgrade of data security and the risk management system, in order to improve the ability of managing the systemic risks, and to prevent the potential damage caused by emerging technological risks. It is essential to improve the collaboration between fintech companies and commercial banks and inter-bank collaborations to expand business scope and reduce innovation costs.
For policymakers, financial regulatory authorities should actively monitor the advancement of fintech by regulating the legal boundaries of fintech, creating industrial standards of fintech, and making relevant laws and regulations. It is important to balance technological innovations and risk compliance in the financial market by providing timely supervision and regulations to emerging fintech products and services and propose regulatory measurements and solutions to ensure the successful reaping of the benefits of fintech development and avoid the systemic risks that fintech may bring to the financial sector with its innovative and sometimes high-risk products.
Author Contributions
Conceptualization, B.C. and Z.M.; data curation, X.Y.; formal analysis, X.Y.; funding acquisition, B.C.; investigation, B.C.; methodology, B.C.; project administration, Z.M.; resources, B.C. and Z.M.; software, X.Y.; supervision, Z.M.; validation, B.C.; visualization, X.Y.; writing—original draft, B.C. and X.Y.; writing—review and editing, Z.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by a RIF Grant from the Odette School of Business, University of Windsor (Grant # 821117).
Data Availability Statement
The data used in this study are available on request from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Anagnostopoulos, Y. Fintech and regtech: Impact on regulators and banks. J. Econ. Bus. 2018, 100, 7–25. [Google Scholar] [CrossRef]
- Kane, E.J. Technological and regulatory forces in the developing fusion of financial-services competition. J. Financ. 1984, 39, 759–772. [Google Scholar]
- Lapavitsas, C.; Santos, P.L. Globalization and contemporary banking: On the impact of new technology. Contrib. Political Econ. 2008, 27, 31–56. [Google Scholar] [CrossRef]
- Lee, I.; Shin, Y.J. Fintech: Ecosystem, business models, investment decisions, and challenges. Bus. Horiz. 2018, 61, 35–46. [Google Scholar] [CrossRef]
- Thakor, A.V. Fintech and banking: What do we know. J. Financ. Intermed. 2020, 43, 10058. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, W.; Li, J.; Mai, F.; Ma, Z. Effect of online review sentiment on product sales: The moderating role of review credibility perception. Comput. Hum. Behav. 2022, 133, 107272. [Google Scholar] [CrossRef]
- Werthamer, N.R.; Raymond, S. Technology and finance: The electronic markets. Technol. Forecast. Soc. Chang. 1997, 55, 39–53. [Google Scholar] [CrossRef]
- Puschmann, T. Fintech. Bus. Inf. Syst. Eng. 2017, 59, 69–76. [Google Scholar] [CrossRef]
- Arner, D.W.; Barberis, J.N.; Buckley, R.P. The evolution of fintech: A new post-crisis paradigm. Soc. Sci. Electron. Publ. 2015, 47, 1271–1319. [Google Scholar] [CrossRef] [Green Version]
- Murinde, V.; Rizopoulos, E.; Zachariadis, M. The impact of the FinTech revolution on the future of banking: Opportunities and risks. Int. Rev. Financ. Anal. 2022, 81, 102–103. [Google Scholar] [CrossRef]
- Bromberg, L.; Godwin, A.; Ramsay, I. Fintech sandboxes: Achieving a balance between regulation and innovation. J. Bank. Financ. Law Pract. 2017, 28, 314–336. [Google Scholar]
- Fung, D.W.H.; Lee, W.Y.; Yeh, J.; Yuen, F.L. Friend or foe: The divergent effects of fintech on financial stability. Emerg. Mark. Rev. 2020, 45, 100727. [Google Scholar] [CrossRef]
- Keeley, M.C. Deposit insurance, risk, and market power in banking. Am. Econ. Rev. 1990, 5, 1183–1200. [Google Scholar]
- Battiston, S.; Gatti, D.D.; Gallegati, M.; Greenwald, B.; Stiglitz, J. Liaisons dangerousness: Increasing connectivity, risk sharing, and systemic risk. J. Econ. Dyn. Control 2012, 36, 1121–1141. [Google Scholar] [CrossRef] [Green Version]
- Goetz, M.R. Competition and bank stability. J. Financ. 2018, 35, 57–69. [Google Scholar] [CrossRef] [Green Version]
- Dong, J.; Yin, L.; Liu, X.; Hu, M.; Li, X.; Liu, L. Impact of internet finance on the performance of commercial banks in China. Int. Rev. Financ. Anal. 2020, 72, 101579. [Google Scholar] [CrossRef]
- Li, W. Development and Supervision of Financial Technology. China Financ. 2017, 8, 14–16. [Google Scholar]
- Wang, D. Research on Transmission, Supervision and Prevention of Systemic Financial Risks; Graduate School of Chinese Academy of Social Sciences: Beijing, China, 2012. [Google Scholar]
- Wang, K.; Wu, Q. Research on the impact of fintech on systemic risk in my country’s banking industry. Manag. Mod. 2018, 3, 112–116. [Google Scholar]
- Liu, M.; Jiang, W. Fintech promotes or hinders the efficiency of commercial banks? An empirical study based on China’s banking industry. Contemp. Econ. Sci. 2020, 3, 56–68. [Google Scholar]
- Ma, Z.; Bu, M. A new research horizon for mass entrepreneurship policy and Chinese firms’ CSR. J. Bus. Ethics 2021, 169, 603–607. [Google Scholar] [CrossRef]
- Ma, Z.; Zhu, J.; Meng, Y.; Teng, Y. The impact of overseas human capital and social ties on Chinese returnee entrepreneurs’ venture performance. Int. J. Entrep. Behav. Res. 2019, 25, 67–83. [Google Scholar] [CrossRef]
- Ma, Z.; Jin, Q. Success factors for product innovation in China’s manufacturing sector: Strategic choice and environment constraints. Int. Stud. Manag. Organ. 2019, 49, 213–231. [Google Scholar] [CrossRef]
- Shang, Q.; Ma, Z.; Wang, X. In search of the best interest rate for group lending: Toward a win-win solution for SMEs and commercial banks in China. Chin. Econ. 2020, 53, 285–299. [Google Scholar] [CrossRef]
- Wu, X. Analysis on the path to improve the efficiency of China’s financial resource allocation. China Mark. 2015, 31, 3–6. [Google Scholar]
- Wu, J.; Ma, Z. Export intensity and MNE customers’ environmental requirements: Effects on local Chinese suppliers’ environment strategies. J. Bus. Ethics 2016, 135, 327–339. [Google Scholar] [CrossRef]
- Wu, J.; Ma, Z.; Liu, Z. The moderated mediating effect of international diversification, technological capability, and market orientation on emerging market firms’ new product performance. J. Bus. Res. 2019, 99, 524–533. [Google Scholar] [CrossRef]
- Xia, H.; Chunsom, N. Third-party payments impact on commercial banks’ non-interest income: Evidence from China. Int. J. Econ. Financ. 2018, 10, 190–199. [Google Scholar] [CrossRef]
- Li, M. Research on the selection and optimization path of financial technology supervision mode and reflection on the supervision sandbox mode. Financ. Superv. Res. 2017, 11, 21–37. [Google Scholar]
- Xuan, C.; Wang, X. Financial innovation and financial stability: A comparative analysis of asset securitization models in Europe and America. Financ. Res. 2009, 5, 35–46. [Google Scholar]
- Yao, M.; Di, H.; Zheng, X.; Xu, X. Impact of payment technology innovations on the traditional financial industry: A focus on China. Technol. Forecast. Soc. Chang. 2018, 135, 199–207. [Google Scholar] [CrossRef]
- Wu, S.; Zhu, Y.; Li, T. Interest rate liberalization, internet finance and commercial bank risk: An empirical test based on panel data dynamic GMM method. Res. Financ. Econ. 2015, 6, 29–38. [Google Scholar]
- Gu, H.; Yang, L. Internet finance and bank risk-taking: Evidence based on China’s banking industry. World Econ. 2018, 10, 75–100. [Google Scholar]
- Guo, P.; Shen, Y. Does internet finance increase the risk-taking of commercial banks? Empirical evidence from China’s banking industry. Nankai Econ. Res. 2015, 4, 82–99. [Google Scholar]
- Guo, P.; Shen, Y. Internet finance, deposit competition and bank risk-taking. Financ. Res. 2019, 8, 58–76. [Google Scholar]
- Wang, Y.; Xing, L.; Li, G. The impact of internet finance development on bank liquidity. Financ. Forum 2016, 8, 42–50. [Google Scholar]
- Manuchehr, S. E-finance: Status, innovations, resources and future challenges. Manag. Financ. 2008, 34, 365–398. [Google Scholar]
- Dai, G.; Fang, P. Interest rate liberalization and bank risk: A study from the perspective of shadow banking and Internet finance. Financ. Forum 2014, 8, 13–19. [Google Scholar]
- Buch, C.M.; Eickmeier, S.; Prieto, E. In search for yield? Survey-based evidence on bank risk taking. J. Econ. Dyn. Control 2011, 43, 12–30. [Google Scholar] [CrossRef] [Green Version]
- Ioannidou, V.; Ongena, S.; Peydrò, J. Monetary policy and subprime lending: A tall tale of low federal funds rates, hazardous loans and reduced loan spreads. In European Banking Centre Discussion Paper; European Banking Authority (EBA): Paris, France, 2009; p. 04S. [Google Scholar]
- Jimenez, G.; Lopez, J.A.; Saurina, J. How does competition affect bank risk-taking? J. Financ. Stab. 2013, 9, 185–195. [Google Scholar] [CrossRef]
- Delis, M.D.; Kouretas, G.P. Interest rates and bank risk-taking. J. Bank. Financ. 2011, 35, 840–855. [Google Scholar] [CrossRef] [Green Version]
- Hoeing, T.M.; Wang, S.; Zeng, Z. Maintaining financial stability in a changing financial system: Lessons from history. New Financ. 2008, 1, 17–20. [Google Scholar]
- Bats, J.V.; Houben, A. Bank-based versus market-based financing: Implications for systemic risk. J. Bank. Financ. 2020, 114, 105776. [Google Scholar] [CrossRef] [Green Version]
- Minto, A.; Voelkerling, M.; Wulff, M. Separating apples from oranges: Identifying threats to financial stability originating from FinTech. Cap. Mark. Law 2017, 12, 428–465. [Google Scholar] [CrossRef]
- Kirilenko, A.A.; Lo, A.W. Moore’s law versus Murphy’s law: Algorithmic trading and its discontents. J. Econ. Perspect. 2013, 27, 51–72. [Google Scholar] [CrossRef]
- Gemayel, R.; Preda, A. Does a scopic regime produce conformism? Herding behavior among trade leaders on social trading platforms. Eur. J. Financ. 2018, 24, 1144–1175. [Google Scholar] [CrossRef]
- Pham, T.N.; Powell, R.; Bannigidadmath, D. Systemically important banks in Asian emerging markets: Evidence from four systemic risk measures. Pac.-Basin Financ. J. 2021, 70, 101670. [Google Scholar] [CrossRef]
- Daud, S.; Ahmad, A.; Khalid, A.; Azman-Saini, W. Fintech and financial stability: Threat or opportunity. Financ. Res. Lett. 2021, 102667. [Google Scholar] [CrossRef]
- King, R.G.; Levine, R. Finance, entrepreneurship, and growth: Theory and evidence. J. Monet. Econ. 1993, 32, 513–542. [Google Scholar] [CrossRef]
- Jagtiani, J.; Lemieux, C. Do fintech lenders penetrate areas that are underserved by traditional banks? J. Econ. Bus. 2018, 100, 43–54. [Google Scholar] [CrossRef] [Green Version]
- Puro, L.; Teich, J.E.; Wallenius, H.; Wallenius, J. Borrower Decision Aid for people-to-people lending. Decis. Support Syst. 2010, 49, 52–60. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yılmaz, K. On the network topology of variance decompositions: Measuring the connectedness of financial firms. J. Econom. 2014, 182, 119–134. [Google Scholar] [CrossRef] [Green Version]
- Altunbaş, Y.; Gambacorta, L.; Marques-Ibanez, D. An Empirical Assessment of the Risk-Taking Channel; Mimeo, Inc.: New York, NY, USA, 2009. [Google Scholar] [CrossRef] [Green Version]
- Laeven, L.; Levine, R. Bank governance, regulation and risk taking. J. Financ. Econ. 2009, 93, 259–275. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Jiang, Z. Fintech development and supervision: A supervisor’s perspective. Financ. Superv. Res. 2017, 3, 1–13. [Google Scholar]
- Allen, F.; McAndrews, J.; Strahan, P. E-finance: An introduction. J. Financ. Serv. Res. 2002, 22, 5–27. [Google Scholar] [CrossRef]
- Kodama, F. Measuring emerging categories of innovation: Modularity and business model. Technol. Forecast. Soc. Chang. 2004, 71, 623–633. [Google Scholar] [CrossRef]
- Ma, Z.; Lee, Y. Patent application and technological collaboration in inventive activities: 1980–2005. Technovation 2008, 28, 379–390. [Google Scholar] [CrossRef]
- Yovanof, G.S.; Hazapis, G.N. Disruptive technologies, services, or business models. Wirel. Pers. Commun. 2008, 45, 569–583. [Google Scholar] [CrossRef]
- Berger, A.N.; Udell, G.F. The institutional memory hypothesis and the procyclicality of bank lending behavior. J. Financ. Intermed. 2004, 13, 458–495. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).