An Artificial-Immune-System-Based Algorithm Enhanced with Deep Reinforcement Learning for Solving Returnable Transport Item Problems
Abstract
1. Introduction
2. Related Work
3. Mathematical Formulation
3.1. Mathematical Model for IRPPDS
3.2. Mathematical Model for DM
- : Quantity of loaded RTIs of type r owned by supplier p and that have been delivered to customer i in period t.
- : Quantity of empty RTIs of type r owned by supplier p and that have been filled with products at his level in period t.
3.3. Mathematical Model for SM
3.3.1. Multi-Period Clustering Problem
3.3.2. SM Model
- Inventory holding at each centre ;
- Pooling cost for each unowned RTI used by each supplier (which is equivalent to the sharing cost in IRPPDS).
- : set of customers for whom the supplier p belongs to the cluster of centre (node ).
- : set of suppliers belonging to the cluster of centre .
- : quantity of empty RTIs of type r belonging to supplier p and sent to centre to which supplier p belongs.
- : quantity of empty RTIs of type r transported from node i to node j in period t and sent to centre .
- : quantity of empty RTIs of type r transported from node p to node in period t and sent by centre .
- : inventory level of empty RTIs of type r at centre in period t.
- : binary variable equal to 1 if node j is visited right after node i by vehicle v, 0 otherwise.
- : binary variable equal to 1 if customer j is visited by v from node (cluster) , 0 otherwise.
- : binary variable equal to 1 if supplier is visited right after supplier p by vehicle v, 0 otherwise.
- binary variable equal to 1 if supplier p is visited by v from node (cluster) , 0 otherwise.
4. Resolution Approach
4.1. Artificial Immune System
4.1.1. Affinity and Cloning Selection
4.1.2. Affinity Maturation
4.2. AIS Enhanced with Deep Q-Learning
4.2.1. AIS and RL
4.2.2. Q-Learning
4.2.3. Deep Q-Learning
4.2.4. Deep Q-Learning Architecture
- : discount-rate parameter to measure the weight of the future awards.
- : current and future action, respectively.
- : current and future state, respectively.
- : future reward.
- : learned action-value function.
- : transpose matrix of network weights.
5. Implementation and Experimental Analysis
Experimental Design and Parameters Tuning
6. Computational Experiments
6.1. Results on Small Instances Solved Using CPLEX
6.2. First Insights into the Effectiveness of the Resolution Approach on Small Instances
6.3. Extra Experiments on Large Instances Solved Using GA-DQL and AIS-DQL
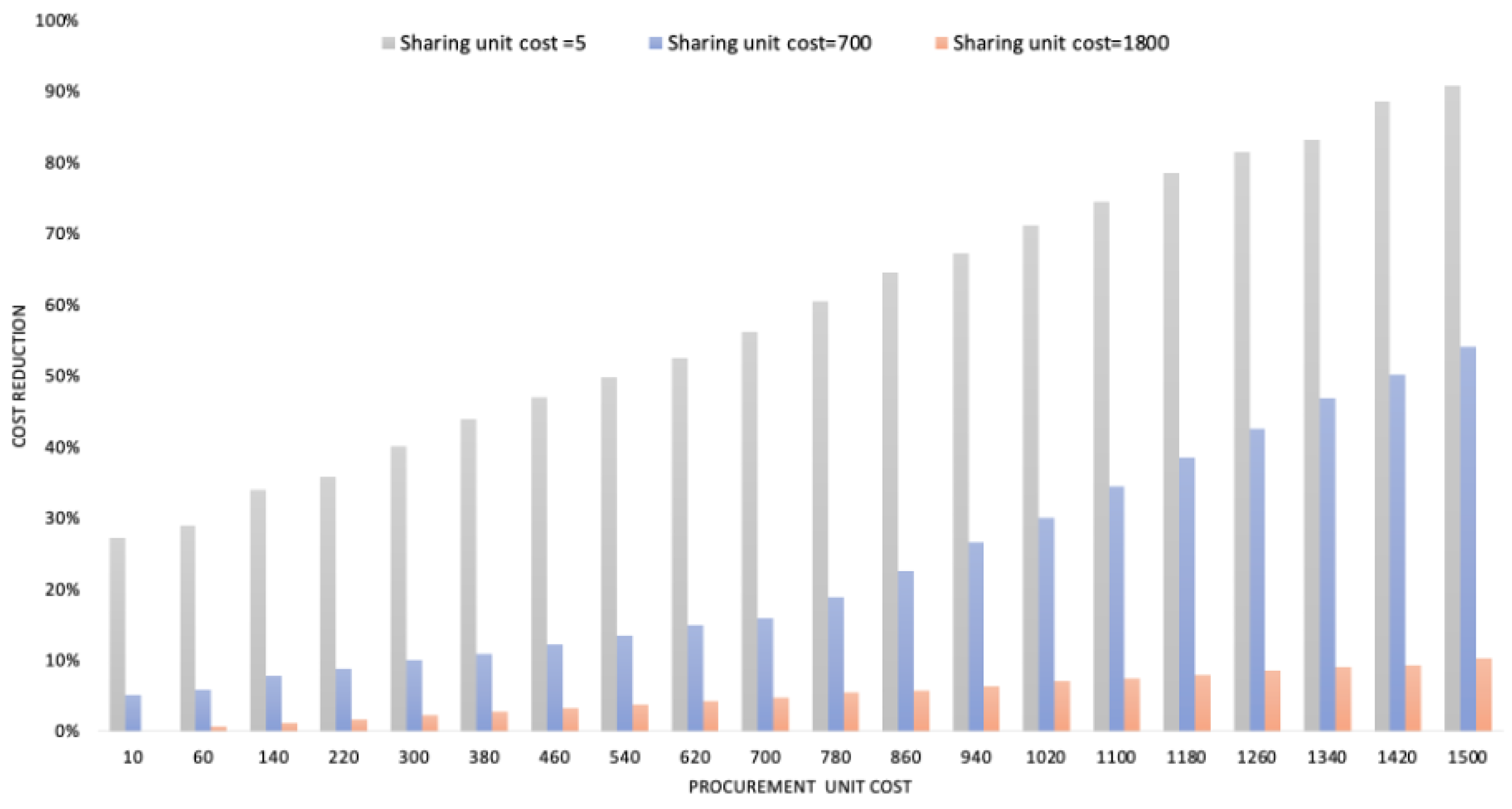
6.4. Sensitivity Analysis on Unit Cost
7. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cobb, B. Inventory control for returnable transport items in a closed-loop supply chain. Transp. Res. Part E Logist. Transp. Rev. 2016, 86, 53–68. [Google Scholar] [CrossRef]
- Kim, T.; Glock, C. On the use of RFID in the management of reusable containers in closed-loop supply chains under stochastic container return quantities. Transp. Res. Part E Logist. Transp. Rev. 2014, 64, 12–27. [Google Scholar] [CrossRef]
- Limbourg, S.; Martin, A.; Paquay, C. Optimal Returnable Transport Items Management. 2016. Available online: https://hdl.handle.net/2268/200983 (accessed on 1 May 2022).
- Iassinovskaia, G.; Limbourg, S.; Riane, F. The inventory-routing problem of returnable transport items with time windows and simultaneous pickup and delivery in closed-loop supply chains. Int. J. Prod. Econ. 2017, 183, 570–582. [Google Scholar] [CrossRef]
- Glock, C.H. Decision support models for managing returnable transport items in supply chains: A systematic literature review. Int. J. Prod. Econ. 2017, 183, 561–569. [Google Scholar] [CrossRef]
- Bortolini, M.; Galizia, F.G.; Mora, C.; Botti, L.; Rosano, M. Bi-objective design of fresh food supply chain networks with reusable and disposable packaging containers. J. Clean. Prod. 2018, 184, 375–388. [Google Scholar] [CrossRef]
- Liu, G.; Li, L.; Chen, J.; Ma, F. Inventory sharing strategy and optimization for reusable transport items. Int. J. Prod. Econ. 2020, 228, 107742. [Google Scholar] [CrossRef]
- Twede, D.; Clarke, R. Supply Chain Issues in Reusable Packaging. J. Mark. Channels 2005, 12, 7–26. [Google Scholar] [CrossRef]
- Sarkar, B.; Ullah, M.; Kim, N. Environmental and economic assessment of closed-loop supply chain with remanufacturing and returnable transport items. Comput. Ind. Eng. 2017, 111, 148–163. [Google Scholar] [CrossRef]
- Talaei, M.; Farhang Moghaddam, B.; Pishvaee, M.S.; Bozorgi-Amiri, A.; Gholamnejad, S. A robust fuzzy optimization model for carbon-efficient closed-loop supply chain network design problem: A numerical illustration in electronics industry. J. Clean. Prod. 2016, 113, 662–673. [Google Scholar] [CrossRef]
- Meherishi, L.; Narayana, S.A.; Ranjani, K.S. Integrated product and packaging decisions with secondary packaging returns and protective packaging management. Eur. J. Oper. Res. 2021, 292, 930–952. [Google Scholar] [CrossRef]
- TrackX. A Return on Returnables. Technical Report. 2017. Available online: https://www.omniq.com/wp-content/uploads/2020/11/Quest-TrackX-WP-RTI-Assets.pdf (accessed on 1 May 2022).
- Na, B.; Sim, M.K.; Lee, W.J. An Optimal Purchase Decision of Reusable Packaging in the Automotive Industry. Sustainability 2019, 11, 6579. [Google Scholar] [CrossRef]
- Zhang, Q.; Segerstedt, A.; Tsao, Y.C.; Liu, B. Returnable packaging management in automotive parts logistics: Dedicated mode and shared mode. Int. J. Prod. Econ. 2015, 168, 234–244. [Google Scholar] [CrossRef]
- GS1 Global Office. Reusable Transport Items within GS1 EANCOM; Technical Report; GS1 Global Office: Brussels, Belgium, 2014. [Google Scholar]
- Accorsi, R.; Baruffaldi, G.; Manzini, R.; Pini, C. Environmental Impacts of Reusable Transport Items: A Case Study of Pallet Pooling in a Retailer Supply Chain. Sustainability 2019, 11, 3147. [Google Scholar] [CrossRef]
- Govindan, K.; Soleimani, H.; Kannan, D. Reverse logistics and closed-loop supply chain: A comprehensive review to explore the future. Eur. J. Oper. Res. 2015, 240, 603–626. [Google Scholar] [CrossRef]
- Paterson, C.; Kiesmüller, G.; Teunter, R.; Glazebrook, K. Inventory models with lateral transshipments: A review. Eur. J. Oper. Res. 2011, 210, 125–136. [Google Scholar] [CrossRef]
- Achamrah, F.E.; Riane, F.; Limbourg, S. Solving inventory routing with transshipment and substitution under dynamic and stochastic demands using genetic algorithm and deep reinforcement learning. Int. J. Prod. Res. 2021, 1–18. [Google Scholar] [CrossRef]
- Toth, P.; Vigo, D. The Vehicle Routing Problem; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Berbeglia, G.; Cordeau, J.F.; Gribkovskaia, I.; Laporte, G. Static pickup and delivery problems: A classification scheme and survey. TOP Off. J. Span. Soc. Stat. Oper. Res. 2007, 15, 1–31. [Google Scholar] [CrossRef]
- Andersson, H.; Christiansen, M.; Fagerholt, K. The Maritime Pickup and Delivery Problem with Time Windows and Split Loads. INFOR Inf. Syst. Oper. Res. 2011, 49, 79–91. [Google Scholar] [CrossRef]
- Rais, A.; Alvelos, F.; Carvalho, M.S. New mixed integer-programming model for the pickup-and-delivery problem with transshipment. Eur. J. Oper. Res. 2014, 235, 530–539. [Google Scholar] [CrossRef]
- Chen, H.K.; Chou, H.W.; Hsueh, C.F.; Yu, Y.J. The paired many-to-many pickup and delivery problem: An application. TOP 2014, 23, 220–243. [Google Scholar] [CrossRef]
- Li, B.; Krushinsky, D.; Van Woensel, T.; Reijers, H. An Adaptive Large Neighborhood Search Heuristic for the Share-a-Ride Problem. Comput. Oper. Res. 2015, 66, 170–180. [Google Scholar] [CrossRef]
- Coelho, L.C.; Laporte, G. Improved solutions for inventory-routing problems through valid inequalities and input ordering. Int. J. Prod. Econ. 2014, 155, 391–397. [Google Scholar] [CrossRef]
- Parragh, S.N.; Doerner, K.F.; Hartl, R.F. A survey on pickup and delivery problems. J. Betr. 2008, 58, 21–51. [Google Scholar] [CrossRef]
- Tarantilis, C.D.; Anagnostopoulou, A.K.; Repoussis, P.P. Adaptive Path Relinking for Vehicle Routing and Scheduling Problems with Product Returns. Transp. Sci. 2012, 47, 356–379. [Google Scholar] [CrossRef]
- Archetti, C.; Christiansen, M.; Grazia Speranza, M. Inventory routing with pickups and deliveries. Eur. J. Oper. Res. 2018, 268, 314–324. [Google Scholar] [CrossRef]
- Van der Heide, G.; Buijs, P.; Roodbergen, K.J.; Vis, I.F.A. Dynamic shipments of inventories in shared warehouse and transportation networks. Transp. Res. Part E Logist. Transp. Rev. 2018, 118, 240–257. [Google Scholar] [CrossRef]
- Archetti, C.; Speranza, M.G.; Boccia, M.; Sforza, A.; Sterle, C. A branch-and-cut algorithm for the inventory routing problem with pickups and deliveries. Eur. J. Oper. Res. 2020, 282, 886–895. [Google Scholar] [CrossRef]
- Meherishi, L.; Narayana, S.A.; Ranjani, K.S. Sustainable packaging for supply chain management in the circular economy: A review. J. Clean. Prod. 2019, 237, 117582. [Google Scholar] [CrossRef]
- Achamrah, F.E.; Bouras, A.; Riane, F.; Darmoul, S. Returnable Transport Items Management: A New Approach to Sidestep Shortage. In Proceedings of the 7th International Conference IEEE on Advanced Logistics and Transport, Marrakech, Morocco, 14–16 June 2019; pp. 92–97. [Google Scholar]
- Singh, S.K.; Gupta, Y.; Mishra, A.; Darla, S. Inventory Routing Problem with Simultaneous Pickup and Delivery of Returnable Transport Items with Consideration of Renting and Repairing. Int. J. Eng. Res. Technol. 2017, 6, 92–97. [Google Scholar]
- Ech-Charrat, M.R.; Amechnoue, K.; Zouadi, T. Dynamic Planning of Reusable Containers in a Close-loop Supply Chain under Carbon Emission Constrain. Int. J. Supply Oper. Manag. 2017, 4, 279–297. [Google Scholar] [CrossRef]
- Ren, J.; Liu, B.; Wang, Z. An optimization model for multi-type pallet allocation over a pallet pool. Adv. Mech. Eng. 2017, 9, 1687814017705841. [Google Scholar] [CrossRef]
- Tornese, F.; Pazour, J.A.; Thorn, B.K.; Roy, D.; Carrano, A.L. Investigating the environmental and economic impact of loading conditions and repositioning strategies for pallet pooling providers. J. Clean. Prod. 2018, 172, 155–168. [Google Scholar] [CrossRef]
- Hassanzadeh Amin, S.; Wu, H.; Karaphillis, G. A perspective on the reverse logistics of plastic pallets in Canada. J. Remanuf. 2018, 8, 153–174. [Google Scholar] [CrossRef]
- Zhou, K.; Song, R. Location Model of Pallet Service Centers Based on the Pallet Pool Mode. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019; pp. 1185–1189. [Google Scholar] [CrossRef]
- Achamrah, F.E.; Riane, F.; Bouras, A.; Sahin, E. Collaboration Mechanism for Shared Returnable Transport Items in Closed Loop Supply Chains. In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems, Valletta, Malta, 22–24 February 2020. [Google Scholar] [CrossRef]
- Karp, R. Reducibility among Combinatorial Problems; Springer: Boston, MA, USA, 1972; Volume 40, pp. 85–103. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Steiglitz, K. On the Complexity of Local Search for the Traveling Salesman Problem. SIAM J. Comput. 1977, 6, 76–83. [Google Scholar] [CrossRef][Green Version]
- Bernardino, H.S.; Barbosa, H.J.C. Grammar-Based Immune Programming for Symbolic Regression BT—Artificial Immune Systems; Springer: Berlin/Heidelberg, Germany, 2009; pp. 274–287. [Google Scholar]
- De Castro, L.; Jos, F.; von Zuben, A.A. Artificial Immune Systems: Part II—A Survey of Applications. 2000. Available online: http://https://www.dca.fee.unicamp.br/~vonzuben/tr_dca/trdca0200.pdf (accessed on 1 May 2022).
- Wong, E.Y.C.; Lau, H.Y.K.; Mak, K.L. Immunity-based evolutionary algorithm for optimal global container repositioning in liner shipping. Spectrum 2010, 32, 739–763. [Google Scholar] [CrossRef][Green Version]
- Tiwari, M.K.; Prakash; Kumar, A.; Mileham, A.R. Determination of an optimal assembly sequence using the psychoclonal algorithm. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2005, 219, 137–149. [Google Scholar] [CrossRef]
- Panigrahi, B.K.; Yadav, S.R.; Agrawal, S.; Tiwari, M.K. A clonal algorithm to solve economic load dispatch. Electr. Power Syst. Res. 2007, 77, 1381–1389. [Google Scholar] [CrossRef]
- Pierrard, T.; Coello Coello, C.A. A Multi-Objective Artificial Immune System Based on Hypervolume BT—Artificial Immune Systems; Springer: Berlin/Heidelberg, Germany, 2012; pp. 14–27. [Google Scholar]
- Navarro, M.; Herath, P.; Villarrubia, G.; Prieto-Castrillo, F.; Venyagamoorthy, G. An Evaluation of a Metaheuristic Artificial Immune System for Household Energy Optimization. Complexity 2018, 2018, 9597158. [Google Scholar] [CrossRef]
- Talbi, E.G. Machine Learning into Metaheuristics: A Survey and Taxonomy of Data-Driven Metaheuristics. 2020. Available online: https://hal.inria.fr/hal-02745295/file/ACM-CR.pdf (accessed on 1 May 2022).
- Bello, I.; Pham, H.; Le, Q.; Norouzi, M.; Bengio, S. Neural Combinatorial Optimization with Reinforcement Learning. arXiv 2016, arXiv:1611.09940. [Google Scholar]
- Dai, H.; Khalil, E.; Yuyu, Z.; Dilkina, B.; Song, L. Learning Combinatorial Optimization Algorithms over Graphs. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Han, M.; Senellart, P.; Bressan, S.; Wu, H. Routing an autonomous taxi with reinforcement learning. In Proceedings of the 25th ACM International on Conference on Information and Knowledge Management, Indianapolis, IN, USA, 24–28 October 2016; pp. 2421–2424. [Google Scholar]
- Kaempfer, Y.; Wolf, L. Learning the multiple traveling salesmen problem with permutation invariant pooling networks. arXiv 2018, arXiv:1803.09621. [Google Scholar]
- Huang, D.; Mao, Z.; Fang, K.; Chen, L. Solving the shortest path interdiction problem via reinforcement learning. Int. J. Prod. Res. 2021, 1–18. [Google Scholar] [CrossRef]
- Ahmadian, S. Approximation Algorithms for Clustering and Facility Location Problems. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2017. Available online: http://hdl.handle.net/10012/11640 (accessed on 1 May 2022).
- OroojlooyJadid, A.; Hajinezhad, D. A review of cooperative multi-agent deep reinforcement learning. arXiv 2019, arXiv:1908.03963. [Google Scholar]
- Lu, H.; Zhang, X.; Yang, S. A Learning-Based Iterative Method for Solving Vehicle Routing Problems. 2019. Available online: https://openreview.net/forum?id=BJe1334YDH (accessed on 1 May 2022).
- Duan, L.; Zhan, Y.; Hu, H.; Gong, Y.; Wei, J.; Zhang, X.; Xu, Y. Efficiently solving the practical vehicle routing problem: A novel joint learning approach. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 3054–3063. [Google Scholar]
- Achamrah, F.E.; Riane, F.; Aghezzaf, E.H. Bi-level programming for modelling inventory sharing in decentralized supply chains. Transp. Res. Procedia 2022, 62, 517–524. [Google Scholar] [CrossRef]
- Nakib, A.; Hilia, M.; Heliodore, F.; Talbi, E.G. Design of metaheuristic based on machine learning: A unified approach. In Proceedings of the 2017 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Lake Buena Vista, FL, USA, 29 May–2 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 510–518. [Google Scholar]
- Seyyedabbasi, A.; Aliyev, R.; Kiani, F.; Gulle, M.U.; Basyildiz, H.; Shah, M.A. Hybrid algorithms based on combining reinforcement learning and metaheuristic methods to solve global optimization problems. Knowl. Based Syst. 2021, 223, 107044. [Google Scholar] [CrossRef]
- Talbi, E.G. Metaheuristics: From Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 74. [Google Scholar]
- Chiang, C.W.; Lee, W.P.; Heh, J.S. A 2-Opt based differential evolution for global optimization. Appl. Soft Comput. 2010, 10, 1200–1207. [Google Scholar] [CrossRef]
- Alom, M.Z.; Taha, T.M.; Yakopcic, C.; Westberg, S.; Sidike, P.; Nasrin, M.S.; Hasan, M.; Van Essen, B.C.; Awwal, A.A.S.; Asari, V.K. A State-of-the-Art Survey on Deep Learning Theory and Architectures. Electronics 2019, 8, 292. [Google Scholar] [CrossRef]
- Mohtashami, A. A Novel Dynamic Genetic Algorithm-Based Method for Vehicle Scheduling in Cross Docking Systems with Frequent Unloading Operation. Comput. Ind. Eng. 2015, 90, 221–240. [Google Scholar] [CrossRef]




| DM | SM | Virtual Pooling Mode | |
|---|---|---|---|
| Owner of RTIs | Each supplier | All suppliers or a pooler company | Each supplier |
| Management of empty RTIs, collection, refurbishing… | Each supplier | One pooler company | All suppliers |
| Storage of empty and shared RTIs | - | In dedicated facilities | At suppliers’ level |
| Sets | |
| N | Set of n customers. |
| P | Set of m suppliers. |
| R | Set of u RTIs. |
| V | Set of k vehicles. |
| T | Set of l periods. |
| Parameters | |
| a | Fixed cost of transportation (€ per km). |
| b | Variable cost of transportation (€ per weight per km). |
| , , , | Cost of holding inventory of loaded and empty RTIs, respectively, for each supplier p and customer i. |
| Cost of buying a new RTI of type r (€ per unit). | |
| Cost of sharing incurred by each supplier which is proportional to the number of unowned empty RTIs of a type r used at his level to deliver products (€ per unit of unowned RTI used). | |
| Cost of maintenance of one RTI of type r (€ per RTI loaded). | |
| , | Weights of a loaded and empty RTIs of type r, respectively. |
| Q | Capacity of vehicle in terms of the number of RTIs. |
| Distance between nodes i and j . | |
| Demand of each customer i for each period t loaded on an RTI r satisfied by supplier p. | |
| , , , | Initial inventory level of loaded and empty RTIs of type r, respectively, for the supplier p and customer i. |
| , , , | Maximum holding capacity for loaded and empty RTIs, respectively, for the supplier p and customer i. |
| Decision variables | |
| Binary variable stating whether the vehicle v visited node j immediately after node i in period t. | |
| Quantity of empty RTIs of type r owned by supplier p that have been filled with products by supplier p in period t. This quantity also includes the case where (supplier uses his RTI). | |
| Inventory level of loaded RTIs of type r held by the supplier p at the end of period t. | |
| Inventory level of RTIs of type r filled with the product of supplier p by customer i at the end of period t. | |
| Quantity of loaded RTIs of type r owned by supplier and delivered by supplier p to customer i in period t. | |
| Quantity of loaded RTIs of type r filled with a product of supplier p transported from node i to node j in period t. | |
| Inventory level of empty RTIs of type r held by the customer i at the end of period t. | |
| Total quantities of all empty RTIs of type r held by the supplier p at the end of period t. | |
| Quantity of empty RTIs of type r owned by supplier p collected from a customer i in period t. | |
| Quantity of empty RTIs of type r owned by supplier p and collected from customer i by supplier p in period t. | |
| Quantity of empty RTIs of type r collected by supplier p transported from node i to node j in period t. | |
| Quantity of RTIs of type r bought by supplier p in period t. | |
| Resolution Approach | F | p-Value |
|---|---|---|
| GA | 2.16 | 0.14 |
| AIS | 1.57 | 0.22 |
| GA-DQL | 0.91 | 0.34 |
| AIS-DQL | 0.49 | 0.49 |
| Tuned Parameter | Value |
|---|---|
| Population size (GA/AIS) | 200 |
| Maximum iteration number (GA/AIS) | 200 |
| Crossover probability (GA/AIS) | 0.81 |
| Mutation probability (GA/AIS) | 0.46 |
| Selection probability | 0.80 |
| Receptor editing rate | 0.28 |
| Instances | Model | T (€) | I-S (€) | I-C (€) | I-K (€) | M (€) | P (€) | S (€) | TC (€) | CS (%) | CPU (s) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1R2S6P40V5T | DM | 106,899 | 1386 | 1428 | 0 | 141 | 280,224 | 0 | 390,078 | - | 424 |
| SM | 105,309 | 592 | 1368 | 751 | 133 | 122,771 | 2371 | 233,294 | 40 | 629 | |
| IRPPDS | 84,854 | 1188 | 1308 | 0 | 141 | 98,739 | 865 | 187,095 | 52 | 451 | |
| 1R2S12P40V5T | DM | 315,279 | 3706 | 1721 | 0 | 299 | 907,085 | 0 | 1,228,090 | - | 5050 |
| SM | 245,866 | 2032 | 1359 | 2390 | 331 | 737,268 | 8940 | 998,186 | 19 | 6445 | |
| IRPPDS | 228,259 | 3562 | 1190 | 0 | 294 | 415,480 | 2998 | 651,784 | 47 | 5265 | |
| 1R2S18P40V5T | DM | 519,475 | 3067 | 4988 | 0 | 366 | 831,051 | 0 | 1,358,947 | - | 8776 |
| SM | 471,330 | 1710 | 2680 | 1765 | 351 | 731,678 | 5504 | 1,215,018 | 11 | 12,115 | |
| IRPPDS | 402,425 | 2532 | 1911 | 0 | 352 | 611,920 | 4835 | 1,023,975 | 25 | 9331 | |
| 1R2S24P40V5T | DM | 853,012 | 4136 | 8040 | 0 | 685 | 3,280,781 | 0 | 4,146,653 | - | 24,314 |
| SM | 711,300 | 3230 | 4061 | 2890 | 688 | 2,758,063 | 7761 | 3,487,994 | 16 | 31,701 | |
| IRPPDS | 552,893 | 4744 | 3046 | 0 | 696 | 1,886,929 | 6107 | 2,454,415 | 41 | 24,399 | |
| 2R2S5P40V5T | DM | 267,334 | 1013 | 4607 | 0 | 152 | 1,306,998 | 0 | 1,580,105 | - | 473 |
| SM | 203,254 | 629 | 2957 | 746 | 171 | 1,188,760 | 3240 | 1,399,757 | 11 | 591 | |
| IRPPDS | 158,771 | 928 | 2011 | 0 | 154 | 781,631 | 1326 | 944,821 | 40 | 496 | |
| 4R2S5P40V5T | DM | 575,795 | 2055 | 11,269 | 0 | 502 | 1,719,310 | 0 | 2,308,932 | - | 1309 |
| SM | 508,117 | 1177 | 5829 | 1432 | 426 | 1,493,784 | 6928 | 2,017,692 | 13 | 1626 | |
| IRPPDS | 413,915 | 1859 | 5141 | 0 | 457 | 1,056,450 | 5324 | 1,483,147 | 36 | 1316 | |
| 6R2S5P40V5T | DM | 984,677 | 3886 | 11,401 | 0 | 645 | 1,953,350 | 0 | 2,953,958 | - | 3013 |
| SM | 601,250 | 1993 | 13,834 | 3007 | 578 | 1,608,985 | 12,681 | 2,242,328 | 24 | 4131 | |
| IRPPDS | 571,245 | 3372 | 6552 | 0 | 562 | 1,499,512 | 14,711 | 2,095,952 | 29 | 4405 | |
| 8R2S5P40V5T | DM | 1,196,050 | 3559 | 19,337 | 0 | 799 | 2,649,398 | 0 | 3,869,143 | - | 5423 |
| SM | 1,027,848 | 2099 | 17,123 | 3738 | 734 | 2,270,434 | 221,00 | 3,344,076 | 14 | 7346 | |
| IRPPDS | 704,453 | 3307 | 11,693 | 0 | 765 | 1,726,959 | 15,446 | 2,462,623 | 36 | 5968 | |
| 10R2S5P40V5T | DM | 1,536,319 | 7376 | 22,048 | 0 | 1005 | 3,674,097 | 0 | 5,240,844 | - | 7981 |
| SM | 1,450,099 | 3844 | 23,893 | 9146 | 1122 | 2,852,572 | 45,735 | 4,386,411 | 16 | 10,675 | |
| IRPPDS | 878,014 | 6777 | 11,199 | 0 | 967 | 2,263,598 | 18,631 | 3,179,185 | 39 | 8687 | |
| 1R5S5P40V5T | DM | 223,327 | 1698 | 3473 | 0 | 257 | 414,556 | 0 | 643,312 | - | 8084 |
| SM | 213,934 | 947 | 3137 | 964 | 241 | 340,187 | 3415 | 562,825 | 13 | 13,686 | |
| IRPPDS | 157,568 | 1591 | 1754 | 0 | 233 | 245,555 | 1440 | 408,141 | 37 | 8969 | |
| 1R10S5P60V5T | DM | 470,266 | 3753 | 6052 | 0 | 544 | 1,040,464 | 0 | 1,521,078 | - | 22,526 |
| SM | 465,720 | 1744 | 5879 | 1869 | 537 | 487,739 | 4204 | 967,693 | 36 | 33,882 | |
| IRPPDS | 383,377 | 2661 | 5856 | 0 | 505 | 209,126 | 2136 | 603,661 | 60 | 24,005 | |
| 1R15S5P40V5T | DM | 1,018,250 | 6620 | 12,547 | 0 | 798 | 882,493 | 0 | 1,920,708 | - | 32,387 |
| SM | 995,463 | 4898 | 6364 | 4941 | 845 | 677,583 | 18,544 | 1,708,639 | 11 | 41,501 | |
| IRPPDS | 715,381 | 6145 | 4966 | 0 | 823 | 612,775 | 7922 | 1,348,012 | 30 | 34,055 | |
| 1R20S5P40V5T | DM | 1,595,794 | 9500 | 21,299 | 0 | 1310 | 1,929,223 | 0 | 3,557,125 | - | 55,543 |
| SM | 1,419,879 | 6413 | 9549 | 7967 | 1139 | 1,724,055 | 25,988 | 3,194,989 | 10 | 67,511 | |
| IRPPDS | 893,618 | 10,265 | 7933 | 0 | 1181 | 754,922 | 9303 | 1,677,222 | 53 | 55,135 | |
| 1R25S5P40V5T | DM | 2,251,175 | 11,306 | 28,742 | 0 | 1488 | 1,758,976 | 0 | 4,051,687 | - | 67,115 |
| SM | 2,044,658 | 6530 | 25,480 | 5387 | 1388 | 1,510,890 | 17,212 | 3,611,545 | 11 | 85,413 | |
| IRPPDS | 1,439,157 | 11,087 | 14,999 | 0 | 1536 | 1,394,438 | 13,932 | 2,875,148 | 29 | 63,468 |
| Instance | Model | CPLEX | GA | AIS | GA-DQL | AIS-DQL | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TC (€) | CPU (s) | TC (€) | CPU (s) | Gap (%) | TC (€) | CPU (s) | Gap (%) | TC (€) | CPU (s) | Gap (%) | TC (€) | CPU (s) | Gap (%) | ||
| 1R2S6P40V5T | DM | 390,078 | 424 | 396,319 | 8 | 1.6 | 395,929 | 28 | 1.5 | 396,319 | 15 | 1.6 | 390,078 | 2 | 0.0 |
| SM | 233,294 | 629 | 257,557 | 9 | 10.4 | 254,757 | 22 | 9.2 | 245,892 | 10 | 5.4 | 234,461 | 31 | 0.5 | |
| IRPPDS | 187,095 | 451 | 204,308 | 9 | 9.2 | 199,443 | 41 | 6.6 | 200,379 | 14 | 7.1 | 187,095 | 4 | 0.0 | |
| 1R2S12P40V5T | DM | 1,228,090 | 5050 | 1,331,250 | 256 | 8.4 | 1,312,828 | 240 | 6.9 | 1,251,424 | 421 | 1.9 | 1,228,090 | 25 | 0.0 |
| SM | 998,186 | 6445 | 1,044,102 | 427 | 4.6 | 1,038,113 | 205 | 4.0 | 1,032,124 | 307 | 3.4 | 1,003,177 | 21 | 0.5 | |
| IRPPDS | 651,784 | 5265 | 677,204 | 401 | 3.9 | 689,587 | 57 | 5.8 | 682,418 | 461 | 4.7 | 651,784 | 21 | 0.0 | |
| 1R2S18P40V5T | DM | 1,358,947 | 8776 | 1,498,919 | 84 | 10.3 | 1,382,049 | 32 | 1.7 | 1,394,280 | 89 | 2.6 | 1,358,947 | 18 | 0.0 |
| SM | 1,215,018 | 12,115 | 1,364,466 | 527 | 12.3 | 1,362,036 | 62 | 12.1 | 1,273,339 | 57 | 4.8 | 1,219,879 | 77 | 0.4 | |
| IRPPDS | 1,023,975 | 9331 | 1,135,588 | 824 | 10.9 | 1,087,461 | 925 | 6.2 | 1,054,694 | 483 | 3 | 1,023,975 | 50 | 0.0 | |
| 1R2S24P40V5T | DM | 4,146,653 | 24,314 | 4,486,679 | 1394 | 8.2 | 4,470,092 | 884 | 7.8 | 4,457,652 | 1674 | 7.5 | 4,146,653 | 47 | 0.0 |
| SM | 3,487,994 | 31,701 | 3,857,721 | 989 | 10.6 | 3,864,697 | 508 | 10.8 | 3,808,889 | 416 | 9.2 | 3,508,922 | 21 | 0.6 | |
| IRPPDS | 2,454,415 | 24,399 | 2,947,752 | 2313 | 20.1 | 2,923,208 | 25 | 19.1 | 2,648,314 | 455 | 7.9 | 2,454,415 | 163 | 0.0 | |
| 2R2S5P40V5T | DM | 1,580,105 | 473 | 1,922,988 | 12 | 21.7 | 1,783,939 | 37 | 12.9 | 1,685,972 | 30 | 6.7 | 1,581,685 | 1 | 0.1 |
| SM | 1,399,757 | 591 | 1,542,532 | 40 | 10.2 | 1,511,738 | 12 | 8.0 | 1,426,353 | 20 | 1.9 | 1,402,557 | 42 | 0.2 | |
| IRPPDS | 944,821 | 496 | 1,037,413 | 18 | 9.8 | 993,952 | 4 | 5.2 | 963,717 | 35 | 2 | 945,766 | 3 | 0.1 | |
| 4R2S5P40V5T | DM | 2,308,932 | 1309 | 2,673,743 | 75 | 15.8 | 2,542,134 | 76 | 10.1 | 2,403,598 | 4 | 4.1 | 2,308,932 | 12 | 0.0 |
| SM | 2,017,692 | 1626 | 2,360,700 | 39 | 17 | 2,209,373 | 41 | 9.5 | 2,031,816 | 51 | 0.7 | 2,017,692 | 22 | 0.0 | |
| IRPPDS | 1,483,147 | 1316 | 1,739,731 | 124 | 17.3 | 1,576,585 | 21 | 6.3 | 1,566,203 | 79 | 5.6 | 1,483,147 | 5 | 0.0 | |
| 6R2S5P40V5T | DM | 2,953,958 | 3013 | 3,202,090 | 63 | 8.4 | 3,190,275 | 42 | 8.0 | 3,140,057 | 227 | 6.3 | 2,953,958 | 6 | 0.0 |
| SM | 2,242,328 | 4131 | 2,679,583 | 58 | 19.5 | 2,684,067 | 6 | 19.7 | 2,419,472 | 8 | 7.9 | 2,249,055 | 53 | 0.3 | |
| IRPPDS | 2,095,952 | 4405 | 2,290,876 | 70 | 9.3 | 2,292,971 | 379 | 9.4 | 2,179,790 | 240 | 4.0 | 2,098,048 | 2 | 0.1 | |
| 8R2S5P40V5T | DM | 3,869,143 | 5423 | 4,604,280 | 538 | 19.0 | 4,016,170 | 527 | 3.8 | 3,927,180 | 392 | 1.5 | 3,873,012 | 29 | 0.1 |
| SM | 3,344,076 | 7346 | 3,691,860 | 525 | 10.4 | 3,410,957 | 604 | 2.0 | 3,390,893 | 209 | 1.4 | 3,347,420 | 41 | 0.1 | |
| IRPPDS | 2,462,623 | 5968 | 2,856,643 | 350 | 16 | 2,570,978 | 46 | 4.4 | 2,561,128 | 31 | 4.0 | 2,462,623 | 44 | 0.0 | |
| 10R2S5P40V5T | DM | 5,240,844 | 7981 | 5,801,614 | 733 | 10.7 | 5,848,782 | 670 | 11.6 | 5,382,347 | 293 | 2.7 | 5,246,085 | 28 | 0.1 |
| SM | 4,386,411 | 10,675 | 4,618,891 | 319 | 5.3 | 4,614,504 | 400 | 5.2 | 4,496,071 | 415 | 2.5 | 4,425,888 | 32 | 0.9 | |
| IRPPDS | 3,179,185 | 8687 | 3,795,947 | 447 | 19.4 | 3,808,664 | 206 | 19.8 | 3,344,503 | 177 | 5.2 | 3,179,185 | 60 | 0.0 | |
| 1R5S5P40V5T | DM | 643,312 | 8084 | 702,497 | 421 | 9.2 | 714,720 | 63 | 11.1 | 656,178 | 30 | 2.0 | 643,955 | 27 | 0.1 |
| SM | 562,825 | 13,686 | 665,259 | 276 | 18.2 | 613,479 | 54 | 9.0 | 602,786 | 38 | 7.1 | 567,328 | 6 | 0.8 | |
| IRPPDS | 408,141 | 8969 | 454,261 | 726 | 11.3 | 422,426 | 702 | 3.5 | 436,711 | 100 | 7.0 | 408,549 | 7 | 0.1 | |
| 1R10S5P60V5T | DM | 1,521,078 | 22,526 | 1,718,818 | 422 | 13.0 | 1,630,596 | 1732 | 7.2 | 1,522,599 | 337 | 0.1 | 1,522,599 | 168 | 0.1 |
| SM | 967,693 | 33,882 | 1,065,430 | 307 | 10.1 | 1,065,430 | 980 | 10.1 | 1,047,043 | 475 | 8.2 | 969,628 | 52 | 0.2 | |
| IRPPDS | 603,661 | 24,005 | 719,564 | 285 | 19.2 | 705,680 | 508 | 16.9 | 644,106 | 295 | 6.7 | 604,265 | 160 | 0.1 | |
| 1R15S5P40V5T | DM | 1,920,708 | 32,387 | 2,214,576 | 2272 | 15.3 | 2,212,656 | 1433 | 15.2 | 2,058,999 | 2871 | 7.2 | 1,920,708 | 48 | 0.0 |
| SM | 1,708,639 | 41,501 | 1,942,722 | 525 | 13.7 | 1,905,132 | 1245 | 11.5 | 1,802,614 | 395 | 5.5 | 1,717,182 | 22 | 0.5 | |
| IRPPDS | 1,348,012 | 34,055 | 1,419,457 | 2947 | 5.3 | 1,443,721 | 1598 | 7.1 | 1,376,320 | 949 | 2.1 | 1,349,360 | 289 | 0.1 | |
| 1R20S5P40V5T | DM | 3,557,125 | 55,543 | 4,197,408 | 1656 | 18.0 | 4,030,223 | 5005 | 13.3 | 3,841,695 | 148 | 8.0 | 3,557,125 | 103 | 0.0 |
| SM | 3,194,989 | 67,511 | 3,600,753 | 910 | 12.7 | 3,466,563 | 406 | 8.5 | 3,252,499 | 510 | 1.8 | 3,201,379 | 12 | 0.2 | |
| IRPPDS | 1,677,222 | 55,135 | 1,893,584 | 902 | 12.9 | 1,893,584 | 5312 | 12.9 | 1,769,469 | 451 | 5.5 | 1,677,222 | 296 | 0.0 | |
| 1R25S5P40V5T | DM | 4,051,687 | 67,115 | 4,590,561 | 3358 | 13.3 | 4,517,631 | 2022 | 11.5 | 4,221,858 | 1636 | 4.2 | 4,051,687 | 524 | 0.0 |
| SM | 3,611,545 | 85,413 | 4,174,946 | 3140 | 15.6 | 4,113,549 | 400 | 13.9 | 3,795,733 | 211 | 5.1 | 3,611,545 | 42 | 0.0 | |
| IRPPDS | 2,875,148 | 63,468 | 3,346,672 | 4064 | 16.4 | 3,197,165 | 3750 | 11.2 | 2,955,652 | 70 | 2.8 | 2,875,148 | 385 | 0.0 | |
| Instances | AIS-DQL | GA-DQL | Diff (%) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DM | SM | IRPPDS | CS (%) | DM | SM | IRPPDS | CS (%) | ||||||||||||
| TC (€) | CPU (s) | TC (€) | CPU (s) | TC (€) | CPU (s) | SM | IRPPDS | TC (€) | CPU (s) | TC (€) | CPU (s) | TC (€) | CPU (s) | SM | IRPPDS | DM | SM | IRPPDS | |
| 15R15S15C90V5T | 1,055,305 | 330 | 979,362 | 274 | 806,191 | 217 | 7 | 24 | 1,217,822 | 527 | 1,074,615 | 318 | 902,934 | 276 | 12 | 26 | 13 | 9 | 11 |
| 15R20S15C120V5T | 2,698,516 | 824 | 2,407,032 | 475 | 1,827,526 | 254 | 11 | 32 | 3,192,344 | 1207 | 2,919,561 | 550 | 2,077,897 | 316 | 9 | 35 | 15 | 18 | 12 |
| 15R30S15C190V5T | 5,826,310 | 44 | 5,075,948 | 1070 | 3,877,637 | 980 | 13 | 33 | 6,659,472 | 70 | 5,079,089 | 1203 | 4,552,346 | 1259 | 24 | 32 | 13 | 0 | 15 |
| 15R40S15C250V5T | 13,140,456 | 181 | 12,054,126 | 335 | 7,920,967 | 391 | 8 | 40 | 15,715,985 | 300 | 14,922,266 | 372 | 9,006,139 | 473 | 5 | 43 | 16 | 19 | 12 |
| 15R50S15C350V5T | 27,632,333 | 513 | 19,565,564 | 395 | 17,761,072 | 329 | 29 | 36 | 31,031,110 | 829 | 27,865,271 | 463 | 20,673,888 | 410 | 10 | 33 | 11 | 30 | 14 |
| 15R60S15C450V5T | 64,334,836 | 135 | 58,442,222 | 165 | 42,490,648 | 256 | 9 | 34 | 72,248,021 | 227 | 71,156,121 | 197 | 49,884,021 | 329 | 2 | 31 | 11 | 18 | 15 |
| 15R70S15C550V5T | 143,862,932 | 97 | 134,278,723 | 156 | 80,904,270 | 156 | 7 | 44 | 172,347,793 | 151 | 134,553,700 | 169 | 97,004,220 | 198 | 22 | 44 | 17 | 0 | 17 |
| 15R80S15C650V5T | 301,974,530 | 717 | 268,660,125 | 922 | 200,455,201 | 1145 | 11 | 34 | 339,721,346 | 1155 | 286,184,629 | 1146 | 225,311,646 | 1454 | 16 | 34 | 11 | 6 | 11 |
| 15R100S15C750V5T | 641,210,086 | 398 | 606,987,781 | 443 | 429,635,068 | 414 | 5 | 33 | 721,361,347 | 615 | 612,861,772 | 471 | 514,273,176 | 536 | 15 | 29 | 11 | 1 | 16 |
| 15R200S15C2000V5T | 1,291,975,415 | 106 | 832,110,939 | 694 | 663,928,176 | 751 | 36 | 49 | 1,536,158,768 | 165 | 1,135,671,285 | 852 | 794,722,027 | 927 | 26 | 48 | 16 | 27 | 16 |
| 15R300S15C4000V5T | 2,721,138,343 | 728 | 2,256,821,880 | 803 | 2,082,860,769 | 665 | 17 | 23 | 3,091,213,158 | 1146 | 2,503,447,969 | 870 | 2,447,361,404 | 827 | 19 | 21 | 12 | 10 | 15 |
| 15R400S15C6000V5T | 5,791,824,472 | 268 | 4,014,243,737 | 268 | 3,126,883,840 | 237 | 31 | 46 | 6,718,516,388 | 409 | 4,960,776,575 | 289 | 3,592,789,532 | 292 | 26 | 47 | 14 | 19 | 13 |
| 15R600S15C8000V5T | 11,431,199,715 | 384 | 8,504,611,093 | 357 | 7,582,649,005 | 178 | 26 | 34 | 13,603,127,661 | 624 | 9,546,143,904 | 391 | 8,507,732,184 | 217 | 30 | 37 | 16 | 11 | 11 |
| 31R20S34C400V5T | 4,428,883 | 740 | 3,736,512 | 845 | 3,445,812 | 971 | 16 | 22 | 5,053,356 | 1105 | 4,036,051 | 954 | 3,979,913 | 1182 | 20 | 21 | 12 | 7 | 13 |
| 31R40S34C900V5T | 10,976,187 | 301 | 7,719,378 | 569 | 7,089,787 | 839 | 30 | 35 | 13,028,734 | 475 | 9,160,248 | 690 | 8,507,744 | 1033 | 30 | 35 | 16 | 16 | 17 |
| 31R60S34C1300V5T | 23,233,219 | 917 | 16,916,596 | 395 | 14,939,103 | 312 | 27 | 36 | 27,368,732 | 1388 | 25,748,719 | 424 | 16,731,795 | 392 | 6 | 39 | 15 | 34 | 11 |
| 31R80S34C2500V5T | 53,970,019 | 595 | 43,722,965 | 622 | 28,413,814 | 603 | 19 | 47 | 62,605,222 | 890 | 57,142,014 | 714 | 31,993,955 | 745 | 9 | 49 | 14 | 23 | 11 |
| 31R110S34C4000V5T | 120,114,263 | 331 | 97,779,299 | 724 | 65,665,251 | 938 | 19 | 45 | 138,972,202 | 492 | 103,217,419 | 858 | 77,288,000 | 1188 | 26 | 44 | 14 | 5 | 15 |
| 31R130S34C5200V5T | 265,313,611 | 515 | 251,439,010 | 284 | 210,348,468 | 214 | 5 | 21 | 315,457,883 | 796 | 299,527,277 | 346 | 243,583,526 | 277 | 5 | 23 | 16 | 16 | 14 |
| 31R150S34C6000V5T | 572,377,195 | 294 | 506,511,145 | 531 | 410,627,455 | 495 | 12 | 28 | 681,701,239 | 456 | 569,930,183 | 608 | 473,453,456 | 614 | 16 | 31 | 16 | 11 | 13 |
| 31R200S34C9000V5T | 1,227,011,538 | 942 | 1,134,046,280 | 346 | 959,955,051 | 172 | 8 | 22 | 1,425,787,407 | 1481 | 1,312,205,027 | 385 | 1,136,586,780 | 221 | 8 | 20 | 14 | 14 | 16 |
| 31R300S34C14000V5T | 2,529,324,214 | 561 | 2,398,032,183 | 563 | 1,745,537,723 | 435 | 5 | 31 | 3,030,130,408 | 869 | 2,645,201,253 | 697 | 2,049,261,287 | 556 | 13 | 32 | 17 | 9 | 15 |
| 31R400S3418000V5T | 5,169,582,108 | 319 | 4,520,814,515 | 483 | 3,311,432,130 | 511 | 13 | 36 | 5,789,931,961 | 516 | 5,245,182,129 | 556 | 3,751,852,603 | 640 | 9 | 35 | 11 | 14 | 12 |
| 31R500S34C20000V5T | 11,050,906,466 | 244 | 8,845,362,928 | 547 | 6,925,392,214 | 728 | 20 | 37 | 13,006,916,910 | 376 | 12,963,475,117 | 614 | 7,964,201,046 | 925 | 0 | 39 | 15 | 32 | 13 |
| 31R600S34C24500V5T | 23,471,937,843 | 1027 | 18,265,998,726 | 1128 | 14,568,743,068 | 1110 | 22 | 38 | 26,734,537,203 | 1598 | 23,081,746,819 | 1420 | 17,278,529,279 | 1412 | 14 | 35 | 12 | 21 | 16 |
| 31R700S34C29000V5T | 49,800,010,407 | 933 | 32,665,152,291 | 1090 | 26,308,338,166 | 1160 | 34 | 47 | 57,270,011,968 | 1439 | 56,207,283,103 | 1185 | 31,096,455,712 | 1430 | 2 | 46 | 13 | 42 | 15 |
| Average | 4,489,886,892 | 479 | 3,287,441,168 | 557 | 2,646,228,016 | 556 | 17 | 35 | 5,185,154,402 | 743 | 4,685,635,081 | 644 | 3,092,258,327 | 697 | 14 | 35 | 14 | 16 | 14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Achamrah, F.E.; Riane, F.; Sahin, E.; Limbourg, S. An Artificial-Immune-System-Based Algorithm Enhanced with Deep Reinforcement Learning for Solving Returnable Transport Item Problems. Sustainability 2022, 14, 5805. https://doi.org/10.3390/su14105805
Achamrah FE, Riane F, Sahin E, Limbourg S. An Artificial-Immune-System-Based Algorithm Enhanced with Deep Reinforcement Learning for Solving Returnable Transport Item Problems. Sustainability. 2022; 14(10):5805. https://doi.org/10.3390/su14105805
Chicago/Turabian StyleAchamrah, Fatima Ezzahra, Fouad Riane, Evren Sahin, and Sabine Limbourg. 2022. "An Artificial-Immune-System-Based Algorithm Enhanced with Deep Reinforcement Learning for Solving Returnable Transport Item Problems" Sustainability 14, no. 10: 5805. https://doi.org/10.3390/su14105805
APA StyleAchamrah, F. E., Riane, F., Sahin, E., & Limbourg, S. (2022). An Artificial-Immune-System-Based Algorithm Enhanced with Deep Reinforcement Learning for Solving Returnable Transport Item Problems. Sustainability, 14(10), 5805. https://doi.org/10.3390/su14105805







