A Novel Model Based on DA-RNN Network and Skip Gated Recurrent Neural Network for Periodic Time Series Forecasting

Abstract

Deep learning models are playing an increasingly important role in time series forecasting with their excellent predictive ability and the convenience of not requiring complex feature engineering. However, the existing deep learning models still have shortcomings in dealing with periodic and long-distance dependent sequences, which lead to unsatisfactory forecasting performance on this type of dataset. To handle these two issues better, this paper proposes a novel periodic time series forecasting model based on DA-RNN, called DA-SKIP. Using the idea of task decomposition, the novel model, based on DA-RNN, GRU-SKIP and autoregressive component, breaks down the prediction of periodic time series into three parts: linear forecasting, nonlinear forecasting and periodic forecasting. The results of the experiments on Solar Energy, Electricity Consumption and Air Quality datasets show that the proposed model outperforms the three comparison models in capturing periodicity and long-distance dependence features of sequences.

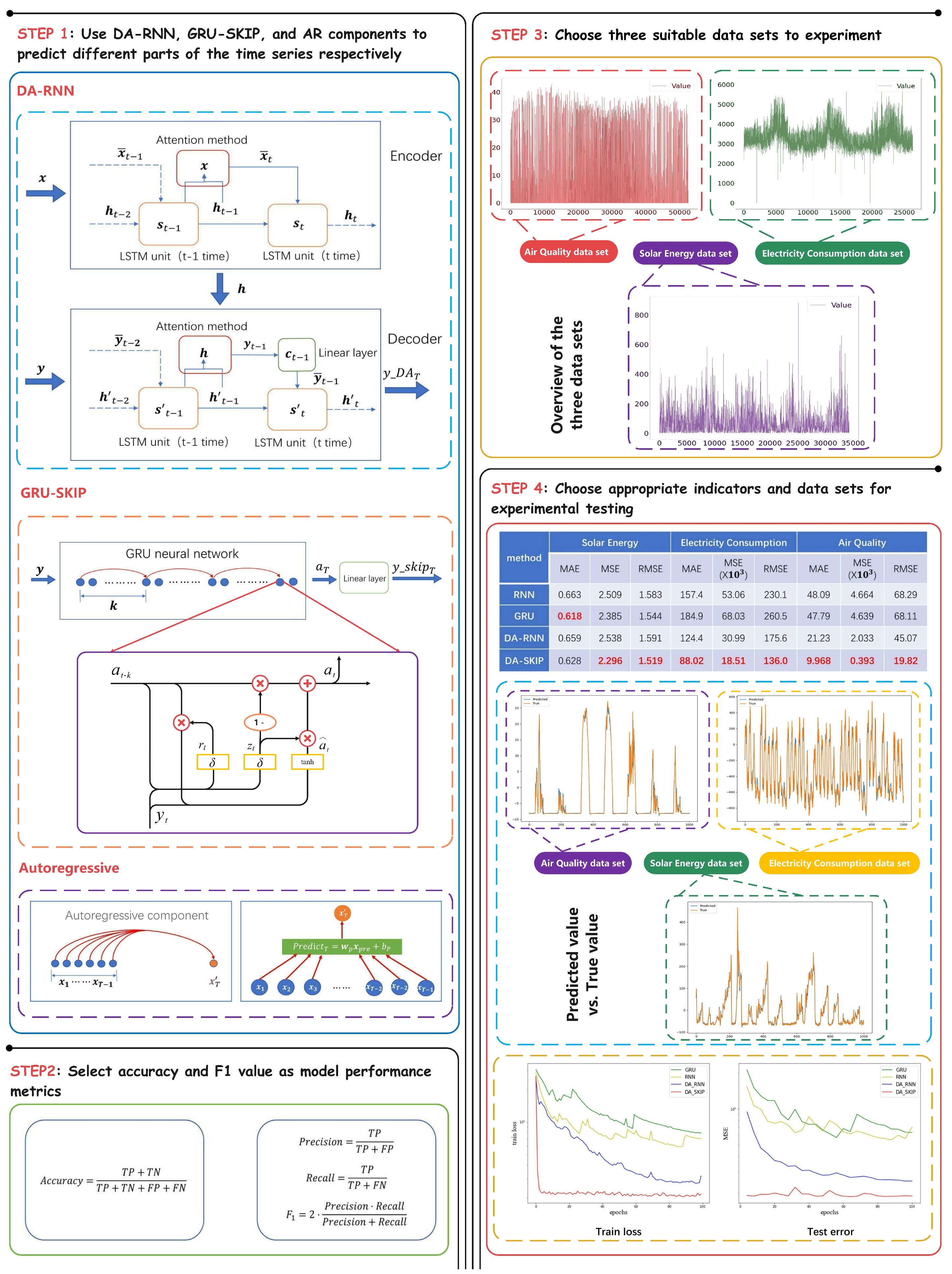
1. Introduction

Time series forecasting can be summarized as a process of extracting useful information from historical records and then forecasting the future value [1]. It has shown great application value in stock trend forecasting [2], traffic flow forecasting [3], power generation [4], electricity consumption forecasting [5], tourism passenger flow forecasting [6], weather forecasting [7] and other fields. Among the problems in time series forecasting, the biggest problem faced by existing models is capturing the long-distance dependence in sequences. From autoregressive models [8] to recurrent neural networks [9], researchers have been trying to improve the model’s prediction performance of long-distance dependent sequences. Furthermore, the periodicity of time series is also an important factor that is worth considering. Traditional time series forecasting models often are not able to achieve the best results on periodic time series datasets [10]. If the periodicity of time series is taken into consideration in optimizing the model, the applicability of the model can be improved such that it can achieve better performance on this type of dataset.

The research methods of time series forecasting have been continuously improving and innovating since the 1970s. Time series forecasting models can be roughly divided into three categories. The first category is time series forecasting methods based on statistical models, such as the Markov model [11] and the autoregressive moving average model (ARIMA) [12]; the second category is time series forecasting methods based on machine learning, such as many methods based on Bayesian network or support vector machine method [13,14]; the third category is time prediction method based on deep learning, such as artificial neural network (ANN) [15], Long Short-Term Memory (LSTM) [16] and Gate Recurrent Unit (GRU) [17], etc.

With the breakthrough in the research of deep learning, deep learning has been playing an increasingly important role in time series forecasting in recent years. In particular, the application of LSTM and GRU has made outstanding contributions to solving the long-distance dependence problem in time series forecasting. Since their introduction, these two methods have achieved great success in time series forecasting [18], time series classification [19], natural language processing [20], machine translation [21], speech recognition [22] and other fields. In recent years, the encoder/decoder network [23] and the attention-based encoder/decoder network [24] have further improved the computational efficiency and prediction accuracy of time series prediction models.

The R2N2 model introduced by Hardik Goel et al. in 2017 [25] decomposes the time series forecasting task into a linear forecasting part and a non-linear forecasting part. The linear forecasting part uses an autoregressive component, and the non-linear part uses an LSTM network for prediction. In 2017, the LSTNet model designed by Guokun Lai et al. [26] embodied the idea of specialized processing for periodic time series data. The model divides the periodic time series forecasting task into a linear forecasting part, a non-linear forecasting part and a periodic forecasting part. The linear forecasting part is composed of an autoregressive model, the non-linear forecasting part is composed of a LSTM network, and the periodic forecasting part is composed of a GRU network. The TPA-LSTM model proposed by Shun-Yao Shih et al. in 2018 [27] introduced the attention mechanism into time series prediction and proposed an attention mechanism in the direction of multivariate. Compared to previous attention models in the dimension of time step, this model has achieved better results on some datasets.

In 2017, based on LSTM and attention mechanism, Yao Qin et al. proposed the DA-RNN network [28]. DA-RNN is a kind of the non-linear autoregressive exogenous (NARX) model [29,30] which means that the data processed by the model has exogenous variables and contains nonlinear relationships inside. This type of model can predict the current value of a time series based on the previous value of the target series and the driving (exogenous) series. Making full use of the information contained in the target series and driving series is the advantage of this type of model [31]. On this basis, the DA-RNN model focuses on processing multivariate series and resolving long-distance dependence problems.

The DA-RNN model comprises two components: encoder and decoder. It is a novel two-stage recurrent neural network based on attention mechanism. In the encoder, the model introduces a new input attention mechanism, which makes it adaptively focus on related driving series and weight them. In the decoder, the model introduces a temporal attention mechanism to adaptively focus on the output of the encoder across all time steps. With the help of this design, the DA-RNN model achieved excellent performance in the test of several multivariate datasets. However, when dealing with periodicity and autocorrelation sequences, DA-RNN is difficult to achieve the best results.

To solve the long-distance dependence problem and sequence periodicity problem in time series forecasting better, this paper introduces the periodic gated recurrent network component (GRU-SKIP) and autoregressive component into the DA-RNN model to construct a new model called DA-SKIP that is more suitable for periodic time series datasets.

The DA-SKIP model combines the multivariate sequence processing and long-distance dependency processing capabilities of the DA-RNN model and the periodic data processing capabilities brought by the GRU-SKIP component. In the processing of periodic datasets, the non-linear law of the data can be captured nicely by the DA-RNN component, the periodic law of the data can be captured by the GRU-SKIP component, and the linear law of the data can be captured by the autoregressive component. The final test shows that on the periodic dataset, the DA-SKIP model performs significantly better than the RNN model, GRU model and DA-RNN model.

The innovations of this paper are as follows:

(1)

The proposed model breaks down the prediction problems of periodic time series into three parts: linear forecasting, nonlinear forecasting and periodic forecasting, and uses three different model components to complete each prediction subtask.

(2)

The characteristics of the DA-RNN components are used in the model to effectively solve the long-distance dependence problem in time series forecasting.

(3)

The characteristics of the DA-SKIP components are used in the model to effectively solve the cyclical problem in time series forecasting.

(4)

The characteristics of autoregressive components are used in the model to effectively solve the linear correlation problem in time series forecasting.

This paper is organized as follows. First, Section 2 introduces the structure of each component of the model. Next, Section 3 presents the datasets, comparison models and evaluation metrics used in the experiment. Then, Section 4 discusses some scientific problems that appeared in the experiment. Finally, Section 5 summarizes the findings and discusses the future research direction. The main content of the paper is shown in Figure 1.

2. Materials and Methods

Generally, the forecasting task of periodic time series data can be divided into three parts: the prediction of non-linear, linear and periodic laws. Three components of our proposed model correspond to these three parts: the DA-RNN encoder/decoder component is used to predict non-linear law, autoregressive component is used to predict linear law, and GRU-SKIP components is used to predict periodic law.

2.1. Model Task

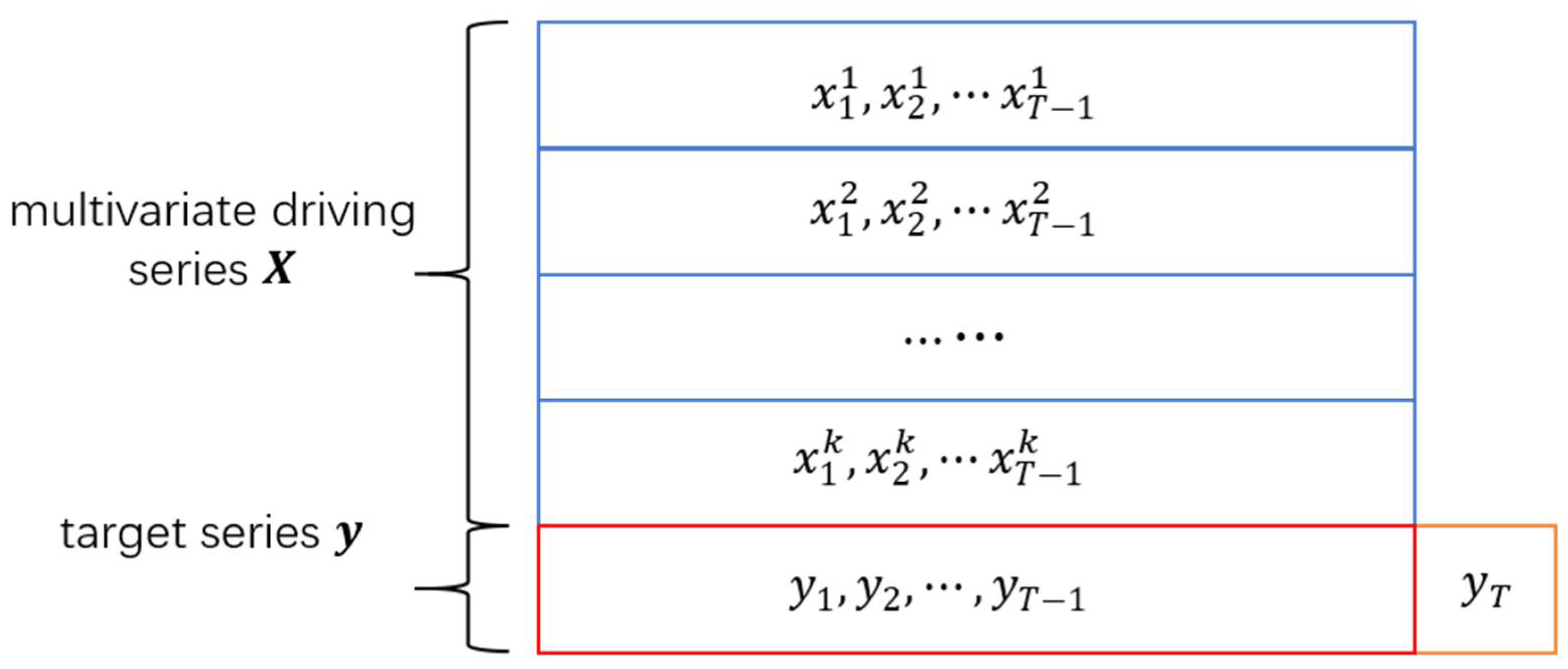
The overall prediction task of the model is to use a multivariate driving series $\mathit{X}=\{{\mathit{x}}_1,{\mathit{x}}_2,\cdots ,{\mathit{x}}_{T-1}\}$ and a target series $\mathit{y}=\{y_1,y_2,\cdots ,y_{T-1}\}$, to predict the target value $y_T$ at time T. Where ${\mathit{x}}_t=\left\{x_t^1,x_t^2,\cdots x_t^n\right\}$ ($1\le t\le T-1$) and ${\mathit{x}}_t\in {ℝ}^n$, n is the number of variables in the input sequence, and T is the length of the input multivariate driving series and target series.

Taking the forecast of people flow in a scenic spot as an example, the multivariate driving series refers to the sequence data related to the people flow, such as the climate, temperature and air quality of the scenic spot. The target series refers to the historical data of the flow of people in the scenic spot. As shown in Figure 2, the task can be summarized as extracting information from k driving series and a target series, using data from time 1 to time T − 1 to predict the flow of people $y_T$ at the scenic spot at time T.

2.2. Encoder Component

The overall structure of the model encoder and decoder component is shown in Figure 3. Among them, the encoder component of the model is broadly the same as the encoder component in DA-RNN. With the support of attention mechanism, the encoder can realize the function of weighting the input multivariate driving series, thereby capturing the correlation between different variables in the multivariate series.

The input series of the encoder is the multivariate drive series $\mathit{X}=\{{\mathit{x}}_1,{\mathit{x}}_2,\cdots ,{\mathit{x}}_{T-1}\}$, where ${\mathit{x}}_t\in {ℝ}^n$ ($1\le t\le T-1$), n is the number of variables in the input sequence. In the encoder, the model uses an LSTM network to map the driving series ${\mathit{x}}_t$ at time t to the hidden state ${\mathit{h}}_t$:

$${\mathit{h}}_t=f_1\left({\mathit{h}}_{t-1},{\mathit{x}}_t\right)$$

(1)

$f_1$ is an LSTM unit, whose input is the hidden state at time t − 1 and the driving series ${\mathit{x}}_t$ at time t and outputs the hidden state at time t ($1\le t\le T-1$) as calculation result. The advantage of LSTM is that it does well in capturing long-distance dependency. Every time step of LSTM has a cell state ${\mathit{s}}_t$, and each ${\mathit{s}}_t$ is controlled by three sigmoid gating components. The three gates are respectively the forget gate ${\mathit{f}}_{\mathit{t}}$, the update gate ${\mathit{u}}_{\mathit{t}}$ and the output gate ${\mathit{o}}_{\mathit{t}}$. The specific calculation formula is as follows:

$${\mathit{s}}_t={\mathit{f}}_{\mathit{t}}\odot {\mathit{s}}_{t-1}+{\mathit{u}}_{\mathit{t}}\odot tanh\left({\mathit{W}}_s\left[{\mathit{h}}_{t-1};{\mathit{x}}_t\right]+{\mathit{b}}_s\right)$$

(2)

$$\mathrm{where}{\mathit{f}}_{\mathit{t}}=\delta \left({\mathit{W}}_f\left[{\mathit{h}}_{t-1};{\mathit{x}}_t\right]+{\mathit{b}}_f\right)$$

(3)

$${\mathit{u}}_{\mathit{t}}=\delta ({\mathit{W}}_u\left[{\mathit{h}}_{t-1};{\mathit{x}}_t\right]+{\mathit{b}}_u)$$

(4)

$${\mathit{o}}_{\mathit{t}}=\delta \left({\mathit{W}}_o\left[{\mathit{h}}_{t-1};{\mathit{x}}_t\right]+{\mathit{b}}_o\right)$$

(5)

$${\mathit{h}}_t={\mathit{o}}_t\odot tan\mathit{h}\left({\mathit{s}}_t\right)$$

(6)

where $\left[{\mathit{h}}_{t-1}:{\mathit{x}}_t\right]$ is the matrix formed by concatenating the hidden state ${\mathit{h}}_{t-1}$ at the previous moment and the input ${\mathit{x}}_t$ at the current moment. ${\mathit{W}}_u$, ${\mathit{W}}_f$, ${\mathit{W}}_o$, ${\mathit{W}}_s$ are the weight matrices that need to be learned and ${\mathit{b}}_u$, ${\mathit{b}}_f$, ${\mathit{b}}_o$, ${\mathit{b}}_s$ are the bias terms that need to be learned. $\delta$ and $\odot$ are the sigmoid function symbol and the dot product symbol, respectively. LSTM here makes the model less prone to the problem of gradient disappearance and brings strong capability to capture long-distance dependency to the model.

After inputting the sequence into the LSTM network, the hidden state ${\mathit{h}}_t$ and the cell state ${\mathit{s}}_t$ in the LSTM network at time t can be calculated. For each variable ${\mathit{X}}^{\mathit{k}}=\left\{x_1^k,x_2^k,\cdots x_{T-1}^k\right\}$ in the multivariate driving series, the model uses an attention component to associate it with the matrix $\left[{\mathit{h}}_{t-1};{\mathit{s}}_{t-1}\right]$ at the previous moment, that is, at time t − 1, and capture the connection between them:

$$e_t^k={\mathit{V}}_e^{\top }tanh\left({\mathit{W}}_e\left[{\mathit{h}}_{t-1};{\mathit{s}}_{t-1}\right]+{\mathit{U}}_e{\mathit{x}}^k\right)$$

(7)

$${\alpha }_t^k=\frac{exp\left(e_t^k\right)}{{{\displaystyle \sum }}_{i=1}^{n}exp\left(e_t^i\right)}$$

(8)

where ${\mathit{V}}_e$, ${\mathit{W}}_e$ and ${\mathit{U}}_e$ are the parameters needed to be learned. The model uses the attention mechanism in Formulas (7) and (8) to capture the association among the hidden state, the cell state and each variable, and the weight ${\alpha }_t^k$ of each variable at time t can be calculated using the softmax formula. Then, with these attention weights provided, the driving series at time t can be weighted: ${\overline{\mathit{x}}}_t={\left({\alpha }_t^1{x}_t^1,{\alpha }_t^2{x}_t^2,\cdots ,{\alpha }_t^n{x}_t^n\right)}^{\top }$. These weights make the model focus on some crucial sequences and selectively ignore less important sequences. This mechanism helps the model to make better use of multivariate data.

The model weights the driving series ${\mathit{x}}_t$ at time t through the hidden state ${\mathit{h}}_{t-1}$ and cell state ${\mathit{s}}_{t-1}$ at time t − 1, and then replace the initial ${\mathit{x}}_t$ with the weighted sequence ${\overline{\mathit{x}}}_t$ in the calculation of the hidden state ${\mathit{h}}_t$ at time t. At this time, Formula (1) should be amended to:

$${\mathit{h}}_t=f_1\left({\mathit{h}}_{t-1},{\overline{\mathit{x}}}_t\right)$$

(9)

where $f_1$ is an LSTM unit, and ${\overline{\mathit{x}}}_t$ is a weighted multivariate sequence. The model map ${\overline{\mathit{x}}}_t$ to the hidden state ${\mathit{h}}_t$ via LSTM, and finally connect the ${\mathit{h}}_t$ at each moment as $\mathit{h}=\{{\mathit{h}}_1,{\mathit{h}}_2,\cdots ,{\mathit{h}}_T\}$ as the output of the encoder and input it to the decoder.

2.3. Decoder Component

The input of the decoder is divided into two parts. The first part is the hidden state of the encoder at each moment $\mathit{h}=\{{\mathit{h}}_1,{\mathit{h}}_2,\cdots ,{\mathit{h}}_T\}$, and the second part is the target series $\mathit{y}=\{y_1,y_2,\cdots ,y_{T-1}\}$. In the decoder, the model firstly uses a LSTM network to decode the input sequence. The LSTM network takes the target series $\mathit{y}$ as input, and the hidden state and cell state at time t are represented by ${\mathit{d}}_t$ and ${\mathit{s}}_t^{\prime }$ ($1\le t\le T-1$), respectively.

To solve the long-distance dependence problem, a time attention mechanism is applied in the decoder to make the model adaptively focus on the important time steps in the hidden state time series. Specifically, the model connects the hidden state ${\mathit{h}}_{t-1}^{\prime }$ of the LSTM network in the decoder at t − 1 with the cell state ${\mathit{s}}_{t-1}^{\prime }$ at the same moment to form the matrix $[{\mathit{h}}_{t-1}^{\prime };{\mathit{s}}_{t-1}^{\prime }$]. Then, a temporal attention mechanism is used to capture the correlation between the $[{\mathit{h}}_{t-1}^{\prime };{\mathit{s}}_{t-1}^{\prime }$] matrix and the hidden state of the encoder at each moment. The attention weight of each hidden state in the encoder can be calculated at this time:

$$l_t^i={\mathit{V}}_h^{\top }tanh\left({\mathit{W}}_{\mathit{h}}\left[{\mathit{h}}_{t-1}^{\prime };s_{t-1}^{\prime }\right]+{\mathit{U}}_h{\mathit{h}}_i\right)$$

(10)

$${\beta }_t^i=\frac{exp\left(l_t^i\right)}{{{\displaystyle \sum }}_{j=1}^{T}exp\left(l_t^j\right)}$$

(11)

where ${\mathit{W}}_h,{\mathit{V}}_h,{\mathit{U}}_h$ are the parameters that need to be learned. ${\mathit{h}}_i$ represents the i-th hidden state in the encoder, and ${\beta }_t^i$ represents the weight of ${\mathit{h}}_i$. By calculating the weight of each moment, the hidden state from the encoder can be weighted at each moment:

$${\mathit{c}}_t={\displaystyle \sum }_{i=1}^T{\beta }_t^i{\mathit{h}}_i$$

(12)

${\mathit{c}}_t$ is called context vector, which is obtained by weighting all hidden state $\mathit{h}=\{{\mathit{h}}_1,{\mathit{h}}_2,\cdots ,{\mathit{h}}_T\}$ in encoder. Then, the model combines the context vector ${\mathit{c}}_t$ with the given target series $\mathit{y}=\{y_1,y_2,\cdots ,y_{t-1}\}$:

$${\overline{y}}_{t-1}={\overline{\mathit{w}}}^{\top }\left[y_{t-1};{\mathit{c}}_{t-1}\right]+\overline{b}$$

(13)

where $\left[y_{t-1};{\mathit{c}}_{t-1}\right]$ is the concatenation of the target value $y_{t-1}$ and the context vector ${\mathit{c}}_{t-1}$ at time t − 1. $\overline{\mathit{w}}$ and $\overline{b}$ are the parameters need to be learned, their role is to reduce the dimensionality of the concatenation vector to a constant. The calculated new target value ${\overline{y}}_{t-1}$ is used to replace the input $y_{t-1}$ of the decoder LSTM at time t. The modified decoder LSTM operation formula is:

$${\mathit{s}}_t^{\prime }={\mathit{f}}_t^{\prime }\odot {\mathit{s}}_{t-1}^{\prime }+{\mathit{u}}_t^{\prime }\odot tanh\left({\mathit{W}}_s^{\prime }\left[{\mathit{h}}_{t-1}^{\prime };{\overline{y}}_{t-1}\right]+{\mathit{b}}_s^{\prime }\right)$$

(14)

$$\mathrm{where}{\mathit{f}}_t^{\prime }=\delta \left({\mathit{W}}_f^{\prime }\left[{\mathit{h}}_{t-1}^{\prime };{\overline{y}}_{t-1}\right]+{\mathit{b}}_f^{\prime }\right)$$

(15)

$${\mathit{u}}_t^{\prime }=\delta ({\mathit{W}}_u^{\prime }\left[{\mathit{h}}_{t-1}^{\prime };{\overline{y}}_{t-1}\right]+{\mathit{b}}_u^{\prime })$$

(16)

$${\mathit{o}}_t^{\prime }=\delta \left({\mathit{W}}_o^{\prime }\left[{\mathit{h}}_{t-1}^{\prime };{\overline{y}}_{t-1}\right]+{\mathit{b}}_o^{\prime }\right)$$

(17)

$${\mathit{h}}_t^{\prime }={\mathit{o}}_t^{\prime }\odot tanh\left({\mathit{s}}_t^{\prime }\right)$$

(18)

where $\left[{\mathit{h}}_{t-1}^{\prime };{\overline{y}}_{t-1}\right]$ is the connection of hidden state ${\mathit{h}}_{t-1}^{\prime }$ and the corrected input ${\overline{y}}_{t-1}$ at t − 1. ${\mathit{W}}_u^{\prime },{\mathit{W}}_f^{\prime },{\mathit{W}}_s^{\prime },{\mathit{W}}_o^{\prime }$ and ${\mathit{b}}_u^{\prime },{\mathit{b}}_f^{\prime },{\mathit{b}}_s^{\prime },{\mathit{b}}_o^{\prime }$ are the parameters that need to be learned. $\delta$ and $\odot$ are respectively the sigmoid function and the dot multiplication operation. The final prediction result can be expressed as:

$$y\_D{A}_T={\mathit{V}}_y^{\top }\left({\mathit{W}}_y\left[{\mathit{h}}_T^{\prime };{\mathit{c}}_T\right]+{\mathit{b}}_w\right)+b_v$$

(19)

where $\left[{\mathit{h}}_T^{\prime };{\mathit{c}}_T\right]$ is the concatenation of the hidden state ${\mathit{h}}_T^{\prime }$ of the decoder at time t and the context vector. The parameters ${\mathit{W}}_y$ and ${\mathit{b}}_w$ adjust the size of concatenation matrix to be the same as the size of hidden state in the decoder. Then, the calculation result is sent into the linear layer whose weight matrix is ${\mathit{v}}_y$ and bias is $b_v$ to generate the decoder’s final prediction value $y\_D{A}_T$.

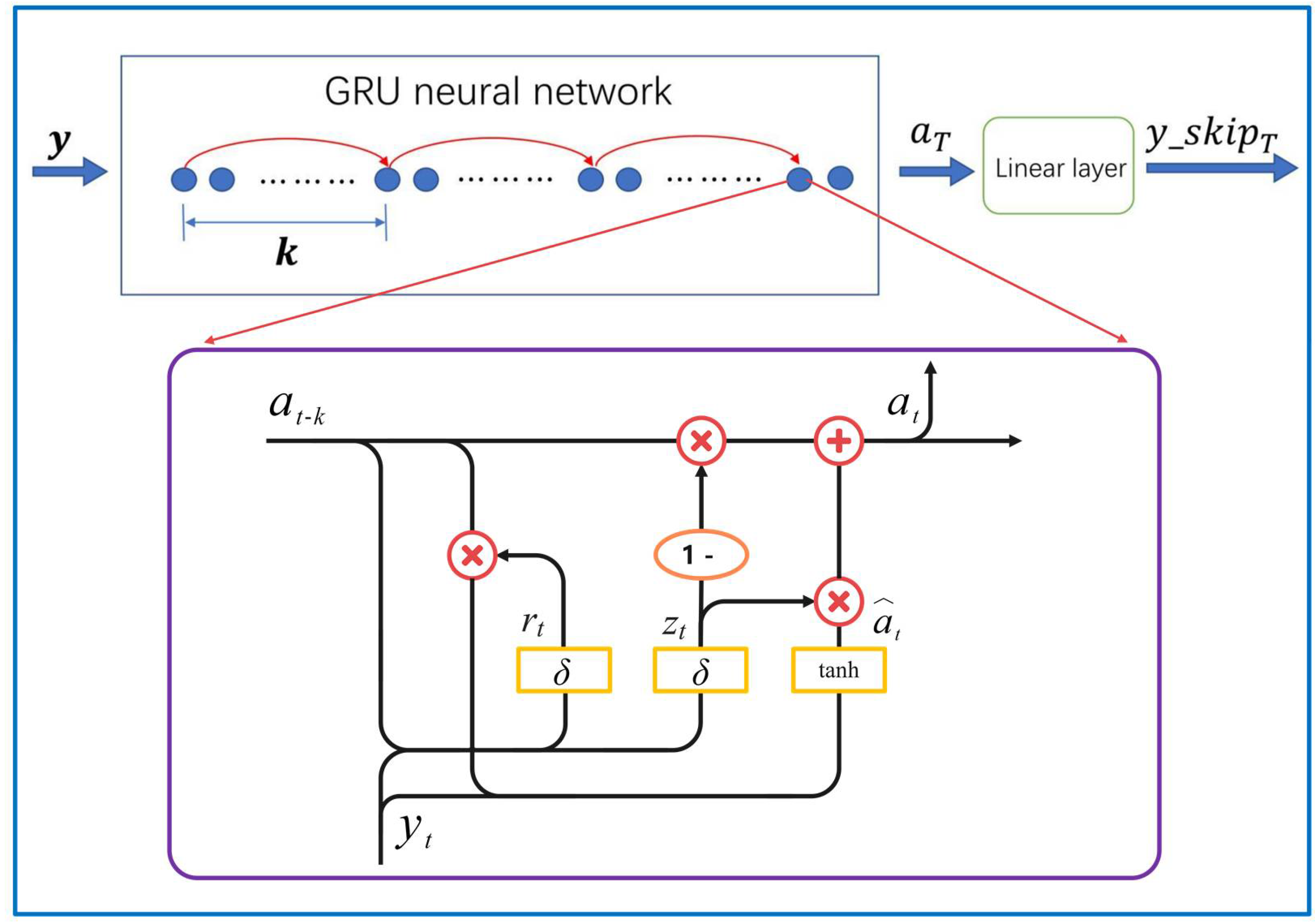
2.4. GRU-SKIP Component

The role of the GRU-SKIP component in the model is to capture the periodicity of the series such that the model performs better in periodic time series datasets. The overall structure of GRU-SKIP components is shown in Figure 4. The model takes the period length k of the sequence as the length of time step and extract the jumping sequence $\mathit{p}=\{y_{T-k\times m},y_{T-k\times \left(m-1\right)},\cdots ,y_{T-k}\}$ ($k\times m\le T$) of length m in the target series $\mathit{y}=\{y_1,y_2,\cdots ,y_{T-1}\}$. For the jumping sequence $\mathit{p}$, the model uses the GRU network to extract its periodic trend.

Similar to the LSTM, the data at each time step in the GRU network is also input into a gated recurrent unit, and each unit is controlled by two gates: update gate $z_t$ and reset gate $r_t$. The detailed calculation formula is as follows:

$${\widehat{a}}_t=tanh(W_a\left[r_t\odot a_{t-k};y_t\right]+b_a)$$

(20)

$$\mathrm{where}{z}_t=\delta (W_z\left[a_{t-k};y_t\right]+b_z)$$

(21)

$$r_t=\delta \left(W_r\left[a_{t-k};y_t\right]+b_r\right)$$

(22)

$$a_t=z_t\odot {\widehat{a}}_t+\left(1-u_t\right)\odot a_{t-k}$$

(23)

where $\delta$ and $\odot$ are respectively the sigmoid function and dot multiplication operation. k is the period length of the time series. $\left[a_{t-k};y_t\right]$ ($1\le t\le T-1$) is the concatenation of the hidden state $a_{t-k}$ at time t − k and the input $y_t$ at time t. $W_a,W_z,W_r$ and $b_a,b_z,b_r$ are all parameters that need to be learned.

The width of the hidden state at time t is equal to the hidden layer width $h_a$ of the GRU_SKIP component. The model inputs the hidden state $a_T$ at time T into a linear layer and reduce its width to 1, and then the periodic prediction value $y\_ski{p}_T$ at time T can be calculated:

$$y\_ski{p}_T=W_j{a}_T+b_j$$

(24)

where $W_j$ and $b_j$ are the weight matrix and bias term in the linear layer, respectively.

In addition to the core part of the GRU-SKIP component, an autoregressive component can be optionally added for predicting the linear part of the data. The autoregressive model can predict the sequence value at a specific time in the future based on the sequence information in the previous period. However, this prediction is limited to the case where there is autocorrelation in the sequence. Thus, autoregressive components are often used to extract linear relationships in the autocorrelation sequence.

The purpose of adding autoregressive components to the model is to enhance the prediction effect of autocorrelation sequences. The operation of the autoregressive component can be regarded as a hyperparameter, which can be selectively added during the tuning process according to the specific performance of the model. If an autoregressive component is added, the output of the GRU-SKIP component should be replaced with:

$$y\_ski{p}_T=W_j{a}_T+b_j+W_i\mathit{y}+b_i$$

(25)

The autoregressive component is implemented by a linear layer, where $W_i$ is the weight matrix, $b_i$ is the bias term, and $\mathit{y}$ is the target series. The prediction target $y\_pre{d}_T$ at time T can be divided into three parts: periodic part, linear-part and non-linear part. The output of the decoder $y\_D{A}_T$ is the forecast of the non-linear part, and the output of the GRU-SKIP component $y\_ski{p}_T$ is the forecast of the periodic part and the linear part. So, the final prediction value $y\_pre{d}_T$ is the sum of $y\_D{A}_T$ and $y\_pre{d}_T$:

$$y\_pre{d}_T=y\_D{A}_T+y\_ski{p}_T$$

(26)

$y\_pre{d}_T$ is the final output of the DA-SKIP model. The overall architecture of DA-skip is shown in Figure 5.

3. Experiments

To test the actual performance of DA-SKIP, it was tested on three datasets and compared with the RNN model, the GRU model and the DA-RNN model. In the test, hyperparameter grid search method was used to adjust each model’s hyperparameter, and then the model ran five times under the optimal parameter combination. Finally, the average value of each evaluation metric in these five tests was taken as the test result of the model. Equipment used in experiment can be find in Appendix A.

3.1. Datasets

Three datasets of Solar Energy, Electricity consumption and Air Quality were used in this experiment. The Solar Energy dataset recorded the power generation of 137 photovoltaic power stations in Alabama, the USA in 2006. Data in this dataset was collected every 15 min [32]. In the experiment, the first 136 rows of data were set as driving series input, and the last row of data was set as target series input. The Electricity consumption dataset recorded the electricity consumption of 321 corporate users in the United States from 2011 to 2014. Data in this dataset was collected every 10 min [33]. In the experiment, the first 320 rows of data were set as driving series input, and the last row of data was set as target series input. The Air Quality dataset recorded 18 indicators of Beijing’s air quality from 2013 to 2017. Data in this dataset was collected every hour [34]. In the experiment, the first indicator was set as target series input, and the other data were set as driving series input. In all three datasets, the first 70% of the data was set as the training set and the last 30% of the data was set as the test set. An overview of the three experimental datasets is shown in

Table 1. Overview of 3 experimental datasets.

Dataset	Driving Series	Train Size	Test Size
Solar Energy	136	32,473	15,768
Electricity Consumption	320	15,533	7892
Air Quality	17	23,284	10,287

.

The training is conducted as the following process: first, the best hyperparameter combination in the test is determined by hyperparameter gradient search. After that, the test is repeated five times under this hyperparameter, and the average of the five test results is used as the final test result.

In all experiments on three datasets, DA-SKIP is trained for 100 rounds, during which the learning rate drops by 10% every 10 rounds of training, while the initial value of learning rate is different: for the Solar Energy dataset its 0.0004, for the Electricity Consumption dataset its 0.08, for the Air Quality dataset its 0.0005. In the experiment, the sequence length corresponding to one day is used as the period length of the GRU-SKIP component.

3.2. Methods for Comparison

In the experiment, RNN, GRU and DA-RNN were selected as comparison models. DA-SKIP model and the three comparison models were trained in three experimental datasets. Finally, the performance of each model in the test sets was used to compare their prediction capabilities.

3.3. Evaluation Metrics

We choose the mean square error MSE, absolute average error MAE and root mean square error RMSE to measure the model’s performance on the dataset. The formulas of these three indicators are as follows:

$$\mathrm{MAE}=\frac{1}{m}{\sum }_{i=1}^m\left|\left(y_{\dot{i}}-{\widehat{y}}_i\right)\right|$$

(27)

$$\mathrm{MSE}=\frac{1}{m}{\sum }_{i=1}^m{\left(y_i-{\widehat{y}}_i\right)}^2$$

(28)

$$\mathrm{RMSE}=\sqrt{\frac{1}{m}{\sum }_{i=1}^m{\left(y_i-{\widehat{y}}_i\right)}^2}$$

(29)

where $y_i$ is the true value of the time series at time i, ${\widehat{y}}_i$ is the predicted value of the model at time i, and m is the length of the test set.

3.4. Results

The test results of each model on the three datasets are shown in

Table 2. Test results of RNN, GRU, DA-RNN, and DA-SKIP models on three datasets. The MSE of the Electricity Consumption and Air Quality datasets are in units of ${10}^3$ .

Method	Solar Energy			Electricity Consumption			Air Quality
	MAE	MSE	RMSE	MAE	MSE	RMSE	MAE	MSE	RMSE
RNN	0.663	2.509	1.583	157.4	53.06	230.1	48.09	4.664	68.29
GRU	0.618	2.385	1.544	184.9	68.03	260.5	47.79	4.639	68.11
DA-RNN	0.659	2.538	1.591	124.4	30.99	175.6	21.23	2.033	45.07
DA-SKIP	0.628	2.296	1.519	88.02	18.51	136.0	9.968	0.393	19.82

.

Table 2 clearly shows that the test results of DA-SKIP on the three datasets are better than DA-RNN, GRU and RNN in most indicators. DA-SKIP achieved the best performance in eight out of nine indicators in the three datasets. On the Electricity Consumption dataset and Air Quality dataset, DA-SKIP has the most significant advantage that it surpasses the second place by 22.55% to 80.66% in all indicators.

DA-SKIP outperforms GRU and RNN mainly because of the advantages in handling long-distance dependence and making full use of external driving series, while DA-SKIP outperforms DA-RNN mainly because of the excellent periodicity forecasting ability of GRU-SKIP components.

On the Electricity Consumption dataset and Air Quality dataset, DA-SKIP has significant advantages, but when it comes to the Solar Energy dataset, DA-SKIP has relatively small advantages. This may be because the data in the Electricity Consumption dataset and the Air Quality dataset show relatively more obvious autocorrelation. As we presented above, DA-SKIP can capture not only the periodicity of data but also the autocorrelation of data by adding autoregressive component. Considering this, that’s the possible reason why DA-SKIP performed significantly better than the comparison model. In the experiment on these two datasets, we found that once the autoregressive component of DA-SKIP is disabled, the advantage of DA-SKIP over other comparison models will reduce. This phenomenon supports the statement from another aspect and also proves the effectiveness of the autoregressive component in the model.

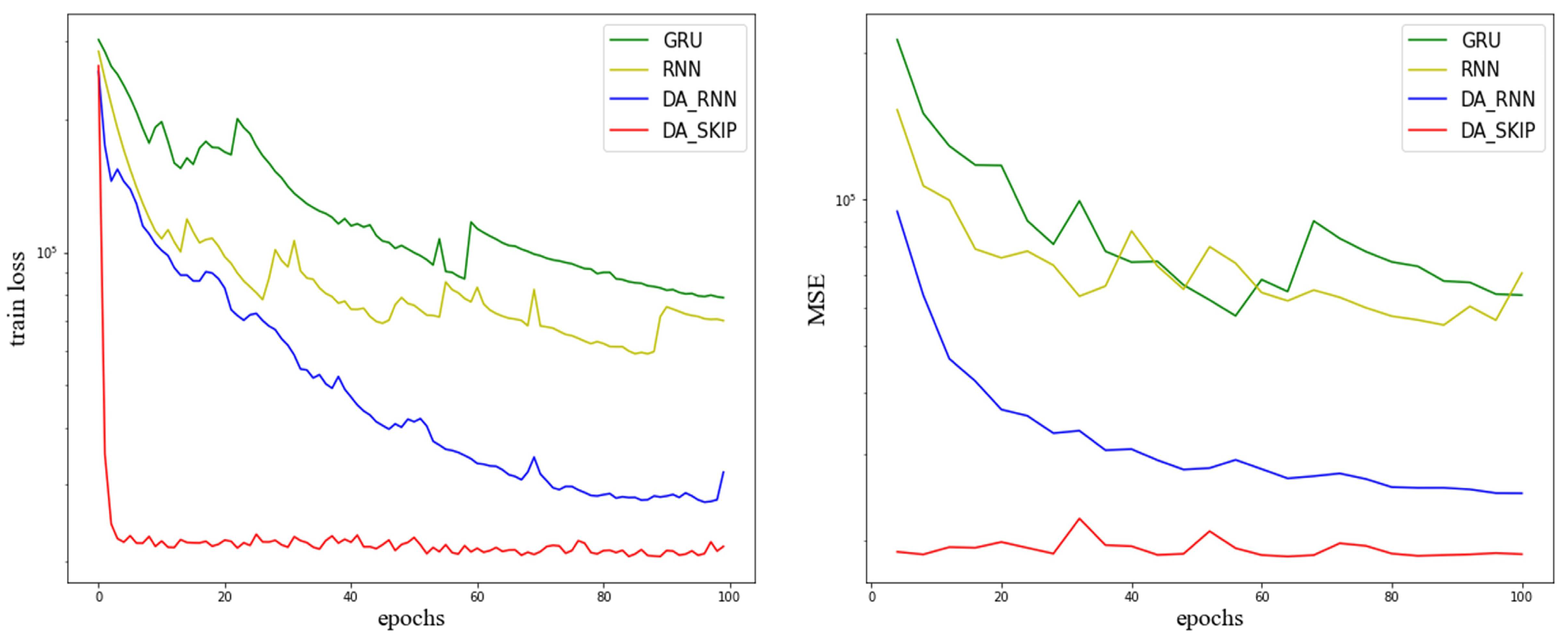
To explore the training efficiency of each model, Figure 6 is plotted to record the change trend of the training loss during the training of the four models on the Electricity Consumption dataset. In the experiment, the model is tested on the test set every four epochs of training. The right part of Figure 6 records the change of the MSE value of each model on the Electricity Consumption test set.

The left part of Figure 6 clearly shows that compared to the other three comparison models; DA-SKIP’s training loss can quickly converge to a smaller value during the training process. The same trend can be seen on the MSE value when testing on the test set. The right part of Figure 6 proves that the MSE value of DA-SKIP model on the test set, shares the same rapid convergence trend as the training loss, and finally it also stays stable at a lower point than the other three models. These prove that DA-SKIP is significantly better than the comparison model in terms of training efficiency and convergence speed while ensuring the accuracy of prediction.

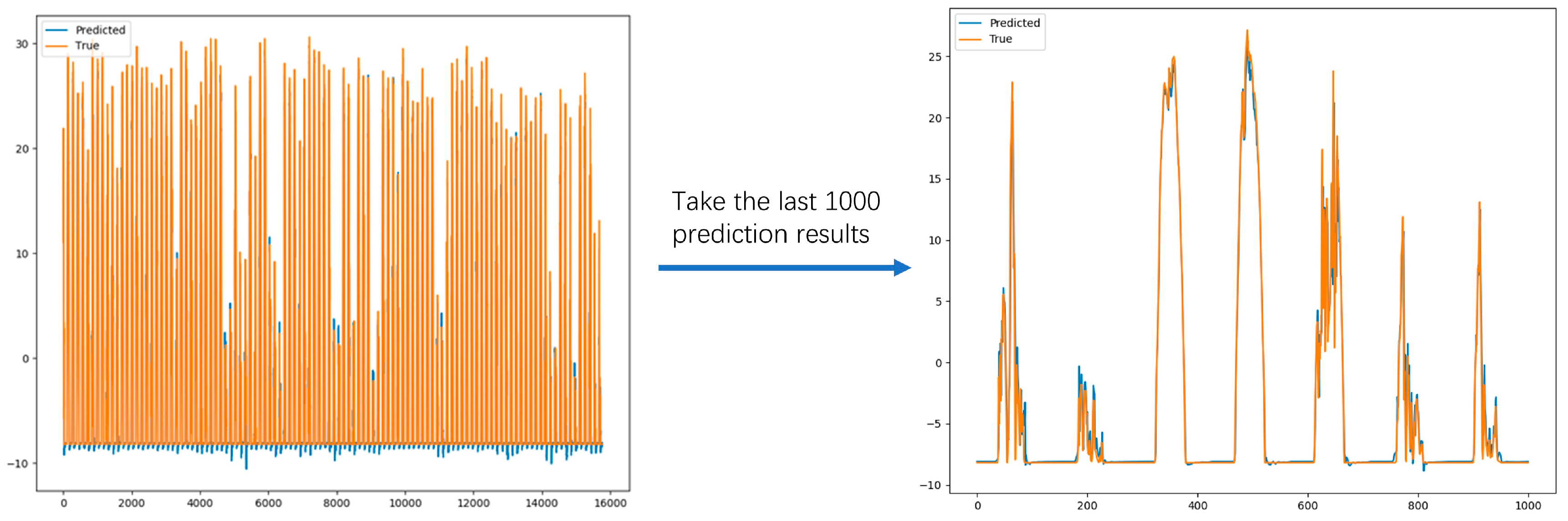
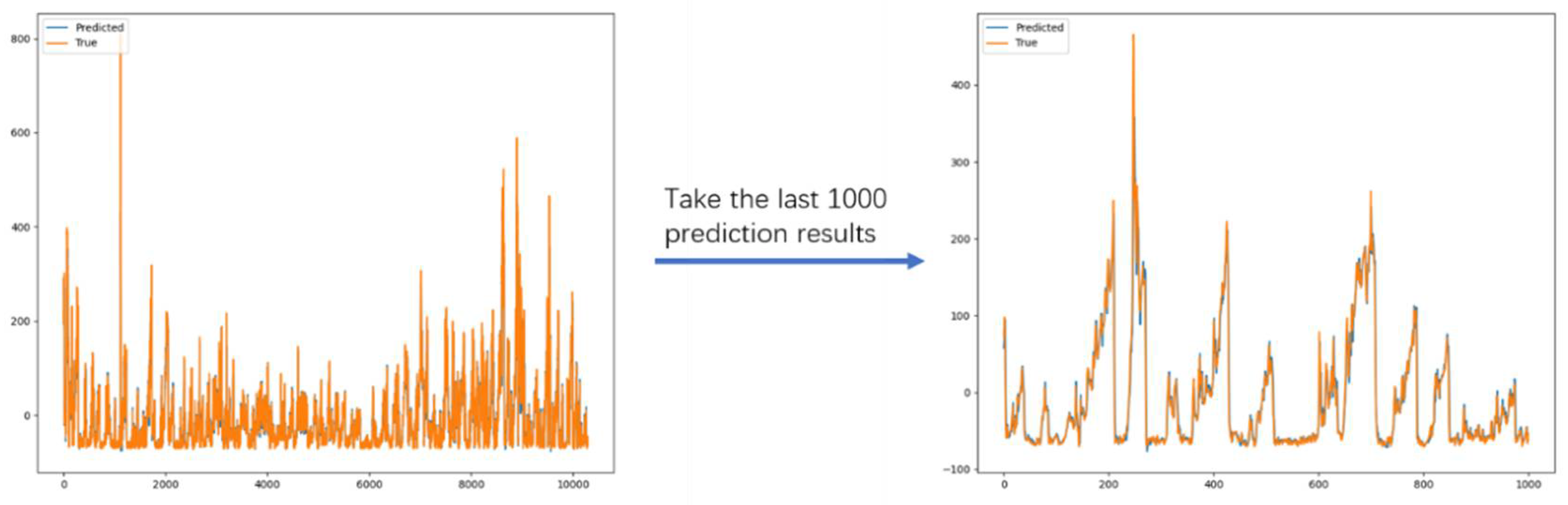
The above experimental results show that the introduction of task segmentation and integrated model ideas brings stronger long-distance prediction capabilities and periodic prediction capabilities to the model. It illustrates the advantages of DA-SKIP in dealing with periodic time series over the comparison models. The final prediction results of the DA-skip model on the three datasets are shown in Figure 7, Figure 8 and Figure 9.

4. Discussion

The result of the experiment proves that the time series prediction accuracy of the DA-SKIP model is significantly improved compared with the existing model, and the degree of improvement is related to the characteristics of the dataset itself. We guess that DA-SKIP model will have a better prediction effect for datasets with strong periodicity and autocorrelation. This conjecture has not been fully verified, and we will collect data on more datasets for in-depth research.

5. Conclusions

The DA-SKIP model designed in this paper is based on the DA-RNN model, and it is optimized for periodic datasets. In this model, the DA-RNN-based encoder/decoder component is used to capture the non-linear law of sequence data, the GRU-SKIP component is used to capture the periodic law of sequence data, and the autoregressive component is used to capture the linear law of sequence data.

DA-SKIP inherits DA-RNN’s excellent processing capabilities for multivariate data and long-distance dependence. At the same time, the introduction of GRU-SKIP components enhances the model’s processing capabilities for periodic sequences, the use of autoregressive components enhances the model’s processing capabilities for autocorrelation sequences. After that, excellent performance was seen on the three datasets of Solar Energy, Electricity Consumption and Air Quality.

The model proposed in this paper is suitable for datasets with clear periodicity and known period length, such as photovoltaic power generation, urban electricity consumption, road traffic flow, tourist flow in scenic spots, and so on. The model is proposed for these kinds of practical problems; therefore, it has a wide range of application prospects in reality. However, the demand for a clear period length also limits the scope of application of our model to some extent. In future research, we can try to use the attention mechanism to adaptively extract the periodicity and period length in order to further expand the application range of the model.