Speed Optimization for Container Ship Fleet Deployment Considering Fuel Consumption
Abstract
1. Introduction
2. Literature Review
3. Mathematical Model Formulation
3.1. Parameter and Variable Definition
3.2. Fuel Consumption Cost
3.3. Container Ships’ Fleet Deployment Model
4. Linearization of the Model
4.1. Linearization of the Reciprocal of Sailing Speeds
4.2. Linearization of the Objective Function of Fuel Consumption Cost
4.3. Underestimating Bilinear Terms
5. Approximation Algorithm
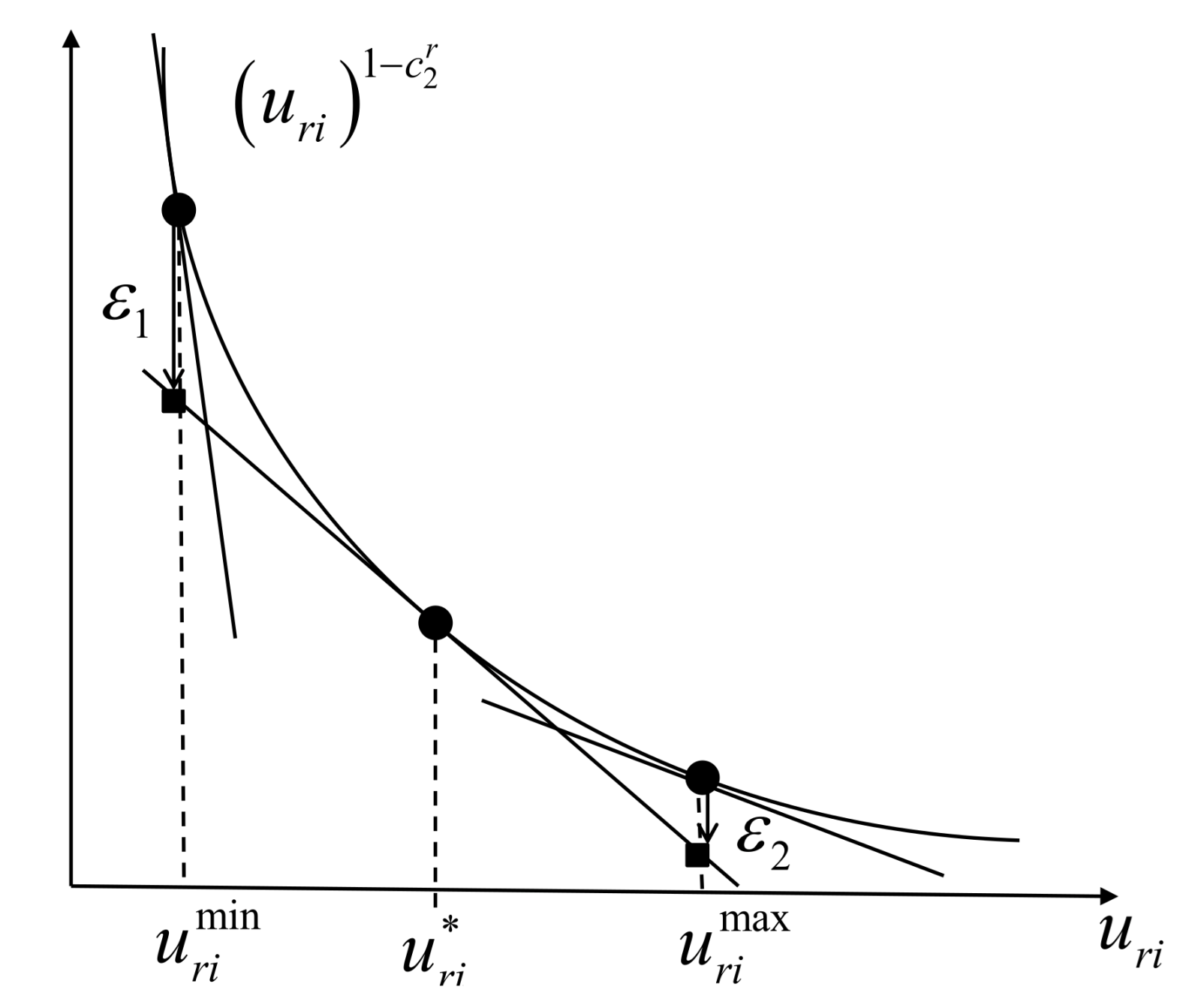
5.1. Linear Outer-Approximation Algorithm
| Algorithm 1. The procedure of linear outer-approximation algorithm to obtain tangent point sets. | |
| Input: | Convex function , the tangent point set . The lower limit and upper limit of is , the approximation relative error |
| Output: | the tangent point set |
| Step 1 | of the interval ; can be carried out by the bisection search method |
| Step 2 | At tangent point , the tangent line is defined as |
| Step 3 | Calculate the relative approximation error of points and according to |
| Step 4 | If or , then branch the feasible range of is divided into two ranges: and , and the tangent point set |
| In one branch , repeat the above step 1 to e step 4 until the stop criterion is reached | |
| In the other branch , repeat the above step 1 to e step 4 until the stop criterion is reached | |
| Stop criterion check: if and , stop and output the current solution. Otherwise, go to Step4. | |
| Step 5 | Return output |
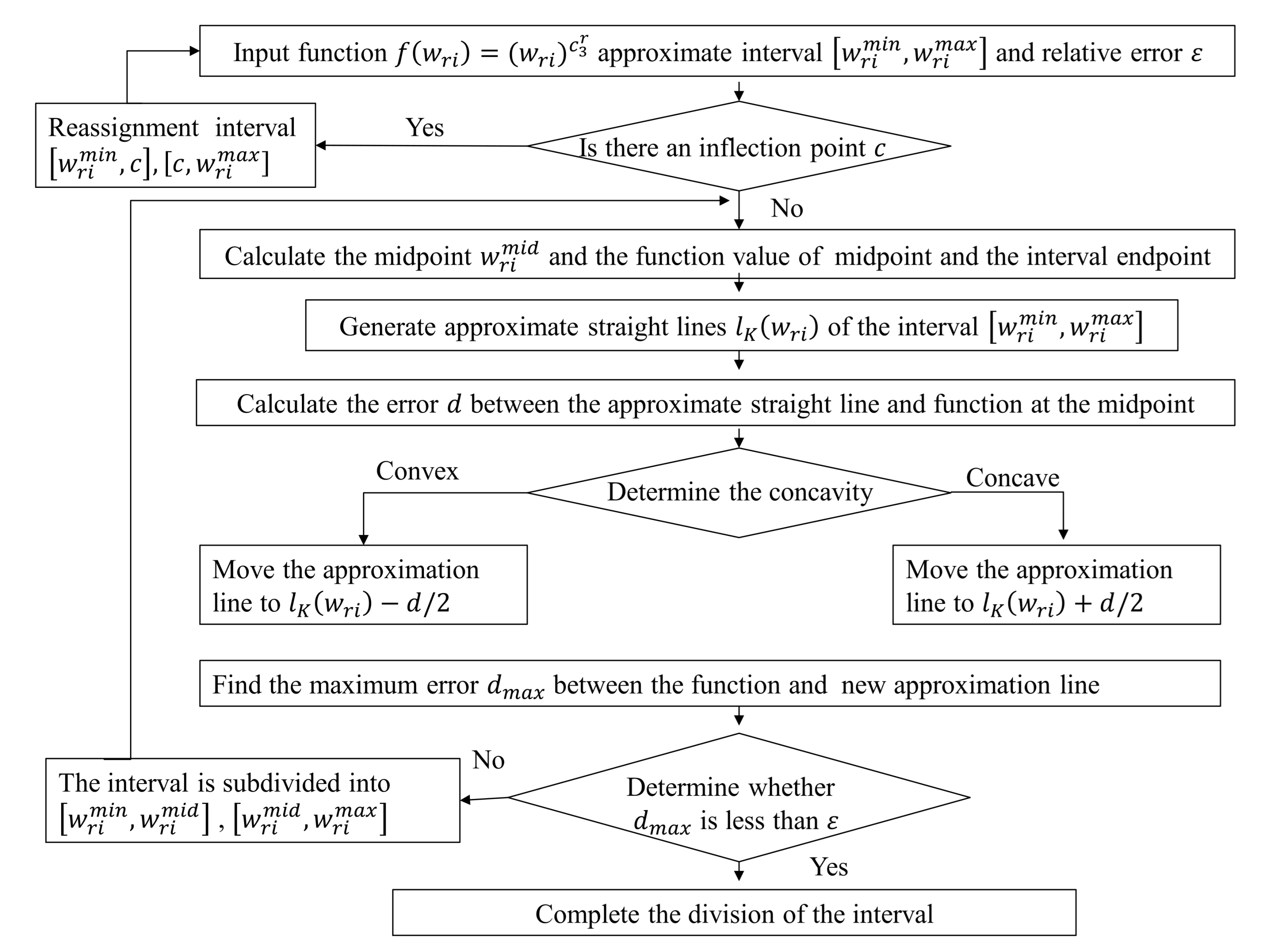
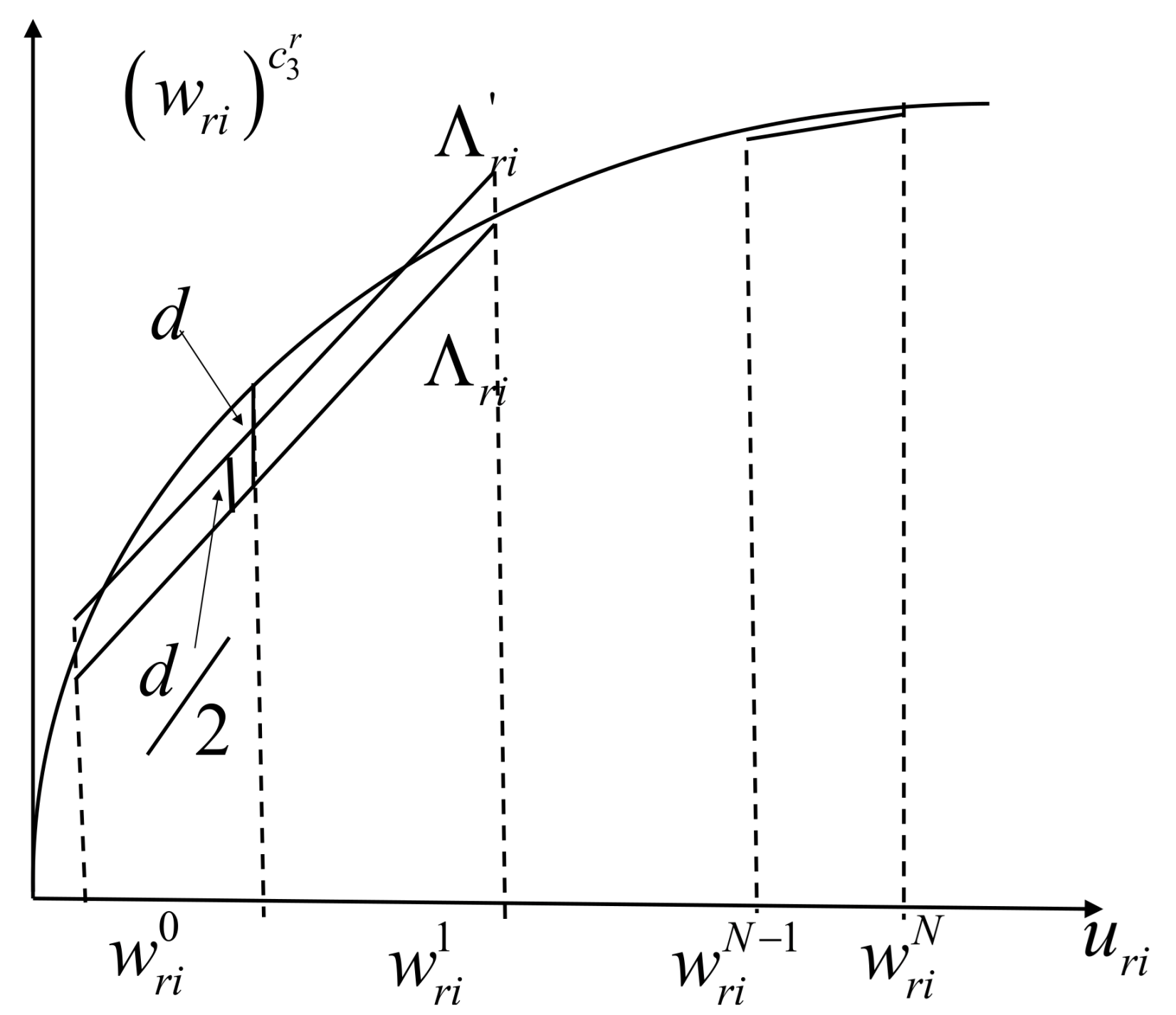
5.2. Improved Piecewise Linear Approximation Algorithm
5.3. Mixed Integer Linear Programming Model
6. Numerical Experiments
6.1. Parameter Setting
6.2. Sensitivity Analysis of Various Fleet Costs
6.3. Analyze the Relationship between Ship Deployment and Sailing Speed
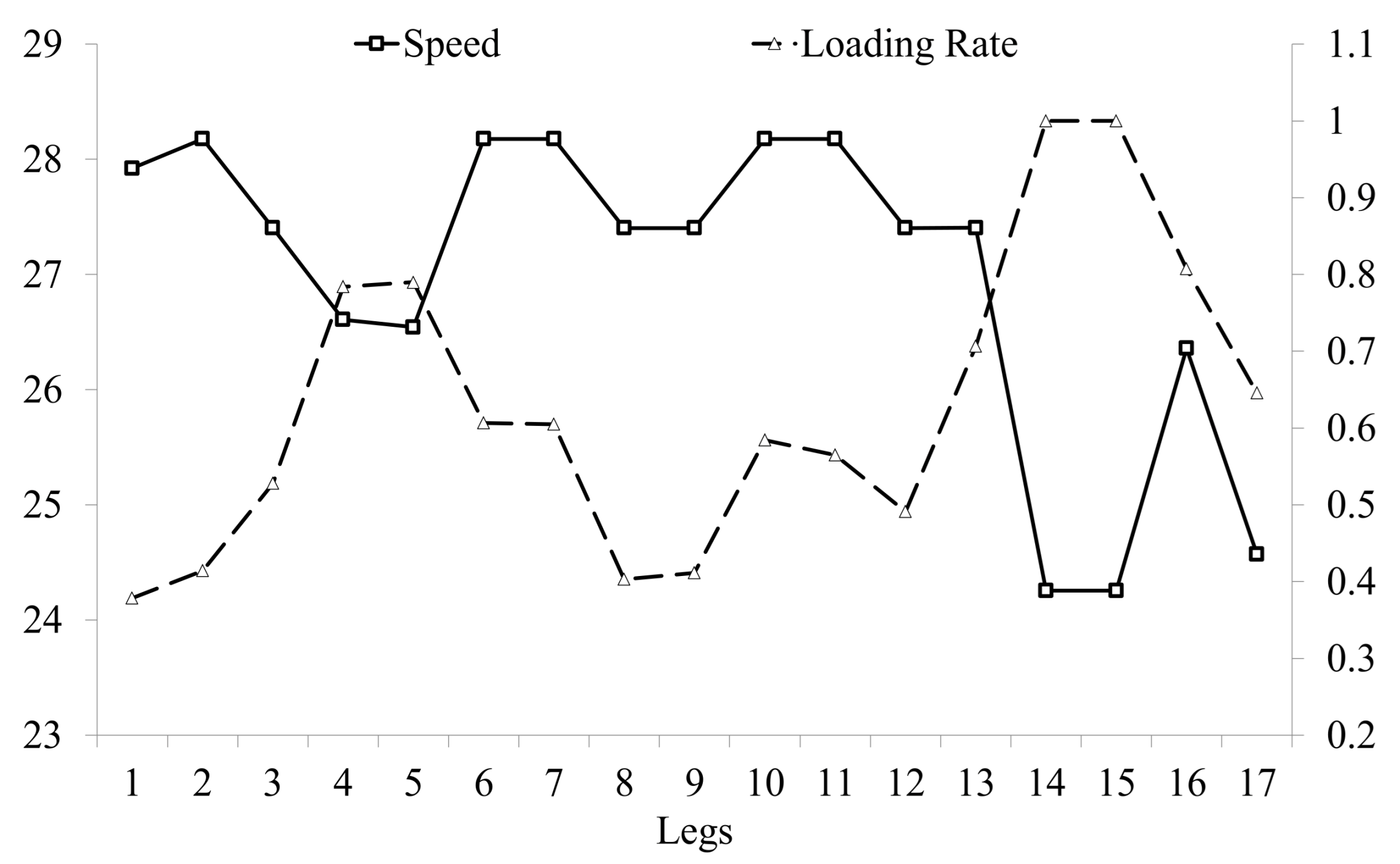
6.4. Analysis of the Relationship between Loading Rate and Sailing Speed
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, S.; Zhuge, D.; Zhen, L.; Lee, C.-Y. Liner Shipping Service Planning Under Sulfur Emission Regulations. Transp. Sci. 2021, 55, 491–509. [Google Scholar] [CrossRef]
- Beşikçi, E.B.; Arslan, O.; Turan, O.; Ölçe, A.I.R. An artificial neural network based decision support system for energy efficient ship operations. Comput. Oper. Res. 2016, 66, 393–401. [Google Scholar] [CrossRef]
- Yang, L.; Chen, G.; Zhao, J.; Rytter, N.G.M. Ship Speed Optimization Considering Ocean Currents to Enhance Environmental Sustainability in Maritime Shipping. Sustainability 2020, 12, 3649. [Google Scholar] [CrossRef]
- Wen, M.; Pacino, D.; Kontovas, C.A.; Psaraftis, H.N. A multiple ship routing and speed optimization problem under time, cost and environmental objectives. Transp. Res. Part D Transp. Environ. 2017, 52, 303–321. [Google Scholar] [CrossRef]
- Acciaro, M. Real option analysis for environmental compliance: LNG and emission control areas. Transp. Res. Part D Transp. Environ. 2014, 28, 41–50. [Google Scholar] [CrossRef]
- Coraddu, A.; Oneto, L.; Baldi, F.; Anguita, D. Vessels fuel consumption forecast and trim optimisation: A data analytics perspective. Ocean Eng. 2017, 130, 351–370. [Google Scholar] [CrossRef]
- Psaraftis, H. Speed Optimization vs Speed Reduction: The Choice between Speed Limits and a Bunker Levy. Sustainability 2019, 11, 2249. [Google Scholar] [CrossRef]
- Christiansen, M.; Fagerholta, K.; Nygreen, B.; Ronenc, D. Ship routing and scheduling in the new millennium. Eur. J. Oper. Res. 2013, 228, 467–483. [Google Scholar] [CrossRef]
- Jaramillo, D.I.; Perakis, A.N. Fleet deployment optimization for liner shipping Part Implementation and results. Marit. Policy Manag. 1991, 18, 235–262. [Google Scholar] [CrossRef]
- Gelareh, S.; Pisinger, D. Fleet deployment, network design and hub location of liner shipping companies. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 947–964. [Google Scholar] [CrossRef]
- Wang, S.; Meng, Q. Liner ship fleet deployment with container transshipment operations. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 470–484. [Google Scholar] [CrossRef]
- Chandra, S.; Christiansen, M.; Fagerholt, K. Combined fleet deployment and inventory management in roll-on/roll-off shipping. Transp. Res. Part E Logist. Transp. Rev. 2016, 92, 43–55. [Google Scholar] [CrossRef]
- Song, Y.; Yue, Y. Optimization Model of Fleet Deployment Plan of Liners. Procedia Eng. 2016, 137, 391–398. [Google Scholar] [CrossRef]
- Gelareh, S.; Meng, Q. A novel modeling approach for the fleet deployment problem within a short-term planning horizon. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 76–89. [Google Scholar] [CrossRef]
- Andersson, H.; Fagerholt, K.; Hobbesland, K. Integrated maritime fleet deployment and speed optimization: Case study from RoRo shipping. Comput. Oper. Res. 2015, 55, 233–240. [Google Scholar] [CrossRef]
- Wang, X.; Fagerholt, K.; Wallace, S.W. Planning for charters: A stochastic maritime fleet composition and deployment problem. Omega 2018, 79, 54–66. [Google Scholar] [CrossRef]
- Zhen, L.; Hu, Y.; Wang, S.; Laporte, G.; Wu, Y. Fleet deployment and demand fulfillment for container shipping liners. Transp. Res. Part B Methodol. 2019, 120, 15–32. [Google Scholar] [CrossRef]
- Norstad, I.; Fagerholt, K.; Laporte, G. Tramp ship routing and scheduling with speed optimization. Transp. Res. Part C Emerg. Technol. 2011, 19, 853–865. [Google Scholar] [CrossRef]
- Zacharioudakis, P.G.; Iordanis, S.; Lyridis, D.V.; Psaraftis, H.N. Liner shipping cycle cost modelling, fleet deployment optimization and what-if analysis. Marit. Econ. Logist. 2011, 13, 278–297. [Google Scholar] [CrossRef]
- Du, Y.; Qiang, M.; Shuaian, W.; Haibod, K. Two-phase optimal solutions for ship speed and trim optimization over a voyage using voyage report data. Transp. Res. Part B Methodol. 2019, 122, 88–114. [Google Scholar] [CrossRef]
- Ronen, D. The effect of oil price on containership speed and fleet size. J. Oper. Res. Soc. 2011, 62, 211–216. [Google Scholar] [CrossRef]
- Wang, S.; Meng, Q. Sailing speed optimization for container ships in a liner shipping network. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 701–714. [Google Scholar] [CrossRef]
- Gkonis, K.G.; Psaraftis, H.N. Modeling tankers’ optimal speed and emissions. Soc. Nav. Archit. Mar. Eng. Trans. 2012, 120, 90–115. [Google Scholar]
- Psaraftis, H.N.; Kontovas, C.A. Ship speed optimization: Concepts, models and combined speed-routing scenarios. Transp. Res. Part C Emerg. Technol. 2014, 44, 52–69. [Google Scholar] [CrossRef]
- Xia, J.; Li, K.X.; Ma, H.; Xu, Z. Joint Planning of Fleet Deployment, Speed Optimization, and Cargo Allocation for Liner Shipping. Transp. Sci. 2015, 49, 922–938. [Google Scholar] [CrossRef]
- Wang, Y.; Meng, Q.; Du, Y. Liner container seasonal shipping revenue management. Transp. Res. Part B Methodol. 2015, 82, 141–161. [Google Scholar] [CrossRef]
- Al-Khayyal, F.A.; Falk, J.E. Jointly Constrained Biconvex Programming. Math. Oper. Res. 1983, 8, 273–286. [Google Scholar] [CrossRef]
- Yang, H.; Xing, Y. Containerships Sailing Speed and Fleet Deployment Optimization under a Time-Based Differentiated Freight Rate Strategy. J. Adv. Transp. 2020, 2020, 1–16. [Google Scholar] [CrossRef]
| Sets | Description |
|---|---|
| Ports set | |
| Parameters | |
| The ith port of call | |
| Unit container transshipment cost | |
| capacity | |
| ship | |
| Costs related to the voyage | |
| Decision Variables | |
| ships | |
| ships | |
| , and 0 otherwise | |
| originating from port o | |
| Ballast water weight required for ship stability sailing on the i-th leg of route r | |
| Ship Type | ||||
|---|---|---|---|---|
| Small | Medium | Large | Giant | |
| Capacity of different types of ships (TEU) | 1500 | 3000 | 5000 | 10,000 |
| Fixed operating costs of different types of ships (week) | 51,923 | 76,923 | 115,384 | 173,076 |
| Unit cost of berthing operation of different types of ships (h) | 500 | 1000 | 1666 | 3333 |
| Per-container operating time of different types of ships (h) | 0.025 | 0.012 | 0.011 | 0.008 |
| Number of ships owned by the shipping lines | 20 | 20 | 20 | 20 |
| Chartering-out profit of different types of ships | 52,500 | 77,000 | 98,000 | 140,000 |
| Chartering-in cost of different types of ships | 66,500 | 94,500 | 122,500 | 175,000 |
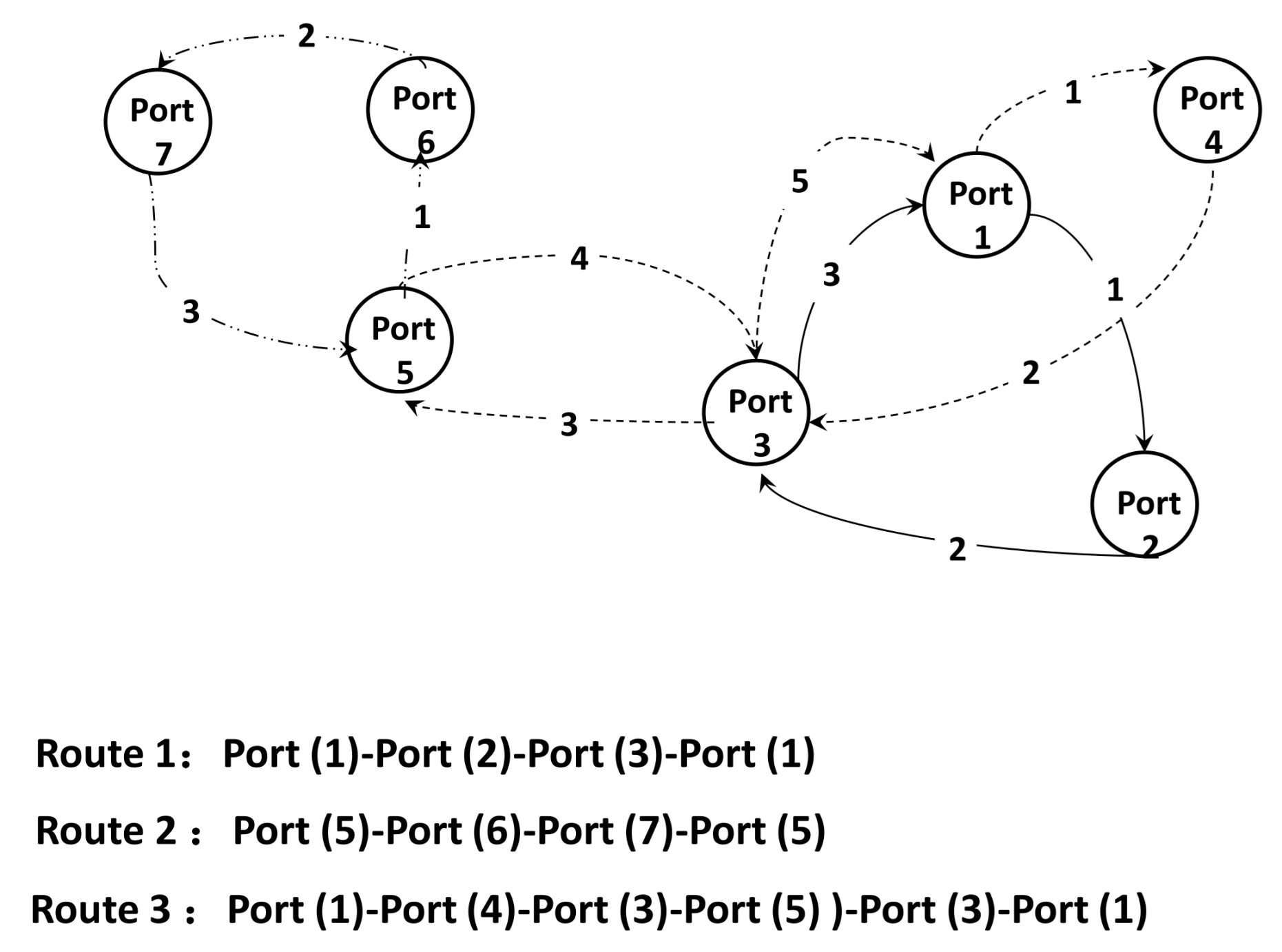
| No. | Ports Corresponding Number, Ports Order (Distance between Ports) |
|---|---|
| 1 | 1Yokohama (15)2Tokyo (177)3Nagoya (201)4Kobe (734)5Shanghai (745)6Hong Kong (1568) 1Yokohama |
| 2 | 7Ho Chi Minh (589)8Laem Chabang (755)9Singapore (187)10Port Klang (830) 7Ho Chi Minh |
| 3 | 11Brisbane (419)12Sydney (512)13Melbourne (470)14Adelaide (1325)15Fremantle (1733)16Jakarta (483)9Singapore (3649)11Brisbane |
| 4 | 17Manila (527) 18Kaohsiung (164)19Xiamen (260) 6Hong Kong (15)20Yantian (19)21Chiwan (17)6Hong Kong (620)17Manila |
| 5 | 22Dalian (187)23Xingang (379)24Qingdao (303)5Shanghai (93)25Ningbo (93)5Shanghai (383)26Kwangyang (72)27Busan (487)22Dalian |
| 6 | 28Chittagong (872)29Chennai (573)30Colombo (306)31Cochin (723)32Nhava Sheva (723)31Cochin (306) 30Colombo (573)29Chennai (872)28Chittagong |
| 7 | 33Sokhna (265)34Aqabah (554)35Jeddah (1268)36Salalah (885)37Karachi (688) 38Jebel Ali (862)36Salalah (1878)33Sokhna |
| 8 | 39Southampton (165)40Thamesport (386)41Hamburg (82) 42Bremerhaven (196)43Rotterdam (42)44Antwerp (51)45Zeebrugge (168)46Le Havre (103)39Southampton |
| 9 | 10Port Klang (187)9Singapore (483)16Jakarta (1917)18Kaohsiung (904)27Busan (904) 18Kaohsiung (342)6Hong Kong (17)21Chiwan (1597)10Port Klang |
| 10 | 39Southampton (3162)33Sokhna (1878)36Salalah (1643)30Colombo (1560)9Singapore (1415)6Hong Kong (260) 19Xiamen (486)5Shanghai (448)27Busan (487)22Dalian (187)23Xingang (379)24Qingdao (303) 5Shanghai (745)6Hong Kong (1415)9Singapore (1560)30Colombo (1643)36Salalah (5029)39Southampton |
| 11 | 11Brisbane (419)12Sydney (512)13Melbourne (470)14Adelaide (1325)15Fremantle (3148)30Colombo (1643)36Salalah (5244)43Rotterdam (5244)36Salalah (1643)30Colombo (5191)11Brisbane |
| 12 | 20Yantian (9956)41Hamburg (3621)33Sokhna (620)35Jeddah (4156)10Port Klang (187)9Singapore (1309)17Manila (629)20Yantian |
| Ship Type | Ship Type | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| No. | Small | Medium | Large | Giant | No. | Small | Medium | Large | Giant |
| 1 | 226,198 | 280,542 | − | 404,000 | 7 | 404,711 | 499,139 | − | 710,000 |
| 2 | 154,791 | 191,900 | − | 276,100 | 8 | − | 129,712 | 149,622 | 199,300 |
| 3 | 533,980 | 656,891 | − | 929,100 | 9 | − | 501,088 | 551,946 | 715,100 |
| 4 | − | 155,123 | 176,013 | 232,200 | 10 | − | − | 1,883,007 | 2,430,000 |
| 5 | 148,807 | 187,600 | − | 279,700 | 11 | 1,504,231 | 1,843,178 | − | 2,583,900 |
| 6 | 322,916 | 400,072 | − | 574,800 | 12 | 1,235,313 | 1,512,755 | − | 2,117,800 |
| Segments | Segments | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | ||
|---|---|---|---|---|---|---|---|
| 1.6 × 10−3 | 68 | 7.6 × 10−3 | 11 | 68 | 68 | 135 | 135 |
| 4.2 × 10−4 | 135 | 9.6 × 10−4 | 22 | 11 | 22 | 11 | 22 |
| Scenario 1 | Scenario 2 | |||||||||||
| Gap | Time | Gap | Time | |||||||||
| 100 | 2.26345 | 1.456898 | 5.4227 | 4.5785% | 157s | 2.25179 | 1.305053 | 5.4227 | 4.1103% | 1320s | −0.5 | −1.0 |
| 200 | 2.38397 | 2.291148 | 5.4082 | 4.7686% | 131s | 2.37363 | 2.203396 | 5.4082 | 4.7209% | 1693s | −0.4 | −3.8 |
| 300 | 2.50588 | 2.978536 | 5.397 | 4.3182% | 116s | 2.4736 | 2.757697 | 5.397 | 4.7709% | 1455s | −1.2 | −7.4 |
| 400 | 2.61124 | 3.153422 | 5.3957 | 4.9317% | 132s | 2.55396 | 2.924008 | 5.3957 | 4.3785% | 1791s | −2.1 | −7.2 |
| 500 | 2.65745 | 3.470209 | 5.3562 | 4.9863% | 170s | 2.67637 | 3.780855 | 5.3562 | 4.7166% | 1422s | −0.7 | 8.9 |
| 600 | 2.71938 | 3.725877 | 5.4509 | 4.8223% | 176s | 2.6914 | 3.686778 | 5.4509 | 4.7034% | 1534s | −1.0 | −1.0 |
| Scenario 3 | Scenario 4 | |||||||||||
| Gap | Time | Gap | Time | |||||||||
| 100 | 2.25775 | 1.53476 | 5.4208 | 4.2802% | 219s | 2.2547 | 1.285647 | 5.3908 | 4.4730% | 1663s | −0.1 | −16 |
| 200 | 2.39083 | 2.230419 | 5.3724 | 4.8466% | 182s | 2.37366 | 2.208508 | 5.3239 | 4.6335% | 1807s | −0.7 | −0.9 |
| 300 | 2.50871 | 3.146133 | 5.408999 | 4.7001% | 160s | 2.47303 | 2.589513 | 5.352 | 4.9580% | 2006s | −1.4 | −18 |
| 400 | 2.59337 | 3.204796 | 5.3449 | 4.7656% | 146s | 2.56488 | 3.067922 | 5.3726 | 4.8849% | 1514s | −1.1 | −4.2 |
| 500 | 2.66613 | 3.596815 | 5.3561 | 4.9071% | 159s | 2.64155 | 3.536123 | 5.3642 | 4.9157% | 1514s | −0.9 | −1.6 |
| 600 | 2.6916 | 3.704831 | 5.346299 | 4.8691% | 167s | 2.69072 | 3.677827 | 5.3619 | 4.8956% | 1606s | −0.0 | −0.7 |
| Ship Deployment | Each Legs Speed of Route 2 | Ship Deployment | Each Legs Speed of Route 6 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | Num | 1 | 2 | 3 | 4 | Type | Num | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 100 | 3000 | 1 | 25.98 | 25.62 | 25.98 | 23.83 | 1500 | 3 | 16.26 | 16.00 | 16.00 | 16.26 | 16.21 | 16.26 | 16.26 | 24.45 |
| 200 | 1500 | 2 | 10.36 | 10.42 | 10.36 | 23.83 | 3000 | 2 | 21.06 | 20.62 | 20.62 | 20.89 | 20.62 | 20.62 | 20.62 | 24.45 |
| 300 | 3000 | 1 | 25.51 | 25.98 | 25.98 | 23.83 | 3000 | 2 | 20.62 | 21.06 | 20.62 | 20.89 | 20.62 | 21.06 | 20.62 | 24.45 |
| 400 | 1500 | 2 | 10.41 | 10.36 | 10.47 | 23.83 | 3000 | 2 | 21.06 | 20.62 | 20.62 | 20.62 | 20.71 | 21.06 | 20.62 | 24.45 |
| 500 | 3000 | 1 | 25.51 | 25.98 | 25.98 | 23.83 | 1500 | 3 | 16.26 | 16.07 | 16.00 | 16.26 | 16.26 | 16.00 | 16.26 | 24.45 |
| 600 | 1500 | 2 | 10.58 | 10.61 | 10.58 | 23.83 | 1500 | 3 | 11.24 | 11.17 | 11.17 | 11.17 | 11.17 | 11.17 | 11.17 | 24.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.-F.; Hu, Z.-H. Speed Optimization for Container Ship Fleet Deployment Considering Fuel Consumption. Sustainability 2021, 13, 5242. https://doi.org/10.3390/su13095242
Gao C-F, Hu Z-H. Speed Optimization for Container Ship Fleet Deployment Considering Fuel Consumption. Sustainability. 2021; 13(9):5242. https://doi.org/10.3390/su13095242
Chicago/Turabian StyleGao, Chao-Feng, and Zhi-Hua Hu. 2021. "Speed Optimization for Container Ship Fleet Deployment Considering Fuel Consumption" Sustainability 13, no. 9: 5242. https://doi.org/10.3390/su13095242
APA StyleGao, C.-F., & Hu, Z.-H. (2021). Speed Optimization for Container Ship Fleet Deployment Considering Fuel Consumption. Sustainability, 13(9), 5242. https://doi.org/10.3390/su13095242







