Path Planning for Autonomous Platoon Formation
Abstract
1. Introduction
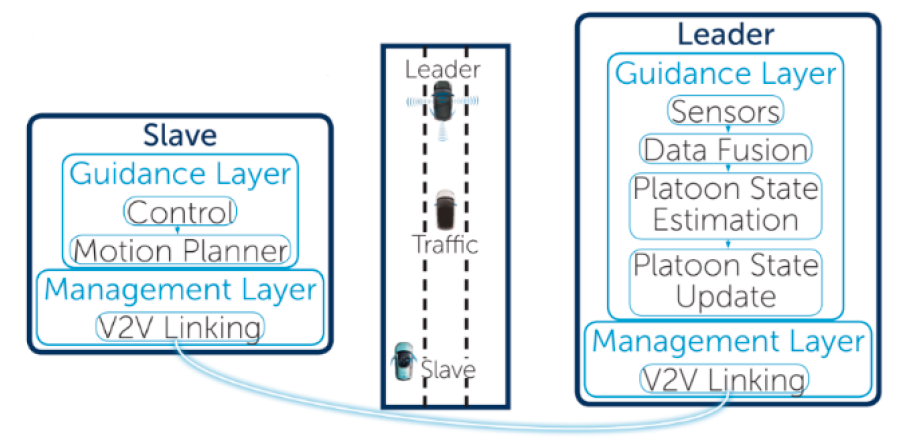
2. Platoon Formation and Path Planning
- Raw path calculation: this first step generates a path that is valid within the configuration space: the path stays inside the road boundaries and prevents the hitting of any road obstacle while making its way to the target position as fast as possible.
- Path optimization: The path calculated in (1) does not guarantee that it is physically achievable for a vehicle. The average driver will not be fond of high acceleration or jerk peaks. This leads to the second operation: path optimization. From the path defined in (1), this step will output a dynamically realistic path for the vehicle to follow.
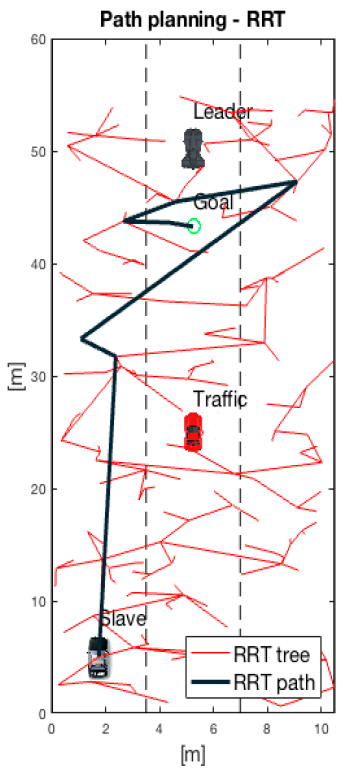
2.1. Path Planning with Rapid-Exploring Random Trees (RRT)
- There is no need to explicitly characterize the configuration space, but instead probe the space and use collision detection on the go.
- They are incremental in nature and efficient which offers the potential for real-time implementation while retaining completeness guarantees.
2.2. Biased RRT Star (RRT*)
2.3. Informed RRT* (i-RRT*)
3. Path Optimization Using Model Predictive Control
- the lateral vehicle coordinate [m].
- the RRT* lateral coordinate [m] (Figure 8).
- the longitudinal distance between leader and slave [m].
- the leader longitudinal coordinate [m].
- the heading angle, the yaw rate and the steering angle, respectively [rad].
- the slave lateral and longitudinal speed, respectively [m/s].
- the weights of the cost function [-].
- the prediction horizon (time over which the dynamic model is solved).
- : deviation between slave lateral position and the RRT* lateral coordinate.
- : distance between the slave and the goal. Minimizing this state variable is the main lever to reach the leader.
- : slave jerk. Minimizing the jerk prevents being too demanding on it.
- slave steering angle. Same justification as for the jerk.
4. Results
4.1. Path Optimization
4.2. Simulation Results
5. Discussion
- Several scenarios are still to be studied (border cases), such as the “leader” being behind “slave” vehicles, or all three lanes being completely blocked by traffic.
- Although the RRT* algorithm provides us with an obstacle-free trajectory, the MPC controller yields a very close but still different trajectory. There is thus a risk of colliding with obstacles if the path planner frequency is too low. To that extent, the real-time performance in embedded systems is an important aspect to be tested, for example, with hardware in-the-loop modelling. Although the results in simulation show a high frequency path calculation, it must be real-time capable for a given hardware.
- The path planner implemented here considered no highway driving protocols, such as knowing the legal way to cross lanes, which gives scope for future study. Another important direction is the usage of informed-RRT* which should result in faster converging paths.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Swaroop, D.; Hedrick, J.K. Constant Spacing Strategies for Platooning in Automated Highway Systems. J. Dyn. Syst. Meas. Control 1999, 121, 462–470. [Google Scholar] [CrossRef]
- Peppard, L. String stability of relative-motion PID vehicle control systems. IEEE Trans. Autom. Control 1974, 19, 579–581. [Google Scholar] [CrossRef]
- Naus, G.J.L.; Vugts, R.P.A.; Ploeg, J.J.; Van De Molengraft, M.J.G.; Steinbuch, M.M. String-Stable CACC Design and Experimental Validation: A Frequency-Domain Approach. IEEE Trans. Veh. Technol. 2010, 59, 4268–4279. [Google Scholar] [CrossRef]
- Xiao, L.; Gao, F. Practical String Stability of Platoon of Adaptive Cruise Control Vehicles. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1184–1194. [Google Scholar] [CrossRef]
- Yanakiev, D.; Kanellakopoulos, I. Nonlinear spacing policies for automated heavy-duty vehicles. IEEE Trans. Veh. Technol. 1998, 47, 1365–1377. [Google Scholar] [CrossRef]
- Seiler, P.; Pant, A.; Hedrick, K. Disturbance Propagation in Vehicle Strings. IEEE Trans. Autom. Control 2004, 49, 1835–1841. [Google Scholar] [CrossRef]
- Shaw, E.; Hedrick, J.K. String Stability Analysis for Heterogeneous Vehicle Strings. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 3118–3125. [Google Scholar]
- Dao, T.S.; Huissoon, J.P.; Clark, C.M. A strategy for optimization of cooperative platoon formation. Int. J. Veh. Inf. Commun. Syst. 2013, 3, 28–43. [Google Scholar]
- Hobert, L.H.X. A Study on Platoon Formations and Reliable Communication in Vehicle Platoons. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2012. [Google Scholar]
- Sheikholeslam, S.; Desoer, C.A. Longitudinal Control of a Platoon of Vehicles. In Proceedings of the 1990 American Control Conference, San Diego, CA, USA, 23–25 May 1990; pp. 291–296. [Google Scholar]
- Tuchner, A.; Haddad, J. Vehicle platoon formation using interpolating control: A laboratory experimental analysis. Transp. Res. Part C Emerg. Technol. 2017, 84, 21–47. [Google Scholar] [CrossRef]
- Rosenzweig, J.; Bartl, M. A Review and Analysis of Literature on Autonomous Driving. 2015. Available online: https://michaelbartl.com/wp-content/uploads/Lit-Review-AD_MoI.pdf (accessed on 21 April 2021).
- Young, B.J.; Beard, R.W.; Kelsey, J.M. A Control Scheme for Improving Multi-Vehicle Formation Maneuvers. In Proceedings of the American Control Conference. (Cat. No.01CH37148), Arlington, VA, USA, 25–27 June 2001; Volume 2, pp. 704–709. [Google Scholar]
- Lam, S.; Katupitiya, J. Cooperative Autonomous Platoon Maneuvers on Highways. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, NSW, Australia, 9–12 July 2013; pp. 1152–1157. [Google Scholar] [CrossRef]
- Lu, X.-Y.; Tan, H.-S.; Shladover, S.E.; Hedrick, J.K. Automated Vehicle Merging Maneuver Implementation for AHS. Veh. Syst. Dyn. 2004, 41, 85–107. [Google Scholar] [CrossRef]
- Claussmann, L.; Revilloud, M.; Gruyer, D.; Glaser, S. A Review of Motion Planning for Highway Autonomous Driving. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1826–1848. [Google Scholar] [CrossRef]
- LaValle, S.M. Motion Planning: The Essentials. IEEE Robot. Autom. Mag. 2011, 18, 79–89. [Google Scholar] [CrossRef]
- Lavalle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning, from the Annual Research Report. 1998. Available online: http://citeseerx.ist.psu.edu/viewdoc/citations;jsessionid=A1AB62F78BC767D0F82777B22AA4B79C?doi=10.1.1.35.1853 (accessed on 21 April 2021).
- Kuwata, Y.; Karaman, S.; Teo, J.; Frazzoli, E.; How, J.P.; Fiore, G.A. Real-Time Motion Planning With Applications to Autonomous Urban Driving. IEEE Trans. Control Syst. Technol. 2009, 17, 1105–1118. [Google Scholar] [CrossRef]
- Cheng, P.; LaValle, S.M. Reducing Metric Sensitivity in Randomized Trajectory Design. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the Next Millennium (Cat. No.01CH37180) 1, Maui, HI, USA, 29 October–3 November 2001; Volume 1, pp. 43–48. Available online: https://pdfs.semanticscholar.org/15e7/f233088f52dffadc0b07b5ff90ad69a71323.pdf (accessed on 21 April 2021).
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Islam, F.; Nasir, J.; Malik, U.; Ayaz, Y.; Hasan, O. RRT-Smart: Rapid Convergence Implementation of RRT towards Optimal Solution. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Chengdu, China, 5–8 August 2012; pp. 1651–1656. [Google Scholar]
- Nasir, J.; Islam, F.; Ayaz, Y. Adaptive Rapidly-Exploring-Random-Tree-Star (RRT*)-Smart: Algorithm Characteristics and Behavior Analysis in Complex Environments. APIJTM 2013, 2, 39–51. [Google Scholar] [CrossRef]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT*: Optimal Sampling-Based Path Planning Focused via Direct Sampling of An Admissible Ellipsoidal Heuristic. In Proceedings of the International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar] [CrossRef]
- Melda Ulusoy, M. Understanding Model Predictive Control, Part 3: MPC Design Parameters Video—MATLAB & Simulink. 2018. Available online: https://fr.mathworks.com/videos/understanding-model-predictive-control-part-3-mpc-design-parameters-530607670393.html (accessed on 21 April 2021).
- Ren, H.; Shim, T.; Ryu, J.; Chen, S. Development of Effective Bicycle Model for Wide Ranges of Vehicle Operations; SAE Technical Paper Series; SAE World Congress & Exhibition: Warrendale, PA, USA, 2014. [Google Scholar] [CrossRef]
- Kong, J.; Pfeiffer, M.; Schildbach, G.; Borrelli, F. Kinematic and Dynamic Vehicle Models for Autonomous Driving Control Design. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 1094–1099. Available online: http://me.berkeley.edu/~frborrel/pdfpub/iv_kinematicmpc_jason.pdf (accessed on 21 April 2021). [CrossRef]
- Polack, P.; Altché, F.; d’Andréa-Novel, B.; de La Fortelle, A. Conference: 2017 IEEE Intelligent Vehicles. Available online: https://www.researchgate.net/publication/318810853_The_kinematic_bicycle_model_A_consistent_model_for_planning_feasible_trajectories_for_autonomous_vehicles (accessed on 21 April 2021).
- Schmitt, C.J.; Basset, M.; Gissger, G.L. European Control Conference, ECC 1999—Conference Proceedings. 2015. Available online: https://www.researchgate.net/publication/267228739_Identification_of_physical_parameters_of_a_passenger_car (accessed on 21 April 2021).










| Weight | ||||
|---|---|---|---|---|
| Value | 150 | 5 | 50 | 1 |
| State Variable | vx | a | j | ||
|---|---|---|---|---|---|
| Minimum | 0 m/s | −5 m/s2 | −10°/s | −5 m/s3 | −10° |
| Maximum | 30 m/s | 5 m/s2 | 10°/s | 5 m/s3 | 10° |
| Bicycle Model | Computational Time |
|---|---|
| Kinematic | 1.3 s |
| Dynamic | 1.6 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Ganaoui-Mourlan, O.; Camp, S.; Hannagan, T.; Arora, V.; De Neuville, M.; Kousournas, V.A. Path Planning for Autonomous Platoon Formation. Sustainability 2021, 13, 4668. https://doi.org/10.3390/su13094668
El Ganaoui-Mourlan O, Camp S, Hannagan T, Arora V, De Neuville M, Kousournas VA. Path Planning for Autonomous Platoon Formation. Sustainability. 2021; 13(9):4668. https://doi.org/10.3390/su13094668
Chicago/Turabian StyleEl Ganaoui-Mourlan, Ouafae, Stephane Camp, Thomas Hannagan, Vaibhav Arora, Martin De Neuville, and Vaios Andreas Kousournas. 2021. "Path Planning for Autonomous Platoon Formation" Sustainability 13, no. 9: 4668. https://doi.org/10.3390/su13094668
APA StyleEl Ganaoui-Mourlan, O., Camp, S., Hannagan, T., Arora, V., De Neuville, M., & Kousournas, V. A. (2021). Path Planning for Autonomous Platoon Formation. Sustainability, 13(9), 4668. https://doi.org/10.3390/su13094668






