A Rigid Cuckoo Search Algorithm for Solving Short-Term Hydrothermal Scheduling Problem
Abstract
1. Introduction
2. Methods
2.1. Mathematical Model of the Hydrothermal System
2.2. Cuckoo Search Algorithm and Lévy Flights
- Concept 1. Individually all cuckoos produce one single egg at a time that regards a proposed solution and randomly throws its egg up into the wanted nest among the set number of possible host nests.
- Concept 2. The egg of high quality thrown up in the best nests regards a better solution transferred to the subsequent generation.
- Concept 3. The possible number of host nests is constant, and the probability that the host bird can find a nest is indicated by the probability constant, Pa, with range [0,1]. Hence, it may either discard the egg or leave this nest and then build a new nest entirely in a different place.
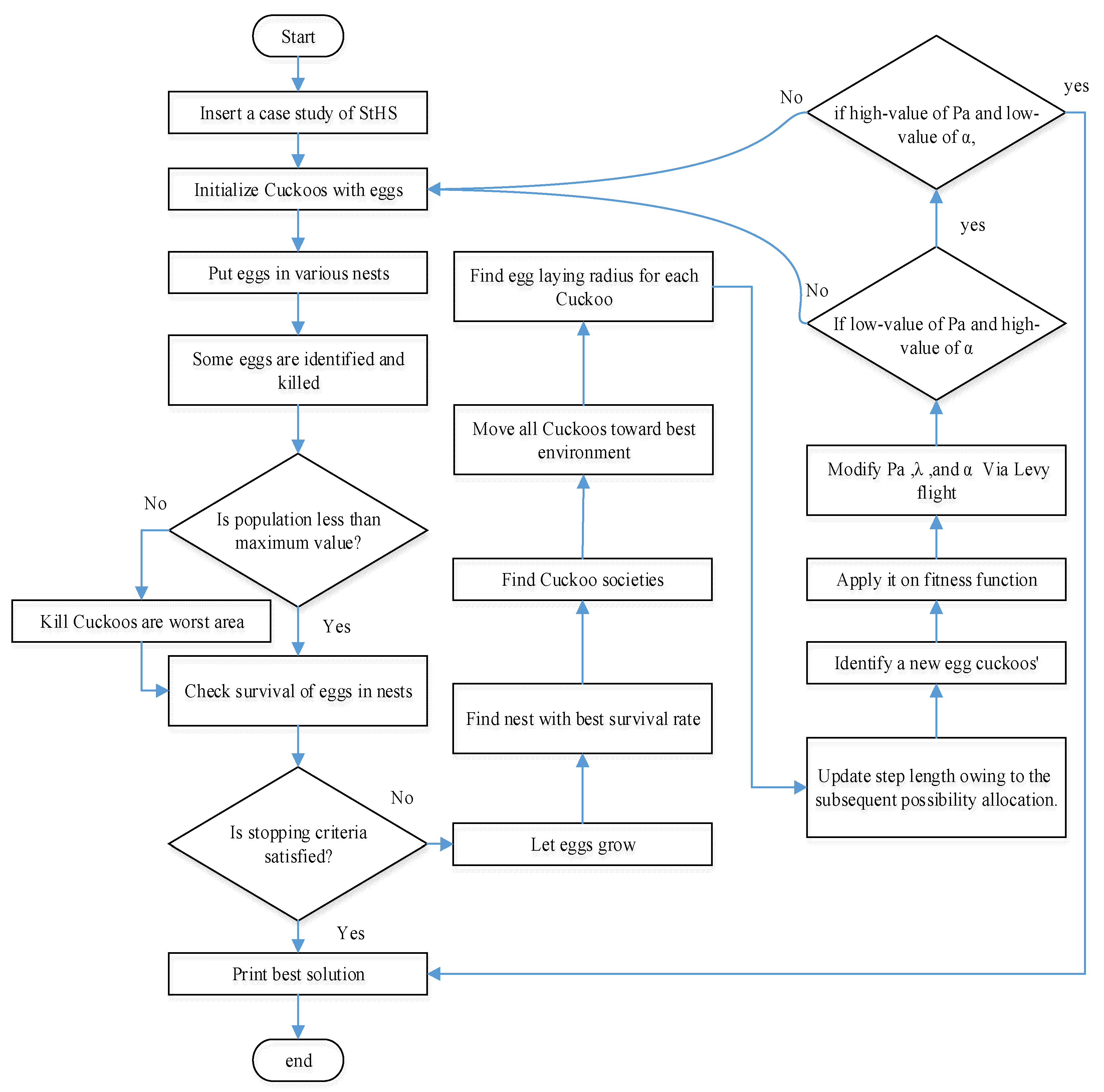
2.3. Rigid Cuckoo Search Algorithm
2.4. Implementation of RCSA on a Hydrothermal System
- Step-1.
- In the StHS problem, the influential variables such as the release rate of water for the whole plants for several hours and thermal unit production for the entire period are chosen irregularly within the operating limitations. The storage capacity of every reservoir has been estimated using Equation (4), the generation of hydro plants has been calculated using Equation (3). Subsequently, the thermal power generation has been computed by applying Equation (2). The population of the host nest (NE) has been explained as:where every nest Yi is expressed as:
- Step-2.
- Set the production number.
- Step-3.
- Compute the objective function using Equation (17). With the equation of restraints, many restrictions irregularly have been limited. Then, enhanced fuel cost has been calculated as Equation (19).
- Step-4.
- The modern solution has been created by using Levy flights. The new solution’s computation has been built in the preceding best nest by using Levy flights. For this technique, the optimal way for levy flights has been computed by Yang XS’s contribution, Deb S [18]. The new solution has been presented in Equation (20)where α > 0 is the updated step size, rand2 is a typical number of allocated stochastic and ΔYi,new has been computed, see Equations (21) and (22):where randA and randB are a couple of commonly allocated stochastic variables with a standard deviation and that has been determined by Equations (23) and (24), respectively.where is between the range from 0.29 to 2.01 and the obtained new solution must satisfy all associated constraints for both of and as well.
- Step-5.
- The effect of the detection of an alien egg in a nest of a host bird with Pa’s possibility produces a new solution for the problem comparable with the Levy flights. The new solution has been computed as following Equations (25)–(27):where was the modernized coefficient defined built in the possibility of a host bird to find out an alien egg in its nest:The increment value of has been defined bywhere is the allocated random number within [0,1], and are the random disorder for locations of nests in . Once more, for the recently produced solution, its lower and upper limits should please the unit’s limitation. The best value has been modernized for every nest and the nest identical to the best fitness function has been defined by Gbest.
- Step-6.
- The technique ends if modern production gives the maximum production number.
3. Results and Discussion
3.1. Parameter Selection
3.2. Obtained Results
3.3. Proposed System Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| F | Gross cost of production |
| Fi(PTj) | Production cost for PTj |
| PTj | Production of power for the thermal unit at period j |
| PH(i, j) | Production of power for hydro unit i at period j |
| Pdj | System load demand at period j |
| qij | Water release rate of hydro unit i at period j |
| rij | Stream rate into the storage reservoir of the hydro plant at a period |
| sij | Spillage of the reservoir at a period |
| Xij | Storage volume of hydro plant i at period j |
| Xi0 | Initial reservoir storage of hydro plant |
| i | Number of units |
| nh, np | Maximum number of unit hydro/thermal |
| j | Number of scheduling intervals |
| NH, NP | Maximum number of scheduling periods of hydro/thermal |
| NC | Total number of constraints |
| Rj | Resource constraint |
| IT | Total iteration numbers |
| IC | Current iterations |
| λk | Penalty value for kth |
| Viok | Violation amount of kth constraint |
| ψ | Distribution factor |
| Φ | Gamma distribution function |
| m | Time period |
References
- Hammid, A.T.; Bin Sulaiman, M.H.; Abdalla, A.N. Prediction of small hydropower plant power production in Himreen Lake dam (HLD) using artificial neural network. Alex. Eng. J. 2018, 57, 211–221. [Google Scholar] [CrossRef]
- Hammid, A.T.; Kadhim, M.B.H.; Sulaiman, A.A.; Kareem, A.N.; Jadaa, K.J. Priority of kaplan turbine and small hydropower plants over other resources: An overview. J. Eng. Appl. Sci. 2017, 12, 8695–8705. [Google Scholar]
- Thaeer Hammid, A.; Awad, O.I.; Sulaiman, M.H.; Gunasekaran, S.S.; Mostafa, S.A.; Manoj Kumar, N.; Khalaf, B.A.; Al-Jawhar, Y.A.; Abdulhasan, R.A. A review of optimization algorithms in solving hydro generation scheduling problems. Energies 2020, 13, 2787. [Google Scholar] [CrossRef]
- Orero, S.; Irving, M. A genetic algorithm modelling framework and solution technique for short term optimal hydrothermal scheduling. IEEE Trans. Power Syst. 1998, 13, 501–518. [Google Scholar] [CrossRef]
- Yuan, X.; Wang, L.; Yuan, Y. Application of enhanced PSO approach to optimal scheduling of hydro system. Energy Convers. Manag. 2008, 49, 2966–2972. [Google Scholar] [CrossRef]
- Sinha, N.; Chakrabarti, R.; Chattopadhyay, P. Fast evolutionary programming techniques for short-term hydrothermal scheduling. IEEE Trans. Power Syst. 2003, 18, 214–220. [Google Scholar] [CrossRef]
- Amjady, N.; Soleymanpour, H.R. Daily hydrothermal generation scheduling by a new modified adaptive particle swarm optimization technique. Electr. Power Syst. Res. 2010, 80, 723–732. [Google Scholar] [CrossRef]
- Lakshminarasimman, L.; Subramanian, S. Short-term scheduling of hydrothermal power system with cascaded reservoirs by using modified differential evolution. IEE Proc. Gener. Transm. Distrib. 2006, 153, 693–700. [Google Scholar] [CrossRef]
- Hota, P.; Barisal, A.; Chakrabarti, R. An improved PSO technique for short-term optimal hydrothermal scheduling. Electr. Power Syst. Res. 2009, 79, 1047–1053. [Google Scholar] [CrossRef]
- Roy, P.K. Teaching learning based optimization for short-term hydrothermal scheduling problem considering valve point effect and prohibited discharge constraint. Int. J. Electr. Power Energy Syst. 2013, 53, 10–19. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vo, D.N.; Ongsakul, W.; Trung, N.T. One rank cuckoo search algorithm for short-term hydrothermal scheduling with reservoir constraint. In Proceedings of the IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015. [Google Scholar]
- Türkay, B.; Mecitoğlu, F.; Baran, S. Application of a fast evolutionary algorithm to short-term hydro-thermal generation scheduling. Energy Sources Part B Econ. Planning, Policy 2011, 6, 395–405. [Google Scholar] [CrossRef]
- Wood, A.J.; Wollenberg, B.F.; Sheblé, G.B. Power Generation, Operation, and Control; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Wong, K.; Wong, Y. Short-term hydrothermal scheduling part. I. Simulated annealing approach. IEE Proc. Gener. Transm. Distrib. 1994, 141, 497–501. [Google Scholar] [CrossRef]
- Swain, R.; Barisal, A.; Hota, P.; Chakrabarti, R. Short-term hydrothermal scheduling using clonal selection algorithm. Int. J. Electr. Power Energy Syst. 2011, 33, 647–656. [Google Scholar] [CrossRef]
- Das, S.; Bhattacharya, A. Symbiotic organisms search algorithm for short-term hydrothermal scheduling. Ain Shams Eng. J. 2018, 9, 499–516. [Google Scholar] [CrossRef]
- Sivasubramani, S.; Swarup, K.S. Hybrid DE–SQP algorithm for non-convex short term hydrothermal scheduling problem. Energy Convers. Manag. 2011, 52, 757–761. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009. [Google Scholar]
- Vo, D.N.; Schegner, P.; Ongsakul, W. Cuckoo search algorithm for non-convex economic dispatch. IET Gener. Transm. Distrib. 2013, 7, 645–654. [Google Scholar] [CrossRef]
- Dubey, H.M.; Pandit, M.; Panigrahi, B. Cuckoo Search Algorithm for Short Term Hydrothermal Scheduling. In Power Electronics and Renewable Energy Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 573–589. [Google Scholar]
- Xinchun, L.; Yongde, K.; Hongna, C.; Hui, L. Hydrothermal Effects of Freeze-Thaw in the Taklimakan Desert. Sustainability 2021, 13, 1292. [Google Scholar] [CrossRef]
- Zeng, X.; Hammid, A.T.; Kumar, N.M.; Subramaniam, U.; Almakhles, D.J. A grasshopper optimization algorithm for optimal short-term hydrothermal scheduling. Energy Rep. 2021, 7, 314–323. [Google Scholar] [CrossRef]
- Zhang, Z.; Fan, W.; Bao, W.; Chen, C.-T.; Liu, S.; Cai, Y. Recent Developments of Exploration and Detection of Shallow-Water Hydrothermal Systems. Sustainability 2020, 12, 9109. [Google Scholar] [CrossRef]
- Kanazawa, K.; Sano, T.G.; Cairoli, A.; Baule, A. Loopy Lévy flights enhance tracer diffusion in active suspensions. Nature 2020, 579, 364–367. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vo, D.N.; Dinh, B.H. A cuckoo bird-inspired meta-heuristic algorithm for optimal short-term hydrothermal generation cooperation. Cogent Eng. 2016, 3, 1266863. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vo, D.N.; Dao, T.T.; Dieu, V.N. Cuckoo search algorithm using different distributions for short-term hydrothermal scheduling with cascaded hydropower plants. In Proceedings of the TENCON 2014—2014 IEEE Region 10 Conference, Bangkok, Thailand, 22–25 October 2014. [Google Scholar]
- Nguyen, T.T.; Vo, D.N.; Truong, A.V. Cuckoo search algorithm for short-term hydrothermal scheduling. Appl. Energy 2014, 132, 276–287. [Google Scholar] [CrossRef]
- Basu, M. Economic environmental dispatch of hydrothermal power system. Int. J. Electr. Power Energy Syst. 2010, 32, 711–720. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vo, D.N. Modified cuckoo search algorithm for short-term hydrothermal scheduling. Int. J. Electr. Power Energy Syst. 2015, 65, 271–281. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vo, D.N.; Dinh, B.H. An effectively adaptive selective cuckoo search algorithm for solving three complicated short-term hydrothermal scheduling problems. Energy 2018, 155, 930–956. [Google Scholar] [CrossRef]
| Pa | Min Cost ($) | Avg. Cost ($) | Max Cost ($) | Std. dev. ($) | CPU (s) |
|---|---|---|---|---|---|
| 0.1 | 709,932.115 | 709,995.586 | 710,655.745 | 327.189 | 17.9 |
| 0.2 | 709,922.44 | 710,768.874 | 711,384.563 | 599.382 | 17.9 |
| 0.3 | 709,911.445 | 709,994.412 | 710,989.321 | 489.733 | 17.8 |
| 0.4 | 709,866.727 | 709,745.236 | 709,999.741 | 103.937 | 18.1 |
| 0.5 | 709,886.651 | 709,887.698 | 709,988.258 | 47.653 | 18.6 |
| 0.6 | 709,862.129 | 709,899.987 | 709,991.951 | 54.512 | 18.5 |
| 0.7 | 709,862.027 | 709,878.852 | 709,996.159 | 59.661 | 18.2 |
| 0.8 | 709,901.478 | 709,910.357 | 710,920.357 | 478.225 | 18.3 |
| 0.9 | 709,902.685 | 709,901.753 | 710,901.753 | 471.185 | 18.7 |
| m | PDm | Vm (acre-ft) | qm (acre-ft/hr) | Psm (MW) | Phm (MW) |
|---|---|---|---|---|---|
| 1 | 1199 | 101,897 | 1832 | 892 | 300 |
| 2 | 1497 | 85,959 | 3328 | 892 | 600 |
| 3 | 1098 | 93,847 | 1340 | 892 | 200 |
| 4 | 1795 | 59,998 | 4817 | 892 | 900 |
| 5 | 948 | 70,428 | 1124 | 783 | 158 |
| 6 | 1289 | 59,998 | 2863 | 783 | 509 |
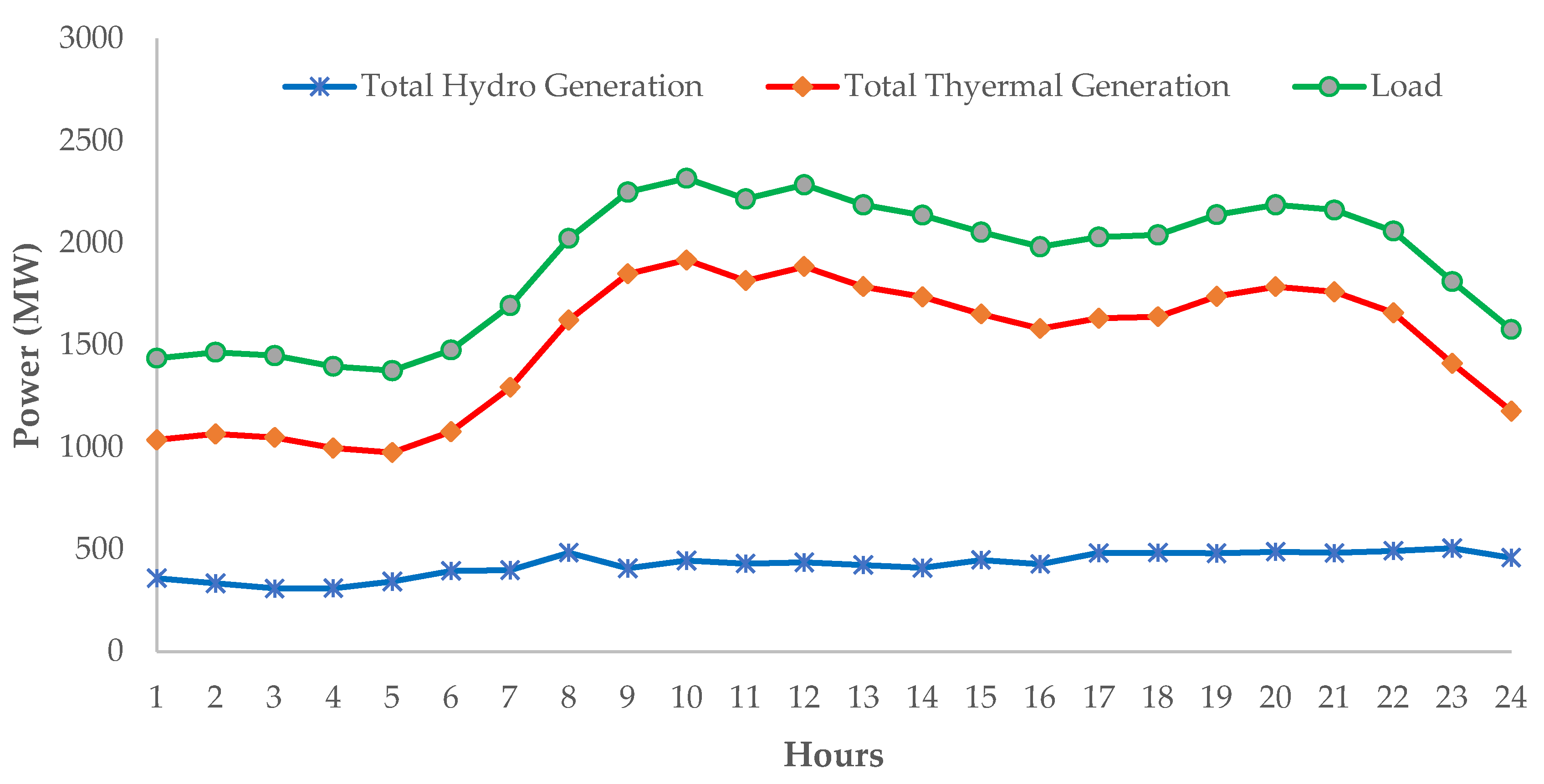
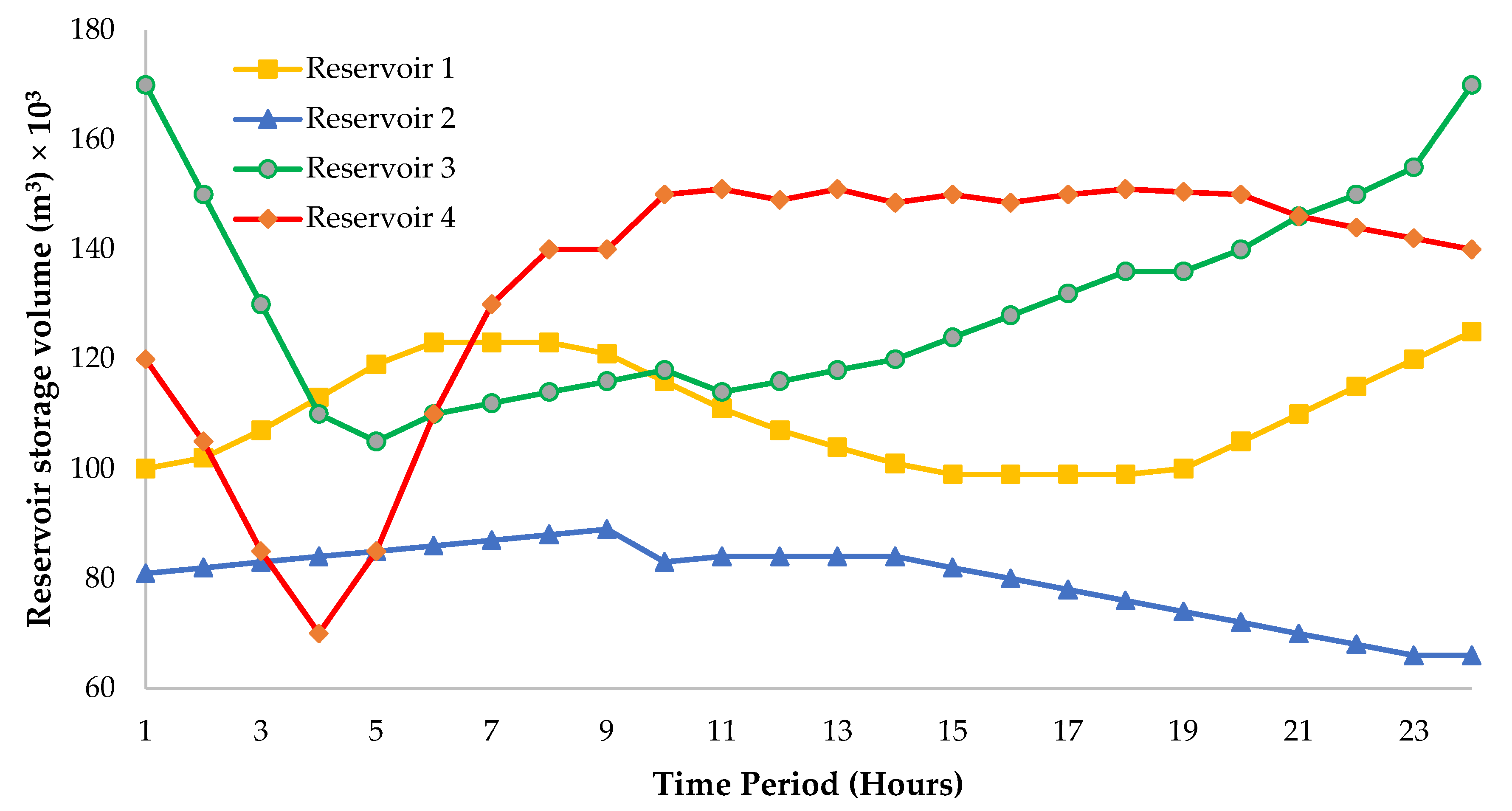
| Hours | Water Discharge (×104 m3) | Ps (MW) | |||
|---|---|---|---|---|---|
| Plant 1 | Plant 2 | Plant 3 | Plant 4 | ||
| 1 | 9.4884 | 6.1377 | 26.3477 | 13.1009 | 1036.249 |
| 2 | 9.4025 | 6.3104 | 25.2088 | 13.1024 | 1066.243 |
| 3 | 9.197 | 6.256 | 24.504 | 13.1035 | 1049.837 |
| 4 | 8.8096 | 6.3038 | 23.8832 | 13.1003 | 996.409 |
| 5 | 8.5269 | 6.2552 | 22.7287 | 13.1009 | 975.264 |
| 6 | 8.3314 | 6.4278 | 21.9238 | 13.1007 | 1076.828 |
| 7 | 8.4101 | 6.821 | 206226 | 13.1005 | 1294.982 |
| 8 | 8.6081 | 7.2309 | 19.2428 | 13.1023 | 1623.787 |
| 9 | 8.8072 | 7.3387 | 18.5775 | 13.1077 | 1849.655 |
| 10 | 8.465 | 7.5783 | 17.8006 | 13.1163 | 1917.3778 |
| 11 | 8.3429 | 7.7186 | 17.0931 | 13 | 1816.169 |
| 12 | 8.4121 | 7.8032 | 16.9969 | 13.4302 | 1885.493 |
| 13 | 8.2444 | 7.8624 | 16.3144 | 14.6742 | 1786.317 |
| 14 | 8.1224 | 8.0001 | 15.439 | 15.9371 | 1737.617 |
| 15 | 7.9417 | 8.1501 | 14.3596 | 17.2956 | 1652.815 |
| 16 | 7.8102 | 8.5518 | 12.9066 | 18.4244 | 1580.968 |
| 17 | 7.8153 | 8.9344 | 11.4353 | 20.0065 | 1630.883 |
| 18 | 7.6626 | 9.3193 | 10.1008 | 21.4157 | 1639.432 |
| 19 | 7.672 | 9.9655 | 10.1316 | 23.0205 | 1739.29 |
| 20 | 7.5945 | 10.5252 | 10.1043 | 24.2843 | 1787.795 |
| 21 | 7.3908 | 11.1875 | 12.1618 | 25.0985 | 1761.32 |
| 22 | 7.586 | 12.2327 | 12.747 | 25.0636 | 1659.735 |
| 23 | 7.5513 | 13.1386 | 13.2403 | 25.0994 | 1411.135 |
| 24 | 7.4103 | 14.2533 | 13.6662 | 25.0972 | 1177.636 |
| Techniques | Min Cost ($) | Average Cost ($) | Max Cost ($) | CPU Time (s) |
|---|---|---|---|---|
| GA [4] | 942,600 | 946,609.1 | 951,087 | 1920 |
| EGA [5] | 934,727.00 | 936,058.00 | 937,339.00 | --- |
| FEP [6] | 930,267.92 | 930,897.44 | 931,396.81 | 1911.2 |
| CEP [6] | 930,166.25 | 930,373.23 | 930,927.01 | 2292.1 |
| IFEP [6] | 930,129.82 | 930,290.13 | 930,881.92 | 1033.2 |
| PSO [5] | 928,878.00 | 933,085.00 | 938,012.00 | --- |
| CSA-Lévy [26] | 927,934.23 | 927,980.45 | 928,000.66 | 79.08 |
| CSA Cauchy [26] | 927,967.66 | 927,981.49 | 927,992.53 | 81.30 |
| CSA Gauss [26] | 927,957.26 | 927,978.911 | 928,003.23 | 85.75 |
| APSO [7] | 926,151.54 | --- | --- | --- |
| EPSO [5] | 922,904.00 | 923,527.00 | 924,808.00 | --- |
| MDE [8] | 922,555.44 | --- | --- | --- |
| IPSO [9] | 922,553.49 | --- | --- | --- |
| MAPSO [7] | 922,421.66 | 922,544.00 | 923,508.00 | --- |
| TLBO [10] | 922,373.39 | 922,462.24 | 922,873.81 | --- |
| CSA [20] | 913,945.87 | 917,624.024 | 921,994.25 | --- |
| RIFEP [12] | 709,862.05 | --- | --- | --- |
| GS [13] | 709,877.38 | --- | --- | --- |
| SA [14] | 709,874.36 | --- | --- | 901 |
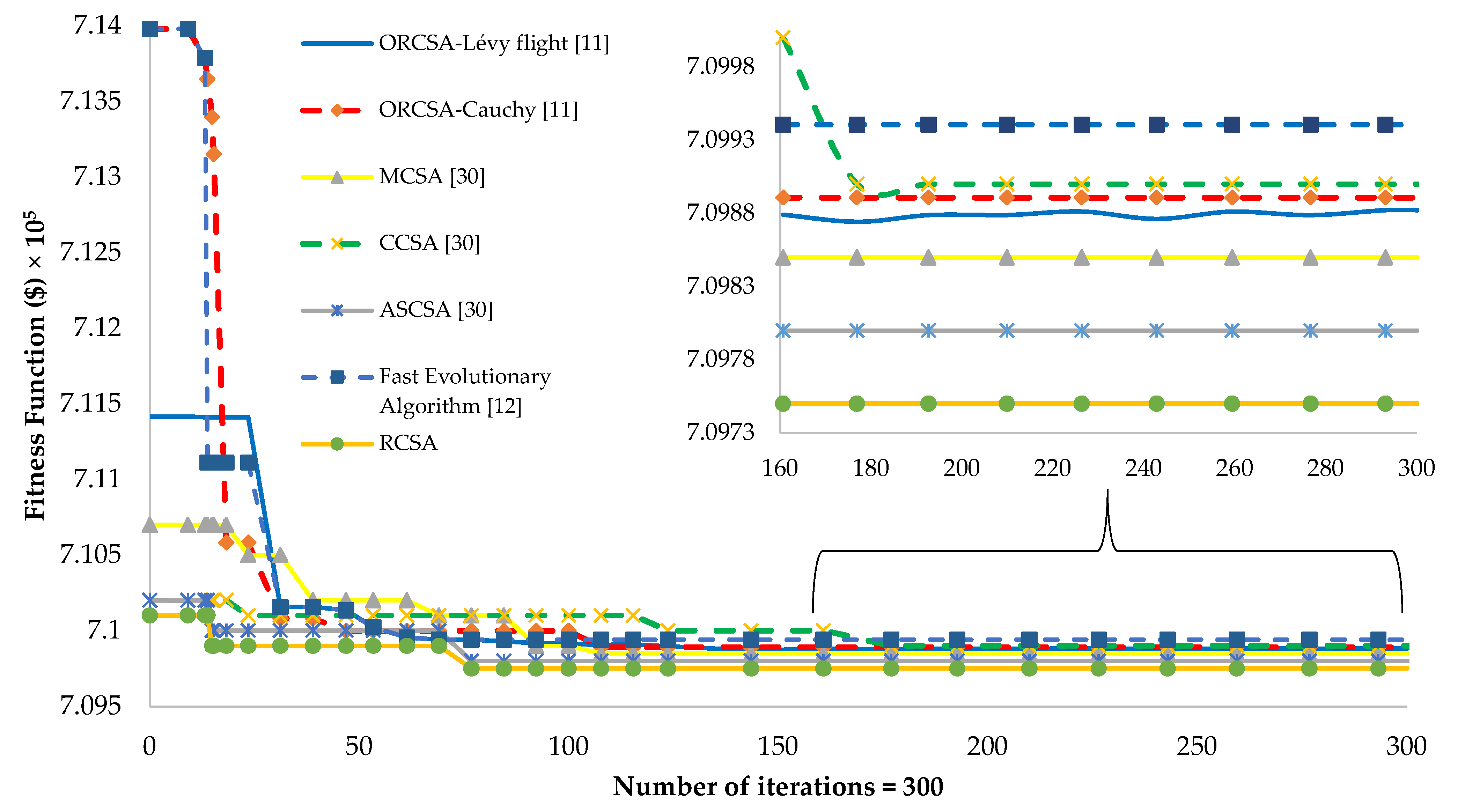
| ORCSA–Lévy flight [11] | 709,862.048 | --- | --- | 18 |
| ORCSA–Cauchy [11] | 709,862.048 | --- | --- | 18 |
| Proposed RCSA | 709,862.027 | --- | --- | 17 |
| Techniques | Min Cost ($) | Average Cost ($) | Max Cost ($) | CPU Time (s) |
|---|---|---|---|---|
| SA [27] | 47,306 | -- | -- | -- |
| CEP [27] | 45,466 | -- | -- | -- |
| CEP-IFS [25] | 45,036.00 | -- | -- | -- |
| PSO [27] | 44,740 | -- | -- | -- |
| DE [28] | 44,526.1 | -- | -- | 200 |
| MDE [28] | 42,611.14 | -- | -- | 125 |
| CSR [15] | 42,440 | -- | -- | 109 |
| TLBO [10] | 42,385.88 | 42,407.23 | 42,441.36 | -- |
| HDE [28] | 42,337.3 | -- | -- | 48 |
| SQP [17] | 42,120.02 | -- | -- | 625.07 |
| KHA [16] | 41,926 | -- | -- | -- |
| MHDE [28] | 41,856.5 | -- | -- | 31 |
| CSA [25] | 41,046.897 | -- | -- | 94.4 |
| Proposed RCSA | 41,013.09 | 41,401.5 | 41,789.9 | 17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheyuan, C.; Hammid, A.T.; Kareem, A.N.; Jiang, M.; Mohammed, M.N.; Kumar, N.M. A Rigid Cuckoo Search Algorithm for Solving Short-Term Hydrothermal Scheduling Problem. Sustainability 2021, 13, 4277. https://doi.org/10.3390/su13084277
Zheyuan C, Hammid AT, Kareem AN, Jiang M, Mohammed MN, Kumar NM. A Rigid Cuckoo Search Algorithm for Solving Short-Term Hydrothermal Scheduling Problem. Sustainability. 2021; 13(8):4277. https://doi.org/10.3390/su13084277
Chicago/Turabian StyleZheyuan, Cui, Ali Thaeer Hammid, Ali Noori Kareem, Mingxin Jiang, Muamer N. Mohammed, and Nallapaneni Manoj Kumar. 2021. "A Rigid Cuckoo Search Algorithm for Solving Short-Term Hydrothermal Scheduling Problem" Sustainability 13, no. 8: 4277. https://doi.org/10.3390/su13084277
APA StyleZheyuan, C., Hammid, A. T., Kareem, A. N., Jiang, M., Mohammed, M. N., & Kumar, N. M. (2021). A Rigid Cuckoo Search Algorithm for Solving Short-Term Hydrothermal Scheduling Problem. Sustainability, 13(8), 4277. https://doi.org/10.3390/su13084277







