Effect of Chia Seed Mucilage on the Rhizosphere Hydraulic Characteristics
Abstract
1. Introduction
2. Materials and Methods
2.1. Mucilage Extraction
2.2. Artificial Rhizosphere Preparation
2.3. Soil Sample Preparation
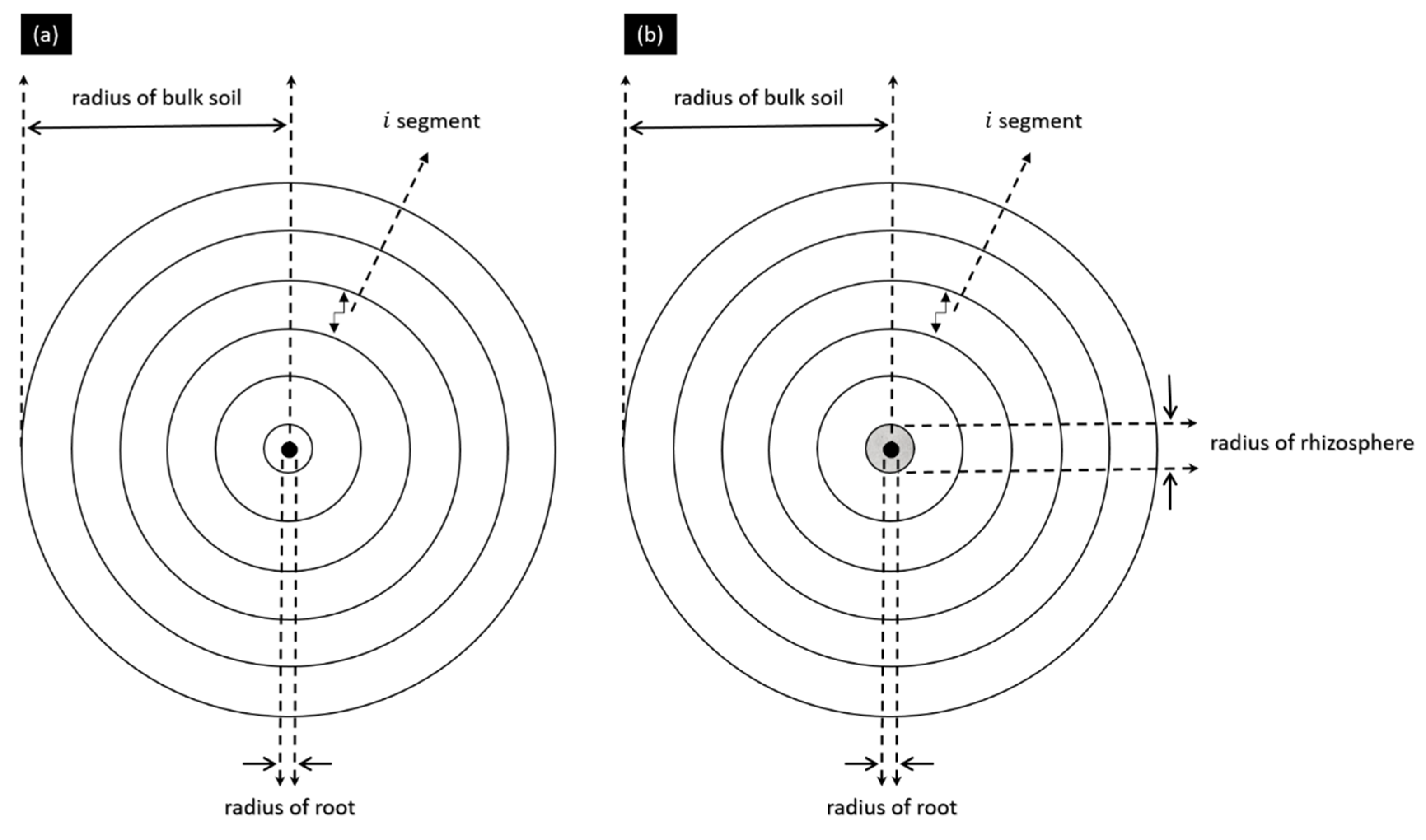
2.4. Experimental Setup
2.5. Numerical Modelling
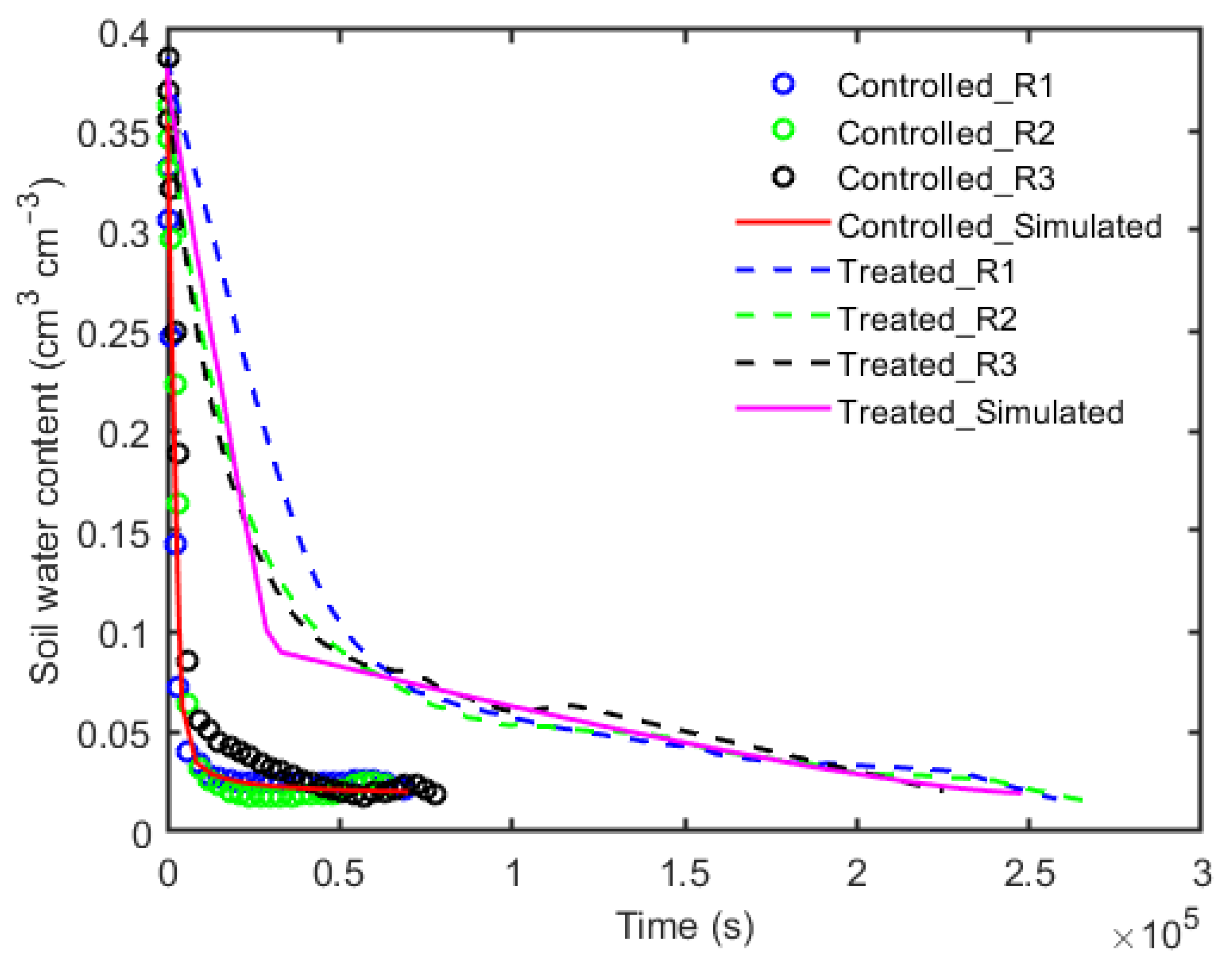
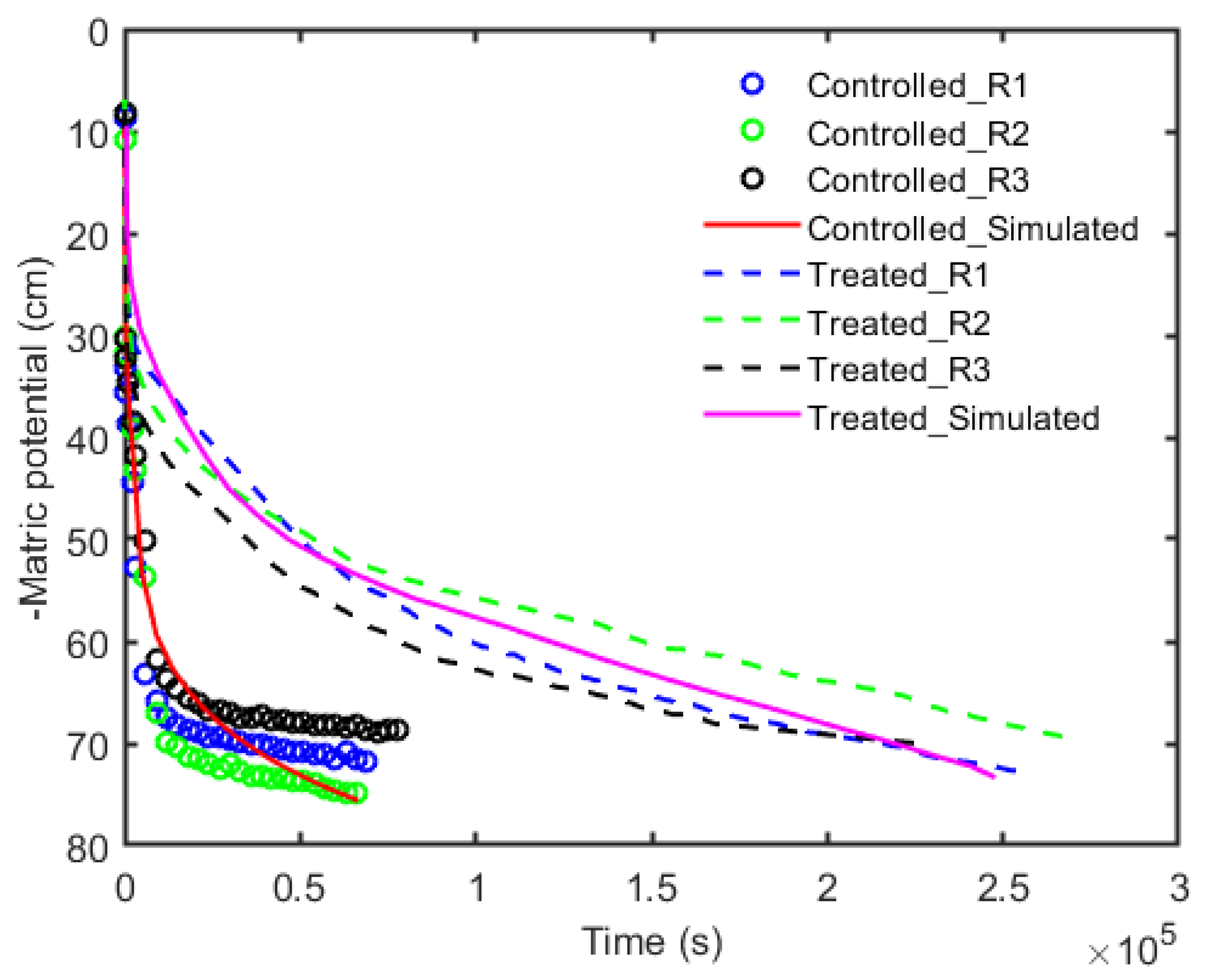
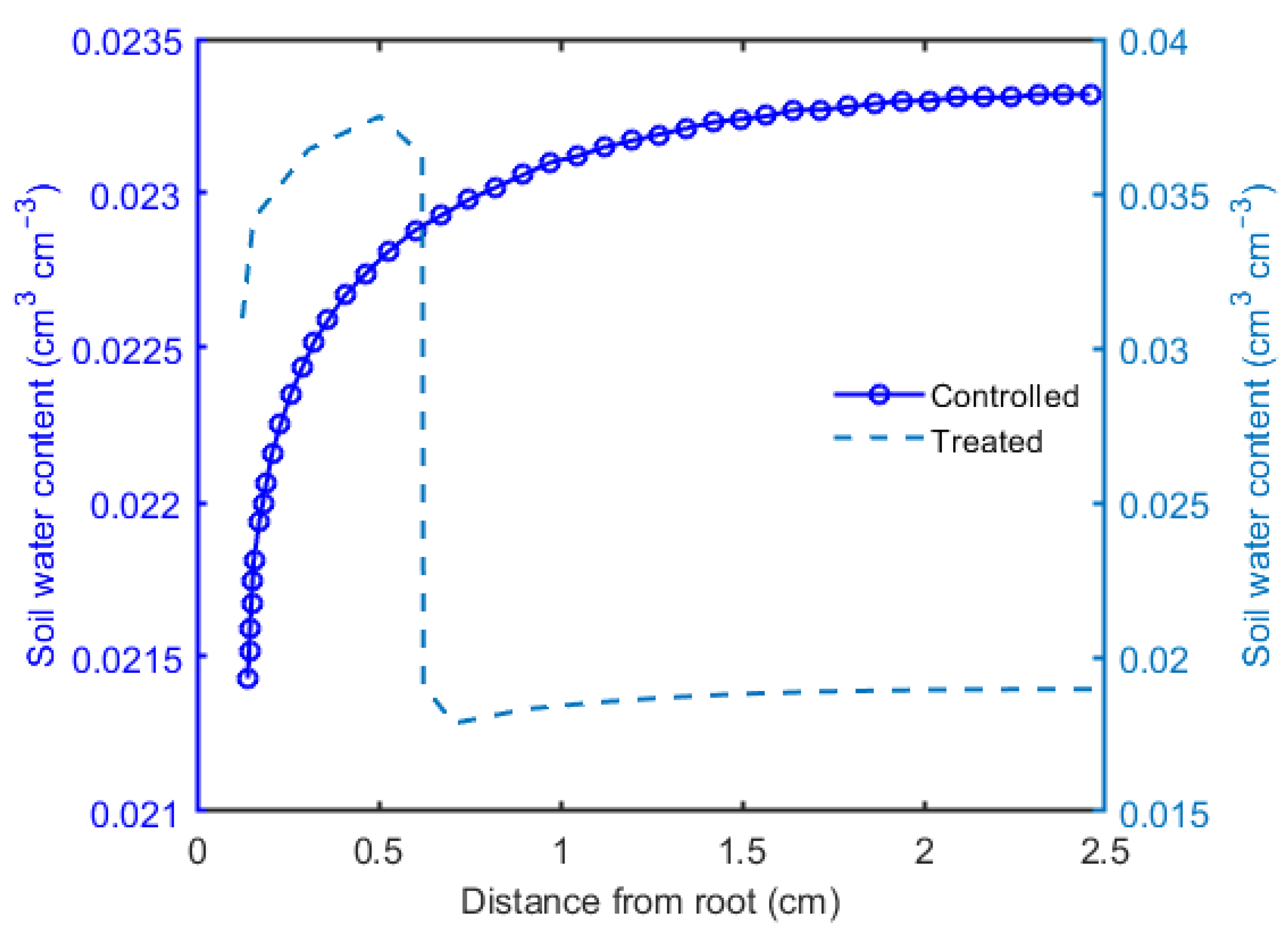
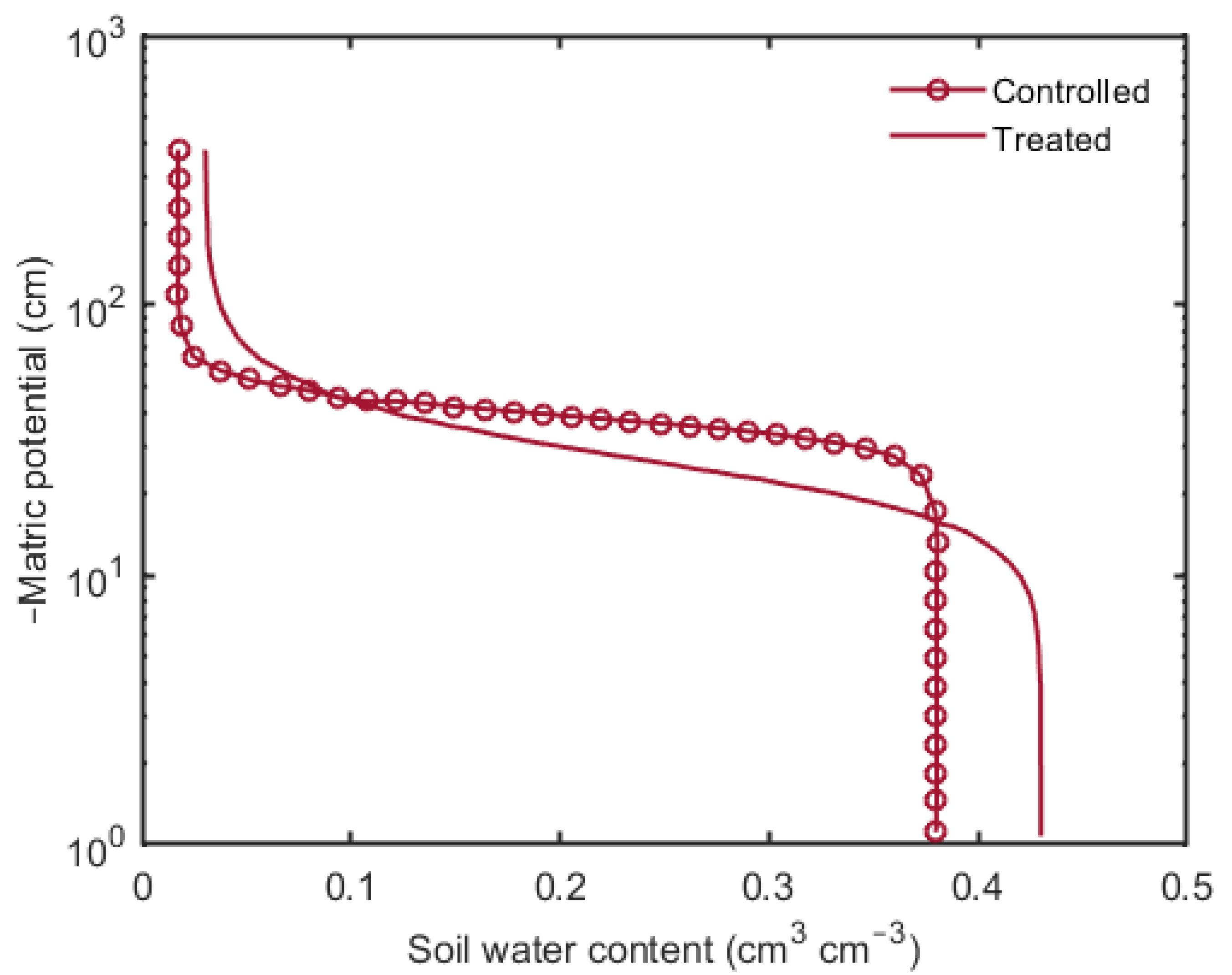
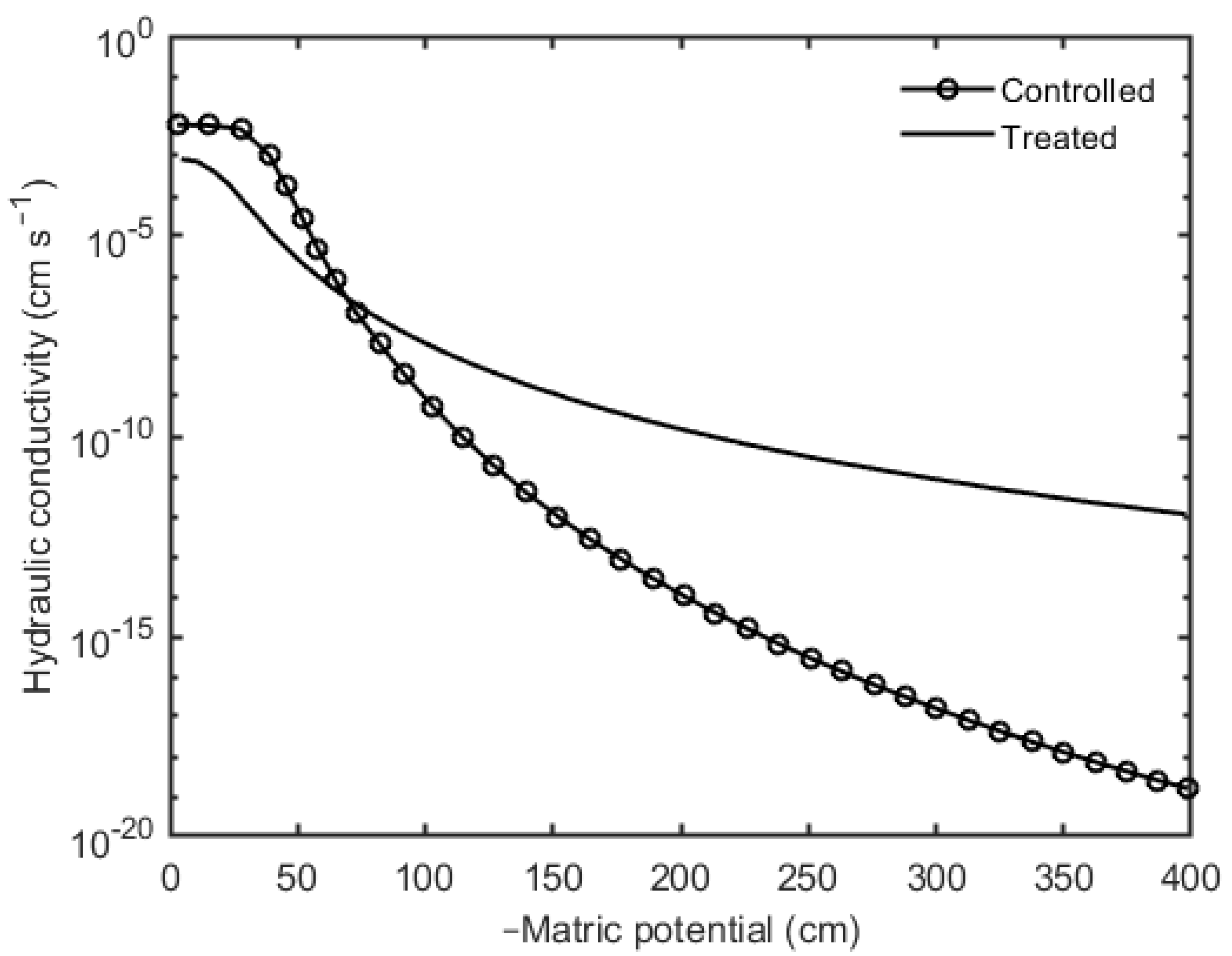
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Martin-StPaul, N.; Delzon, S.; Cochard, H. Plant resistance to drought depends on timely stomatal closure. Ecol. Lett. 2017, 20, 1437–1447. [Google Scholar] [CrossRef]
- Lynch, J.P. Steep, cheap and deep: An ideotype to optimize water and N acquisition by maize root systems. Ann. Bot. 2013, 112, 347–357. [Google Scholar] [CrossRef] [PubMed]
- Sharp, R.E.; Davies, W.J. Root growth and water uptake by maize plants in drying soil. J. Exp. Bot. 1985, 36, 1441–1456. [Google Scholar] [CrossRef]
- Zegada-Lizarazu, W.; Iijima, M. Hydrogen stable isotope analysis of water acquisition ability of deep roots and hydraulic lift in sixteen food crop species. Plant Prod. Sci. 2004, 7, 427–434. [Google Scholar] [CrossRef]
- Doussan, C.; Pierret, A.; Garrigues, E.; Pagès, L. Water uptake by plant roots: II—Modelling of water transfer in the soil root-system with explicit account of flow within the root system—Comparison with experiments. Plant Soil 2006, 283, 99–117. [Google Scholar] [CrossRef]
- Hayat, F.; Ahmed, M.A.; Zarebanadkouki, M.; Cai, G.; Carminati, A. Measurements and simulation of leaf xylem water potential and root water uptake in heterogeneous soil water contents. Adv. Water Resour. 2018, 124, 96–105. [Google Scholar] [CrossRef]
- Caldwell, M.M.; Richards, J.H. Hydraulic lift: Water efflux from upper roots improves effectiveness of water uptake by deep roots. Oecologia 1989, 79, 1–5. [Google Scholar] [CrossRef]
- Brooks, J.R.; Meinzer, F.C.; Coulombe, R.; Gregg, J. Hydraulic redistribution of soil water during summer drought in two contrasting Pacific Northwest coniferous forests. Tree Physiol. 2002, 22, 1107–1117. [Google Scholar] [CrossRef]
- Smart, D.R.; Carlisle, E.; Goebel, M.; Núñez, B.A. Transverse hydraulic redistribution by a grapevine. Plant Cell Environ. 2005, 28, 157–166. [Google Scholar] [CrossRef]
- Hayat, F.; Zarebanadkouki, M.; Ahmed, M.A.; Buecherl, T.; Carminati, A. Quantification of hydraulic redistribution in maize roots using neutron radiography. Vadose Zone J. 2020, 99, 1–10. [Google Scholar] [CrossRef]
- Philippot, L.; Raaijmakers, J.M.; Lemanceau, P.; Van Der Putten, W.H. Going back to the roots: The microbial ecology of the rhizosphere. Nat. Rev. Microbiol. 2013, 11, 789–799. [Google Scholar] [CrossRef]
- Gregory, P.J. Roots, rhizosphere and soil: The route to a better understanding of soil science? Eur. J. Soil Sci. 2006, 57, 2–12. [Google Scholar] [CrossRef]
- Hinsinger, P.; Bengough, A.G.; Vetterlein, D.; Young, I.M. Rhizosphere: Biophysics, biogeochemistry and ecological relevance. Plant Soil 2009, 321, 117–152. [Google Scholar] [CrossRef]
- Carminati, A.; Moradi, A.B.; Vetterlein, D.; Vontobel, P.; Lehmann, E.; Weller, U.; Vogel, H.J.; Oswald, S.E. Dynamics of soil water content in the rhizosphere. Plant Soil 2010, 332, 163–176. [Google Scholar] [CrossRef]
- Young, I.M. Variation in moisture contents between bulk soil and the rhizosheath of wheat (Triticum aestivum L. cv. Wembley). New Phytol. 1995, 130, 135–139. [Google Scholar] [CrossRef]
- Naveed, M.; Brown, L.K.; Raffan, A.C.; George, T.S.; Bengough, A.G.; Roose, T.; Sinclair, I.; Koebernick, N.; Cooper, L.; Hackett, C.A.; et al. Plant exudates may stabilize or weaken soil depending on species, origin and time: Effect of plant exudates on rhizosphere formation. Eur. J. Soil Sci. 2017, 68, 806–816. [Google Scholar] [CrossRef]
- Flemming, H.C.; Wingender, J. Relevance of microbial extracellular polymeric substances (EPSs)—Part I: Structural and ecological aspects. Water Sci. Technol. 2001, 43, 1–8. [Google Scholar] [CrossRef]
- Aravena, J.E.; Berli, M.; Ghezzehei, T.A.; Tyler, S.W. Effects of root-induced compaction on rhizosphere hydraulic properties - X-ray microtomography imaging and numerical simulations. Environ. Sci. Technol. 2011, 45, 425–431. [Google Scholar] [CrossRef]
- Sposito, G. Green Water and Global Food Security. Vadose Zone J. 2013, 12, 2–6. [Google Scholar] [CrossRef]
- Carminati, A.; Javaux, M. Soil Rather Than Xylem Vulnerability Controls Stomatal Response to Drought. Trends Plant Sci. 2020, 25, 868–880. [Google Scholar] [CrossRef]
- Hayat, F.; Ahmed, M.A.; Zarebanadkouki, M.; Javaux, M.; Cai, G.; Carminati, A. Transpiration Reduction in Maize (Zea mays L) in Response to Soil Drying. Front. Plant Sci. 2020, 10, 1695. [Google Scholar] [CrossRef]
- Rodriguez-Dominguez, C.M.; Brodribb, T.J. Declining root water transport drives stomatal closure in olive under moderate water stress. New Phytol. 2020, 225, 126–134. [Google Scholar] [CrossRef]
- Abdalla, M.; Carminati, A.; Cai, G.; Javaux, M.; Ahmed, M.A. Stomatal closure of tomato under drought is driven by an increase in soil-root hydraulic resistance. Plant Cell Environ. 2021, 44, 425–431. [Google Scholar] [CrossRef]
- Cuneo, I.F.; Knipfer, T.; Brodersen, C.R.; McElrone, A.J. Mechanical failure of fine root cortical cells initiates plant hydraulic decline during drought. Plant Physiol. 2016, 172, 1669–1678. [Google Scholar] [CrossRef]
- Carminati, A.; Ahmed, M.A.; Zarebanadkouki, M.; Cai, G.; Lovric, G.; Javaux, M. Stomatal closure prevents the drop in soil water potential around roots. New Phytol. 2020, 226, 1541–1543. [Google Scholar] [CrossRef] [PubMed]
- Zha, J.; Roggendorf, H. Sol-gel science, the physics and chemistry of sol-gel processing, Ed. by C. J. Brinker and G. W. Scherer, Academic Press, Boston 1990, xiv, 908 pp., bound?ISBN 0-12-134970-5. Adv. Mater. 1991, 3, 522. [Google Scholar] [CrossRef]
- Flemming, H.C.; Wingender, J. The biofilm matrix. Nat. Rev. Microbiol. 2010, 8, 623–633. [Google Scholar] [CrossRef] [PubMed]
- Read, D.B.; Gregory, P.J. Surface tension and viscosity of axenic maize and lupin root mucilages. New Phytol. 1997, 137, 623–628. [Google Scholar] [CrossRef]
- Read, D.B.; Gregory, P.J.; Bell, A.E. Physical properties of axenic maize root mucilage. Plant Soil 1999, 211, 87–91. [Google Scholar] [CrossRef]
- Segura-Campos, M.R.; Ciau-Solís, N.; Rosado-Rubio, G.; Chel-Guerrero, L.; Betancur-Ancona, D. Chemical and functional properties of chia seed (Salvia hispanica L.) gum. Int. J. Food Sci. 2014, 2014, 1–5. [Google Scholar] [CrossRef]
- McCully, M.E.; Boyer, J.S. The expansion of maize root-cap mucilage during hydration. 3. Changes in water potential and water content. Physiol. Plant. 1997, 99, 169–177. [Google Scholar] [CrossRef]
- Read, D.B.; Bengough, A.G.; Gregory, P.J.; Crawford, J.W.; Robinson, D.; Scrimgeour, C.M.; Young, I.M.; Zhang, K.; Zhang, X. Plant roots release phospholipid surfactants that modify the physical and chemical properties of soil. New Phytol. 2003, 157, 315–326. [Google Scholar] [CrossRef]
- Raaijmakers, J.M.; de Bruijn, I.; Nybroe, O.; Ongena, M. Natural functions of lipopeptides from Bacillus and Pseudomonas: More than surfactants and antibiotics. FEMS Microbiol. Rev. 2010, 34, 1037–1062. [Google Scholar] [CrossRef] [PubMed]
- Naveed, M.; Brown, L.K.; Raffan, A.C.; George, T.S.; Bengough, A.G.; Roose, T.; Sinclair, I.; Koebernick, N.; Cooper, L.; Hallett, P.D. Rhizosphere-Scale Quantification of Hydraulic and Mechanical Properties of Soil Impacted by Root and Seed Exudates. Vadose Zone J. 2018, 17, 170083. [Google Scholar] [CrossRef]
- Moradi, A.B.; Carminati, A.; Vetterlein, D.; Vontobel, P.; Lehmann, E.; Weller, U.; Hopmans, J.W.; Vogel, H.-J.; Oswald, S.E. Three-dimensional visualization and quantification of water content in the rhizosphere. New Phytol. 2011, 192, 653–663. [Google Scholar] [CrossRef]
- Carminati, A.; Vetterlein, D. Plasticity of rhizosphere hydraulic properties as a key for efficient utilization of scarce resources. Ann. Bot. 2013, 112, 277–290. [Google Scholar] [CrossRef] [PubMed]
- Lin, K.Y.; Daniel, J.R.; Whistler, R.L. Structure of chia seed polysaccharide exudate. Carbohydr. Polym. 1994, 23, 13–18. [Google Scholar] [CrossRef]
- Singh, B.; Chauhan, G.S.; Kumar, S.; Chauhan, N. Synthesis, characterization and swelling responses of pH sensitive psyllium and polyacrylamide based hydrogels for the use in drug delivery (I). Carbohydr. Polym. 2007, 67, 190–200. [Google Scholar] [CrossRef]
- Steudle, E. Water uptake by plant roots: An integration of views. Plant Soil 2000, 226, 45–56. [Google Scholar] [CrossRef]
- Maurel, C.; Verdoucq, L.; Luu, D.T.; Santoni, V. Plant aquaporins: Membrane channels with multiple integrated functions. Annu. Rev. Plant Biol. 2008, 59, 595–624. [Google Scholar] [CrossRef]
- Benard, P.; Zarebanadkouki, M.; Brax, M.; Kaltenbach, R.; Jerjen, I.; Marone, F.; Couradeau, E.; Felde, V.J.M.N.L.; Kaestner, A.; Carminati, A. Microhydrological Niches in Soils: How Mucilage and EPS Alter the Biophysical Properties of the Rhizosphere and Other Biological Hotspots. Vadose Zone J. 2019, 18, 1–10. [Google Scholar] [CrossRef]
- Kroener, E.; Holz, M.; Zarebanadkouki, M.; Ahmed, M.; Carminati, A. Effects of Mucilage on Rhizosphere Hydraulic Functions Depend on Soil Particle Size. Vadose Zone J. 2018, 17, 170056. [Google Scholar] [CrossRef]
- GUINEL, F.C.; McCULLY, M.E. Some water-related physical properties of maize root-cap mucilage. Plant Cell Environ. 1986, 9, 657–666. [Google Scholar] [CrossRef]
- Ahmed, M.A.; Kroener, E.; Holz, M.; Zarebanadkouki, M.; Carminati, A. Mucilage exudation facilitates root water uptake in dry soils. Funct. Plant Biol. 2014, 41, 1129–1137. [Google Scholar] [CrossRef] [PubMed]
- Carminati, A.; Schneider, C.L.; Moradi, A.B.; Zarebanadkouki, M.; Vetterlein, D.; Vogel, H.-J.; Hildebrandt, A.; Weller, U.; Schüler, L.; Oswald, S.E. How the Rhizosphere May Favor Water Availability to Roots. Vadose Zone J. 2011, 10, 988–998. [Google Scholar] [CrossRef]
- Dakora, F.D.; Phillips, D.A. Root exudates as mediators of mineral acquisition in low-nutrient environments. Plant Soil 2002, 245, 35–47. [Google Scholar] [CrossRef]
- Benard, P. Microhydrological Niches in Soils: How Mucilage and EPS alter Soil Hydraulic Properties and Water Dynamics. Ph.D. Thesis, University of Bayreuth, Bayreuth, Germany, 2020. [Google Scholar]
- Kroener, E.; Zarebanadkouki, M.; Kaestner, A.; Carminati, A. Nonequilibrium water dynamics in the rhizosphere: How mucilage affects water flow in soils. Water Resour. Res. 2014, 50, 6479–6495. [Google Scholar] [CrossRef]
- Kroener, E.; Zarebanadkouki, M.; Bittelli, M.; Carminati, A. Simulation of root water uptake under consideration of nonequilibrium dynamics in the rhizosphere. Water Resour. Res. 2016, 52, 5755–5770. [Google Scholar] [CrossRef]
- Carminati, A.; Zarebanadkouki, M.; Kroener, E.; Ahmed, M.A.; Holz, M. Biophysical rhizosphere processes affecting root water uptake. Ann. Bot. 2016, 118, 561–571. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.; Hallett, P.D.; Jeng, D.S.; Squire, G.R.; Toorop, P.E.; Iannetta, P.P.M. The effect of natural seed coatings of Capsella bursa-pastoris L. Medik. (shepherd’s purse) on soil-water retention, stability and hydraulic conductivity. Plant Soil 2015, 387, 167–176. [Google Scholar] [CrossRef]

| Intrinsic Properties | Root Mucilage | Seed Mucilage |
|---|---|---|
| Viscosity | Viscosity increases with increase in concentration of root exudate | Viscosity increases with increase in concentration of seed exudate |
| Water Adsorption | Up to 5.25 g water/g exudate | Up to 44 g water/g mucilage |
| Surface tension | Surface tension decreases with increase in concentration of root exudate | Surface tension decreases with increase in concentration of seed exudate |
| Parameters | (-) | (-) | (cm−1) | (-) | (cm s−1) | (-) | (cm s−1) |
|---|---|---|---|---|---|---|---|
| Lower Limit | 0.34 | 0.017 | 0.001 | 3 | 0.07 × 10−4 | −6 | 0.1 × 10−6 |
| Upper Limit | 0.47 | 0.06 | 0.06 | 10 | 0.01 | 6 | 10 × 10−6 |
| Parameters | (-) | (-) | (cm−1) | (-) | (cm s−1) | (-) | (cm s−1) |
|---|---|---|---|---|---|---|---|
| Controlled | 0.3803 | 0.0170 | 0.0260 | 8.0875 | 0.0060 | 0.0883 | 1 × 10−6 |
| Treated | 0.4302 | 0.0300 | 0.0409 | 3.8000 | 0.0009 | −0.1676 | 6.58 × 10−7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayat, F.; Abdalla, M.; Munir, M.U. Effect of Chia Seed Mucilage on the Rhizosphere Hydraulic Characteristics. Sustainability 2021, 13, 3303. https://doi.org/10.3390/su13063303
Hayat F, Abdalla M, Munir MU. Effect of Chia Seed Mucilage on the Rhizosphere Hydraulic Characteristics. Sustainability. 2021; 13(6):3303. https://doi.org/10.3390/su13063303
Chicago/Turabian StyleHayat, Faisal, Mohanned Abdalla, and Muhammad Usman Munir. 2021. "Effect of Chia Seed Mucilage on the Rhizosphere Hydraulic Characteristics" Sustainability 13, no. 6: 3303. https://doi.org/10.3390/su13063303
APA StyleHayat, F., Abdalla, M., & Munir, M. U. (2021). Effect of Chia Seed Mucilage on the Rhizosphere Hydraulic Characteristics. Sustainability, 13(6), 3303. https://doi.org/10.3390/su13063303





