Predict the Influence of Environmental Vibration from High-Speed Railway on Over-Track Buildings
Abstract
:1. Introduction
2. A Simulation of the Vertical Vibration Load from a Train
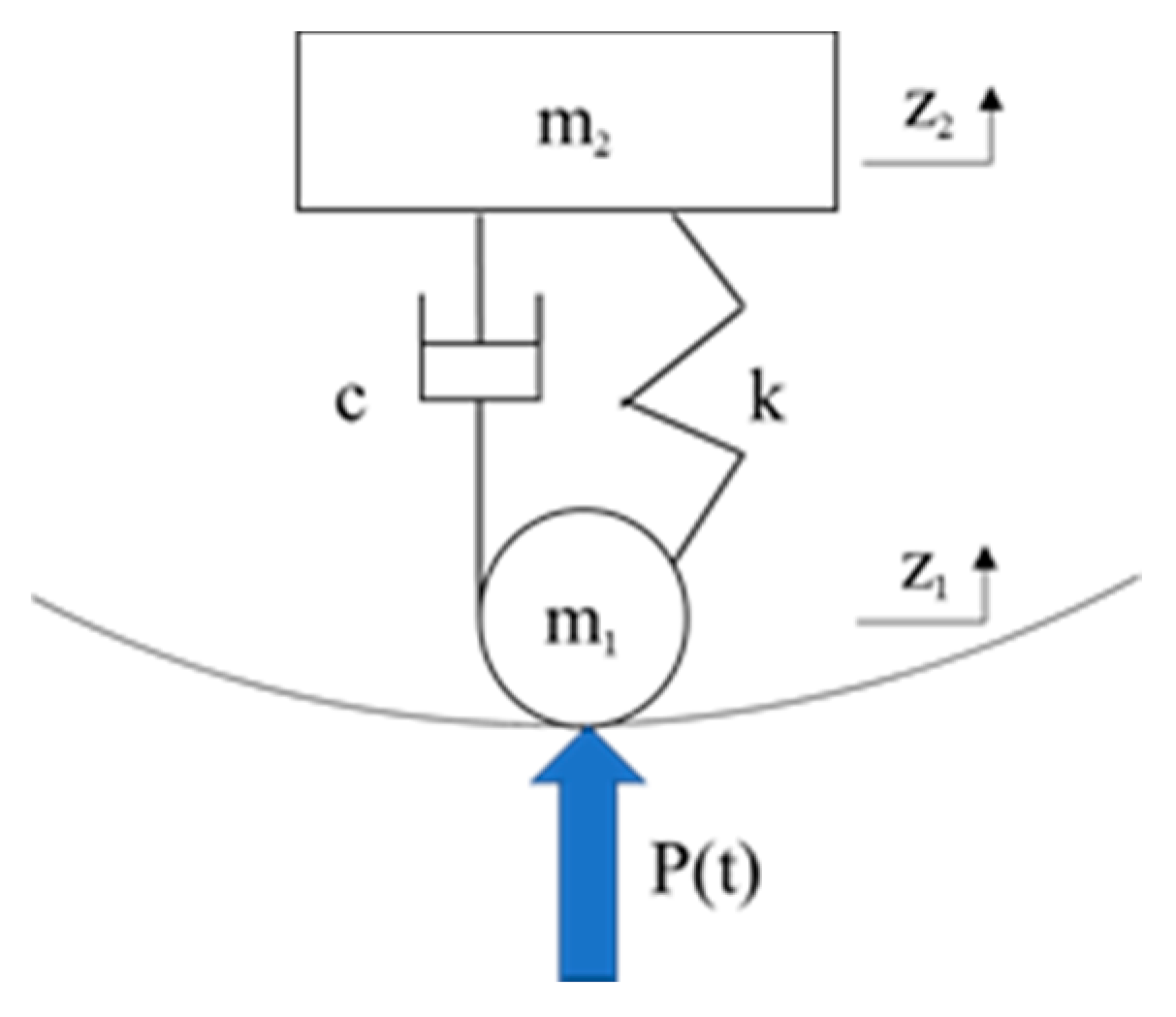
2.1. A Simplified Model of Vertical Vibration of a Train
2.2. Fourier Transformation of Vertical Vibration Acceleration of Rails
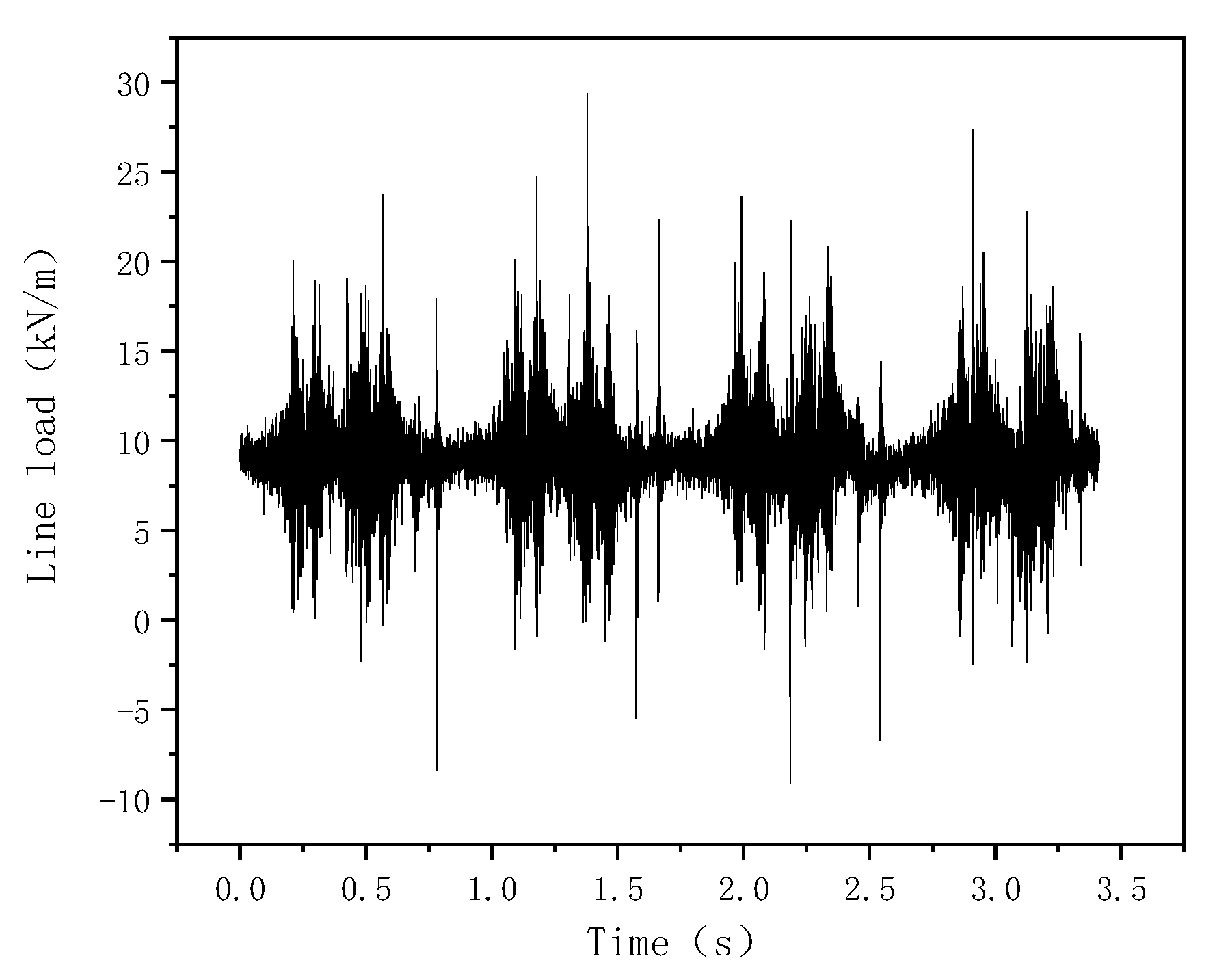
2.3. Equivalent Load of Vertical Vibration of a Train
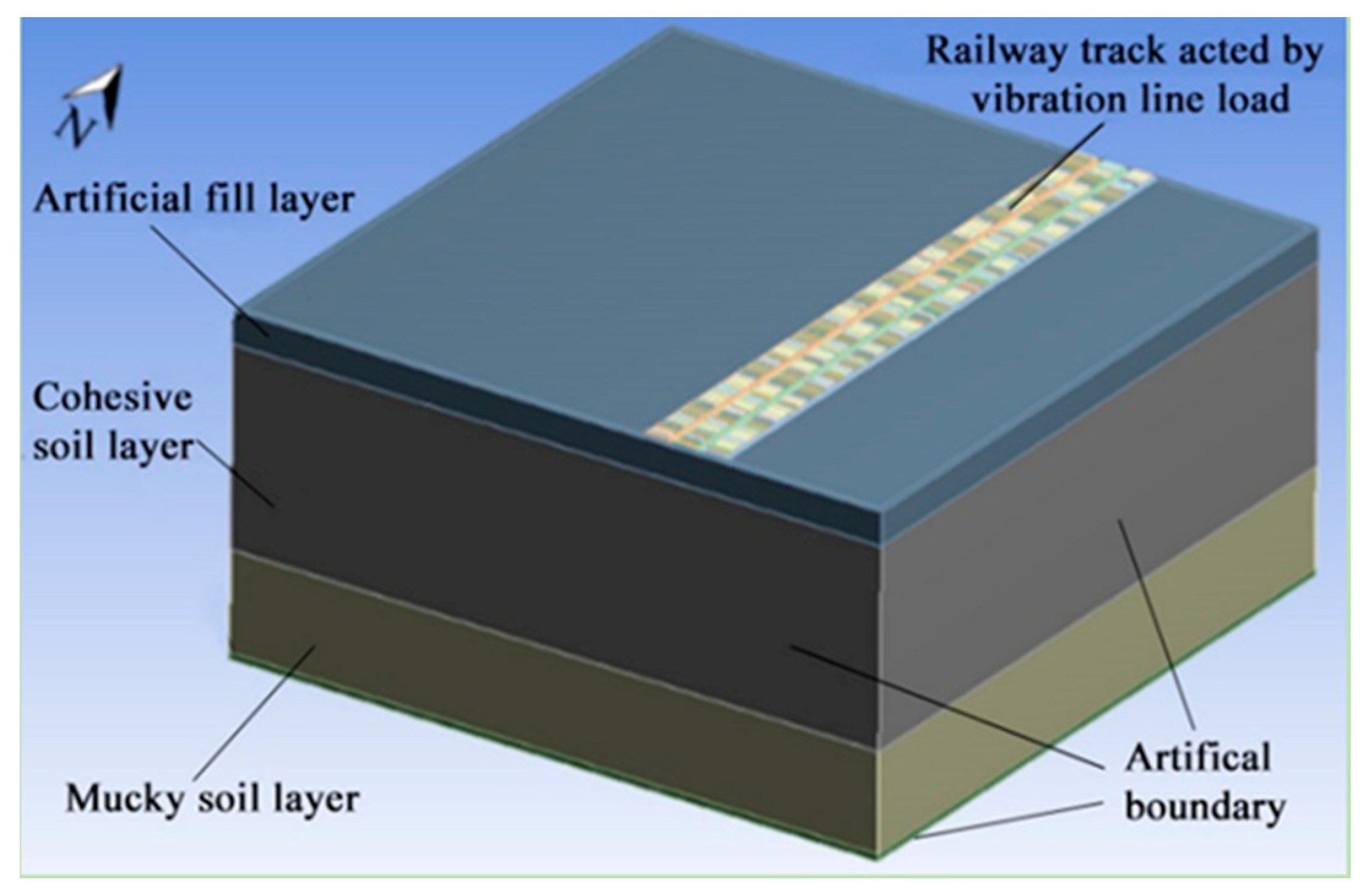
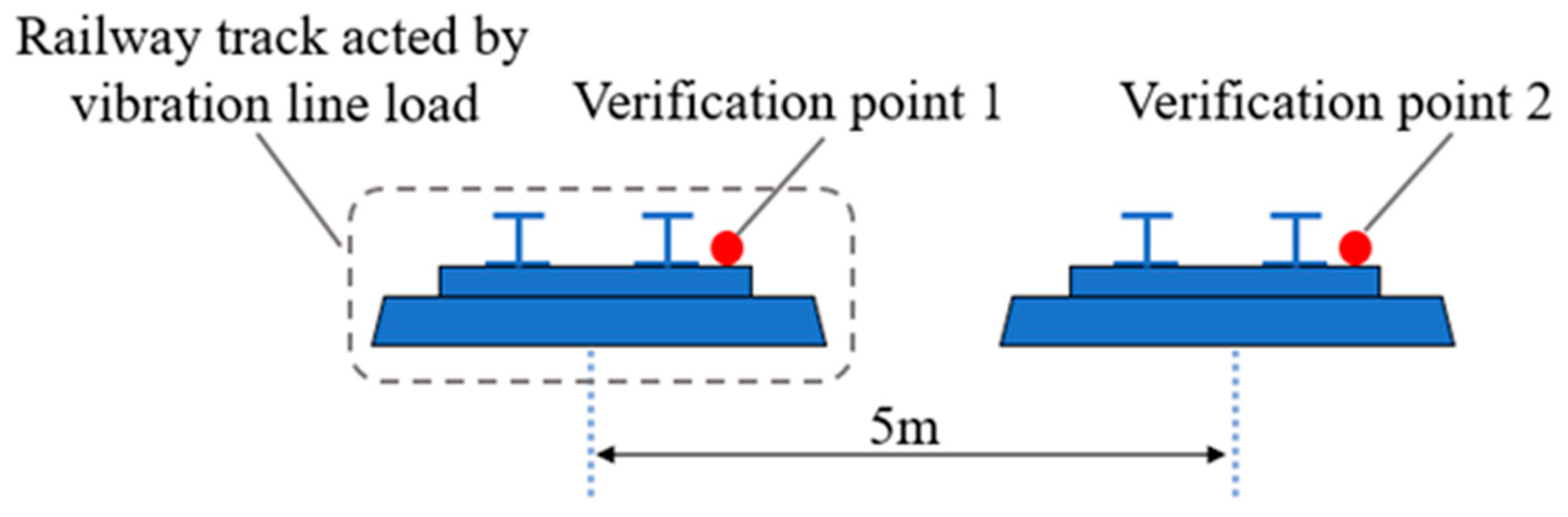
3. An Finite Element Model and Its Verification of Reasonability
4. A Single Factor Analysis of Environmental Vibration Influence on Over-Track Buildings
4.1. A Simulation Model and Its Parameters Setting
4.2. An Analysis of Influence Factors on Environmental Vibration
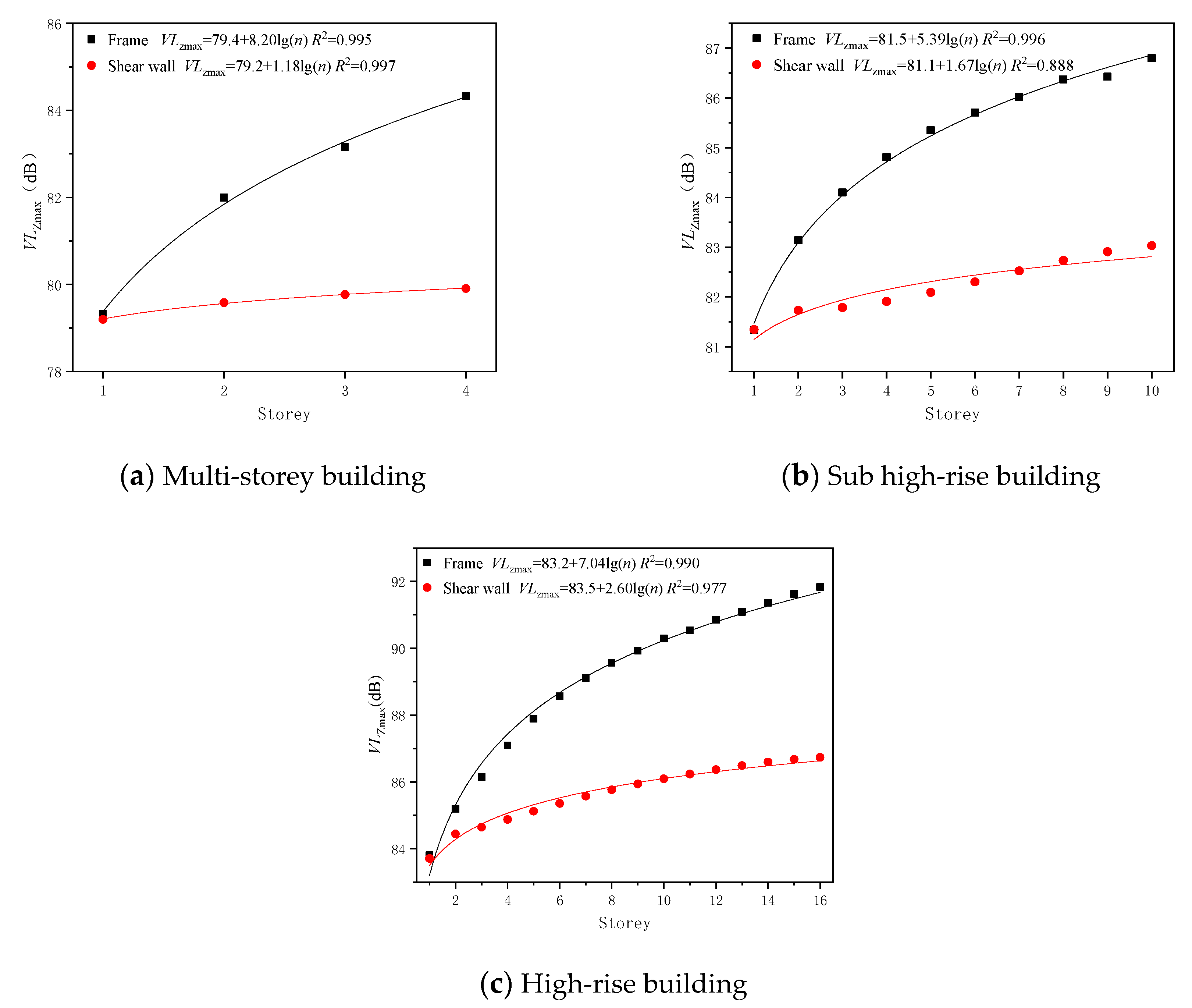
4.2.1. The Influence of Building Structure Type and Total Storey Number
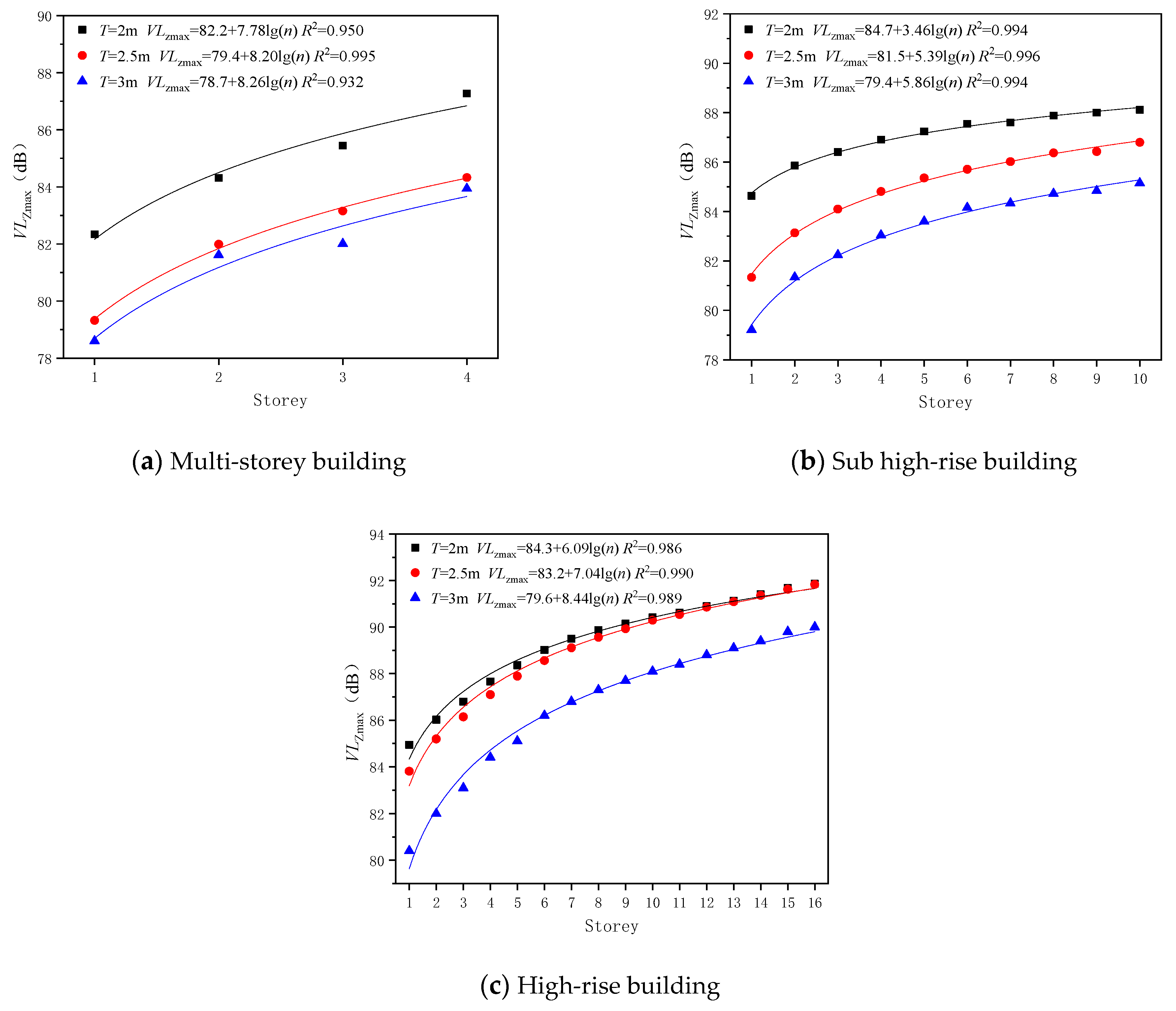
4.2.2. The Influence of Over-Track Platform Thickness
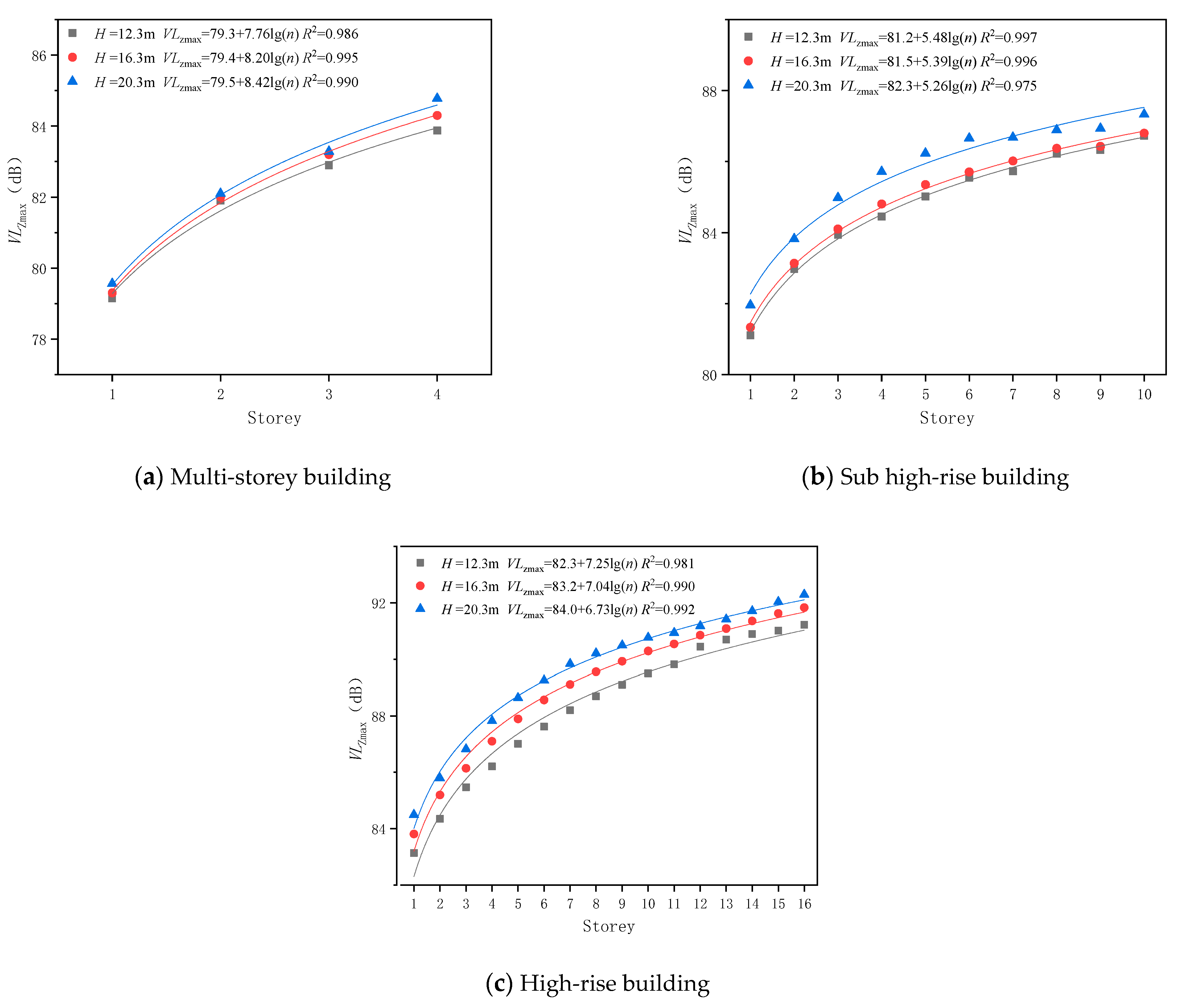
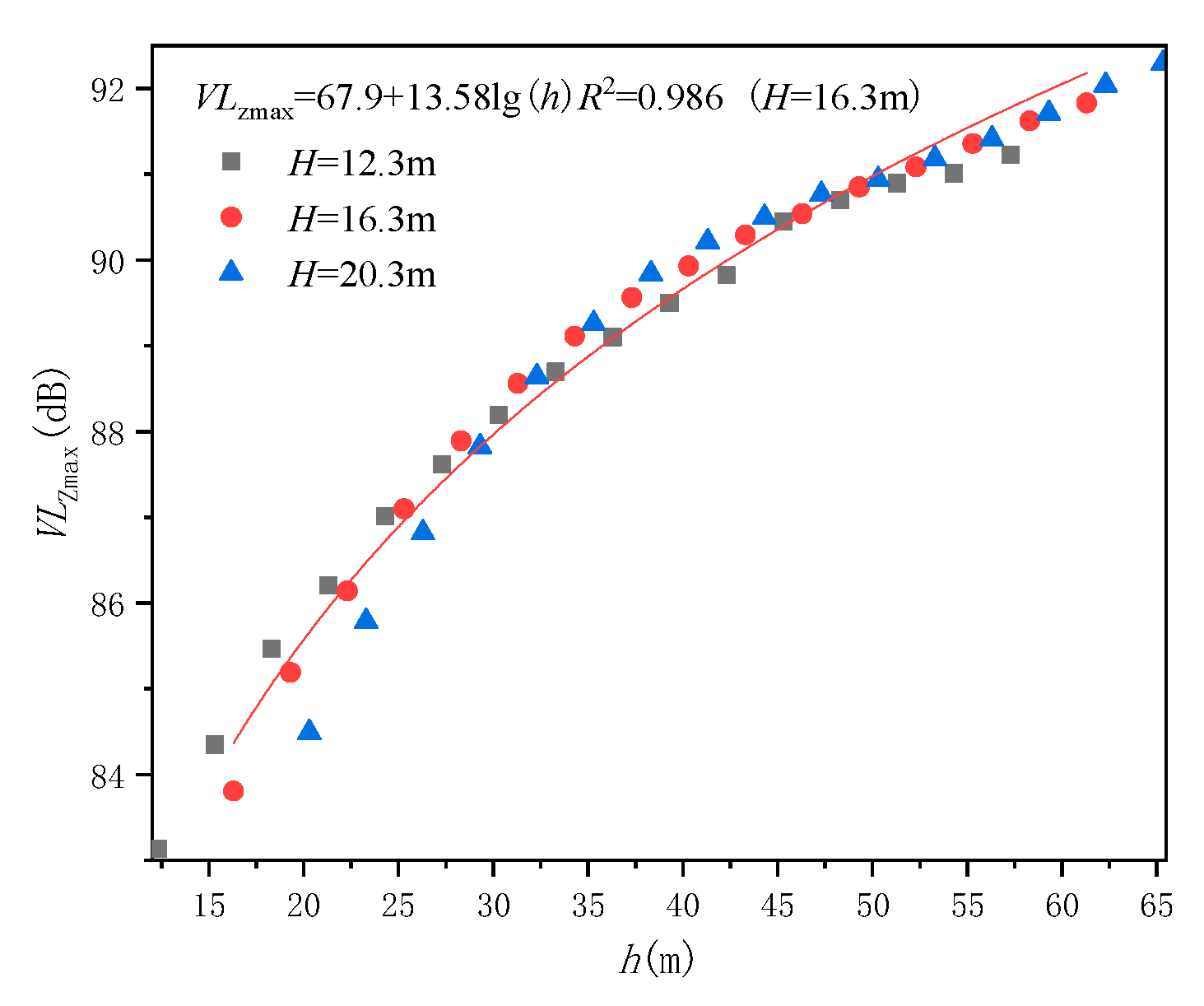
4.2.3. The Influence of Over-Track Platform Height Away from Ground
5. A Prediction Model of the Environment Vibration Impact from High-Speed Railway on Over-Track Buildings
5.1. The Correction Term of the Thickness of Over-Track Platform and Its Height Away from Ground, CP
5.2. The Correction Term of Storey,
5.3. The Correction Term of Building Structure,
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Zhang, J. Comprehensive Evaluation of Operating Speeds for High-Speed Railway: A Case Study of China High-Speed Railway. Math. Probl. Eng. 2021, 2021, 8826193. [Google Scholar]
- Nering, K.; Kowalska-Koczwara, A.; Stypuła, K. Annoyance Based Vibro-Acoustic Comfort Evaluation of as Summation of Stimuli Annoyance in the Context of Human Exposure to Noise and Vibration in Buildings. Sustainability 2020, 12, 9876. [Google Scholar] [CrossRef]
- Eizaguirre-Iribar, A.; Grijalba, O.; Hernández-Minguillón, R.J. An Integrated Approach to Transportation and Land-Use Planning for the Analysis of Former Railway Nodes in Sustainable Transport Development: The Case of the Vasco-Navarro Railway. Sustainability 2021, 13, 322. [Google Scholar] [CrossRef]
- Martínez Fernández, P.; Villalba Sanchís, I.; Botello Rojas, F.; Franco, R.I. Monitoring and analysis of vibration transmission for various track typologies. A case study. Transp. Res. Part D Transp. Environ. 2013, 24, 98–109. [Google Scholar] [CrossRef]
- U.S. Department of Transportation Federal Railroad Administration. High-Speed Ground Transportation Noise and Vibration Impact Assessment; U.S. Department of Transportation Federal Railroad Administration: Washington, DC, USA, 2005.
- Ferdous, W.; Manalo, A. Failures of mainline railway sleepers and suggested remedies—Review of current practice. Eng. Fail. Anal. 2014, 44, 17–35. [Google Scholar] [CrossRef]
- Ministry of Railways of the People’s Republic of China. Guidance on Noise and Vibration Source Values and Governance Principles for Environmental Impact Assessment of Railway Construction Projects (2010 Revision). Available online: https://www.sooooob.cn/information/2674.htm (accessed on 27 May 2010).
- Paneiro, G.; Durão, F.O.; de Silva, M.C.; Neves, P.F. Prediction of ground vibration amplitudes due to urban railway traffic using quantitative and qualitative field data. Transp. Res. Part D Transp. Environ. 2015, 40, 1–13. [Google Scholar] [CrossRef]
- Colaco, A.; Costa, P.A.; Amado-Mendes, P.; Godinho, L. Prediction of vibrations and reradiated noise due to railway traffic: A comprehensive hybrid model based on a finite element method and of fundamental solutions approach. J. Vib. Acoust. 2017, 139, 061009. [Google Scholar] [CrossRef]
- Madshus, C.; Bessason, B.; Rvik, L.H. Prediction model for low frequency vibration from high speed railways on soft ground. J. Sound Vib. 1996, 193, 195–203. [Google Scholar] [CrossRef]
- Verbraken, H.; Lombaert, G.; Degrande, G. Verification of an empirical prediction method for railway induced vibrations by means of numerical simulations. J. Sound Vib. 2011, 330, 1692–1703. [Google Scholar] [CrossRef]
- Auersch, L. Building response due to ground vibration-simple prediction model basedon experience with detailed models and measurements. Int. J. Acoust. Vib. 2010, 15, 101–112. [Google Scholar]
- Wang, X.Q.; Hu, Z.X.; Zhang, H.J. Analysis of vibration characteristics of adjacent buildings near the high speed railway of Wuhan to Guangzhou. Noise Vib. Control 2018, 38, 132–136. [Google Scholar]
- Sanayei, M.; Zhao, N.; Maurya, P.; Moore, J.A.; Zapfe, J.A.; Hines, E.M. Prediction and mitigation of building floor vibrations using a blocking floor. J. Struct. Eng. 2012, 138, 1181–1192. [Google Scholar] [CrossRef]
- Sanayei, M.; Anish, K.P.; Moore, J.A.; Brett, C.R. Measurement and prediction of train-induced vibrations in a full-scale building. Eng. Struct. 2014, 77, 119–128. [Google Scholar] [CrossRef]
- Zheng, X.D.; Geng, C.Z. Vibration effect simulation analysis of superstructure in Xinzhuang Hub project. J. Tongji Univ. Nat. Sci. 2014, 42, 1557–1561. [Google Scholar]
- Alabi, B. A parametric study on some aspects of ground-borne vibrations due to rail traffic. J. Sound Vib. 1992, 153, 77–87. [Google Scholar] [CrossRef]
- Sheng, X.; Jones, C.J.C.; Thompson, D.J. A theoretical study on the influence of the track on train-induced ground vibration. J. Sound Vib. 2004, 272, 909–936. [Google Scholar] [CrossRef]
- Zou, C. Train-Induced Vibration Transmission and Mitigation in Metro Depot and Over-Track Buildings; South China University of Technology: Guangzhou, China, 2017. [Google Scholar]
- Wu, C.F.; Zhu, X.R.; Liu, X.M. Studies on variability of shear strength indexes for several typical stratums in Hangzhou area. Chin. J. Geotech. Eng. 2005, 94–99. Available online: https://en.cnki.com.cn/Article_en/CJFDTotal-YTGC20050100F.htm (accessed on 14 March 2021).
- Ferdous, W.; Manalo, A.; AlAjarmeh, O.; Mohammed, A.A.; Salih, C.; Yu, P.; Mehrinejad Khotbehsara, M.; Schubel, P. Static behaviour of glass fibre reinforced novel composite sleepers for mainline railway track. Eng. Struct. 2021, 229, 111627. [Google Scholar] [CrossRef]
- GB 50352-2019. Uniform Standards for Civil Building Design; China Building Standard Design and Research Institute Co., Ltd.: Beijing, China, 2019. [Google Scholar]
- Xia, H.; Chen, J.G.; Wei, P.B.; Xia, C.; De Roeck, G.; Degrande, G. Experimental investigation of railway train-induced vibrations of surrounding ground and a nearby multi-story building. Earthq. Eng. Eng. Vib. 2009, 8, 137–148. [Google Scholar] [CrossRef]
- Xia, H.; Zhang, N.; Cao, Y.M. Experimental study of train-induced vibrations of environments and buildings. J. Sound Vib. 2005, 280, 1017–1029. [Google Scholar] [CrossRef]

| Materials | Density (kg/m3) | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|
| Rail | 7850 | 205,900 | 0.30 |
| Sleeper | 2400 | 30,000 | 0.20 |
| Track-bed | 1800 | 300 | 0.35 |
| Artificial fill layer | 1980 | 205 | 0.31 |
| Cohesive soil layer | 1940 | 175 | 0.44 |
| Mucky soil layer | 1530 | 120 | 0.35 |
| Verification Point | ||||
|---|---|---|---|---|
| Measured Result | Simulated Result | Difference | Relative Error | |
| Point 1 | 113.0 | 109.0 | 4.0 | 3.54% |
| Point 2 | 88.9 | 92.9 | 4.0 | 4.50% |
| The Number of Storey of Over-Track Building | The Structural Type of Over-Track Building | The Thickness of Over-Track Platform (m) | The Height of Over-Track Platform Away from Ground (m) |
|---|---|---|---|
| Multi-layer (4 storeys), sub high-rise (10 storeys), high-rise (16 storeys) | Frame structure or shear wall structure | 2, 2.5, 3 | 12.3, 16.3, 20.3 |
| Building Types | a (dB) | ||||
|---|---|---|---|---|---|
| T = 2.0~2.5 (m) | T = 2.5~3.0 (m) | H = 12.3~16.3 (m) | H = 16.3~20.3 (m) | ||
| Multi-storey | −2.5 | −6.0 | −1.4 | 0.025 | 0.075 |
| Sub high-rise | −0.5 | −6.6 | −4.2 | 0.05 | 0.15 |
| High-rise | 2.0 | −6.8 | −2.2 | 0.15 | 0.2 |
| Building Types | K |
|---|---|
| Multi-story | 7.76~8.42 |
| Sub high-rise | 3.46~5.86 |
| High-rise | 6.09~8.44 |
| Building Types | ||||
|---|---|---|---|---|
| Frame | Shear Wall | Frame | Shear Wall | |
| Multi-storey | 0 | −7.02 | 0 | −0.2 |
| Sub high-rise | 0 | −3.72 | 0 | −0.4 |
| High-rise | 0 | −4.44 | 0 | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di, G.; Xie, Z.; Guo, J. Predict the Influence of Environmental Vibration from High-Speed Railway on Over-Track Buildings. Sustainability 2021, 13, 3218. https://doi.org/10.3390/su13063218
Di G, Xie Z, Guo J. Predict the Influence of Environmental Vibration from High-Speed Railway on Over-Track Buildings. Sustainability. 2021; 13(6):3218. https://doi.org/10.3390/su13063218
Chicago/Turabian StyleDi, Guoqing, Ziyin Xie, and Jingyi Guo. 2021. "Predict the Influence of Environmental Vibration from High-Speed Railway on Over-Track Buildings" Sustainability 13, no. 6: 3218. https://doi.org/10.3390/su13063218
APA StyleDi, G., Xie, Z., & Guo, J. (2021). Predict the Influence of Environmental Vibration from High-Speed Railway on Over-Track Buildings. Sustainability, 13(6), 3218. https://doi.org/10.3390/su13063218






