Abstract
This article presents a methodology for predicting the fluid dynamic behavior of a gear pump over its operating range. Complete pump parameterization was carried out through standard tests, and these parameters were used to create a bond graph model to simulate the behavior of the unit. This model was experimentally validated under working conditions in field tests. To carry this out, the pump was used to drive the auxiliary movements of a drilling machine, and the experimental data were compared with a simulation of the volumetric behavior under the same conditions. This paper aims to describe a method for characterizing any hydrostatic pump as a “black box” model predicting its behavior in any operating condition. The novelty of this method is based on the correspondence between the variation of the parameters and the internal changes of the unit when working in real conditions, that is, outside a test bench.
1. Introduction
The challenge of fluid-dynamically characterizing hydrostatic units began more than ninety years ago and continues to be a valuable and cutting-edge area of research. Several researchers have significantly contributed to the field, with the works of Wilson [1], Edge [2], and Ivantysynova [3] being excellent examples. Several studies have been carried out with gear pumps [4] and gerotor machines [5].
Fluid-dynamic characterization has to be based on testing the hydrostatic unit in order to ascertain its steady performance (volumetric and mechanical efficiency), unsteady characteristics (flow ripple and source impedance), noise generation, and reliability. The authors have gathered experience in this field over the past twenty years [6,7].
A survey of the scientific literature reveals a great amount of work in this field that has been pursued by using different models, numerical simulations, and experimental techniques, in order to describe the gear pump behavior from different points of view [8,9]. In terms of the current state of external gear pumps in the research field, there are two topics that the major efforts are concentrated on: Efficiency evaluation and tribological assessment.
With regard to efficiency evaluation, Batarra and Mucchi [10] performed an exhaustive experimental campaign, resulting in a reliable evaluation of a population of pumps based on a statistical approach, rather than a single pump sample. The experimental procedure was carried out in laboratory facilities and not in in-field working conditions. Zardin et al. [11] describe a model that takes into account the position of the gears in the losses, friction, and viscous leakage during the meshing process. The model results show a good agreement with the tested commercial unit, although they do not take into account hard operating conditions, such as a high pressure during in-field machine tests.
With regard to tribological assessment, the wear and its degradation state in an external gear pump have been evaluated by Guo et al. [12]. The authors proved that the instantaneous flow rate of the gear pump gradually decreases once the wear clearance increases, and presented the degradation characteristics. In addition, a high pressure accelerates the internal wear of the pump. In a very recent work, Casoli et al. [13] analyzed the effectiveness of textured surfaces, paying special attention to the influence of introducing dimples in the lubricated couplings of hydraulic pumps. As a result, the tribological properties are improved.
Over the years, a great amount of numerical research has been conducted on the phenomena of different natures that occur inside a gear pump, determining its performance. In the extensive review carried out by Rundo [14], a compendium of the different methodologies used in the simulation of flow generated by gear machines in shown. The use of 2D and 3D computational fluid dynamics (CFD) techniques to evaluate volumetric losses and friction losses in complex geometries shows the great effort that has been made to use simulation models for the design and optimization of this type of machine.
However, the experimental verifications of numerical models are often carried out in laboratory conditions that have little to do with the working conditions in a real machine. The question is no longer related to whether the model has been validated, but to under what conditions this validation has been performed. Therefore, the main objective of this work is to address the lack of experimental validation of the loss models applied to positive displacement pumps in real conditions. To carry this out, experiments were conducted on an external gear pump working in in-field operating conditions on a drilling rig. In this type of machine, an open hydraulic circuit equipped with a load sensing piston pump is used for both high power and auxiliary drives. The use of an external gear pump to conduct the latter would allow the use of a simpler control block.
The work presented in this paper consists of two parts: modeling and testing. When the pump runs, the oil is transported to the outlet side and the pressure rises due to the system impedance, involving more leakage from the outlet side to inlet side. Considering Figure 1b, this occurs between the tooth peak and the casing (path A), between the end side plates and gears (path B), and in the area of meshing (path C). To compensate for this increasing leakage due to a higher working pressure, the rear area of the end side plates is pushed by the working pressure, pressing the end side plate against the gear and reducing the leakage clearance, as shown in Figure 1c (axial clearance compensation, Thiagarajan et al. [15]). In this way, these types of pumps are able keep their volumetric efficiency quite constant in a wide range of working conditions (pressure, oil temperature, and rotation speed). Therefore, to create a good model that simulates its behavior, it is necessary to establish the variations of the parameters that define it according to the working conditions. This work must be carried out in the laboratory by corresponding international organization for standardization (ISO) tests and treating the results, in order to parameterize the pump. This work is introduced in the first part of the research presented in this paper.
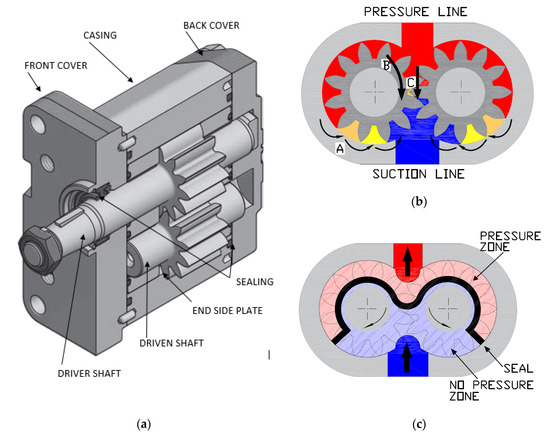
Figure 1.
Inside of a gear pump: (a) parts of a gear pump (source: ROQUET Group S.A.); (b) leakage paths; and (c) rear of the side plate.
However, in a real system, there are pressure fluctuations that depend on both the hydraulic circuit and the pump flow pulsations. Then the “end plate-oil film” system is being excited with an oscillatory movement, which is unpredictable a priori, and consequently, the related losses. The dynamics of internal parts are fundamental for defining the volumetric and mechanical efficiency, and therefore, it is not known if the parameterization carried out under stable laboratory conditions is valid when the pump has to be operating under real working conditions. In this study, experiments were carried out in the second part of the investigation, verifying that the model works correctly in stable conditions, having certain limitations under unstable conditions.
The parameterization of hydrostatic pumps can be approached from two points of view: On one hand, by evaluating the flow and torque losses in their range of operating conditions according to standard ISO 4409:2007 [16], and on the other hand, by studying the machine as a flow ripple and impedance source according to standard ISO 10767-1:2015 [17]. Both models lead to parameterization of the unit, either through the loss coefficients with the mathematical treatment of the results at different temperatures or through the flow ripple and the pump impedance.
ISO 4409 is usually used to quantify the volumetric and mechanic losses in a steady state, while ISO 10,767 is usually used to quantify the noise generating capacity and the unsteady behavior of the tested machine. Oil-hydraulic pumps have been widely studied from both points of view, but the knowledge on the relationship between the results of both methodologies needs to be advanced. In this research, both types of studies were carried out, and the authors consider that flow losses are included in the pump impedance definition. The uncertainty of the ISO 10,767 results does not allow the volumetric behavior of the unit to be ascertained with enough precision. In addition, the pump impedance does not allow the nature of different types of leaks to be determined. For these reasons, only the ISO4407:2007 results are presented for the pump parameterization, and the oil inertia and compressibility terms have been included in the model to guarantee that the same information on the source impedance is obtained, and accordingly, that it is possible to evaluate the unsteady behavior.
2. Parameterization of the Pump
In a positive volumetric displacement pump, such as the gear pump of Figure 1a, not all torque applied to the shaft is used to increase the pressure, as there is hydro-mechanical friction quantified by the mechanical efficiency (this parameter is not mentioned in the ISO 4409 standard). The leakage occurring through the internal pump clearance means that not all of the shaft speed is used to deliver flow. The losses are quantified by the volumetric efficiency.
A loss model is a mathematical formulation of these performances under different operating conditions. The work published by Wilson [1] describes the nature of the flow inside volumetric displacement machines, and has been taken as a reference by most authors, producing models with physical significance in terms of both the shaft torque and the delivered flow. In these expressions, there are the loss coefficients, and their behavior can significantly help us to understand how the pump geometry varies according to the working conditions. Specifically, the expressions used in this paper are very similar to those proposed by McCandlish et al. [18], adding a turbulent leakage term proposed by Schlosser [19].
To develop a good model, first of all, it is necessary to evaluate the main parameter of a positive displacement pump—the derived capacity—according to ISO 8426:2008 [20]. Then, the ISO 4409:2007 test is carried out to ascertain the behavior in a steady state, determining the volumetric and mechanical efficiency in the range of operating conditions.
Mainly, the flow regime for the clearance of an hydrostatic unit can be laminar (the friction torque is proportional to the rotational speed and viscosity, and the leakage is proportional to the pressure difference between the pump outlet and inlet and inversely proportional to the viscosity) or turbulent (the friction torque is proportional to the working pressure and the leakage is proportional to the square root of the pressure difference between the pump outlet and the inlet and independent of the viscosity). Other aspects of the nature of the flow inside a hydrostatic machine can be considered, such as the presence of air and steam or the temperature increase during fluid compression, but they will not be taken into account in the model presented in this paper because they cannot easily be quantified from the results of standardized tests.
It should be noted that there is considerable controversy surrounding the standard tests, which is beyond the scope of this article. The first and main parameter to evaluate is the derived capacity. This is defined as the volumetric flow driven by the positive displacement pump per shaft revolution, under zero internal and external leakage flow conditions. First of all, these zero leak conditions are impossible to obtain in a real test as there is always a pressure gradient between the suction and discharge line, with corresponding leaks. Additionally, the method described in the ISO 8426:2007 of extrapolating results to zero pressure conditions has often been misunderstood. This is due to the fact that both geometric displacement and Couette flow dragged by the unit have to be included in the derived capacity. A further problem is that experimental methods for investigating Couette flow separation from leaks have not yet been developed.
The occurrence of volumetric efficiencies greater than 100% is quite common, as a consequence of an incorrect procedure for determining the derived capacity. This scenario has been analyzed by Toet et al. [21] in a revised translation of a work developed more than 40 years ago by the author, which has been the basis of successive editions of the ISO 8426 standard.
Achten et al. [22] present a review on ISO 4409:2007, analyzing the efficiency and losses of pumps (and motors) in an alternative way, by taking into account the change of the internal fluid energy that is neglected in the methodology of the standard test. In particular, the effects of the bulk modulus are considered in a different and more inclusive manner. New definitions for the losses and efficiencies of hydrostatic pumps and motors are derived on the basis of thermodynamic analysis. The new methodology results in a lower total loss for pumps than the current ISO 4409 standard.
Next, a brief explanation of the classical loss model deduction from expressions of the flow and friction generated in the internal oil films and orifices will be presented, in order to show the relationship between loss coefficients and the internal geometry of the unit.
2.1. Flow Losses
Accordingly, the flow delivered by a pump is
where
- Qi is the ideal flow without losses,
- Qs represents laminar flow losses,
- Qst represents turbulent flow losses and,
- Qc represents flow reduction due to compressibility.
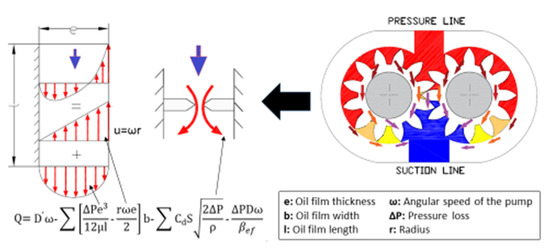
Figure 2.
Nature of leakage in a gear pump.
- The derived capacity according to ISO 8426 has to take the dragging effects of oil by the gears into account. Therefore, the derived capacity iswhere the Couette term can be positive or negative, depending on whether it contributes to increasing or decreasing the derived capacity, respectively;
- Regarding , although dimensionally it is equivalent to D, it does not always have to be proportional to the volumetric displacement. If the pump displacement is modified by increasing the tooth width, maintaining its modulus (as occurs in pumps of the same group), the considered term will be the same. In any case, most authors have adopted the Poiseuille term:where Cs is the laminar slip coefficient;
- Regarding , taking into account that d3 is proportional to D,where Cst is the turbulent slip coefficient.
Finally, the proposed flow model depending on the pump operating conditions is as follows, which contemplates both laminar and turbulence slip, and flow losses due to the oil compressibility:
Since both turbulent leaks and flow losses due to compressibility do not depend on the viscosity, any change in temperature will only affect laminar leaks. Therefore, having obtained the flow at θ1 = 22 °C and θ2 = 60 °C according to ISO 4409, we could calculate Cs.
The turbulent leaks were evaluated by subtracting the measured laminar leaks and the losses due to compressibility of the delivered flow:
The turbulent slip coefficient was calculated as
2.2. Torque Losses
Consequently, the applied pump torque is
where
- Ti is the ideal torque,
- Tfr is the fluid friction torque,
- Tk is the Coulombian friction torque,
- Tv is the viscous friction torque,
- Tf is the load dependent friction torque and,
- Te is the small friction torque loss independent of speed and pressure (p.e. shaft seal friction).
It should be noted that in a pump with good lubrication, the oil film does not have to be broken (this would cause damage by seizure), and therefore, there should be no Coulombian friction. It can be demonstrated that the friction dependent on the working pressure and independent of the viscosity can be justified by only taking into account the hydrodynamic lubrication. The overall friction torque by all considered fluid films can be evaluated by the following expression (Couette and Poiseuille):
The first term only depends on the working pressure of the pump, but has been deduced from the hydrostatic forces that must be overcome when rotating, irrespective of whether or not there is Coulombian friction. If we assume that the oil film has broken, so that metal-to-metal contact occurs, qualitatively, the friction torque can be determined by
Therefore, the hydrodynamic, hydrostatic, and possible Coulombian friction depend on a dimensionally cubic length term that can be associated with the derived capacity. This statement is more truthful if the derived capacity variation occurs by modifying the gear diameter. In any case, we could evaluate the torque to rotate the pump with the following expressions.
With Cv representing the viscous friction coefficient and Cf representing the Coulombian friction coefficient, and not taking into account Te due to its low values, the model of mechanical losses is
Since Coulombian friction does not depend on the viscosity, any change in temperature will only affect the laminar friction. Therefore, having obtained the torque at θ1 = 22 °C and θ2 = 60 °C according to ISO 4409, we can calculate Cv.
The Coulombian friction is evaluated by subtracting the measured laminar friction of the shaft torque.
The Coulombian coefficient is calculated as
The previously deduced loss models, as already argued, have a physical meaning and are valid for any hydrostatic machine. However, the assumption of constant leakage coefficients means that these models are only valid for a certain range of operating conditions. To use them in the whole operation range, it is necessary to take into account the changes of the losses coefficients with the pressure and the rotation speed. These changes will reflect the variations in the internal unit geometry, and are basically related to the balance of the lubrication regime, that is, the position of the side plates in external gear pumps.
3. Experimental Procedure
3.1. Test Benches
According to ISO 8426:2008, the test employed to determine the volumetric capacity was carried out with flow rates recorded for a pressure range over which the capacity was nominally constant. Approximately, this occurs at around 5% of the maximum working pressure, as indicated in the previous edition ISO 8426:1988. Hence, for two different speeds, it was evaluated as D = ∆qve/∆n, and the results have been extrapolated at the point where ∆P = 0. Annex B of the ISO 8426: 2008 standard presents the principle of calculation of the derived capacity using a zero-pressure intercept method. However, this method can lead to values of volumetric efficiency higher than 100%. Neglecting the evaluation of the dragged Couette flow or the compensating mechanisms (for example, lateral plate axial clearance in a gear pump) means that the theoretical flow calculated based on the volumetric capacity is lower than the real one, and inevitably, that volumetric efficiencies are higher than 100%. That is mentioned in the paper of Toet et al. [21]. The value of the test presented a derived capacity of 14.7 cm3, identical to the manufacturer information.
The ISO 4409 established a methodology for determining the pump performance. Volumetric and overall efficiencies were calculated based on the volumetric displacement obtained with the previous test, also producing the loss coefficients, as explained above. The relationship between the leakage coefficients and the operating conditions is shown in Figure 3. Brief considerations of the loss coefficients’ behavior and the pump internal changes are as follows:
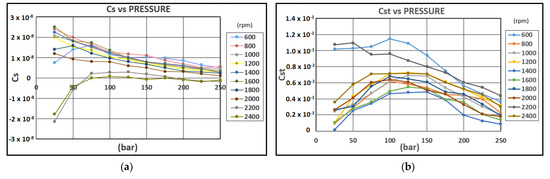
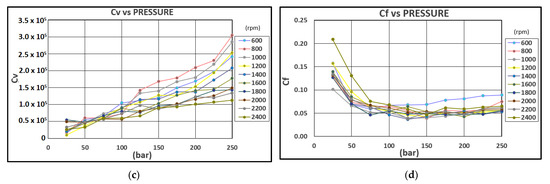
Figure 3.
Loss coefficients versus pressure and speed: (a) laminar slip coefficient; (b) turbulent slip coefficient; (c) laminar friction coefficient; and (d) Coulomb friction coefficient.
- The side end plate movement is reflected in the laminar slip coefficient variation. This coefficient decreases as the working pressure increases because the oil film thickness between the side plate and the gear also decreases due to the axial compensation mechanism. This is the main reason why a pressure rise does not cause a significant increase in leakage, keeping the volumetric efficiency above 90% in the entire range of operation;
- This coefficient decreases slightly as the rotational speed increases because end plate balance between the hydrodynamic forces on the gear side and the hydrostatic forces on the back side is achieved with smaller oil film thicknesses. This phenomenon is more significant at high rotational speeds, even reaching negative values at low pressures (2200 and 2400 rpm). An explanation for this is that the Couette flow dragged to the pump outlet is higher than the Poiseulle slip at the pump suction. This behavior reaffirms the fact that the variation of the laminar slip coefficient is closely related to the separation between the side plates and the gear face, and also that it is not experimentally possible to separate Poiseuille leaks from Couette leaks;
- The viscous friction coefficient behavior is inverse, since an increase in its value indicates a decrease in the oil film thickness. The mechanical efficiency remains approximately constant, since the Coulomb friction coefficient decreases quickly from 0 to 100 bar. The explanation for this behavior is that the slip intensifies turbulent flow until 100 bar. This can be seen with the growth of the turbulent slip coefficient until 150 bar. The conclusion is that the pump, when working at high pressures and speeds between 1200 and 1800 rpm, mainly exhibits laminar slip and a good lubrication regime.
- Assuming that both turbulent leakage and Coulomb friction mainly occur between the tooth peak and the casing, the variation of the coefficients Cst and Cf is related to the oil film thickness between the gear shaft and the hydrodynamic bearings located on the side plates. An increase in pressure up to about 100 bar leads to movement of the side plate until it comes into contact with the casing. Then, higher pressures lead to a decrease in the oil film thickness between the shaft and the hydrodynamic bearing located on these plates and the teeth peaks approach the casing in the suction zone. Due to the side plate configuration, it is in this area where the separation between the high-pressure and low-pressure area occurs.
3.2. In-Field Machine Test
The machine chosen to install the tested gear pump was a drilling rig manufactured by Construcciones Mecanicas LLAMADA Type P140, which can be seen in Figure 4a. Basically, this machine has three oil hydraulic systems: A closed circuit system for the drilling rotary table (piston pump 210 cm3 and maximum pressure 400 bar); a load sensing LS system for winch, tracks, and auxiliary drives (piston pump 165 cm3 and maximum pressure 350 bar); and an open circuit system for the fluid conditioning system (gear pump 43 cm3 and maximum pressure 20 bar). The diesel engine can run from 800 to 2000 rpm, and units are coupled by means of a pump drive with a ratio of 1:1. The operator sets the engine speed, selects the drive to move, and controls the direction and flow from the hydraulic joysticks installed in the machine cabin.

Figure 4.
LLAMADA P140 machine: (a) overview; (b) gear pump assembly and instrumentation; and (c) acquisition system.
Regarding the LS system, a compensated proportional control block allows sixteen movements to be driven. These can be the main high-flow motors (tracks and winches), or one of the cylinders for auxiliary drives, mainly linear actuators (tower lift, counterweight, auger guide, tower feet, feet of platform, tower head, etc.). Each movement has a maximum flow defined by the calibrated spool, and a maximum working pressure according to the setting of the LS relief valve of the element. The working pressure is the highest required by the actuators plus the pump stand-by, while the delivered flow is the sum of the flows of all the actuators. The objective of this in-field machine test is to carry out predetermined movements with the gear pump in real conditions, in order to check the goodness of the model developed with the losses coefficients. In this way, we will have a tool to study the feasibility of replacing the piston pump with the gear pump in auxiliary movements, in order to economize the system by using a simpler and more efficient control block.
3.2.1. Adaptation of the Gear Pump
This assembly was made by coupling the gear pump on the rear cover of the LS pump, which was ready to couple to an auxiliary pump, as can be seen in Figure 4b. Therefore, an SAE J498B 9 teeth 16/32 pitch spline shaft pump was installed, instead of the one tested on the test bench, coupled to an electric motor, with a UNI 5589 tapered shaft and European mounting flange. This is the only difference between the one mounted on the test bench and the one used on the real machine. To cancel the flow supplied by the original pump, the LS line was depressurized and its standby was regulated at the minimum value (11 bar), as can be seen in Figure 5. The pressure line from the gear pump was a connecter after a check valve was installed at the outlet of the LS pump, so that the incoming flow to the main distributor only came from the gear pump.
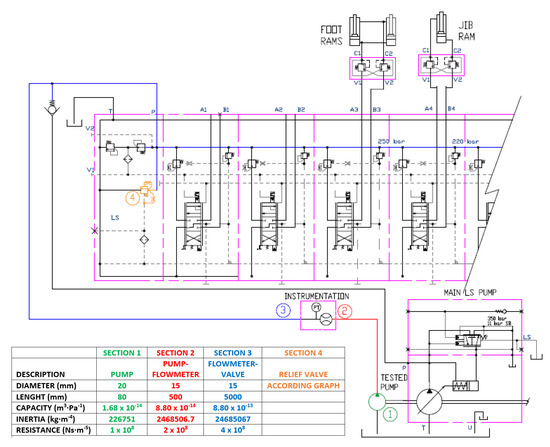
Figure 5.
Adaptation circuit with instrumentation and section characteristics.
The main control block was a combination of two sizes of pressure compensated proportional load sensing valves. One of these was converted from a closed center to open center configuration to perform the tests, by mounting the conversion kit on the inlet cover (Figure 6). Therefore, the system’s regulation behaves like a compensating 3-way flow regulator, where the throttle opening (element spool) is controlled by the operator through the cabin joystick and the system stand-by is determined by the compensator spring (theoretical value 14 bar).
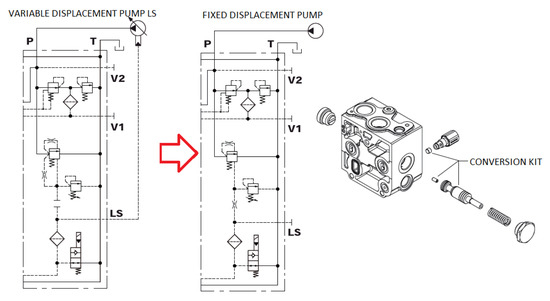
Figure 6.
Transformation of the control block from a closed center to open center (source: WALVOIL).
Finally, the instrumentation used was PARKER Serviceman Plus equipment [23], specially designed for data acquisition in-field tests. A pressure transducer with a precision ±0.25% and a flowmeter with a precision ±1% were used together with the software SensoWin 7.1.
3.2.2. Selection of the Movements to Work
The mast foot and jib movements were chosen because they work perfectly within the operating range of the gear pump, being subjected to load oscillations that allow us to monitor the system in both steady and non-steady conditions. The sampling frequency will be low when the intension is to study the behavior in a steady state, since the duration of the data acquisition is relatively long. For unsteady behavior, acquisition will be carried out every 30 ms, moving the tower foot near its end of the stroke, in order to generate pressure oscillations. In this way, the behavior of the model can be studied in both permanent and transitory conditions. The study of the flow fluctuations with an acquisition time lower than 30 ms was dismissed owing to two opposed effects: the flow fluctuations by the pump (interesting to validate the model of this work) against the compressibility of the installation (not interesting for the aim of this work).
During the movement of the mast foot, the forces involved were the friction of tubular guides, the structure weight, and the pressure needed to open the overcenter valve, with a setting of 350 bar and a ratio of 1:4. The pressure was approximately 90 bar when it was lowering and 135 bar when it was rising, but these values depended on both the controlled flow and the speed of the diesel engine, since they determined the mechanical friction of cylinder guides and the pressure losses of the hydraulic system. The setting of the LS relief valve of this element was approximately 250 bar. When this value is reached, it indicates that the cylinder has reached the end of its stroke.
In terms of the jib, the pressure was not constant during the movement, since there was variation in the geometry of the mechanism. The pressure required for lowering it was between 90 and 110 bar, while for raising it, it was between 130 and 160 bar. The setting of the LS relief valve of this element was approximately 220 bar. When the graphs of the results show that the pressure dropped to approximately 20 bar, it indicates that the operator had centered the joystick, stopping the movement, and therefore, the pump worked at standby plus the pressure in the return line. Pressure oscillations indicate that the operator varied the flow supplied to the cylinder by acting on the control joystick.
The tests were carried out at different speeds of the diesel engine, trying to cover the pump speed range from 1000 to 2000 rpm. The engine regulation procedure did not allow the speed to be set with precision, because it could only be regulated step by step, but the value shown on the cabin display was very exact, since the sensor signal came directly from the engine. Therefore, the test speeds were 1030, 1467, and 1961 rpm. The fact that the engine had a power of 345 kW made the speed variation with the pump pressure negligible. The pump worked within its operating range, being subjected to load variations of different intensities. This work on a real system, with its inductive, resistive, and capacitive impedances, made it the ideal framework to validate the goodness of the leakage model.
4. System Simulation
Once the behavior of the pump was studied, ascertaining the volumetric and mechanical losses in different operating conditions and the parameters that govern them, a model to simulate this behavior was designed using bond graph diagrams. This is a method of modeling dynamic systems that can be applied to different fields, being very common in oil hydraulic systems [24]. 20-SIM software [25] was used to process the bond graph diagram.
A model of the system is shown in Figure 7, defining the pump behavior by Equation (6) (supplied flow) and Equation (16) (input torque). The different parts of the bond graph are equivalent to those of the scheme in Figure 5. Section 1 corresponds to the tested pump, Section 2 to the hose between the pump and the instrumentation, Section 3 to the hose between the instrumentation and the control block, and Section 4 to the relief valve. The diagram represents the pump connected to a pressure source (MSe SYSTEM), which corresponds to the duty cycle of the machine to be studied. This cycle was established by experimentally measuring the working pressure and temperature. The input pump conditions are the rotation speed (MSf ENGINE) and the derived capacity (DISPLACEMENT). The fluid density was considered to be constant and the pump inertia was considered to be negligible.
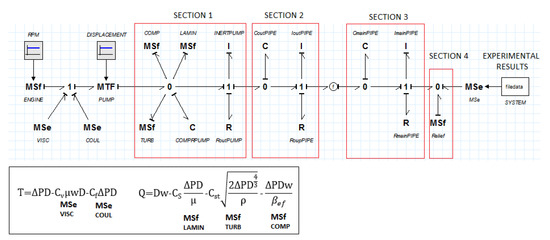
Figure 7.
Bond graph system edited in 20SIM.
The first 1 node on the left determines the mechanical efficiency of the pump. MSe VISC and MSe COUL introduce the viscous and Coulombian friction losses, respectively. It should be noted that these blocks need the viscous and Coulomb friction coefficients (Cv and Cf), whose values were tuned by polynomial adjustments of the values versus pressure. Since the simulated machine operates at the constant speed of the diesel engine that drives the pump, the speed dependence of the friction coefficients was not taken into account, although it was known from experimental tests on the test bench.
The MTF PUMP transformer corresponds to a theoretical ideal pump. The following 0 node determines the volumetric efficiency of the pump. MSf LAMIN and MSf TURB introduce the laminar and turbulent leakage, respectively. We should note that these blocks need the laminar and turbulent slip coefficients (Cs and Cst), which were tuned by polynomial adjustments of the values versus pressure. MSf COMP introduces the volume reduction due to the compression of suctioned fluid and C COMPRPUMP introduces the fluid compressibility in the outlet passage. Moreover, the inertia and resistance of the outlet passage were taken into account in INERTPUMP and RoutPUMP, respectively. Therefore, the pump is represented as a flow source, together with its impedance, with resistive, capacitive, and inertial terms.
Each hose used (Section 2 and Section 3) was parameterized with its capacity, inertia, and resistance, according to its diameter, length, and effective bulk modulus, and the relief valve (Section 4) was introduced by means of the mathematical expression of the pressure versus flow graph supplied by the control block manufacturer.
The interaction with the machine was introduced by means of the SYSTEM file, which was obtained during the simulation with 20SIM. This functionality allows the model to know the real pressure, flow, and temperature during the duty cycle. The measured temperature was used to obtain the real value of viscosity during the simulation time, since its value is not constant during the tests. Hence, by comparing the flow generated by the model with that measured in the machine working in the same conditions, we could analyze the correlation between simulated and real behavior and verify the goodness of the model.
Finally, the model shown in Figure 7 is a simplified diagram of the bond graph used for the simulation, where there are calculation blocks and links between different parts of the system. The representation of the complete diagram complicates the conceptual understanding of the system.
5. Results and Discussion
Figure 8, Figure 9 and Figure 10 show the evolution of the experimental pressure and temperature measurements versus time, which were introduced into the bond graph model through the SYSTEM file. With these data, the simulation program was started, obtaining the modeled flow versus time. In the graphs, this result is compared with the measured flow. The ratios between the modeled flow rate and the measured flow versus the theoretical flow rate were also calculated, producing the modeled and real volumetric efficiency, respectively. Finally, the mechanical efficiency was modeled. In this work, only the volumetric losses were validated experimentally, because the installation of the torque transducer between the pump drive of the machine and the pump was very difficult. These tests were carried out at different engine speeds, both for the movement of the tower foot and for the jib.
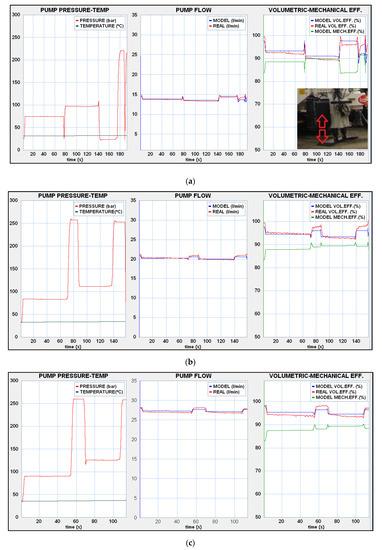
Figure 8.
In-field machine test results: (a) lowering-raising foot (1030 rpm); (b) lowering-raising foot (1467 rpm); and (c) lowering-raising foot (1961 rpm).
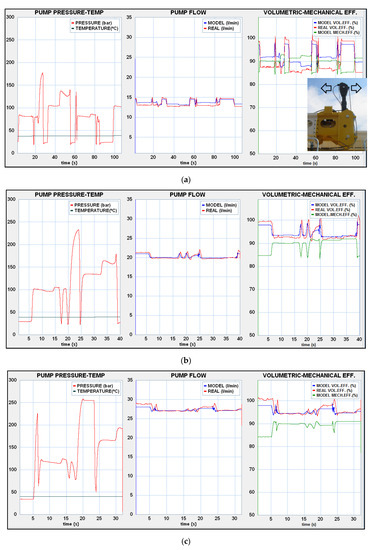
Figure 9.
In-field machine test results: (a) lowering-raising jib (1030 rpm); (b) lowering-raising jib (1467 rpm); and (c) lowering-raising jib (1961 rpm).
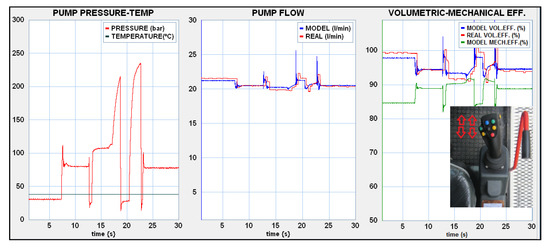
Figure 10.
In-field machine test results. Unsteady foot motion (1480 rpm).
In all the graphs, there was a slight offset between the modeled and measured flow, which was more noticeable at 1030 rpm. This was due to a minor error in the speed engine indication, which was directly entered into the model using the RPM parameter.
Figure 8a shows that the flow decreased slightly during a prolonged period of the pump operating at constant pressure (approximately 70 and 100 bar), while the model remained constant as the operating conditions were not changing (the temperature variation is negligible). The reason for this could be that the hydrodynamic balance in pump lubrication was difficult to achieve at low speeds. This was also observed in the ISO4409 tests, noting a difficulty in keeping the flow constant with steady operating conditions and an appreciable hysteresis (different flow measured with the same working conditions). This only happened at low speeds, not being noticeable in Figure 8b and Figure 7c. This behavior could be related to the instability of the loss coefficients at low speeds (600–1000 rpm) and low pressures. Although the ISO 4409 tests were also carried out at 5 and 10 bar, the results were omitted from the model as they considerably distorted the polynomial adjustments of the loss coefficients. Toet, G., et al. [22] specifically noticed “the kinematic uncertainty of the pumps and motors at low pressures”. In Figure 9a, the offset between the measured flow and the modeling flow considerably increases. In spite of the fact that the working temperature was approximately 8–10 °C higher than the tests with the tower foot, the modeled flow already takes into account the correlation between the viscosity of oil SHELL Tellus S2 V46 [26] and temperature when calculating the leakage in the model. Therefore, this difference can only be explained by the randomness of the internal balance of the pump at low speeds.
At speeds of 1467 and 1961 rpm, a real volumetric efficiency greater than the modeling is observed when increasing the pressure, especially in situations of sudden changes. The differences between the flow rate and efficiency modeled with the experimental values are not due to uncertainty of the viscosity correlation or the inaccuracy in capturing the rotational speed of the engine. These reasons did not justify the divergences observed when there were sudden load changes. If a pressure increase carries a greater flow, this means that the axial compensation mechanism of the pump acts with more energy than that modeled by the leakage coefficients Cs and Cst. Additionally, when the pressure dropped to a stand-by value because the operator stopped the movement, a flow peak occurred.
The pressure peak stuck the side plate against the gears, so the leakage remained constant or decreased. Then, when the pressure decreased, the plate did not separate with the same magnitude of the gears, suddenly increasing the flow rate. This phenomenon could be significantly appreciated in Figure 9b between t = 15 and 25(s), and it is surely also related to the hysteresis mentioned above. An explanation may be that the compensation mechanism is not immediate because the pump lubrication regime requires some time to reach equilibrium. Working in real conditions, before reaching this equilibrium, the impedance may have changed, in such a way that it can explain the slight differences between the behavior on the test bench (the modeling) and the real behavior under unsteady conditions.
There is a peak flow in the model when simulating an unstable operation that did not show up on the measured flow graph (Figure 10). As the data acquisition time was 30 ms, the flowmeter might not be able to capture these peaks of the order of milliseconds. These peaks could be minimized by introducing capacities smaller than those corresponding to the dimensions of the pipe and the outlet passage of the pump in the model. When a sudden decompression occurred, there was an increase in the volumetric flow due to the internal energy of the fluid.
In Figure 10, an interesting curiosity could also be seen. The real flow was slightly delayed versus the modeled flow. While the latter perfectly followed the evolution of the pressure, since the calculation of the leakage coefficients occurred immediately, the measured flow shows the time required for internal hydrodynamic adjustment of the pump parts, and therefore, a delay occurred.
The pump used in the field tests was not the same as the unit used in the laboratory tests. Although the manufacturing inaccuracies and tolerances caused a statistical spread in the geometric capacity, which, in many cases, was too large for a correct determination of the losses, this was not the reason why the model flow differs from the real one, especially at low or very high pressures. The leakage coefficients were calculated based on a polynomial fit as a function of pressure, minimizing the mean square error. However, at some points, there was a substantial difference between the experimental coefficients and the values used in the model, especially at low pressures.
6. Conclusions
A gear pump was parameterized from the results of standard tests, building a classic loss model where the coefficients should have a physical meaning related to the internal kinematics of the unit. This model was implemented by using the bond graph technique, simulating the pump performance under different operating conditions. Finally, the experimental volumetric behavior during in-field tests, driving auxiliary movements in a pile drilling machine, was compared with the simulated volumetric behavior under identical conditions, checking the model goodness. This also took into account the resistance, capacity, and inertia of the pump’s output passage, so it intrinsically included the concept of the impedance of the pump.
The correlation between the measured flow rate and the modeling was reasonably accurate and therefore, it could be concluded that laboratory tests under stable conditions could be used to model the pump and simulate its operation under quasi-steady conditions.
As expected, the model had certain limitations. At low speeds and pressures, the predicted results did not exactly follow the measured ones. This could be due to randomness in the internal hydrodynamic equilibrium. The model did not take into account the hysteresis in the operation of the pump, that is, under the same operating conditions, the flow is not the same. Finally, the hydrodynamic equilibrium was not immediately achieved, as the model predicted. For these reasons, the model could be improved in non-stationary conditions, introducing additional terms in the bond graph to include the response time of the end side plates and its influence on the pump behavior. For validation of the resulting model, specific studies of transients will have to be carried out with time scales smaller than those presented in this research.
The great dependence of the loss coefficients with the operating conditions makes it advisable to introduce three-dimensional polynomial correlations in the model, that is, the coefficients as a function of pressure and rotation speed. When reaching this complexity, it might be more convenient to simply work with the volumetric and mechanical efficiency, instead of the four loss coefficients considered.
Methodically, the knowledge acquired in the laboratory was applied in real working conditions, having revealed certain limitations in the ISO standard tests on positive displacement pumps. Although there was some controversy regarding these standards, they were a very powerful tool for characterizing the operation of this type of machine, as was demonstrated in this research.
Finally, it was proposed that similar tests with mechanical losses were carried out, by installing a torque transducer between the pump drive and the tested unit. Comparing the pump impedance in the bond graph model with the results of the ISO 10,767 tests and introducing the pumping mechanism in the model are also interesting challenges that can be addressed.
Author Contributions
The investigation was led and supervised by E.C. Experimental works, bond graph simulation models, data processing, and illustrations were completed by M.T. The manuscript was finalized by M.T., P.J.G.-M., and E.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy reasons.
Acknowledgments
The authors would like to thank ROQUET GROUP (https://www.pedro-roquet.com, accessed on 03 March 2021) and CONSTRUCCIONES MECANICAS LLAMADA (https://cm-llamada.es, accessed on 03 March 2021) for the facilities used to perform the tests with the pump and machine, respectively.
Conflicts of Interest
The funding sponsors had no role in the design of the study; in the collection, analyses or interpretation of data; in the writing of the conclusions; and in the decision to publish the results. The authors declare no conflict of interest.
Nomenclature
| Symbol | Description | Units |
| Oil film width | m | |
| Discharge coefficient | - | |
| Coulombian friction coefficient | - | |
| Laminar slip coefficient | - | |
| Turbulent slip coefficient | - | |
| Viscous friction coefficient | - | |
| Orifice diameter | m | |
| Derived capacity | m3rad−1 | |
| Geometrical derived capacity | m3rad−1 | |
| Oil film thickness | m | |
| Oil film length | m | |
| Flow rate pump at outlet ISO 4409 at pressure p and temperature θ | m3s−1 | |
| Flow rate pump at outlet ISO 4409 at pressure p and temperature θ1 | m3s−1 | |
| Flow rate pump at inlet ISO 4409 at pressure p temperature θ2 | m3s−1 | |
| Real pump flow rate | m3s−1 | |
| Compressed flow rate | m3s−1 | |
| Ideal pump flow rate | m3s−1 | |
| Laminal leakage flow rate | m3s−1 | |
| Turbulent leakage flow rate | m3s−1 | |
| Radius in oil film | m | |
| Orifice area | m2 | |
| Real torque | Nm | |
| Shaft seal frictional torque | Nm | |
| Load dependent frictional torque | Nm | |
| Frictional torque (Fluid) | Nm | |
| Ideal torque | Nm | |
| Friction torque (Coulomb) | Nm | |
| Viscous frictional torque | Nm | |
| Torque pump ISO 4409 at pressure p and temperature θ | Nm | |
| Torque pump ISO 4409 at pressure p and temperature θ1 | Nm | |
| Torque pump ISO 4409 at pressure p and temperature θ2 | Nm | |
| (Greek letters) | ||
| Pressure increase in the pump | Pa | |
| Effective bulk modulus | Pa | |
| Dynamic viscosity | Pa s | |
| Dynamic viscosity at temperature θ1 | Pa s | |
| Dynamic viscosity at temperature θ2 | Pa s | |
| Mass density | Kg m−3 | |
| Rotation speed of the pump | rad s−1 |
References
- Wilson, W.E. Rotary pump theory. Trans. ASME 1946, 68, 371–383. [Google Scholar]
- Edge, K.A.; Johnston, D.N. The ‘secondary source’ method for the measurement of pump pressure ripple characteristics part 1: Description of method. Proc. IMechE Part A J. Power Energy 1990, 204, 33–40. [Google Scholar] [CrossRef]
- Ivantysyn, J.; Ivantysynova, M. Hydrostatic Pumps and Motors: Principles, Design, Performance, Modelling, Analysis, Control, and Testing; Akademia Books International: New Delhi, India, 2001. [Google Scholar]
- Frosina, E.; Senatore, A.; Rigosi, M. Study of a High-Pressure External Gear Pump with a Computational Fluid Dynamic Modeling Approach. Energies 2017, 10, 1113. [Google Scholar] [CrossRef]
- Gamez-Montero, P.J.; Codina, E.; Castilla, R. A review of gerotor technology in hydraulic machines. Energies 2019, 12, 2423. [Google Scholar] [CrossRef]
- Torrent, M.; Codina, E. Modelización de las pérdidas volumétricas y mecánicas en una bomba de engranajes externos. In Proceedings of the XII Congreso Nacional de Ingeniería Mecánica, Bilbao, Spain, 11 February 1997; pp. 151–5072. [Google Scholar]
- Castilla, R.; Gamez-Montero, P.J.; Del Campo, D.; Raush, G.; Garcia-Vilchez, M.; Codina, E. Three-dimensional numerical simulation of an external gear pump with decompression slot and meshing contact point. J. Fluids Eng. 2015, 137, 041105. [Google Scholar] [CrossRef]
- Antoniak, P.; Stryczek, J. Visualization study of the flow processes and phenomena in the external gear pump. Arch. Civ. Mech. Eng. 2018, 18, 1103–1115. [Google Scholar] [CrossRef]
- Zhao, X.; Vacca, A. Theoretical Investigation into the Ripple Source of External Gear Pumps. Energies 2019, 12, 535. [Google Scholar] [CrossRef]
- Battarra, M.; Mucchi, E. On the assessment of lumped parameter models for gear pump performance prediction. Simul. Model. Pract. Theory 2020, 99, 102008. [Google Scholar] [CrossRef]
- Zardin, B.; Natali, E.; Borghi, M. Evaluation of the Hydro—Mechanical Efficiency of External Gear Pumps. Energies 2019, 12, 2468. [Google Scholar] [CrossRef]
- Guo, R.; Li, Y.; Shi, Y.; Li, H.; Zhao, J.; Gao, D. Research on Identification Method of Wear Degradation of External Gear Pump Based on Flow Field Analysis. Sensors 2020, 20, 4058. [Google Scholar] [CrossRef] [PubMed]
- Casoli, P.; Scolari, F.; Rundo, M.; Lettini, A.; Rigosi, M. CFD Analyses of Textured Surfaces for Tribological Improvements in Hydraulic Pumps. Energies 2020, 13, 5799. [Google Scholar] [CrossRef]
- Rundo, M. Models for flow rate simulation in gear pumps: A review. Energies 2017, 10, 1261. [Google Scholar] [CrossRef]
- Thiagarajan, D.; Vacca, A. Mixed Lubrication Effects in the Lateral Lubricating Interfaces of External Gear machines: Modelling and Experimental Validation. Energies 2017, 10, 111. [Google Scholar] [CrossRef]
- ISO 4409:2007. Hydraulic Fluid Power; Positive Displacement Pumps and Motors; Methods of Testing and Presenting Basic Steady State Perfomance. (Revised by ISO 4409:2019). Available online: https://www.iso.org/standard/37528.html (accessed on 19 January 2021).
- ISO 10767-1:2015. Hydraulic Fluid Power; Positive Displacement Pumps and Motors; Determination of Pressure Ripple Levels Generated in Systems and Components—Part 1: Method for Determining Source Flow Ripple and Source Impedance of Pumps. Available online: https://www.iso.org/standard/59414.html (accessed on 19 January 2021).
- McCandlish, D.; Dorey, R. The mathematical modelling of hydrostatic pumps and motors. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 1984, 198, 165–174. [Google Scholar] [CrossRef]
- Schlosser, W.M.J.; Hilbrands, J.W. Das volumetrische Wirkungsgrad von Verdrongerpumpen. Oilhydraulik Pneum. 1963, 7, 469–476. [Google Scholar]
- ISO 8426:2008. Hydraulic Fluid Power; Positive Displacement Pumps and Motors; Determination of Derived Capacity. Available online: https://www.iso.org/standard/40351.html (accessed on 19 January 2021).
- Toet, G.; Johnson, J.; Montague, J.; Torres, K.; Garcia-Bravo, J. The Determination of the Theoretical Stroke Volume of Hydrostatic Positive Displacement Pumps and Motors from Volumetric Measurements. Energies 2019, 12, 415. [Google Scholar] [CrossRef]
- Achten, P.; Mommers, R.; Nishiumi, T.; Murrenhoff, H.; Sepehri, N.; Stelson, K.; Palmberg, J.; Schmitz, K. Measuring the Losses of Hydrostatic Pumps and Motors: A Critical Review of ISO4409:2007. In Proceedings of the ASME/BATH 2019, Symposium on Fluid Power and Motion Control, Longboat Key, FL, USA, 7–9 October 2019. [Google Scholar]
- Available online: https://ph.parker.com/es/en/sensocontrol-serviceman-plus-measuring-device (accessed on 20 November 2020).
- De Las Heras, S.; Codina, E. Modelización de Sistemas Fluidos Mediante Bond Graph; Cardellach Còpies: SA. Terrassa, Spain, 1997; ISBN 84-605-7035-5. [Google Scholar]
- 20SIM Version 4.2; Controllab Products B.V.: Enchede, The Netherlands; Available online: http://www.rt.el.utwente.nl/20sim (accessed on 20 November 2020).
- Available online: https://www.shell-livedocs.com/data/published/es/81c4c41c-b9f7-40da-9a57-fa8881dbc2da.pdf (accessed on 20 November 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).