Abstract
Bike-sharing systems (BSS) have raised in popularity in the last years due to their potential share in sustainable cities. Although the first attempts to implement a bike-sharing public service date back to 1965 (Amsterdam), their widespread use arrived with the millennium becoming a vibrant research area whose activity has increased steadily in the last decade. Several authors have attempted to summarize the current state of the art, but the literature on BSS is still scattered in different fields. Thus, there is a lack of literature that summarizes and categorizes the available research on BSS. In this paper, we perform a thorough review of the challenges behind rebalancing in bike-sharing systems. The objectives of this paper are to collect papers on the repositioning problem in dock-based bike-sharing services, classify them and point to novel research venues. We render a keyword analysis in the literature and a timeline that shows the evolution of those keywords throughout the last decade. We also include an exhaustive table that will assist researchers from different disciplines to address the open challenges in the field and to transition towards more sustainable cities.
Keywords:
bike-sharing; reposition; balancing; relocation; algorithm; review; sustainable vehicle-sharing 1. Introduction
Population concentration in big cities brings higher levels of pollution (due to traffic jams) and has raised the interest in the so-called businesses “as a service” and the sharing economy. Interestingly, the Covid-19 crisis has been a push back for services such as car-sharing while increased awareness about bike-sharing systems (BSS).
Bike-sharing systems (BSS) have probably become the most widespread implementation of the concept of Mobility as a Service (MaaS) [1]. BSS started as a public service in 1965 in Amsterdam with the program named “White Bike”. However, it was not until the past decade that they spread their popularity worldwide [2]. The number of BSS implementations increased from 13 in 2004 to 1956 operational local schemes and approximately 15,254,400 shared bicycles in 2019 [3] (see also [4,5,6]). Visual inspection of the Bike-sharing World Map shows its widespread use, especially in north America, western Europe and Asia [7,8].
The idea behind BSS is simple: a pool of publicly available bicycles placed around the city and ready to be used for a low payment. Each implementation indeed has its own characteristics like:
- Public or private service depending on if it is managed by a private company or by a government administration.
- Dock-based (if it is based on stations picking areas) or free-floating (if just can be picked and dropped around city).
- With a restricted area of use (a delimited perimeter) or without any geographical restriction.
- Implementing different payment methods, incentives to the use of the service, discounts, and prices plans.
Attending to their characteristics and according to [9,10,11] there are five generations of BSS shown in Table 1.

Table 1.
A brief chronology of Bike-sharing systems (BSS) generations according to Refs. [9,10,11].
Focusing our attention on the BSS based on docking-stations, we can define them as a set of stations distributed in different locations around the city. Each station has bike slots where users can pick-up a bike or leave the one that they have already used. Due to imbalanced demands, some stations might out of bikes while others get fully occupied and can be overloaded by concurrent end trips. This problem has been identified in literature with several names: imbalance, rebalance, repositioning, and balancing are the most used.
BSS operators (namely company or government administration that owns the service) mitigate the effect of this asymmetric demand, getting the bicycles to be replenished at the top origin stations and releasing docking-bases at the top destination stations. It is worth remarking that how the owners manage this problem is directly translated into the user level satisfaction of the service.
Options used to solve this situation can be divided into two strategies [12]: Operator-based or User-based repositioning. The former consists of using some vehicles (typically trucks) to move bikes from one station to another one. Alternatively, in user-based repositioning, the users, instead of BSS employees, are incentivized to leave or pick-up bikes in specific stations. As mentioned in [13] Operator-based strategy seems to be more effective in docking-station based BSS, while user-based strategy retrieves better results in dockless BSS. Both strategies can be implemented from the static point of view (redistributing bikes on specific time frames) or dynamic one (the operator redistributes them in real time [13]). The current trend shows a hybrid solution, combining the different rebalancing modes.
Because there are several possible solutions for this problem, we decided to identify available review literature focused on the repositioning problem. Firstly, we decided to classify available research in BSS area. Although BSS implementations started years ago, it is not until 2010 that relevant research appears in this field. According to [14] BSS research can be classified into four stages shown in Table 2.

Table 2.
Four stages in which BSS research can be classified according to Ref. [14] and attending to publish period, research topic and bike generation.
In the fourth one (2016–2018) research is mainly focused on demand, rebalancing, and redistributions of bikes among stations problem. However, the literature on BSS is scattered in different fields which makes it hard for new researchers to bring ideas that can push further this service as a competing strategy to achieve more sustainable cities. For example, in the last years, there is a growing interest in understanding patterns that explain the use of BSS. References for docking-based BSS like [15,16] or dockless ones like [17,18] can be found. However, rebalance data is not used for that purpose. In this review paper, we attempt to review BSS research focused on the “rebalancing problem”. Only for BSS implementations based on docking-stations (fourth generation of BSS). This paper addresses four key themes: (a) Overview of the state-of-the-art related to the BSS research, (b) identification of available literature regarding reviews of bike relocation problem, (c) list and classification of studies related to algorithms used to solve bike repositioning problem and (d) evaluation of further research to be done. We combine systematic analysis of the literature as well as automatic feature extraction to identify research opportunities that can pave the ground for new and exciting achievements in the field. In this work, we have focused on dock-based BSS, although we expect a considerable raise of publications in dockless (free-floating) BSS in the next decade.
2. Methods and Data Acquisition
In order to identify papers related to the review topic (rebalancing problem) the following steps have been followed:
- Perform a search in Google Scholar by term “Bike sharing” applying the following scope restrictions:
- Limit scope to literature written in English.
- Time range is set from 2010 to the 3rd quarter of 2020. As stated in the introduction section is not until 2010 that relevant research appears in BSS field.
- Research related to balancing problem in BSS based on stations picking-areas (Dock-based). This means that other studies focused on solving the same problem for free-floating BSS implementations like [19] are out of the scope of this review
- With that, we retrieved a sorted by relevance list of bike-sharing topic papers. Google Scholar automatically will produce alternative searches related to those keywords, like: “Bicycle sharing, bike sharing, bikeshare, shared bikes, bikesharing, etc.” For the first entries of the previous search, we use the “Cited by” option provided by Google scholar to identify papers that reference the most relevant ones related to our general topic (bike sharing). After that, we filter the “Cited by” papers using several terms that are used to refer to the rebalancing problem. As mentioned in [20] a variety of terms had been used in the available literature to refer to rebalancing problem: balancing, rebalancing, repositioning, relocation, and redistribution. Classify and analyze papers focusing attention on the state-of-art, proposed algorithms, and their respective references mainly. Studies belong to several disciplines (economics, logistics, computer science, mathematics, etc.) Only papers that are focused on algorithms to solve the balancing problem are going to be analyzed.
We are aware that Google Scholar is not a curated-human database but a search engine on the Internet but, in our case, it simplifies the queries as it unifies keywords such as “bike-sharing”, “bike sharing” or “bikesharing”. It also retrieves documents related to the “rebalancing problem” that other databases only include if the right keywords are included in the query. However, we have doubled checked our results with Web of Science and Crossref.
3. Results and Discussion
3.1. Contextualization of Research in Bike-Sharing Field
We began our research by conducting an exploratory work on the research carried out in the field of bikesharing. To do this, we have made a graphic representation of the main key-words and topics that appear in Titles and abstracts on the bike-sharing related papers. Figure 1 shows mentioned keyword graph summarizing the inter-concept relationship in the BSS field, using a free computer software for representing bibliometric maps (VOSviewer). As their authors commented in [21], VOSviewer unlike other Bibliometric tools, it is focused on visual representation in an easy way (VOSViewer files could be found in the Supplementary.
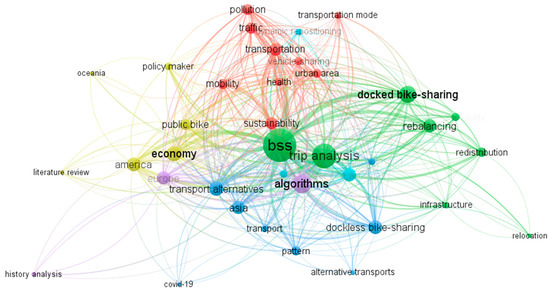
Figure 1.
BSS research concepts clustered by similarity using VOSviewer [9] Different colors stand for different groups and the size is proportional to occurrence number of the concept.
Research topics have been clustered in five groups: 1—Green: represents research focused on trips analysis, docked BSS implementations and rebalancing problem; 2—Red: groups research related to social concepts like health, mobility etc; 3—Blue: shows the last research trends (dockless BSS) and it is very interesting to remark that this type of research in mainly done in Asia; 4—Yellow: research done in fields related to economy and government. It is very interesting to see that this type of research has been done mainly in America; 5—Purple: research focused on algorithms applied to BSS that has been mainly addressed using European data. VOSviewer software performs this clustering using modularity clustering technique. Further information related to this clustering technique has been addressed by [22].
If we include the temporal variable (year of the research) in the chart, we obtain Figure 2 that shows the trend of research topics according to the years:
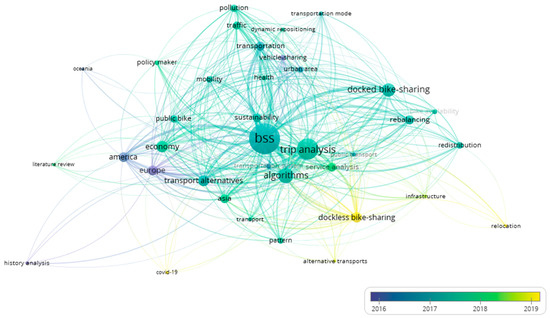
Figure 2.
BSS research trend movement across years showing a current focus on dockless bike-sharing.
Interestingly, simple inspection of Figure 2 emphasizes the fact that trending research topics are shifting progressively towards research conducted in Asia, and especially, in the fifth generation (dockless BSS). Regarding the role of rebalancing, we can see a highlighted version of the keyword graph in Figure 3 (left).
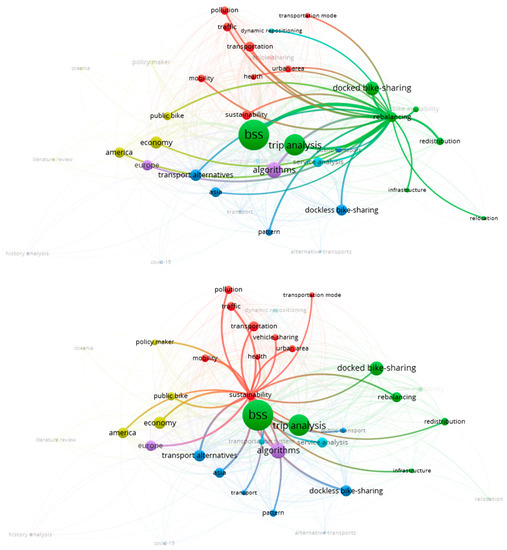
Figure 3.
Version of the keyword graph highlighting the rebalancing word (up) and sustainability word (down) showing its relationship with other relevant words.
“Rebalancing problem” has been clustered in the green-colored cluster with important links to concepts like “docked bike sharing”, synonyms of the problem (like redistribution or relocation) and “Trip analysis” (it is very common to perform a trip analysis before adopting a rebalancing policy).
Another relevant insight obtained from Figure 3 (up) is that “rebalancing problem” is linked with other research topics. For example, it affects economic measures and social behaviors. It is solved using specific algorithms. As a concept, “rebalance”, also affects dockless bikes. Although they do not have stations, it is also required to redistribute bikes around the city. However, this kind of redistribution problem (Dockless bike redistribution) is out of the scope of this paper.
Finally, we can see that the rebalance problem is tightly connected with “sustainability”. In fact, if we focus our attention on sustainability in the chart, we obtain Figure 3 (down), basically showing that most of relevant research topics in BSS have a kind of link with sustainability.
After a general and visual classification of available studies, we have identified the ones that are review papers on BSS. The first review of BSS state-of-the-art was performed by [23] in which it is provided: 1. An overview of the Bike-sharing programs, 2. A critical check of available literature and 3 An identification of the gaps in the knowledge.
After that, [3,24] provided their respective reviews, focused on specific themes related to BSS and taking into account the available literature before 2015. Finally, in Ref. [14] the authors summarize BSS research done between 2010 and 2018, done with a scientometric approach. It consists of applying mathematical and statistical methods to create a quantitative analysis of the knowledge related to BSS.
Table 3 shows the characteristics of the available BSS Literature review paper (LRP) but also establishes the position of the present work in the context of previously published LRPs.

Table 3.
Comparative among the available BSS Literature review paper (LRP) and the present work.
3.2. BSS Rebalancing Problem Review Analysis
The number of studies related to BSS has been growing over recent years, specifically since 2010 [25]. Therefore, the main aim of our work is to provide an updated and broad view of the literature that can guide future research on the topic. Thus, having analyzed the BSS literature, we can conclude that there are only a few review studies in this research area. Additionally, those review papers provide a high-level overview of the BSS research, mixing different knowledge fields, and not giving enough detail on main BSS research topics. Focusing on one of the main BSS problems (“rebalancing problem”), we detect that there are not specific review papers that summarize available studies. State-of-the-art related to rebalancing problem is split thought the different papers that are providing solutions to the problem being this one of the topics covered by the present work.
Literature Review Timeline
The balancing problem has been identified as one of the main challenges that BSS implementations have faced since their earliest implementations. BSS operators identified the need of improving the bike’s distribution methods and, in some cases, they also evaluated its associated costs [9]. Therefore, there is a need to find methods that make redistribution more efficient [2].
Several approaches have been proposed in the last ten years. Nair and Miller-Hooks [26], using stochastic programming, assumed that the cost of moving vehicles (cars or bikes) can be represented by a fixed pus-linear function, not taking into accounting routing constraints and costs. The model assumes a static demand but does not consider fluctuations in demand in different periods. Therefore, this model is considered too simplistic for the BSS repositioning problem.
Another early approach [27] describes the problem as an alternative to the classical traveling salesman problem (TSP) and proposes a methodology based on approximation algorithms to reduce the cost. In the same year, another study [28] use Station Origin-Destiny visualization techniques to show trip flows among docking-stations. Apart from identifying possible rebalancing strategies, the main contribution of this paper is the recognition of the need for a demand study to find an optimal balancing strategy. In addition, they find a clear dependence between the rebalancing strategy and the concrete implementation of the BSS, also shown in [29].
Chemla et al. [30] introduced a more rigorous theoretical framework in order to better understanding the critical factors affecting the optimal solution. Moreover, this was the first time in which a metaheuristic approach was used in this context. They proposed an integer program with several constraints solved with a branch-and-cut algorithm.
In 2012, Labadi et al. [31] proposed the use of Petri nets to create a modular dynamic model. The goal was to search for optimal values of the model minimizing empty and full stations scenarios. Lin and Chou [32] realized that bike redistribution is part of the vehicle routing problem (VPR) and traditionally it has been solved using Euclidean distance to calculate transport cost. They propose to include geographical information, (like road conditions, traffic regulations, etc.) provided by geographic information systems (GIS), in the transport cost calculation. With this approach, and testing different constructions methods, they conclude that farthest insertion performs better than a nearest-neighbor approach.
Until 2013, the main idea was to address the problem assuming that there is an optimal occupation level per station and the goal is to achieve those levels with the minimum bike-reposition cost. Raviv et al. [33] offered two formulations of the problem, using a Mixed-integer linear program (MILP), thus obtaining solutions with acceptable optimally gaps for moderate size BSS implementations (up to 60 stations). For larger systems, they suggest applying their method in conjunction with a geographical approach or decide to use heuristics methods such as Tabu search or Genetic Algorithms.
Another approach to solve the balancing problem was Variable Neighborhood Search (VNS) [34,35]. In general, VNS performs well and scales much better than linear programming approaches. Nair et al. [36] decided to obtain a quantitative analysis of a large-scale BSS implementation (Vélib’ system in Paris). They analyzed the redistribution problem by using stochastic historical information. This research builds on a previous study of the same main author [26]. Furthermore, in the same year, Lin et al. [37] proposed a strategic design for BSS taking into account stock considerations and formulating the problem as a hub location inventory model. They used heuristics to cost out the objective function. Their weak point is that they do not consider in their model that check-in bikes can be reused.
Alternatively, Di Gaspero et al. [38] tackled the problem using the so-called constraint programming. In order to speed-up the search of the most promising routes they used a Large Neighborhood Search (LNS) approach. In 2014, Erdogan et al. [39] introduced, modeled, and solved a variant of the One Commodity Pickup and Delivery Traveling Salesman Problem (1-PDTSP) called Static Bicycle Relocation Problem with Demand Intervals (SBRP-DI). The problem consists of relocating bikes among different stations considering the initial inventory of each station and some fixed lower and upper bounds. They solved it by applying integer programming with a branch-and-cut algorithm. In the same year, Kloimüllner et al. [40] extended their previous work done from a static point of view (Using Greedy–PILOT Heuristics with Variable Neighborhood Search). Other authors F [41] proposed a framework to solve the repositioning problem based on four models: 1—demand forecasting, 2—station inventory, 3—redistribution needs, and 4—vehicle routing, within the dynamic programming paradigm.
From the cost-benefit side, in Ref. [42] the authors combined the classical redistribution method done by the owner of the BSS implementation with a pricing incentive approach to the customers. This was the first example of a user-based approach mixed with the classical operator-based one and illustrated that cost reductions can be achieved, making dynamic changes in the rewards given to the users if their park in one or in another bike station. Basically, they proposed to compute how users acts to variable rewards and then they re-calculate the routing bike distribution plan for the staff.
Dell’Amico et al. [43] addressed the problem by combining four different methods and comparing their results. All of the alternatives had in common that they involve an exponential number of constraints, so a branch-and-cut algorithm was adopted to solve them. After testing it with several datasets, they concluded that this approach works fine for instances up to 50 vertices. For larger ones, computing time is increased. They suggest treating them with heuristics and metaheuristics algorithms.
In the same year, a method to identify commuting behaviors to identify user’s travel patterns was introduced in Ref. [44]. Classical analysis of peak-times demand, according to their research, caused more problems to the rebalancing, than the visual classification techniques used in this research (weighted mean-centers calculation, spatial k-means clustering, and kernel-density estimation). With this approach, they identified the main sources of imbalance (mornings vs. evenings, travels originated inside London vs. outside ones, etc.).
Ho [45] used an iterated tabu search heuristic producing with this approach high-quality solutions with short computer times. Apart from the improved solution, this paper contributed to increasing the realism and reducing the solution space of the rebalancing problem. They finally commented that this approach could be used with other objective functions and they recommended to extend research to multiple reportioning vehicle scenarios.
Finally, also in 2014, Zhan et al. [46] analyzed the degree of success of bike sharing exploring BSS in China. Although no algorithm or possible solution to the rebalance problem was provided in this paper, it is important to remark that they concluded that the adopted rebalance strategy influences on the service level, begin this and often neglected key factors to address to achieve a successful BSS implementation. At the beginning of 2015, a three-step heuristic approach was proposed in [47]. First, divide and group stations considering geographic and inventory considerations (clustering). Second, vehicles routes are set through the clusters taking the inventory level decision for each station. Finally, the third step consists of only allowing transfers between stations of the same cluster or the one that belongs to consecutive clusters. In the same year, Erdolan et al. [48] introduced a linear programming algorithm, converting general variables into binary ones. They proved this solution with several datasets, being able to scale up the computation up to 60 stations.
In 2016, Álvarez-Valdés et al. [49] discussed the role of the repositioning plan as a key factor of the quality of the service. They provided a summary of the research done until then, and they conclude that although each system has its own characteristics all of them share two parts. The first one is the prediction/forecasting of the stochastic demand and the second one is the routing plan. Their contribution consisted of designing a procedure that joins both parts. Finally, they recommend extending research to dynamic solutions.
In Ref. [50] Szeto and Shui reframed the problem and analyzed it as a Chemical reaction optimization (CRO) algorithm, obtaining better solutions with less computing time.
Regarding computation time, in Ref. [51] Dell’Amico et al. claimed that their proposed solution strongly improved previous alternatives by combining a new heuristic with local searches and adapting it with a branch-and-cut technique to consider the maximum duration time to reposition.
Li et al. [52] addressed the scenario of having different types of bikes. They propose to reduce the total cost of the rebalancing task, formulating a mixed-linear programming problem and solving it with a hybrid genetic algorithm.
In another interesting research published in 2016 by Medard de Chardon et al. [20] the rebalancing process of nine BSS is described. They conclude that the relationship between trips and rebalancing is more complex than expected. Although they do not provide a new rebalancing algorithm, one of their conclusions is highly relevant: the simple fact of applying a rebalancing policy to a station directly affects its demand level. Other authors like Cruz et al. [53] focused on a simpler version of the problem (only having one car to rebalance bikes among stations). The proposed algorithm in this research is Iterated local search (ILS) based heuristic, and they also perform a comparison with earlier proposed solutions [30,48].
Zhang et al. [54] highlighted the division of the rebalancing problem into two parts: first one related to the decision of the target inventory level and second one about the routing plan to distribute bikes in order to accomplish with previous mentioned target inventory level. They use a Meteorology Similarity Weighted K-Nearest-Neighbor (MSWK) regressor to predict the demand based on historical data, and a mixed-integer nonlinear programming (MINLP) trying to minimize the distance traveled by the routing vehicle. Finally, to cluster the stations, the authors use an Adaptive-Capacity Constrained K-centers Clustering (AdaCCKC) algorithm.
Finally, also in 2016, Zhang et al. [55] proposed a dynamic bicycle-repositioning methodology. With the inventory level and user arrivals forecasting, bicycle repositioning data, and vehicle routing the crated a time-space network model translated into an underlying complex nonlinear optimization problem analyzed a custom heuristic algorithm. Along those lines, Ho and Szeto [56] provided a heuristic algorithm based on a large neighborhood search, with tabu search and various insertion and removal operators to improve the algorithmic performance. This algorithm performs better than the previous ones but has a limitation: the possibility of moving bikes from already balanced stations to neighbor stations reducing travel costs. Similarly, in Ref. [57], and based on the artificial bee colony (EABC) algorithm Shui and Szeto put their focus in reducing CO2 emissions outperforming the classic Genetic Algorithm.
Chiaiotti et al. [58] used a combination of Birth–Death Processes to decide the time to redistribute bikes and graph theory to select the rebalancing route.
Additionally, in 2017, Elthenawy and Rakha [59] proposed a solution based on game theory, specifically on the deferred acceptance algorithm. This algorithm has two phases: building the route for rebalancing and improving this route. In the end, the problem is modeled as two disjoint sets of players, each of them with their own.
Finally, in 2017 Schuijbroek et al. [60] combined two aspects that traditionally were handled separately: the service level of each bike station and the optimization of vehicle routes to rebalance bikes. To combine both subproblems they used a clustering algorithm first and after that they applied some heuristics.
Bulhoes et al. [61] included the possibility of having multiple vehicles with several visits to execute the rebalance among stations. They suggested an integer programming problem, solved with a branch-and-cut algorithm. Their main contribution is that multiple visits are only interesting for vehicles with a capacity higher than 20 bikes. They also concluded that the number of required revisits decreased with the number of available vehicles.
Szeto and Sui [50] proposed an enhanced artificial bee colony (EABC) algorithm concluding that EABC has a better performance and also returns better approximated solutions than the classical CPLEX algorithm. They also provide a list of recommendations regarding routes durations, service time, number of vehicles and demand satisfaction. All those recommendations have been demonstrated. Legros [62] provided a decision-support tool based on a Markov decision process, that allows the operator to decide in a specific time the numbers of bikes that should be moved from or to each station. Alternatively, Dell’Amico et al. [63] provided a heuristic solution to the problem but focusing on a stochastic demand version. In parallel, Ref. [64] contributed to the solution of the problem improving the prediction of the demand with machine learning techniques.
Another example of a dynamic bike repositioning model was provided by Li et al. [65], using a spatial-temporal reinforcement learning based on clustering algorithms. They divided the BSSS into several clusters and they applied the model to each cluster. Doing that they reduced the problem complexity and learned optimal reposition policies training the model.
In 2019, You [66] proposed a constrained nonlinear mixed-integer programming model. In order to address the complexity of the problem, it is split into time-independent subproblems. Then, they solved the remaining problems with selected linear programming models. Evidence shows that their approach is better than GAMS/CEPLEX and better also than a mixed approach (genetic algorithm plus linear programming).
Tang et al. [67] solved a bilevel model using iterated local and tabu search algorithms. The upper level manages the number of bikes that should be moved among target stations while the lower level is focused on reducing transportation costs. Their performance, according to their tests, is better than previously available solutions. In parallel, they provide some insights that affects the cost of repositioning: size of the repositioning vehicle, the value of loading/unloading time for a single bike, and the length of repositioning time.
Wang and Wu [68] included additional variables into the problem (unusable bikes and stations, multiple vehicle and visits and restrictions due to the repair requirements of stations). They proposed a model tested with a small problem and solved with simple heuristics mathematical algorithms. They concluded that for further and larger research it is required to use metaheuristic algorithms like the iterated local search, the large neighborhood search or the tabu search.
Warrington and Ruchti [69] proposed a two-stage stochastic approximation applied not only for BSS but also for other sharing vehicles. We have included it in this review because they use a BSS system to evaluate their solution.
During 2020, many works were focused on anticipating future demand. In particular, Brinkmann et al. [70] introduced a stochastic-dynamic inventory routing problem modeled as a Markov decision process to solve the problem.
In addition, Tang et al. [71] focused their research on minimizing several costs that are aligned with the rebalancing procedure: 1—transportation cost, 2—penalty cost of all stations for not fulfilling the demand, and 3—holding costs. For that purpose, they used a two-stage stochastic programming model solved with a simulated annealing algorithm. In parallel, Maleki et al. [72] modeled the problem as a Jackson network and a genetic algorithm was used to solve it. They obtained acceptable improvements and they also provide feedback regarding fleet size and BSS capacity.
Another solution was proposed by Zhang et al. [73] by modeling the problem as a classic linear programming problem but solving it with an adaptative tabu search (ATP) algorithm.
Jia et al. [74], instead of focusing their research in obtaining the balance point as classical literature, introduced the concept of “balance interval”. They modeled it as a bi-objective integer-mixed program problem, using a multi-start multi-objective particle swarm optimization (MS-MOPSO) algorithm.
Finally, Lu et al. [75] proposed a memetic algorithm that combines a greedy construction method to generate solutions, a route-copy algorithm for solution recombination, and a local search for solution improvement. This solution provided a double improvement: first 46% of cases obtained a better-known result and second near two to six time faster than available solutions in the literature.
In recent year, research on the rebalancing problem has focused on dockless BSS implementations. Because of dockless BSS is out of scope of this review, they are not mentioned in this work. Free floating BSS require to take into account additional variables like the classification of the city area in zone types (residential, commercial, leisure areas, etc.) and transport administration policies among others. It would be interesting, for further research, to analyze the redistribution algorithms used in dockless and compare them with the ones used in dockbased BSS.
4. Summary of Results and Discussion
Dock-based BSS Rebalancing problem has been addressed by several authors, referencing it with different names (can be seen in Table A1). There was a clear need to gather in a paper all the references related to the solution of the problem, regardless of how the author had named it. This is one of the motivations for our research.
Once we have identified the target papers, it was required to classify them. According to Ho and Szeto [56] and Shui and Szeto [57] algorithms for solving the rebalance problem can be clustered in four families: (1) Exact Methods; (2) Approximation; (3) Heuristics/Metaheuristics; and (4) Hybrid methods. The papers of family (1) (Exact methods), it has been included the initial solutions, focused on solving linear integer programming problems. The inconvenience of the exact methods is that, for large and realistic problems, they become intractable. Therefore, most of the research had focused on approximate algorithms, trying to achieve better solutions with less computer analysis cost. During our research we have identified some solution approaches that do not fit on previous mentioned families. We are referring to the approaches that use modern techniques like visualization and machine learning, among others. We decided to refer them in Table A1 as “others”.
We have also identified, for each proposed solution, the choice distribution time of the bikes. It could be static distribution (the operator redistributes bikes on specific time frames) or dynamic one (the operator redistributes them in real time). We have checked that most of solutions opt for a static approach.
Taking into account the strategy followed to rebalance bikes, approaches can be divided into three groups (1—operator-based, 2—user-based, and 3—operator-based mixed with user-based) as we have described in the introduction. Considering that our scope is limited to dock-based BSS implementation and remembering that operator-based strategy seems to be more effective in docking-station based BSS (as mentioned by [13]), what was expected is that most of the analyzed papers described an operator-based strategy. We have verified that this is indeed the case.
Regarding temporal and spatial location, we have also classified the papers by year, by continent of the authors and, in case that a dataset is used to validate the algorithm, which is the BSS implementation involved. Since 2020, rebalancing problem is a topic that has been treated several times per year with little increase in the last ones. At the beginning of the decade most of the works addressed BSS in Europe and America and the datasets were also from BSS implementations in cities of those continents. But, by the end of the present decade, the trend has changed, and many works are now addressing BSS in Asia (almost exclusively in China).
As a result of our review work, we have identified a list of open questions research lines in the BSS rebalancing problem. In the following Table 4 we show this list, with the already research done and the research niches that are still pending to be addressed.

Table 4.
Summary table of main analysis results.
5. Conclusions
Bicycle-sharing systems (BSS) has been recognized as an important actor towards the construction of sustainable cities and it has experienced an unprecedented expansion worldwide. In this work, we have reviewed all the available algorithms reported in the literature for solving the rebalance problem in dock-based BSS (often referred to as rebalance, redistribution, distribution, reallocation, balance, imbalance and reposition). In order to overcome a systematic bias and to provide an exhaustive review of the literature, we have created a thesaurus that as allowed to broaden the scope of the review.
Once the target papers had been identified, we have created a taxonomy/classification of proposed algorithms and, to make our analysis more helpful we have summarized our exhaustive discussions in Table A1 in Appendix A. In that table, the available literature has been classified by year, type of algorithm, rebalance strategy and distribution time. Additional information is related to the source of the used datasets and the main differentiating contribution of the paper.
Although several algorithms have been proposed in the literature for solving this problem, all of them have concluded that the rebalancing problem entails the conjunction of two subproblems. The first one consists of analyzing and modeling the demand of the service and obtaining a generic analysis for several BSS implementations is not an easy task. There are a lot of variables that directly affect the demand and, what is more, they do not affect the different BSS implementation in the same way. The second one involves the optimization of the bike-rebalancing process, respecting the desired service level and minimizing cost.
We have clearly seen, as it was also recognized in Ref. [32], that BSS in different cities have different characteristics which means that different redistribution mechanisms will be required (as a consequence of the topology, socioeconomic factors and climatology). A common characteristic in the practical totality of the proposed redistribution mechanisms, is the use of a fleet of vehicles to perform this action. The contradictory part is that most of them use highly polluting vehicles what contradicts the goal of alleviating the problem of a sustainable transport. Interestingly, to our knowledge, except for Ref. [57], there are not others works computing the carbon footprint of different BSS rebalancing strategies, so our work paves the ground to this sort of approach.
We have also identified that, in the last years, modern algorithms like visualization or machine leaning based ones, has been used to provide possible solutions to the rebalancing problem. Those algorithms do not fit in the classical used algorithm taxonomy in this field, and because of that we suggest to include a new group for include inside it this kind of new approaches.
Finally, we identify the following open questions and research lines in the BSS rebalancing problem. (1) Surprisingly, all the existing works addresses the BSS as a sustainable alternative in a non-sustainable way as they ignore the impact of rebalancing using polluting vehicles. (2) The “rebalance problem” has been studied in other scenarios (other vehicle-sharing systems, classical pickup and drop problems of deliverable services, etc.). However, we have not retrieved comparative studies comparing solutions adopted in other fields and how it would be adopted in the BSS. (3) Currently, most of the newly implanted BSS solutions are dockless, so we expect a considerable raise of publications in that direction in the next decade. We anticipate that most of the solutions adopted for BSS would be obsolete what paves the ground for further developments adapted to its idiosyncrasies. (4) Currently, most of the solutions do not exploit the vast amount of user-centric data using machine learning techniques that could improve considerably the personalization of the service. (5) Finally, we guess that comparative analyses (in terms of sustainability as well as economic or social penetration) between dock-based and dockless BSS systems would assist public administrations and companies to evaluate the decision of migrating from a one BSS type to another.
Supplementary Materials
The following are available online at https://github.com/cvallez/BSS-rebalancing-review, VOSViewer files: BSSKeywordsMapFile.txt, BSSKeywordsNetworkFile.txt and BSSRebalancingPapers.ris, Thesaurus file: ThesaurusBSSKeywords.txt, Table S1 Excel file: BSSRebalancingPapersClassif.xlsx.
Author Contributions
All authors have read and agreed to the published version of the manuscript, contributing in the same proportion to the realization of the review paper.
Funding
This research has been partially funded by the Spanish Ministerio de Ciencia, Innovación y Universidades (MICINN)-Fondo Europeo de Desarrollo Regional funds of the European Union support, under Projects FIS2016-78883-C2-2-P and PID2019-106339GB-I00.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Summarized information of research done in rebalancing problem of dock-based BSS.
Table A1.
Summarized information of research done in rebalancing problem of dock-based BSS.
| Authors Reference | Year | Continent of the Paper | Data Analysis Country | Algorithm Classification | Algorithm | Distribution Time | Strategy | Term Used to Name the Problem | Main Contribution | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Nair and Miller-Hooks, 2011 | 2011 | America | Singapore city Singapore | Heuristics/ metaheuristics | Stochastic MIP | Static | Operator-based | Imbalance, Redistribution | Very simplistic model for BBS but valid for |
| 2 | Benchimol et al., 2011 | 2011 | Europe | France Paris | Approximation | Approximation algorithms and polynomial algorithm | Static | Operator-based | Balancing | Treat the problem as an alternative of the classic traveling salesman problem (TSP) |
| 3 | Wood, Slingsby, and Dykes, 2011 | 2011 | Europe | UK London | Other | Visualization Techniques | N/A | N/A | Rebalancing | Identifies that service demand and implementation of BSS affect to rebalancing strategy. Any solution will require a kind of study of both characteristics. |
| 4 | Chemla, Meunier, and Wolfler Calvo, 2012 | 2012 | Europe | N/A | Hybrid exact and heuristics | A branch-and-cut algorithm applied to a integer program with several constraints. | Static | Operator-based | Rebalancing, repositioning | First time a metaheuristic approach is applied to this problem. |
| 5 | Labadi, Benarbia, Hamaci, and Darcherif, 2012 | 2012 | Europe | France Paris | Other | Petri nets | Dynamic | N/A | Rebalance, Balance, Imbalance | First study to include Petri nets to simulate and validate models of this transportation service. |
| 6 | Lin & Chou, 2012 | 2012 | Asia | Taipei | Other | Gis information + farthest insertion and nearest neighbor algorithms | Static | Operator-based | Rebalance, Imbalance | Use GIS information |
| 7 | Contardo, Morency, and Rousseau, 2012 | 2012 | America | Canada Montreal | Heuristics/ metaheuristics | Column generation and Benders decomposition applied to a model based on arc-flow | Dynamic | Operator-based | Balance, Balancing | Develop a scalable methodology that provides lower and upper bounds in short computing times |
| 8 | Raviv et al., 2013 | 2013 | Asia | France Paris Washington DC USA | Heuristics/ metaheuristics | Mixed-integer linear program (MILP), | Static | Operator-based | Repositioning, Pickup and delivery problem | Use of MILP models |
| 9 | Rainer-Harbach, Papazek, Hu, and Raidl, 2013 | 2013 | Europe | Austria Vienna | Heuristics/ metaheuristics | Variable Neighborhood Search (VNS) with an embedded Variable Neighborhood Descent (VND) plus use of greedy heuristic, a maximum flow calculation, and linear programming | Static | Operator-based | Balancing, Rebalance | Shows (experimentally) that VNS in general performs well and scales much better than other two used MIP approaches |
| 10 | Raidl, Hu, Rainer-Harbach, and Papazek, 2013 | 2013 | Europe | Austria Vienna | Hybrid exact and heuristics | Variable Neighborhood Search (VNS) combined with Greedy Heuristics (GH), maximum flow approach for the monotonic case (MF-MC) and maximum flow based, general case(MF-GC) | Static | Operator-based | Balancing, Rebalance | Shows (experimentally) that this combined approach yields significantly better results than the original variable neighborhood search. |
| 11 | Nair, Miller-Hooks, Hampshire, and Bušić, 2013 | 2013 | America | France Paris | Heuristics/ metaheuristics | Stochastic MIP | Static | Operator-based | Redistributing, Redistribution | They show the efficacy of generating redistribution strategies using stochastic information applied to a large-scale BSS implementation. |
| 12 | J. R. Lin, Yang, and Chang, 2013 | 2013 | Asia | N/A | Heuristics/ metaheuristics | Heuristics | Static | Operator-based | Redistribution | A hub location inventory model. |
| 13 | Di Gaspero, L., Rendl, A., and Urli, T. 2013 | 2013 | Europe | Vienna Austria | Heuristics/ metaheuristics | Constraints programming speed-up with Large Neighborhood Search (LNS) | Static | Operator-based | Rebalancing | Not outperforms current solutions but allows a more general formulation of a BSS |
| 14 | Erdoğan, G., Laporte, G., and Calvo, R. W. 2014 | 2014 | Europe | N/A | Exact method | A branch-and-cut algorithm applied to a integer program | Static | Operator-based | Relocation Redistributing, Redistribution | Consider lower and upper bounds |
| 15 | Kloimüllner, C., Papazek, P., Hu, B., and Raidl, G. R. 2014, | 2014 | Europe | Austria Vienna | Heuristics/ metaheuristics | Variable Neighborhood Search (VNS) combined with Greedy Heuristics (GH), | Dynamic | Operator-based | Balancing, Rebalance | Improvement of the paper Raidl, Hu, Rainer-Harbach, & Papazek, 201 done for a dynamical scenario. |
| 16 | Regue, R., and Recker, W. 2014 | 2014 | America | USA Boston | Exact method | Framework based on four models | Dynamic | Operator-based | Rebalancing | Proactive approach (repositioning is done before unbalances happens) opposite to the traditional reactive approach |
| 17 | Pfrommer, J., Warrington, J., Schildbach, G., and Morari, M. 2014 | 2014 | Europe | UK London | Other | Solution based on mix of intelligent routing plan plus dynamic rewards incentives to the users | Dynamic | Operator-based mixed with User-based | Redistribution | First paper that evaluates the approach of using customer incentives (User-based approach) |
| 18 | Dell’Amico, M., Hadjicostantinou, E., Iori, M., and Novellani, S. 2014 | 2014 | Europe | Several instances | Exact method | Four proposals ways all of them compared and solved with branch-and-cut algorithm | Static | Operator-based | Reposition, Rebalancing | Evaluation based on computational benchmarks |
| 19 | Beecham, Wood, and Bowerman, 2014 | 2014 | Europe | UK London | Other | Visual classification techniques | Static | Operator-based | Redistribution | Identification of imbalances sources (mornings vs evenings, travels originated inside London vs outside ones |
| 20 | Ho, S. C., and Szeto, W. Y. 2014 | 2014 | Europe Asia | Several instances | Heuristics/ metaheuristics | Iterated tabu search heuristic | Static | Operator-based | Repositioning | High-quality solutions with shorter computer times |
| 21 | Forma, I. A., Raviv, T., and Tzur, M. 2015 | 2015 | Europe | France Paris | Hybrid exact and heuristics | 3-step heuristic method | Static | Operator-based | Repositioning | Reduces the routing problem by clustering techniques |
| 22 | Erdoğan, G., Battarra, M., and Calvo, R. W. 2015 | 2015 | Europe | Several instances | Heuristics/ metaheuristics | Algorithm based on linear programming solution | Static | Operator-based | Rebalancing, reposition | Test on benchmarks instances of the literature. |
| 23 | Alvarez-Valdes, R., Belenguer, J. M., Benavent, E., Bermudez, J. D., Muñoz, F., Vercher, E., and Verdejo, F. 2016 | 2016 | Europe | Palma de Mallorca Spain | Heuristics/ metaheuristics | Mathematical solution based to obtain the predictions and heuristics to decide routing part. | Static | Operator-based | Repositioning | Identifies that two parts need to be addressing the repositioning problem. Provide a solution that merges both and suggest to extend research to dynamic solutions |
| 24 | Dell, M., Iori, M., Novellani, S., and Stützle, T. 2016 | 2016 | Europe | Several instances | Heuristics/ metaheuristics | New heuristic with local searches and adapting it with a branch-and-cut technique | Static | Operator-based | Reposition, Rebalancing | An improvement in computational time. |
| 25 | Li, Y., Szeto, W. Y., Long, J., and Shui, C. S. 2016 | 2016 | Asia | Experimental Data | Heuristics/ metaheuristics | Mixed-linear programming problem and solving it with a hybrid genetic algorithm | Static | Operator-based | Repositioning | They consider scenarios having different types of bikes. |
| 26 | Cruz, F., Subramanian, A., Bruck, B. P., and Iori, M. 2016 | 2016 | America, Europe | N/A | Heuristics/ metaheuristics | Iterated Local Search (ILS) based heuristic | Static | Operator-based | Rebalancing | Comparison with the solutions proposed by (Erdoʇan et al., 2015) and (Chemla et al., 2012). |
| 27 | Liu, J., Sun, L., Chen, W., and Xiong, H. (2016 | 2016 | America, Asia | New York USA | Hybrid exact and heuristics | 1 a Meteorology Similarity Weighted K-Nearest-Neighbor (MSWK) regressor to predict the demand based on historical data, 2 a mixed-integer nonlinear programming (MINLP) trying to minimize travel distance of routing vehicle, and 3 a Adaptive Capacity Constrained K-centers Clustering (AdaCCKC) algorithm to create clusters of stations | Static | Operator-based | Rebalancing | Large scale rebalance optimization |
| 28 | Zhang, D., Yu, C., Desai, J., Lau, H. Y. K., and Srivathsan, S. 2016 | 2016 | Asia | Washington DC USA Paris France | Heuristics/ metaheuristics | Mixed-integer problem solved with a novel heuristic algorithm. | Dynamic | Operator-based | Repositioning | Significant reduction in rejected user requests compared with existing methodology |
| 29 | Szeto, W. Y., Liu, Y., and Ho, S. C. 2016 | 2016 | Europe, Asia | Vienna, Europe | Heuristics/ metaheuristics | Chemical reaction optimization (CRO) | Static | Operator-based | Repositioning | Improve the solution quality reducing computing time |
| 30 | Ho, S. C., and Szeto, W. Y. 2017 | 2017 | Europe, Asia | 3 Datasets | Heuristics/ metaheuristics | Heuristic based on large neighborhood search, with tabu search and various insertion and removal operators | Static | Operator-based | Repositioning | Improve performance |
| 31 | Shui, C. S., and Szeto, W. Y. (2017) | 2017 | Asia | Numerical examples | Heuristics/ metaheuristics | Artificial bee colony (EABC) algorithm and a route truncation heuristic | Static | Operator-based | Repositioning | Focus objective on CO2 emissions reduction |
| 32 | Chiariotti, F., Pielli, C., Zanella, A., and Zorzi, M. 2018 | 2017 | Europe | New York USA | Other | Combination of Birth-Death Processes and graph theory | Dynamic | Operator-based | Rebalancing, rebalance | Clear benefits of dynamic vs static approach. |
| 33 | Elhenawy, M., and Rakha, H. 2017 | 2017 | America | Several datasets | Other | Game theory: based on the deferred acceptance algorithm | Static | Operator-based | Rebalancing, rebalance | An approach that sometimes is better than known solution and other times close to it but with a better computational performance. |
| 34 | Schuijbroek, J., Hampshire, R. C., and Van Hoeve, W. J. 2017 | 2017 | Europe America | Boston, Washington USA | Heuristics/ metaheuristics | Cluster-first route-second heuristic, | Static | Operator-based | Rebalancing | First paper that unifies the level of station inventory constraints with vehicle routing for static rebalancing |
| 35 | Bulhões, T., Subramanian, A., Erdoğan, G., and Laporte, G. 2018 | 2018 | America/Europe | Several datasets | Heuristics/ metaheuristics | Integer programming problem solved with a branch-and-cut algorithm | Static | Operator-based | Relocation | Relationship between the number of revisits, number of vehicles and capacity of them |
| 36 | Szeto, W. Y., and Shui, C. S. 2018 | 2018 | Asia | Several datasets | Heuristics/ metaheuristics | Enhanced artificial bee colony (EABC) algorithm | Static | Operator-based | Repositioning | Better performance and higher quality solutions than CPLEX. A set of best practices that have been demonstrated. |
| 37 | Legros, B. 2019 | 2018 | Europe | Paris France | Other | Markov decision process | Dynamic | Operator-based | Repositioning | Provide a solution with simpler prioritization rules and better performance. |
| 38 | Dell’Amico, M., Iori, M., Novellani, S., and Subramanian, A. 2018 | 2018 | Europe | Several instances | Hybrid exact and heuristics | Heuristic with Deterministic Equivalent Program, L-Shaped methods, and branch-and-cut algorithms | Static | Operator-based | Rebalancing | Treat stochastic version of the problem. |
| 39 | Li, Y., Zheng, Y., and Yang, Q. 2018, July | 2018 | Asia | New York USA | Other | Spacio-temporal reinforcement learning based on clustering algorithms | Dynamic | Operator-based | Reposition | Dynamical approach based on clustering and tested with a real dataset, providing a better solution than the used one. |
| 40 | You, P. S. 2019 | 2019 | Asia | N/A | Heuristics/ metaheuristics | Constrained nonlinear mixed-integer programming model. | Static | Operator-based | Repositioning | Better solution than GAMS/CEPLEX and a mixed approach (genetic algorithm plus linear programming) |
| 41 | Tang, Q., Fu, Z., and Qiu, M. 2019 | 2019 | Asia | Several instances | Hybrid exact and heuristics | Bi-level model solve with iterated local search and tabu search algorithms | Static | Operator-based | Repositioning | Better performance and demonstrates some insights that affect the cost of repositioning |
| 42 | Wang, S., and Wu, R. 2019 | 2019 | Asia | N/A | Heuristics/ metaheuristics | Heuristics based mathematical algorithms | Static | Operator-based | Rebalancing | Include the concept of unusable bikes and stations into the variables of the problem. |
| 43 | Warrington, J., & Ruchti, D. 2019 | 2019 | America Europe | Philadelphia USA | Heuristics/ metaheuristics | A two-stage stochastic approximation | Dynamic | Operator-based | Rebalancing, Rebalance | Demonstrate a better performance than real options and provide a solution for other vehicle-sharing systems |
| 44 | Brinkmann, J., Ulmer, M. W., and Mattfeld, D. C. 2020 | 2020 | Europe | Minneapolis and San Francisco USA | Other | Stochastic-dynamic inventory routing problem modeled as a Markov decision process | Dynamic | Operator-based | Repositioning, Rebalancing | Outperforms benchmark policies from the literature |
| 45 | Tang, Q., Fu, Z., Zhang, D., Guo, H., and Li, M. 2020 | 2020 | Asia | N/A | Heuristics/ metaheuristics | A two-stage stochastic programming model solved with simulated annealing algorithm | Static | Operator-based | Repositioning | Focus objectives on costs reduction |
| 46 | Vishkaei, B. M., Mahdavi, I., Mahdavi-Amiri, N., and Khorram, E. 2020 | 2020 | Asia | N/A | Other | A Jackson network solved with a genetic algorithm | Static | Operator-based | Rebalancing | Acceptable improvement and provide advice regarding fleet size and the BSS capacity |
| 47 | Zhang, D., Xu, W., Ji, B., Li, S., and Liu, Y. 2020 | 2020 | Asia | New York USA | Hybrid exact and heuristics | Linear programming model solved with adaptative tabu search algorithm | Static | Operator-based | Repositioning | Better performance compared with tabu search (TS) and variable neighborhood search (VNS). |
| 48 | Jia, Y., Xu, Y., Yang, D., and Li, J. 2020 | 2020 | Asia | N/A | Hybrid exact and heuristics | A bi-objective integer-mixed programming model, using a multi-start multi-objective particle swarm optimization (MS-MOPSO) algorithm to solve it. | Static | Operator-based | Rebalance, Repositioning | Introduce the concept of balance interval. |
| 49 | Lu, Y., Benlic, U., and Wu, Q. (2020). | 2020 | Asia | Several instances | Other | Memetic algorithm | Static | Operator-based | Rebalancing, Repositioning | Two to six times faster than existing heuristics |
Note: BSSRebalancingPapersClassif.xlsx could be found in the Supplementary.
References
- Kamargianni, M.; Li, W.; Matyas, M.; Schäfer, A. A Critical Review of New Mobility Services for Urban Transport. Transp. Res. Procedia 2016, 14, 3294–3303. [Google Scholar] [CrossRef]
- Shaheen, A.; Guzman, S.; Zhang, S. Bikesharing in Europe, the Americas, and Asia: Past, Present, and Future. Transp. Res. Rec. J. Transp. Res. Board 2010, 2143, 159–167. [Google Scholar] [CrossRef]
- Nikitas, A. How to Save Bike-Sharing: An Evidence-Based Survival Toolkit for Policy-Makers and Mobility Providers. Sustainability 2019, 11, 3206. [Google Scholar] [CrossRef]
- Ma, Y.; Lan, J.; Thornton, T.; Mangalagiu, D.; Zhu, D. Challenges of Collaborative Governance in the Sharing Economy: The Case of Free-Floating Bike Sharing in Shanghai. J. Clean. Prod. 2018, 197, 356–365. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, X.; Zhao, J. Understanding the Usage of Dockless Bike Sharing in Singapore. Int. J. Sustain. Transp. 2018, 12, 686–700. [Google Scholar] [CrossRef]
- Shi, J.G.; Si, H.; Wu, G.; Su, Y.; Lan, J. Critical Factors to Achieve Dockless Bike-Sharing Sustainability in China: A Stakeholder-Oriented Network Perspective. Sustainability 2018, 10, 2090. [Google Scholar] [CrossRef]
- DeMaio Metrobike Web. Available online: http://www.metrobike.net/the-bike-sharing-world-map/ (accessed on 2 May 2019).
- O’Brien, O. Bike Share Map Web. Available online: https://oobrien.com/bikesharemap/ (accessed on 7 June 2019).
- DeMaio, P. Bike-Sharing: History, Impacts, Models of Provision, and Future. J. Public Transp. 2009, 12, 41–56. [Google Scholar] [CrossRef]
- Mátrai, T.; Tóth, J. Comparative Assessment of Public Bike Sharing Systems. Transp. Res. Procedia 2016, 14, 2344–2351. [Google Scholar] [CrossRef]
- Midgley, P. Bicycle-Sharing Schemes: Enhancing Sustainable Mobility in Urban Areas; United Nations, Department of Economic and Social Affairs: New York, NY, USA, 2011; Volume 8, pp. 1–12. [Google Scholar]
- Dötterl, J.; Bruns, R.; Dunkel, J.; Ossowski, S. Towards Dynamic Rebalancing of Bike Sharing Systems: An Event-Driven Agents Approach. In Proceedings of the Progress in Artificial Intelligence; Oliveira, E., Gama, J., Vale, Z., Lopes Cardoso, H., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 309–320. [Google Scholar]
- Ban, S.; Hyun, K.H. Curvature-Based Distribution Algorithm: Rebalancing Bike Sharing System with Agent-Based Simulation. J. Vis. 2019, 22, 587–607. [Google Scholar] [CrossRef]
- Si, H.; Shi, J.G.; Wu, G.; Chen, J.; Zhao, X. Mapping the Bike Sharing Research Published from 2010 to 2018: A Scientometric Review. J. Clean. Prod. 2019, 213, 415–427. [Google Scholar] [CrossRef]
- Nikitas, A. Understanding Bike-Sharing Acceptability and Expected Usage Patterns in the Context of a Small City Novel to the Concept: A Story of ‘Greek Drama’. Transp. Res. Part F Traffic Psychol. Behav. 2018, 56, 306–321. [Google Scholar] [CrossRef]
- Kou, Z.; Cai, H. Understanding Bike Sharing Travel Patterns: An Analysis of Trip Data from Eight Cities. Phys. A Stat. Mech. Appl. 2019, 515, 785–797. [Google Scholar] [CrossRef]
- Bakogiannis, E.; Siti, M.; Tsigdinos, S.; Vassi, A.; Nikitas, A. Monitoring the First Dockless Bike Sharing System in Greece: Understanding User Perceptions, Usage Patterns and Adoption Barriers. Res. Transp. Bus. Manag. 2019, 33, 100432. [Google Scholar] [CrossRef]
- Yang, Y.; Heppenstall, A.; Turner, A.; Comber, A. A Spatiotemporal and Graph-Based Analysis of Dockless Bike Sharing Patterns to Understand Urban Flows over the Last Mile. Comput. Environ. Urban Syst. 2019, 77, 101361. [Google Scholar] [CrossRef]
- Guidon, S.; Becker, H.; Axhausen, K. Avoiding Stranded Bicycles in Free-Floating Bicycle-Sharing Systems: Using Survival Analysis to Derive Operational Rules for Rebalancing. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 1703–1708. [Google Scholar] [CrossRef]
- Médard de Chardon, C.; Caruso, G.; Thomas, I. Bike-Share Rebalancing Strategies, Patterns, and Purpose. J. Transp. Geogr. 2016, 55, 22–39. [Google Scholar] [CrossRef]
- van Eck, N.J.; Waltman, L. Software Survey: VOSviewer, a Computer Program for Bibliometric Mapping. Scientometrics 2010, 84, 523–538. [Google Scholar] [CrossRef]
- Waltman, L.; van Eck, N.J.; Noyons, E.C.M. A Unified Approach to Mapping and Clustering of Bibliometric Networks. J. Informetr. 2010, 4, 629–635. [Google Scholar] [CrossRef]
- Fishman, E.; Washingtion, S.; Haworth, N. Bike Share. Transp. Rev. 2013, 33, 1–26. [Google Scholar] [CrossRef]
- Ricci, M. Bike Sharing: A Review of Evidence on Impacts and Processes of Implementation and Operation. Res. Transp. Bus. Manag. 2015, 15, 28–38. [Google Scholar] [CrossRef]
- Ricci, M.; Parkhust, G.; Jain, J. Transport Policy and Social Inclusion. Soc. Incl. 2016, 4, 1–6. [Google Scholar] [CrossRef]
- Nair, R.; Miller-Hooks, E. Fleet Management for Vehicle Sharing Operations. Transp. Sci. 2011, 45, 524–540. [Google Scholar] [CrossRef]
- Benchimol, M.; Benchimol, P.; Chappert, B.; De La Taille, A.; Laroche, F.; Meunier, F.; Robinet, L. Balancing the Stations of a Self Service “Bike Hire” System. RAIRO Oper. Res. 2011, 45, 37–61. [Google Scholar] [CrossRef]
- Wood, J.; Slingsby, A.; Dykes, J. Visualizing the Dynamics of London’s Bicycle-Hire Scheme. Cartographica 2011, 46, 239–251. [Google Scholar] [CrossRef]
- Borgnat, P.; Abry, P.; Flandrin, P.; Robardet, C.; Rouquier, J.B.; Fleury, E. Shared Bicycles in a City: A Signal Processing and Data Analysis Perspective. Adv. Complex Syst. 2011, 14, 415–438. [Google Scholar] [CrossRef]
- Chemla, D.; Meunier, F.; Wolfler Calvo, R. Bike Sharing Systems: Solving the Static Rebalancing Problem. Discret. Optim. 2012, 10, 120–146. [Google Scholar] [CrossRef]
- Labadi, K.; Benarbia, T.; Hamaci, S.; Darcherif, A.-M. Petri Nets Models for Analysis and Control of Public Bicycle-Sharing Systems. Petri Nets Manuf. Comput. Sci. 2012. [Google Scholar] [CrossRef]
- Lin, J.H.; Chou, T.C. A Geo-Aware and VRP-Based Public Bicycle Redistribution System. Int. J. Veh. Technol. 2012, 2012. [Google Scholar] [CrossRef]
- Raviv, T.; Tzur, M.; Forma, I.A. Static Repositioning in a Bike-Sharing System: Models and Solution Approaches. EURO J. Transp. Logist. 2013, 2, 187–229. [Google Scholar] [CrossRef]
- Raidl, G.R.; Hu, B.; Rainer-Harbach, M.; Papazek, P. Balancing Bicycle Sharing Systems: Improving a VNS by Efficiently Determining Optimal Loading Operations. Lect. Notes Comput. Sci. 2013, 7919 LNCS, 130–143. [Google Scholar] [CrossRef]
- Rainer-Harbach, M.; Papazek, P.; Hu, B.; Raidl, G.R. Balancing Bicycle Sharing Systems: A Variable Neighborhood Search Approach. Lect. Notes Comput. Sci. 2013, 7832 LNCS, 121–132. [Google Scholar] [CrossRef]
- Nair, R.; Miller-Hooks, E.; Hampshire, R.C.; Bušić, A. Large-Scale Vehicle Sharing Systems: Analysis of Vélib’. Int. J. Sustain. Transp. 2013, 7, 85–106. [Google Scholar] [CrossRef]
- Lin, J.R.; Yang, T.H.; Chang, Y.C. A Hub Location Inventory Model for Bicycle Sharing System Design: Formulation and Solution. Comput. Ind. Eng. 2013, 65, 77–86. [Google Scholar] [CrossRef]
- Di Gaspero, L.; Rendl, A.; Urli, T. Constraint-Based Approaches for Balancing Bike Sharing Systems. Lect. Notes Comput. Sci. 2013, 8124 LNCS, 758–773. [Google Scholar] [CrossRef]
- Erdoǧan, G.; Laporte, G.; Wolfler Calvo, R. The Static Bicycle Relocation Problem with Demand Intervals. Eur. J. Oper. Res. 2014, 238, 451–457. [Google Scholar] [CrossRef]
- Kloimüllner, C.; Papazek, P.; Hu, B.; Raidl, G.R. Balancing Bicycle Sharing Systems: An Approach for the Dynamic Case. Lect. Notes Comput. Sci. 2014, 8600, 73–84. [Google Scholar] [CrossRef]
- Regue, R.; Recker, W. Proactive Vehicle Routing with Inferred Demand to Solve the Bikesharing Rebalancing Problem. Transp. Res. Part E Logist. Transp. Rev. 2014, 72, 192–209. [Google Scholar] [CrossRef]
- Pfrommer, J.; Warrington, J.; Schildbach, G.; Morari, M. Dynamic Vehicle Redistribution and Online Price Incentives in Shared Mobility Systems. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1567–1578. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Hadjicostantinou, E.; Iori, M.; Novellani, S. The Bike Sharing Rebalancing Problem: Mathematical Formulations and Benchmark Instances. Omega 2014, 45, 7–19. [Google Scholar] [CrossRef]
- Beecham, R.; Wood, J.; Bowerman, A. Studying Commuting Behaviours Using Collaborative Visual Analytics. Comput. Environ. Urban Syst. 2014, 47, 5–15. [Google Scholar] [CrossRef]
- Ho, A. Solving a Static Repositioning Problem in Bike-Sharing Systems Using Iterated Tabu Search. Logist. Transp. Rev. 2014, 69, 180–198. [Google Scholar] [CrossRef]
- Zhao, J.; Deng, W.; Song, Y. Ridership and Effectiveness of Bikesharing: The Effects of Urban Features and System Characteristics on Daily Use and Turnover Rate of Public Bikes in China. Transp. Policy 2014, 35, 253–264. [Google Scholar] [CrossRef]
- Forma, I.A.; Raviv, T.; Tzur, M. A 3-Step Math Heuristic for the Static Repositioning Problem in Bike-Sharing Systems. Transp. Res. Part B Methodol. 2015, 71, 230–247. [Google Scholar] [CrossRef]
- Erdoʇan, G.; Battarra, M.; Wolfler Calvo, R. An Exact Algorithm for the Static Rebalancing Problem Arising in Bicycle Sharing Systems. Eur. J. Oper. Res. 2015, 245, 667–679. [Google Scholar] [CrossRef]
- Alvarez-Valdes, R.; Belenguer, J.M.; Benavent, E.; Bermudez, J.D.; Muñoz, F.; Vercher, E.; Verdejo, F. Optimizing the Level of Service Quality of a Bike-Sharing System. Omega 2016, 62, 163–175. [Google Scholar] [CrossRef]
- Szeto, W.Y.; Shui, C.S. Exact Loading and Unloading Strategies for the Static Multi-Vehicle Bike Repositioning Problem. Transp. Res. Part B Methodol. 2018, 109, 176–211. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Iori, M.; Novellani, S.; Stützle, T. A Destroy and Repair Algorithm for the Bike Sharing Rebalancing Problem. Comput. Oper. Res. 2016, 71, 149–162. [Google Scholar] [CrossRef]
- Li, Y.; Szeto, W.Y.; Long, J.; Shui, C.S. A Multiple Type Bike Repositioning Problem. Transp. Res. Part B Methodol. 2016, 90, 263–278. [Google Scholar] [CrossRef]
- Cruz, F.; Subramanian, A.; Bruck, B.P.; Iori, M. A Heuristic Algorithm for a Single Vehicle Static Bike Sharing Rebalancing Problem. Comput. Oper. Res. 2016, 79, 19–33. [Google Scholar] [CrossRef]
- Liu, J.; Sun, L.; Chen, W.; Xiong, H. Rebalancing Bike Sharing Systems: A Multi-Source Data Smart Optimization. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Franscisco, CA, USA, 13–17 August 2016; pp. 1005–1014. [Google Scholar] [CrossRef]
- Zhang, D.; Yu, C.; Desai, J.; Lau, H.Y.K.; Srivathsan, S. A Time-Space Network Flow Approach to Dynamic Repositioning in Bicycle Sharing Systems. Transp. Res. Part B Methodol. 2017, 103, 188–207. [Google Scholar] [CrossRef]
- Ho, S.C.; Szeto, W.Y. A Hybrid Large Neighborhood Search for the Static Multi-Vehicle Bike-Repositioning Problem. Transp. Res. Part B Methodol. 2017, 95, 340–363. [Google Scholar] [CrossRef]
- Shui, C.S.; Szeto, W.Y. Dynamic Green Bike Repositioning Problem—A Hybrid Rolling Horizon Artificial Bee Colony Algorithm Approach. Transp. Res. Part D Transp. Environ. 2017, 60, 119–136. [Google Scholar] [CrossRef]
- Chiariotti, F.; Pielli, C.; Zanella, A.; Zorzi, M. A Dynamic Approach to Rebalancing Bike-Sharing Systems. Sensors 2017, 18, 512. [Google Scholar] [CrossRef] [PubMed]
- Elhenawy, M.; Rakha, H. A Heuristic for Rebalancing Bike Sharing Systems Based on a Deferred Acceptance Algorithm. In Proceedings of the 2017 5th IEEE International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Naples, Italy, 26–28 June 2017; pp. 188–193. [Google Scholar] [CrossRef]
- Schuijbroek, J.; Hampshire, R.C.; van Hoeve, W.J. Inventory Rebalancing and Vehicle Routing in Bike Sharing Systems. Eur. J. Oper. Res. 2017, 257, 992–1004. [Google Scholar] [CrossRef]
- Bulhões, T.; Subramanian, A.; Erdoğan, G.; Laporte, G. The Static Bike Relocation Problem with Multiple Vehicles and Visits. Eur. J. Oper. Res. 2018, 264, 508–523. [Google Scholar] [CrossRef]
- Legros, B. Dynamic Repositioning Strategy in a Bike-Sharing System; How to Prioritize and How to Rebalance a Bike Station. Eur. J. Oper. Res. 2019, 272, 740–753. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Iori, M.; Novellani, S.; Subramanian, A. The Bike Sharing Rebalancing Problem with Stochastic Demands. Transp. Res. Part B Methodol. 2018, 118, 362–380. [Google Scholar] [CrossRef]
- Hulot, P.; Aloise, D.; Jena, S.D. Towards Station-Level Demand Prediction for Effective Rebalancing in Bike-Sharing Systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 378–386. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, Y.; Yang, Q. Dynamic Bike Reposition. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1724–1733. [Google Scholar] [CrossRef]
- You, P.S. A Two-Phase Heuristic Approach to the Bike Repositioning Problem. Appl. Math. Model. 2019, 73, 651–667. [Google Scholar] [CrossRef]
- Tang, Q.; Fu, Z.; Qiu, M. A Bilevel Programming Model and Algorithm for the Static Bike Repositioning Problem. J. Adv. Transp. 2019, 2019. [Google Scholar] [CrossRef]
- Wang, S.; Wu, R. The Static Rebalancing Problem in Bicycle-Sharing Systems with Unusable Bicycles. In Proceedings of the 2019 16th International Conference on Service Systems and Service Management (ICSSSM), Shenzhen, China, 13–15 July 2019. [Google Scholar] [CrossRef]
- Warrington, J.; Ruchti, D. Two-Stage Stochastic Approximation for Dynamic Rebalancing of Shared Mobility Systems. Transp. Res. Part C Emerg. Technol. 2019, 104, 110–134. [Google Scholar] [CrossRef]
- Brinkmann, J.; Ulmer, M.W.; Mattfeld, D.C. The Multi-Vehicle Stochastic-Dynamic Inventory Routing Problem for Bike Sharing Systems. Bus. Res. 2020, 13, 69–92. [Google Scholar] [CrossRef]
- Tang, Q.; Fu, Z.; Zhang, D.; Guo, H.; Li, M. Addressing the Bike Repositioning Problem in Bike Sharing System: A Two-Stage Stochastic Programming Model. Sci. Program. 2020, 2020. [Google Scholar] [CrossRef]
- Maleki, B.; Mahdavi, I.; Mahdavi-amiri, N.; Khorram, E. Balancing Public Bicycle Sharing System Using Inventory Critical Levels in Queuing Network. Comput. Ind. Eng. 2020, 141, 106277. [Google Scholar] [CrossRef]
- Zhang, D.; Xu, W.; Ji, B.; Li, S.; Liu, Y. Computers and Operations Research An Adaptive Tabu Search Algorithm Embedded with Iterated Local Search and Route Elimination for the Bike Repositioning and Recycling Problem. Comput. Oper. Res. 2020, 123, 105035. [Google Scholar] [CrossRef]
- Jia, Y.; Xu, Y.; Yang, D.; Li, J. The Biobjective Bike-Sharing Rebalancing Problem with Balance Intervals: A Multistart Multiobjective Particle Swarm Optimization Algorithm. Complexity 2020, 2020. [Google Scholar] [CrossRef]
- Lu, Y.; Benlic, U.; Wu, Q. An Effective Memetic Algorithm for the Generalized Bike-Sharing Rebalancing Problem. Eng. Appl. Artif. Intell. 2020, 95, 103890. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).