Multi-Objective Optimization for Sustainable Supply Chain and Logistics: A Review

Abstract

There are several methods available for modeling sustainable supply chain and logistics (SSCL) issues. Multi-objective optimization (MOO) has been a widely used method in SSCL modeling (SSCLM), nonetheless selecting a suitable optimization technique and solution method is still of interest as model performance is highly dependent on decision-making variables of the model development process. This study provides insights from the analysis of 95 scholarly articles to identify research gaps in the MOO for SSCLM and to assist decision-makers in selecting suitable MOO techniques and solution methods. The results of the analysis indicate that economic and environmental aspects of sustainability are the main context of SSCLM, where the social aspect is still limited. More SSCLMs for sourcing, distribution, and transportation phases of the supply chain are required. Additionally, more sophisticated techniques and solution methods, including hybrid metaheuristics approaches, are needed in SSCLM.

1. Introduction

Supply chain modeling has become more applied and feasible in supply chain management and logistics research as it facilitates decision-making to achieve various objectives, including economic, environmental, and social [1]. Traditional supply chain models have focused only on operational efficiency by reducing the total cost, lead time, defective items, unused capacity, and processing time [2,3,4], but novel supply chain models incorporate environmental and social objectives in addition to economic performance [5,6,7,8]. This phenomenon is evident by the growing research on sustainable supply chain and logistics modeling (SSCLM) [9,10]. SSCLM is aimed at optimizing economic, environmental, and social objectives simultaneously. SSCLM is a complex process as it involves diverse stakeholders from suppliers to customers for managing products and services accounting for economic, environmental, and social impacts [11]. This complexity becomes more emphasized when different phases of the supply chain (sourcing, manufacturing, warehousing, distribution, and transportation), different types of a supply chain (forward, reverse, and close loop), different levels of decision-making (strategic, tactical, and operational), and supply chain environment (certainty or uncertainty) are considered.

In this study, the authors explore the scholarly literature to identify the research gaps in multi-objective optimization (MOO) for SSCLM and to assist decision-makers in selecting suitable optimization techniques and solution methods based on various SSCL issues. Numerous review studies are currently available; however, they are limited to certain factors. Some have concentrated more broadly on operational research (OR) methods not specific to MOO [11,12] while others have focused on limited aspects of different sustainability dimensions [4,13] or have not considered decision levels and supply chain phases [14,15,16]. Further, most of these research efforts did not take uncertainty into account [17,18,19].

Given these limitations in this research, the authors reviewed SSCL problems with a modeling perspective focusing on various aspects such as sustainability dimensions, indicators, different supply chain phases, decision levels, optimization techniques, and solution methods. The structure of the paper is outlined as follows. Section 2 provides the methodology. Section 3 presents the data analysis. Section 4 shows the results and discussion. Lastly, Section 5 presents the conclusion and recommendations for future research.

2. Methodology

The study at hand follows a semi-systematic review methodology where formulating research questions, locating studies, screening, and selection were carried out according to the review methodology proposed by Denyer and Transfield [20], and reviewing and analyzing were carried out according to the narrative review methods [21]. The authors described these review steps as follows.

• Step 1: Formulation of research questions

Adhering to Denyer and Transfield [20], the current study used an acronym CIMO (context, intervention, mechanism, outcome) to specify well-built review questions. As the aim of this paper is to identify the research gaps in MOO for SSCLM (C) and to assist decision-makers (I) in selecting suitable MOO techniques and solution methods (O) based on their varied SSCL issues addressed by the literature (M), the authors developed the following research questions.

(i)

What dimensions and indicators of sustainability are over-presented in MOO of supply chain and logistics models?

(ii)

Which supply chain phases and decision levels are discussed in the SSCLM?

(iii)

Which type of optimization technique and solution method is used to address SSCLM?

(iv)

To what extent uncertainty has been incorporated into SSCLM and what optimization techniques and solution methods are used to address uncertainty in SSCLM?

• Step 2: Locating studies

The authors searched for publications from the Science Direct and Google Scholar databases for the last decade (2010–2020). The authors used specific keywords of ‘sustainable supply chain’ OR ‘sustainable logistics’ AND ‘multi-objective optimization’ to identify the relevant high-quality papers. The total results as of 1 December 2020, were 323 including review papers, research articles, conference papers, book chapters, and editorials.

• Step 3: Screening and selection

The authors selected 122 for the current study of which 27 papers are reviews articles. The authors used these 27 papers to identify the gap in the existing reviews and the remaining 95 papers for the main analysis. The relevancy was determined by considering several inclusion criteria: (1) included the papers published in peer-reviewed scientific journals in English, (2) content including any supply chain decision variable, and (3) included at least two out of three sustainability dimensions for the MOO model, (4) excluded review papers, conference papers, book chapters, and journal papers with no citations (except papers published in 2020).

• Step 4: Reviewing and analyzing

First, the authors analyzed the selected 27 review papers to confirm the validity, relevance, and contribution of our article to the overall literature. A summary of the existing review analysis is provided in

Table 1. Overview of the available review studies.

Reference	No of Papers	Time-Period	a	b	c	d	e	f	g	h	i	j
[4]	60	n/a	*			*			*
[11]	220	1999–2016	*	*	*	*	*	*
[12]	188	2000–2015	*	*			*		*		*	*
[13]	89	2007–2017	*		*			*			*	*
[14]	174	1987–2015	*
[15]	445	1989–2012	*	*
[16]	134	1994–2012	*								*	*
[17]	145	1995–2018	*	*							*	*
[18]	384	2000–2003	*								*
[19]	36	1994–2010	*						*
[22]	98	2005–2015			*		*			*	*	*
[23]	113	2015–2018	*	*	*		*
[24]	207	1995 –2017	*	*	*	*	*			*		*
[25]	300	1980–2020	*	*	*		*		*	*		*
[26]	540	1999–2010	*			*	*	*
[27]	134	1983–2011	*			*
[28]	87	2000–2010	*	*
[29]	56	n/a				*		*
[30]	160	1980–2013			*		*
[31]	185	1994–2004	*				*
[32]	190	1999–2010							*		*	*
[33]	87	1990–2014	*	*			*				*	*
[34]	115	n/a	*	*
[35]	190	2000–2015	*	*		*		*
[36]	40	1900–2018	*	*		*				*
[37]	142	2009–2019	*	*		*		*	*			*
[38]	247	1997–2019	*	*			*				*	*

Notes: (a) sustainability dimension focus, (b) sustainability indicator categorization, (c) supply chain decision levels, (d) type of supply chain, (e) supply chain environment, (f) OR methods, (g) multi-criteria decision-making, (h) multi-objective framework, (i) optimization techniques, and (j) solution method. * Consideration of above categories (a–j) in the review papers.

. Most papers covered sustainability objectives (a) and their indicators (b), but a thorough review of how these objectives are optimized in a model is limited—only four appear to have the MOO focus. Of these studies, Trisna et al. [22] did not consider sustainability aspects, Moreno-Camacho et al. [23] did not discuss optimization methods and solution techniques, Van Engeland et al. [24] limited their study to one phase of the supply chain (reverse logistics), and Zahraee et al. [25] explored specific supply chain (biomass supply chain) in their reviews. Supply chain decision levels (c), types of the supply chain (d), and supply chain environment (e) were also considered, but no clear idea on which supply chain decision, type, and environment were addressed with a sustainability dimension. Eleven papers looked at different assessment methods (f) or multi-criteria decision-making approaches (g), but they were not specific to the MOO (h) except one study [25]. Optimization techniques (i) and solution methods (j) were widely addressed but not in SSCLM. These general findings emphasize the need for a study that specifically focuses on MOO methods and solutions for SSCLM. According to the analysis of review papers and the best of our knowledge, the authors found that no studies covered all the factors considered here (a–j in Table 1) within one study before. Therefore, the current study provides a detailed and comprehensive analysis of the existing literature of MOO for SSCL. Following the content analysis as a narrative review method [21], the authors reviewed the other 95 research papers using the categories based on authors, supply chain problem, sustainability dimensions, sustainability indicators, supply chain phases, decision levels, supply chain environment, optimization techniques, and solution methods. These categories were carefully analyzed using descriptive analysis to respond to each research question.

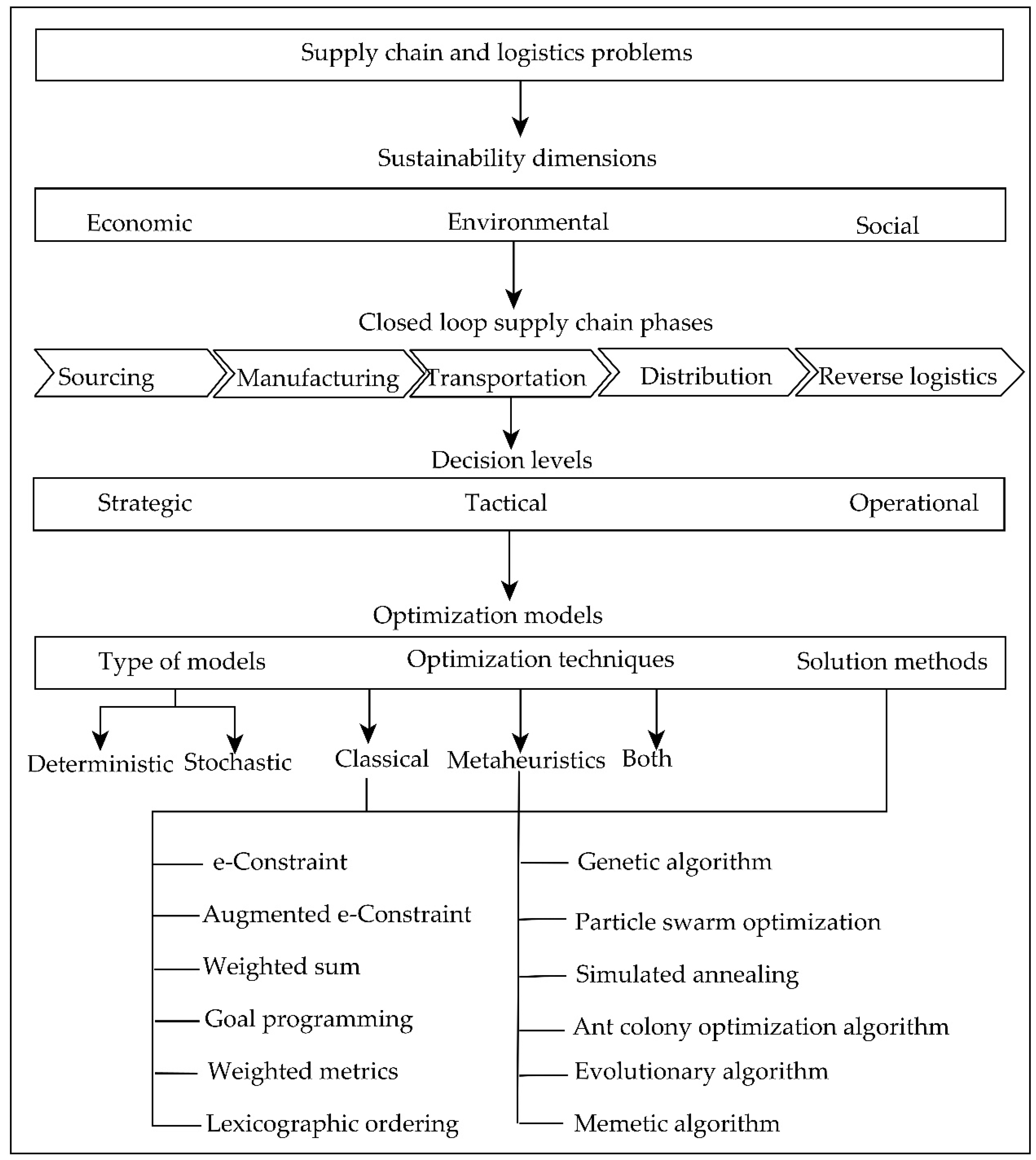
Framework of the Study

The multi-objective optimization problem is traditionally aimed at addressing forward supply chain issues where raw materials are converted to the final product and carried through suppliers, manufacturers, warehouses, transporters, and distributors, to end customers. This tradition has now changed to considering closed-loop supply chains in the MOO problem. A closed-loop supply chain considers reverse logistics in addition to a forward supply chain. The authors classify closed-loop supply chain phases as sourcing, manufacturing, transportation, distribution, and reverse logistics. To incorporate sustainability in to supply chain and logistics context, the authors consider three pillars of economic, environmental, and social dimensions as addressed by the literature [11,23,35]. MOO problems in the supply chain are based on the different phases in a closed-loop supply chain and those problems are addressed through strategic, tactical, and operational level decisions. Decisions that have long-term implications are considered strategic decisions, such as supplier selection and facility location. Tactical decisions have medium-term implications that support strategic decisions such as order allocation, and vehicle routine problems. Operational decisions are related to day-to-day operations and have short-term implications. Examples include scheduling logistics tasks and the quantity discount model. Addressing MOO problems becomes complex and dynamic due to uncertain factors. Therefore, SSCLM can be designed as a deterministic or stochastic model. These models can be solved using different solution methods mainly categorized as classical, metaheuristics, or both. Accordingly, the authors present this review paper for MOO in SSCLM based on the following framework (Figure 1).

3. Data Analysis

The data analysis includes the descriptive analysis of the distribution of reference papers by time and journal, reference papers by sustainability dimensions and indicators, supply chain phases, and decision levels from a sustainable perspective, optimization techniques, and solution methods.

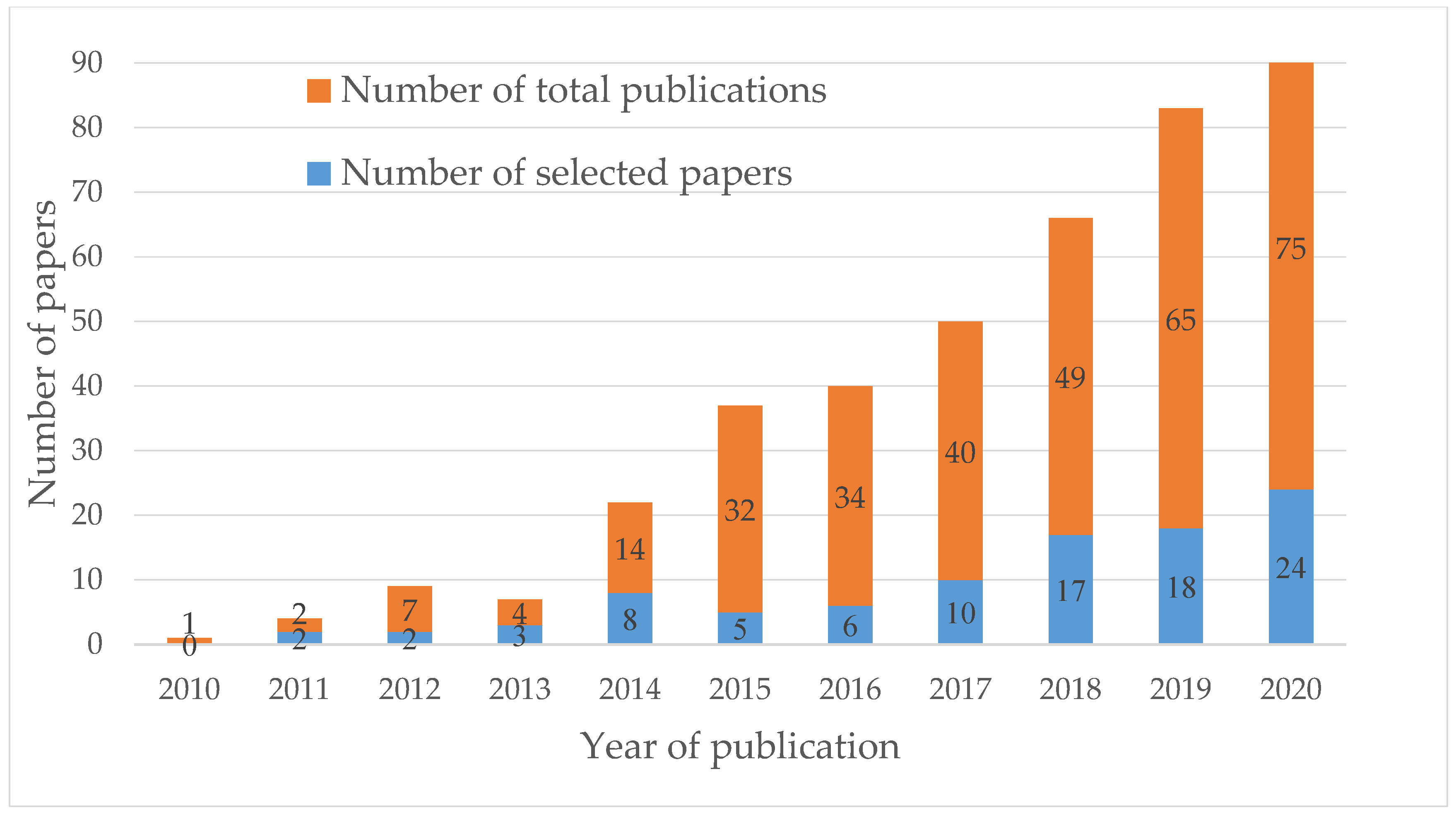
3.1. Distribution of Articles by Time and Outlet

Figure 2 shows the distribution of papers over the last decade (2010–2020). There has been a growing trend of publishing papers during the considered period. In terms of selected papers, the highest number of selected papers are from the last three years, respectively. No publication was found in 2010 relating to the considered criteria of the current study.

Figure 3 shows papers are distributed across 39 journals, and 30 journals have only one publication. The highest number of selected papers are from the Journal of Cleaner Production, which is approximately 34% of the total papers selected.

3.2. Analysis of Articles by Sustainability Dimensions and Indicators

Most of the sustainable supply chain models are multi-objective and many authors consider economic objectives as traditional objectives and incorporate environmental or social objectives as extensions [33]. The authors analyzed the distribution of reference papers among the sustainability dimensions and found that more than half (55%) of the reference papers (52 papers) focused on economic and environmental combinations and 42% of the reference papers (40 papers) focused on all three dimensions of sustainability. Two papers focused on the economic and social combination [39,40], and only one paper focused on environmental and social combinations [41]. Furthermore, most of the papers (99%) considered economic and environmental pillars as one of the objectives in SSCLM. These facts reveal the importance of economic and environmental pillars for assessing sustainability in supply chain and logistics models. Social dimension was considered in limited papers (45%) compared to economic and environmental dimensions. The reason for the limited consideration in the social dimension is the difficulty of measuring social sustainability as most of the social indicators are qualitative. There remains an imbalance in the distribution of papers among these three dimensions, thus in SSCL research, there is still outstanding work as these three pillars are equally important for sustainability.

In MOO models, numerous indicators were used from each sustainability dimension (

Table 2. Summary of sustainability objectives by articles.

Economic Objectives (Min./Max)	No. of Papers	Environmental Objectives (Min./Max.)	No. of Papers	Social Objectives (Min./Max.)	No. of Papers
Total cost/Profit/ Operational performance	85	GHG/CO2 emission/Global warming potential	49	Social benefit/ social impact	25
Delivery lead time/ traveling time	12	Environmental impact/performance	41	Job opportunities	14
Economic benefits	5	Energy consumption/energy recovery	8	Employee injuries	2
NPV/PV of costs	4	Water consumption	5	Human resource variations	1
Resilience	2	Waste	4	Lost working days	1
Total quality	2	Noise pollution	1	Community development	1
Financial risk	1
Travel distance	1
Reliability	2
Responsiveness	1
Supplier performance	1

). From the economic aspect, widely used indicators were the minimization of cost, maximization of profit, or operational performance. From the environmental dimension, most of the models used minimization of greenhouse gas (GHG), CO₂ emission, or global warming potential. From the social perspective, the highest number of models focused on minimizing the social impact or maximizing the social benefit. The detailed analysis of reference papers by each sustainable objective with its indicators is presented in Appendix A and Appendix B.

3.3. Supply Chain Phases and Decision Levels from a Sustainable Perspective

Table 3. Distribution of decision levels across the supply chain phases.

Decision Levels	Total	OSC	S	M	D	T	RL	S/D	M/D	T/RL	T/D	S/M/D	S/M/T
Strategic	55	23	5	6	3	-	8	2	4	-	3	1	-
Tactical	20	1	-	5	4	3	3	-	2	1	-	-	1
Operational	1	-	-	-	-	-	-	-	1	-	-	-	-
Strategic/Tactical	14	10	1	-	-	-	-	-	1	-	-	1	1
Strategic/Operational	1	-	-		1	-	-	-	-	-	-	-	-
Tactical/Operational	1	1	-		-	-	-	-	-	-	-	-	-
Strategic/Tactical/Operational	3	2	-	1	-	-	-	-	-	-	-	-	-
Total	95	37	6	12	8	3	11	2	8	1	3	2	2

Notes: OSC: overall supply chain, S: sourcing, M: manufacturing, D: distributing, T: transporting, RL: reverse logistics. All the references relating to Table 3 are presented in Appendix C. Full references can be found in Supplementary Materials.

shows the decision levels distributed across every phase in the supply chain. Most of the researchers analyzed the strategic decisions (55 out of 95), such as supply chain network design, supplier selection, hub location, facility location, logistic network configuration, and most of these (23 out of 55) focused on the overall supply chain [5,14,42,43] focused on strategic level decisions in the overall supply chain. Tactical decisions were integrated into 20 papers; those decisions involve order allocation, vehicle routine problem, aggregate production planning, and selecting transportation mode. Most of the tactical decisions were related to the manufacturing phase [44,45,46,47]. Operational decisions, such as the quantity discount model, the selection of transport mode, and production methods were incorporated into only one paper, which is related to manufacturing and distribution phases [48]. Only Govindan et al. [49] focused on strategic and operational decisions, which are related to the distribution phase and only Wang et al. [50] focused on tactical and operational decisions in the overall supply chain. In total, 14 papers have investigated strategic and tactical decisions, most of which are related to the overall supply chain [51,52,53,54,55]. Only three papers have looked at all three decision levels, two of which are related to the overall supply chain [56,57] and the other one is related to the manufacturing phase [58].

Table 4. Sustainability aspects of supply chain phases.

Sustainability Dimensions	OSC	S	M	D	T	RL	S/D	M/D	T/RL	T/D	S/M/D	S/M/T	Total
Eco/Env/Soc	16	3	3	2	1	7	1	5	-	-	1	1	40
Eco/Env	19	3	9	6	2	3	1	3	1	3	1	1	52
Eco/Soc	1	-	-	-	-	1	-	-	-	-	-	-	2
Env/Soc	1	-	-	-	-	-	-	-	-	-	-	-	1
Total	37	6	12	8	3	11	2	8	1	3	2	2	95

Notes: OSC: overall supply chain, S: sourcing, M: manufacturing, D: distributing, T: transporting, RL: reverse logistics, Eco: economic, Env: environmental, Soc: social. All the references relating to Table 4 are presented in Appendix C. Full references can be found in Supplementary Materials.

indicates the sustainability aspects of supply chain phases in MOO models. Most of the models are designed on the overall supply chain and 16 papers considered all three dimensions and 19 papers considered economic and environmental dimensions. The second and third most frequent focus was on manufacturing (12 papers) and reverse logistics (11 papers) phases in MOO models. In manufacturing issues, nine papers investigated economic and environmental aspects e.g., [46,47,59], and three papers investigated all three dimensions [58,60,61]. In reverse logistics models, seven papers considered all three dimensions [62,63,64,65,66,67,68] and three papers considered economic and environmental aspects [69,70,71]. Overall, the highest number of papers (52) have considered economic and environmental aspects of sustainability, whereas 40 papers have incorporated all three aspects of sustainability. Two papers have focused on economic and social aspects of the overall supply chain [40] and reverse logistics [39], only one paper looked at the environmental and social aspects of sustainability, which is also focused on the overall supply chain [72].

In terms of sustainability aspects of decision levels (

Table 5. Sustainability aspects of supply chain decision levels.

Decision Levels	Total	Eco/Env/Soc	Eco/Env	Eco/Soc	Env/Soc
Strategic	55	22	31	1	1
Tactical	20	6	13	1	-
Operational	1	1	-	-	-
Strategic/Operational	1	1	-	-	-
Tactical/Operational	1	1	-	-	-
Strategic/Tactical	14	8	6	-	-
Strategic/Tactical/Operational	3	1	2	-	-
Total	95	40	52	2	1

Note: All the references relating to Table 5 are presented in Appendix C. Full references can be found in Supplementary Materials.

), 58% of the SSCLM was used to make strategic decisions and 40% of which have focused on all three dimensions of sustainability, and 56% of which focused on economic and environmental aspects; 21% of the SSCLM were used for tactical decisions, 30% of which focused on all three dimensions, and 65% focused on economic and environmental aspects. Only 1% of the models was used for operational decisions and focused on all three dimensions.

3.4. Optimization Techniques and Solution Methods

Most of the optimization models are deterministic models (consider certain environment) (58%) and 42% of the models are stochastic models (consider uncertain environment) (

Table 6. Classification of articles by modeling techniques and type of model.

Modeling Technique	Number of Papers	Deterministic Models	Stochastic Models
Classical	63	32	31
Metaheuristics	31	22	9
Hybrid (C/M)	1	1	-
Total	95	55	40

Note: All the references relating to Table 6 are presented in Appendix C. Full references can be found in Supplementary Materials.

). In terms of modeling technique, 66% of the reference papers used classical optimization methods, 33% of the optimization models used metaheuristics methods and 1% used both methods. Of the classical methods, e-constraint, augmented e-constraint, and weighted sum were largely used (

Table 7. Distribution of classical solution methods.

Classical Methods	Total	Certain	Uncertain
e-Constraint	22	13	9
Augmented e-constraint	9	4	5
Weighted sum	7	2	5
Fuzzy programming	5	-	5
Normalized normal constraint methods	3	3	-
Weighted goal programming	2	1	1
Fuzzy goal programming	1	-	1
Weighted comprehensive criteria method	1	-	1
Weighted min max	1	-	1
Weighted metrics	1	-	1
LP metric based compromising programming	1	-	1
Meta goal programming and simulation	1	-	1
Scenario method	1	1	-
AHP and ordered weighted averaging (OWA)	1	1	-
Augmented e-constraint and TOPSIS.	1	1	-
Exact solution approach (non-dominated points)	1	1	-
Goal programming/e-constraint	1	1	-
Goal programming MINMAX	1	1	-
Lexicographic ordering	1	1	-
PROMTHEE and goal programming	1	1	-
Weighted sum/Augmented e-constraint	1	1	-
Total	63	32	31

Note: All the references relating to Table 7 are presented in Appendix C. Full references can be found in Supplementary Materials.

). From metaheuristics methods, hybrid metaheuristic algorithms, particle swarm optimization, and genetic algorithm were largely used methods (

Table 8. Distribution of metaheuristics solution methods.

Metaheuristics Methods	Total	Certain	Uncertain
Hybrid meta-heuristic algorithm	6	4	2
Genetic algorithm (GA) *	4	4	-
Particle swarm optimization (PSO)	4	3	1
GA/PSO	2	1	1
Non-dominated sorting genetic algorithm (NSGA II)/PSO	2	2	-
Non-dominated sorting genetic algorithm (NSGA II)	2	-	2
Simulated-annealing (SA)/NSGA-II	1	1	-
Swarm intelligence	1	1	-
Hybrid swarm intelligence meta-heuristic	1	1	-
Memetic algorithm	1	1	-
Non-dominated ranking generic algorithm (NRGA)	1	1	-
Ant colony optimization (ACO)	1	1	-
AugMathFix	1	1	-
Centre of gravity/K means clustering	1	1	-
Evolutionary Algorithm (EA)	1	-	1
Simulated annealing (SA)	1	-	1
Lagrangian relaxation (LR)	1	-	1
Total	31	22	3

Note: All the references relating to Table 8 are presented in Appendix C. Full references can be found in Supplementary Materials. * Some papers have not specified which GA methods they have used.

).

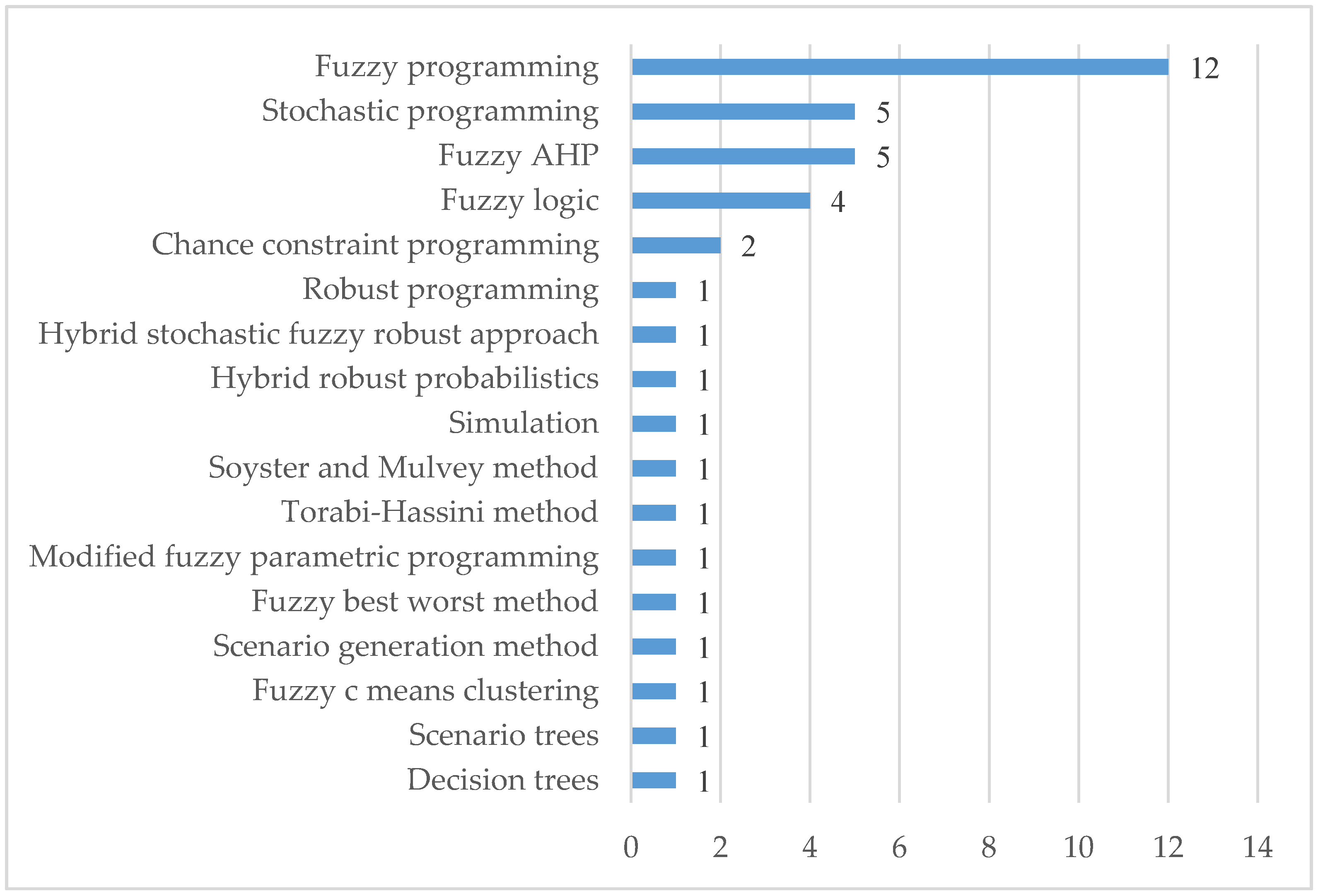
3.5. Uncertainty in Supply Chains

Different solution methods were used to address the uncertainty in optimization models, the most common being fuzzy programming (Figure 4). Azadeh et al. [53] used fuzzy programming to solve their model of the crude oil supply chain. The uncertain parameters considered in their model were cost and production capacity of refined products along with the consumption rate of petroleum products. Govindan et al. [68] used this method for uncertainty in a sustainable reverse logistics network design model. Pourjavad and Mayorga [73] considered uncertain parameters of return rates of products from customers, the capacity of all facilities, and product demand in designing a closed-loop supply chain model. The fuzzy AHP method for uncertain input including purchasing and transportation costs, purchasing quantities, demands, CO₂ emission, and capacity levels were used by Mohammad et al. [74] (for green and resilient supply chain network design) and Mohammad et al. [75] (for supplier selection and order allocation problem). Stochastic programming was used by Rahimi et al. [76] (for sustainable supply chain network design with uncertain parameters of transportation cost, demand, and price), Ebrahimi et al. [77] (for supplier selection and location-allocation model with demand uncertainty), Ruiz Femenia [78] (to incorporate the effect of demand uncertainty on the chemical supply chains). Wang et al. [79] used robust optimization for CLSC network design under the uncertainty factors of the supply side, customer demand, and return quantities. Sharifi et al. [40] used a hybrid stochastic fuzzy robust approach in designing biofuel supply chain network designing. Rabbani et al. [80] used a hybrid robust probabilistic method for location-allocation network designing with uncertain factors of transportation cost and CO₂ emission.

4. Results and Discussion

Most of the optimization models used the e-constraint method to solve the sustainable supply chain issues because of the following advantages [64,81]: (i) it is simple and computationally faster, (ii) it helps produce a set of non-extreme Pareto solutions, (iii) it is not necessary to scale the objective functions to a common scale, and (iv) we can control the number of generated efficient solutions by properly adjusting the number of grid points in each one of the objective function ranges. The second most used solution method was the augmented e-constraint method. This method was developed using appropriate slack variables to the objective function due to the weekly solutions produced using the e-constraint method [77,80,81]. To find approximate solutions for large complex models, metaheuristics methods are recommended [32,82]. Our results show hybrid metaheuristics algorithms, GA and PSO are largely used metaheuristics methods. GA leads to accurate Pareto front identification as it does not depend on the objective and constraint functions but requires a large computational effort [83]. Azadeh et al. [53] and Chiandussai et al. [83] found that EA seems particularly suitable for large-size multi-objective optimization problems, but its computational cost is high.

In sustainability aspects, most of the referenced models focused on economic and environmental dimensions, and less than 50% focused on all three dimensions of sustainability, especially in the overall supply chain, manufacturing, and reverse logistics phases. For the sourcing, distribution, and transportation phases, limited studies were incorporated into sustainability aspects. Minimization of cost and CO₂ emission were the popular objectives for most of these phases of the supply chain. From the social dimension, minimization of social impact and maximization of job opportunities were described. Although the consideration of social dimension in the SSCLM is still less than the economic and environmental dimensions, it is now being considered in the SSCLM. This trend is facilitated using quantitative social indicators such as social cost, social investments, number of job opportunities, lost working days, and number of employee injuries. However, qualitative aspects of the social dimension such as customer or employee satisfaction, employee discrimination, and social equality are still be missed.

In sustainability modeling, selecting indicators of economic objectives should be carefully chosen as it depends on the purpose of analysis, such as operational purpose (cost) or investment purpose (NPV) [11]. The authors highlighted the cost of implementing sustainability practices should also be incorporated into economic objectives. For environmental objectives, the use of energy, water, and other natural resources should be incorporated into the optimization model together with greenhouse gas (GHG) emissions. For that purpose, the LCA (life cycle analysis) method can be used, which is largely neglected in optimization models [84,85]. For the social component, social-LCA (S-LCA) may be a better option to address social sustainability. To consider the qualitative indicators of the social dimension, optimization methods are needed to be combined with other OR methods, such as decision analysis, expert systems, data analysis, and neural networks. Researchers suggest interdisciplinary approaches combining exact science and social sciences to quantify the social impact of sustainability [11,31].

The design of SSCLM is a critical decision and most of the SSCLM were designed to make strategic and tactical decisions such as supplier selection, order allocation, location-allocation, vehicle routine problems. The design of SSCLM for operational decision-making has largely been neglected in the reviewed papers. This phenomenon happens because sustainability is complex, has upfront costs, is time-consuming, and operational decisions are short-term. However, the integration of strategic, tactical, and operational decisions within one model has considerable potential to study sustainability aspects.

Uncertainty is a crucial factor that supply chain decision-makers should handle carefully. Researchers face difficulty in incorporating uncertainty into SSCLM due to the dynamic and complex nature of such models. In the literature, three main approaches were used to incorporate uncertainty into the model including fuzzy programming, stochastic programming, and robust programming. Fuzzy programming is applicable when there is no specific distribution for uncertain data, but it is possible to determine the boundaries and association functions for the data [53]. Stochastic programming is used when the collected data have specific distribution [53]. Robust methods are more restricted to convex problems, such as linear, linear discrete problems, and convex constrained continuous minimax problems [86]. Our results revealed that most of the uncertainty models used fuzzy programming. This highlights the lack of data regarding the uncertainty of the supply chain.

In uncertainty, several parameters were considered in SSCLM, the majority of which focused on uncertain data relating to economic dimensions, such as cost, demand, price, and capacity level. Uncertainty on environmental and social data has more space in research on SSCLM. In addition to the demand-side uncertainty, uncertainty at supply-side resources can be considered in SSCLM [87]. Barbosa Povoa et al. [11] described three challenges in optimization modeling, including sustainability modeling, uncertainty modeling, and risk and resilience. In our review, modeling sustainability and uncertainty were adequately addressed, but risk and resilience were barely studied. Silva et al. [88] are the only authors who considered risk objective in their model and used the conditional value-at-risk (CVaR) as a measure of risk in this review. Cardoso et al. [89] state that CVaR is one of the most used risk methods within the literature. Resilience was considered by Sharifi et al. [40] and Mohammad et al. [74] and in a later study, the resilience pillar was represented in terms of robustness, agility, leanness, and flexibility.

5. Conclusions and Recommendations for Future Research

This study provided a review of 95 published papers in the field of MOO for SSCLM. The review aimed to identify the research gaps in MOO for SSCLM and to assist decision-makers in selecting suitable MOO methods and solutions in developing SSCLM. These purposes were achieved through different research questions covering sustainability dimensions, indicators, supply chain phases, decision levels, optimization techniques, solution methods, and uncertainty in SSCLM. The results revealed that the economic and environmental aspects of sustainability still dominate in the SSCLM, and they are limited to a few indicators. Sourcing, distribution, and transportation issues in the supply chain were not adequately addressed. Most of the models used classical methods of optimization of which the epsilon constraint (e-constraint) method is widely used and from metaheuristics methods, hybrid metaheuristics methods were highlighted. Less than 50% of the reference papers considered uncertainty in the models, and fuzzy programming was commonly used to address the uncertainty. There are several optimization techniques and solution methods available but selecting one of them depends on several factors such as the purpose of the decision-maker, nature of the problem, and availability of the data. This study has presented a comprehensive analysis of the MOO of SSCLM, and the results of the study significantly contributed to the development of the field of sustainable supply chain and logistics modeling. Specifically, the current study provided the research gaps in the MOO of SSCLM from sustainability dimensions, sustainability indicators, different supply chain phases, decision levels, optimization techniques, and solution methods. Accordingly, future researchers and decision-makers can use the following key considerations for their potential works in modeling sustainable supply chain and logistics issues.

• In the absence of broad indicators of sustainability assessment and limited focus on the social dimension, the authors suggest incorporating more social aspects and integrating economic, environmental, and social indicators into the future of SSCLM. For example, innovation can be considered as an economic indicator in addition to cost, quality, and delivery flexibility to maximize competitive advantage [90], which is one of the main economic objectives in supply chain modeling. As indicated in the GRI (Global Reporting Initiative) standard [91], indirect economic impact, anti-corruption, and anti-competitive behavior from economic aspects, the material used, biodiversity, supplier environmental assessment from environmental aspects, training and development, non-discrimination, human rights, and supplier social assessment from social aspects can be considered as sustainability indicators. Comprehensive economic, environmental, and social indicators proposed by [92] can also be used in SSCLM.
• To incorporate the sustainability indicators into the optimization models, quantification is a barrier. Direct and indirect economic benefits can be quantified using the cost of implementing green practices, cost savings of using reverse logistics practices, and return on environmental and social investment. Social impact can be quantified using factors, including the number of health and safety training, cost of health and safety training, average hours of training on anti-corruption policies and procedures, reported cases of corruption and bribery, employee happiness index, community satisfaction rate, and number of CSR initiatives. The use of comprehensive techniques, including LCA and S-LCA, for measuring environmental and social impact have more research potential in this case. The authors propose to combine social science research techniques, including surveys and case research, especially for social sustainability assessment in optimization models, to avoid its limitations and ensure data quality.
• More SSCLMs for sourcing, distribution, and transportation phases of the supply chain are required. Of these phases, the transportation phase requires more focus on strategic decisions, for example, a decision to use electric vehicles to reduce Co2 emissions. The integration of all levels of decision with uncertainty factors to the model is also emphasized as a solution method to address uncertainty is limited to fuzzy programming. Incorporating more demand and supply-related uncertainty factors in a model can lead to exploring other solution methods, such as simulation, scenario and robust programming. Dividing the optimization model into different phases, including decision levels or supply chain phases, is recommended as it will help reduce problem space and the solution time. As all these considerations make optimization models more complex and larger, more sophisticated techniques and solution methods, the inclusion of hybrid metaheuristics approaches will be more useful in SSCLM. Furthermore, the authors propose the use of more hybrid and decomposed optimization methods that have direct implications for solving many real-world cases. Other OR methods, including simulation and system dynamics modeling, can also be applied and combined in future research, which facilitates decision-makers to acquire a more comprehensive picture of the sustainable supply chain and logistics issues.

The authors acknowledge that the current study was conducted using the publications of limited databases. Future studies can expand the search databases and enhance the contribution to developing the field of sustainable supply chain and logistics modeling.