Control of Laser Scanner Trilateration Networks for Accurate Georeferencing of Caves: Application to El Castillo Cave (Spain)
Abstract
:1. Introduction
2. Materials and Methods
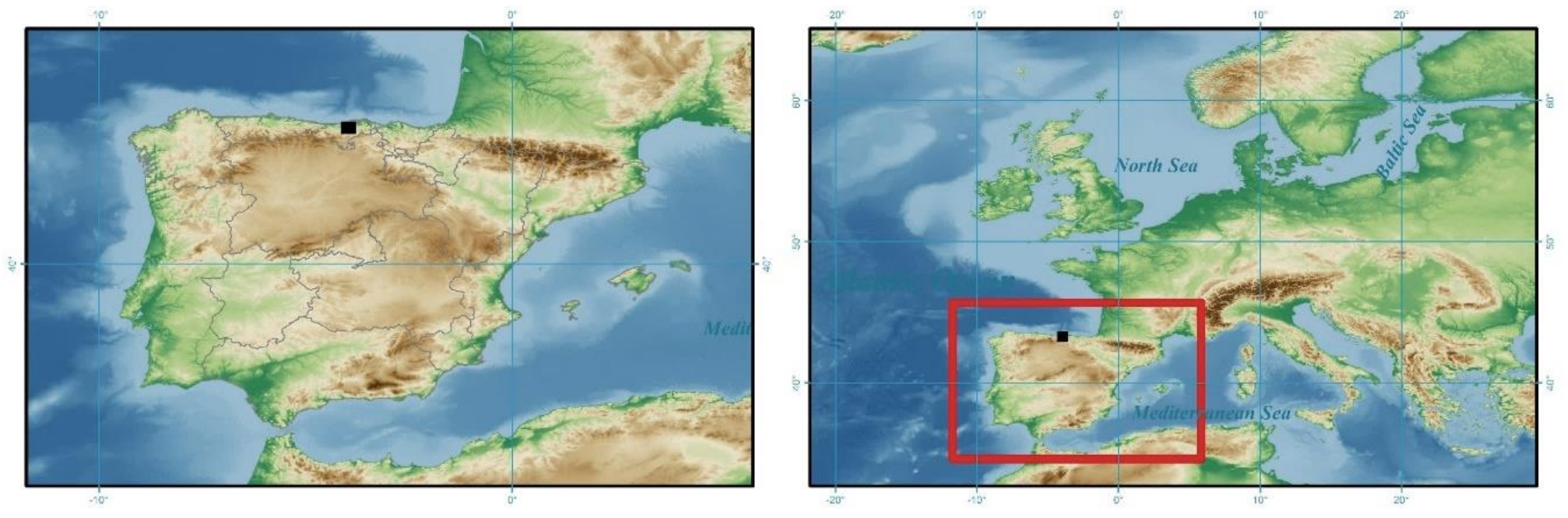
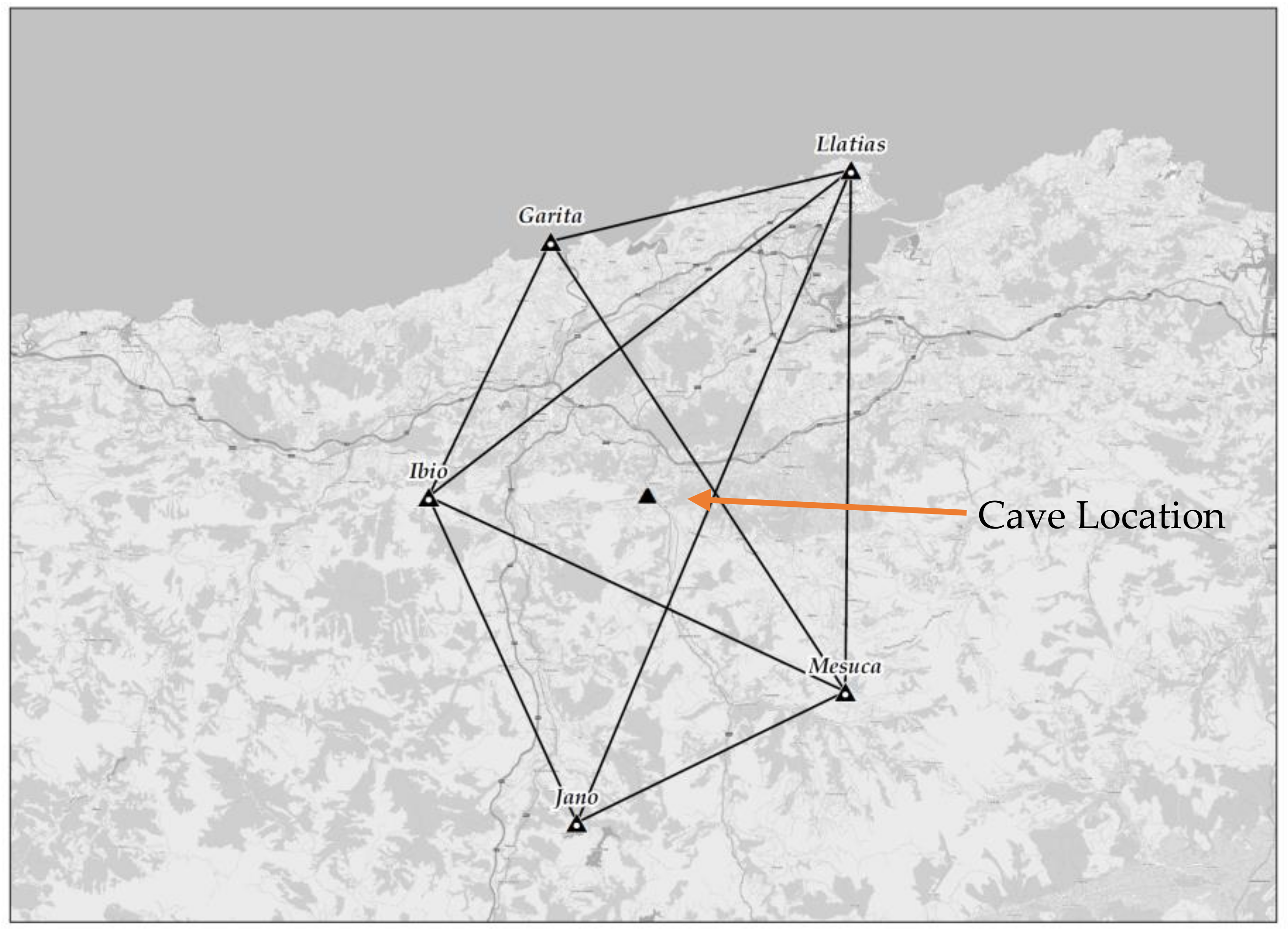
2.1. Study Area
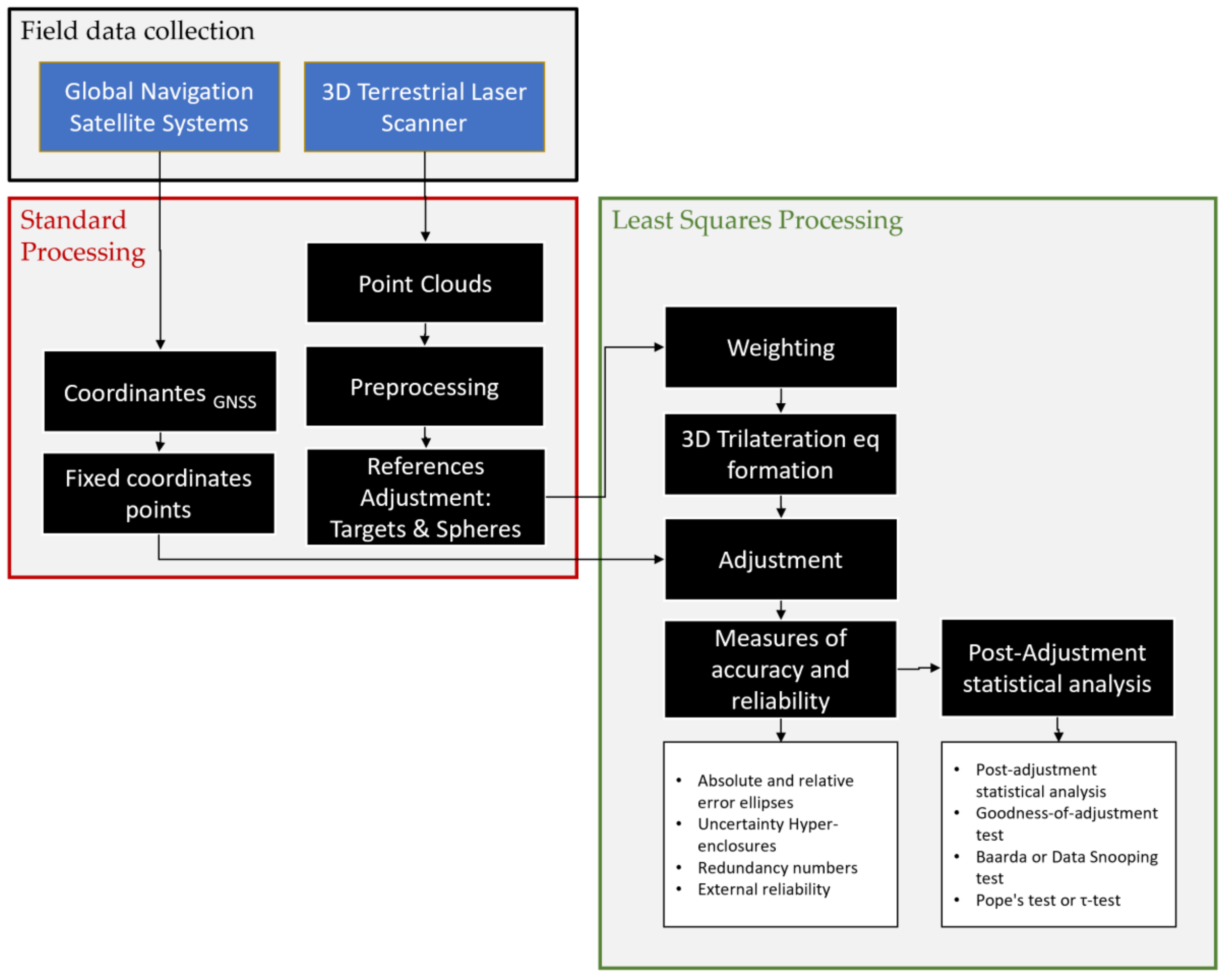
2.2. Overall Workflow
2.3. Propagation and Accuracy of Random Errors in Indirectly Measured Quantities
2.3.1. Introduction
2.3.2. Basic Error Propagation Equation
2.3.3. Accuracy of Indirectly Determined Quantities
Development of the Covariance Matrix
Standard Deviation of the Calculated Quantities
2.3.4. Fitting Spherical Objects from Point Clouds
2.4. Fitting Spherical Objects from Point Clouds
2.4.1. Problem Definition
2.4.2. Method of Adjustment
2.4.3. Different Measures of Distances
2.4.4. Canonical Analysis of the Quadratic Form
2.4.5. Adjustment of the Sphere
2.5. 3DTLS Networks
2.5.1. General Adjustment Model
Observation Equation Modelling
Conditional Equation Model
2.5.2. Traditional Topogeodetic Observation Equations
Points of Known Coordinates
Distances
Azimuth
Horizontal Angle Readings
Trilateration Network Adjustment
2.5.3. Network Datum, Constraints, and Degrees of Freedom
- A correction to the coordinates of all vertices represented by the solution vector of the adjustment;
- A geometric transformation to the previously formed and adjusted network that keeps it the same as itself and refers it to new axes (adjusted datum).
Points of Known Coordinates
Fixed Azimuth
Horizontal Angular Reading to a Fixed External Point
Network Internal Constraint
- The coordinates of the network centroid must remain unchanged after the adjustment. Therefore, if the centroid coordinates are:the restrictions to be fulfilled would be that the corrections to the centroid coordinates are zero, that is, that the centroid remains unchanged due to the adjustment:which implies that:
- The mean azimuth from the centroid to each network point must remain unchanged. As it can be written for the azimuth between the centroid and any point on the network that:differentiating
- 3D trilateration: No fixed point and no orientation. There is a translation in X, Y, Z = (da, db, dc) and a rotation of axes (dω, dθ). Here, there are five degrees of freedom, and the constraint matrix will be as follows:
- 2.
- 3D trilateration with known azimuth; no fixed point but with orientation. There is a translation in X, Y, Z = (da, db, dc) and an axis rotation (dθ). Here, there are four degrees of freedom, and the constraint matrix will be as follows:
- 3.
- 3D trilateration with a fixed elevation. No fixed planimetric point, with a fixed height (or altitude) point and no orientation. There is a translation in X, Y = (da, db) and a rotation of axes (dω, dθ). Here, there are four degrees of freedom, and the constraint matrix will be as follows;
- 4.
- 2D trilateration, altimetry with a known fixed elevation and a fixed azimuth. No fixed planimetric point, with a fixed elevation point and orientation. There is a translation in X, Y = (da, db) and an axis rotation (dθ). Here, there are three degrees of freedom, and the constraint matrix will look like this:
- 5.
- 3D trilateration with fixed point: with a fixed point and no orientation. There is one axis rotation (dω, dθ). Here there are two degrees of freedom and the constraint matrix is:
- 6.
- 3D trilateration with fixed point and known azimuth. With a fixed point and orientation. There is an axis rotation (dθ). Here, there is one degree of freedom, and the constraint matrix is:
2.5.4. Resolution Methods
Imposition of Constraints by Elimination of Parameters
Adjustment with Parameter Functions
Weighted Method
2.5.5. Weighting of Observations
Introduction
Weighted Average
Relationship between Weights and Standard Errors
Statistics of Weighted Averages
2.5.6. Termination of Iteration
- There is a gross error in the data, and it is impossible to find a solution, or
- The maximum size of the correction is smaller than the precision of the observations.
2.5.7. Main Design Problem: Measures of Accuracy and Reliability
Absolute and Relative Error Ellipses
Uncertainty Hyper-Enclosures
- Projections of the a priori or a posteriori hyperquadric on any plane defined by two coordinate axes. This gives rise to another meaning of vertex and correlation ellipses, geometrically representative of the location of the exact vertex if the reference vertex is that of the grid or, otherwise, that of a point determined by the correlation between two vertex coordinates.
- Projection of the pairs of semi-axes on the coordinate planes formed by the generic axes. This gives rise to another meaning of ellipses of vertices and correlation of the survey, which is just as representative as the previous case. They consider issues related to the range of the design matrices.
- Projections of the hyperquadric a priori or a posteriori onto any three-dimensional space defined by three coordinate axes. This gives rise to another meaning of vertex ellipses and correlation ellipses, geometrically representative of the location of the exact vertex if the reference vertex is of the network or, otherwise, of that of a point determined by the correlation between two vertex coordinates.
- Projection of triads of semi-axes onto any three-dimensional space defined by three coordinate axes. This gives rise to another meaning of vertex ellipses and survey correlation, which is equally representative as the previous case. The solutions depend on the range of the design matrices.
Redundancy Numbers
External Reliability
2.5.8. Post-Adjustment Statistical Analysis
Goodness-of-Adjustment Test
Baarda or Data Snooping Test
Pope’s Test or -Test
2.6. Global Navigation Satellite Systems (GNSS)
- Pseudoranging: This implies determining distances (or ranges) between satellites and receivers by measuring the time that transmitted signals take to travel from satellites to ground receivers. Precise travel times are determined due to known frequency of the PRN codes. It is usually known as code measurement procedure.
- Carrier-phase measurements: The phase changes of the carrier from the satellites to receivers is observed. The clocks in the satellites and receivers should have been synchronised to observe true phase-shift, which is impossible. Differencing techniques (differences between phase observations) are used to solve this timing problem and to remove other errors in the system. Single differencing removes satellite clock biases. Double differencing removes receiver clock biases and other systematic errors. Triple differencing cancels out the ambiguity of the number of full cycles in the travel distance being unknown.
3. Results
3.1. Preliminary 3DTLS Tests
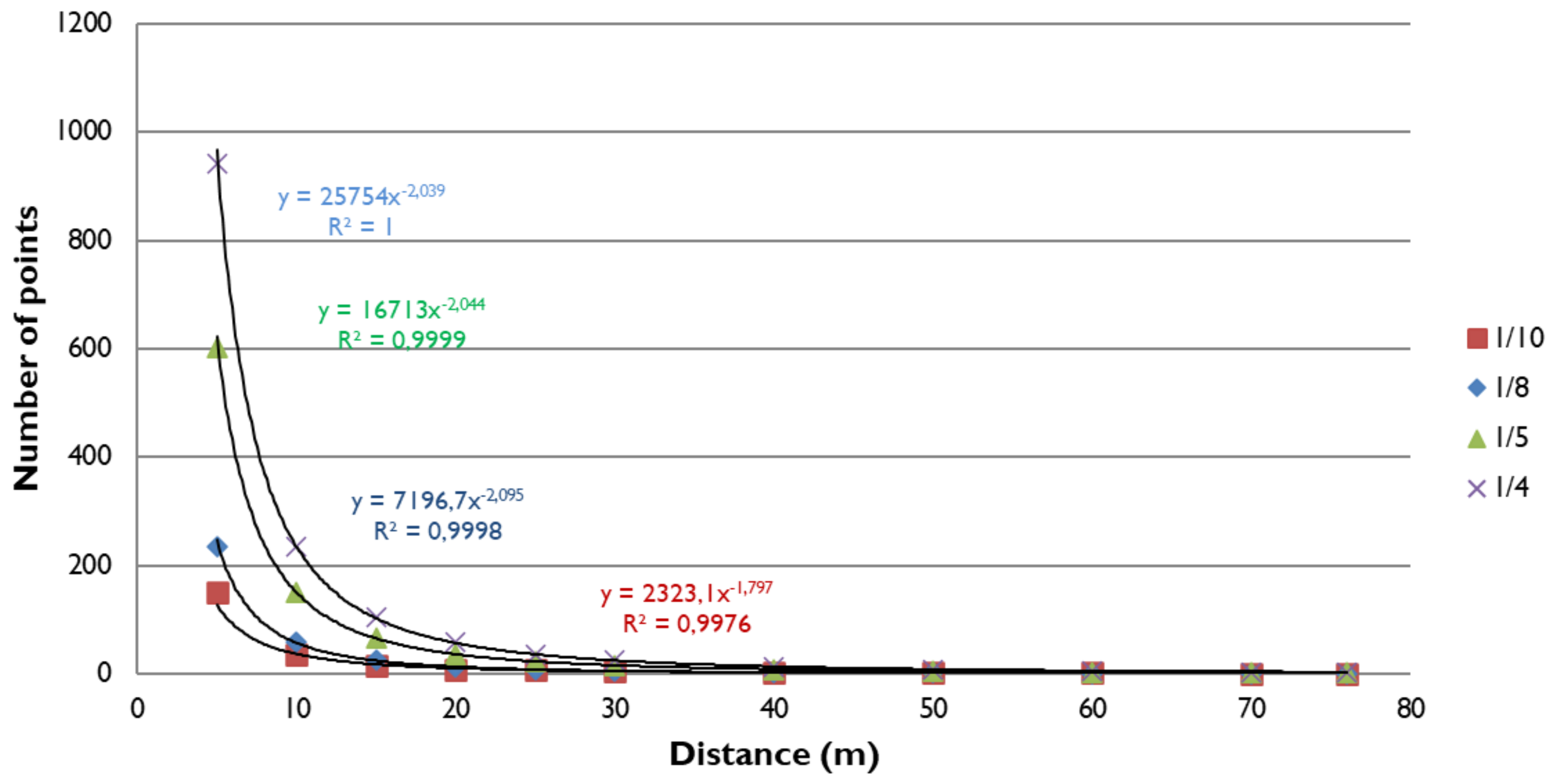
3.1.1. Calculation of the Theoretical Resolution
- For 1/10 resolution, high accuracy is only possible with scan distances less than 8.25 m, at best;
- If the scanning resolution is 1/8, it is not recommended to use distances greater than 10.35 m to calculate the least square spheres;
- A maximum of 16.55 m would be recommended for 1/5 resolutions;
- The theoretical maximum distance is 20.65 m for 1/4 scanning resolutions;
- Theoretically, with a resolution of 1/2, spheres up to 41.35 m could be recognised with guarantees;
- At maximum resolution, it should be possible to recognise a sphere over 82.7 m.
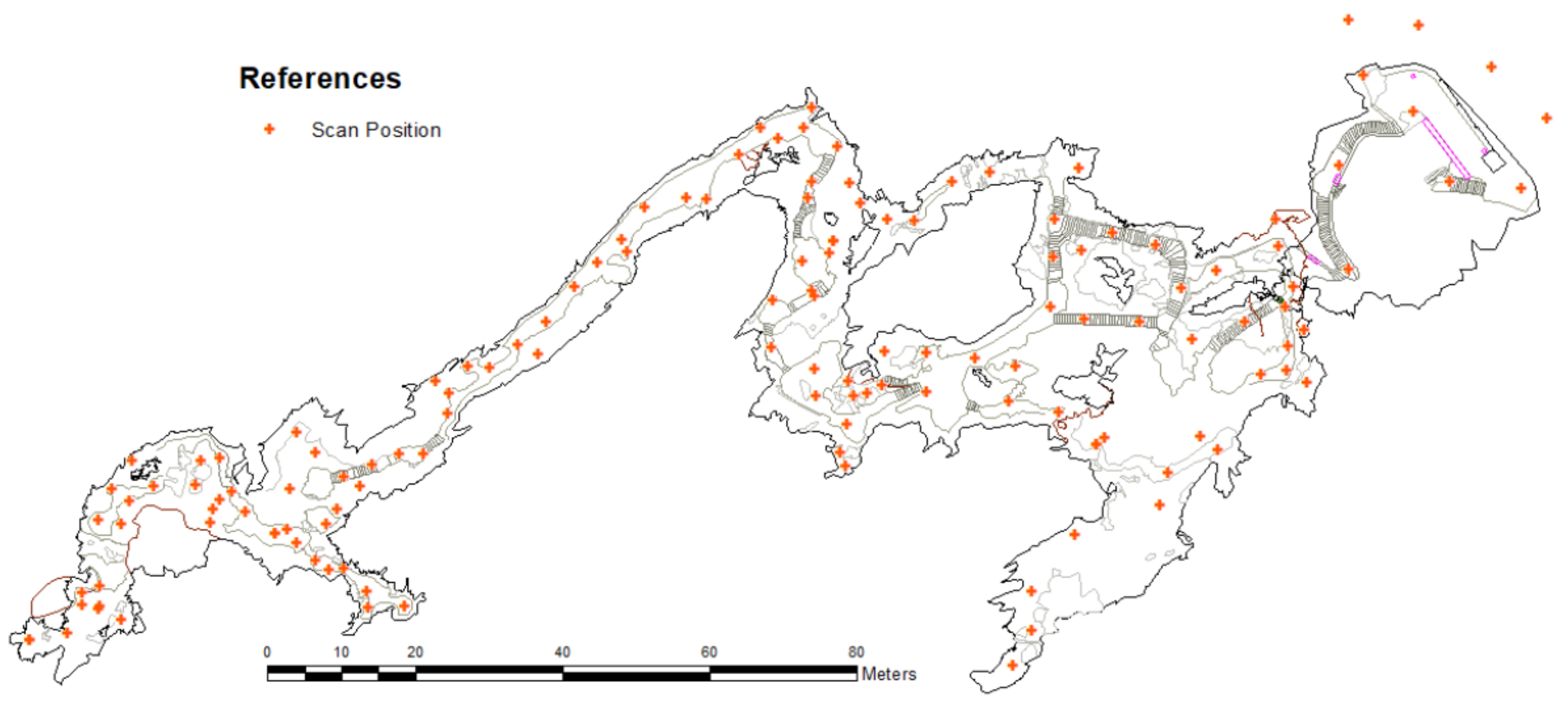
3.1.2. Data Capture for the Tests
3.1.3. Measurement Accuracy Test
Applied Method
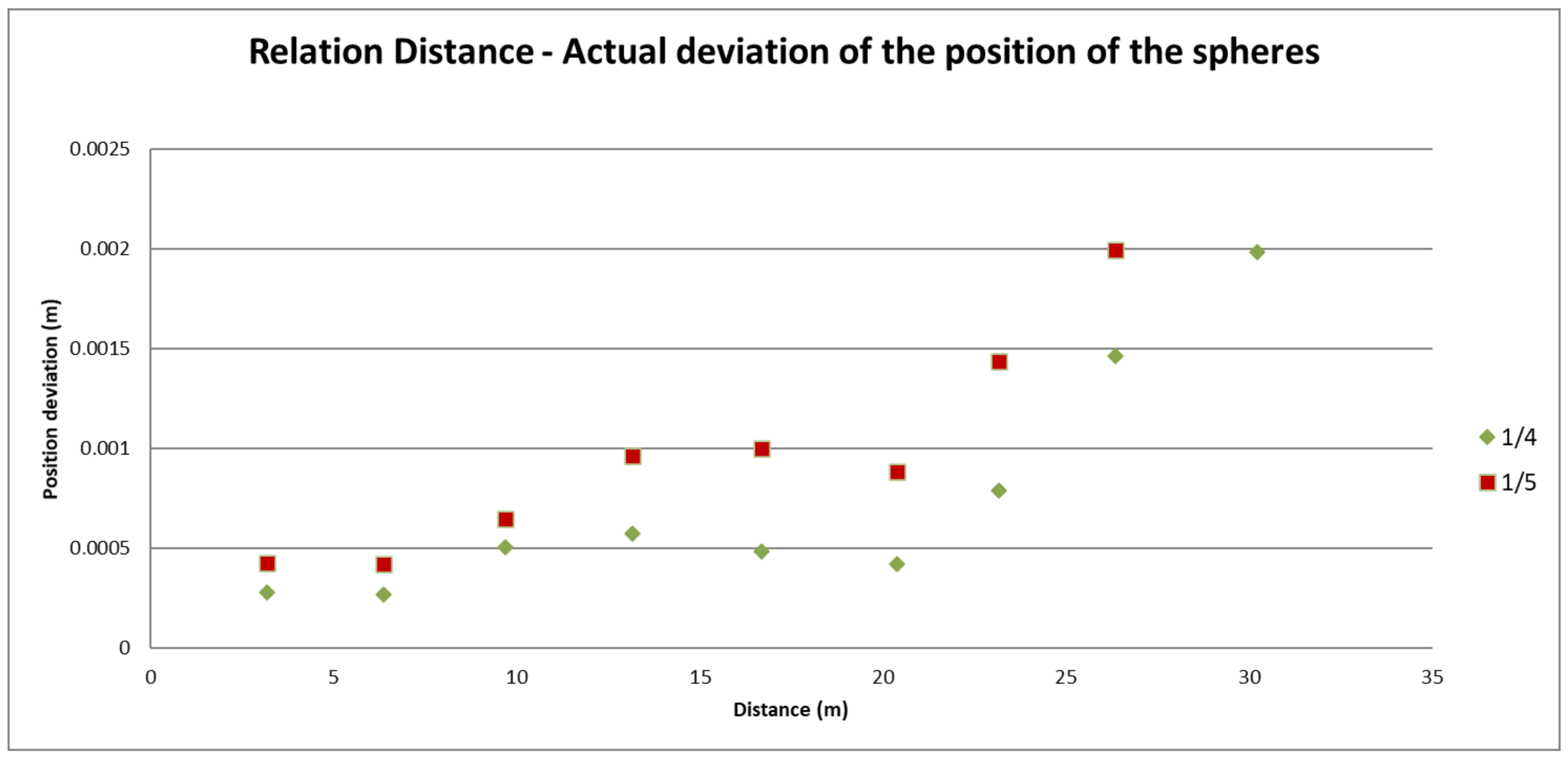
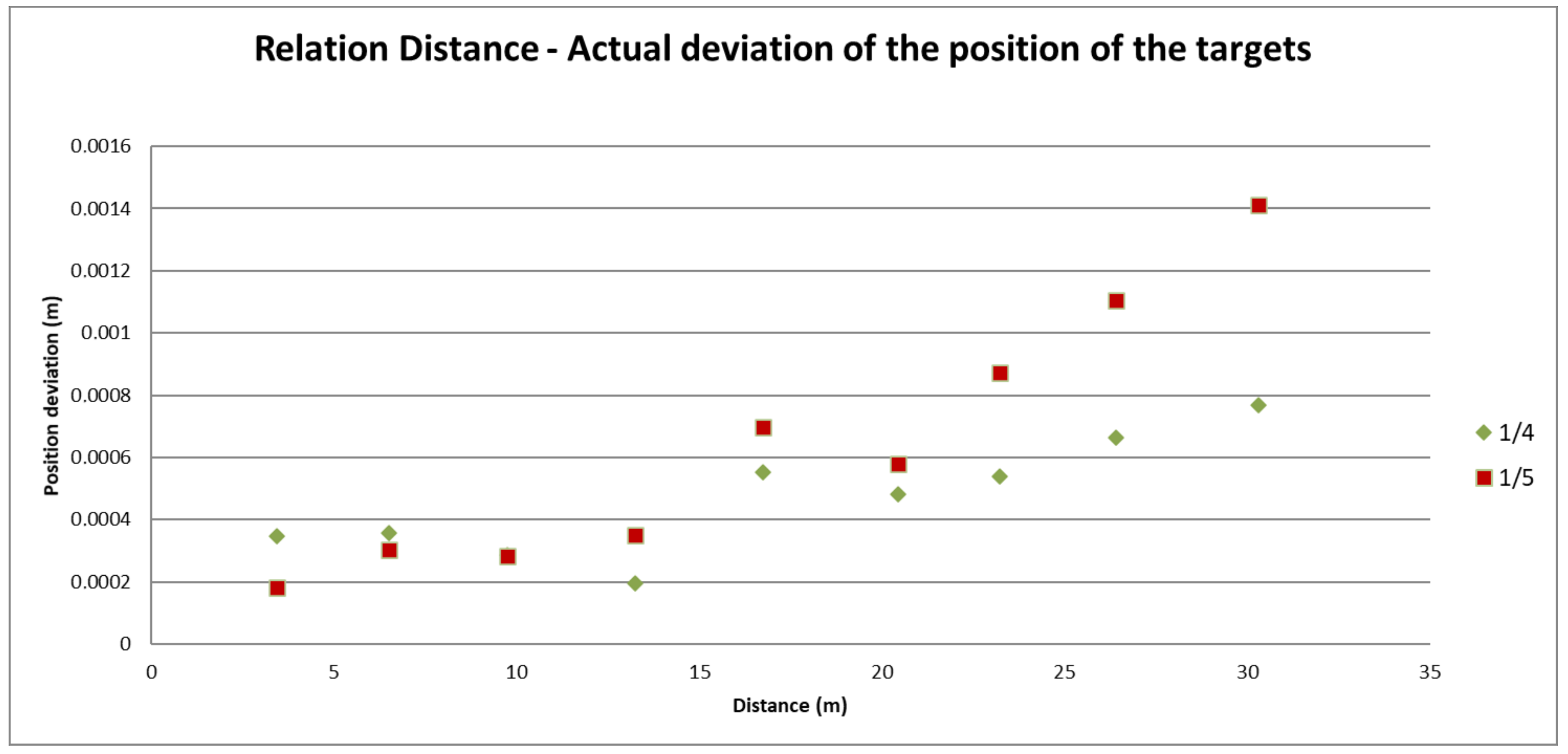
Results Obtained from the Test
Conclusions
3.1.4. Normality Test
Applied Method
- The range of values that the random variable of the distribution can take is divided into K adjacent intervals:
- 2.
- Let be the number of values of the data we have that belong to the interval .
- 3.
- Calculate the probability that the random variable of the candidate distribution is in the interval .
- 4.
- The following test statistic is formed:
Results Obtained from the Test
Conclusions
3.1.5. Conclusion on Fitness
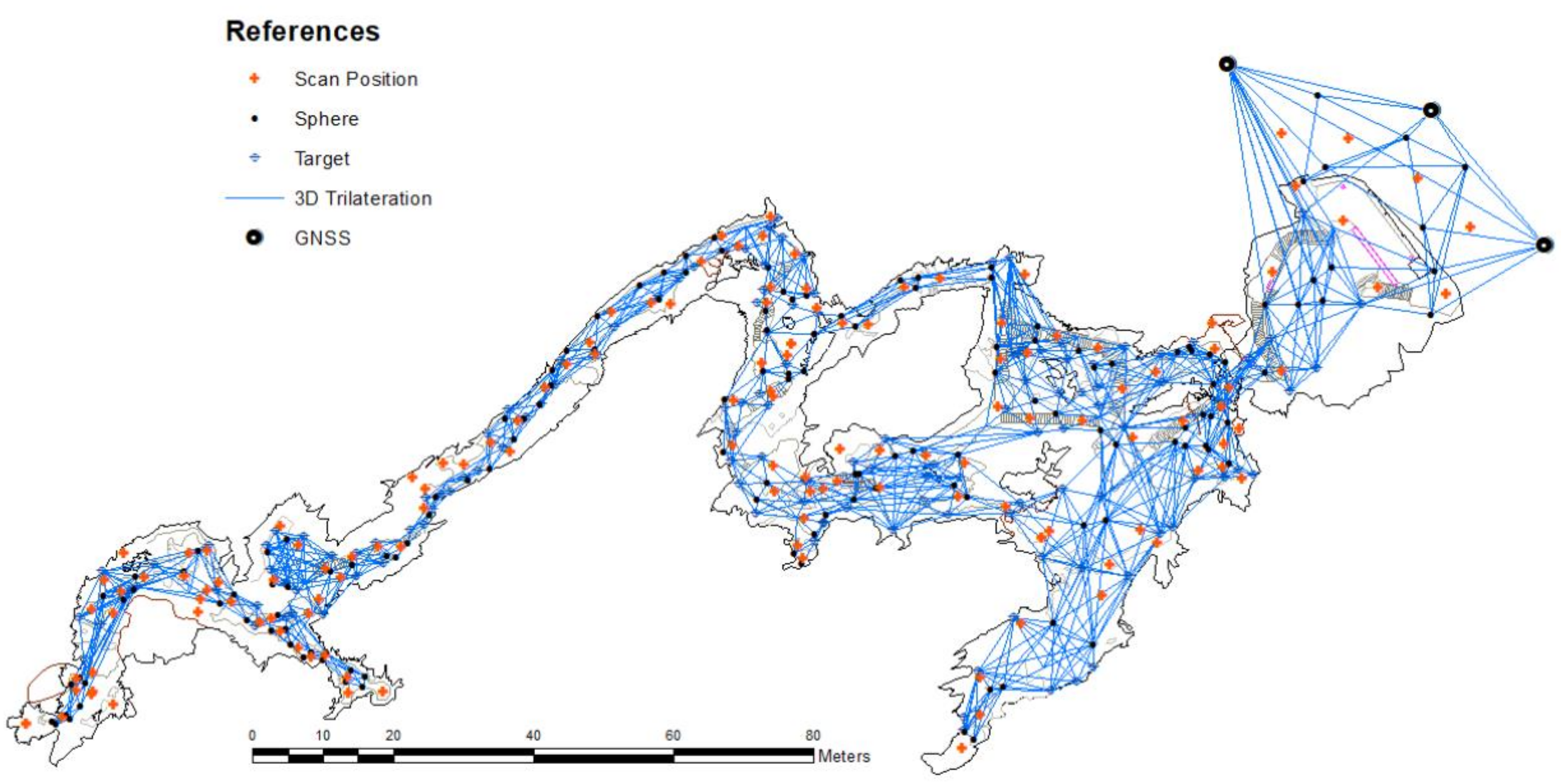
3.2. Practical Case: Cave Adjustment
3.2.1. Global Navigation Satellite Systems (GNSS)
3.2.2. Observation Generation from Scan Points
Name_Of_Reference, Scan_Position, X_coordinate, Y_coordinate, Z_coordinate, Radius, number_of_points used to calculate the reference, normal_transversal_deviation, normal_longitudinal_deviation, and distance to scan point.
3.2.3. D Trilateration
Reference_Name_1; Reference_Type_1; Reference_Name_2; Reference_Type_2; Mean_Value; Standard_Deviation_Estimation;
3.2.4. Measures of Accuracy and Reliability
Absolute Standard Ellipses
Name_Of_Ellipse, X_coordinate, Y_coordinate, Z_coordinate, Semi-major axis, Semi-minor axis, Orientation.
Relative Standard Ellipses
Name_Of_Ellipse, Reference_1, Reference_2, X_coordinate, Y_coordinate, Z_coordinate, Semi-major axis, Semi-minor axis, Orientation
Uncertainty Hyper-Enclosures
3.2.5. Post-Adjustment Statistical Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Ontañon, R.; Bayarri, V.; Herrera, J.; Gutierrez, R. The conservation of prehistoric caves in Cantabria, Spain. In The Conservation of Subterranean Cultural Heritage; CRC Press/Balkema: Boca Raton, FL, USA; Taylor & Francis Group: London, UK, 2014; ISBN 978-1-315-73997-7. [Google Scholar]
- Bayarri-Cayón, V.; Castillo, E. Caracterización geométrica de elementos complejos mediante la integración de diferentes técnicas geomáticas. Resultados obtenidos en diferentes cuevas de la Cornisa Cantábrica. In Proceedings of the VIII Semana Geomática Internacional, Barcelona, Spain, 3–5 March 2009. [Google Scholar]
- Bayarri, V. Algoritmos de Análisis de Imágenes Multiespectrales e Hiperespectrales para la Documentación e Interpretación del Arte Rupestre. Ph.D. Thesis, Universidad Nacional de Educación a Distancia, Madrid, Spain, May 2020. Available online: http://e-spacio.uned.es/fez/view/tesisuned:ED-Pg-TecInd-Vbayarri (accessed on 25 July 2021).
- Matsuoka, M.T.; Rofatto, V.F.; Klein, I.; Roberto Veronez, M.; da Silveira, L.G., Jr.; Neto, J.B.S.; Alves, A.C.R. Control Points Selection Based on Maximum External Reliability for Designing Geodetic Networks. Appl. Sci. 2020, 10, 687. [Google Scholar] [CrossRef] [Green Version]
- Baarda, W. S-transformations and criterion matrices. Publ. Geod. New Ser. 1973, 5, 168. [Google Scholar]
- Grafarend, E.W. Optimization of Geodetic Networks. Can. Surv. 1974, 28, 716. [Google Scholar] [CrossRef]
- Klein, I.; Matsuoka, M.T.; Guzatto, M.P.; Nievinski, F.G.; Veronez, M.R.; Rofatto, V.F. A new relationship between the quality criteria for geodetic networks. J. Geod. 2019, 93, 529. [Google Scholar] [CrossRef]
- Seemkooei, A.A. Comparison of reliability and geometrical strength criteria in geodetic networks. J. Geod. 2001, 75, 227–233. [Google Scholar] [CrossRef]
- Seemkooei, A.A. Strategy for Designing Geodetic Network with High Reliability and Geometrical Strength. J. Surv. Eng. 2001, 127, 104–117. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, P.J.G. Quality Control in Geodetic Networks. In Optimization and Design of Geodetic Networks; Grafarend, E.W., Sansò, F., Eds.; Springer: Berlin/Heidelberg, Germany, 1985; pp. 526–547. [Google Scholar]
- Gargula, T. Adjustment of an Integrated Geodetic Network Composed of GNSS Vectors and Classical Terrestrial Linear Pseudo-Observations. Appl. Sci. 2021, 11, 4352. [Google Scholar] [CrossRef]
- Vanícek, P.; Craymer, M.R.; Krakiwsky, E.J. Robustness analysis of geodetic horizontal networks. J. Geod. 2001, 75, 199–209. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A. A new method for second order design of geodetic networks: Aiming at high reliability. Surv. Rev. 2004, 37, 552–560. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.; Sharifi, M.A. Approach for Equivalent Accuracy Design of Different Types of Observations. J. Surv. Eng. 2004, 130, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Hekimoglu, S.; Erenoglu, R.C.; Sanli, D.U.; Erdogan, B. Detecting Configuration Weaknesses in Geodetic Networks. Surv. Rev. 2011, 43, 713–730. [Google Scholar] [CrossRef]
- Hekimoglu, S.; Erdogan, B. New Median Approach to Define Configuration Weakness of Deformation Networks. J. Surv. Eng. 2012, 138, 101–108. [Google Scholar] [CrossRef]
- Besl, P.J.; Mckay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Fritsch, D.; Wagner, J.F.; Ceranski, B.; Simon, S.; Niklaus, M.; Zhan, K.; Mammadov, G. Making Historical Gyroscopes Alive—2D and 3D Preservations by Sensor Fusion and Open Data Access. Sensors 2021, 21, 957. [Google Scholar] [CrossRef]
- Koch, K.R. Parameter Estimation and Hypothesis Testing in Linear Models; Springer: Berlin/Heidelberg, Germany, 1999; 333p. [Google Scholar]
- Bayarri, V.; Sebastián, M.A.; Ripoll, S. Hyperspectral Imaging Techniques for the Study, Conservation and Management of Rock Art. Appl. Sci. 2019, 9, 5011. [Google Scholar] [CrossRef] [Green Version]
- Alcalde Del Río, H.; Breuil, H.; Sierra, L. Les Cavernes de la Région Cantabrique (Espagne); Impr. V A. Chêne: Rabat, Monaco, 1911. [Google Scholar]
- Espeleo Club de Gràcia. El Sector Oriental del Massís del Dobra (Puente Viesgo); Exploracions Nº 6; Espeleo Club de Gràcia: Barcelona, Spain, 1982. [Google Scholar]
- Ripoll, S.; Bayarri, V.; Muñoz, F.J.; Latova, J.; Gutiérrez, R.; Pecci, H. El arte rupestre de la cueva de El Castillo (Puente Viesgo, Cantabria): Unas reflexiones metodológicas y una propuesta cronológica. In Capítulo en Libro Cien Años de Arte Rupestre Paleolítico Centenario del Descubrimiento de la Cueva de la Peña de Candamo (1914–2014); Ediciones Universidad de Salamanca: Salamanca, Spain, 2014; ISBN 978-84-9012-480-2. [Google Scholar]
- FARO. FARO Laser Scanner Focus 3D X 330 TEchnical Datasheet. Available online: https://faro.app.box.com/s/nn8swfhtez68lo88uhp6u8bchdfl1ay9/file/441669546444 (accessed on 11 June 2021).
- Chueca Pazos, M.; Herráez Boquera, J.; Berné Valero, J.L. Redes Topográficas y Locales. Microgeodesia; Paraninfo: Madrid, Spain, 1996. [Google Scholar]
- Hogg, R.V.; Johannes, L. Applied Statistics for Engineers and Physical Scientists; Macmillan: New York, NY, USA, 1992. [Google Scholar]
- Mikhail, E.M.; Gordon, G. Analysis /& Adjustment of Survey Measurements; Van Nostrand Reinhold Company: New York, NY, USA, 1981. [Google Scholar]
- Ghilani, C.D. Statistics and Adjustments Explained, Part 3: Error Propagation. Surv. Land Inf. Sci. 2004, 64, 29–33. [Google Scholar]
- Jorge, R.; Eduardo, B. Medical image segmentation, volume representation and registration using spheres in the geometric algebra framework. Pattern Recogn. 2007, 40, 171–188. [Google Scholar] [CrossRef]
- Franaszek, M.; Cheok, G.; Witzgall, C. Fast automatic registration of range images from 3D imaging systems using sphere targets. Automat. Constr. 2009, 18, 265–274. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, H.; Zhang, Y.; Zhang, D. Automatic registration of laser point cloud using precisely located sphere targets. J. Appl. Remote Sens. 2014, 8, 083588. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in C: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Rabbani, T. Automatic Reconstruction of Industrial Installations Using Point Clouds and Images; Publications on Geodesy 62; Netherlands Geodetic Commission: Delft, The Netherlands, 2006. [Google Scholar]
- Eberly, D. 3D Game Engine Design: A Practical Approach to Real- Time Computer Graphics; Academic Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Box, G.E.P.; Draper, N.R. Empirical Model-Building and Response Surface; John Wiley & Sons: Hoboken, NJ, USA, 1986. [Google Scholar]
- Boro, K.R.; Bielajew, A.F. Quadplot: A Programme to Plot Quadric Surfaces; Technical Report NRCC/PIRS-0491; Institute for National Measurement Standards, National Research Council of Cañada: Ottawa, ON, Cañada, 1995. [Google Scholar]
- Bookstein, F. Fitting Conic Sections to Scattered Data. Comput. Graph. Image Process. 1979, 9, 56–71. [Google Scholar] [CrossRef]
- Leick, A. GPS Satellite Surveying, 2nd. ed.; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Mikhail, E.M.; Ackermann, F. Observations and Least Squares; Harper & Row Publishers: New York, NY, USA, 1976. [Google Scholar]
- Cooper, M.A.R. Control Survegs in Civil Engineering; Coliins Profesional and Technical Books; Nichols Pub. Co: New York, NY, USA, 1987. [Google Scholar]
- Wolf, P.R.; Charles, D.G. Adjustment Computations: Statistics and Least Squares in Surveying and GIS; Wiley Interscience: Hoboken, NJ, USA, 1997. [Google Scholar]
- Harvey, B.R. Practical Least Squares and Statistics for Surveyors; En Monograph 13 (University of New South Wales, ed.); Kensington: Sidney, Australia, 1991. [Google Scholar]
- Chueca Pazos, M.; Anquela Julián, A.B.; Baselga Moreno, S. Diseño de Redes y Control de Deformaciones. Los Problemas del da Tum y Principal de Diseño; Editorial Universidad Politécnica de Valencia: Valencia, Spain, 2007. [Google Scholar]
- Strang, G.; Kai, B. Linear Algebra, Geodesy and GPS; Wellesley Cambridge Press: Cambridge, UK, 1997. [Google Scholar]
- Caspary, W.F. Monograph 11: Concepts of Network and Deformation Analysis; The University of New South Wales: Sydney, Australia, 1988. [Google Scholar]
- Kuang, S. Geodetic Network Analysis and Optimal Design. Concepts and Applications; Ann Arbor Press Inc.: Chelsea, MI, USA, 1996. [Google Scholar]
- Dracup, J.F. Squares Adjustment by the Method of Observation Equations with Accuracy Estimates. Surv. Land Inf. Sci. 1994, 55, 2. [Google Scholar]
- De La Fuente, J.L.O. Técnicas de Cálculo Para Sistemas de Ecuaciones, Programación Lineal y Programación Entera; Reverte S.A.: Barcelona, Spain, 1998. [Google Scholar]
- Harvey, B. Practical Least Squares and Statistics for Surveyors; School of Surveying, University of New South Wales: Sydney, Australia, 1994. [Google Scholar]
- Gruëndig, L. Special Adjustment tools for Surveying Networks. In Papers for the Precise Engineering and Deformation Surveys Workshop; University of Calgary. Publ.: Calgary, AB, Canada, 1985; Volume 60004. [Google Scholar]
- Haim, B.P.; David, S. Relative error of geodetic Networks. J. Surv. Eng. ASCE 1985, 111. [Google Scholar] [CrossRef]
- Leick, A. Adjustment Computations; University of Maine: Orono, ME, USA, 1980. [Google Scholar]
- Alian, A.L. Practical Surveging and Computations; Butter-Worth/Heinemann: Oxford, UK, 1993. [Google Scholar]
- Dewitt, B.A. An Efficient Memory Paging Scheme for Least Squares Adjustment of Horizontal Surveys. Surv. Land Inf. Sci. 1994, 54, 147–156. [Google Scholar]
- Pope, A.J. The Statistics of Residuals and the Detection of Outliers; NOAA Technical Report, NOS 65, NGS 1; National Geodetic Survey: Rockville, MD, USA, 1976. [Google Scholar]
- Barnes, D. GPS Status and Modernization. Presentation at Munich Satellite Navigation Summit 2019. Available online: https://www.gps.gov/cgsic/international/2019/munich/barnes.pdf (accessed on 28 July 2021).
- Zrinjski, M.; Barković, Đ.; Matika, K. Razvoj i modernizacija GNSS-a. Geod. List 2019, 73, 45–65. Available online: https://hrcak.srce.hr/218855 (accessed on 16 July 2021).
- Hein, G.W. Status, perspectives and trends of satellite navigation. Satell. Navig. 2020, 1, 22. [Google Scholar] [CrossRef]
- Cross, P.A. Advanced Least Squares Applied to Positionjixing; Working papers; Univrsity of East London: London, UK, 1983. [Google Scholar]
- Rüeger, J.M. Electronic Distance Measurement: An Introduction; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Gielsdorf, F.; Rietdorf, A.; Gruendig, L. A Concept for the calibration of terrestrial láser scanners. In Proceedings of the FIG Working Week, Athens, Greece, 22–27 May 2004; In CD-ROM. Available online: https://m.fig.net/resources/proceedings/fig_proceedings/athens/papers/pdf/ts_26_2_gielsdorf_etal_ppt.pdf (accessed on 28 July 2021).
- Boehler, W.; Bordas, M.; Marbs, A. Investigating Láser Scanner Accuracy. In Proceedings of the XIXth CIPA Sgmposium, Working Group 6, Antalya, Turkey, 30 September–4 October 2003. [Google Scholar]
- Amiri Parían, J.; Grün, A. Integrated láser scanner and intensity image calibration and accuracy assessment. Int. Arch. Photogramm. Remóte Sens. Spat. Inf. Sci. 2005, 36, 18–23. [Google Scholar]
- Bayarri, V.; Castillo, E.; Ripoll, S.; Sebastián, M.A. Improved Application of Hyperspectral Analysis to Rock Art Panels from El Castillo Cave (Spain). Appl. Sci. 2021, 11, 1292. [Google Scholar] [CrossRef]
- Ripoll, S.; Bayarri, V.; Muñoz, F.J.; Ortega, R.; Castillo, E.; Latova, J.; Herrera, J.; Moreno-Salinas, D.; Martín, I. Hands Stencils in El Castillo Cave (Puente Viesgo, Cantabria, Spain). An Interdisciplinary Study. Proc. Prehist. Soc. 2021, 1–21. [Google Scholar] [CrossRef]
- Bayarri-Cayón, V.; Latova, J.; Castillo, E.; Lasheras, J.A.; De Las Heras, C.; Prada, A. Nueva ortoimagen verdadera del Techo de Polícromos de la Cueva de Altamira, ARKEOS | perspectivas em diálogo, nº 37. In XIX International Rock Art Conference IFRAO 2015. Symbols in the Landscape: Rock Art and Its Context. Conference Proceedings; Instituto Terra e Memória: Tomar, Portugal, 2015; pp. 2308–2320. [Google Scholar]
- Barrera, S.; Otaola, A.; Bayarri-Cayón, V. Explotación Turística no Intrusita de la Cueva de Santimamiñe (Vizcaya) Mediante Realidad Virtual. II Congreso Español de Cuevas Turísticas; Asociación de Cuevas Turísticas Española: Madrid, Spain, 2009; pp. 359–371. [Google Scholar]
- Bayarri, V.; Latova, J.; Castillo, E.; Lasheras, J.A.; De Las Heras, C.; Prada, A. Nueva documentación y estudio del arte empleando técnicas hiperespectrales en la Cueva de Altamira. ARKEOS | perspectivas em diálogo, nº 37. In XIX International Rock Art Conference IFRAO 2015. Symbols in the Landscape: Rock Art and Its Context. Conference Proceedings; Instituto Terra e Memória: Tomar, Portugal, 2015. [Google Scholar]
- Muñoz, E.; Ontañón, R.; Bayarri-Cayón, V.; Montes, R.; Morlote, J.M.; Bayarri-Cayón, V.; Herrera, J.; Gómez, A.J.G. La Cueva de Cueto Grande (Miengo, Cantabria-España). Un Nuevo Conjunto de Grabados Paleolíticos en la Región Cantábrica., in: ARKEOS | Perspectivas Em Diálogo, No 37. Symbols in the Landscape: Rock Art and Its Context. Presented at the XIX International Rock Art Conference IFRAO. 2015, pp. 945–967. Available online: http://www.apheleiaproject.org/apheleia/Articles/COLLADO%20et%20al%202015%20Symbols%20in%20the%20Landscape%20Rock%20Art%20and%20its%20Context.%20Arkeos%2037.pdf (accessed on 28 July 2021).
- Ontañón, R.; Bayarri, V.; Castillo, E.; Montes, R.; Morlote, J.M.; Muñoz, E.; Palacio, E. New discoveries of pre-Magdalenian cave art in the central area of the Cantabrian region (Spain). J. Archaeol. Sci. Rep. 2019, 28, 102020. [Google Scholar] [CrossRef]
- Montes, R.; Bayarri-Cayón, V.; Muñoz, E.; Morlote, J.M.; Ontañon, R. Avance al Estudio del Registro Gráfico Paleolítico de la Cueva de Solviejo (Voto, Cantabria, España). Cuadernos de Arte Prehistórico Número 3. 2017. Available online: https://cuadernosdearteprehistorico.com/index.php/cdap/article/view/21 (accessed on 28 July 2021).
- Ripoll-López, S.; Bayarri-Cayón, V.; Latova Fernández-Luna, J.; Herrera-López, J.; Benavides Miguel, M. El Proyecto de Investigación: Elaboración de una Sistema Gestor para la protección, puesta en valor y divulgación de Arte Rupestre y Estaciones Prehistóricas (SIGAREP I y II). X Jornadas de Patrimonio Arqueológico en la Comunidad de Madrid. Dirección General de Patrimonio Histórico. Museo Arqueológico Regional. Alcalá de Henares (Madrid). November 2014. Available online: https://www.researchgate.net/publication/283489912_El_Proyecto_de_Investigacion_Elaboracion_de_una_Sistema_Gestor_para_la_proteccion_puesta_en_valor_y_divulgacion_de_Arte_Rupestre_y_Estaciones_Prehistoricas_SIGAREP_I_y_II (accessed on 28 July 2021).
- Hatzopoulos, J.; Stefanakis, D.; Georgopoulos, A.; Tapinaki, S.; Pantelis, V.; Liritzis, I. Use of various surveying technologies to 3d digital mapping and modeling of cultural heritage structures for maintenance and restoration purposes: The tholos in Delphi, Greece. Mediterr. Archaeol. Archaeom. 2017, 17, 311–336. [Google Scholar]
- Jamhawi, M.; Alshawabkeh, Y.; Freewan, A.; Al-Gharaibeh, R. Combined Laser Scanner and Dense Stereo Matching Techniques For 3d Modelling Of Heritage Sites: Dar Es-Saraya Museum. Mediterr. Archaeol. Archaeom. 2016, 16, 185–192. [Google Scholar] [CrossRef]








| Type of Quadratic | Standard Equation | Figure |
|---|---|---|
| Sphere |  | |
| Elliptic Cylinder |  |
| Network Type | Parameters Defining the DATUM | No. Parameters Required |
|---|---|---|
| Altimetric network | 1 translation Tz | 1 |
| Triangulated planimetric network | 2 translations Tx, Ty, 1 rotation κ 1 scale factor S | 4 |
| Trilateral planimetric network | 2 translations Tx, Ty 1 rotation κ | 3 |
| 3D network (with distances) | 3 translations Tx, Ty, Tz 3 rotations ω, φ, κ | 6 |
| 3D network (without distances) | 3 translations Tx, Ty, Tz 3 rotations ω, φ, κ 1 scale factor S | 7 |
| Datum Parameters | |||||||
|---|---|---|---|---|---|---|---|
| Observations | Tx | Ty | Tz | S | |||
| Angles and Angular Readings | - | - | - | - | - | - | - |
| Distances | - | - | - | - | - | ✓ | ✓ |
| Azimuths | - | - | - | - | - | - | - |
| Zenith Angles | - | - | - | ✓ | ✓ | - | - |
| Elevations | - | - | - | - | ✓ | ✓ | ✓ |
| GNSS Positions | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| GNSS Baselines | - | - | - | ✓ | ✓ | ✓ | ✓ |
| Type of Network | Typical Redundancy Number |
|---|---|
| Radiations | 0 |
| Polygonal | 0.1–0.2 |
| Level | 0.2–0.5 |
| Trilateral Nets | 0.3–0.6 |
| Networks with Distances and Angular Readings | 0.5–0.8 |
| Resolution | 1/1 | 1/2 | 1/4 | 1/5 | 1/8 | 1/10 |
|---|---|---|---|---|---|---|
| Pts/400 g | 40,000 | 20,000 | 10,000 | 8000 | 5000 | 4000 |
| 5 | 0.0008 | 0.0016 | 0.0031 | 0.0039 | 0.0063 | 0.0079 |
| 10 | 0.0016 | 0.0031 | 0.0063 | 0.0079 | 0.0126 | 0.0157 |
| 15 | 0.0024 | 0.0047 | 0.0094 | 0.0118 | 0.0188 | 0.0236 |
| 20 | 0.0031 | 0.0063 | 0.0126 | 0.0157 | 0.0251 | 0.0314 |
| 25 | 0.0039 | 0.0079 | 0.0157 | 0.0196 | 0.0314 | 0.0393 |
| 30 | 0.0047 | 0.0094 | 0.0188 | 0.0236 | 0.0377 | 0.0471 |
| 40 | 0.0063 | 0.0126 | 0.0251 | 0.0314 | 0.0503 | 0.0628 |
| 50 | 0.0079 | 0.0157 | 0.0314 | 0.0393 | 0.0628 | 0.0785 |
| 60 | 0.0094 | 0.0188 | 0.0377 | 0.0471 | 0.0754 | 0.0942 |
| 70 | 0.0110 | 0.0220 | 0.0440 | 0.0550 | 0.0880 | 0.1100 |
| 76 | 0.0119 | 0.0239 | 0.0478 | 0.0597 | 0.0955 | 0.1194 |
| Resolution Pts/400 g | 1/1 40,000 | 1/2 20,000 | 1/4 10,000 | 1/5 8000 | 1/8 5000 | 1/10 4000 |
|---|---|---|---|---|---|---|
| 5 | 15,058 | 3765 | 941 | 602 | 235 | 151 |
| 10 | 3765 | 941 | 235 | 151 | 59 | 38 |
| 15 | 1673 | 418 | 105 | 67 | 26 | 17 |
| 20 | 941 | 235 | 59 | 38 | 15 | 9 |
| 25 | 602 | 151 | 38 | 24 | 9 | 6 |
| 30 | 418 | 105 | 26 | 17 | 7 | 4 |
| 40 | 235 | 59 | 15 | 9 | 4 | 2 |
| 50 | 151 | 38 | 9 | 6 | 2 | 2 |
| 60 | 105 | 26 | 7 | 4 | 2 | 1 |
| 70 | 77 | 19 | 5 | 3 | 1 | 1 |
| 80 | 59 | 14 | 3 | 2 | 1 | 1 |
| 90 | 46 | 11 | 2 | 1 | 0 | 0 |
| Time | Temperature (°C) | Pressure (hPa) | Humidity (%) |
|---|---|---|---|
| 10:15 | 16.7 | 1003 | 74 |
| 10:30 | 16.9 | 1003 | 74 |
| 10:45 | 17.0 | 1003 | 74 |
| 10:00 | 17.2 | 1003 | 73 |
| 11:15 | 17.4 | 1004 | 73 |
| 11:30 | 17.6 | 1004 | 73 |
| 11:45 | 17.9 | 1004 | 73 |
| 12:00 | 18.1 | 1004 | 73 |
| 12:15 | 18.2 | 1004 | 74 |
| 12:30 | 18.4 | 1004 | 74 |
| Confidence Interval at 1.5 mm | Empiric Confidence Interval | |||||||
|---|---|---|---|---|---|---|---|---|
| Out of Range | Out of Range | Empiric Conf. Interval 1/5 | Empiric Conf. Interval 1/4 | |||||
| Sphere 1 | 0.1823 | 0 | 0.6192 | 0 | 0.00035 | 0.7166 | 0.00037 | 0.7118 |
| Sphere 2 | 0.0056 | 0 | 0.1371 | 0 | 0.00053 | 0.2627 | 0.00025 | 0.5308 |
| Sphere 3 | 0.3849 | 0 | 0.1793 | 0 | 0.00032 | 0.3636 | 0.00067 | 0.2295 |
| Sphere 4 | 0.1735 | 0 | 0.2388 | 0 | 0.00067 | 0.2809 | 0.00056 | 0.6710 |
| Sphere 5 | 0.4130 | 0 | 0.9993 | 0 | 0.00071 | 0.2241 | 0.00128 | 0.7716 |
| Sphere 6 | 0.2013 | 0 | 0.4106 | 1 | 0.00090 | 0.2129 | 0.00116 | 0.2754 |
| Sphere 7 | 0.7345 | 0 | 0.6390 | 1 | 0.00113 | 0.3011 | 0.00109 | 0.3011 |
| Sphere 8 | 0.7749 | 1 | 0.6117 | 0 | 0.00150 | 0.7823 | 0.00126 | 0.2530 |
| Target 1 | 0.0008 | 0 | 0.1665 | 0 | 0.00021 | 0.8476 | 0.00037 | 0.2440 |
| Target 2 | 0.0076 | 0 | 0.3475 | 0 | 0.00023 | 0.3709 | 0.00054 | 0.2278 |
| Target 3 | 0.0581 | 0 | 0.0081 | 0 | 0.00033 | 0.0604 | 0.00027 | 0.2553 |
| Target 4 | 0.1366 | 0 | 0.0100 | 0 | 0.00036 | 0.3702 | 0.00021 | 0.7815 |
| Target 5 | 0.0131 | 0 | 0.4957 | 0 | 0.00067 | 0.7934 | 0.00039 | 0.9690 |
| Target 6 | 0.3546 | 0 | 0.4134 | 0 | 0.00060 | 0.4936 | 0.00048 | 0.0944 |
| Target 7 | 0.0077 | 0 | 0.1608 | 0 | 0.00058 | 0.7777 | 0.00101 | 0.0876 |
| Target 8 | 0.8822 | 0 | 0.6536 | 0 | 0.00041 | 0.9789 | 0.00055 | 0.7992 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bayarri, V.; Castillo, E.; Ripoll, S.; Sebastián, M.A. Control of Laser Scanner Trilateration Networks for Accurate Georeferencing of Caves: Application to El Castillo Cave (Spain). Sustainability 2021, 13, 13526. https://doi.org/10.3390/su132413526
Bayarri V, Castillo E, Ripoll S, Sebastián MA. Control of Laser Scanner Trilateration Networks for Accurate Georeferencing of Caves: Application to El Castillo Cave (Spain). Sustainability. 2021; 13(24):13526. https://doi.org/10.3390/su132413526
Chicago/Turabian StyleBayarri, Vicente, Elena Castillo, Sergio Ripoll, and Miguel A. Sebastián. 2021. "Control of Laser Scanner Trilateration Networks for Accurate Georeferencing of Caves: Application to El Castillo Cave (Spain)" Sustainability 13, no. 24: 13526. https://doi.org/10.3390/su132413526
APA StyleBayarri, V., Castillo, E., Ripoll, S., & Sebastián, M. A. (2021). Control of Laser Scanner Trilateration Networks for Accurate Georeferencing of Caves: Application to El Castillo Cave (Spain). Sustainability, 13(24), 13526. https://doi.org/10.3390/su132413526







