An Air Route Network Planning Model of Logistics UAV Terminal Distribution in Urban Low Altitude Airspace
Abstract
:1. Introduction
2. Models
2.1. Problem Description
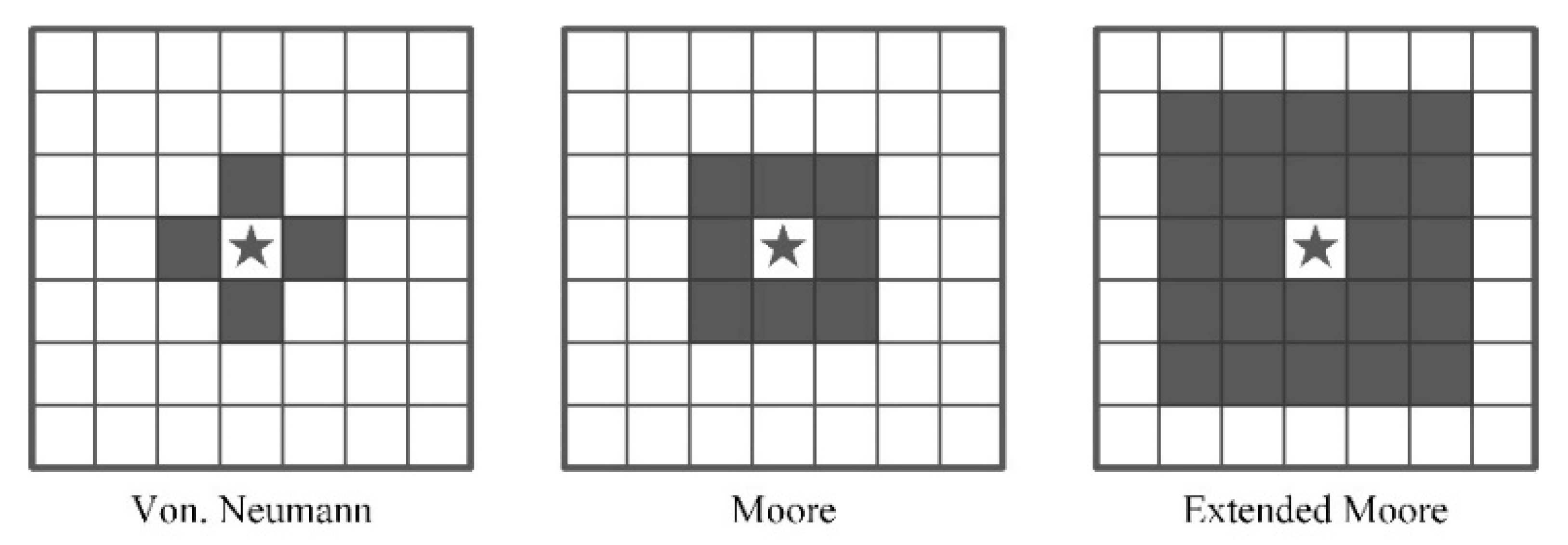
2.2. Airspace Grid
2.3. Single Air Route Planning Model of Logistics UAV
2.3.1. Objective Functions
2.3.2. Constraint Conditions
2.4. Air Route Network Planning Model of Logistics UAV
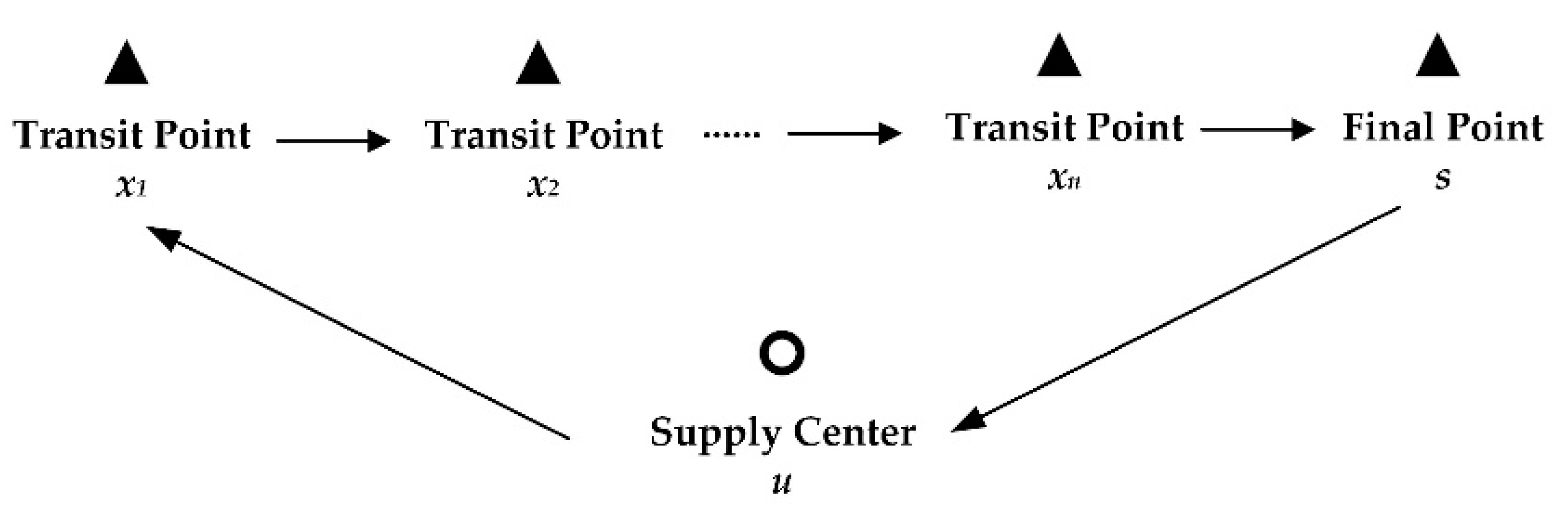
2.4.1. Related Conception
2.4.2. Objective Functions
2.4.3. Constraint Conditions
3. Algorithms
3.1. Single Air Route Generation Based on the Improved CA
3.1.1. Basic Principle
3.1.2. Parameters
3.1.3. Cost Function
3.1.4. Pseudo-Code


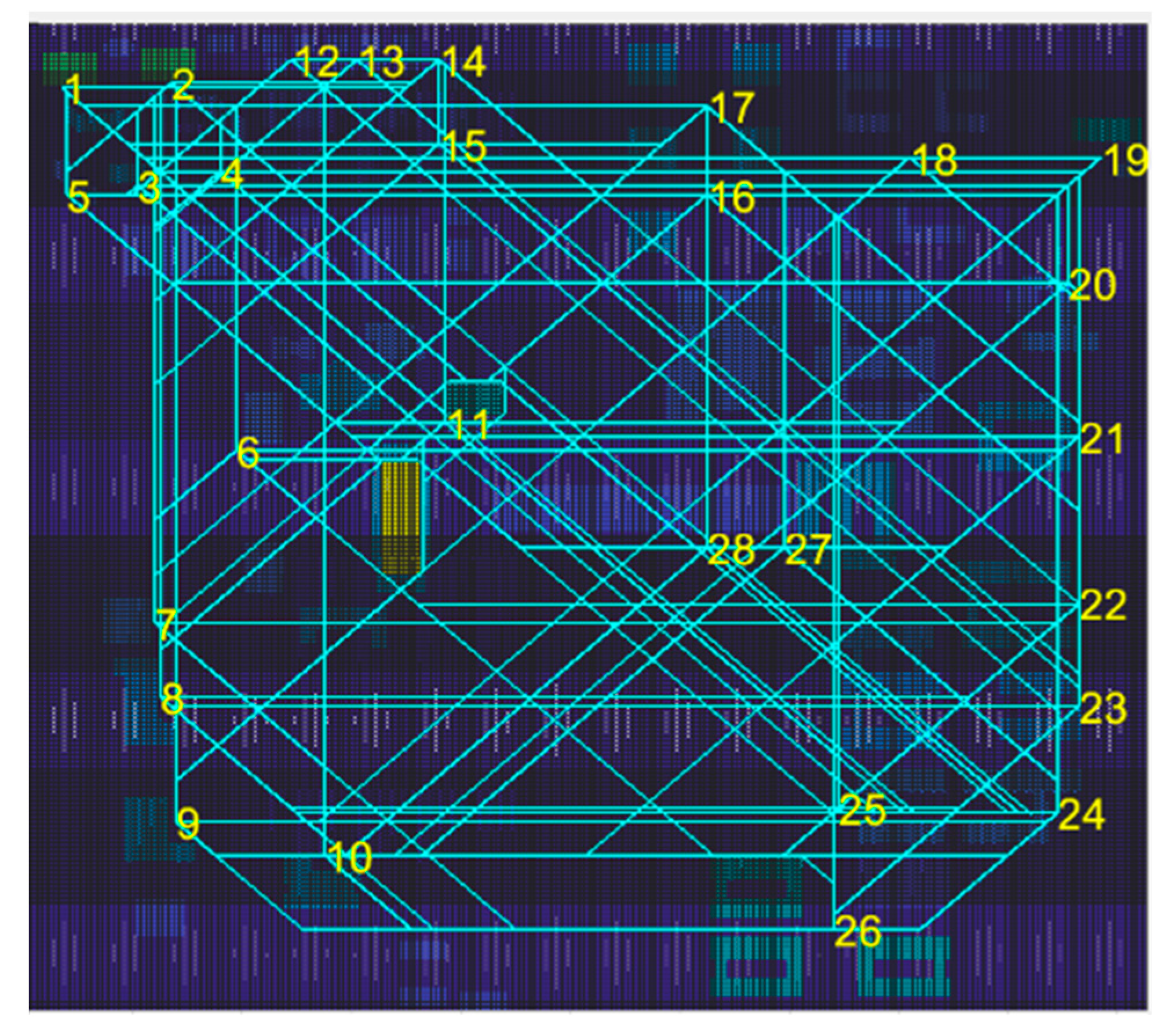
3.2. Air Route Network Planning Based on the Optimal Spanning Tree
3.2.1. Basic Principle
3.2.2. Algorithm Flow
4. Simulation and Analysis
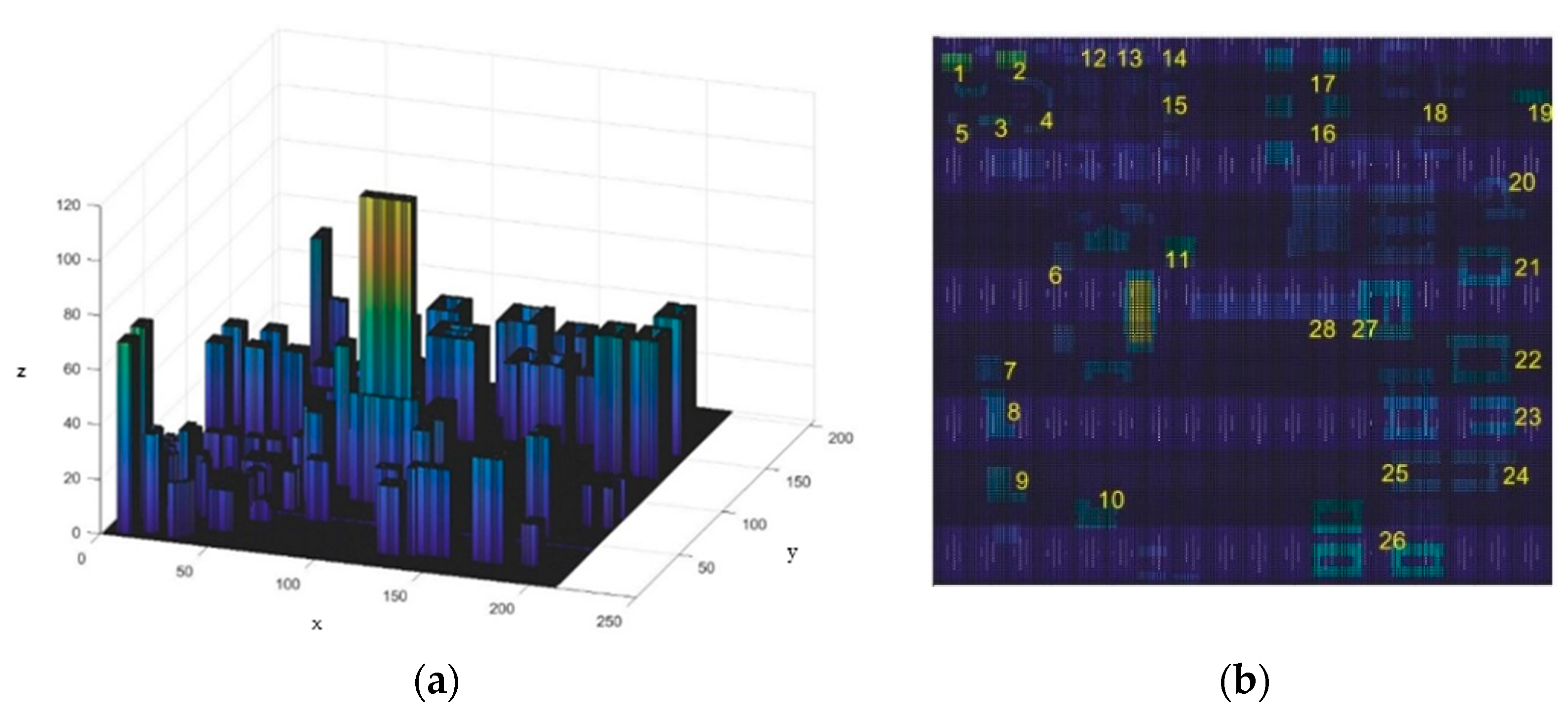
4.1. Simulation Environment
4.2. Performance of Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, C.L.; Qu, W.Q.; Li, Y.D.; Huang, L.Y.; Wei, P. Overview on traffic management of urban air mobility (UAM) with eVTOL aircraft. J. Trfc. Trnsp. Eng. 2020, 20, 35–54. [Google Scholar]
- Zhang, H.H.; Zou, Y.Y.; Zhang, Q.Q.; Liu, H. Review of Research on Future Urban Air Mobility (UAM) Management. Acta Aeronaut. Astronaut. Sin. 2020, 42, 1–28. [Google Scholar]
- Menouar, H.; Guvenc, I.; Akkaya, K.; Uluagac, A.S.; Kadri, A.; Tunce, A. UAV-Enabled Intelligent Transportation Systems for the Smart City: Applications and Challenges. IEEE Commun. Mag. 2017, 55, 22–28. [Google Scholar] [CrossRef]
- Holden, J.; Goel, N. Fast-Forwarding to a Future of on-Demand Urban Air Transportation. Available online: https://www.uber.com/elevate.pdf (accessed on 27 October 2016).
- Airbus. Blueprint for the Sky: The Roadmap for the Safe Integration of Autonomous Aircraft. Available online: https://storage.googleapis.com/blueprint/Airbus_UTM_Blueprint.pdf (accessed on 5 September 2018).
- Thipphavong, D.P.; Apaza, R.; Barmore, B.; Battiste, V.; Verma, S.A. Urban air mobility airspace integration concepts and considerations. In Proceedings of the Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Xu, H.X. Ehang Intelligent City Air Traffic System White Paper. Available online: https://www.ehang.com/app/%E4%BA%BF%E8%88%AA%E6%99%BA%E8%83%BD%E5%9F%8E%E5%B8%82%E7%A9%BA%E4%B8%AD%E4%BA%A4%E9%80%9A%E7%B3%BB%E7%BB%9F%E7%99%BD%E7%9A%AE%E4%B9%A6.pdf (accessed on 18 January 2020).
- Amazon.com Inc. Amazon Prime Air. Available online: http://www.amazon.com/b?node=8037720011 (accessed on 12 June 2021).
- Dew Atlas. DHL Parcelcopter Takes to Tanzanian Skies. Available online: https://newatlas.com/dhl-parcelcopter-africa/56663/ (accessed on 5 October 2018).
- Zhao, J.; Xie, F. Cognitive and artificial intelligence system for logistics industry. Int. J. Innov. Comput. Appl. 2020, 11, 84–88. [Google Scholar] [CrossRef]
- Zhao, Y.; Zheng, Y. Construction and optimization of flight mission profile of urban logistics UAV. Flt. Dyn. 2021, 39, 54–59. [Google Scholar]
- Gong, Y.H. Research on Air Route Network Planning Technology. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2015. [Google Scholar]
- Fan, H.D.; Ma, X.L.; Ye, W. Aircraft Low Altitude Penetration Route Planning Technology; National Defense Industry Press: Beijing, China, 2007. [Google Scholar]
- Zhang, Q.Q.; Xu, W.W.; Zhang, H.H.; Zou, Y.Y.; Chen, Y.T. Path planning for logistics UAV in complex low-altitude airspace. J. Beijing. Univ. Aeronaut. Astronaut. 2020, 46, 1275–1286. [Google Scholar]
- Zhang, H.H.; Li, H.; Liu, H.; Xu, W.W.; Zou, Y.Y. Path Planning for Logistics Unmanned Aerial Vehicle in Urban Area. J. Trnsp. Syst. Eng. Inf. Technol. 2020, 20, 22–29. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In MHS’95, Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; IEEE: Manhattan, NY, USA, 1995. [Google Scholar]
- Tang, X.L.; Li, L.M.; Jiang, B.J. Mobile robot SLAM method based on multi-agent particle swarm optimized particle filter. J. China Univ. Posts Telecommunications 2014, 21, 78–86. [Google Scholar] [CrossRef]
- Xu, C.C.; Liao, X.H.; Yue, H.Y.; Lu, M.; Chen, X.W. Construction of a UAV Low-altitude Public Air Route based on an Improved Ant Colony Algorithm. J. Geo-Inf. Sci. 2019, 21, 570–579. [Google Scholar]
- Xu, C.; Liao, X.; Ye, H.; Yue, H. Iterative construction of low-altitude UAV air route network in urban areas: Case planning and assessment. J. Geogr. Sci. 2020, 30, 1534–1552. [Google Scholar] [CrossRef]
- Duan, H.B.; Zhang, X.Y.; Wu, J.; Ma, G.J. Max-Min Adaptive Ant Colony Optimization Approach to Multi-UAVs Coordinated Trajectory Replanning in Dynamic and Uncertain Environments. J. Bionic Eng. 2009, 6, 161–173. [Google Scholar] [CrossRef]
- Wang, S.J.; Gong, Y.H. Research on air route network nodes optimization with avoiding the three areas. Saf. Sci. 2014, 66, 9–18. [Google Scholar] [CrossRef]
- Mccaskill, J.S.; Packard, N.H. Analysing Emergent Dynamics of Evolving Computation in 2D Cellular Automata. In Proceedings of the International Conference on Theory and Practice of Natural Computing, Kingston, ON, Canada, 9–11 December 2019. [Google Scholar]
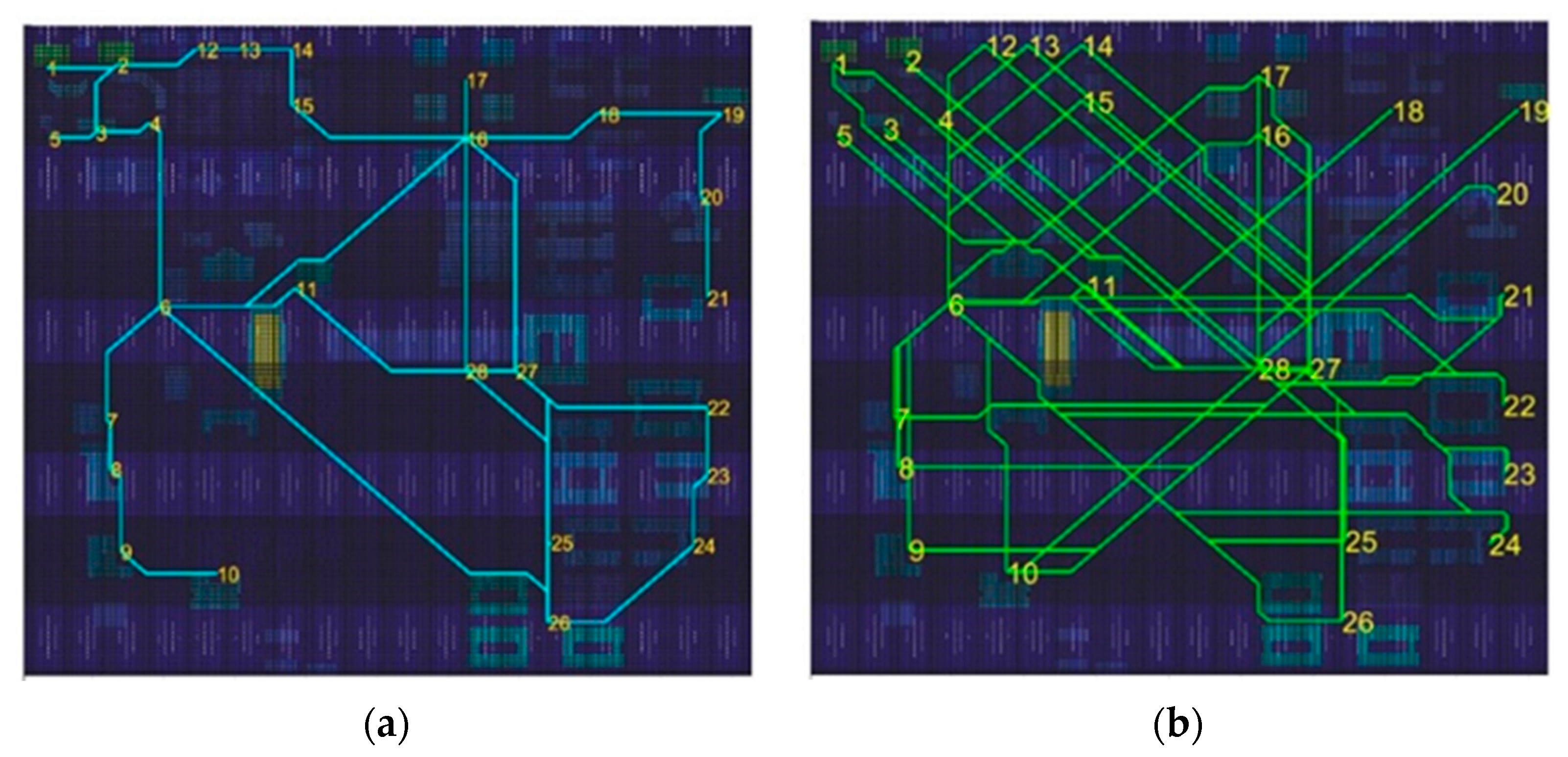
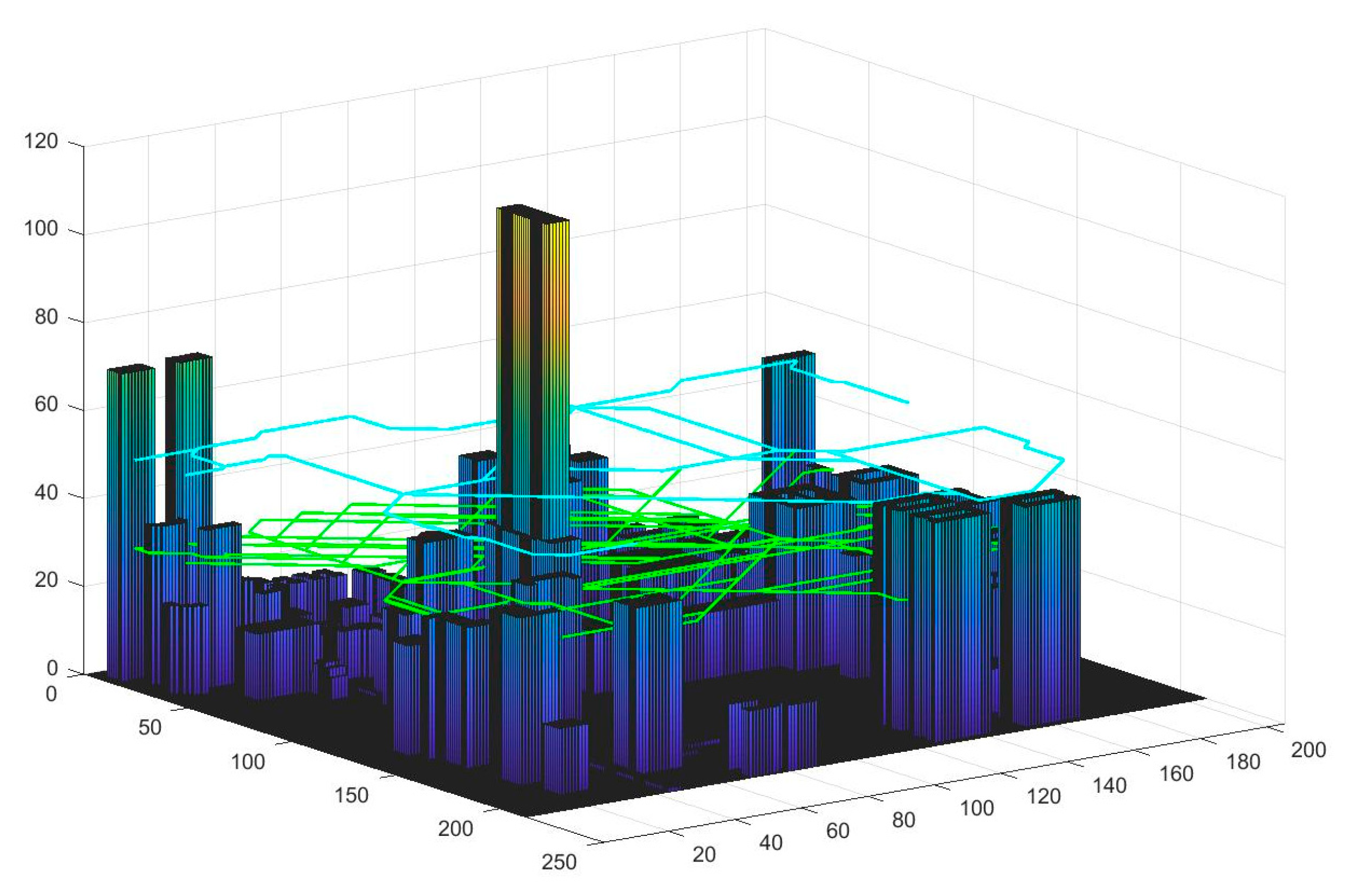
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Length of grid cell | 5 m | Width of grid cell | 5 m |
| Planned area | 1.0865 km2 | Supply centers’ number | 3 |
| Distance weight | 0.6 | Demand points’ number | 25 |
| Risk degree weight | 0.4 | Weight of segment gravity | 0.5 |
| Scaling factor of risk degree | 100 | Weight of segment distance | 0.5 |
| Maximum turning Angle | Scaling factor of segment | 100 | |
| Turning buffer distance | 5 m | Maximum range of UAV | 2800 m |
| Service providers’ number | 2 | UAV speed | 5 m/s |
| No. | Type | Coordinate | Node Importance | No. | Type | Coordinate | Node Importance |
|---|---|---|---|---|---|---|---|
| 1 | D | (14, 7) | 0.059638 | 15 | D | (26, 76) | 0.036818 |
| 2 | D | (13, 27) | 0.0601 | 16 | D | (37, 125) | 0.115057 |
| 3 | D | (35, 21) | 0.024546 | 17 | D | (18, 125) | 0.050571 |
| 4 | D | (32, 36) | 0.012273 | 18 | D | (29, 162) | 0.050571 |
| 5 | D | (37, 8) | 0.012273 | 19 | D | (29, 197) | 0.019176 |
| 6 | S of A | (92, 39) | 0.7 | 20 | D | (56, 191) | 0.019176 |
| 7 | D | (129, 24) | 0.024546 | 21 | D | (89, 193) | 0.019176 |
| 8 | D | (145, 25) | 0.024546 | 22 | D | (125, 193) | 0.019176 |
| 9 | D | (172, 28) | 0.024546 | 23 | D | (147, 193) | 0.019176 |
| 10 | D | (179, 55) | 0.024546 | 24 | D | (170, 189) | 0.019176 |
| 11 | D | (86, 77) | 0.024546 | 25 | D | (169, 149) | 0.019176 |
| 12 | D | (8, 49) | 0.02654 | 26 | D | (195, 148) | 0.115057 |
| 13 | D | (8, 61) | 0.02654 | 27 | S of A | (113, 139) | 0.3 |
| 14 | D | (8, 76) | 0.024546 | 28 | S of B | (113, 125) | 0.5 |
| Index | Traditional CA | Improved CA |
|---|---|---|
| Total time consuming/s | 1826 | 1410.1 |
| Average time consuming/s | 4.7 | 3.5 |
| Average number of search steps | 135 | 108 |
| Average single route length/m | 716 | 625.3 |
| Average flight time/s | 143.2 | 125.1 |
| Average number of turns | 17 | 6 |
| Index | Optimized Network |
|---|---|
| Total length | 7233.3 |
| Nonlinear coefficient | 1.25 |
| Segment number | 30 |
| Intersection number | 5 |
| Network connectivity | 2.14 |
| Network density | 6.657 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Zhang, H.; Li, Z.; Liu, H. An Air Route Network Planning Model of Logistics UAV Terminal Distribution in Urban Low Altitude Airspace. Sustainability 2021, 13, 13079. https://doi.org/10.3390/su132313079
Li S, Zhang H, Li Z, Liu H. An Air Route Network Planning Model of Logistics UAV Terminal Distribution in Urban Low Altitude Airspace. Sustainability. 2021; 13(23):13079. https://doi.org/10.3390/su132313079
Chicago/Turabian StyleLi, Shan, Honghai Zhang, Zhuolun Li, and Hao Liu. 2021. "An Air Route Network Planning Model of Logistics UAV Terminal Distribution in Urban Low Altitude Airspace" Sustainability 13, no. 23: 13079. https://doi.org/10.3390/su132313079
APA StyleLi, S., Zhang, H., Li, Z., & Liu, H. (2021). An Air Route Network Planning Model of Logistics UAV Terminal Distribution in Urban Low Altitude Airspace. Sustainability, 13(23), 13079. https://doi.org/10.3390/su132313079







