1. Introduction
Worldwide, there is an increasing trend toward the massive consumption of all electrical and electronic equipment (EEE) such as cell phones, tablets, smart televisions and computers [
1]. The increase in EEE consumption has been accelerated by several factors such as international trade conditions, decreasing cost of products, the rise of social media and continuous technological innovations [
1,
2,
3]. As a consequence, the EEE life cycles are shorter, the generation of waste of electrical and electronic equipment (WEEE) has increased over the past years, and it is expected that it will increase even more in the foreseeable future [
1,
4,
5,
6,
7]. In 2016, estimations suggest that global WEEE exceeded 44 Megatons (Mt); however, by 2019, the amount was surpassing a value of nearly 53.6 Mt worldwide and is projected to reach 74.7 Mt by 2030 [
2,
8]. In China alone, it is expected that the growth of obsolete electronic devices would average 18% per year, where the growth rate of some items like air conditioners would increase at rates of near 40% annually [
5,
9].
While several (developed) countries have improved their WEEE management systems, WEEE management remains a challenge for almost all countries since only 20% of the total global WEEE is currently recycled [
3,
4,
10,
11]. The main difficulty lies in the establishment of a fully functional and integrated disposal management system that is able to process and benefit from the WEEE recovered [
12,
13]. In emerging countries, the lack of suited WEEE management systems is especially pressing because environmental and human health impacts are directly linked to the exposure of WEEE toxic materials [
14,
15,
16,
17]. Additionally, the WEEE recycling industry brings opportunities for new sources of employment and development [
4,
6,
18].
To establish an integrated WEEE management system, it is necessary to consider its main stages: (i) product acquisition/gate keeping, (ii) collection, (iii) inspection and sorting and (iv) disposition [
19]. Each of these stages are subject to be optimized in their design and performance [
20]. That is why much of the literature on WEEE management systems has focused mainly on the optimization of one or two stages of the whole process [
5,
19,
21,
22]. However, there is the need of approaches that are able to address the coordination of these four stages in a scheme of integration capable of guaranteeing future and systemic performance [
5,
19,
21,
22]. Optimization techniques are ideal when the context of the problem is static, linear and deterministic, but as the modeling of the system incorporates time and nonlinear behavior, optimization techniques face limitations.
Given their capacity for eliciting complex systems nature, simulation techniques such as Discrete-Event Simulation (DES), System Dynamics (SD) and Agent-Based Simulation (ABS) are among the most used quantitative approaches. They are designed to understand the interaction between policy and behavior [
23]. DES and ABS approaches are more commonly implemented to address problems whose nature is operative and detail-oriented [
24]. Conversely, SD allows a strategic/tactical approach which is ideal for modeling the interaction of components in large systems [
4,
5,
19,
25]. Thus, all of them have been widely applied to improve the performance of either one or several WEEE management processes. However, the main use of SD and ABS simulation techniques is for the analysis of the process of generation and acquisition [
26,
27], while DES models are mainly used for modeling the processes of collection and disposition [
28]. Overall, these methodologies are able to incorporate the stochastic and dynamic nature of the WEEE management systems and also target the analysis considering either the strategic or the operative nature of the problem [
29,
30].
In modeling the interaction of the four aforementioned process, most of the literature uses SD as a primary methodology given its versatility to elicit complex and large systems [
25]. This is mainly due to the fact that SD modeling is well-suited for eliciting the effects of delays and feedbacks in the performance of interrelated variables describing complex behavior [
23]. The works by [
31,
32] can be taken as examples of this. The first study analyzes the long-term behavior of a closed-loop supply chain with recycling activities under scenarios of ecological motivations and technological innovations. The second work evaluates the impact of regulations, activities, and practices on closed-loop supply chains measuring their environmental and economic performance. In analyzing the WEEE management dynamics in specific geographical contexts, the work by [
33] uses SD to evaluate the impact of Chinese policies to promote WEEE recycling, while the work by [
34] pursues a similar analysis in Latin America. In addressing WEEE management problems, SD has been used to model the whole system from an aggregated perspective [
4,
5,
19,
25]. This approach conveys a holistic analysis of the integration of the WEEE management system stages. As a result, the SD approach provides future performance scenarios of waste recovery and profit, given the policy decisions and the system structure [
4,
5,
19,
25,
35].
In addition to the use of SD as a tool for operative or strategic planning, there is a recurrent topic of contributions addressing strategies to improve the recovery of WEEE. Consider, for instance, the work by [
5], which assesses the role of the informal sector as a main contributor in the process of collection of used electric and electronic devices in India. The work by [
36] uses an SD approach to explore the formalization of Brazilian waste pickers as a strategy for social empowerment and WEEE recolection. Similarly, the work by [
37] develops a novel approach on the use of SD to determine policies for used mobile phone recycling in China. In the same context, [
38] introduces an SD methodology to study the effects of retailer-led recycling of WEEE. The contribution by [
4] introduces a mobile phone case study which explores the main determining factors influencing electronic waste generation in Colombia. A recent contribution addresses the mitigation of lead pollution due to recycling in India [
25].
All these aforementioned contributions illustrate how the use of SD methodology is well established as a suited approach for guiding policy and strategy in WEEE management systems. However, there is the need of a new set of hybrid simulation models with the purpose of exploding the SD reach even further [
39]. This is because SD as a methodology has some limitations that prevent the capture of WEE management systems’ more realistic behavior. The simulation approach rests upon the use of constants. It models state or decision variables whose change is assumed to be constant over the time horizon of interest [
23]. This assumption constrains the use of SD to an aggregated representation of the WEEE managing systems, since tactical and operative processes require frequent updates of state and decisions variables. This updates need to convey the changes in products, process and market constrains [
24]. Then, the use of SD to understand the behavior of the WEEE managing systems over time is prone to provide an unrealistic representation of the real behavior as the time horizon of interest is larger. Thus, by using an SD modeling, there is a limitation in capturing how operative and tactical decisions in the short run affect the overall performance of the system in the long run [
24].
The WEEE management systems literature presents few examples of the integration of simulation and optimization as an approach to overcome the limitations of both methodologies. Consider, for instance, the work by [
35], which implements an ABS model seeking to maximize the profit of a remanufacturing company. Similarly, [
40] developed a DES simulation-based optimization model to determine the best locations for the collection centers and recycling plants for managing WEEE. The integration of SD and optimization for the improvement of WEEE management systems does not have examples that have been reported in the literature. However, the combination of both methodologies has been implemented in different fields as a complementary approach for policy analysis and systems design [
41]. Dangerfield and Roberts [
42] used optimization in SD as an approach to accomplish two main tasks: optimization to fit data and policy optimization to improve systems performance. In consequence, such efforts to integrate SD and optimization had produced a group of applications in several fields: coal industry [
43], energy consumption [
44] and water supply [
45]. Our study argues that given the widespread use of SD in the improvement of WEEE management systems, there is a need to develop more research illustrating the possibilities that optimization brings to the SD models and thus to the study of WEEE management systems. Therefore, an optimization-based simulation (OBS) approach is proposed as an approach able to overcome the limitations/assumptions that SD operates on. The purpose of the present research is to illustrate how such integration provides a more comprehensive and realistic approach for improving WEEE management performance.
This paper is organized as follows.
Section 2 describes the proposed OBS approach.
Section 3 describes the experimental validation of the proposed approach and the results of the Colombian mobile phone supply chain case study. Finally,
Section 4 presents the conclusions of this work and outlines some opportunities for further research.
2. Optimization-Based Simulation for WEEE Management
This section describes the proposed methodology integrating SD and optimization under an optimization-based simulation approach (OBS with iterative refinement [
46]). This is contrary to classical SD models, where system parameters are fixed in advance and remain constant during the entire simulation horizon. In order to accommodate changing conditions, OBS with iterative refinement models solve an optimization problem periodically to refine parameters and improve system performance. In the SD literature, this approach is also known as policy optimization [
42]. Optimization techniques that are embedded within SD models with this aim often include heuristic and metaheuristic methods [
47]. In contrast, we rely on an exact method for this iterative refinement. Following an OBS with iterative refinement approach, with SD it is possible to better represent the complexity (e.g., variable interactions, feedbacks and delays) of the WEEE generation process. At the same time, using the optimization periodically, the WEEE management system adjusts the repurchase price, flows, processing capacities and cost of WEEE processing.
2.1. Reverse Logistics Process
A description of the reverse logistics (RL) stages is necessary before introducing in detail the proposed OBS approach [
48,
49]. Following [
21,
50], we include the following stages of the RL process in the proposed OBS model:
Acquisition: is the inflow of the system, which consists of consolidating and repurchasing used products, components or materials.
Collection: is the process that moves products from the acquisition points to inspection/sorting facilities.
Inspection and sorting: consists of evaluating the general appearance and condition of the products. After inspection, the returned goods go to either the
processing stage or are diverted to an
export process for treatment and disposition abroad [
3].
Processing: includes different practices such as renovation through the repair and/or replacement of damaged parts, disassembly for cannibalization through the use of its components in different products, recycling for obtaining raw materials such as gold, silver, etc., and finally, elimination/deactivation for the proper final disposal of probably hazardous materials.
Disposition: is the final reintroduction of the products in an appropriated channel or market depending on the previous treatment. These markets include the following: remanufactured markets for second-hand products, component markets resulting from cannibalization and recycled materials markets. If there are no more possibilities of waste profiting, disposal is the final option.
2.2. System Dynamics Model
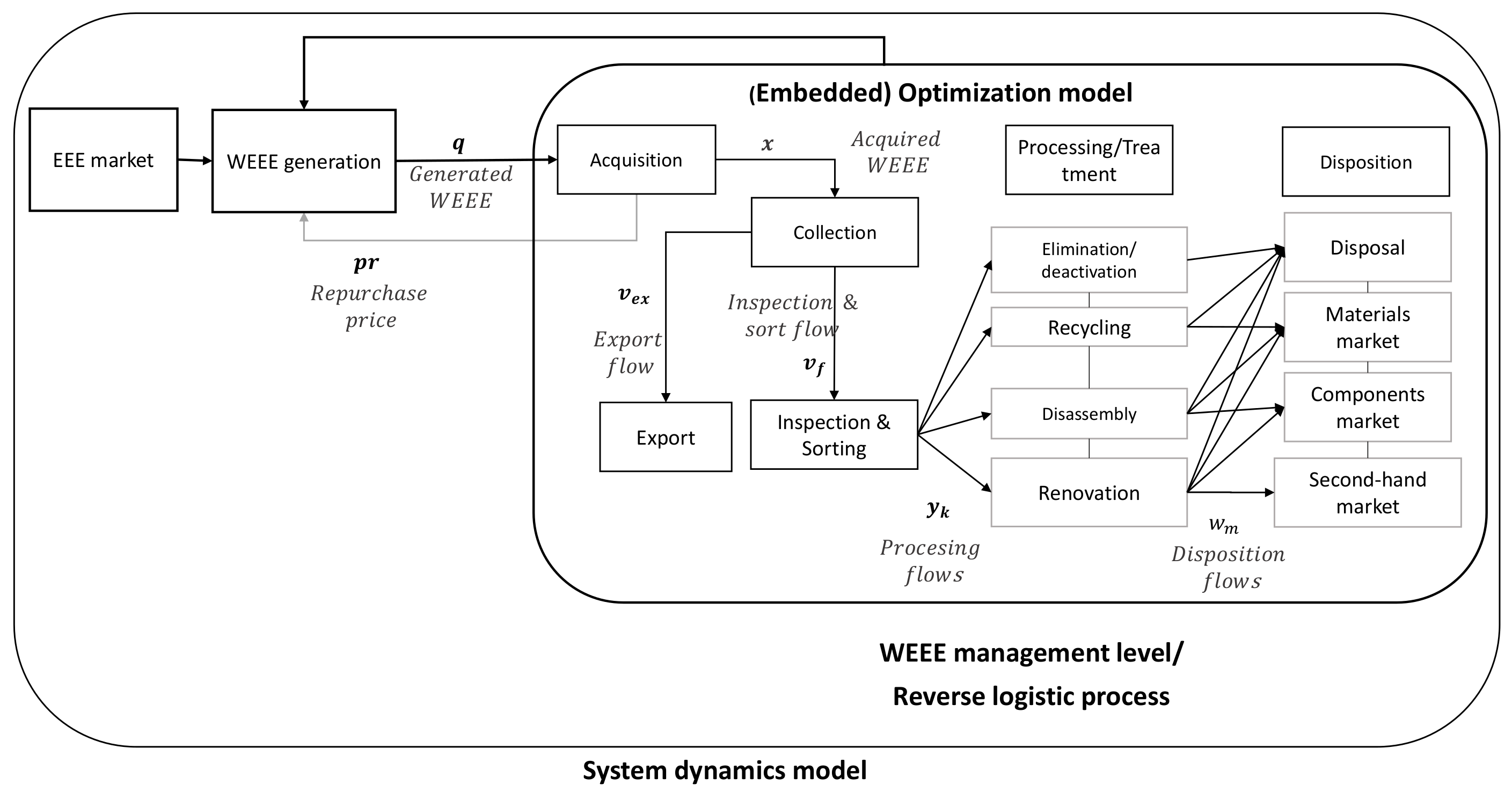
Figure 1 shows an aggregated representation of the flows and stocks structure of the EEE generation process and WEEE management system. For reference,
Appendix A.1 presents all nomenclature of the SD model.
In the WEEE management system, the market behavior depends on the flow of equipment and the interaction of supply (
) and demand (
) of EEE (units). The circulation of EEE in the market (
) represents the equipment in use. When the equipment leaves circulation, it enters a transitional storage level (
) or a final stage for disposition, corresponding to the disposal process (
). Meanwhile, the output of the storage level depends on the rate of user waste, and this increases the level of WEEE units generated (
). Finally, the acquisition of WEEE allows for the transition from
to the WEEE management level (
). Once WEEE enters the management level, its processing is performed following the different stages of the RL process described in
Section 2.1. It is at this level where the optimization model defines key operation parameters periodically.
Equation (
1) corresponds to the demand of EEE, namely, the number of people who purchase the equipment (Equation (2)). The flow
is equivalent to the amount of EEE sold per person per week.
The marketing of new and second-hand equipment (
and
, respectively) increases the supply of EEE (
) (Equation (
3)) and decreases it by its sales (
). Equation (4) represents the flow of new EEE, a stock that is subject to the rate of supply growth (
). Equation (5) shows how the flow of second-hand EEE is determined by the arrival of remanufactured equipment (
) thanks to the recovery management of WEEE.
The flow
represents the amount of equipment available to be sold (
) (Equation (
6)), whose value is the minimum quantity between the supply (
) and the equipment demanded by new customers (Equation (7)). Equations (8) and (9) explain how the new demand of EEE (
) depends on the number of customers (
) and their growth rate (
). The average amount of EEE per person (
) multiplies the resulting value to express it in units.
The circulation of EEE (
) (Equation (
10)) increases due to sales of new equipment and decreases by the following two flows: first, the flow of disposal (
) that depends on a disposal rate (
) (Equation (11)), and second, the disposition flow of WEEE (
), which is subject to the previous level of storage (Equation (12)).
The storage level in Equation (
13) (
) increases by the amount of equipment replaced (
, as defined in Equation (14), and decreases by the output of the accumulated EEE (
, as defined in Equation (
18). The replacement of equipment depends on two variables: the frequency of equipment replacement (
) and the rate of unit replacement according to customer behavior (
) (Equation (14)). Equation (15) indicates that the replacement rate varies due to the purchase price (
). This effect is represented by the GRAPH function (Equation (16)) that explains the average purchase price fluctuations (
) with respect to the initial average price of new EEE (
) (Equation (17)) at the beginning of the simulation.
The EEE output of the storage level (
) depends on the potential disposal rate (Equation (
18)). This rate varies according to the effect of the economic incentive (Equation (19)). This is modeled using a GRAPH function (Equation (20)). Equation (21) describes the main argument of Equation (20) in terms of the ratio of the repurchase price (
) (fixed periodically by the optimization model (
25)–(57)) and the average purchase price (
).
Equation (
22) corresponds to the generation of WEEE (
), which increases by the WEEE disposition flow (
) and decreases by the acquisition flow (
), and this is the first stage of WEEE management. The acquisition decision depends on the acquisition rate (
) (Equation (23)) as an input from the optimization model.
Finally, Equation (
24) represents WEEE stock, which increases by the acquisition of WEEE (
) and decreases thanks to each stage of the RL process denoted by
.
At this point, the optimization model determines all the decisions inside the WEEE management systems (repurchase price, acquired WEEE, export, processing and disposition flows and processing capacities).
Figure 2 shows the detailed RL process performed at the
level.
2.3. Optimization Model
The optimization model used for the iterative refinement of the SD model is a mixed-integer nonlinear program (MINLP). The decision variables (represented in grey in
Figure 2) of the MINLP cover the different stages of the RL process. Meanwhile, the WEEE generation process is represented according to the structure of the SD model as depicted in
Figure 1.
In the acquisition stage, the model makes three main decisions. The first one determines the repurchase price (
). The second one is the amount of WEEE generated (
q), which depends on the repurchase price as stated in Equation (16). The third decision is the amount of WEEE that enters the management system (
x), which determines the acquisition rate (
) in the SD model. Following [
51], we use a piecewise linear approximation to model the WEEE generation process (i.e., to connect different repurchase price values (
P) with their corresponding WEEE generation quantities (
Q) in a nonlinear fashion).
Table 1 presents an example of different
P values and their effect on
Q. In this piecewise linear approximation, we use binary variables (
) to select a single segment of it.
corresponds to the weights of the extreme points of each segment in the convex combination that defines the linear interpolation used to determine the values
and
q. This piecewise modeling option gives the flexibility to represent different customer behaviors that will be explored in the scenarios analyzed with the model.
Once WEEE enters the system and becomes part of the collection stage flow (x), the first decision of the RL process is to split it into two variables: WEEE sent to the inspection and sorting process () and WEEE exported to be treated in another country (). After inspection and sorting, the WEEE splits again into the different processing options () represented with variables (). In this stage, we assume a lexicographic order of the different processing options. This means that the decision making process has to assign the processing options in the aforementioned order based on increasing quality. That is, lower-quality WEEE cannot be processed with an upper-quality process. For instance, WEEE suitable for cannibalization (through the disassembly process) can also be treated for recycling or elimination. On the other hand, WEEE suitable for recycling can be treated in its own process or alternatively through elimination/deactivation. Finally, after the processing option or the export phase, the resulting (valorized) materials go to the corresponding alternative markets () for disposition according to set m.
Additionally, the MINLP model also decides on the technologies used for the different RL processes. This decision determines for each stage of the process the available capacity, the fixed costs and the avoided environmental burden [
52,
53]. To model these technology-choice decisions, we use binary variables for each stage of the RL process (with
for collection,
for inspection and sorting,
for exports and
for the
k-th treatment alternative). Here, index
i indicates the available options for each RL process. For ease of reference,
Appendix A.2 presents the sets, parameters and decision variables of the MINLP model.
2.3.1. Objective Function
The main goal of the optimization model is to maximize the total profit (Equation (
25)). This equation comprises four main components. The first one is the income obtained by the sales of the valorized waste (
) in each market at price
. The second one is a quadratic term that represent the cost of the repurchase of WEEE. The third component represents the variable costs of the RL process that depend on the quantities that are either exported at unitary cost
or processed through the different treatment options at unitary cost
. Finally, the last component sums up the fixed costs of the different processes determined by the technological choices (
z variables) and their corresponding cost (
).
2.3.2. Constraints
The optimization model considers the following constraints to describe the WEEE generation and acquisition process: the flows inside the RL process and the capacity of the WEEE management system.
WEEE generation process. The piecewise linear approximation that relates the repurchase price and the generation of WEEE variables is given in Equations (
26)–(32). The structure of these equations follows the approach described by [
51]. Equation (
26) ensures the choice of a single interval in the approximation. Equation (27) indicates that the point obtained is a convex combination of the extreme points of the interval. Equations (28)–(30) show the relations between the values of the variables
and
using a type-2 special ordered set (SOS2) [
51]. This is to calculate the convex combination where only two consecutive extreme points (in the same interval) are activated.
Finally, Equations (31) and (32) establish the values of the repurchase price and WEEE generation, respectively, using the linear combination of the extreme points of the selected interval.
Acquisition process. Two conditions must be met at this point. The amount of WEEE acquired cannot exceed the amount of WEEE generated (Equation (
33)). Additionally, a minimum acquisition amount is considered in Equation (34). In this equation,
represents a minimum percentage of the WEEE generated to ensure an inflow into the WEEE management system.
Balance constraints. This set of constraints ensures that the flow of elements is continuous through the RL process. Equation (
35) indicates the collection flow splitting into inspection/sorting and export processes. Likewise, Equation (36) indicates that after inspection, the flow of WEEE is split into the different processing options.
WEEE state constraints. These constraints define the appropriate processing alternatives according to the initial status of the WEEE determined after inspection and sorting, and consequently, its ideal market alternative. To model the WEEE entering status, we use parameters
to express the percentage of WEEE entering the system that is suitable for the treatment option
k (
, i.e., the options of the RL processing stage). Equations (
37) and (38) indicate the amount of WEEE that can enter each processing option according to their initial status. Particularly, Equation (39) ensures the amount of WEEE that has to be eliminated because no other option is available given its initial status (that is, the percentage of WEEE with status
). Finally, Equation (40) determines the amount of materials available in each market (
) after treated with the different processes (
). In this last equation, we resort to parameter
to represent the percentage of WEEE suitable for market
m after process
k. In a special case, the amount of WEEE that is directly exported and does not enter the internal RL process is given in Equation (41).
Capacity constraints. Equations (
42)–(49) define (respectively) the capacities of the different stages of the RL process according to the selected technologies. In these constraints, available capacities are represented by the following parameters:
for collection,
for inspection and sorting,
for export and
for the treatments of the processing stage.
Market demand. Finally, at the disposition stage, the amount of valorized material that goes to each market is limited by its demand (Equation (
50)).
Variable domain constraints. Constraints (
51) to (57) define the decision variables and their domains.
2.3.3. Environmental Indicator (Alternative Objective Function)
To measure the environmental effect of the system, we used the Avoided Environmental Burden (AEB) indicator. Introduced by [
53], the AEB is an alternative multidimensional metric to assess WEEE management systems that focuses its attention on the recovery of raw materials and the environmental benefits of recycling them. The dimensions of the AEB include cumulative energy demand, global warming potential, human toxicity potential, acidification and nutrification, among others. In our computational experiments, we explore the effect of the WEEE management system on profits if the AEB indicator is used as alternative objective function. To measure the AEB, we use the primary material extraction avoidance that comes from the different RL processes as presented by [
53]. Equation (
58) presents the AEB metric used in the proposed approach. Note that the AEB expression has a non-linear structure since it includes in each one of its terms the multiplication of the volume disposed in each market (
and
), its environmental burden (
), the AEB obtained (
and
) by the (technological) option chosen for the export stage and each treatment process (
).
2.4. OBS Implementation
Figure 3 summarizes the implementation of the OBS approach following the procedure depicted on it. The simulation step is equivalent to one week (
t), and the simulation ends when it reaches the time horizon (
T). In general, the steps described in
Figure 3 are:
Estimate WEEE generation. Initially, at the beginning of each cycle, SD is used to estimate the effect of several repurchase prices and its corresponding generation of WEEE according to the dynamics of the market described in
Section 2.2. This procedure updates the values used in the piecewise linear approximation of the optimization model (Equations (
26)–(32)) and in the GRAPH function for the WEEE generation process of the SD model (Equation (20)). In this step, we test iteratively increasing values of
(beginning at a given value
equal to 0) and store the corresponding values of
q.
Run the optimization model. Using the previous estimates, in this step, the optimization model (of
Section 2.3) chooses the optimal point for the repurchase price (
) and its corresponding generation of WEEE (
q). Simultaneously, the optimization model also specifies the flow entering the RL process
x and the flows inside it (variables
and
w), as well as the capacities of the different stages (variables
z).
Simulate the WEEE management system. At this step, the SD model (
Section 2.2) considers the output of the optimization model and uses the Euler integration method to model the interaction between flows and levels of the WEEE management system (
). At the WEEE generation level (
), the simulation uses again the estimates of the piecewise linear approximation (
) and represents the WEEE management level (
) with the RL processes inside it. The SD model runs under these conditions for a period of
weeks. Once the reoptimization period (
) is reached, the procedure runs step 1 for a new WEEE generation estimate and step 2 for a reoptimization of the RL process.
Report performance metrics. Once the simulation horizon (T) is reached, four different performance metrics of the system are reported: (i) the total profit, (ii) the total AEB, (iii) the total number of units of WEEE processed by the WEEE management system and (iv) the average repurchase price.
The SD model was implemented in Excel for its connection with the optimization model. The optimization model was developed on the OpenSolver platform [
54] using Couenne [
55] as the non-linear optimizer under the NEOS optimization service [
56]. The OBS approach was implemented through Visual Basic for Applications to automate the information transfer and to provide the end-user with a visual interface where it is possible to select the conditions of the desired experimental runs [
57].
4. Conclusions and Perspectives
This paper presents an OBS approach that allows the design of sustainable WEEE management system policies. By integrating optimization and system dynamics in the hybrid approach described in this paper, the analysis profits from the complementary strengths of each methodology. Optimization methodologies find optimal solutions in defined and limited sets of time. The simulation describes the behavior of polices over time, which are unable to optimally self-correct. The model presented here is an example of how the OBS approach could be implemented to tackle interdependent strategic and systemic problems governed by feedback and nonlinearities such as those of WEEE management systems and the circular economy.
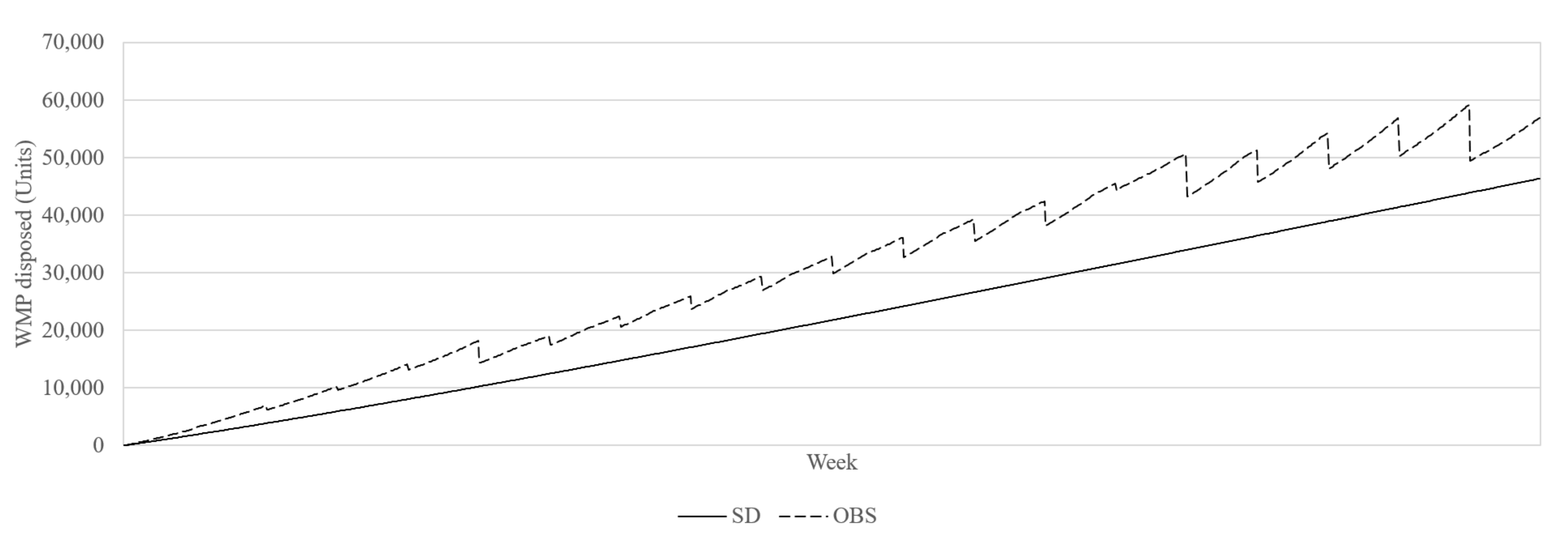
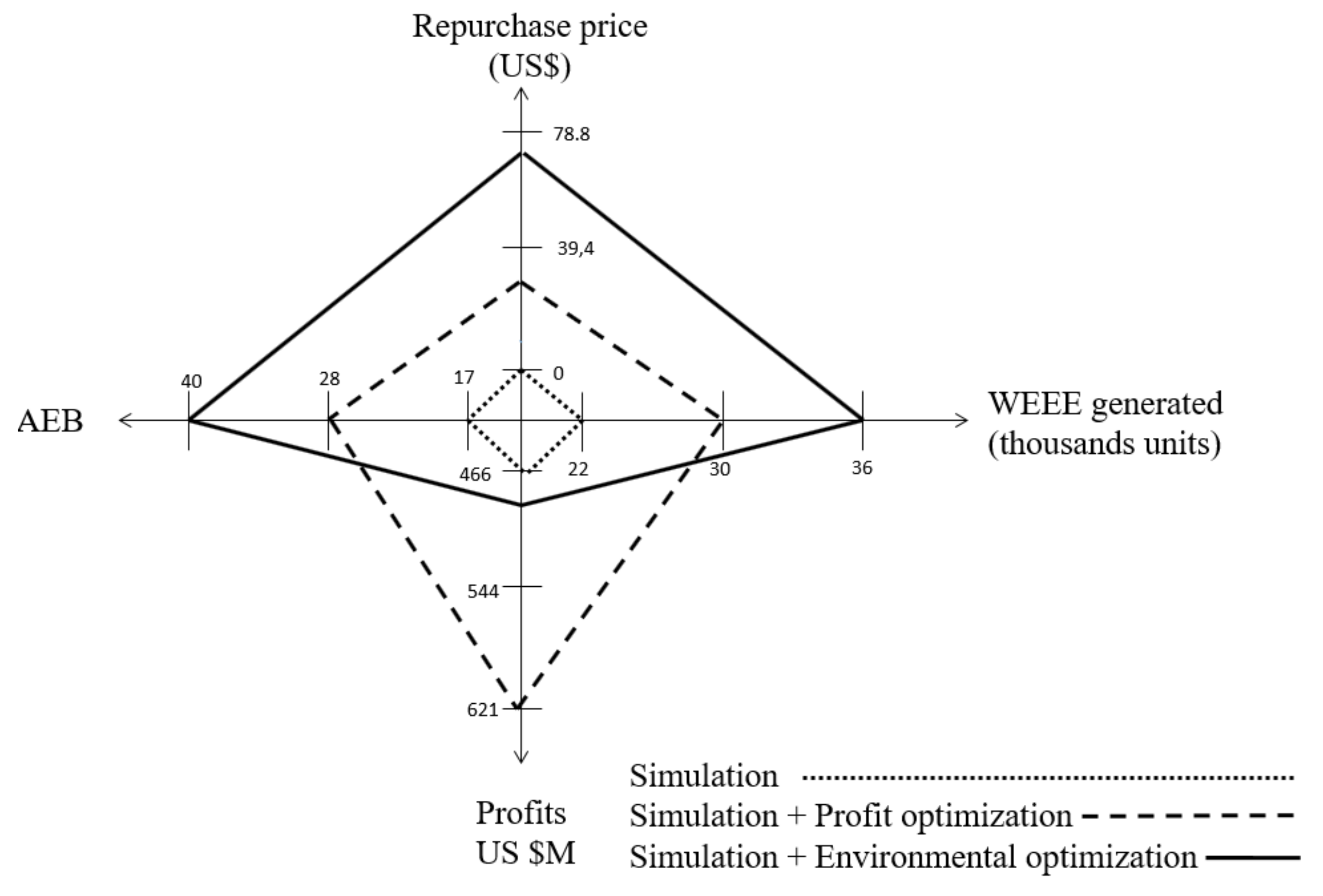
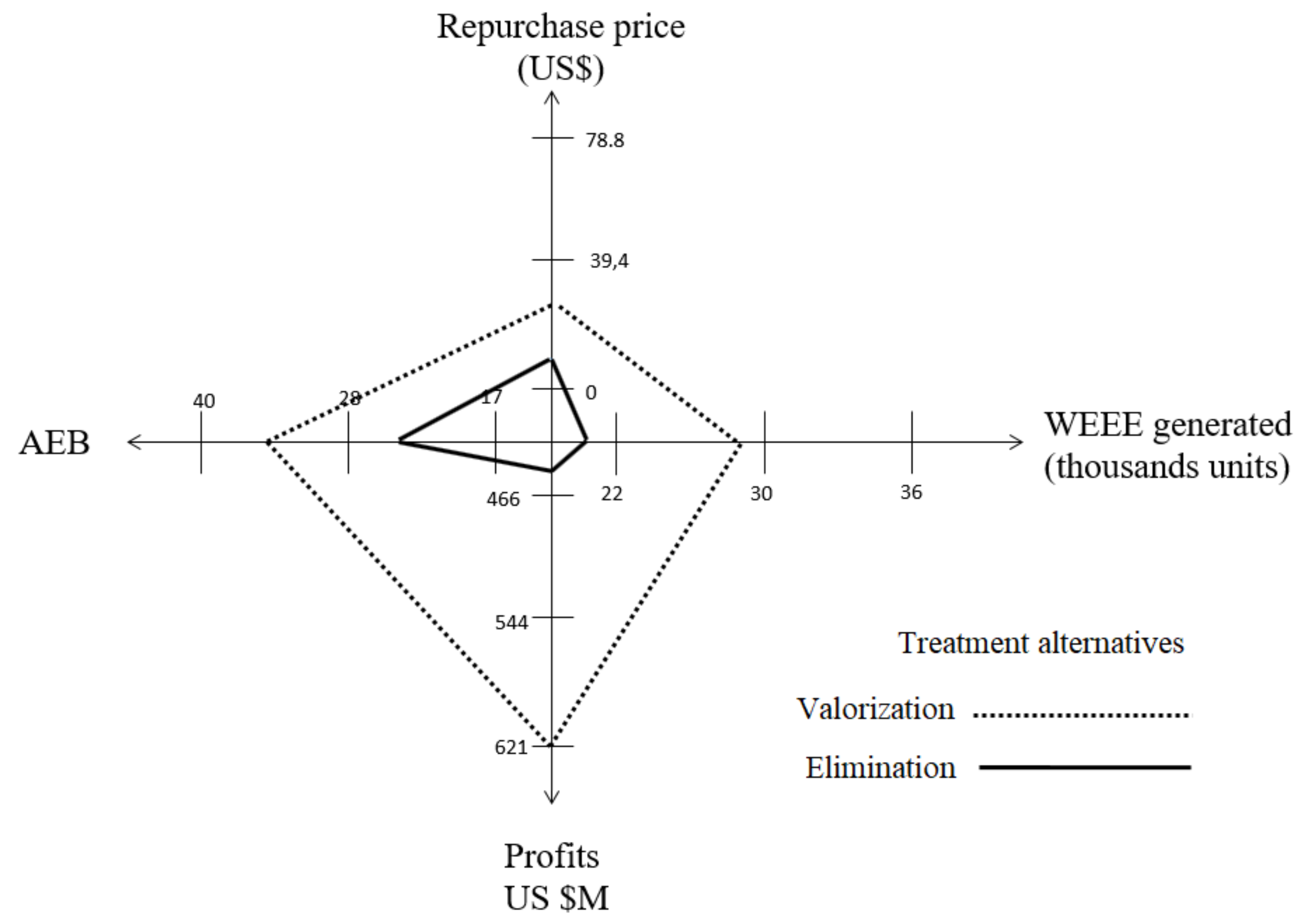
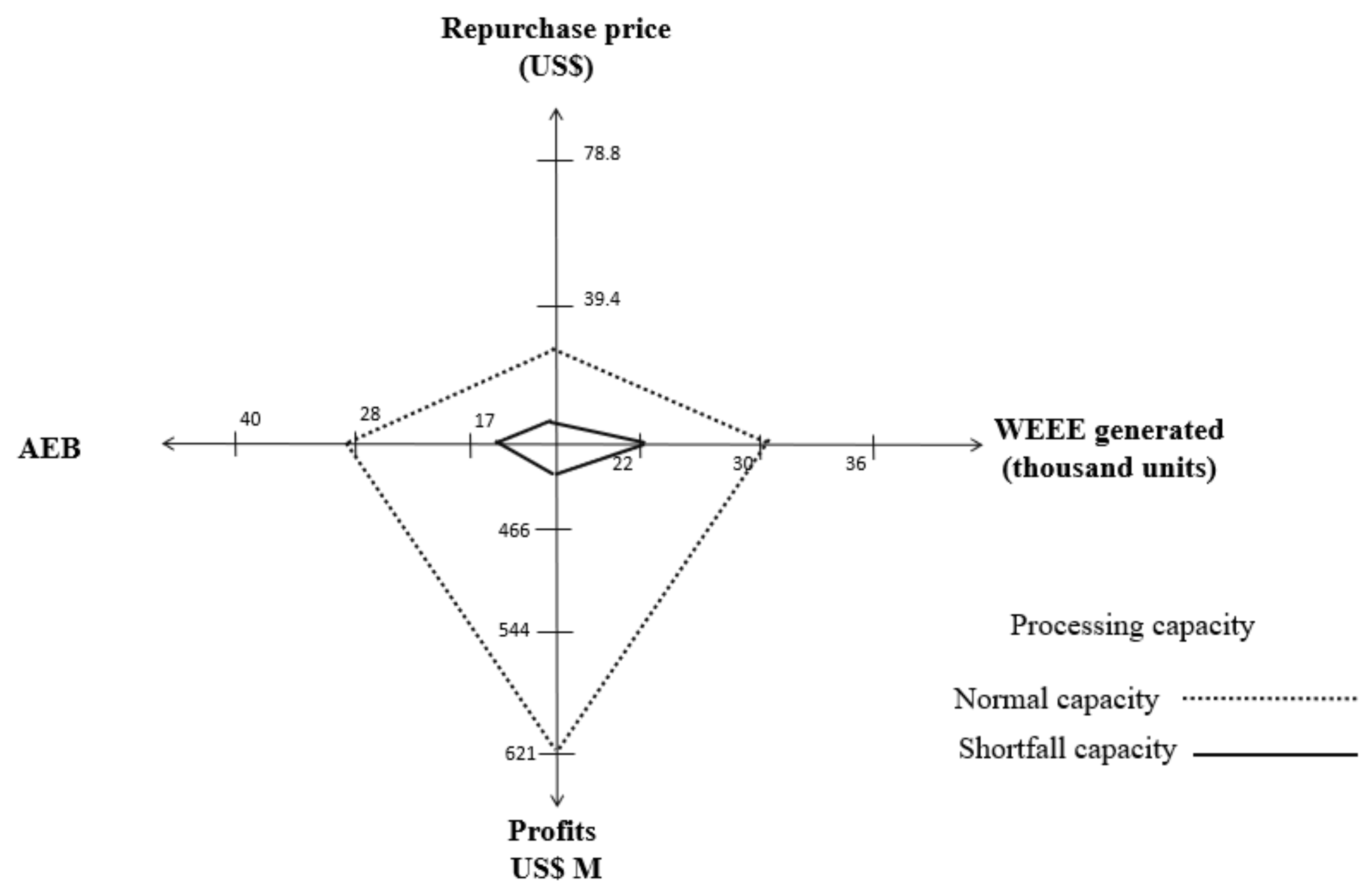
The computational results in a case study based on WEEE from Colombian mobile phones illustrates how an approach solely based on simulation (under the widely used system dynamics paradigm) is unable to capture the operative-strategic nature of the system and perform optimal parameter updates. In contrast, the OBS approach of this paper outperforms the SD approach in several dimensions. In general, it is able to obtain 33% more profits and 65% more environmental benefits mainly obtained by a 36% greater quantity of WEEE entering the system to be treated and valorized.
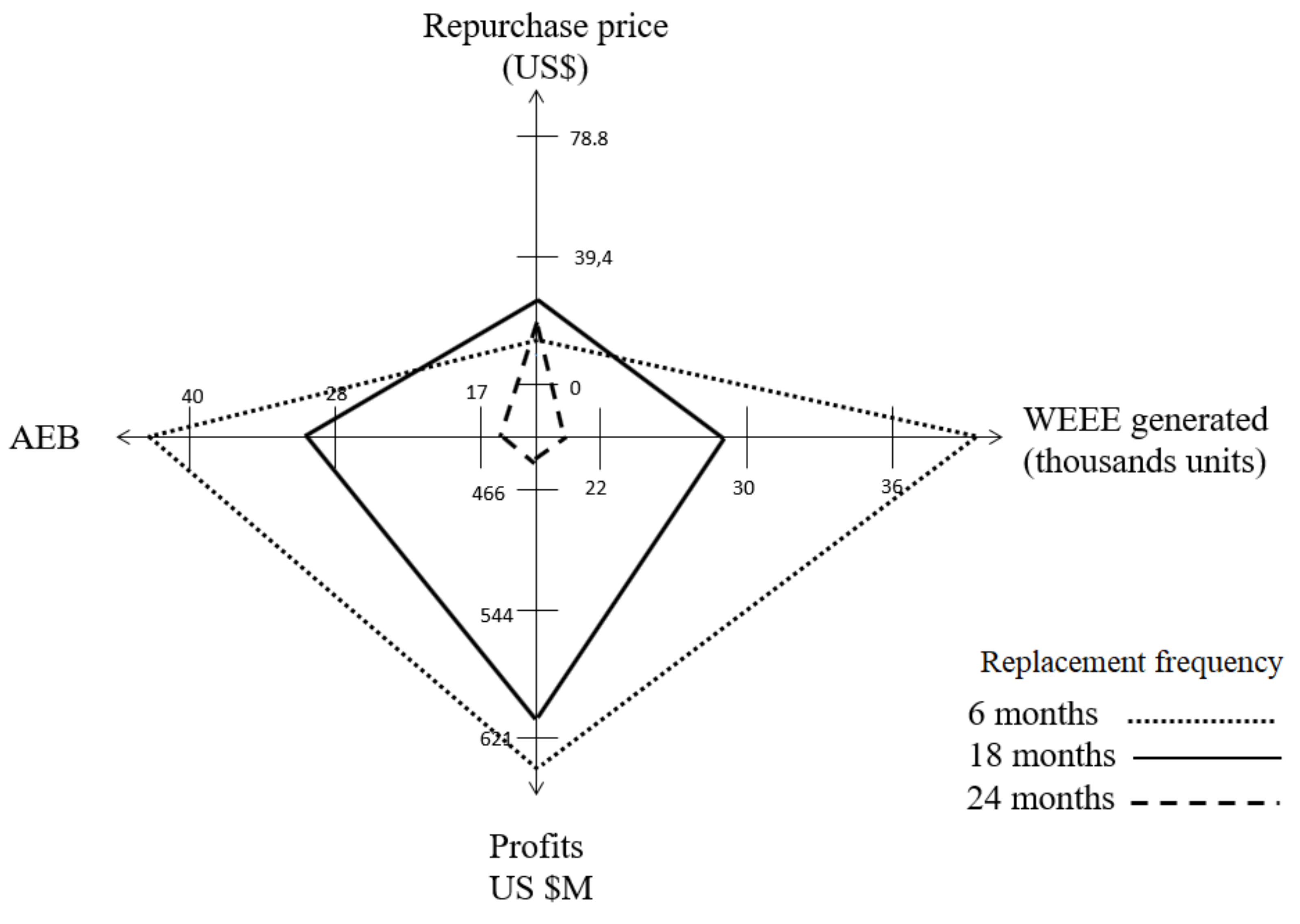
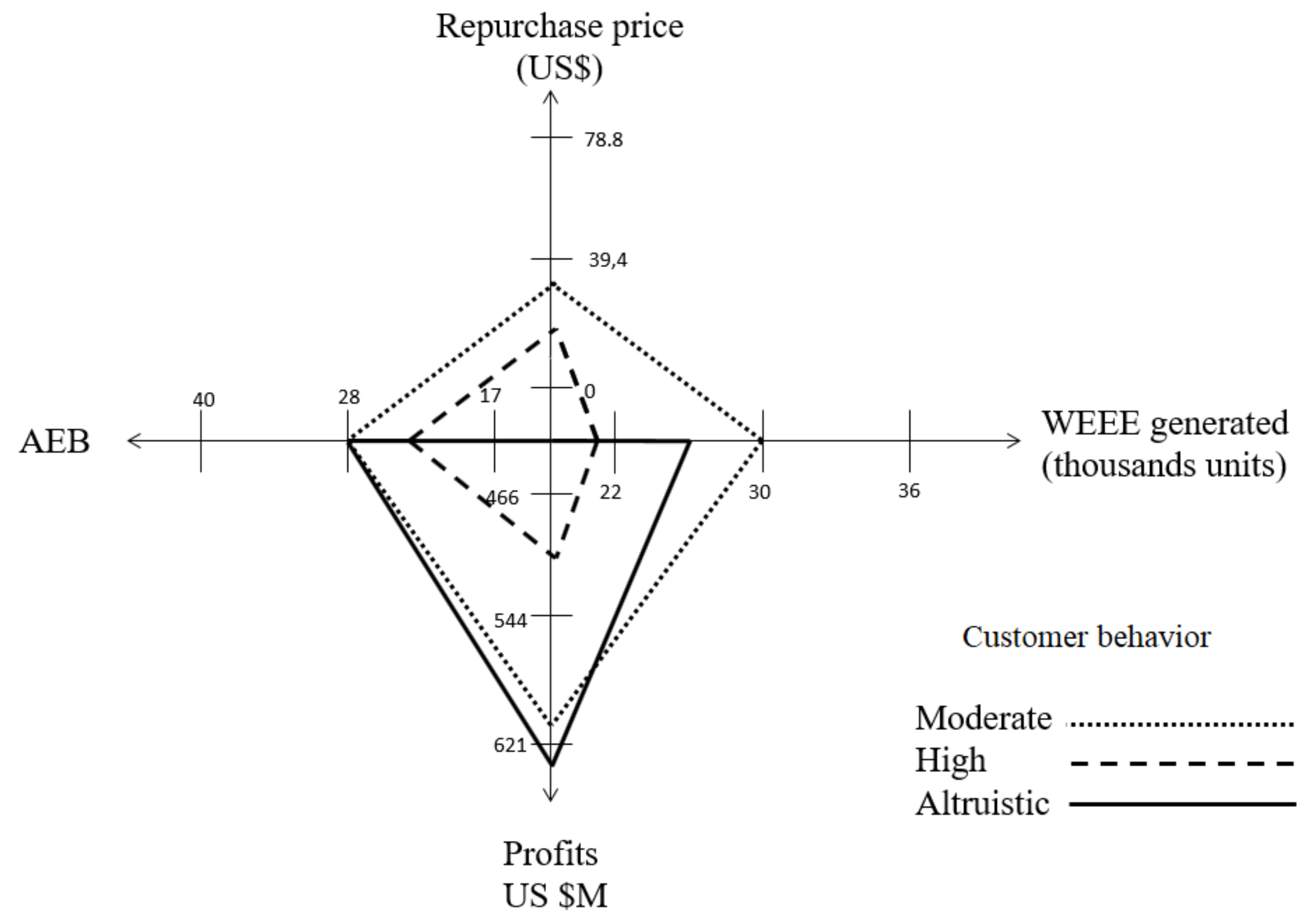
Moreover, by dynamically adjusting the repurchase price of WEEE and the structure (flows and capacities) of the reverse logistics process, the OBS is capable of positively reacting to a wide variety of scenarios with different replacement frequencies, customer expectations towards an economic incentive or different prevailing alternatives in the treatment of WEEE and processing capacities. The analysis of these scenarios allows the identification of the main drivers used in the design of optimal WEEE management system policies. The results presented here suggest that a maximization of profits can yield both economic profits and environmental savings in this kind of industry. The model suggests that the cornerstone of the WEEE management system is the replacement rate which is influenced by two main drivers: the frequency of replacement and the customer repurchase price expectations.
The OBS approach proposed in this paper can be extended in different ways. The first possible extension is considering a bi-objective model that explicitly includes the economic/environmental trade-off. This extension will need a multi-objective approach for the optimization component. Another possible extension is to include randomness into the SD model to better describe some of the system elements (e.g., WEEE generation, status and prices). Finally, the role of the informal sector (an important factor in developing economies [
70,
71,
73]) could be added to the system dynamics model.