Superiority of Hybrid Soft Computing Models in Daily Suspended Sediment Estimation in Highly Dynamic Rivers
Abstract
1. Introduction
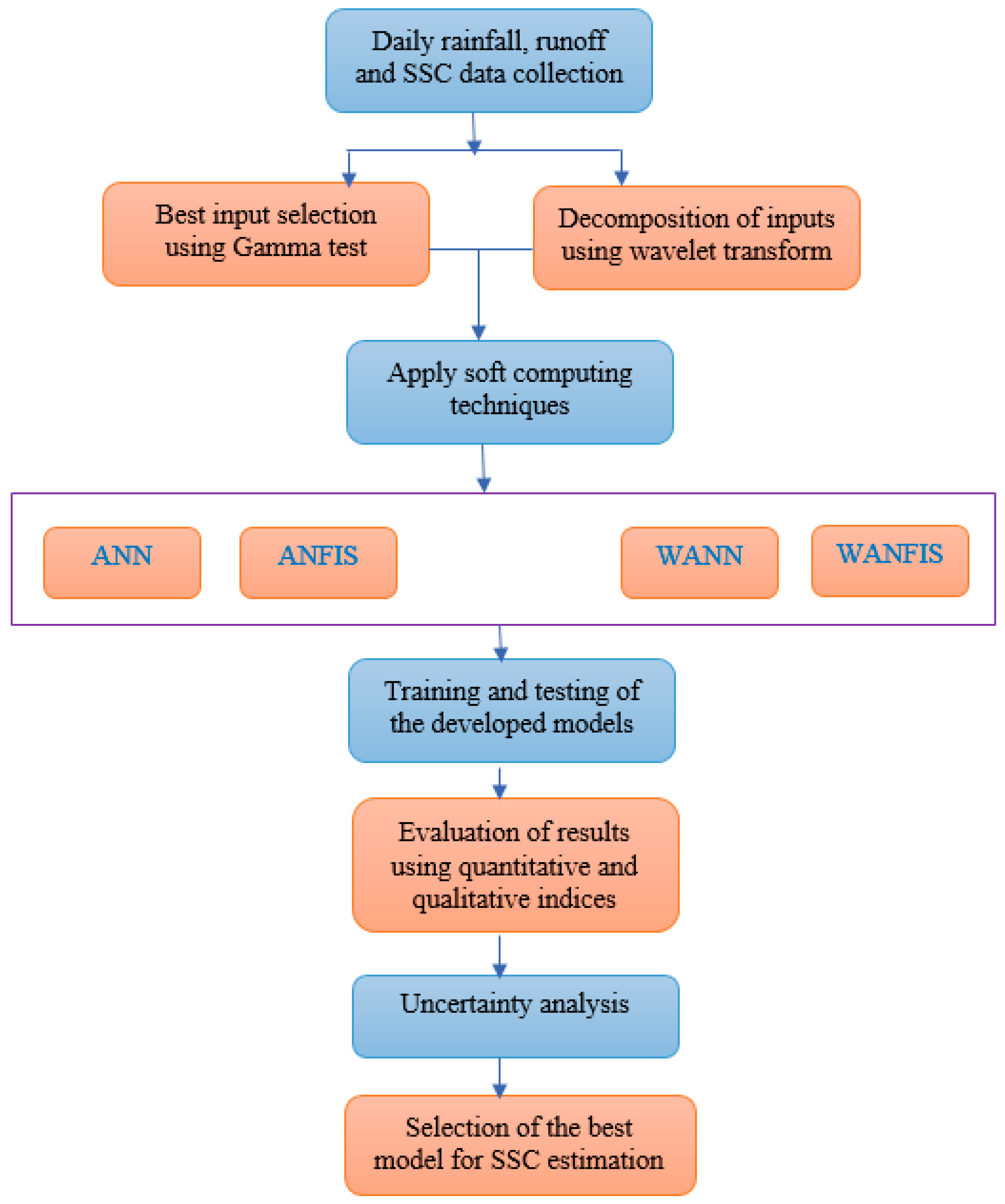
2. Materials and Methods
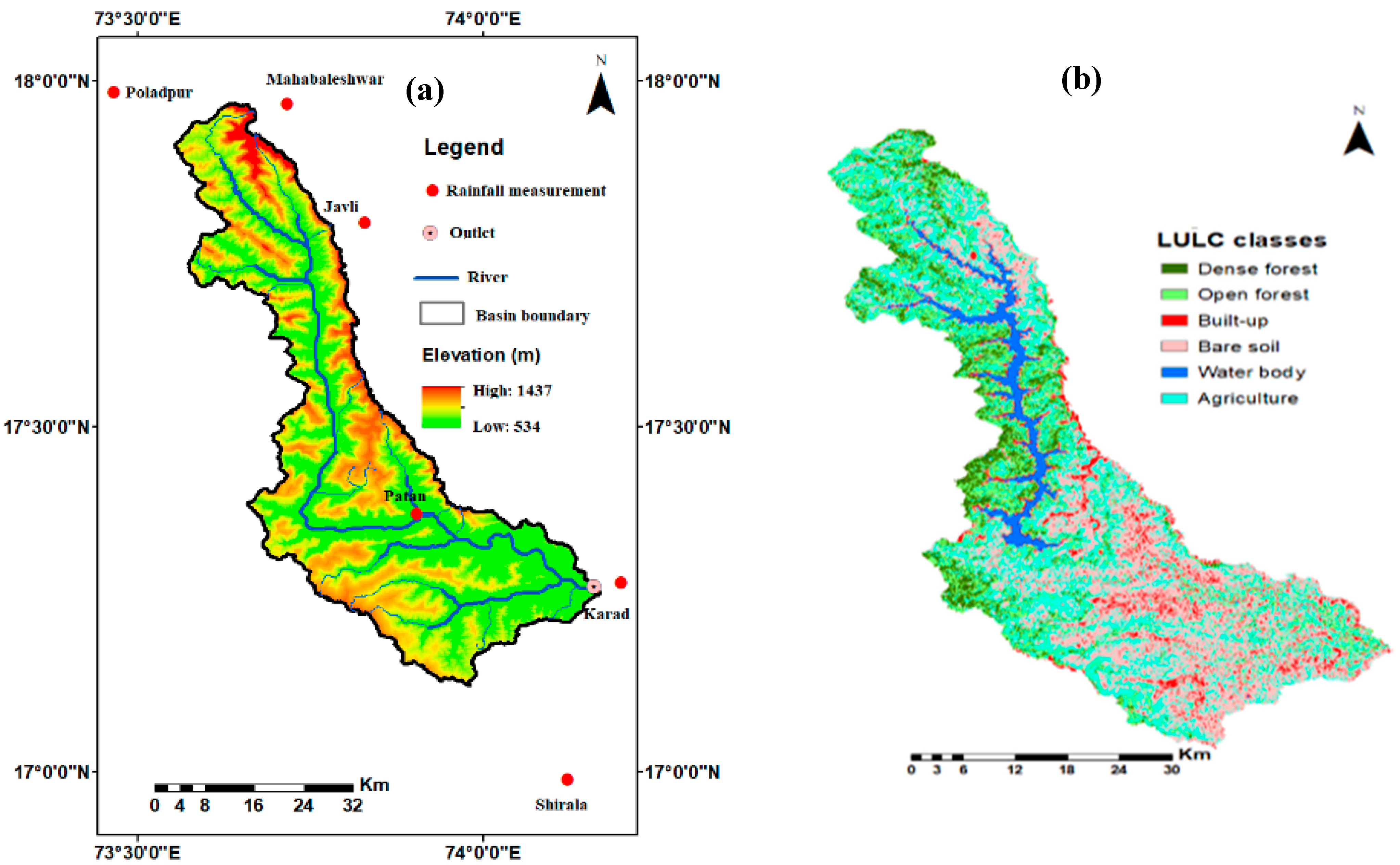
2.1. Study Area and Data Collection
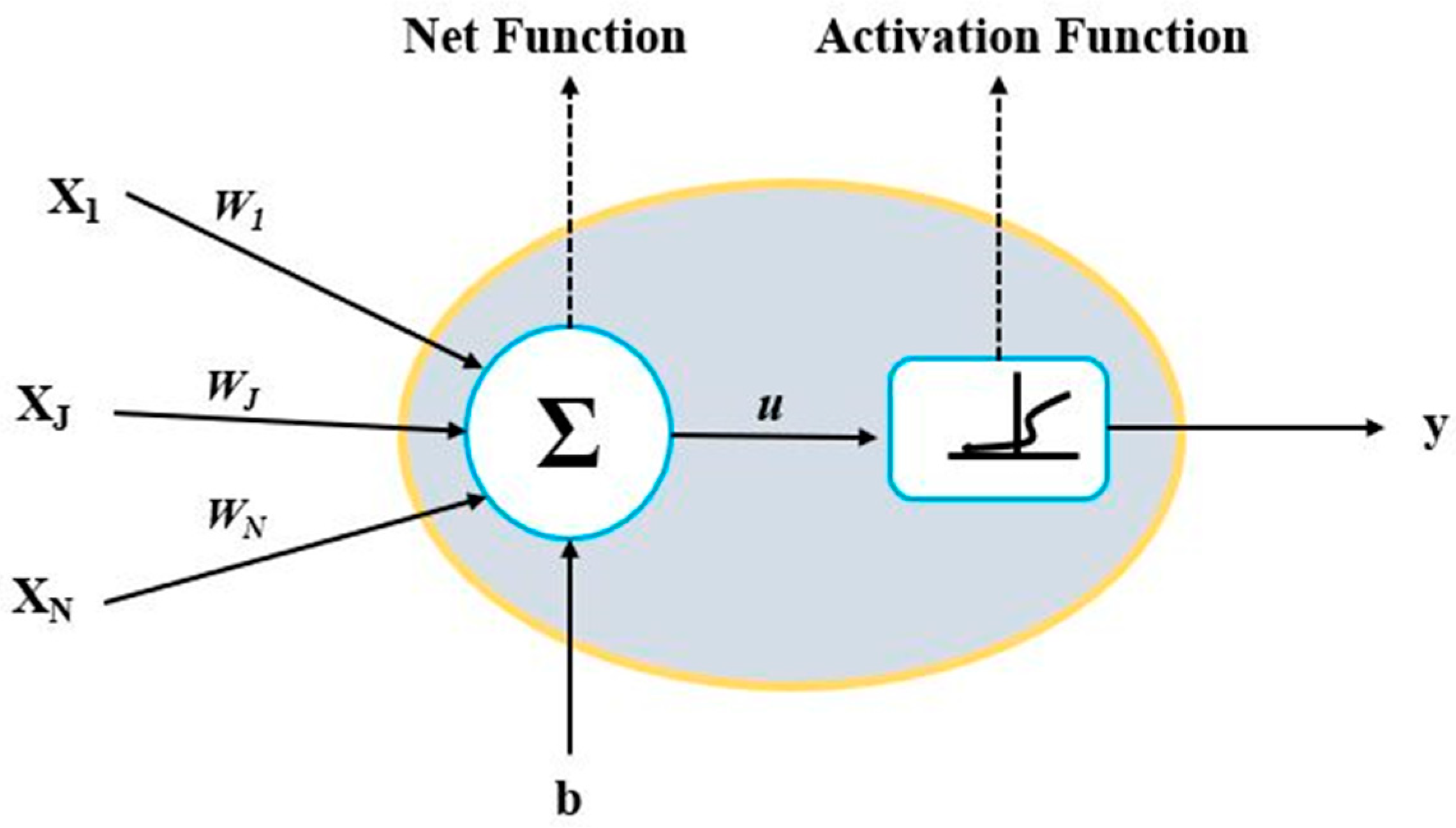
2.2. ANN
2.3. ANFIS
2.4. Subtractive Clustering
2.5. Wavelet Transform
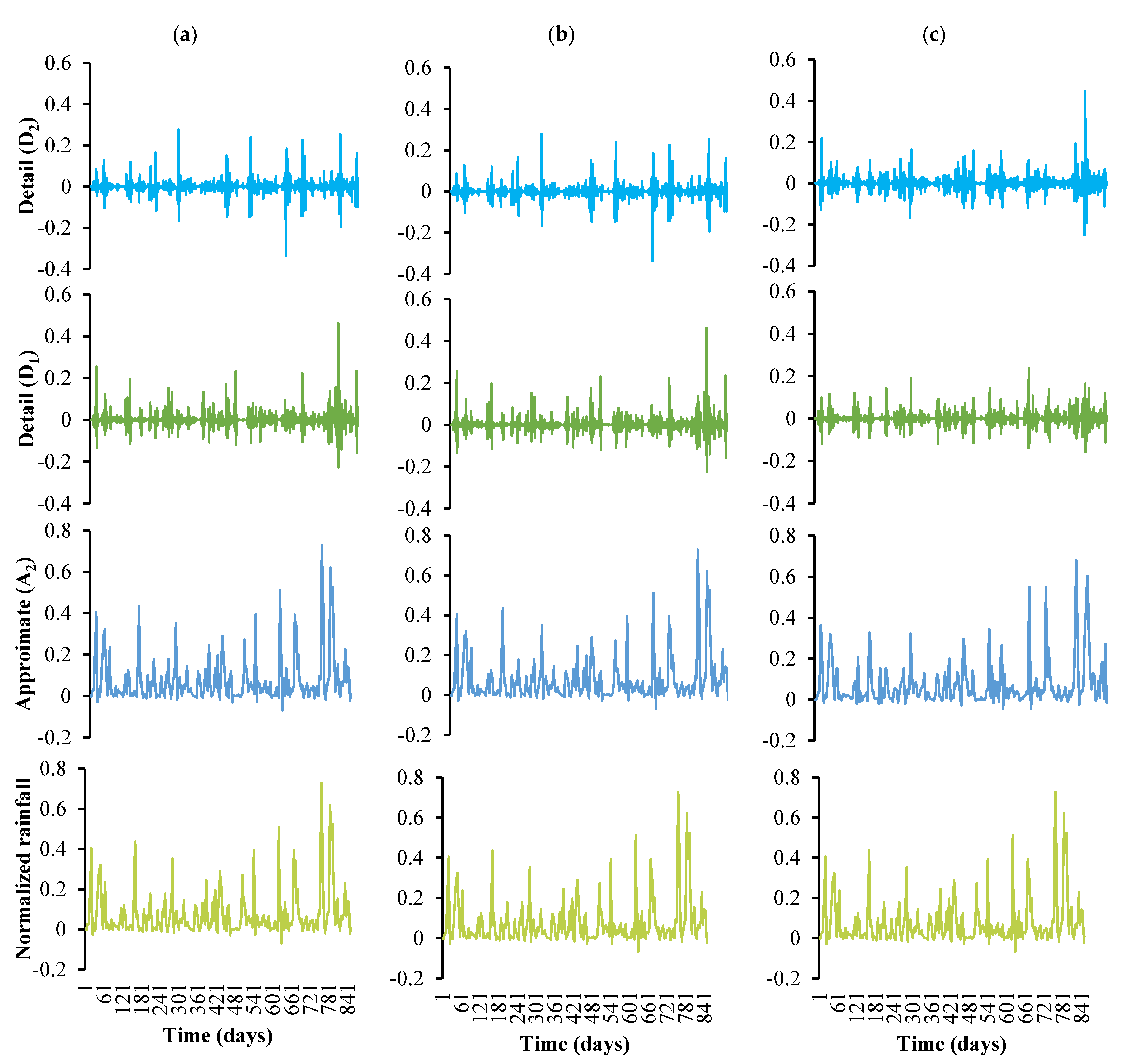
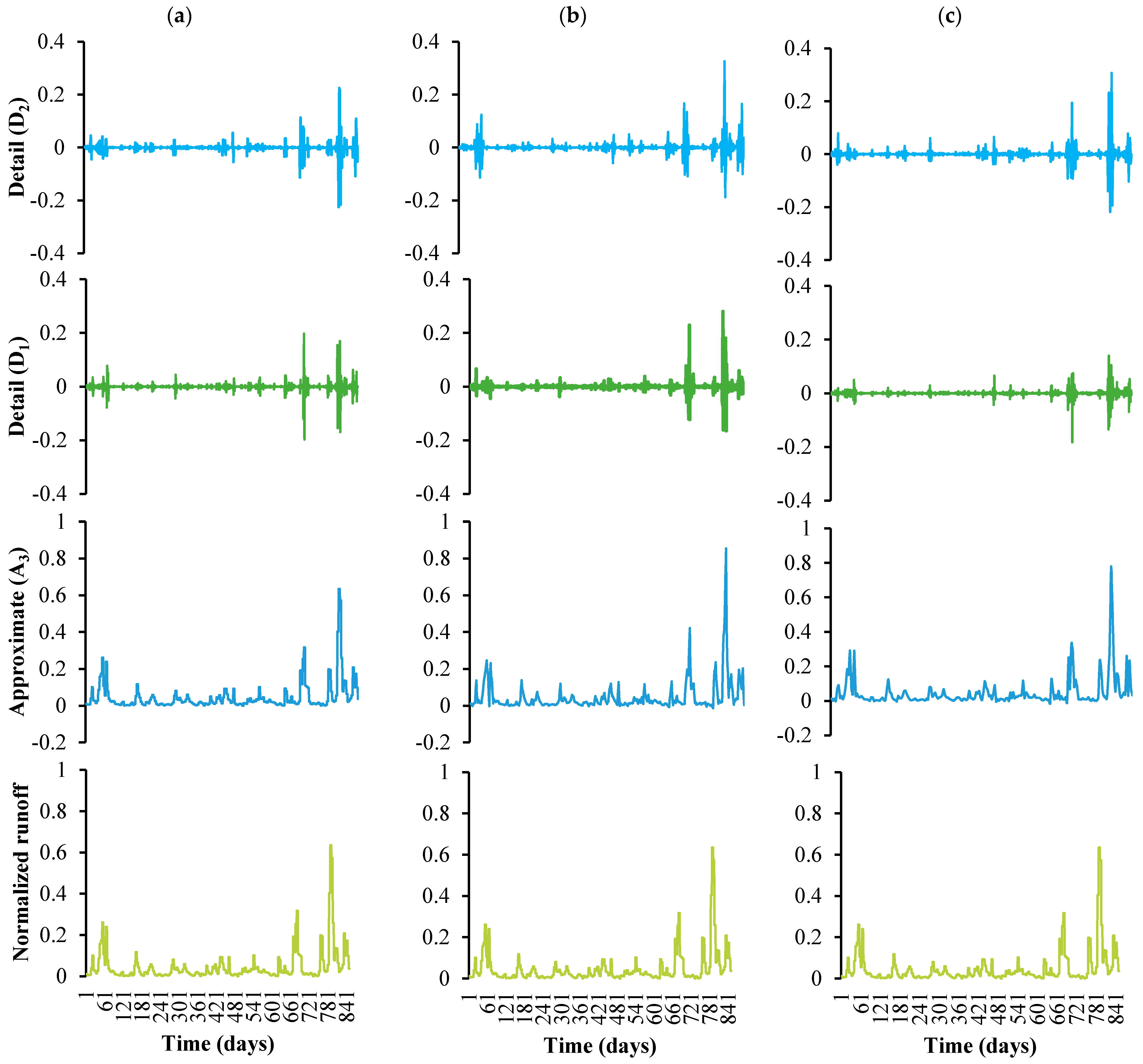
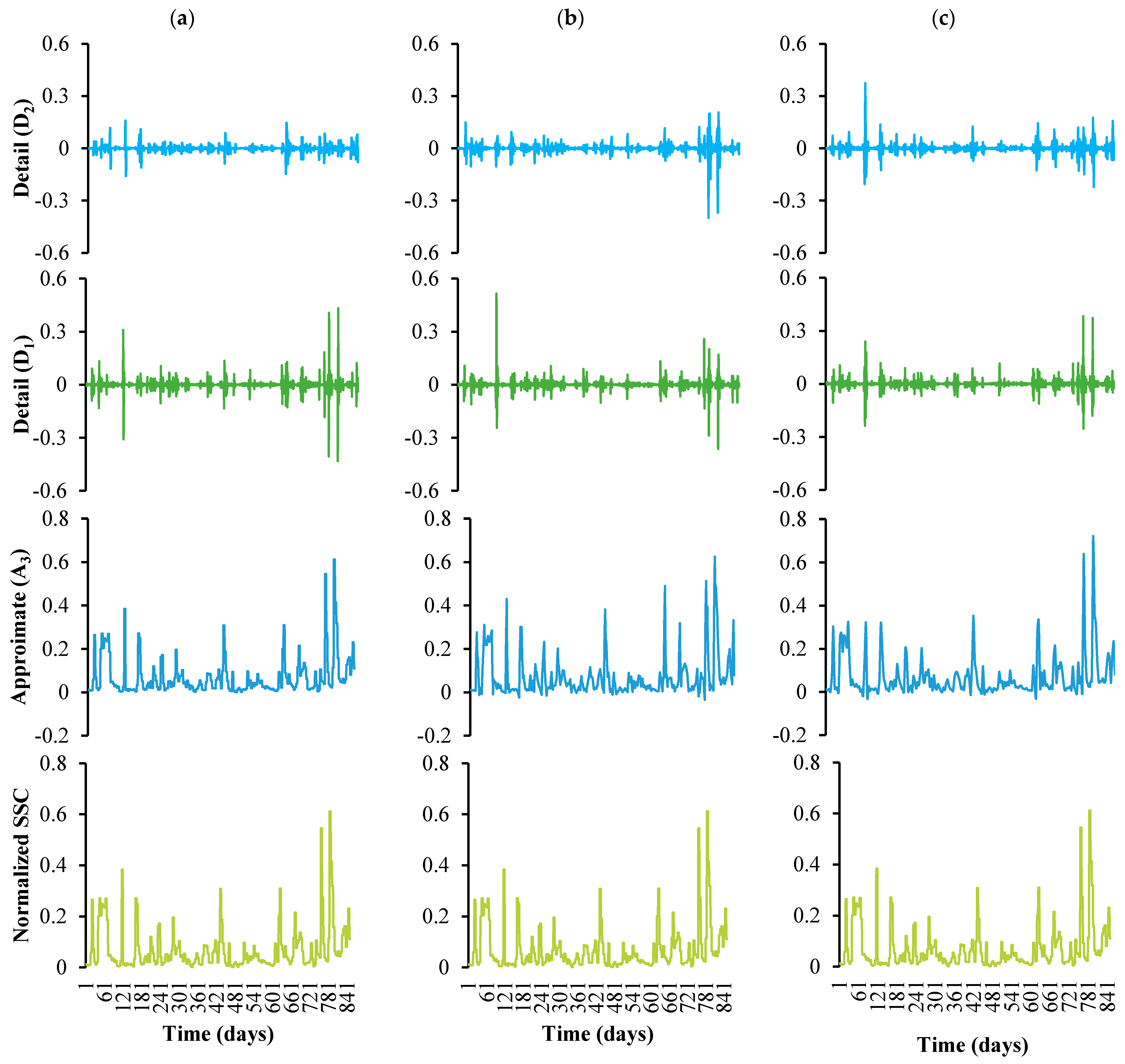
2.6. Mother Wavelets
2.7. Gamma Test (GT)
2.8. Data Normalization
2.9. Training and Testing of Developed Models
2.10. Performance Evaluation of Developed Models
2.10.1. Quantitative Evaluation
2.10.2. Hydrological Indices
Coefficient of Efficiency (CE)
Pooled Average Relative Error (PARE)
2.11. Qualitative Evaluation
2.12. Uncertainty Analysis
2.12.1. Width of Uncertainty Band of Error Prediction (We)
2.12.2. 95% Confidence Interval of Error Prediction (CIe)
3. Results
3.1. Data Analysis
3.2. GT for Input Selection
3.3. Hydrological Model Development
3.3.1. ANN/ANFIS Models for Daily SSC Prediction
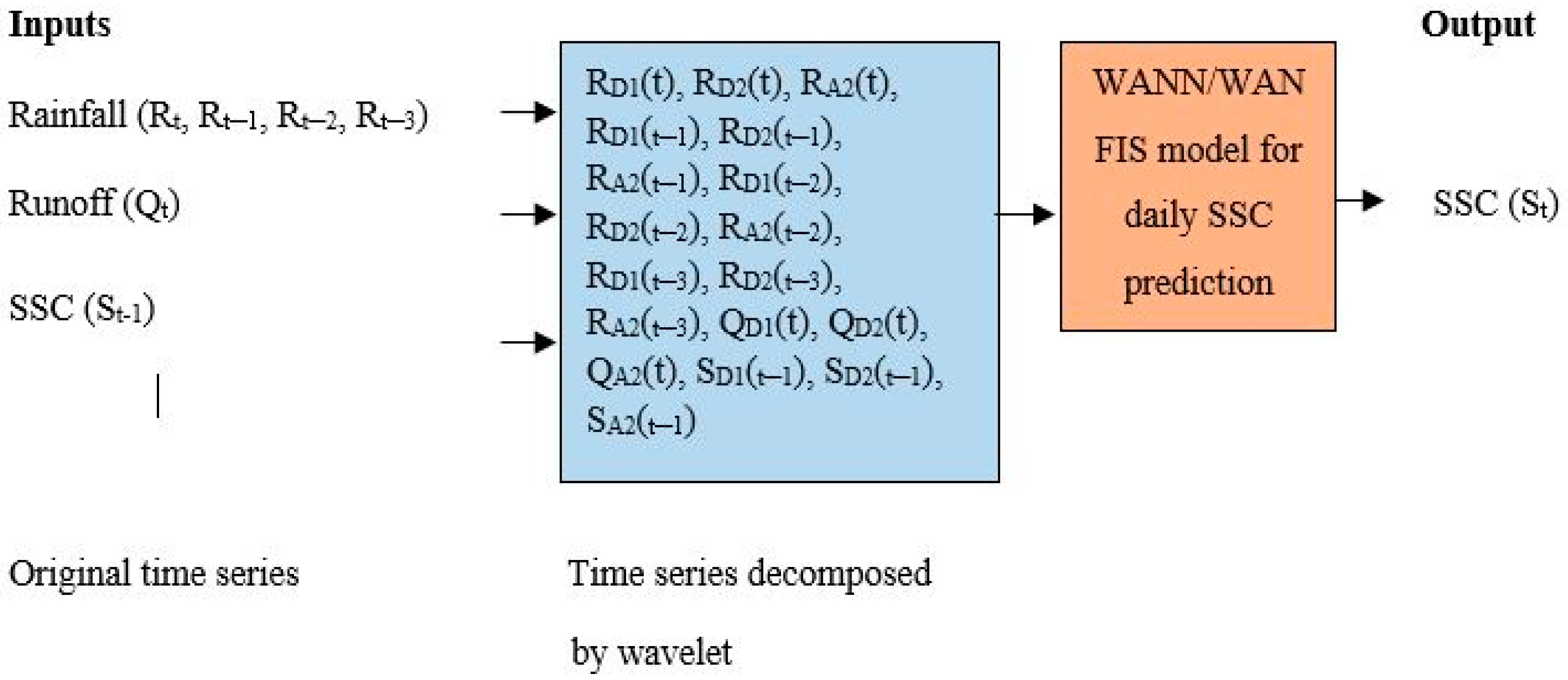
3.3.2. WANN/WANFIS Models for Daily SSC Prediction
3.4. Quantitative Performance Evaluation of Developed Models for Daily SSC Prediction
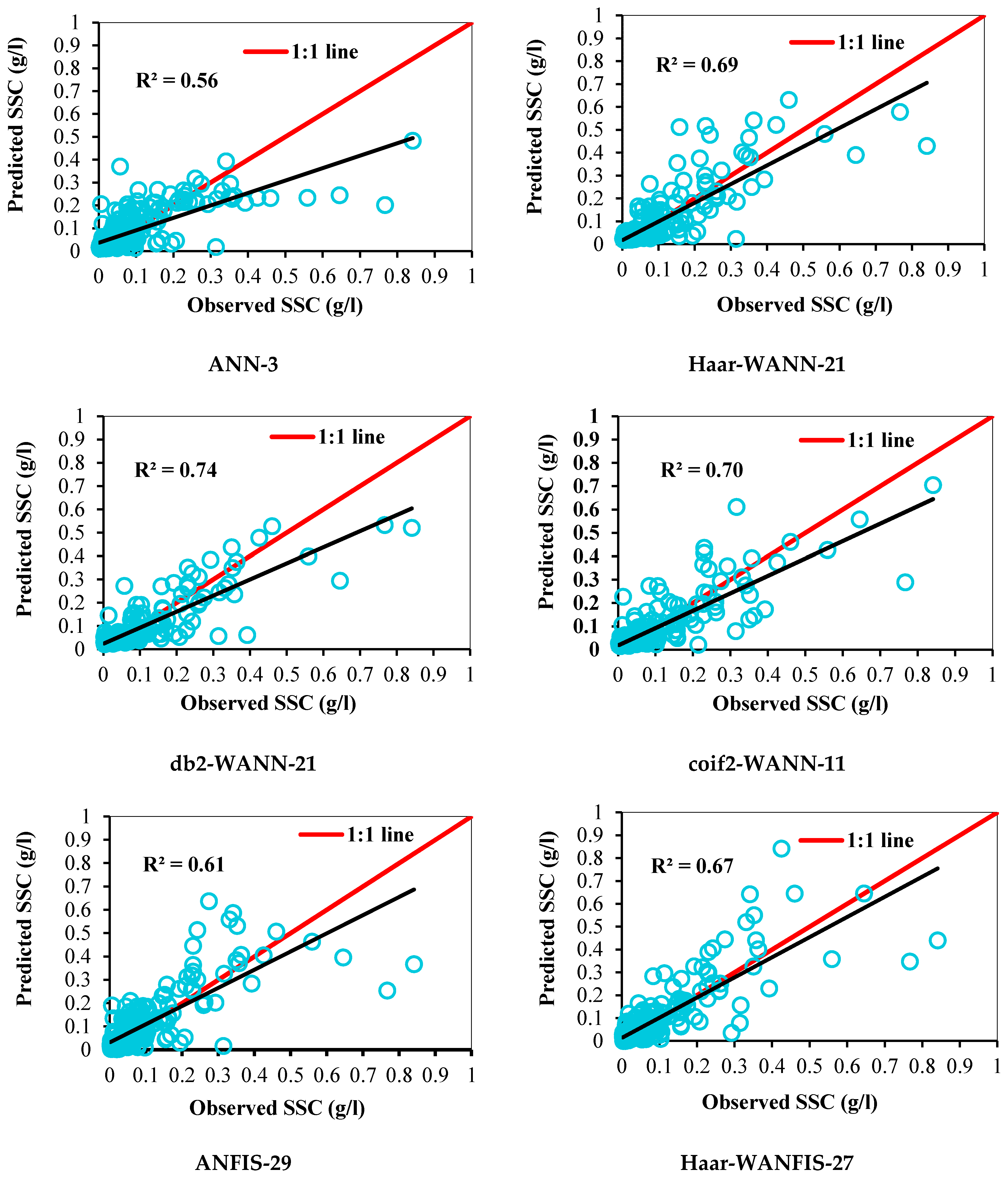
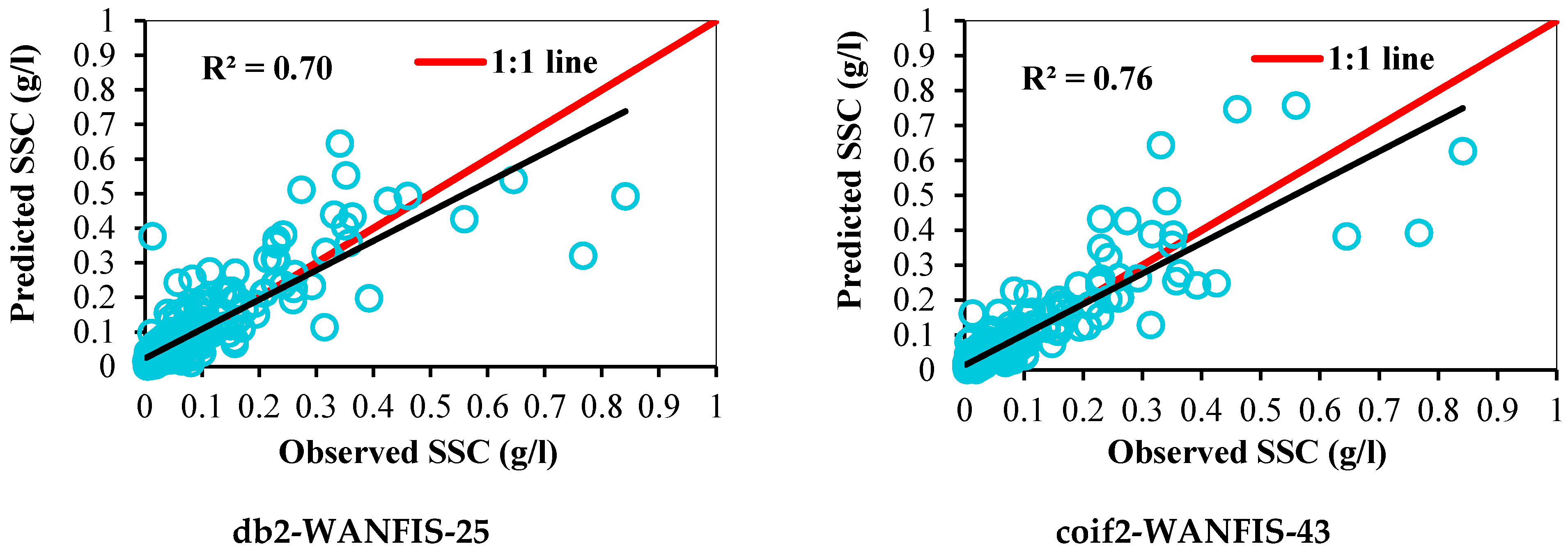
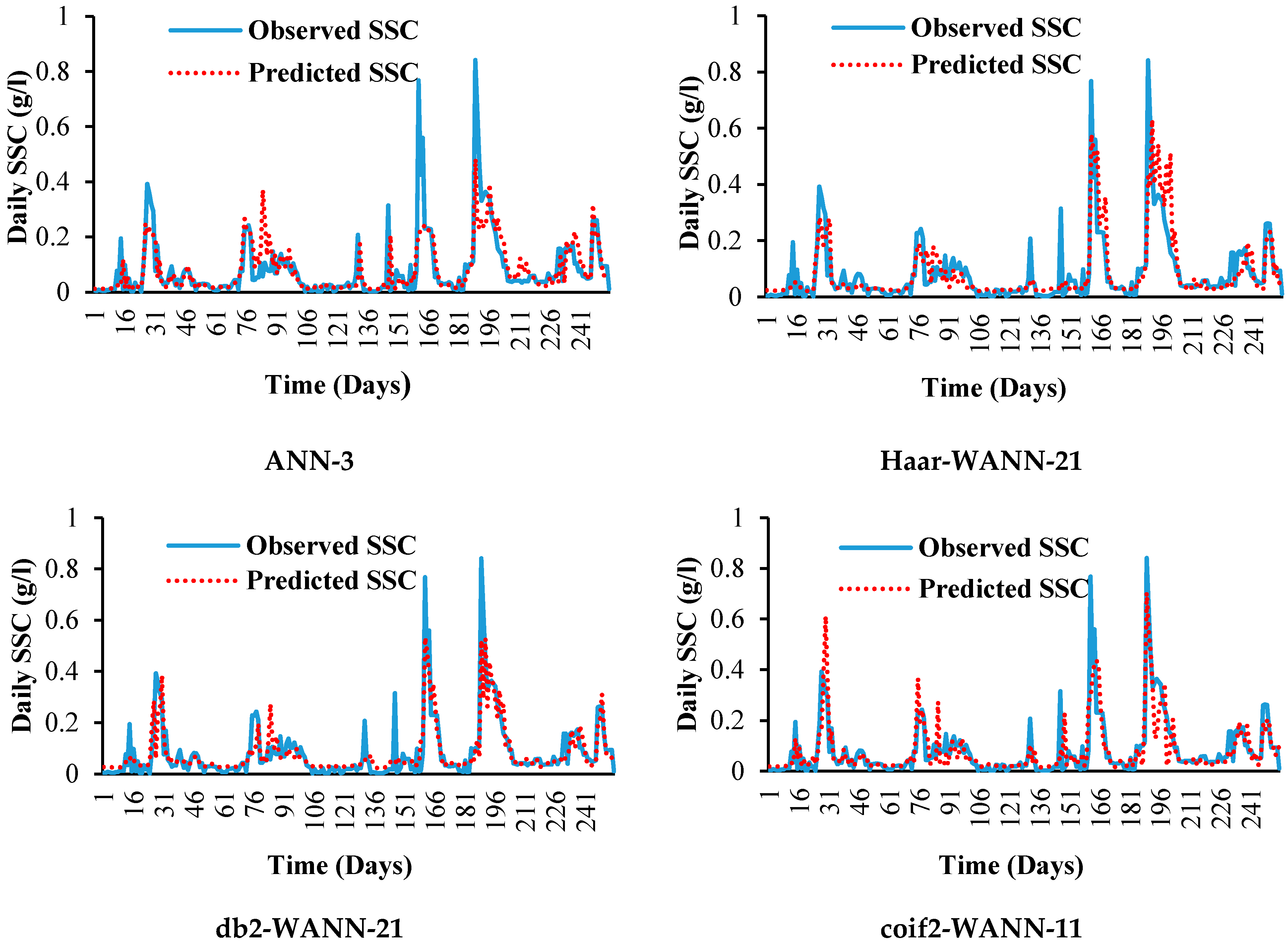
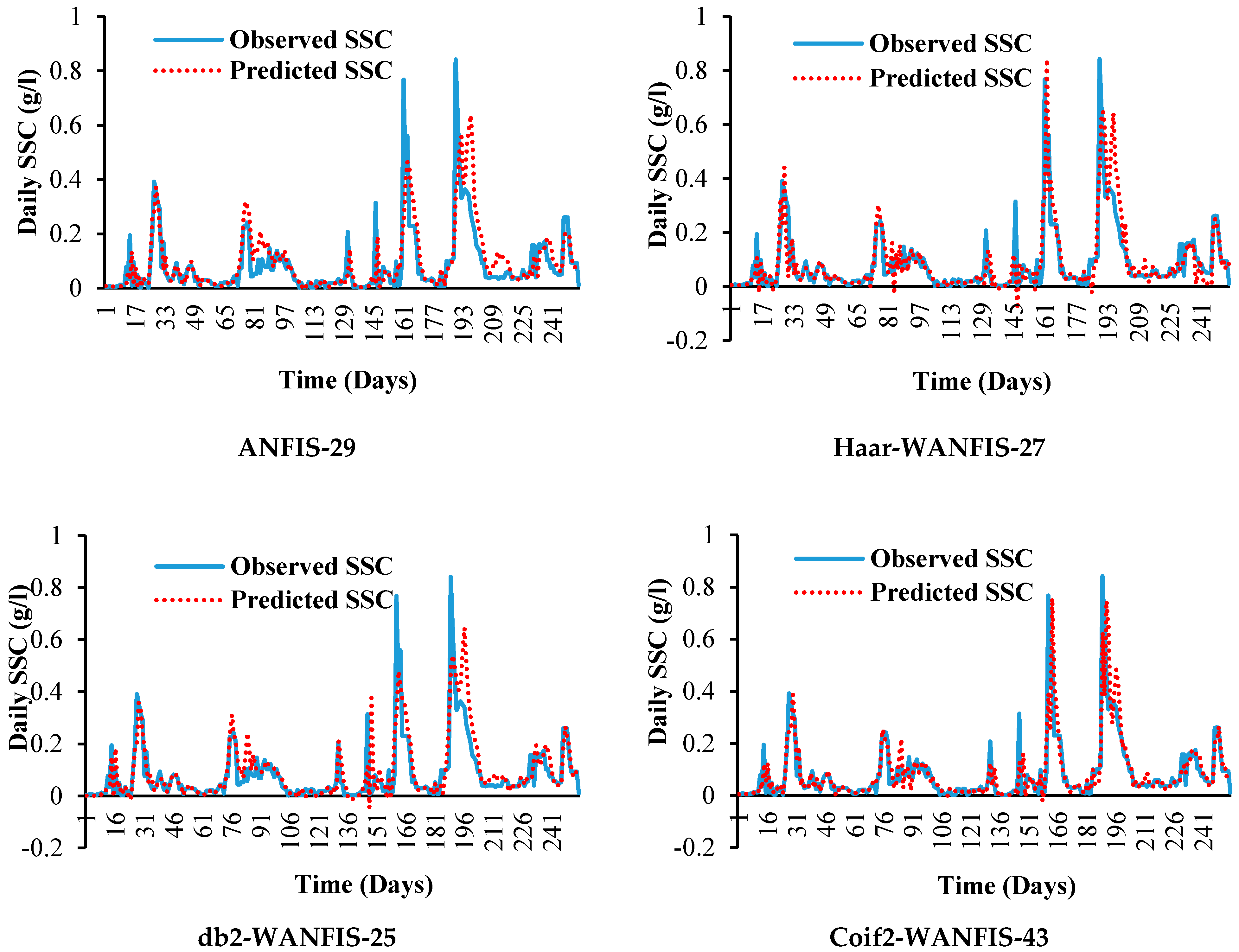
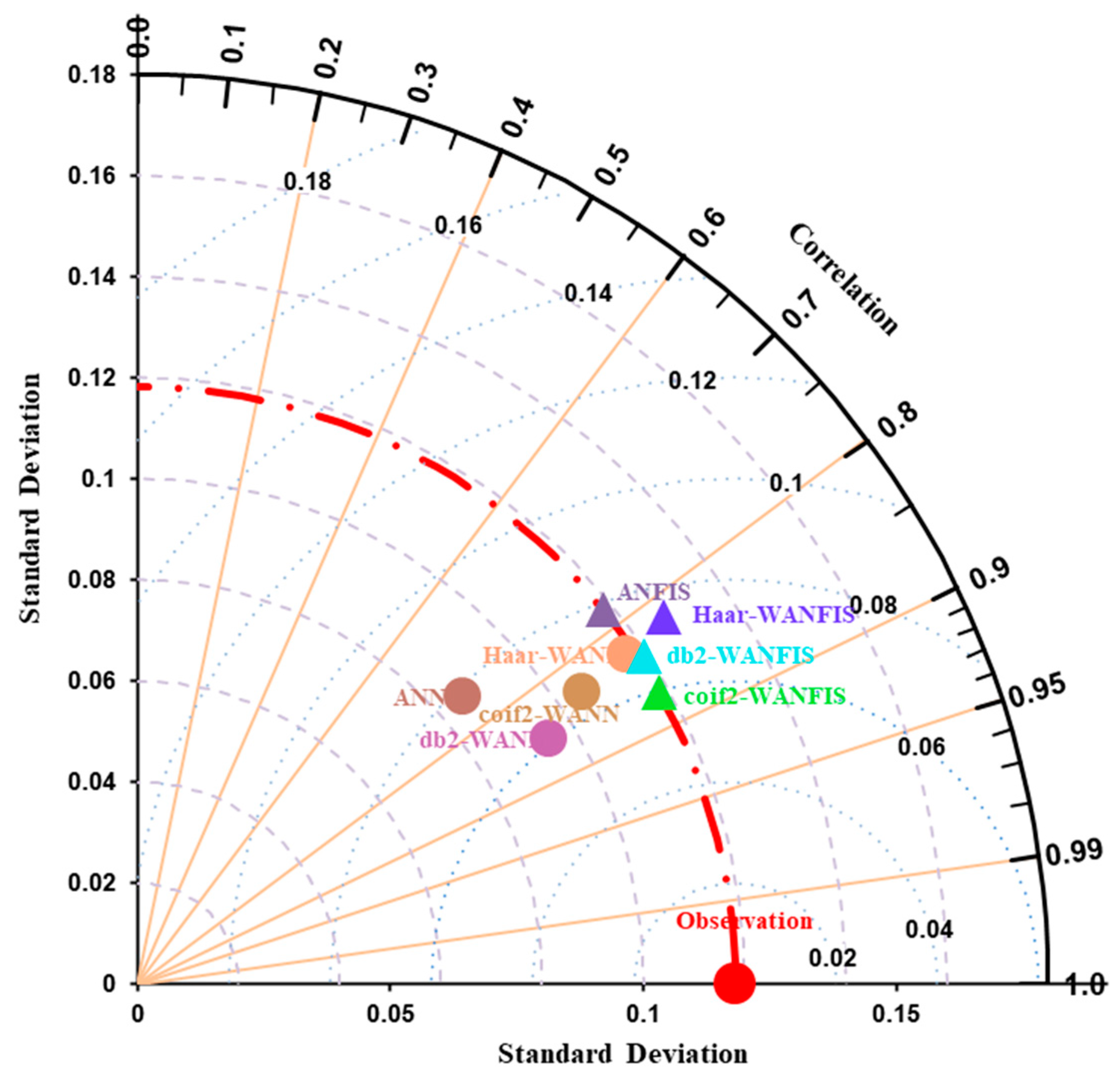
3.5. Qualitative Performance Evaluation of Developed Models for Daily SSC Prediction
3.6. Uncertainty Analysis
3.7. Sensitivity Analysis
4. Discussion
Comparison of ANN, WANN, ANFIS, and WANFIS Models for Daily SSC Prediction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
Appendix D.1. Root Mean Squared Error (RMSE)
Appendix D.2. The Correlation Coefficient (r)
Appendix D.3. Willmott Index (WI)
References
- Kuriqi, A.; Koçileri, G.; Ardiçlioğlu, M. Potential of Meyer-Peter and Müller approach for estimation of bed-load sediment transport under different hydraulic regimes. Model. Earth Syst. Environ. 2020, 6, 129–137. [Google Scholar] [CrossRef]
- Ardıçlıoğlu, M.; Kuriqi, A. Calibration of channel roughness in intermittent rivers using HEC-RAS model: Case of Sarimsakli creek, Turkey. SN Appl. Sci. 2019, 1, 1080. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; El-Shafie, S.; Zounemat, K.; Kisi, O. Prediction of Suspended Sediment Load Using Data-Driven Models. Water 2019, 11, 2060. [Google Scholar] [CrossRef]
- Melesse, A.M.; Ahmad, S.; McClain, M.E.; Wang, X.; Lim, Y.H. Suspended sediment load prediction of river systems: An artificial neural network approach. Agric. Water Manag. 2011, 98, 855–866. [Google Scholar] [CrossRef]
- Towfiqul Islam, A.R.M.; Talukdar, S.; Mahato, S.; Kundu, S.; Eibek, K.U.; Pham, Q.B.; Kuriqi, A.; Linh, N.T.T. Flood susceptibility modelling using advanced ensemble machine learning models. Geosci. Front. 2020. [Google Scholar] [CrossRef]
- Kuriqi, A.; Pinheiro, A.N.; Sordo-Ward, A.; Garrote, L. Water-energy-ecosystem nexus: Balancing competing interests at a run-of-river hydropower plant coupling a hydrologic-ecohydraulic approach. Energy Convers. Manag. 2020, 223, 113267. [Google Scholar] [CrossRef]
- Buyukyildiz, M.; Kumcu, S.Y. An Estimation of the Suspended Sediment Load Using Adaptive Network Based Fuzzy Inference System, Support Vector Machine and Artificial Neural Network Models. Water Resour. Manag. 2017, 31, 1343–1359. [Google Scholar] [CrossRef]
- Kisi, O. Suspended sediment estimation using neuro-fuzzy and neural network approaches/Estimation des matières en suspension par des approches neurofloues et à base de réseau de neurones. Hydrol. Sci. J. 2005, 50, 696. [Google Scholar] [CrossRef]
- Kumari, A.; Kumar, M.; Kumar, A.; Amitabh, A. Daily Gauge-Discharge Simulation using ANN and Wavelet-ANN Models for Muri Station, Jharkhand. Indian J. Ecol. 2020, 47, 645–649. [Google Scholar]
- Zhu, Y.-M.; Lu, X.X.; Zhou, Y. Suspended sediment flux modeling with artificial neural network: An example of the Longchuanjiang River in the Upper Yangtze Catchment, China. Geomorphology 2007, 84, 111–125. [Google Scholar] [CrossRef]
- Olyaie, E.; Banejad, H.; Chau, K.-W.; Melesse, A.M. A comparison of various artificial intelligence approaches performance for estimating suspended sediment load of river systems: A case study in United States. Environ. Monit. Assess. 2015, 187, 189. [Google Scholar] [CrossRef] [PubMed]
- Güldal, V.; Tongal, H. Comparison of Recurrent Neural Network, Adaptive Neuro-Fuzzy Inference System and Stochastic Models in Eğirdir Lake Level Forecasting. Water Resour. Manag. 2010, 24, 105–128. [Google Scholar] [CrossRef]
- Valizadeh, N.; El-Shafie, A. Forecasting the Level of Reservoirs Using Multiple Input Fuzzification in ANFIS. Water Resour. Manag. 2013, 27, 3319–3331. [Google Scholar] [CrossRef]
- Samantaray, S.; Ghose, D.K. Assessment of Suspended Sediment Load with Neural Networks in Arid Watershed. J. Inst. Eng. Ser. A 2020, 101, 371–380. [Google Scholar] [CrossRef]
- Rajaee, T.; Jafari, H. Two decades on the artificial intelligence models advancement for modeling river sediment concentration: State-of-the-art. J. Hydrol. 2020, 588, 125011. [Google Scholar] [CrossRef]
- Meshram, S.G.; Singh, V.P.; Kisi, O.; Karimi, V.; Meshram, C. Application of Artificial Neural Networks, Support Vector Machine and Multiple Model-ANN to Sediment Yield Prediction. Water Resour. Manag. 2020, 34, 4561–4575. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, P. Daily Suspended-sediment Concentration simulation using ANN and Wavelet ANN models. Int. Arch. Appl. Sci. Technol. 2019, 11, 60–69. [Google Scholar]
- Hussan, W.; Khurram Shahzad, M.; Seidel, F.; Nestmann, F. Application of Soft Computing Models with Input Vectors of Snow Cover Area in Addition to Hydro-Climatic Data to Predict the Sediment Loads. Water 2020, 12, 1481. [Google Scholar] [CrossRef]
- Talebizadeh, M.; Morid, S.; Ayyoubzadeh, S.A.; Ghasemzadeh, M. Uncertainty Analysis in Sediment Load Modeling Using ANN and SWAT Model. Water Resour. Manag. 2010, 24, 1747–1761. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Kisi, O.; Shiri, J. Evaluating the performance of four different heuristic approaches with Gamma test for daily suspended sediment concentration modeling. Environ. Sci. Pollut. Res. 2019, 26, 22670–22687. [Google Scholar] [CrossRef]
- Yin, D.; Shu, L.; Chen, X.; Wang, Z.; Mohammed, M.E. Assessment of Sustainable Yield of Karst Water in Huaibei, China. Water Resour. Manag. 2011, 25, 287–300. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S.; Kisi, O.; Singh, V.P. Daily water level forecasting using wavelet decomposition and artificial intelligence techniques. J. Hydrol. 2015, 520, 224–243. [Google Scholar] [CrossRef]
- Singh, V.K.; Kumar, D.; Kashyap, P.S.; Kisi, O. Simulation of suspended sediment based on gamma test, heuristic, and regression-based techniques. Environ. Earth Sci. 2018, 77, 708. [Google Scholar] [CrossRef]
- Agarwal, A.; Mishra, S.K.; Ram, S.; Singh, J.K. Simulation of Runoff and Sediment Yield using Artificial Neural Networks. Biosyst. Eng. 2006, 94, 597–613. [Google Scholar] [CrossRef]
- Dadaser-Celik, F.; Cengiz, E. A neural network model for simulation of water levels at the Sultan Marshes wetland in Turkey. Wetl. Ecol. Manag. 2013, 21, 297–306. [Google Scholar] [CrossRef]
- Nourani, V.; Komasi, M. A geomorphology-based ANFIS model for multi-station modeling of rainfall–runoff process. J. Hydrol. 2013, 490, 41–55. [Google Scholar] [CrossRef]
- Samantaray, S.; Ghose, D.K. Evaluation of suspended sediment concentration using descent neural networks. Procedia Comput. Sci. 2018, 132, 1824–1831. [Google Scholar] [CrossRef]
- Lohani, A.K.; Goel, N.K.; Bhatia, K.K.S. Improving real time flood forecasting using fuzzy inference system. J. Hydrol. 2014, 509, 25–41. [Google Scholar] [CrossRef]
- Alizadeh, M.J.; Kavianpour, M.R.; Kisi, O.; Nourani, V. A new approach for simulating and forecasting the rainfall-runoff process within the next two months. J. Hydrol. 2017, 548, 588–597. [Google Scholar] [CrossRef]
- Ravansalar, M.; Rajaee, T. Evaluation of wavelet performance via an ANN-based electrical conductivity prediction model. Environ. Monit. Assess. 2015, 187, 366. [Google Scholar] [CrossRef]
- Shoaib, M.; Shamseldin, A.Y.; Melville, B.W. Comparative study of different wavelet based neural network models for rainfall–runoff modeling. J. Hydrol. 2014, 515, 47–58. [Google Scholar] [CrossRef]
- Shoaib, M.; Shamseldin, A.Y.; Khan, S.; Khan, M.M.; Khan, Z.M.; Sultan, T.; Melville, B.W. A Comparative Study of Various Hybrid Wavelet Feedforward Neural Network Models for Runoff Forecasting. Water Resour. Manag. 2018, 32, 83–103. [Google Scholar] [CrossRef]
- Grossmann, A.; Morlet, J. Decomposition of Hardy Functions into Square Integrable Wavelets of Constant Shape. Fundam. Pap. Wavelet Theory 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Kisi, O. Wavelet Regression Model as an Alternative to Neural Networks for River Stage Forecasting. Water Resour. Manag. 2011, 25, 579–600. [Google Scholar] [CrossRef]
- Partal, T.; Kişi, Ö. Wavelet and neuro-fuzzy conjunction model for precipitation forecasting. J. Hydrol. 2007, 342, 199–212. [Google Scholar] [CrossRef]
- Nayak, P.C.; Venkatesh, B.; Krishna, B.; Jain, S.K. Rainfall-runoff modeling using conceptual, data driven, and wavelet based computing approach. J. Hydrol. 2013, 493, 57–67. [Google Scholar] [CrossRef]
- Prahlada, R.; Deka, P.C. Forecasting of Time Series Significant Wave Height Using Wavelet Decomposed Neural Network. Aquat. Procedia 2015, 4, 540–547. [Google Scholar] [CrossRef]
- Hassan, M.; Ali Shamim, M.; Sikandar, A.; Mehmood, I.; Ahmed, I.; Ashiq, S.Z.; Khitab, A. Development of sediment load estimation models by using artificial neural networking techniques. Environ. Monit. Assess. 2015, 187, 686. [Google Scholar] [CrossRef]
- Kişi, Ö. Daily suspended sediment estimation using neuro-wavelet models. Int. J. Earth Sci. 2010, 99, 1471–1482. [Google Scholar] [CrossRef]
- Genç, O.; Kişi, Ö.; Ardıçlıoğlu, M. Determination of Mean Velocity and Discharge in Natural Streams Using Neuro-Fuzzy and Neural Network Approaches. Water Resour. Manag. 2014, 28, 2387–2400. [Google Scholar] [CrossRef]
- Sharghi, E.; Nourani, V.; Najafi, H.; Molajou, A. Emotional ANN (EANN) and Wavelet-ANN (WANN) Approaches for Markovian and Seasonal Based Modeling of Rainfall-Runoff Process. Water Resour. Manag. 2018, 32, 3441–3456. [Google Scholar] [CrossRef]
- Nourani, V.; Kisi, Ö.; Komasi, M. Two hybrid Artificial Intelligence approaches for modeling rainfall–runoff process. J. Hydrol. 2011, 402, 41–59. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Bonakdari, H. Performance Evaluation of Adaptive Neural Fuzzy Inference System for Sediment Transport in Sewers. Water Resour. Manag. 2014, 28, 4765–4779. [Google Scholar] [CrossRef]
- Jang, J.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Rajaee, T. Wavelet and ANN combination model for prediction of daily suspended sediment load in rivers. Sci. Total Environ. 2011, 409, 2917–2928. [Google Scholar] [CrossRef]
- Sudhishri, S.; Kumar, A.; Singh, J.K. Comparative Evaluation of Neural Network and Regression Based Models to Simulate Runoff and Sediment Yield in an Outer Himalayan Watershed. J. Agric. Sci. Technol. 2016, 18, 681–694. [Google Scholar]
- Rajaee, T.; Mirbagheri, S.A.; Nourani, V.; Alikhani, A. Prediction of daily suspended sediment load using wavelet and neurofuzzy combined model. Int. J. Environ. Sci. Technol. 2010, 7, 93–110. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Haghiabi, A.H.; Parsaie, A. Prediction of side weir discharge coefficient by support vector machine technique. Water Supply 2016, 16, 1002–1016. [Google Scholar] [CrossRef]
- Kumar, M.; Kumari, A.; Kushwaha, D.P.; Kumar, P.; Malik, A.; Ali, R.; Kuriqi, A. Estimation of Daily Stage–Discharge Relationship by Using Data-Driven Techniques of a Perennial River, India. Sustainability 2020, 12, 7877. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Willmott, C.J. On the Evaluation of Model Performance in Physical Geography. In Spatial Statistics and Models; Gaile, G.L., Willmott, C.J., Eds.; Springer: Dordrecht, The Netherlands, 1984; pp. 443–460. [Google Scholar] [CrossRef]

| Statistical Parameters | Whole Data | Training Data Set | Testing Data Set | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Rt (mm) | Qt (m3/s) | SSCt (g/L) | Rt (mm) | Qt (m3/s) | SSCt (g/L) | Rt (mm) | Qt (m3/s) | SSCt (g/L) | |
| Mean | 14.60 | 215.65 | 0.059 | 12.00 | 141.03 | 0.048 | 20.61 | 388.02 | 0.084 |
| Standard Deviation | 22.91 | 405.67 | 0.088 | 17.33 | 191.73 | 0.069 | 31.53 | 646.81 | 0.118 |
| Kurtosis | 11.85 | 41.33 | 20.03 | 7.62 | 14.54 | 17.105 | 6.81 | 15.67 | 13.261 |
| Skewness | 3.01 | 5.38 | 3.643 | 2.51 | 3.41 | 3.175 | 2.47 | 3.48 | 3.180 |
| Range | 193.32 | 4641 | 0.841 | 119.51 | 1397.00 | 0.717 | 193.32 | 4640.50 | 0.839 |
| Minimum | 0.00 | 0.00 | 0.000 | 0.00 | 0.00 | 0.000 | 0.00 | 0.50 | 0.002 |
| Maximum | 193.32 | 4641 | 0.841 | 119.51 | 1397.00 | 0.717 | 193.32 | 4641.00 | 0.841 |
| Count | 854 | 854 | 854 | 596 | 596 | 596 | 258 | 258 | 258 |
| Variable | St | Rt | Rt-1 | Rt-2 | Rt-3 | Qt | Qt-1 | Qt-2 | Qt-3 | St-1 | St-2 | St-3 | p-Values |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| St | 1.00 | - | |||||||||||
| Rt | 0.70 | 1.00 | 5.65 × 10−26 | ||||||||||
| Rt − 1 | 0.68 | 0.74 | 1.00 | 0.73 | |||||||||
| Rt − 2 | 0.61 | 0.58 | 0.74 | 1.00 | 0.97 | ||||||||
| Rt − 3 | 0.51 | 0.45 | 0.58 | 0.74 | 1.00 | 0.27 | |||||||
| Qt | 0.62 | 0.66 | 0.68 | 0.63 | 0.56 | 1.00 | 0.04 | ||||||
| Qt − 1 | 0.54 | 0.48 | 0.66 | 0.68 | 0.63 | 0.89 | 1.00 | 0.78 | |||||
| Qt − 2 | 0.44 | 0.37 | 0.48 | 0.66 | 0.68 | 0.75 | 0.89 | 1.00 | 0.93 | ||||
| Qt − 3 | 0.35 | 0.29 | 0.37 | 0.48 | 0.66 | 0.65 | 0.75 | 0.89 | 1.00 | 0.10 | |||
| St − 1 | 0.72 | 0.51 | 0.70 | 0.68 | 0.61 | 0.59 | 0.62 | 0.54 | 0.44 | 1.00 | 1.82 × 10−27 | ||
| St − 2 | 0.60 | 0.41 | 0.51 | 0.70 | 0.68 | 0.56 | 0.59 | 0.62 | 0.54 | 0.72 | 1.00 | 0.00016 | |
| St − 3 | 0.49 | 0.33 | 0.41 | 0.51 | 0.70 | 0.52 | 0.56 | 0.59 | 0.62 | 0.60 | 0.72 | 1.00 | 0.18 |
| Model | Model Input Combination | Mask | Gamma | V − Ratio |
|---|---|---|---|---|
| M1 | Rt | 10000000000 | 0.0047802000 | 0.5471600 |
| M2 | Rt, Rt − 1 | 11000000000 | 0.0042625000 | 0.4879000 |
| M3 | Rt, R t− 1, Rt−2 | 11100000000 | 0.0041758000 | 0.4779800 |
| M4 | Rt, Rt − 1, Rt − 2, Rt − 3 | 11110000000 | 0.0032813667 | 0.4219459 |
| M5 | Rt, Rt − 1, Rt − 2, Qt | 11110000000 | 0.0038298000 | 0.4383700 |
| M6 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt | 11111000000 | 0.0030169776 | 0.3879486 |
| M7 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt, Qt − 1 | 11111100000 | 0.0034506204 | 0.4437100 |
| M8 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt, Qt − 1, Qt − 2 | 11111110000 | 0.0034489278 | 0.4434924 |
| M9 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt, Qt − 1, Qt − 2, Qt − 3 | 11111111000 | 0.0032920565 | 0.4233205 |
| M10 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt, Qt − 1, Qt − 2, Qt − 3, St − 1 | 11111111100 | 0.0032920565 | 0.4233205 |
| M11 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt, Qt − 1, Qt − 2, Qt − 3, St − 1, St − 2 | 11111111110 | 0.0032920306 | 0.4233172 |
| M12 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt, Qt − 1, Qt − 2, Qt − 3, St − 1, St − 2, St − 3 | 11111111111 | 0.0032920306 | 0.4233172 |
| M13 | Rt, Rt − 1, Rt − 2, Qt, St − 1, St − 2 | 11101000110 | 0.0034097067 | 0.4384490 |
| M14 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt, St − 1 | 11111000100 | 0.0030159990 | 0.3878227 |
| M15 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt, St − 1, St − 2 | 11111000110 | 0.0030159998 | 0.3878228 |
| M16 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt, St − 1, St − 2, St − 3 | 11111000111 | 0.0030165903 | 0.3878988 |
| M17 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt, Qt − 1, St − 1, St − 2, St − 3 | 11111100111 | 0.0034493755 | 0.4435500 |
| M18 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt, Qt − 1, Qt − 2, St − 1, St − 2, St − 3 | 11111110111 | 0.0034489289 | 0.4434925 |
| M19 | Rt, Rt − 1, Rt − 2, Qt, Qt − 1, Qt − 2, Qt − 3, St − 1, St − 2, St − 3 | 11101111111 | 0.0033026471 | 0.4246824 |
| M20 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt, Qt − 1, Qt − 2, Qt − 3, St − 1, St − 2 | 11111111110 | 0.0032920306 | 0.4233172 |
| M21 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt, Qt − 1, Qt − 2, St − 1, St − 2, St − 3 | 11111110111 | 0.0034489289 | 0.4434925 |
| M22 | Rt, Rt − 1, Rt − 2, Qt, Qt − 1 | 11101100000 | 0.0042706000 | 0.4888370 |
| M23 | Rt, Rt − 1, Rt − 2, Rt − 3, Qt, Qt − 1 | 11111100000 | 0.0034506204 | 0.4437100 |
| M24 | Rt, Rt − 1, Rt − 2, Qt, Qt − 1, Qt − 2 | 11111100000 | 0.0040742000 | 0.4663550 |
| M25 | Rt, Rt − 1, Rt − 2, Qt, Qt − 1, Qt − 2, St − 1 | 11101110100 | 0.0040742000 | 0.4663550 |
| M26 | Rt, Rt − 1, Rt − 2, Qt, Qt − 1, Qt − 2, St − 1, St − 2 | 11101110110 | 0.0040742000 | 0.4663550 |
| M27 | Rt, Rt − 1, Rt − 2, St − 2 | 11100000010 | 0.0041747000 | 0.4778580 |
| M28 | Rt, Rt − 1, Rt − 2, St − 1, St − 2 | 11100000110 | 0.0041719000 | 0.4775350 |
| M29 | Rt, Rt − 1, Rt − 2, Qt, St − 1 | 11101000100 | 0.0038292000 | 0.4383100 |
| M30 | Rt, Rt − 1, Rt − 2, Qt, St − 1, St − 2 | 11101000110 | 0.0038289000 | 0.4382700 |
| M31 | Rt, Rt − 1, Rt − 2, Qt, Qt − 1, St − 1, St − 2 | 11111100110 | 0.0042695000 | 0.4887090 |
| M32 | Rt − 1 | 01000000000 | 0.0045396000 | 0.5196200 |
| M33 | Rt − 1, Rt − 2 | 01100000000 | 0.0046157000 | 0.5283400 |
| M34 | Rt − 1, Rt − 2, Qt | 01101000000 | 0.0048902000 | 0.5597500 |
| M35 | Rt − 1, Rt − 2, Qt, St − 1 | 01101000100 | 0.0048889000 | 0.5596100 |
| M36 | Rt − 1, Rt − 2, Qt, St − 1, St − 2 | 01101000110 | 0.0048885000 | 0.5595600 |
| M37 | Rt − 1, Rt − 2, Qt, Qt − 1, St − 1, St − 2 | 01101100110 | 0.0045635000 | 0.5223630 |
| M38 | Rt − 1, Rt − 2, Qt, Qt − 1, Qt − 2, St − 1, St − 2 | 01101110110 | 0.0044611000 | 0.5106410 |
| M39 | Rt − 2 | 00100000000 | 0.0059649000 | 0.6827700 |
| M40 | Rt − 2, Qt | 00101000000 | 0.0049465000 | 0.5662000 |
| M41 | Rt − 2, Qt, St − 1 | 00101000100 | 0.0049457000 | 0.5661100 |
| M42 | Rt − 2, Qt, St − 1, St − 2 | 00101000110 | 0.0049452000 | 0.5660450 |
| M43 | Qt | 00001000000 | 0.0053284000 | 0.6099170 |
| M44 | Qt, St − 1 | 00001000100 | 0.0053036000 | 0.6070760 |
| M45 | Qt, St − 1, St − 2 | 00001000110 | 0.0052017000 | 0.5954070 |
| M46 | St − 1 | 00000000100 | 0.0045528000 | 0.5211380 |
| M47 | St − 1, St − 2 | 00000000110 | 0.0046496000 | 0.5322160 |
| M48 | St − 2 | 00000000010 | 0.0060325000 | 0.6905120 |
| M49 | Rt, Rt − 2, Qt, St − 1, St − 2 | 10101000110 | 0.0041118000 | 0.4706530 |
| M50 | Rt, Qt, St − 1, St − 2 | 10001000110 | 0.0042217000 | 0.4832370 |
| M51 | Rt, St − 1, St − 2 | 10000000110 | 0.0039567000 | 0.4529040 |
| M52 | Rt, St − 2 | 10000000010 | 0.0042196000 | 0.4830030 |
| M53 | Rt, Rt − 1, Qt, St − 1, St − 2 | 11001000110 | 0.0038594000 | 0.4417640 |
| M54 | Rt, Rt − 1, St − 1, St − 2 | 11000000110 | 0.0042129000 | 0.4822330 |
| M55 | Rt, Rt − 1, St − 2 | 11000000010 | 0.0042181000 | 0.4828270 |
| M56 | Rt, Rt − 1, Rt − 2, St − 1, St − 2 | 11100000110 | 0.0041719000 | 0.4775350 |
| M57 | Rt, Rt − 1, Rt − 2, St − 2 | 11100000010 | 0.0041747000 | 0.4778580 |
| M58 | Rt, Rt − 1, Rt − 2, Qt, St − 2 | 11101000010 | 0.0038293000 | 0.4383140 |
| Model | Architecture | Training | Testing | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE (g/L) | r | WI | CE | PARE (%) | RMSE (g/L) | r | WI | CE | PARE (%) | ||
| ANN-3 | 6-3-1 | 0.040 | 0.81 | 0.78 | 0.655 | 0.0017 | 0.078 | 0.75 | 0.73 | 0.560 | −0.013 |
| Haar-WANN-21 | 18-21-1 | 0.042 | 0.80 | 0.73 | 0.633 | 0.0041 | 0.069 | 0.83 | 0.74 | 0.661 | 0.006 |
| db2-WANN-21 | 18-21-1 | 0.031 | 0.90 | 0.72 | 0.801 | 0.0236 | 0.061 | 0.86 | 0.75 | 0.734 | −0.012 |
| coif2-WANN-11 | 18-11-1 | 0.021 | 0.95 | 0.81 | 0.903 | 0.0134 | 0.065 | 0.84 | 0.76 | 0.696 | −0.017 |
| Model | Training | Testing | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE (g/L) | R | WI | CE | PARE (%) | RMSE (g/L) | r | WI | CE | PARE (%) | |
| ANFIS-29 | 0.041 | 0.80 | 0.78 | 0.638 | 6.6 × 10−9 | 0.080 | 0.78 | 0.73 | 0.545 | 0.060 |
| Haar-WANFIS-27 | 0.032 | 0.88 | 0.83 | 0.782 | 1.7 × 10−9 | 0.074 | 0.82 | 0.76 | 0.605 | 0.017 |
| db2-WANFIS-25 | 0.023 | 0.94 | 0.85 | 0.892 | 2.1 × 10−10 | 0.068 | 0.84 | 0.77 | 0.666 | 0.051 |
| coif2-WANFIS-43 | 0.029 | 0.91 | 0.83 | 0.821 | 3 × 10−11 | 0.060 | 0.87 | 0.80 | 0.745 | 0.015 |
| Model | We (g/L) | CIe(g/L) |
|---|---|---|
| ANN-3 | ±0.0096 | −0.0125 to 0.0067 (0.0192) |
| Haar-WANN-121 | ±0.0084 | −0.0071 to 0.0097 (0.0168) |
| db2-WANN-21 | ±0.0074 | −0.0100 to 0.0049 (0.0149) |
| coif2-WANN-11 | ±0.0080 | −0.0118 to 0.0042 (0.0160) |
| ANFIS-29 | ±0.0096 | 0.0226 to 0.0034 (0.0260) |
| Haar-WANFIS-27 | ±0.0091 | −0.0054 to 0.0128 (0.0182) |
| db2-WANFIS-25 | ±0.0083 | 0.0028 to 0.0193 (0.0221) |
| coif2-WANFIS-43 | ±0.0073 | −0.0041 to 0.0105 (0.0146) |
| Inputs | Training | Testing | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE (g/L) | r | WI | CE | PARE (%) | RMSE (g/L) | r | WI | CE | PARE (%) | |
| Rt, Rt − 1, Rt − 2, Rt − 3, Qt, St − 1 | 0.040 | 0.81 | 0.78 | 0.655 | 0.0017 | 0.078 | 0.75 | 0.73 | 0.560 | −0.013 |
| Rt − 1, Rt − 2, Rt − 3, Qt, St − 1 | 0.043 | 0.78 | 0.72 | 0.612 | 0.0037 | 0.091 | 0.71 | 0.67 | 0.409 | 0.032 |
| Rt, Rt − 2, Rt − 3, Qt, St − 1 | 0.040 | 0.82 | 0.77 | 0.666 | 0.0015 | 0.080 | 0.73 | 0.72 | 0.539 | 0.008 |
| Rt, Rt − 1, Rt − 3, Qt, St − 1 | 0.043 | 0.79 | 0.68 | 0.613 | 0.0138 | 0.089 | 0.66 | 0.68 | 0.427 | −0.054 |
| Rt, Rt − 1, Rt − 2, Qt, St − 1 | 0.045 | 0.77 | 0.63 | 0.570 | 0.0327 | 0.096 | 0.68 | 0.67 | 0.342 | 0.054 |
| Rt, Rt − 1, Rt − 2, Rt − 3, St − 1 | 0.041 | 0.80 | 0.73 | 0.639 | 0.0207 | 0.087 | 0.69 | 0.69 | 0.455 | −0.046 |
| Rt, Rt − 1, Rt − 2, Rt − 3, Qt | 0.045 | 0.75 | 0.69 | 0.563 | 0.0071 | 0.108 | 0.45 | 0.59 | 0.160 | −0.027 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bajirao, T.S.; Kumar, P.; Kumar, M.; Elbeltagi, A.; Kuriqi, A. Superiority of Hybrid Soft Computing Models in Daily Suspended Sediment Estimation in Highly Dynamic Rivers. Sustainability 2021, 13, 542. https://doi.org/10.3390/su13020542
Bajirao TS, Kumar P, Kumar M, Elbeltagi A, Kuriqi A. Superiority of Hybrid Soft Computing Models in Daily Suspended Sediment Estimation in Highly Dynamic Rivers. Sustainability. 2021; 13(2):542. https://doi.org/10.3390/su13020542
Chicago/Turabian StyleBajirao, Tarate Suryakant, Pravendra Kumar, Manish Kumar, Ahmed Elbeltagi, and Alban Kuriqi. 2021. "Superiority of Hybrid Soft Computing Models in Daily Suspended Sediment Estimation in Highly Dynamic Rivers" Sustainability 13, no. 2: 542. https://doi.org/10.3390/su13020542
APA StyleBajirao, T. S., Kumar, P., Kumar, M., Elbeltagi, A., & Kuriqi, A. (2021). Superiority of Hybrid Soft Computing Models in Daily Suspended Sediment Estimation in Highly Dynamic Rivers. Sustainability, 13(2), 542. https://doi.org/10.3390/su13020542







