Estimation of Iodine Leaching in Soil Amended with Organic and Inorganic Materials Using HYDRUS 1-D Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Column Study
2.2. Iodine Determination
2.2.1. HYDRUS Model Setup
2.2.2. Simulation and Calibration of the Model
2.2.3. Assessment of the Model Performance
3. Results and Discussion
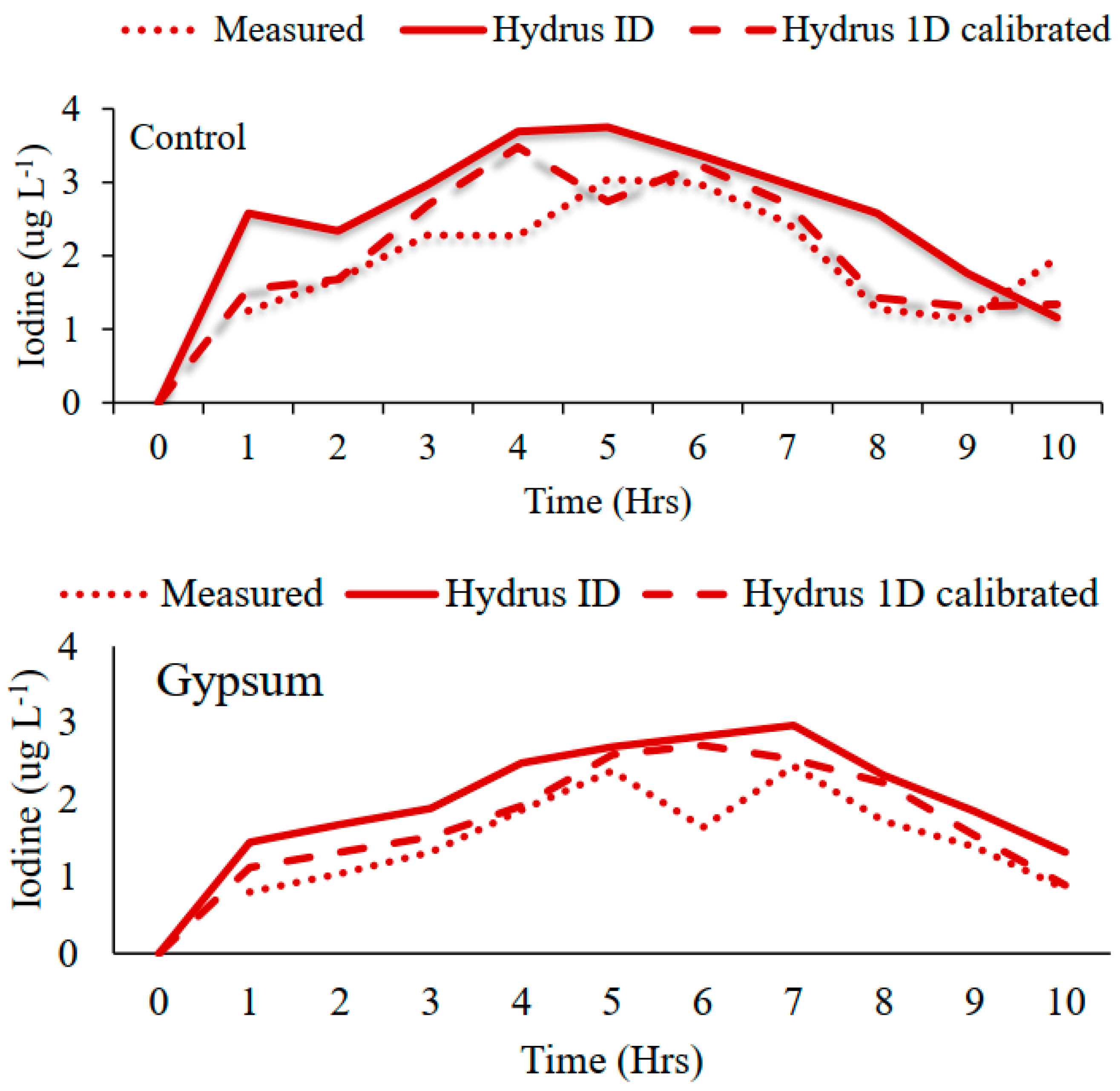
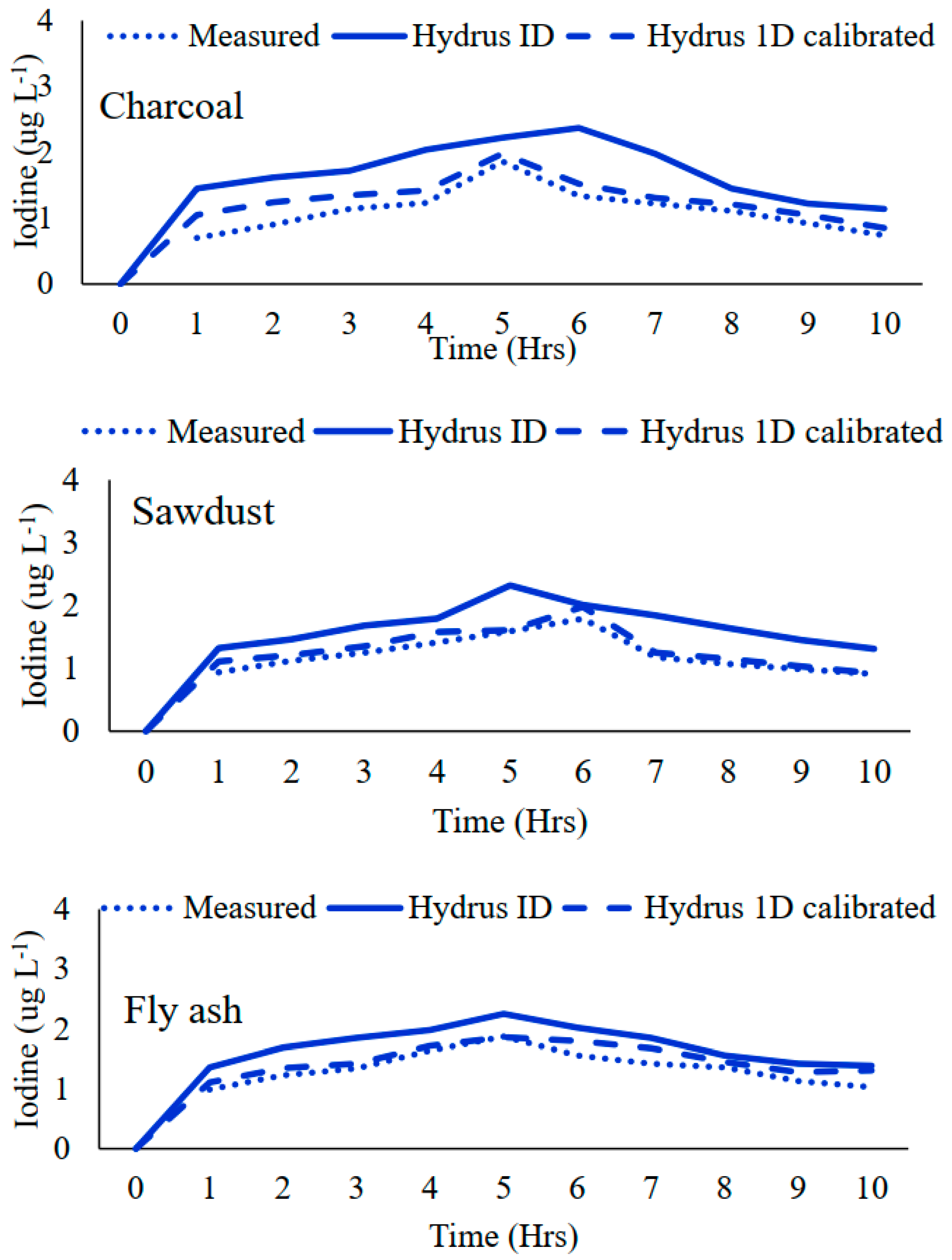
3.1. Calibration of HYDRUS 1D Model
3.2. Solute Movement
3.3. Model Efficiency Parameters
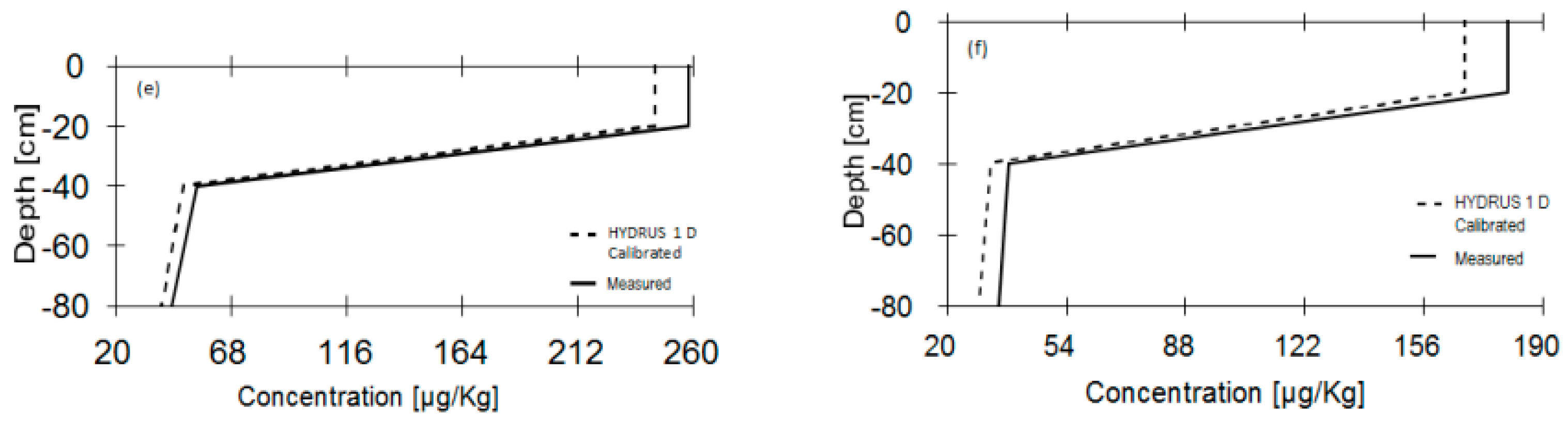
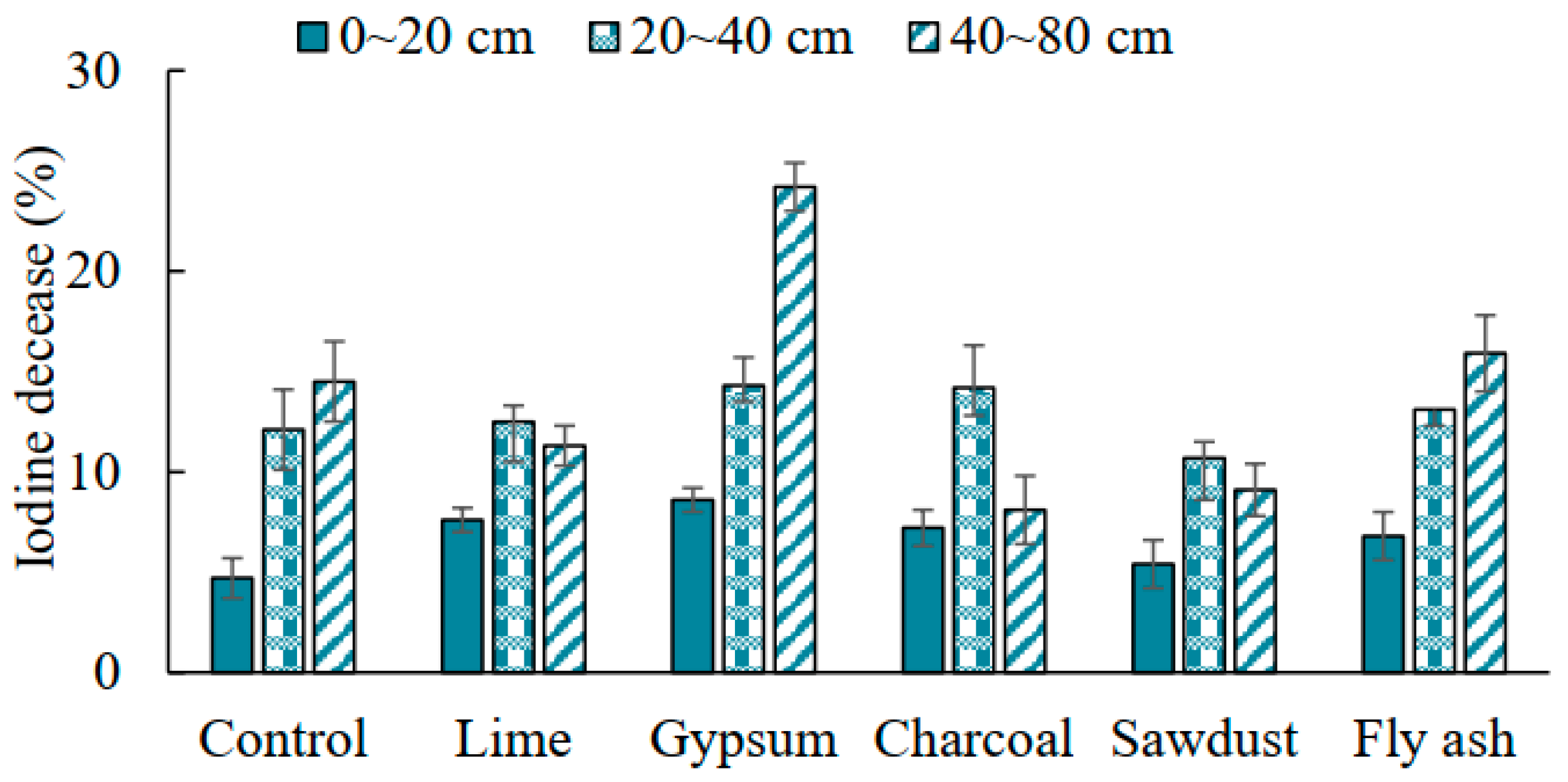
3.4. Iodine Retention in Soil
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Inobeme, A.; Adetunji, C.O.; Akram, M.; Munirat, M.; Laila, U.; Okonkwo, S.; Islam, S.; Inobeme, J. Benefits of Geochemistry and Its Impact on Human Health. Geochem. Concepts Appl. 2021, 23–35. [Google Scholar] [CrossRef]
- Zimmermann, M.B.; Jooste, P.L.; Pandav, C.S. Iodine-deficiency disorders. Lancet 2008, 372, 1251–1262. [Google Scholar] [CrossRef]
- Andersson, M.; de Benoist, B.; Rogers, L. Epidemiology of iodine deficiency: Salt iodisation and iodine status. Best Pract. Res. Clin. Endocrinol. Metab. 2010, 24, 1–11. [Google Scholar] [CrossRef]
- Hetzel, B.S. Towards the global elimination of brain damage due to iodine deficiency-the role of the International Council for Control of Iodine Deficiency Disorders. Int. J. Epidemiol. 2005, 34, 762–764. [Google Scholar] [CrossRef] [PubMed]
- Faško, P.; Lapin, M.; Pecho, J. 20-year extraordinary climatic period in Slovakia. Meteorol. Časopis 2008, 11, 99–105. [Google Scholar]
- Muramatsu, Y.; Wedepohl, K.H. The distribution of iodine in the earth’s crust. Chem. Geol. 1998, 147, 201–216. [Google Scholar] [CrossRef]
- Hou, X.; Hansen, V.; Aldahan, A.; Possnert, G.; Lind, O.C.; Lujaniene, G. A review on speciation of iodine-129 in the environmental and biological samples. Anal. Chim. Acta 2009, 632, 181–196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hassanien, M.H.; Hussein, L.A.; Robinson, E.N.; Mercer, L.P. Human iodine requirements determined by the saturation kinetics model. J. Nutr. Biochem. 2003, 14, 280–287. [Google Scholar] [CrossRef]
- Kodešová, R.; Vignozzi, N.; Rohošková, M.; Hájková, T.; Kočárek, M.; Pagliai, M.; Kozák, J.; Šimůnek, J. Impact of varying soil structure on transport processes in different diagnostic horizons of three soil types. J. Contam. Hydrol. 2009, 104, 107–125. [Google Scholar] [CrossRef]
- Pang, L.; Close, M.E.; Watt, J.P.; Vincent, K.W. Simulation of picloram, atrazine, and simazine leaching through two New Zealand soils and into groundwater using HYDRUS-2D. J. Contam. Hydrol. 2000, 44, 19–46. [Google Scholar] [CrossRef]
- Phillips, I. Modelling water and chemical transport in large undisturbed soil cores using HYDRUS-2D. Soil Res. 2006, 44, 27–34. [Google Scholar] [CrossRef]
- Ma, Y.; Feng, S.; Su, D.; Gao, G.; Huo, Z. Modeling water infiltration in a large layered soil column with a modified Green–Ampt model and HYDRUS-1D. Comput. Electron. Agric. 2010, 71, S40–S47. [Google Scholar] [CrossRef]
- Gee, G.W.; Bauder, J.; Klute, A. Methods of Soil Analysis, part 1, Physical and Mineralogical Methods; American Society of Agronomy: Madison, WI, USA, 1986. [Google Scholar]
- Nelson, D.; Sommers, L.E. Total Carbon, Organic Carbon, and Organic Matter. Methods of Soil Analysis: Part 2 Chemical and Microbiological Properties; American Society of Agronomy Inc.: Madison, WI, USA, 1983; pp. 539–579. [Google Scholar] [CrossRef]
- Kesari, R.; Rastogi, R.; Gupta, V. A simple and sensitive spectrophotometric method for the determination of iodine in environmental samples. Chem. Anal. 1998, 43, 201–207. [Google Scholar]
- Jha, R.K.; Sahoo, B.; Panda, R.K. Modeling the water and nitrogen transports in a soil–paddy–atmosphere system using HYDRUS-1D and lysimeter experiment. Paddy Water Environ. 2017, 15, 831–846. [Google Scholar] [CrossRef]
- Simunek, J.; Van Genuchten, M.T.; Sejna, M. The HYDRUS-1D software package for simulating the one-dimensional movement of water, heat, and multiple solutes in variably-saturated media. Univ. Calif. -Riverside Res. Rep. 2005, 3, 1–240. [Google Scholar]
- Simunek, J.; Jacques, D.; Bradford, S.A.; van Genuchten, M.T. Numerical modeling of contaminant transport using HYDRUS and its specialized modules. J. Indian Inst. Sci. 2013, 93, 265–284. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Vogel, T.; Cislerova, M. On the reliability of unsaturated hydraulic conductivity calculated from the moisture retention curve. Transp. Porous Media 1988, 3, 1–15. [Google Scholar] [CrossRef]
- Kosugi, K.I. Lognormal distribution model for unsaturated soil hydraulic properties. Water Resour. Res. 1996, 32, 2697–2703. [Google Scholar] [CrossRef]
- Dai, J.; Zhang, M.; Hu, Q.; Huang, Y.; Wang, R.; Zhu, Y. Adsorption and desorption of iodine by various Chinese soils: II. Iodide and iodate. Geoderma 2009, 153, 130–135. [Google Scholar] [CrossRef]
- Kočárek, M.; Kodešová, R.; Kozák, J.; Drábek, O.; Vacek, O. Chlorotoluron behaviour in five different soil types. Plant Soil Environ. 2005, 51, 304–309. [Google Scholar] [CrossRef] [Green Version]
- Singh, P.; Kanwar, R.S. Preferential Solute Transport through Macropores in Large Undisturbed Saturated Soil Columns; Wiley Online Library: Hoboken, NJ, USA, 1991. [Google Scholar] [CrossRef]
- Li, Y.; Ghodrati, M. Transport of Nitrate in Soils as Affected by Earthworm Activities; Wiley Online Library: Hoboken, NJ, USA, 1995. [Google Scholar] [CrossRef]
- Enfield, C.G.; Phan, T.; Walters, D.M.; Ellis Jr, R. Kinetic model for phosphate transport and transformation in calcareous soils: I. Kinetics of transformation. Soil Sci. Soc. Am. J. 1981, 45, 1059–1064. [Google Scholar] [CrossRef]
- Irshad, M.; Waseem, A.; Umar, M.; Sabir, M.A. Leachability of nitrate from sandy soil using waste amendments. Commun. Soil Sci. Plant Anal. 2014, 45, 680–687. [Google Scholar] [CrossRef]
- Mohiuddin, M.; Irshad, M.; Farig, M.; Shahzad, M. Extractability of iodine from soils using different methods in relation to soil properties. Arab. J. Geosci. 2021, 14, 1–9. [Google Scholar] [CrossRef]
- Mohiuddin, M.; Irshad, M.; Ping, A.; Hussain, Z.; Shahzad, M. Bioavailability of iodine to mint from soil applied with selected amendments. Environ. Pollut. Bioavailab. 2019, 31, 138–144. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, S.; Muramatsu, Y.; Uchida, S. Studies on the sorption of I−(iodide) and IO 3−(iodate) onto andosols. Water Air Soil Pollut. 1992, 63, 321–329. [Google Scholar] [CrossRef]
- Liu, N.; Wang, M.; Zhou, F.; Zhai, H.; Qi, M.; Liu, Y.; Li, Y.; Zhang, N.; Ma, Y.; Huang, J. Selenium bioavailability in soil-wheat system and its dominant influential factors: A field study in Shaanxi province, China. Sci. Total. Environ. 2021, 770, 144664. [Google Scholar] [CrossRef] [PubMed]
- Leta, M.K.; Demissie, T.A.; Tränckner, J. Hydrological Responses of Watershed to Historical and Future Land Use Land Cover Change Dynamics of Nashe Watershed, Ethiopia. Water 2021, 13, 2372. [Google Scholar] [CrossRef]
- Leta, M.K.; Demissie, T.A.; Tränckner, J. Modeling and Prediction of Land Use Land Cover Change Dynamics Based on Land Change Modeler (LCM) in Nashe Watershed, Upper Blue Nile Basin, Ethiopia. Sustainability 2021, 13, 3740. [Google Scholar] [CrossRef]


| Parameter | Unit | Values |
|---|---|---|
| Sand | % | 75.6 |
| Silt | % | 16.6 |
| Clay | % | 7.8 |
| Texture | - | Sandy loam |
| C | g/kg1 | 21.6 |
| Moisture | % | 18.2 |
| Iodine | mg/kg1 | 0.34 |
| Exch. Ca | mg/kg1 | 76.3 |
| Exch. Mg | mg/kg1 | 56.7 |
| Exch. K | mg/kg1 | 156 |
| Exch. Na | mg/kg1 | 35.6 |
| CEC | mg/kg1 | 324.6 |
| EC (1:5) | µS/m1 | 125 |
| pH (1:5) | - | 7.6 |
| Soil Amendment | K1 | α | R2 |
|---|---|---|---|
| Control | 1.42 | 1.71 | 0.91 |
| Lime | 1.51 | 1.82 | 0.94 |
| Gypsum | 1.64 | 1.98 | 0.96 |
| Charcoal | 1.72 | 2.08 | 0.923 |
| Sawdust | 1.82 | 2.2 | 0.912 |
| Fly ash | 1.69 | 2.04 | 0.943 |
| Soil Amendment | Column 1 Calibration | Column 2 Validation | ||||||
|---|---|---|---|---|---|---|---|---|
| Depth (cm) | Experiment Value | Model Value | Absolute Difference | Experimental Value | Model Value | Absolute Difference | pH | |
| (µg/kg1) | ||||||||
| Control | 0~20 | 94.6 | 79.25 | 15.35 | 92.1 | 87.7 | 4.3 | 7.48 |
| 20~40 | 31.5 | 24 | 7.5 | 33.4 | 29.3 | 4 | 7.5 | |
| 40~80 | 32.4 | 19 | 13.4 | 28.7 | 24.5 | 4.1 | 7.51 | |
| Lime | 0~20 | 138.2 | 118 | 20.2 | 148.5 | 137.1 | 11.4 | 7.75 |
| 20~40 | 31.5 | 13.2 | 18.2 | 33.4 | 29.2 | 4.1 | 7.79 | |
| 40~80 | 28.4 | 11.7 | 16.6 | 26.5 | 23.5 | 3 | 7.82 | |
| Gypsum | 0~20 | 147.5 | 110.5 | 37 | 142.6 | 130.2 | 12.3 | 7.89 |
| 20~40 | 37.4 | 23.5 | 13.9 | 34.8 | 29.8 | 4.9 | 7.91 | |
| 40~80 | 29.8 | 17 | 12.8 | 31.5 | 23.8 | 7.6 | 7.92 | |
| Charcoal | 0~20 | 186.5 | 173.5 | 13 | 184.5 | 171 | 13.4 | 7.87 |
| 20~40 | 42.5 | 33.7 | 8.8 | 44.8 | 38.4 | 6.3 | 7.89 | |
| 40~80 | 34.5 | 25.2 | 9.3 | 32.1 | 29.5 | 2.6 | 7.85 | |
| Sawdust | 0~20 | 251.2 | 217 | 34.2 | 258.7 | 244.6 | 14 | 7.15 |
| 20~40 | 57.6 | 44 | 13.6 | 54.3 | 48.4 | 5.8 | 7.19 | |
| 40~80 | 48.4 | 27.2 | 21.15 | 43.5 | 39.5 | 3.9 | 7.2 | |
| Fly ash | 0~20 | 184.2 | 166.7 | 17.45 | 180.2 | 167.7 | 12.4 | 7.15 |
| 20~40 | 41.3 | 29.5 | 11.8 | 37.6 | 32.6 | 4.92 | 7.18 | |
| 40~80 | 32.8 | 21.25 | 11.55 | 34.8 | 29.2 | 5.53 | 7.21 | |
| Soil Amendment | Parameters of Model Calibration | Parameter of Model Validation | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | D | R2 | ME | EF | RMSE | D | R2 | ME | EF | |
| Control | 0.57 | 0.684 | 0.81 | 1.82 | 0.92 | 0.58 | 0.67 | 0.87 | 1.79 | 0.91 |
| Gypsum | 0.82 | 0.261 | 0.95 | 2.61 | 0.94 | 0.84 | 0.28 | 0.94 | 2.56 | 0.92 |
| Lime | 0.92 | 0.292 | 0.87 | 2.92 | 0.9 | 0.89 | 0.31 | 0.86 | 2.87 | 0.9 |
| Charcoal | 0.57 | 0.182 | 0.95 | 1.82 | 0.86 | 0.62 | 0.18 | 0.94 | 0.17 | 0.85 |
| Sawdust | 0.29 | 0.094 | 0.98 | 0.94 | 0.91 | 0.32 | 0.08 | 0.96 | 0.89 | 0.9 |
| Fly ash | 0.44 | 0.141 | 0.96 | 1.41 | 0.94 | 0.48 | 0.15 | 0.94 | 1.45 | 0.93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohiuddin, M.; Ali, J.; Leta, M.K.; Waseem, M.; Irshad, M.; Hussain, Z. Estimation of Iodine Leaching in Soil Amended with Organic and Inorganic Materials Using HYDRUS 1-D Model. Sustainability 2021, 13, 10967. https://doi.org/10.3390/su131910967
Mohiuddin M, Ali J, Leta MK, Waseem M, Irshad M, Hussain Z. Estimation of Iodine Leaching in Soil Amended with Organic and Inorganic Materials Using HYDRUS 1-D Model. Sustainability. 2021; 13(19):10967. https://doi.org/10.3390/su131910967
Chicago/Turabian StyleMohiuddin, Muhammad, Jawad Ali, Megersa Kebede Leta, Muhammad Waseem, Muhammad Irshad, and Zahid Hussain. 2021. "Estimation of Iodine Leaching in Soil Amended with Organic and Inorganic Materials Using HYDRUS 1-D Model" Sustainability 13, no. 19: 10967. https://doi.org/10.3390/su131910967
APA StyleMohiuddin, M., Ali, J., Leta, M. K., Waseem, M., Irshad, M., & Hussain, Z. (2021). Estimation of Iodine Leaching in Soil Amended with Organic and Inorganic Materials Using HYDRUS 1-D Model. Sustainability, 13(19), 10967. https://doi.org/10.3390/su131910967









