1. Introduction
The Construction Embankment Technical Guide [
1] continues to be relevant in landfill monitoring. It recommends compaction control at stone fillings by procedure. It limits the maximum size to 800 mm for the operation of the compaction rollers. The guide recommends procedural control, limiting the application to materials with a maximum size of less than 800 mm. Compaction is defined according to the ratio Q/S compaction intensity, where Q is the volume of the compacted embankment in cubic meters and S is the area swept by the compactor in square meters, the maximum thickness of the compacted layers in meters, the maximum speed of the compactor in kilometers per hour, and the number of roller passes.
Eurocode 7 (EC7) provides a long list of possible limit states and serviceability limit states that should be checked for embankments. It has specific provisions for the supervision of the construction of embankments and the monitoring of embankments during and after construction. It considers that when determining the weight of the embankment from the specific gravity of the soil, care should be taken to include particles bigger than 20 mm and up to 60 mm in the density tests as they are often not included, although this can have a considerable effect on the specific weight determined. Teijón–López–Zuazo et al. [
2] show that in the construction of fillings with stone materials, compaction have limitations that avoid the optimal quality control.
The General Specifications for Roads and Bridges Works PG-3 [
3] prescribes macro pits with a minimum surface of 1 m
2 and 1 m
3 of volume. So, it is complex to obtain gradings weighing fractions of different aggregates. For Teijón el al. [
4], the nuclear methods for the obtention of density and humidity in situ are not adequate in random fillings for a tested thickness of 300mm when the layer thicknesses are usually 600mm. Also, the particle sizes reduce the significance of the test. The density by substitution methods such as sand are not correct, the high hollow introduces errors, limiting its application to 50mm. For larger sizes the vibration table is recommended.
The modified Proctor test is not a correct reference for the degree of compaction, since it is carried out by substituting material bigger than 20 mm, which in this case is the biggest fraction. Even with these size limitations, the Proctor test is still recommended. Finally, as the plate bearing test (PBT) is a point test, to be representative the diameter of the plate must be 5 times the maximum size, which results in sizes outside the test procedure. The control of topographic settlements needs adequate references, according to Sopeña [
5]. The French standard NF P98-736 [
6] classifies the compactors according to their load per wheel (CR) as P1, with CR values between 25–40 kN, P2 for CR between 40–60 kN, and P3 for CR > 60 kN. For Fernandez and others [
7], test sections are necessary because of the limitations of the compaction control. The tests carried out in this research are shown in
Table 1.
Nowadays, the quality control methods for earthworks are highly developed through several research projects that made it possible to use inadequate quality materials. The current specifications are sufficient for the control of this type of material. However, the specifications for the control of the laying of stone materials (rockfills and random fillings) are underdeveloped.
The granulometric analysis of stone formations by inspection pits can be carried out by weighing the fractions, although it is of limited operability. Average density control has the limitations of nuclear methods for density and moisture determinations. The limitations of the test also affect the layer thickness tested. A more accurate method for compaction control in rockfills is the measurement of settlement by topographic procedures, although practical reference values need to be defined. The values required for the wheel impression test do not impose any limitations on the usual compaction conditions.
The procedure for testing the wheel impression test on fillings involves the measuring points being measured by means of a tape measure attached to two survey markers. The measuring element on which the survey marker is placed consists of a set of welded metal frames which, because of their interlocking arrangement, is usually known as ‘H’. The measurement is carried out by placing the metal device on each measuring point, before and after the loaded truck has passed. The wheel impression value is calculated as the arithmetic mean of the 10 points (δm). This value is called the compaction degree index.
The main reasons proposed are to define a new method of compaction control, applying only representative tests and thresholds, and the revision of procedures in the wheel-tracking test and in the topographic settlement, avoiding limitations. Among the different types of rock, research is focused on the family of slate rocks. Fernandez et al. [
7] consider that rocks with a single compressive strength below 25 MPa produce random fillings of sufficient quality, performing test sections with excellent results. Rahman et al. [
8] relate the compactor placed on the vibratory rollers with the calculation of the instantaneous density, finishing the compaction when the dynamic module is reached. This method can be used to locate soft spots by means of a global positioning system (GPS). Oteo [
9] considers granulometry and density as the main parameters to be defined for use in the formation of fillings. Lim [
10] says that Korean road specifications include a 30 cm layer thickness that avoids the use of rocks. There are also no specifications for quality control with stone materials. He proposes obtaining the density on site by the “water replacement method” within the inspection pit. For Sakaia et al. [
11], the revision of the Road Embankment Earthquake Manual does not sufficiently consider the influence on the mechanical behavior of soil compaction. Triaxial tests have associated the highest load deviation with the compaction degree. One-dimensional consolidation tests allowed a linear adjustment of the compression curve. The highest dry density corresponds to the lowest compressibility, although overconsolidation can produce the collapse of the structure.
The compaction procedure for random fillings, in accordance with PG-3 [
3], should define the optimum moisture content, the number of passes, the maximum layer thickness, and the machinery to be used for earthworks. Kyung–Tae et al. [
12] investigate the execution of a rock embankment built by dynamic compaction performing PBT. Due to dynamic compaction, an increase in pressure can develop in the foundation. A hyperbolic model associated with the construction method was adjusted to the seat. The estimated results were compared to the settlements and the results of PBT.
Oteo [
9] considers that geophysical prospecting techniques, in addition to the plastic sheet substitution method, are suitable for the control of random fills. Nuclear methods present problems, such as the penetration of the emitting rod between rock fragments. It can be measured by backscattering, that is, by direct emission from the surface, although the results are not reliable because they correspond to the most compacted area. In the study of space exploration, research was carried out to estimate soil density by means of drone drilling. Similar methods can be applied to quality control in compaction. Iai et al. [
13] fit a model by obtaining the density of the raked soil by raking force. The application of the method allows the support of the drone on the moon or Mars in addition to the Earth. Scale models were made with JSC-1
a (artificial lunar regolite), obtaining relationships between the density of the soil or lunar regolite, the ripple force, and the spacing and number of scarifiers. The instrumentation allows a high-resolution mapping of the density of the raked site, providing an in situ calibration of the ground by remote control from the Earth. For Wu and Wang [
14], the effect of the time between the layers on field compaction must be considered in the construction of filler. For longer surface exposures, moisture tends to evaporate, and test results change. With the Clegg soil impact test hammer, compacted Xiangshan sand was practical for dry density measurement. The force of compacted sand and compaction effort correlated well with the soil impact test hammer. The main factors influencing the compacted Xiangshan sand were moisture and degree of compaction. Lower compaction effort results in lower soil strength as moisture content increases. The stability of the embankments depends on the quality of the compaction of the fill. Nondestructive testing techniques have more advantages than that of conventional field density tests. Therefore, the use of nondestructive testing techniques in fill monitoring seems interesting in geotechnical applications. Using the Clegg impact tester, impact (Iv) values varying in compaction effort, moisture content, and density were observed in the laboratory. The variations of Iv with moisture are equal to the moisture-density ratio. The Iv has a strong relationship, for each compaction effort, with the moisture-density ratio. With a simple moisture test, the dry density can be predicted using the Iv values. This allows efficient quality control compaction.
Cacciola et al. [
15] performed a geo-analytical investigation. The use of frequent surveys adds both costs and delays to earthwork projects. With continuous compaction control and intelligent compaction systems, they provide a real-time monitoring. This is the Real-Time Kinematic Global Positioning System. This process can be used with great benefit by ensuring the quality of the compacted soil. In addition, Liu et al. [
16] proposed an innovative process for quality control in earth rock engineering. The compaction monitoring technology integrated into the rollers was combined with real-time global positioning kinematics, adopting the value of compaction as real-time monitoring. The compaction value has decreased with the speed of the rollers, increased with the decrease of the layer thickness, and increased with the increase of the dry density. Thus, the compaction value has a relation with the quality control of the compaction. Therefore, the compaction value is similar to the compaction meter value used by the geodynamic engine drive power. Therefore, it can serve as a real-time characterization, identifying the quality control of the compaction. Regression models were used with compaction value, moisture, and gradation as independent variables. Rapid and continuous evaluations of the compaction quality control prevent quality defects and improve the quality of the embankment construction, traditionally controlled through compaction thickness, vibration condition, compaction passes, and roller speed. These are limited point samples to represent the construction quality of the entire work area can be unreliable, with delays in rectification of problems at the paving site.
Sawangsuriya et al. [
17] commented that quality control in road compaction in Thailand is based on in-situ density measurements using the sand method. Quality monitoring is basically carried out through the sand cone test, UNE 103503 [
18]. This is a simple test, although it generally requires a long testing time and is a destructive procedure. A laboratory machine provides a rapid impedance-based measurement of density and moisture in electrical spectroscopy. They investigated the density and moisture results with other tests such as nuclear methods, PBT, sand method, etc. Anjan Kumar et al. [
19] proposed an alternative method by setting target values according to soil characteristics, trying to avoid test sections. By measurement of rollers and nondestructive tests, different soils were analyzed. The in-situ tests carried out were the dynamic penetrometer, the light deflectometer and the density measurement by radioactive isotopes. With the use of the intelligent compaction, they established correlations between the values of the in-situ ensembles and the measurements of the rollers, quantifying the improvement of the material at the passing of the compacting rollers.
Nazarian et al. [
20] evaluate modules as a function of moisture from the portable seismic analyzer. While all sections tested with the nuclear density meter exceeded the traditional 95% maximum dry density acceptance limit of the modified Proctor test, the modules estimated with ultrasonic surface wave technologies are higher than the moisture-dependent adjusted module. Mansour and Aly [
21] adopted the Modflow program for modelling groundwater flow conditions. Using a genetic algorithm, they achieve optimization to minimize the number of wells. Road construction requires high water consumption for compaction. Thus, groundwater optimization contributes to future drainage projects and can be applied in construction excavations to obtain satisfactory quality control.
The Portancimeter, developed at the Laboratoire Central des Ponts et Chaussées, consists of the passing of a one meter diameter wheel of 400 kg with an eccentric introducing a vibration of 35 Hz, the reaction being a suspended mass of 600 kg. The modulus of stiffness is obtained with an accelerometer on the wheel axle which measures the experienced settlement.
Similar techniques are used in the compactometer, using intelligent compaction rollers, IC rollers. IC rollers have an accelerometer in the bracket and a gauge on the dashboard, visible to the operator. The ratio between the amplitude of the acceleration of the first harmonic of the wave and the amplitude of the fundamental frequency is evaluated at time intervals between 5 and 30 s. The accelerometer changes its shape with increasing number of passes. With the first pass, the signal is almost sinusoidal; a distortion is produced which increases with the number of passes. The test depth can exceed 150 cm. The compactometer measurement is correlated with the density instantaneously. Once the minimum value of the required dynamic modulus is obtained, the operator stops making additional roller passes over the compacting layer. The method can be used in checks to locate soft spots, and the information can be completed with a global positioning system (GPS).
The statistical analysis of the main compaction trials was carried out, obtaining correlations. Due to the large size of the explanations, the study was particularized to the core zone, with a maximum layer thickness of 800 mm. The tests carried out were applied the revised procedures of the topographic settlement and the wheel impression test [
2].
3. Results
Linear correlations between 225 lots were evaluated. There was no relation between density–topographic settlement test, wheel-tracking–topographic settlement test, or first–second modulus PBT (ɸ 600mm). The variables were entered into the SPSS Statistics calculation program. An analysis of variance ANOVA shows the sums of squares and the degrees of freedom associated with each: is significant at p < 0,05. A multitude of nonlinear models were analyzed, although finally all the adjustments were linear because no curve was found that has significantly improved the adjustments.
3.1. Relation Wheel-Tracking—Topographic Settlement Tests
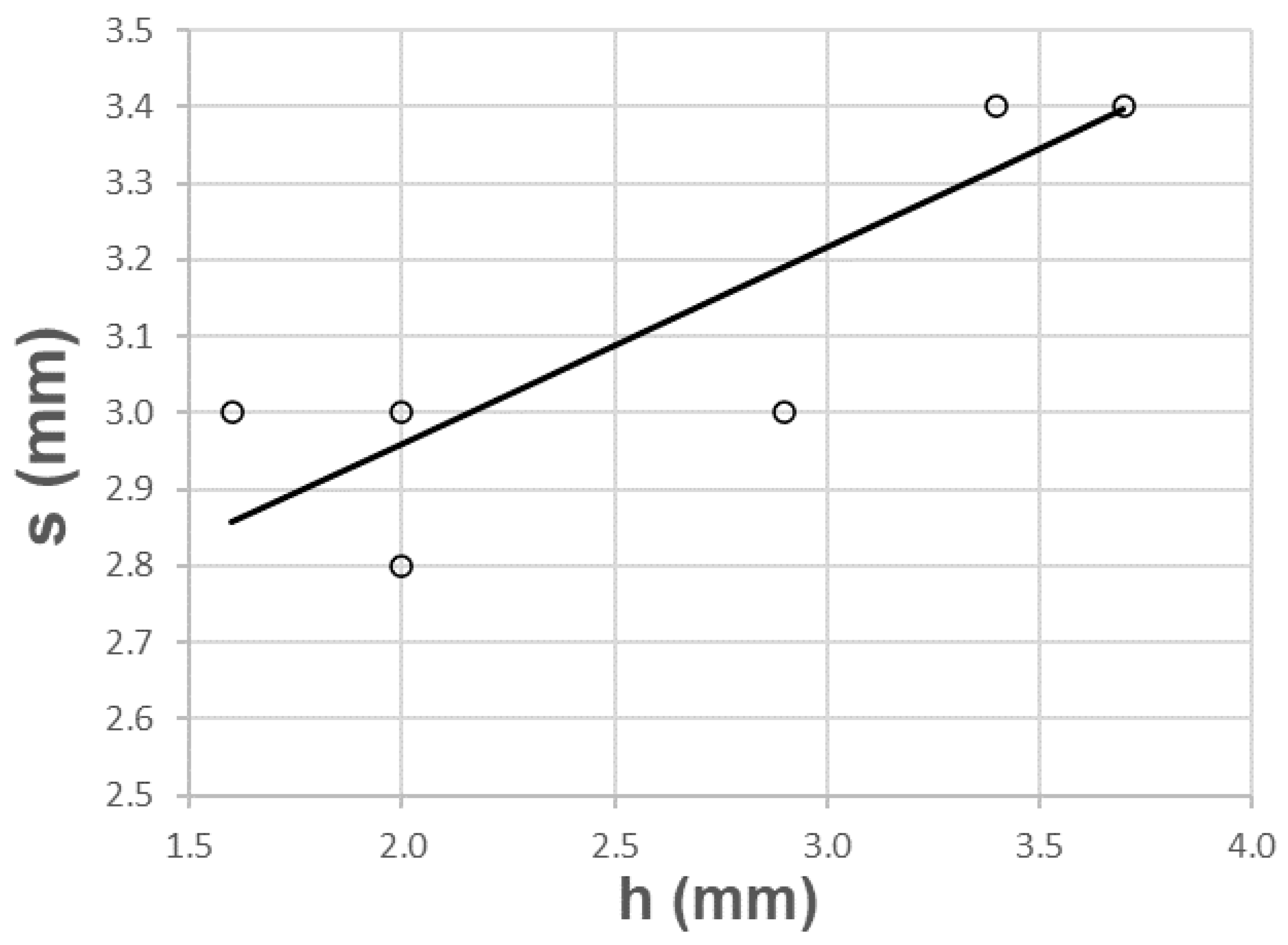
As shown in
Figure 7, there is a correlation between the wheel-tracking and the topographic settlement tests. The association is directly proportional, with higher values of the wheel rut corresponding to higher topographic settlements.
The high value of the Pearson correlation coefficient ρ = 0.843 (R in table) shows a strong relationship between the wheel-tracking and the topographic settlement tests, as detailed in
Table 6. The coefficient of determination R
2 = 0.710 means a variance percentage of 71.0%. The standard error is 0.1475 mm.
As shown in
Table 7, Levene test is significant with a value of F = 9.786 (Hartley’s F). Consequently, the homoscedasticity criterion is not met. The variances are different. The variables, therefore, are related.
Table 8 shows high
t-values (Student’s
t test) of 11.237 and 3.128, both significant. The wheel-tracking test permits an accurate prediction of the topographic settlement values, which allows for the substitution of the compaction control procedure and vice versa.
According to the coefficients, the linear fit equation for the topographic settlement and the wheel-tracking tests is:
The function domain uses the intervals of [2.5 ≤ s ≤ 3.5] and [1.5 ≤ h ≤ 4.0].
3.2. Relation Wheel-Tracking Test—First PBT Modulus
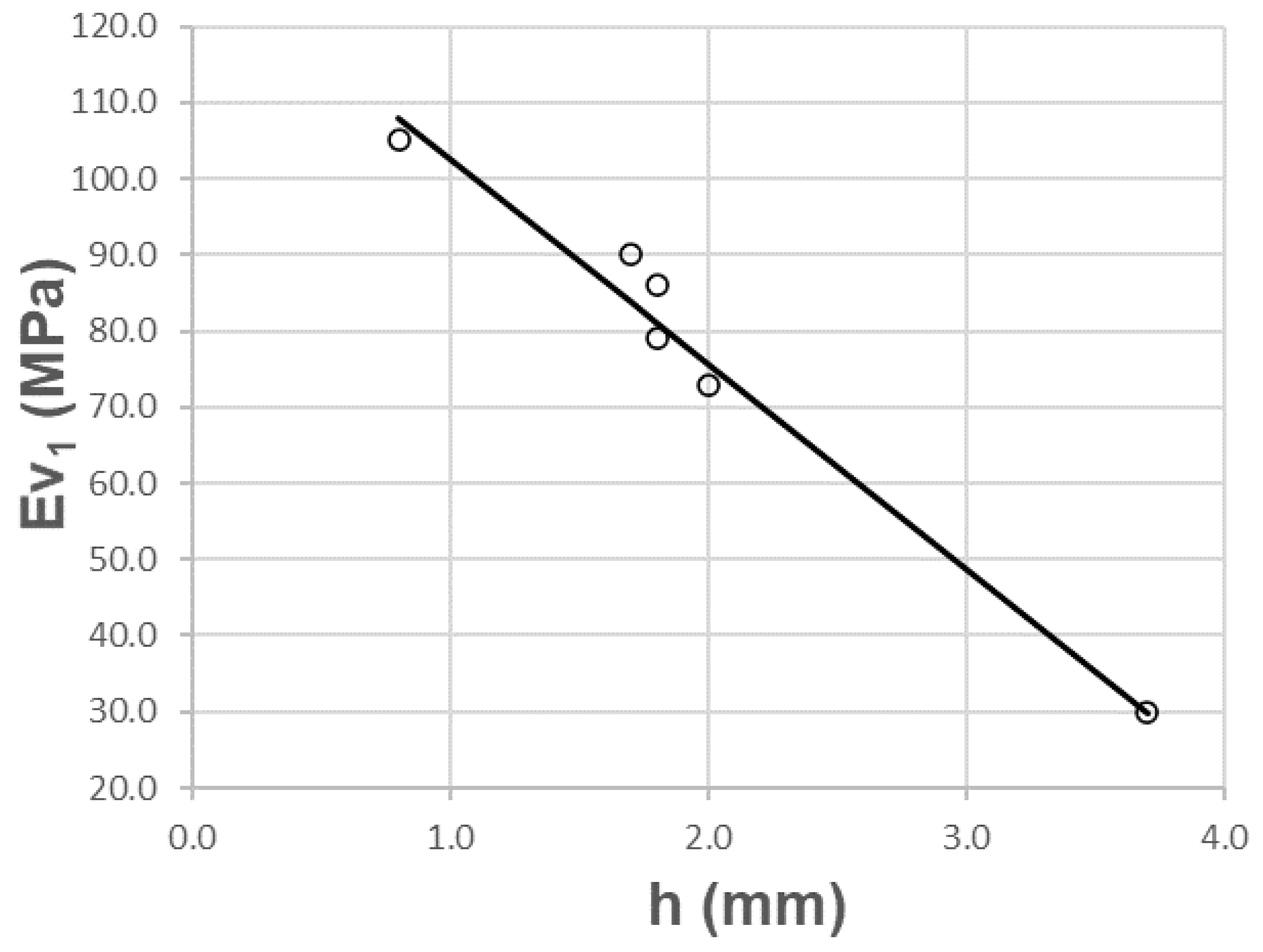
As shown in
Figure 8, there is a high correlation between the wheel-tracking test and the first PBT modulus (ɸ 600 mm), with inverse proportionality. In this case, high values for the wheel-tracking test correspond to low values for the first PBT modulus.
Table 9 shows a high Pearson correlation coefficient value, ρ = 0.990, which is associated with low dispersion. The coefficient of determination R
2 = 0.980 yields a variance of 98%. The standard error is only 4.1934 MPa.
Table 10 shows the ANOVA results. Levene’s test proved significant sig = 0.000 with a value of F = 199.826. Therefore, the null hypothesis of homoscedasticity is rejected, and variances are significantly different.
The
t-test in
Table 11 offers high values, 32.576 and −14.136, both significant (sig = 0).
Moreover, the wheel impression test predicts the first vertical modulus of the plate bearing test. Besides the linear regression coefficients, the fit between the wheel impression test and the first modulus of the PBT (ɸ 600 mm) is:
The domain of the function between the intervals is [20 ≤ Ev1 ≤ 110] and [0.5 ≤ h ≤ 4.5].
3.3. Relation Topographic Settlement Test—First PBT Modulus
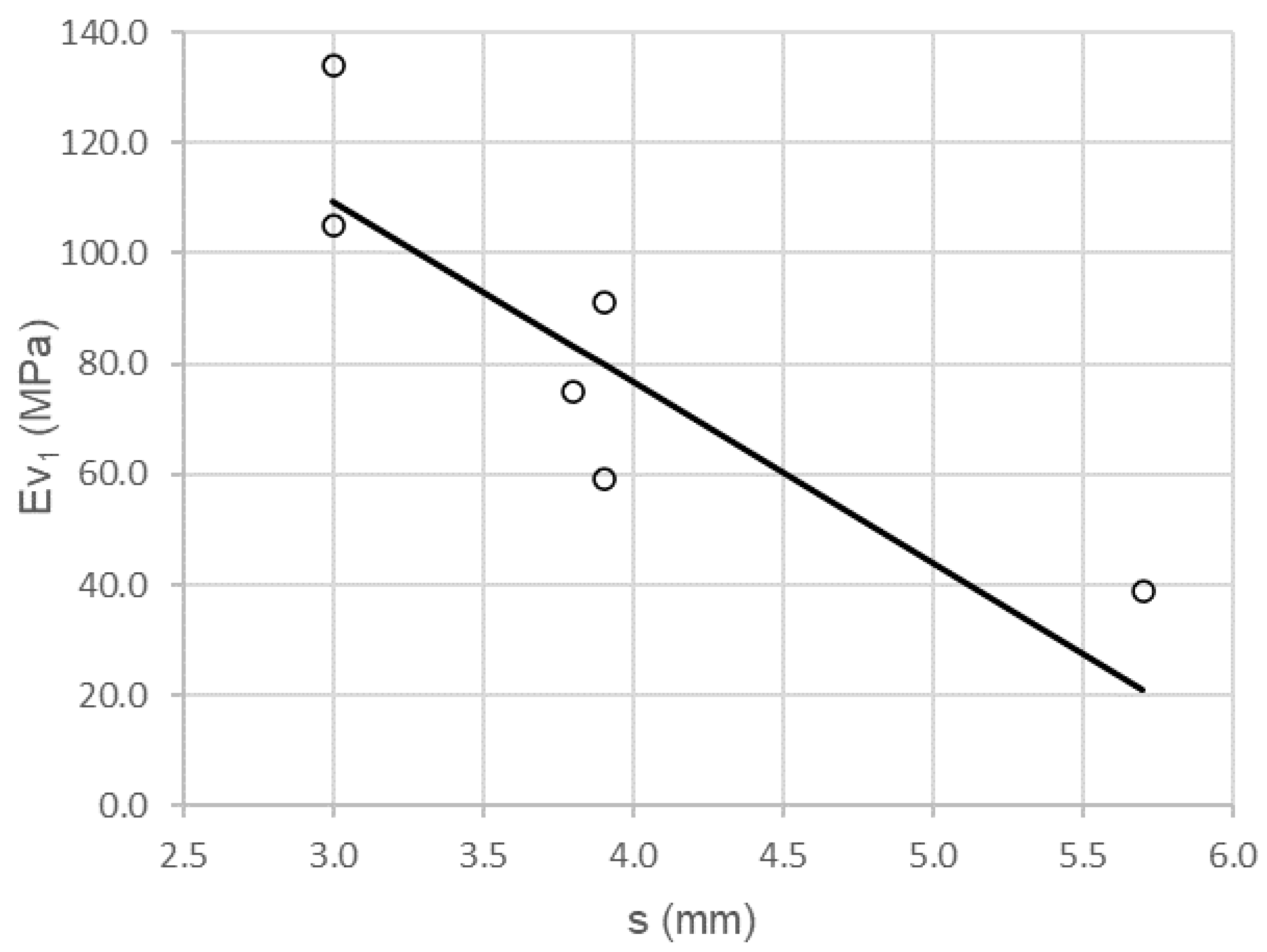
As shown in
Figure 9, there is a strong correlation between the topographic settlement test and the first modulus plate bearing test (ɸ 600 mm).
Table 12 shows a high Pearson correlation coefficient value, ρ = 0.962, and a low standard error of Se = 7.1343 MPa. The coefficient of determination validates a variance of 92.5%. All the parameters suggest a high correlation between both variables.
ANOVA parameters are in
Table 13. Levene’s test is significant, F = 36.847, sig = 0.009. The homoscedasticity criterion is not clearly met. Since the variables are strongly related, variances are significantly different.
Table 14 shows high
t-values of 9.884 and −6.070, which are both significant. The topographic settlement test predicts the first PBT modulus (ɸ 600 mm).
According to the linear regression coefficients, the adjustment line is:
The domain of the function uses the [20 ≤ Ev1 ≤ 100] and [3.0 ≤ s ≤ 6.0] intervals.
3.4. Relation Topographic Settlement Test—Second PBT Modulus
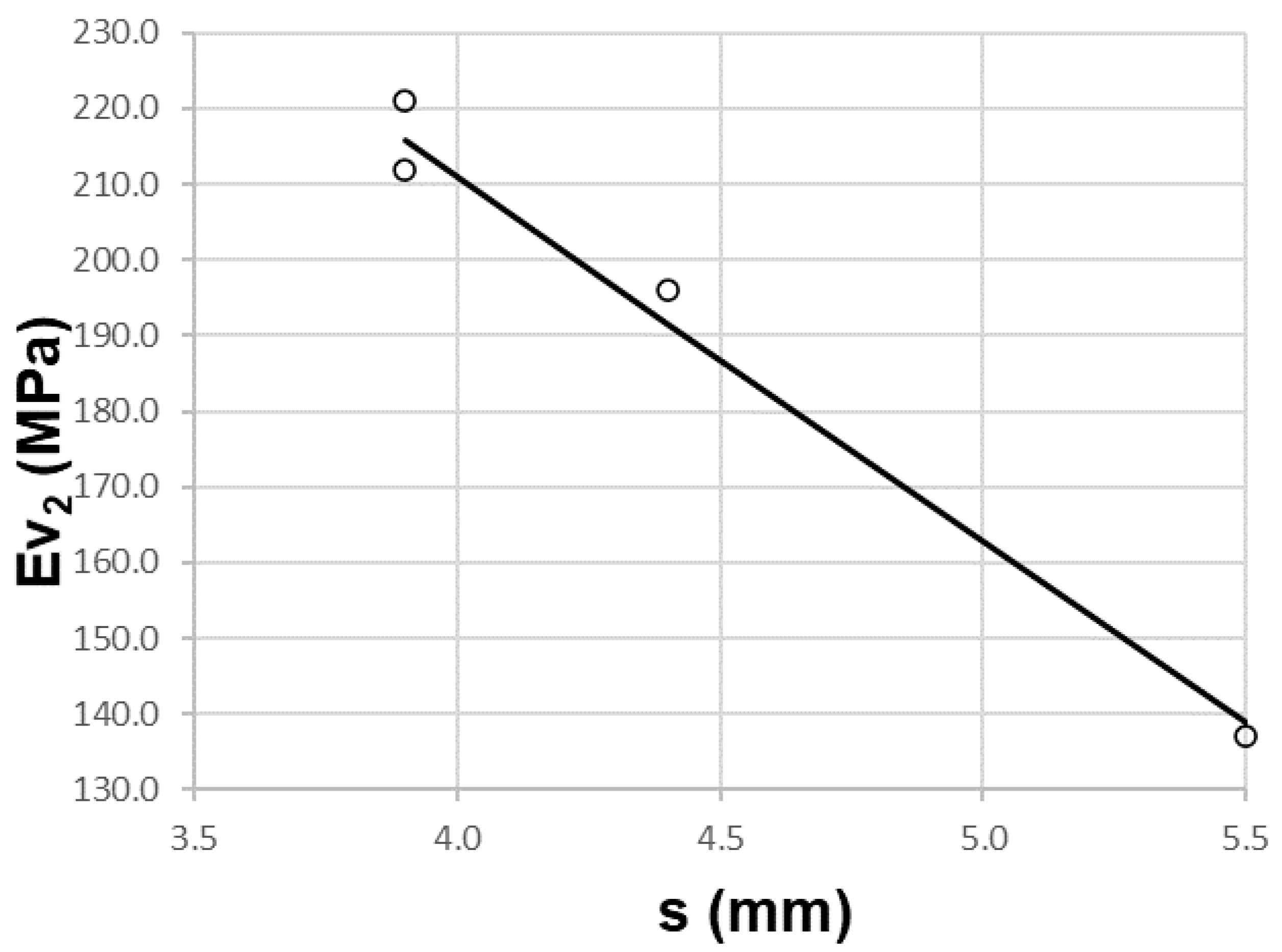
As shown in
Figure 10, there is a high correlation between topographic settlement and first PBT modulus. The distribution is inversely proportional to the lower settlement values corresponding to the higher values of the second PBT modulus (ɸ 600 mm).
Table 15 illustrates a high Pearson correlation coefficient, ρ = 0.995. There is a low standard error Se = 4.5260 MPa and a high coefficient of determination R
2 = 0.990. There is low dispersion.
The ANOVA analysis parameters are shown in
Table 16. Levene’s test is significant, sig = 0.005 with F = 19.251, and therefore, the assumption of homoscedasticity criterion is not met, since variances are different and have a dependency relationship.
Student’s
t test values are significant. As shown in
Table 17, there is a significant contribution of the topographic settlement in the second modulus plate bearing test (ɸ 600 mm).
The expression of the adjustment line is:
The domain of the function has values between [140 ≤ Ev2 ≤ 240] and [3.5 ≤ s ≤ 6.0].
3.5. Significance Matrix
For better understanding, a matrix of significance is shown in
Table 18 with the results obtained. If no relationship was obtained, the numerical value is replaced by ns (nonsignificant). Some elements of the matrix are not considered because they are easily deduced.
The values of the student
t test were grouped in
Table 19.
3.6. Discussion
The wheel impression test has a reduced test length in the batch on a single margin and a low precision due to levelling in soils. With the alternative method, levelling pikes were defined, a higher number of determinations on both ruts and over a larger length. This revision was implemented satisfactorily. In the wheel impression test, a high correlation with other compaction control tests was obtained, which made it possible to replace it as redundant. In addition, the low sensitivity of the test made it possible to further restrict the acceptance threshold to 4 mm. The classical procedure by topographic settlement control is insufficient. A new origin was defined in the penultimate roller pass and the acceptance measure was quantified satisfactorily according to the test section. It is considered essential to limit the execution of big pits due to the operational complexity associated with large sizes. Also, it is necessary to consider the execution of plate load tests on 600 mm plate in random fillings.
The advantages of the revised procedure, compared to the French standard SNV 670 365 “Contrôle du Compactage par essieu de 10 t” are:
Obtaining the compaction degree index in a length five times longer than the initial one, with twice as many measurements for the same section of all-in-one backfill;
Reduction of levelling errors by having a fixed point on the metal levelling spike and not on the ground, guaranteeing millimetric precision;
Increased performance by reducing test times, with the first measurement being made on the picks without the need to move the heavy metal support used in the measurement;
The possible dynamic effects of acceleration/braking of the truck are minimized by increasing the distance travelled and increasing the time taken for the truck to establish a constant speed when passing over the cutting tools;
With two measurements per profile, a more complete check of the all-one fill section is made than with a single point. By measuring in two parallel and independent tracks, any deficiencies in one track are corrected. In addition, second-order effects such as the weight of the driver or the fuel tank are no longer considered in the test;
The in-situ density did not correlate with any other variable. Alternatively, with the first PBT modulus (ɸ 600 mm), the wheel-tracking and topographic settlement tests proved to have a strong relationship. A revised control method was designed for the in-situ density test and the PBT.
There is a strong correlation between the revised topographic settlement test and the plate bearing test (ɸ 600 mm) so the PBT can be easily replaced. With significant improvements in both the topographic settlement test and the wheel impression test, the PBT is associated with both, so the PBT (ɸ 600 mm) can replace these tests in quality control.
The nuclear methods have a low efficiency, limited by a maximum test thickness of 300 mm and the high variability of the materials. Therefore, the PBT (ɸ 600 mm) is proposed as the most representative test to define the degree of compaction in the new control method. As this test is strongly associated with surface moisture, it should be carried out in the same area of validity as the optimum moisture obtained in the modified Proctor.
As factors that can potentially produce errors in the results, the Proctor test is rarely used as a reference in such heterogeneous and unconventional materials as random fillings. The nuclear densimeter offers specific problems of the presence of rock, with the absence of fines, which does not allow the gamma radiation emitting stem to be introduced into the compacted layer in the presence of rock with medium–high hardness. Thus, the comparison with a reference Proctor loses interest due to its low representativeness, as it is mostly made with the less common fraction by replacing the larger sizes with fines, specifically those retained by the 20 mm sieve.