Target-Oriented User Equilibrium Considering Travel Time, Late Arrival Penalty, and Travel Cost on the Stochastic Tolled Traffic Network
Abstract
1. Introduction
2. Target-Oriented Multi-Attribute Travel Utility Model
2.1. Review of the Target-Oriented Methodology
2.2. Network Representation and Attributes
2.2.1. Stochastic Route Travel Time and Its Corresponding Target
2.2.2. Stochastic Route LAP and Its Corresponding Target
2.2.3. Deterministic Route Travel Cost and Its Corresponding Target
2.3. Joint Probability Evaluation Derived from the Marginal Distributions
2.4. Target Interaction
3. Target-Oriented Multi-Attribute User Equilibrium
3.1. Equilibrium Condition
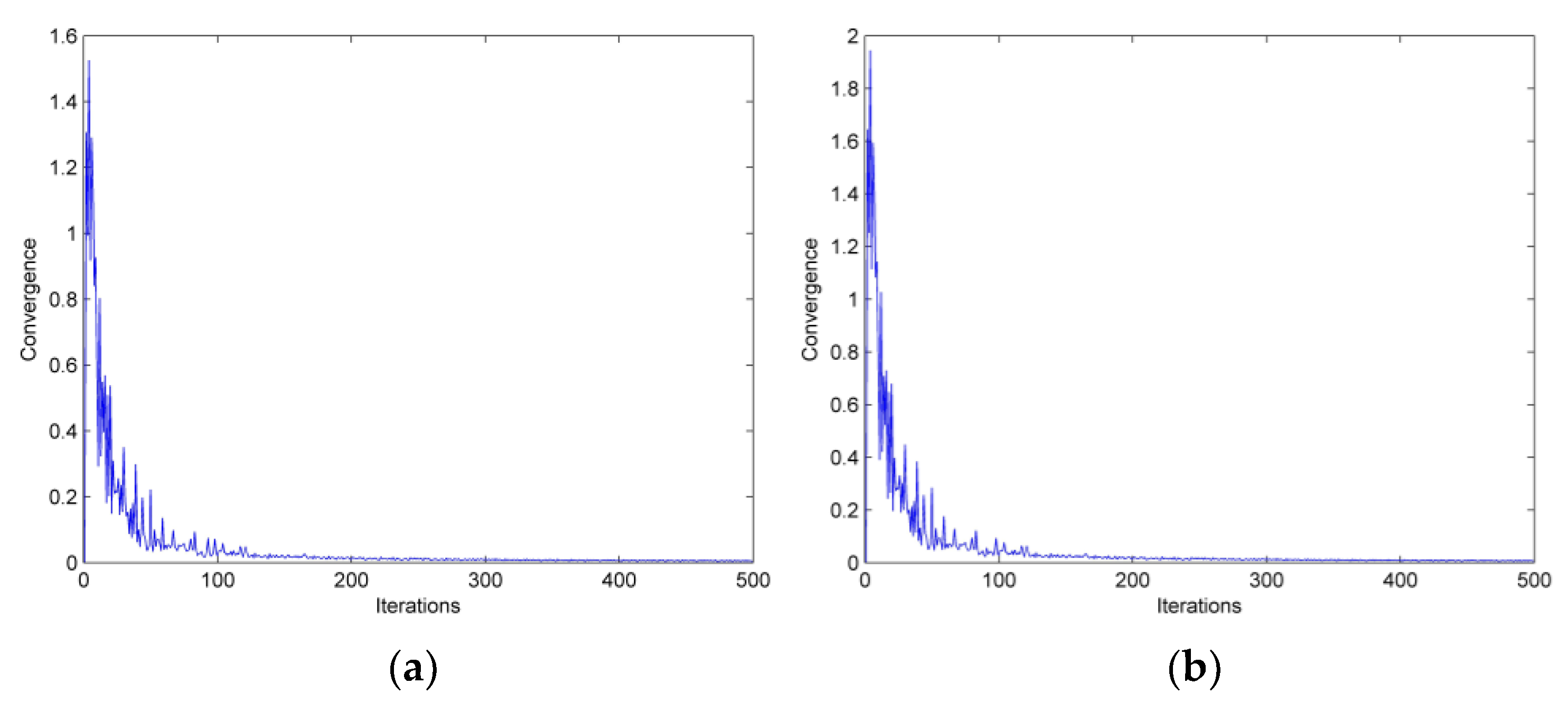
3.2. Solution Algorithm
- Stage 0: Initialization. Set the value of the convergence tolerance as , which means the maximum number of iterations, as well as .
- Stage 1: All-Or-Nothing assignment. Conduct all-or-nothing assignment in terms of the present vacant link flow , as well as obtain the flow of route connecting each pair.
- Stage 2: Link flow, route travel time distribution and route LAP distribution updating. According to the present flow of route, orderly update the flow of its link, the route travel time distribution, and the route LAP distribution.
- Stage 3: Calculation for ToMaTU. Acquire the value of ToMaTU based on Equation (10) or (11), and obtain the maximum route utility .
- Stage 4: Check the Convergence. Set . Stop the algorithm if or the maximum number of iterations is reached, if not, go to Stage 5.
- Stage 5: Route flow updating. Detect the direction of search () and the step size () judging from the present values, and the flow of route is updated as the rule , and go the Stage 2. Set the direction of search as , where is called as auxiliary flow. If , with being the number of routes that have the maximum value of ToMaRUs in step for pair , and otherwise, is 0. The step size is set as .
4. Numerical Analysis
4.1. Test on the Braess Traffic Network
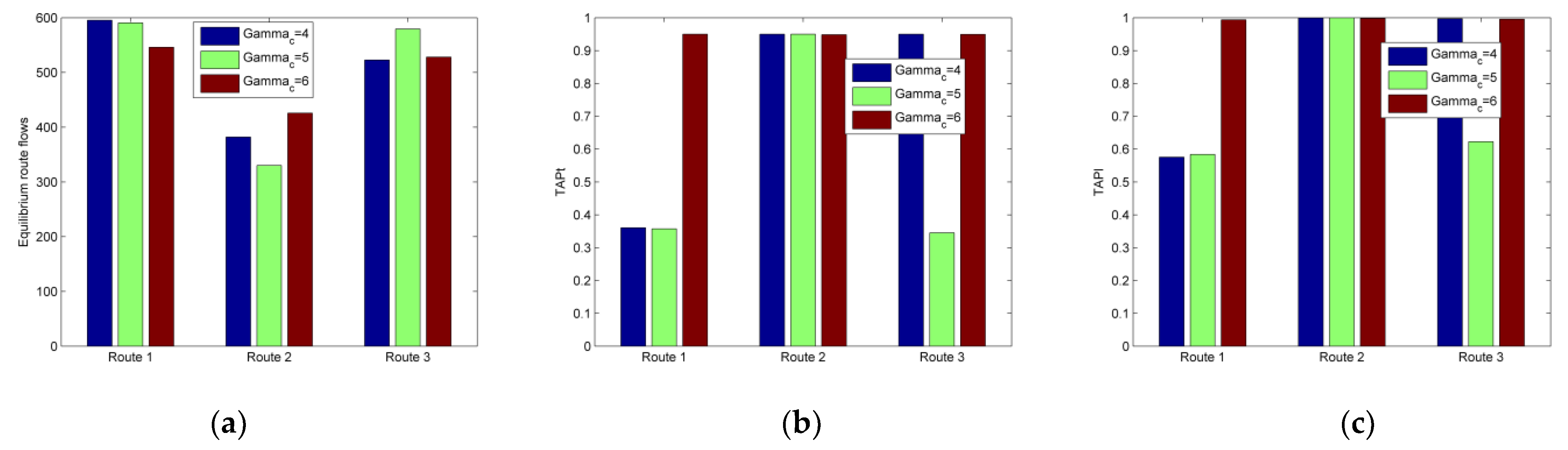
4.1.1. Sensitivity Analysis via Changing
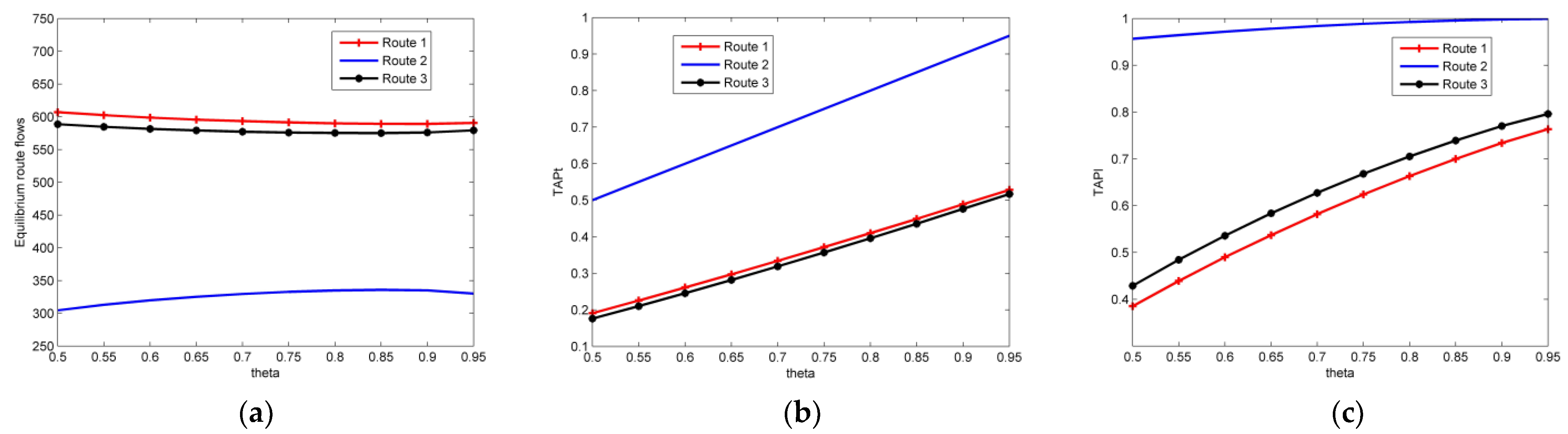
4.1.2. Sensitivity Analysis via Changing
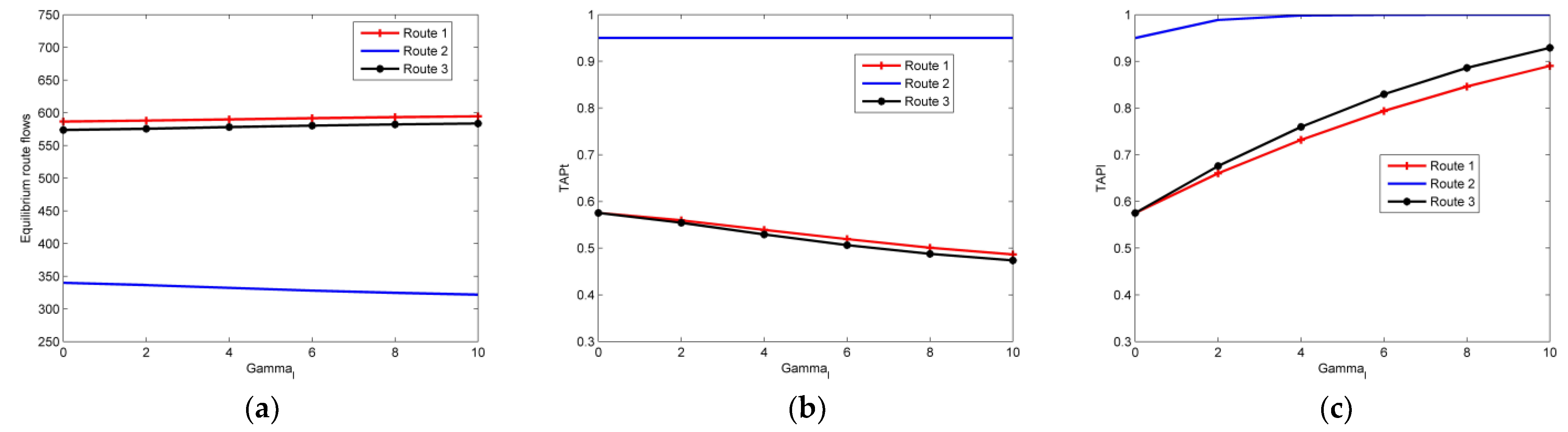
4.1.3. Sensitivity Analysis via Changing
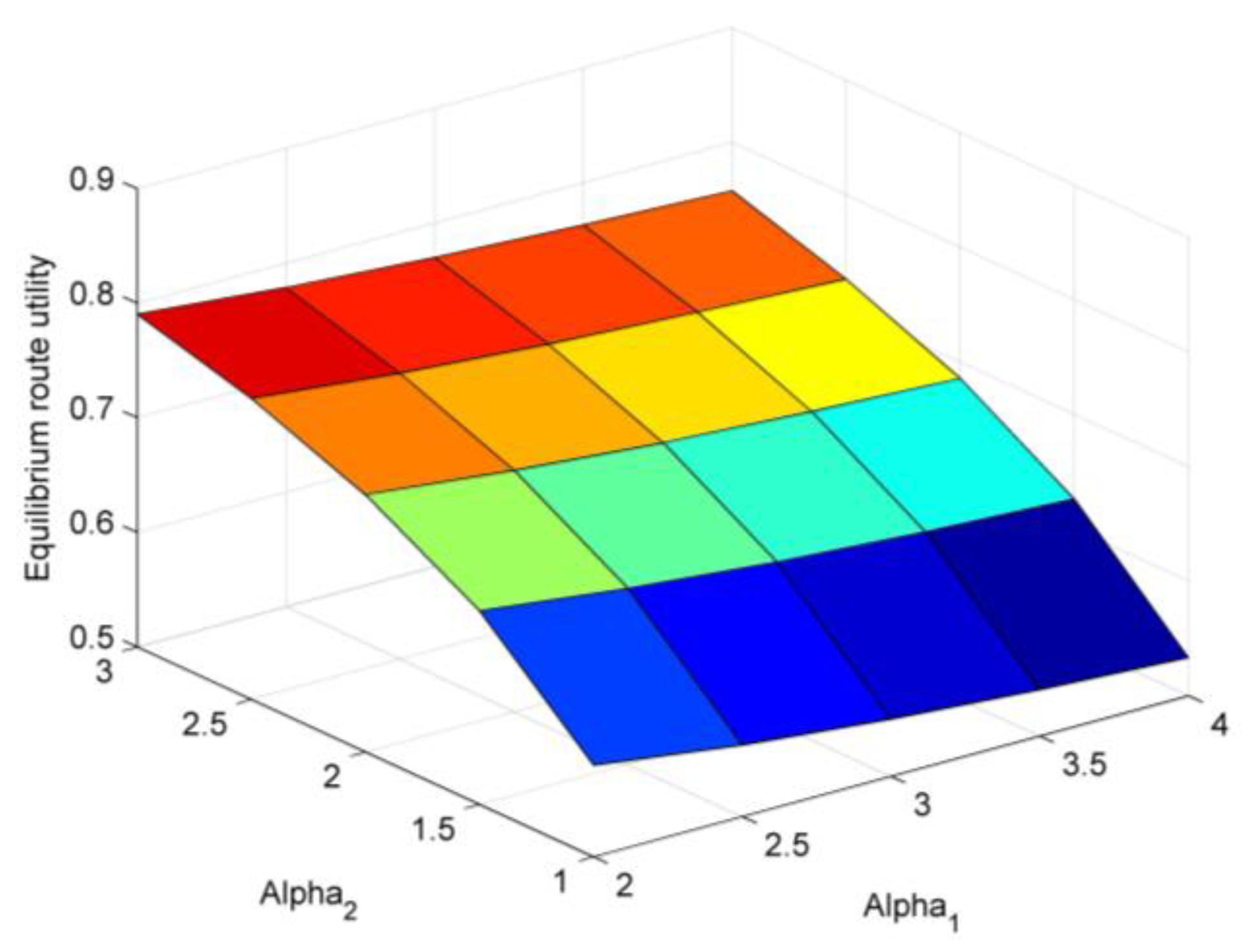
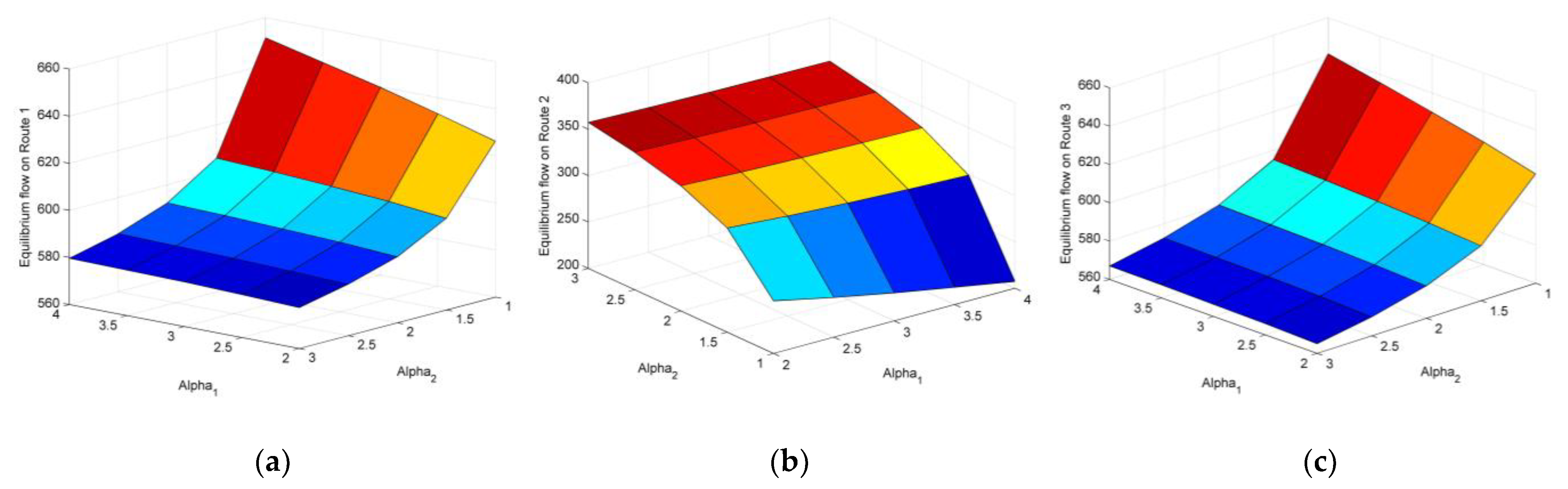
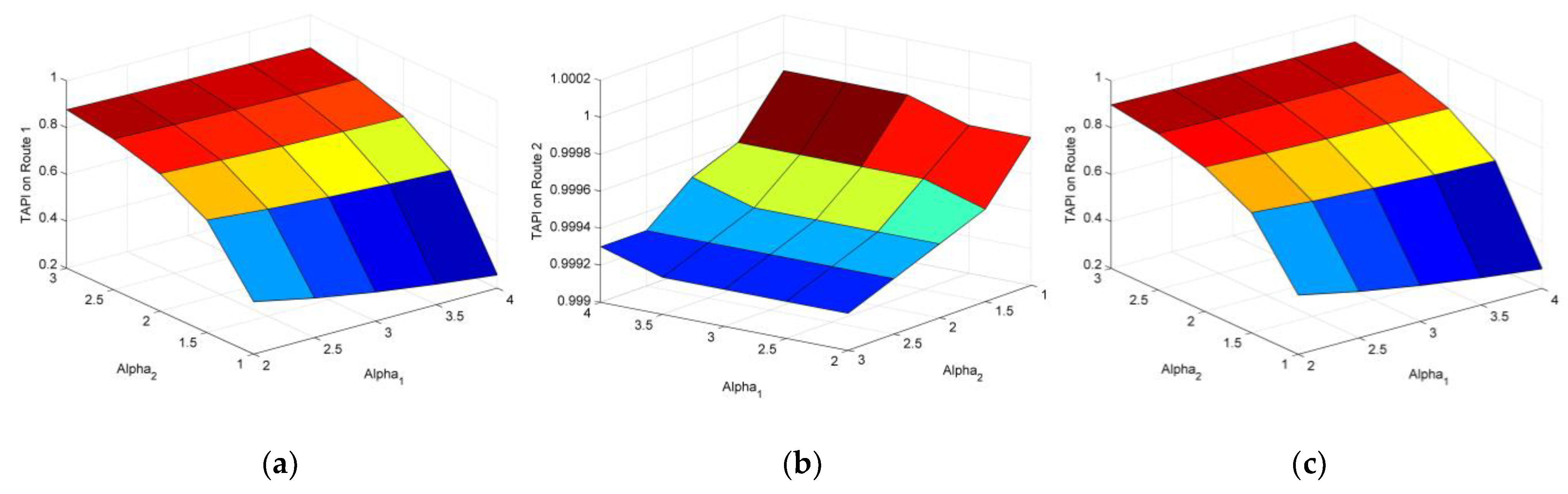
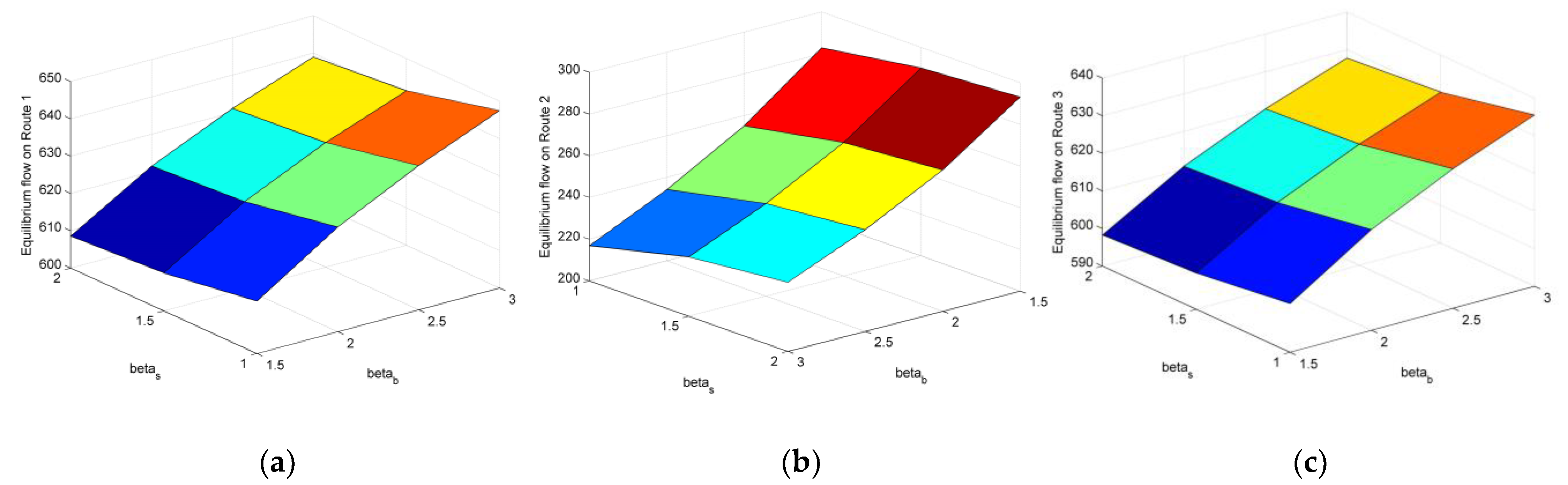
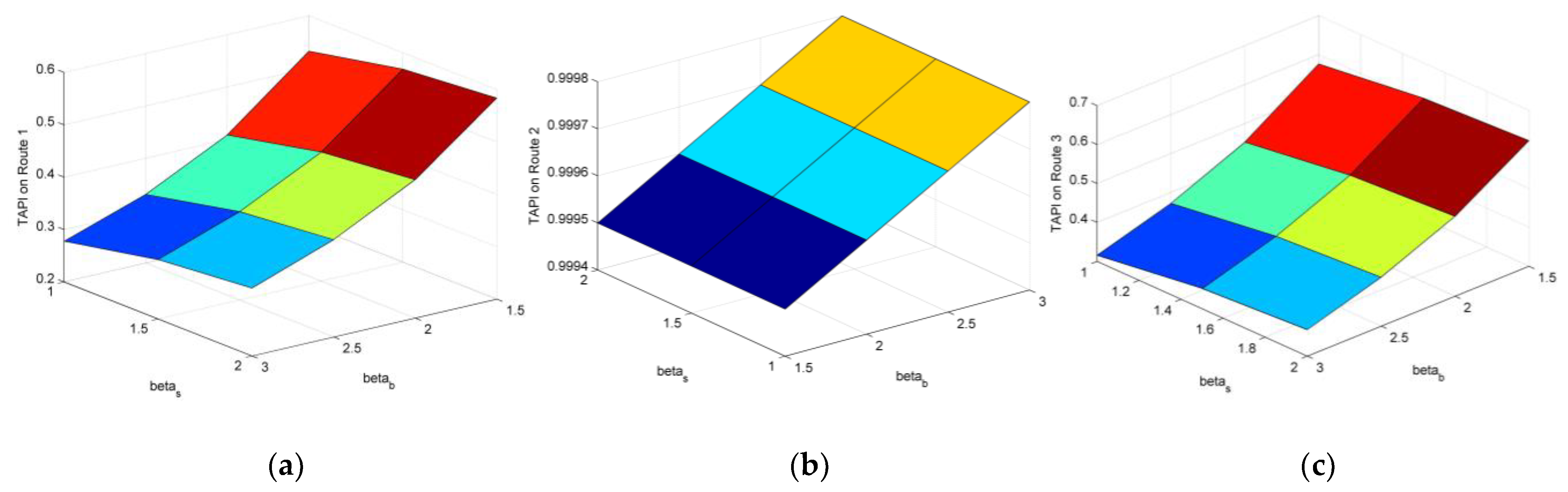
4.1.4. Sensitivity Analysis via Changing and
4.1.5. Sensitivity Analysis via Changing and
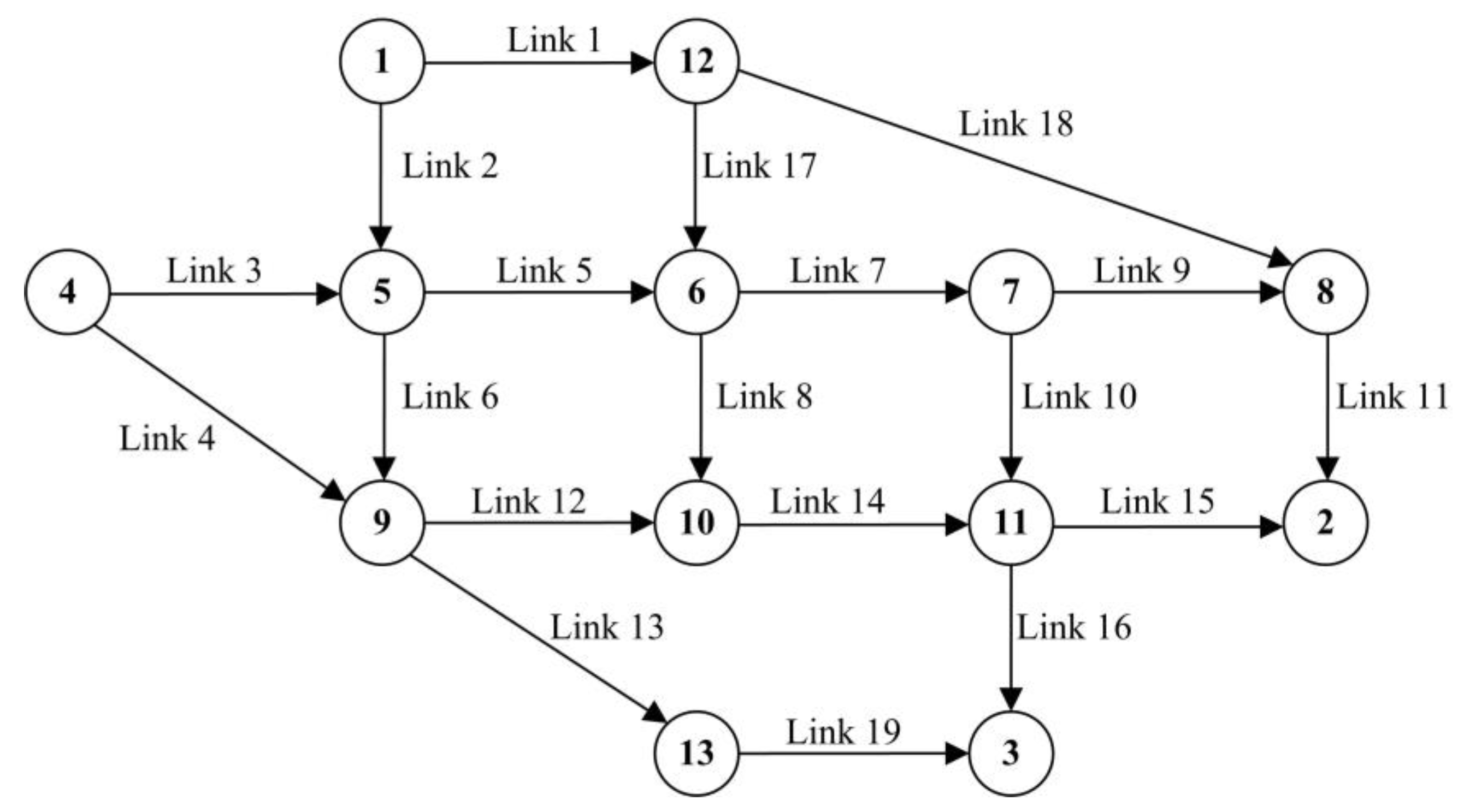
4.2. Test on the Nguyen and Dupuis’s Traffic Network
4.3. Insights of the Sensitivity Analysis
- (1)
- For some routes, where the target set for travel cost can be successfully reached (depending on travelers’ acceptable expense), target achievement probability for travel time is smaller than travelers’ on-time arrival probability, which means travelers become less risk-averse or even risk-seeking in order to achieve the three targets simultaneously. Meanwhile, on these kinds of routes, target achievement probability for late arrival penalty is also not very large, unless the allowable delay of the company is large; the relative significance between the achievements of the target set for travel cost and travel time is relatively large, or the extent of target interaction among three targets is small. That is, travelers usually bear the risk of violating the allowable delay of the company in order to achieve the three targets simultaneously, unless the aforementioned situations happen.
- (2)
- For some routes, where the target set for travel cost fails to be reached (depending on travelers’ acceptable expense), the probability of achieving the target for travel time is travelers’ on-time arrival probability, and the probability of achieving the target for late arrival penalty is almost 1, which are always valid in all the testing.
- (3)
- The equilibrium route flow distribution changes when the values of the three targets, the relative importance between different target achievements, and the target interaction change. Usually, travelers prefer the routes where the target set for travel cost can be successfully reached, which can be impacted by their risk-averse attitude, and the allowable delay of the company, but our testing shows that these impacts are not significant. If achieving the target for travel cost takes on greater importance, flows will shift from the routes where this target cannot be achieved to the routes where this target can be achieved in general, but the target achievements of travel time and late arrival penalty have impact on this flow shift. Meanwhile, the impact of the former one is larger. When the extent of the interaction among three targets become stronger, more travelers will choose the routes where the three targets can be achieved simultaneously, but stronger extent of the interaction between two targets could weaken this impact.
- (4)
- The equilibrium route utility changes when the values of the three targets, the relative importance between different target achievements, and the target interaction change. From our testing, travelers’ larger acceptable expense and stronger extent of risk-averse attitude leads to the larger equilibrium route utility, but the allowable delay of the company has almost no impact on this. When the relative significance between the achievements of the target set for travel cost and travel time becomes larger, the equilibrium route utility is larger, but the target interaction, among three targets or between two targets, can decrease the equilibrium route utility.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Umar, M.; Ji, X.; Kirikkaleli, D.; Xu, Q. COP21 Roadmap: Do Innovation, Financial Development, and Transportation Infrastructure Matter for Environmental Sustainability in China? J. Environ. Manag. 2020, 271, 111026. [Google Scholar] [CrossRef]
- Wardrop, J.G. Road paper. Some theoretical aspects of road traffic research. Proc. Inst. Civ. Eng. 1952, 1, 325–362. [Google Scholar] [CrossRef]
- Xu, H.; Lou, Y.; Yin, Y.; Zhou, J. A prospect-based user equilibrium model with endogenous reference points and its application in congestion pricing. Transp. Res. Part B-Methodol. 2011, 45, 311–328. [Google Scholar] [CrossRef]
- Chen, A.; Zhou, Z. The α-Reliable mean-excess traffic equilibrium model with stochastic travel times. Transp. Res. Part B-Methodol. 2010, 44, 493–513. [Google Scholar] [CrossRef]
- Ji, X.; Ban, X.; Zhang, J.; Ran, B. Moment-based travel time reliability assessment with Lasserre’s relaxation. Transp. B-Transp. Dyn. 2019, 7, 401–422. [Google Scholar] [CrossRef]
- Khight, F.H. Risk, Uncertainty, and Profit; Houghton Mifflin: Boston, MA, USA, 1921. [Google Scholar]
- Ji, X.; Ban, X.; Zhang, J.; Ran, B. Subjective-utility travel time budget modeling in the stochastic traffic network assignment. J. Intell. Transport. Syst. 2017, 21, 439–451. [Google Scholar] [CrossRef]
- Ji, X.; Ban, X.; Li, M.; Zhang, J.; Ran, B. Non-expected route choice model under risk on stochastic traffic networks. Netw. Spat. Econ. 2017, 17, 777–807. [Google Scholar] [CrossRef]
- Li, X.; Natarajan, K.; Teo, C.-P.; Zheng, Z. Distributionally robust mixed integer linear programs: Persistency models with applications. Eur. J. Oper. Res. 2014, 233, 459–473. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, S.; Shen, Z.-J.M.; Wu, C. Robust shortest path problem with distributional uncertainty. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1080–1090. [Google Scholar] [CrossRef]
- Wang, Z.; You, K.; Song, S.; Zhang, Y. Wasserstein distributionally robust shortest path problem. Eur. J. Oper. Res. 2020, 284, 31–43. [Google Scholar] [CrossRef]
- Lo, H.K.; Luo, X.W.; Siu, B.W.Y. Degradable transport network: Travel time budget of travelers with heterogeneous risk aversion. Transp. Res. Part B-Methodol. 2006, 40, 792–806. [Google Scholar] [CrossRef]
- Abdel-Aty, M.; Kitamura, R.; Jovanis, P. Investigating effect of travel time variability on route choice using repeated measurement stated preference. Data. Transp. Res. Rec. 1995, 1493, 39–45. [Google Scholar]
- Brownstone, D.; Ghosh, A.; Golob, T.F.; Kazimi, C.; Van Amelsfort, D. Drivers’ willingness-to-pay to reduce travel time: Evidence from the San Diego I-15 Congestion Pricing Project. Transp. Res. Part A-Policy Pract. 2003, 37, 373–387. [Google Scholar] [CrossRef]
- Ji, X.; Ao, X. Travelers’ bi-attribute decision making on the risky mode choice with flow-dependent salience theory. Sustainability 2021, 13, 3901. [Google Scholar] [CrossRef]
- Xu, Q.; Ji, X. User equilibrium analysis considering travelers’ context-dependent route choice behavior on the risky traffic network. Sustainability 2020, 12, 6706. [Google Scholar] [CrossRef]
- Yang, H.; Huang, H.-J. The multi-class, multi-criteria traffic network equilibrium and systems optimum problem. Transp. Res. Part B-Methodol. 2004, 38, 1–15. [Google Scholar] [CrossRef]
- Watling, D. User equilibrium traffic network assignment with stochastic travel times and late arrival penalty. Eur. J. Oper. Res. 2006, 175, 1539–1556. [Google Scholar] [CrossRef]
- Wang, J.Y.T.; Ehrgott, M.; Chen, A. A bi-objective user equilibrium model of travel time reliability in a road network. Transp. Res. Part B-Methodol. 2014, 66, 4–15. [Google Scholar] [CrossRef]
- Ehrgott, M.; Wang, J.Y.T.; Watling, D.P. On multi-objective stochastic user equilibrium. Transp. Res. Part B-Methodol. 2015, 81, 704–717. [Google Scholar] [CrossRef][Green Version]
- Sun, C.; Cheng, L.; Zhu, S.; Han, F.; Chu, Z. Multi-criteria user equilibrium model considering travel time, travel time reliability and distance. Transport. Res. Part D-Transport. Environ. 2019, 66, 3–12. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Kemel, E.; Paraschiv, C. Prospect theory for joint time and money consequences in risk and ambiguity. Transp. Res. Part B-Methodol. 2013, 56, 81–95. [Google Scholar] [CrossRef]
- Avineri, E. The effect of reference point on stochastic network equilibrium. Transp. Sci. 2006, 40, 409–420. [Google Scholar] [CrossRef]
- Schwanen, T.; Ettema, D. Coping with unreliable transportation when collecting children: Examining parents’ behavior with cumulative prospect theory. Transp. Res. Part A-Policy Pract. 2009, 43, 511–525. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, T.-L.; Huang, H.-J.; Chen, J. A cumulative prospect theory approach to commuters’ day-to-day route-choice modeling with friends’ travel information. Transp. Res. Part C-Emerg. Technol. 2018, 86, 527–548. [Google Scholar] [CrossRef]
- Ghader, S.; Darzi, A.; Zhang, L. Modeling effects of travel time reliability on mode choice using cumulative prospect theory. Transp. Res. Part C-Emerg. Technol. 2019, 108, 245–254. [Google Scholar] [CrossRef]
- Hu, L.; Dong, J.; Lin, Z. Modeling charging behavior of battery electric vehicle drivers: A cumulative prospect theory based approach. Transp. Res. Part C-Emerg. Technol. 2019, 102, 474–489. [Google Scholar] [CrossRef]
- Ji, X.; Chu, Y. A target-oriented bi-attribute user equilibrium model with travelers’ perception errors on the tolled traffic network. Transp. Res. Part E-Logist. Transp. Rev. 2020, 144, 102150. [Google Scholar] [CrossRef]
- Ji, X. User-equilibrium-based investigation on the usage of tolled routes: A target-oriented perspective. Transp. Res. Part E-Logist. Transp. Rev. 2021. under review. [Google Scholar]
- Gao, S.; Frejinger, E.; Ben-Akiva, M. Adaptive route choices in risky traffic networks: A prospect theory approach. Transp. Res. Part C-Emerg. Technol. 2010, 18, 727–740. [Google Scholar] [CrossRef]
- Boyles, S.D.; Waller, S.T. Optimal information location for adaptive routing. Netw. Spat. Econ. 2011, 11, 233–254. [Google Scholar] [CrossRef]
- Gao, S.; Huang, H. Real-time traveler information for optimal adaptive routing in stochastic time-dependent networks. Transp. Res. Part C-Emerg. Technol. 2012, 21, 196–213. [Google Scholar] [CrossRef]
- Miller-Hooks, E. Adaptive least-expected time paths in stochastic, time-varying transportation and data networks. Networks 2001, 37, 35–52. [Google Scholar] [CrossRef]
- Unnikrishnan, A.; Waller, S.T. User equilibrium with recourse. Netw. Spat. Econ. 2009, 9, 575–593. [Google Scholar] [CrossRef]
- Unnikrishnan, A.; Lin, D.-Y. User equilibrium with recourse: Continuous network design problem. Comput-Aided Civ. Inf. 2012, 27, 512–524. [Google Scholar] [CrossRef]
- Wijayaratna, K.P.; Dixit, V.V.; Denant-Boemont, L.; Waller, S.T. An experimental study of the online information paradox: Does en-route information improve road network performance? PLoS ONE 2017, 12, e0184191. [Google Scholar] [CrossRef]
- Wijayaratna, K.P.; Dixit, V.V. Impact of information on risk attitudes: Implications on valuation of reliability and information. J. Choice Model. 2016, 20, 16–34. [Google Scholar] [CrossRef]
- Lo, H.K.; Tung, Y.-K. Network with degradable links: Capacity analysis and design. Transp. Res. Part B-Methodol. 2003, 37, 345–363. [Google Scholar] [CrossRef]
- Shao, H.; Lam, W.H.K.; Tam, M.L. A reliability-based stochastic traffic assignment model for network with multiple user classes under uncertainty in demand. Netw. Spat. Econ. 2006, 6, 173–204. [Google Scholar] [CrossRef]
- Ji, X.; Cheng, H.; Ao, X.; Zhou, X. Modeling travel time reliability and unreliability on the stochastic traffic network with target-oriented analysis. Ann. Oper. Res. 2021. under review. [Google Scholar]
- Isac, G.; Bulavsky, V.A.; Kalashnikov, V.V. Complementarity, Equilibrium, Efficiency and Economics; Springer: Boston, MA, USA, 2013. [Google Scholar]
- Nagurney, A. Network Economics: A Variational Inequality Approach; Springer: Boston, MA, USA, 2013. [Google Scholar]
- Facchinei, F.; Pang, J.-S. Finite-Dimensional Variational Inequalities and Complementarity Problems; Springer Series in Operations Research and Financial Engineering; Springer: Boston, MA, USA, 2003. [Google Scholar]
- Nikolova, E.; Stier-Moses, N. A mean-risk model for the traffic assignment problem with stochastic travel times. Oper. Res. 2014, 62, 366–382. [Google Scholar] [CrossRef]
- Sheffi, Y. Urban Transportation Networks: Equilibrium Analysis With Mathematical Programming Methods; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Nguyen, S.; Dupuis, C. An efficient method for computing traffic equilibria in networks with asymmetric transportation costs. Transp. Sci. 1984, 18, 185–202. [Google Scholar] [CrossRef]
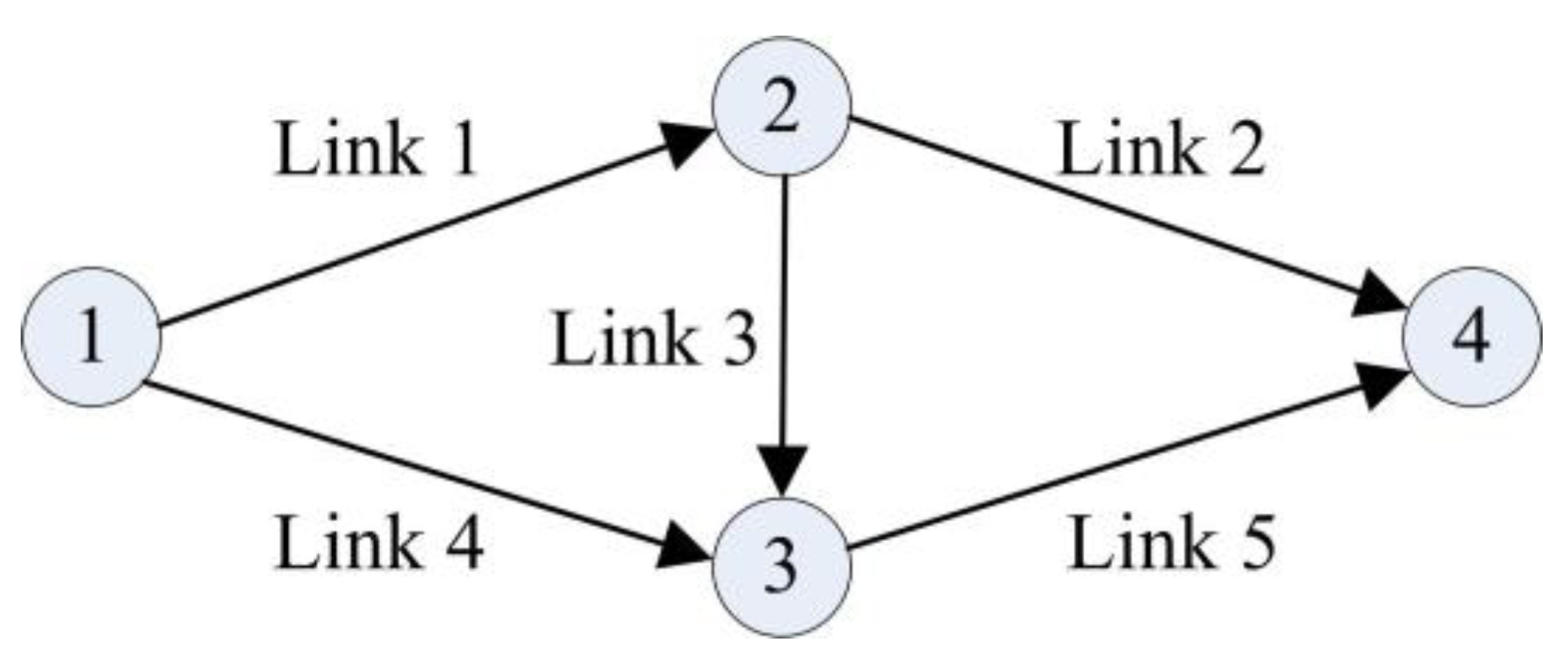



| Link Number | Free-Flow Travel Time | Capacity | Toll | ϕ |
|---|---|---|---|---|
| 1 | 5 | 600 | 2 | 0.8 |
| 2 | 12 | 400 | 2 | 0.7 |
| 3 | 7 | 400 | 2 | 0.9 |
| 4 | 10 | 400 | 3 | 0.7 |
| 5 | 8 | 600 | 2 | 0.8 |
| Link Number | Free-Flow Travel Time | Capacity | Toll | ϕ |
|---|---|---|---|---|
| 1 | 5 | 600 | 3.5 | 0.8 |
| 2 | 12 | 400 | 8 | 0.9 |
| 3 | 7 | 400 | 5 | 0.8 |
| 4 | 10 | 400 | 6 | 0.8 |
| 5 | 8 | 600 | 6 | 0.7 |
| 6 | 6 | 500 | 4 | 0.8 |
| 7 | 10 | 500 | 7 | 0.6 |
| 8 | 10 | 400 | 8 | 0.8 |
| 9 | 8 | 600 | 5 | 0.8 |
| 10 | 6 | 500 | 4 | 0.9 |
| 11 | 12 | 400 | 9 | 0.9 |
| 12 | 11 | 600 | 8 | 0.9 |
| 13 | 6 | 600 | 4 | 0.7 |
| 14 | 8 | 500 | 5 | 0.8 |
| 15 | 9 | 500 | 6 | 0.8 |
| 16 | 10 | 400 | 6 | 0.9 |
| 17 | 12 | 400 | 10 | 0.8 |
| 18 | 8 | 600 | 5 | 0.9 |
| 19 | 10 | 500 | 7 | 0.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zang, X.; Guo, Z.; Ma, J.; Zhong, Y.; Ji, X. Target-Oriented User Equilibrium Considering Travel Time, Late Arrival Penalty, and Travel Cost on the Stochastic Tolled Traffic Network. Sustainability 2021, 13, 9992. https://doi.org/10.3390/su13179992
Zang X, Guo Z, Ma J, Zhong Y, Ji X. Target-Oriented User Equilibrium Considering Travel Time, Late Arrival Penalty, and Travel Cost on the Stochastic Tolled Traffic Network. Sustainability. 2021; 13(17):9992. https://doi.org/10.3390/su13179992
Chicago/Turabian StyleZang, Xinming, Zhenqi Guo, Jingai Ma, Yongguang Zhong, and Xiangfeng Ji. 2021. "Target-Oriented User Equilibrium Considering Travel Time, Late Arrival Penalty, and Travel Cost on the Stochastic Tolled Traffic Network" Sustainability 13, no. 17: 9992. https://doi.org/10.3390/su13179992
APA StyleZang, X., Guo, Z., Ma, J., Zhong, Y., & Ji, X. (2021). Target-Oriented User Equilibrium Considering Travel Time, Late Arrival Penalty, and Travel Cost on the Stochastic Tolled Traffic Network. Sustainability, 13(17), 9992. https://doi.org/10.3390/su13179992







