Characterization of Ionic Exchange and Macroporous Resins for Their Application on the Separation and Recovery of Chlorogenic Acid from the Wastewater of Artichoke Blanching
Abstract
:1. Introduction
2. Materials and Methods
2.1. Feed Solution
2.2. Adsorbents
2.3. Resin Performance
2.4. Effect of the pH on the Adsorption Process
2.5. Adsorption Isotherms
2.6. Adsorption and Desorption Kinetics
2.7. Analytical Determinations
3. Results and Discussion
3.1. Resin Performance
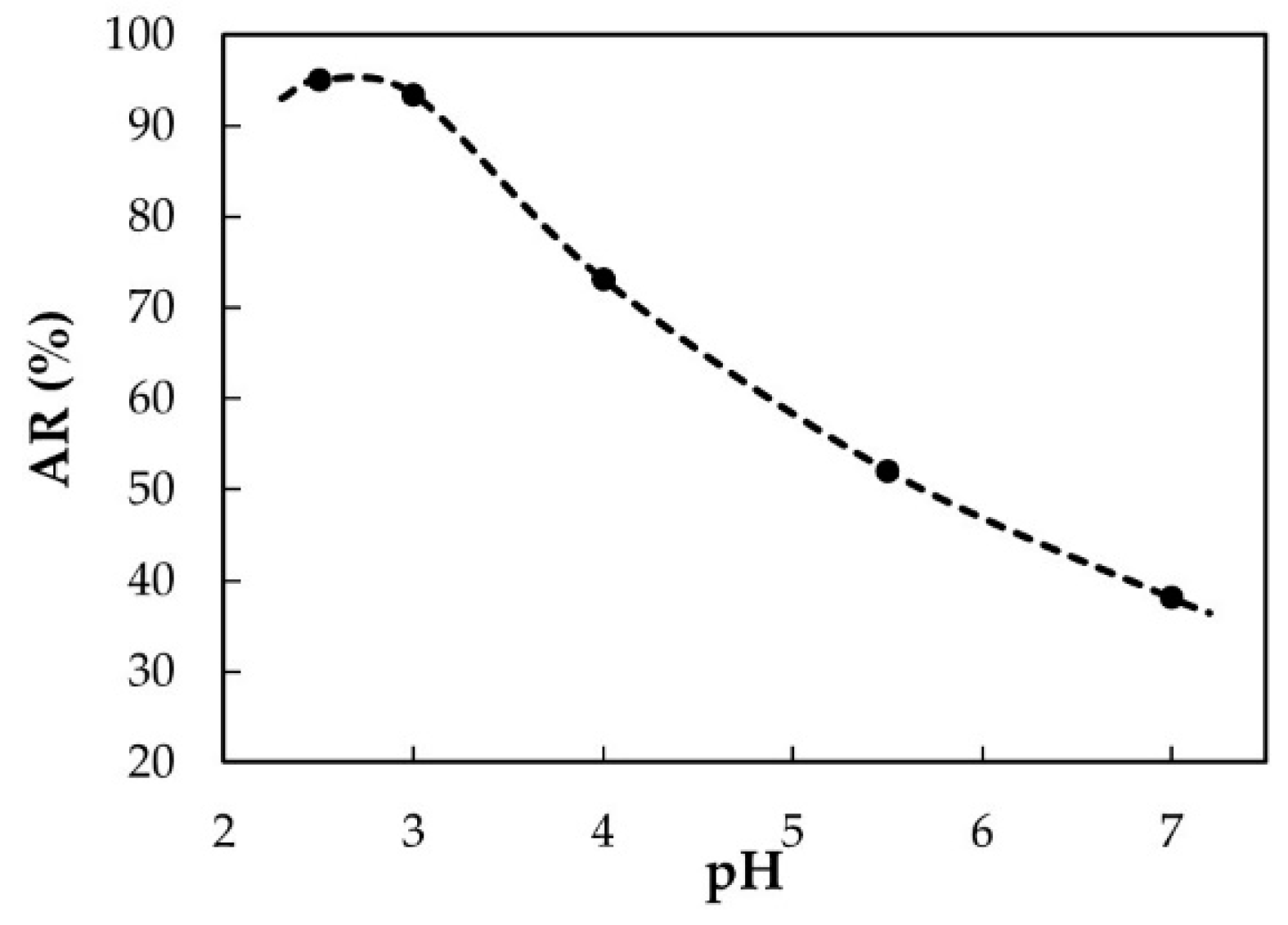
3.2. Effect of pH on the Chlorogenic Acid Adsorption
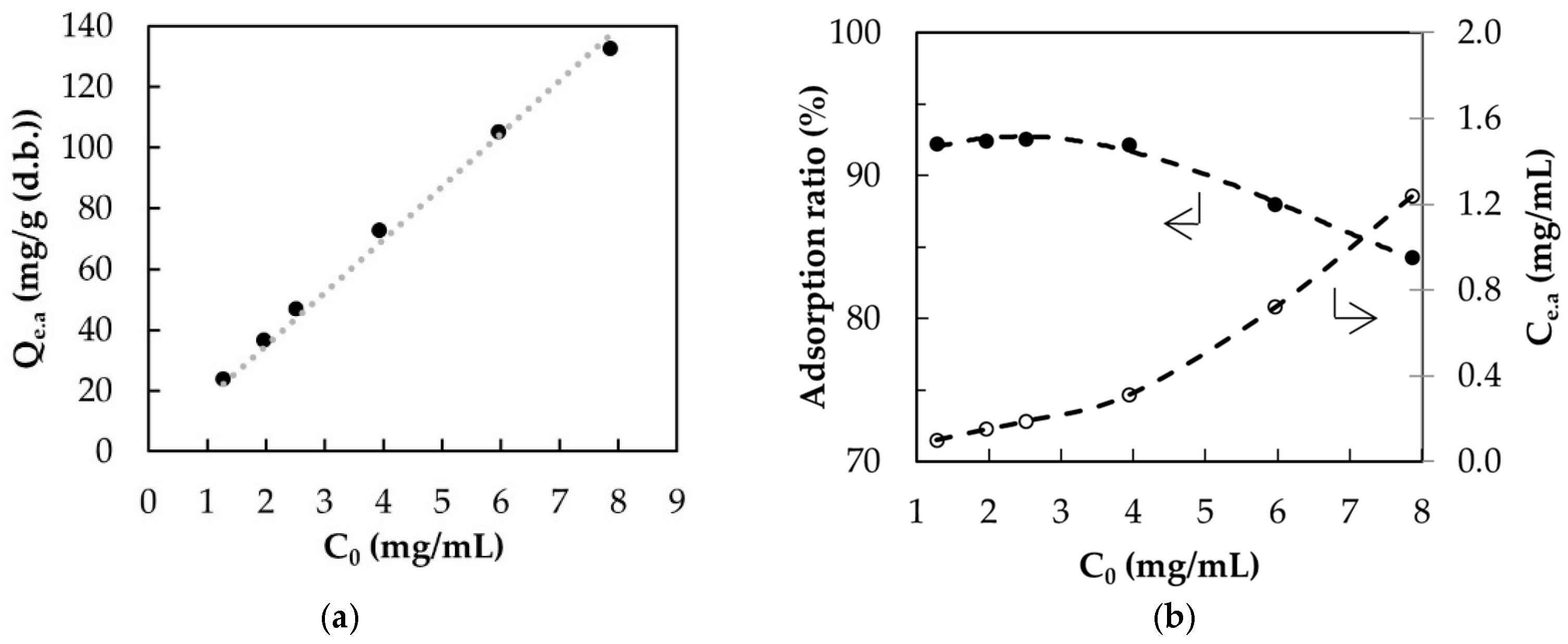
3.3. Adsorption Studies
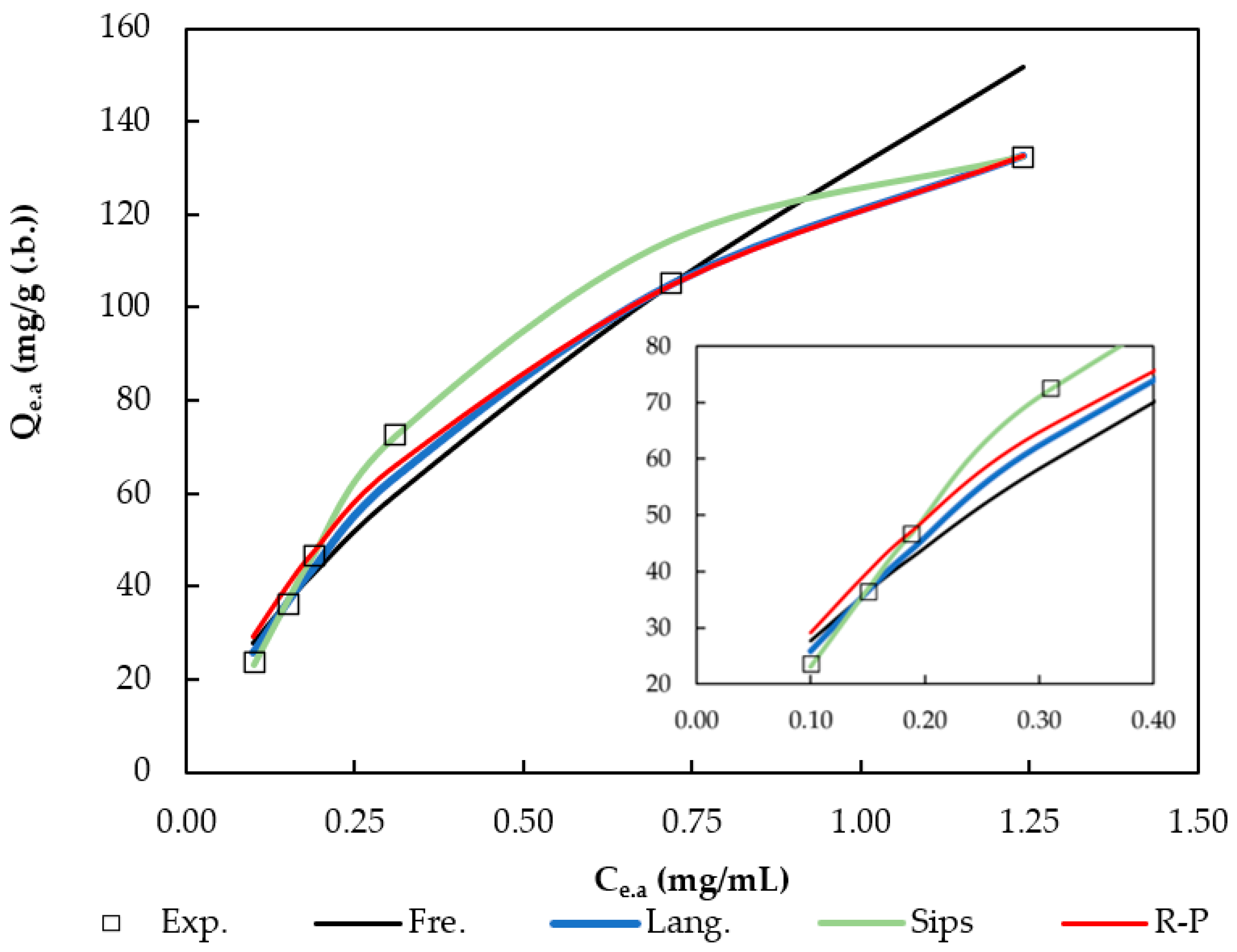
3.4. Adsorption Isotherms
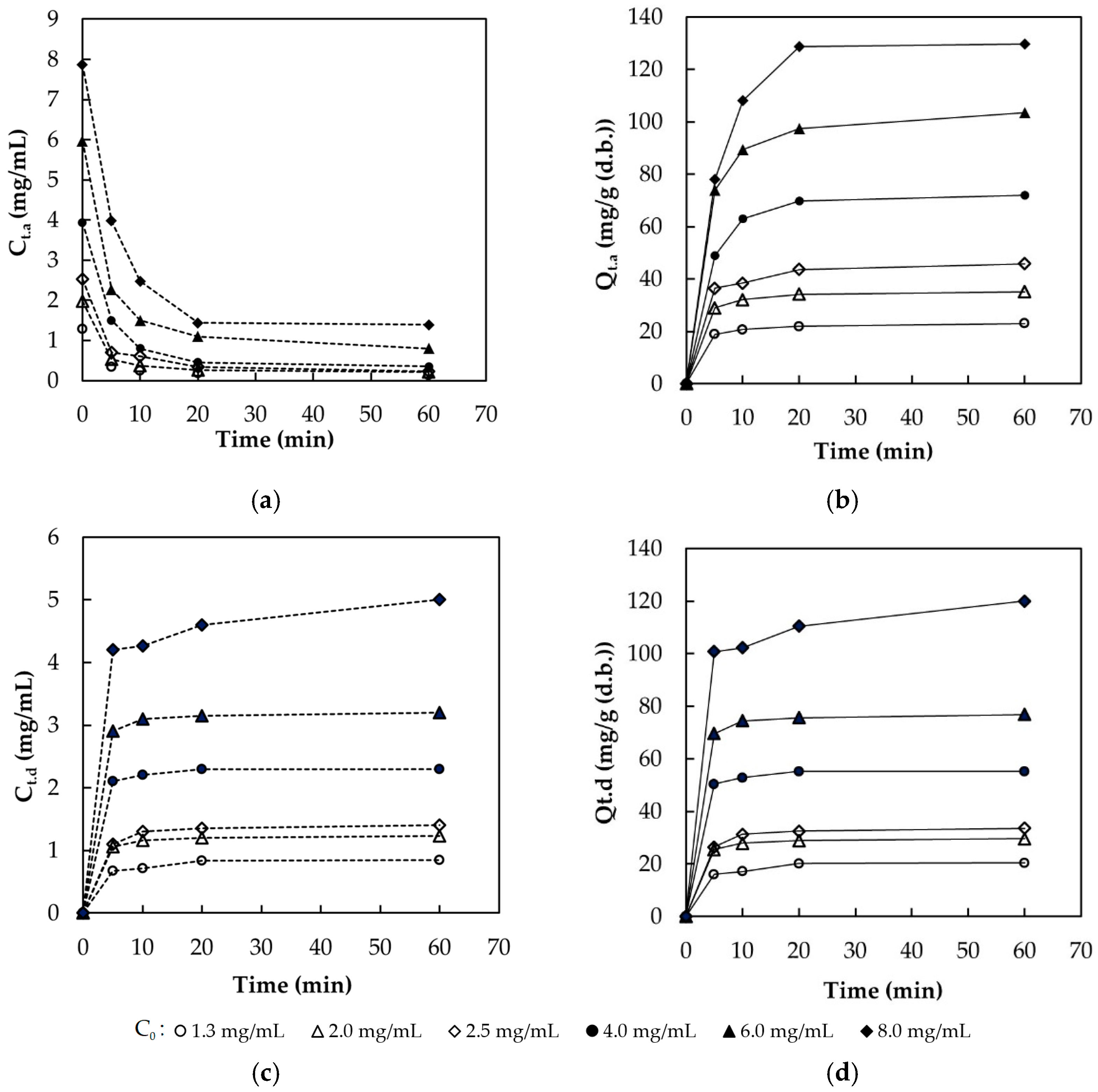
3.5. Adsorption and Desorption Kinetics
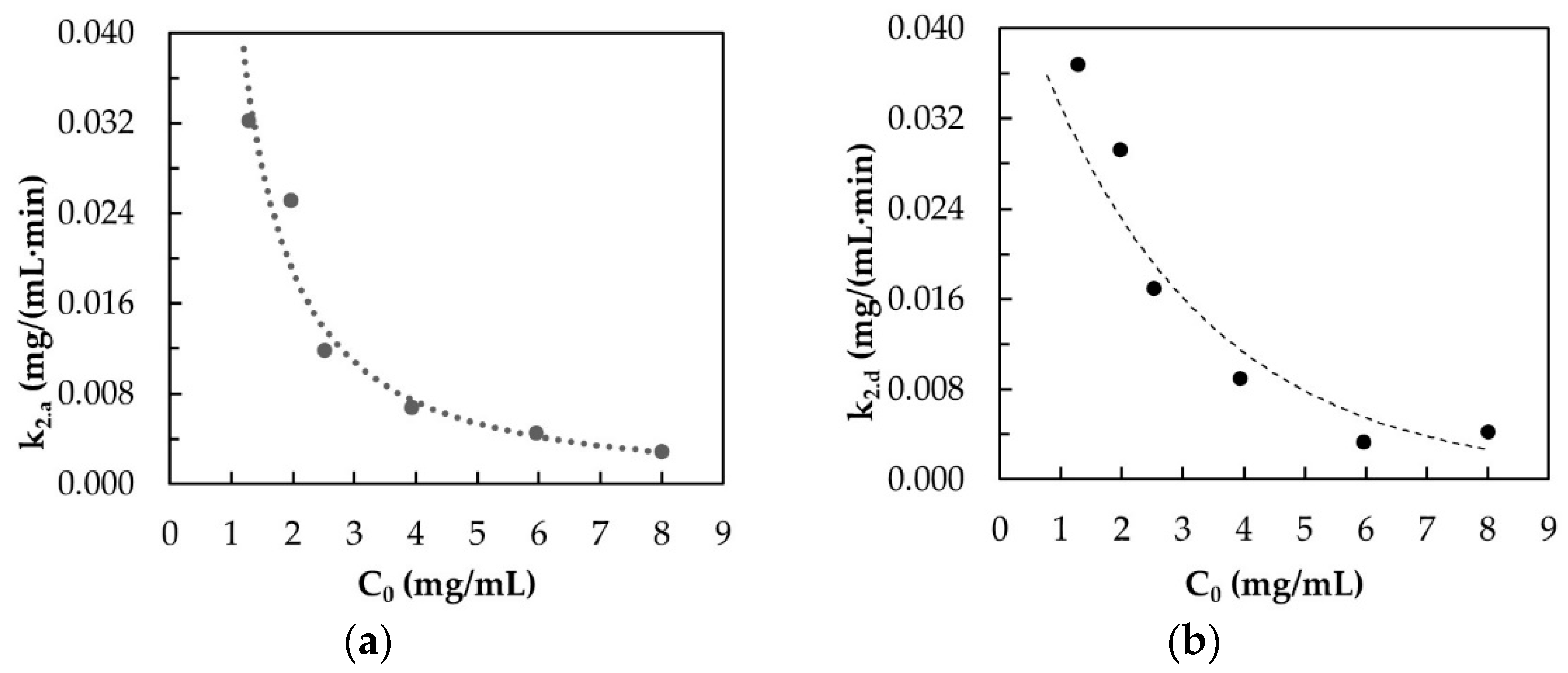
3.5.1. Sorption Kinetics
3.5.2. Sorption Control Mechanisms
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zagklis, D.P.; Papageorgiou, C.S.; Paraskeva, C.A. Technoeconomic Analysis of the Recovery of Phenols from Olive Mill Wastewater through Membrane Filtration and Resin Adsorption_Desorption. Sustainability 2021, 13, 2376. [Google Scholar] [CrossRef]
- Garcia-Castello, E.M.; Rodriguez-Lopez, A.D.; Mayor, L.; Ballesteros, R.; Conidi, C.; Cassano, A. Optimization of conventional and ultrasound assisted extraction of flavonoids from grapefruit (Citrus paradisi L.) solid wastes. LWT Food Sci. Technol. 2015, 64, 1114–1122. [Google Scholar] [CrossRef]
- Scherhaufer, S.; Moates, G.; Hartikainen, H.; Waldron, K.; Obersteiner, G. Environmental impacts of food waste in Europe. Waste Manag. 2018, 77, 98–113. [Google Scholar] [CrossRef]
- Rodriguez-Lopez, A.D.; Melgar, B.; Conidi, C.; Barros, L.; Ferreira, I.C.F.R.; Cassano, A.; Garcia-Castello, E.M. Food industry by-products valorization and new ingredients: Cases of study. In Sustainability of the Food System; Noelia, B., Ester, B., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 71–99. [Google Scholar] [CrossRef]
- Carciochi, R.A.; D’Alessandro, L.G.; Vauchel, P.; Rodriguez, M.M.; Nolasco, S.M.; Dimitrov, K. Valorization of agrifood by-products by extracting valuable bioactive compounds using green processes. In Ingredients Extraction by Physicochemical Methods in Food; Academic Press: Cambridge, MA, USA, 2017; pp. 191–228. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations (FAOSTAT). Available online: http://www.fao.org/faostat/en/#data/QC (accessed on 22 June 2021).
- Saavedra, M.I.; Doval Miñarro, M.; Angosto, J.M.; Fernández-López, J.A. Reuse potential of residues of artichoke (Cynara scolymus L.) from industrial canning processing as sorbent of heavy metals in multimetallic effluents. Ind. Crop. Prod. 2019, 141, 111751. [Google Scholar] [CrossRef]
- Mármol, I.; Quero, J.; Ibarz, R.; Ferreira-Santos, P.; Teixeira, J.A.; Rocha, C.M.R.; Pérez-Fernández, M.; García-Juiz, S.; Osada, J.; Martín-Belloso, O.; et al. Valorization of agro-food by-products and their potential therapeutic applications. Food Bioprod. Process. 2021. [Google Scholar] [CrossRef]
- Conidi, C.; Cassano, A.; Garcia-Castello, E. Valorization of artichoke wastewaters by integrated membrane process. Water Res. 2014, 48, 363–374. [Google Scholar] [CrossRef]
- Conidi, C.; Rodriguez-Lopez, A.D.; Garcia-Castello, E.M.; Cassano, A. Purification of artichoke polyphenols by using membrane filtration and polymeric resins. Sep. Purif. Technol. 2015, 144, 153–161. [Google Scholar] [CrossRef]
- Sandhu, A.K.; Gu, L. Adsorption/desorption characteristics and separation of anthocyanins from muscadine (Vitis rotundifolia) juice pomace by use of macroporous adsorbent resins. J. Agric. Food Chem. 2013, 61, 1441–1448. [Google Scholar] [CrossRef] [PubMed]
- Soto, M.L.; Moure, A.; Domínguez, H.; Parajó, J.C. Recovery, concentration and purification of phenolic compounds by adsorption: A review. J. Food Eng. 2011, 105, 1–27. [Google Scholar] [CrossRef]
- Buran, T.J.; Sandhu, A.K.; Li, Z.; Rock, C.R.; Yang, W.W.; Gu, L. Adsorption/desorption characteristics and separation of anthocyanins and polyphenols from blueberries using macroporous adsorbent resins. J. Food Eng. 2014, 128, 167–173. [Google Scholar] [CrossRef]
- De Araújo Padilha, C.E.; Da Costa Nogueira, C.; Oliveira Filho, M.A.; De Sousa Júnior, F.C.; De Assis, C.F.; De Santana Souza, D.F.; De Oliveira, J.A.; Dos Santos, E.S. Fractionation of green coconut fiber using sequential hydrothermal/alkaline pretreatments and Amberlite XAD-7HP resin. J. Environ. Chem. Eng. 2019, 7, 103474. [Google Scholar] [CrossRef]
- Kammerer, J.; Kammerer, D.R.; Carle, R. Impact of saccharides and amino acids on the interaction of apple polyphenols with ion exchange and adsorbent resins. J. Food Eng. 2010, 98, 230–239. [Google Scholar] [CrossRef]
- Kammerer, J.; Boschet, J.; Kammerer, D.R.; Carle, R. Enrichment and fractionation of major apple flavonoids, phenolic acids and dihydrochalcones using anion exchange resins. LWT Food Sci. Technol. 2011, 44, 1079–1087. [Google Scholar] [CrossRef]
- Silva, E.M.; Pompeu, D.R.; Larondelle, Y.; Rogez, H. Optimisation of the adsorption of polyphenols from Inga edulis leaves on macroporous resins using an experimental design methodology. Sep. Purif. Technol. 2007, 53, 274–280. [Google Scholar] [CrossRef]
- Šimko, I.; Roriz, E.; Gramblička, M.; Illeová, V.; Polakovič, M. Adsorption separation of 2-phenylethanol and L-phenylalanine on polymeric resins: Adsorbent screening, single-component and binary equilibria. Food Bioprod. Process. 2015, 95, 254–263. [Google Scholar] [CrossRef]
- Liang, L.; Bao, S.; Zhang, Y.; Tang, Y. Separation and recovery of V(IV) from sulfuric acid solutions containing Fe(III) and Al(III) using bis(2-ethylhexyl)phosphoric acid impregnated resin. Chem. Eng. Res. Des. 2016, 111, 109–116. [Google Scholar] [CrossRef]
- Zhang, B.; Yang, R.; Zhao, Y.; Liu, C.Z. Separation of chlorogenic acid from honeysuckle crude extracts by macroporous resins. J. Chromatogr. B Anal. Technol. Biomed. Life Sci. 2008, 867, 253–258. [Google Scholar] [CrossRef]
- Sun, P.C.; Liu, Y.; Yi, Y.T.; Li, H.J.; Fan, P.; Xia, C.H. Preliminary enrichment and separation of chlorogenic acid from Helianthus tuberosus L. leaves extract by macroporous resins. Food Chem. 2015, 168, 55–62. [Google Scholar] [CrossRef] [PubMed]
- Ahammad, N.A.; Zulkifli, M.A.; Ahmad, M.A.; Hameed, B.H.; Mohd Din, A.T. Desorption of chloramphenicol from ordered mesoporous carbon-alginate beads: Effects of operating parameters, and isotherm, kinetics, and regeneration studies. J. Environ. Chem. Eng. 2021, 9, 105015. [Google Scholar] [CrossRef]
- Shazeli, M.; Zain, C.; Lee, S.Y.; Teo, C.Y.; Shaari, K. Adsorption/Desorption Characteristics and Simultaneous Enrichment of Orientin, Isoorientin, Vitexin and Isovitexin from Hydrolyzed Oil Palm Leaf Extract Using Macroporous Resins. Processes 2021, 9, 659. [Google Scholar] [CrossRef]
- Ray, S.S.; Gusain, R.; Kumar, N. Adsorption equilibrium isotherms, kinetics and thermodynamics. In Carbon Nanomaterial-Based Adsorbents for Water Purification; Elsevier: Amsterdam, The Netherlands, 2020; pp. 101–118. [Google Scholar] [CrossRef]
- Bretag, J.; Kammerer, D.R.; Jensen, U.; Carle, R. Adsorption of rutin onto a food-grade styrene-divinylbenzene copolymer in a model system. Food Chem. 2009, 114, 151–160. [Google Scholar] [CrossRef]
- Sahoo, T.R.; Prelot, B. Adsorption processes for the removal of contaminants from wastewater. In Nanomaterials for the Detection and Removal of Wastewater Pollutants; Elsevier: Amsterdam, The Netherlands, 2020; pp. 161–222. [Google Scholar] [CrossRef]
- Paredes-Laverde, M.; Salamanca, M.; Silva-Agredo, J.; Manrique-Losada, L.; Torres-Palma, R.A. Selective removal of acetaminophen in urine with activated carbons from rice (Oryza sativa) and coffee (Coffea arabica) husk: Effect of activating agent, activation temperature and analysis of physical-chemical interactions. J. Environ. Chem. Eng. 2019, 7, 103318. [Google Scholar] [CrossRef]
- Che Zain, M.S.; Lee, S.Y.; Teo, C.Y.; Shaari, K. Adsorption and Desorption Properties of Total Flavonoids from Oil Palm (Elaeis guineensis Jacq.) Mature Leaf on Macroporous Adsorption Resins. Molecules 2020, 25, 778. [Google Scholar] [CrossRef] [Green Version]
- Yuanfeng, W.; Lei, Z.; Jianwei, M.; Shiwang, L.; Jun, H.; Yuru, Y.; Lehe, M. Kinetic and thermodynamic studies of sulforaphane adsorption on macroporous resin. J. Chromatogr. B Anal. Technol. Biomed. Life Sci. 2016, 1028, 231–236. [Google Scholar] [CrossRef]
- Li, R.; Liang, N.; Ma, X.; Chen, B.; Huang, F. Study on the adsorption behavior of glycerin from fatty acid methyl esters by a tertiary amine-type anion exchange resin. J. Chromatogr. A 2019, 1586, 62–71. [Google Scholar] [CrossRef]
- Wu, F.C.; Tseng, R.L.; Juang, R.S. Initial behavior of intraparticle diffusion model used in the description of adsorption kinetics. Chem. Eng. J. 2009, 153, 1–8. [Google Scholar] [CrossRef]
- Lv, C.; Yang, J.; Liu, R.; Lu, Q.; Ding, Y.; Zhang, J.; Deng, J. A comparative study on the adsorption and desorption characteristics of flavonoids from honey by six resins. Food Chem. 2018, 268, 424–430. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.T.; Zhang, R.; Chen, S.S.; Wen, K.; Han, R.P. Adsorption of phosphate from solution by iron modified macroporous chelating resin. Desalination Water Treat. 2019, 170, 187–198. [Google Scholar] [CrossRef]
- Wen, Z.; Huang, K.; Niu, Y.; Yao, Y.; Wang, S.; Cao, Z.; Zhong, H. Kinetic study of ultrasonic-assisted uranium adsorption by anion exchange resin. Colloids Surf. A Physicochem. Eng. Asp. 2020, 585, 124021. [Google Scholar] [CrossRef]
- Sparks, D.L.; Zelazny, L.W.; Martens, D.C. Kinetics of Potassium Desorption in Soil using Miscible Displacement. Soil Sci. Soc. Am. J. 1980, 44, 1205–1208. [Google Scholar] [CrossRef] [Green Version]
- Paredes-Laverde, M.; Salamanca, M.; Diaz-Corrales, J.D.; Flórez, E.; Silva-Agredo, J.; Torres-Palma, R.A. Understanding the removal of an anionic dye in textile wastewaters by adsorption on ZnCl2 activated carbons from rice and coffee husk wastes: A combined experimental and theoretical study. J. Environ. Chem. Eng. 2021, 9, 105685. [Google Scholar] [CrossRef]
- Ho, Y.S.; Ng, J.C.Y.; McKay, G. Kinetics of pollutant sorption by biosorbents: Review. Sep. Purif. Methods 2000, 29, 189–232. [Google Scholar] [CrossRef]



| S 2328 | S 6328 A | S 7968 | XAD 7HP | XAD 16HP N | |
|---|---|---|---|---|---|
| Functional group | Sulphonic acid | Quaternary ammine | None | None | None |
| Ionic form as shipped | H+ | Cl− | Neutral | Neutral | Neutral |
| Surface area (m2/g) | - | - | 800 | 380 | 800 |
| Particle size (mm) | 0.40–1.20 | 0.40–1.25 | 0.49 | 0.56–0.71 | 0.60–0.75 |
| Pore diameter (nm) | 55 | 50 | 5–10 | 55 | 20 [19] |
| Maximum operating temperature (°C) | 120 | 85 | 120 | 80–100 | 150 |
| Moisture content (%): | |||||
| Manufacturer | 65–75 | 58–63 | 50–60 | 61–69 | 62–70 |
| Measured | 67.3 | 48.7 | 61.3 | 69.3 | 67.3 |
| pH range | 0–14 | 0–14 | 0–14 | 0–14 | 0–14 |
| Conditioning solutions | 6% HCl aq. solution | 6% HCl and 4% NaOH aq. solutions | 6% HCl and 4% NaOH aq. solutions | 20 g/L of NaOH and 0.5% of HCl | 20 g/L of NaOH and 20 g/L of H2SO4 |
| General Model | Eq. | Linearized | Eq. |
|---|---|---|---|
| Langmuir | |||
| (6) | (6′) [26] | ||
| Freundlich | |||
| (7) | (7′) [26] | ||
| Sips | |||
| (8) | (8′) [24] | ||
| Redlich-Peterson | |||
| (9) | (9′) adapted from [24] | ||
| Model | General | Eq. | Integrated | Eq. |
|---|---|---|---|---|
| Pseudo-first order | (10) | (11) | ||
| Pseudo-second order | (12) | (13) | ||
| Intraparticle diffusion | (14) | |||
| Resin | AR (%) | Qe.a (mg/g (d.b.)) | DR (%) | Qe.d (mg/g (d.b.)) | TADY (%) |
|---|---|---|---|---|---|
| S 2328 | 46.9 | 14.4 | 49.7 | 8.1 | 23.3 |
| S 6328 A | 98.3 | 33.5 | 3.9 | 1.3 | 3.8 |
| S 7968 | 11.3 | 2.0 | 96.8 | 1.9 | 11.0 |
| XAD 7HP | 94.6 | 31.3 | 76.9 | 25.3 | 72.8 |
| XAD 16HP N | 24.3 | 2.3 | 49.5 | 1.6 | 12.0 |
| Freundlich | Langmuir | Sips | Redlich–Peterson |
|---|---|---|---|
| KF = 131.08 (mg/g)·(mL/mg)1/n | KL = 1.42 mL/mg | QS = 152.94 mg/g | KRP = 377.06 (mL/mg)·(mg/g) |
| n = 1.48 | Qm = 208.09 mg/g | KS = 4.79 mL/mg | BRP = 2.10 (mL/mg)g |
| RL = 0.082 | α = 1.43 | β = 0.85 | |
| r2 = 0.972 | r2 = 0.994 | r2 = 0.996 | r2 = 0.836 |
| APE = 9.8% | APE = 4.7% | APE = 2.2% | APE = 7.2% |
| Experimental | Pseudo-First Order | Pseudo-Second Order | |||||
|---|---|---|---|---|---|---|---|
| Adsorption | |||||||
| Co | Qe.a exp. | k1.a | Qe.a | Qe.a relative deviation | k2.a | Qe.a | Qe.a relative deviation |
| mg/mL | mg/g | 1/min | mg/g | % | mg/(mL·min) | mg/g | % |
| 1.3 | 23.61 | 8.34 | 13.87 | 41.25 | 0.03215 | 23.48 | 0.55 |
| 2.0 | 36.42 | 7.86 | 22.03 | 39.51 | 0.02512 | 35.76 | 1.81 |
| 2.5 | 46.76 | 8.13 | 31.08 | 33.53 | 0.01180 | 47.18 | 0.90 |
| 4.0 | 72.61 | 6.26 | 59.71 | 17.77 | 0.00672 | 74.44 | 2.52 |
| 6.0 | 105.05 | 7.99 | 74.59 | 29.00 | 0.00449 | 107.10 | 1.95 |
| 8.0 | 132.70 | 5.74 | 133.99 | 0.97 | 0.00278 | 136.18 | 2.62 |
| Desorption | |||||||
| Co | Qe.dexp. | k1.d | Qe.d | Qe.a relative deviation | k2.d | Qe.d | Qe.a relative deviation |
| mg/mL | mg/g | 1/min | mg/g | % | mg/(mL·min) | mg/g | % |
| 1.3 | 20.64 | 0.1778 | 16.76 | 4.84 | 0.0368 | 20.76 | 0.58 |
| 2.0 | 30.24 | 0.1397 | 16.02 | 47.02 | 0.0292 | 30.37 | 0.43 |
| 2.5 | 34.80 | 0.1264 | 21.39 | 38.54 | 0.0169 | 35.02 | 0.63 |
| 4.0 | 59.04 | 0.1197 | 30.07 | 49.07 | 0.0089 | 59.37 | 0.56 |
| 6.0 | 87.21 | 0.0872 | 46.89 | 46.23 | 0.0033 | 88.06 | 0.97 |
| 8.0 | 123.08 | 0.0977 | 68.60 | 44.26 | 0.0042 | 123.04 | 0.03 |
| Co (mg CA/mL) | |||||||
|---|---|---|---|---|---|---|---|
| 1.3 | 2.0 | 2.5 | 4.0 | 6.0 | 8.0 | ||
| Adsorption | |||||||
| No stages approach | |||||||
| r2 | 0.840 | 0.747 | 0.860 | 0.655 | 0.768 | 0.627 | |
| kpa (mg/(g (d.b.)·min0.5) | 0.673 | 0.983 | 1.683 | 3.497 | 4.651 | 7.972 | |
| Ca (mg/g (d.b.)) | 18.1 | 28.2 | 33.7 | 47.9 | 70.6 | 75.9 | |
| Rpa | 0.231 | 0.225 | 0.280 | 0.340 | 0.328 | 0.428 | |
| Two stages approach | |||||||
| 1 | r12 | 0.958 | 0.952 | 0.972 | 0.919 | 0.924 | 0.958 |
| kpa1 (mg/(g (d.b.)·min0.5) | 1.338 | 2.286 | 3.252 | 9.123 | 10.229 | 22.253 | |
| Ca1 (mg/g (d.b.)) | 16.1 | 24.2 | 28.8 | 30.5 | 53.3 | 31.6 | |
| Rpa1 | 0.319 | 0.336 | 0.384 | 0.581 | 0.493 | 0.762 | |
| 2 | r22 | 1 | 1 | 1 | 1 | 1 | 1 |
| kpa2 (mg/(g (d.b.)·min0.5) | 0.326 | 0.295 | 0.664 | 0.611 | 1.831 | 0.278 | |
| Ca2 (mg/g (d.b.)). | 20.5 | 32.8 | 40.7 | 67.3 | 89.3 | 127.4 | |
| Rpa2 | 0.134 | 0.099 | 0.130 | 0.074 | 0.150 | 0.040 | |
| Desorption | |||||||
| No stages approach | |||||||
| r2 | 0.520 | 0.616 | 0.579 | 0.846 | 0.938 | 0.794 | |
| kpd (mg/(g (d.b.)·min0.5) | 0.283 | 0.273 | 0.458 | 0.549 | 1.164 | 1.672 | |
| Cd (mg/g (d.b.)) | 17.0 | 26.6 | 28.6 | 50.9 | 69.0 | 100.2 | |
| Rpd | 0.176 | 0.122 | 0.177 | 0.138 | 0.209 | 0.186 | |
| Two stages approach | |||||||
| 1 | r12 | 0.974 | 0.876 | 0.826 | 0.989 | 0.825 | 0.921 |
| kpd1 (mg/(g (d.b.)·min0.5) | 1.859 | 1.463 | 2.572 | 2.100 | 2.566 | 4.422 | |
| Cd1 (mg/g (d.b.)) | 11.7 | 22.6 | 21.5 | 45.9 | 64.8 | 89.9 | |
| Rpd1 | 0.434 | 0.254 | 0.381 | 0.223 | 0.257 | 0.269 | |
| 2 | r22 | 0.948 | 0.948 | 0.949 | 0.923 | 0.961 | 0.754 |
| kpd2 (mg/(g (d.b.)·min0.5) | 0.041 | 0.124 | 0.205 | 0.379 | 1.106 | 1.015 | |
| Cd2 (mg/g (d.b.)). | 20.0 | 28.4 | 31.7 | 53.0 | 69.7 | 108.50 | |
| Rpd2 | 0.030 | 0.062 | 0.089 | 0.103 | 0.201 | 0.119 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez-Lopez, A.D.; Reig, M.; Mayor, L.; Ortiz-Climent, M.; Garcia-Castello, E.M. Characterization of Ionic Exchange and Macroporous Resins for Their Application on the Separation and Recovery of Chlorogenic Acid from the Wastewater of Artichoke Blanching. Sustainability 2021, 13, 8928. https://doi.org/10.3390/su13168928
Rodriguez-Lopez AD, Reig M, Mayor L, Ortiz-Climent M, Garcia-Castello EM. Characterization of Ionic Exchange and Macroporous Resins for Their Application on the Separation and Recovery of Chlorogenic Acid from the Wastewater of Artichoke Blanching. Sustainability. 2021; 13(16):8928. https://doi.org/10.3390/su13168928
Chicago/Turabian StyleRodriguez-Lopez, Antonio D., Milagro Reig, Luis Mayor, Mireia Ortiz-Climent, and Esperanza M. Garcia-Castello. 2021. "Characterization of Ionic Exchange and Macroporous Resins for Their Application on the Separation and Recovery of Chlorogenic Acid from the Wastewater of Artichoke Blanching" Sustainability 13, no. 16: 8928. https://doi.org/10.3390/su13168928
APA StyleRodriguez-Lopez, A. D., Reig, M., Mayor, L., Ortiz-Climent, M., & Garcia-Castello, E. M. (2021). Characterization of Ionic Exchange and Macroporous Resins for Their Application on the Separation and Recovery of Chlorogenic Acid from the Wastewater of Artichoke Blanching. Sustainability, 13(16), 8928. https://doi.org/10.3390/su13168928








