Public Transport Network Vulnerability and Delay Distribution among Travelers
Abstract
1. Introduction
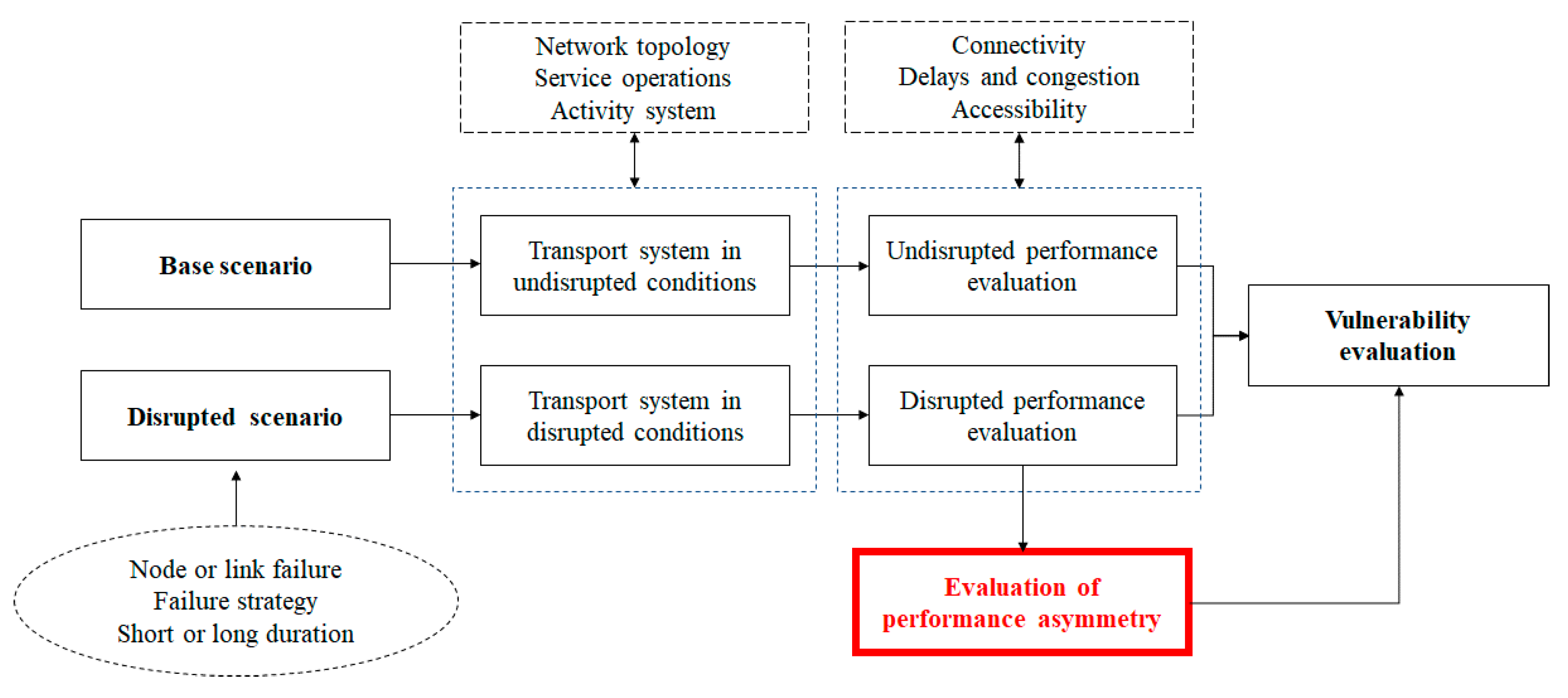
2. Methodological Framework
3. Model
3.1. Public Transport System Model
3.2. Simulation Model
3.3. Disrupted Scenario and Vulnerability Evaluation
4. Case Study
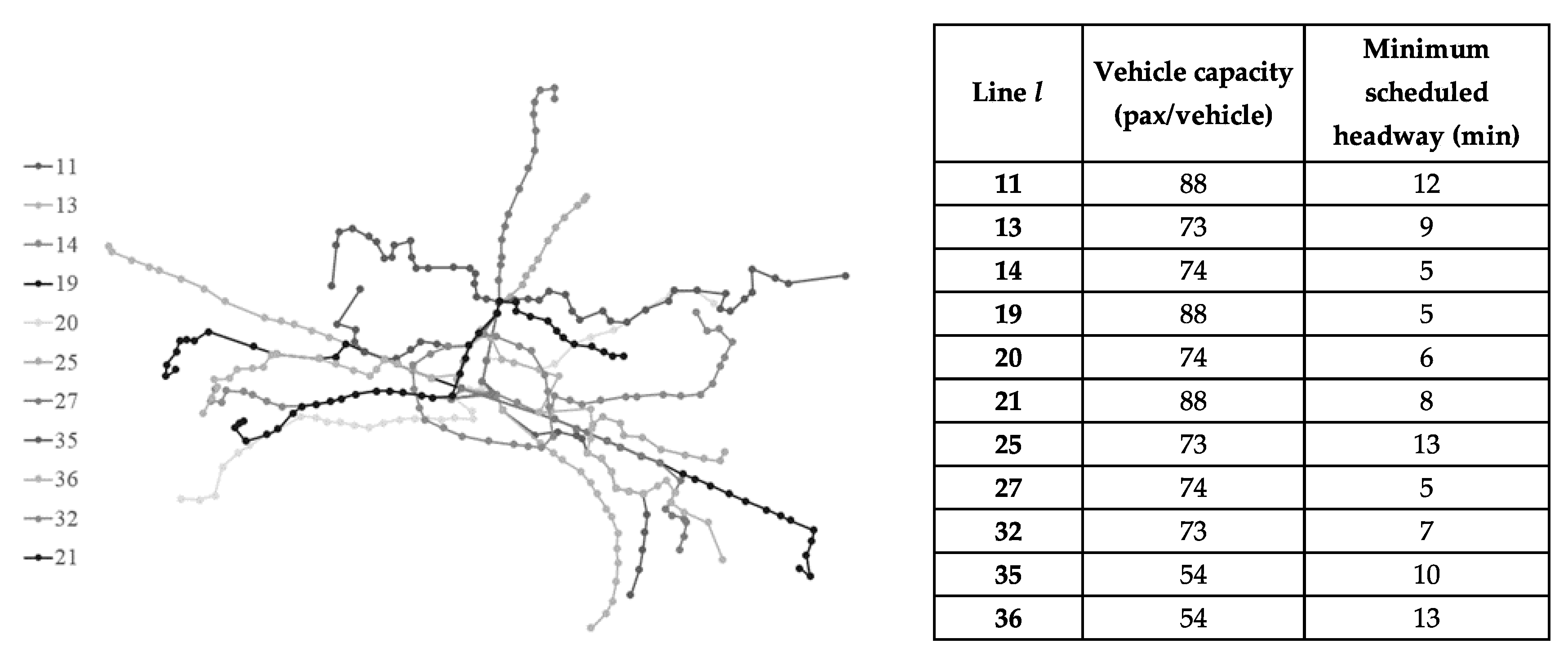
4.1. Public Transport System Description and Implementation
4.2. Disrupted Scenario Definition: Central Links Identification
5. Results and Discussion
6. Conclusions and Further Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saxena, N.; Rashidi, T.H.; Auld, J. Studying the tastes effecting mode choice behavior of travelers under transit service disruptions. Travel Behav. Soc. 2019, 17, 86–95. [Google Scholar] [CrossRef]
- Xia, T.; Nitschke, M.; Zhang, Y.; Shah, P.; Crabb, S.; Hansen, A. Traffic-related air pollution and health co-benefits of alternative transport in Adelaide, South Australia. Environ. Int. 2015, 74, 281–290. [Google Scholar] [CrossRef]
- Moniruzzaman, M.; Páez, A. Accessibility to transit, by transit, and mode share: Application of a logistic model with spatial filters. J. Transp. Geogr. 2012, 24, 198–205. [Google Scholar] [CrossRef]
- Gu, Y.; Fu, X.; Liu, Z.; Xu, X.; Chen, A. Performance of transportation network under perturbations: Reliability, vulnerability, and resilience. Transp. Res. Part E Logis. Transp. Rev. 2020, 133, 101809. [Google Scholar] [CrossRef]
- Li, T.; Rong, L.; Yan, K. Vulnerability analysis and critical area identification of public transport system: A case of high-speed rail and air transport coupling system in China. Transp. Res. Part A Policy Pract. 2019, 127, 55–70. [Google Scholar] [CrossRef]
- Zhu, S.; Levinson, D.M. Disruptions to transportation networks: A review. In Network Reliability in Practice; Levinson, D.M., Liu, H.X., Bell, M., Eds.; Springer: New York, NY, USA, 2012; pp. 5–20. [Google Scholar]
- de Oliveira, E.L.; da Silva Portugal, L.; Junior, W.P. Indicators of reliability and vulnerability: Similarities and differences in ranking links of a complex road system. Transp. Res. Part A Policy Pract. 2016, 88, 195–208. [Google Scholar] [CrossRef]
- Lu, Q.C.; Lin, S. Vulnerability analysis of urban rail transit network within multi-modal public transport networks. Sustainability 2019, 11, 2109. [Google Scholar] [CrossRef]
- Rodríguez-Núñez, E.; García-Palomares, J.C. Measuring the vulnerability of public transport networks. J. Transp. Geogr. 2014, 35, 50–63. [Google Scholar] [CrossRef]
- Yap, M.; Cats, O. Predicting disruptions and their passenger delay impacts for public transport stops. Transportation 2020, 48, 1703–1731. [Google Scholar] [CrossRef]
- Hörcher, D.; Graham, D.J.; Anderson, R.J. Crowding cost estimation with large scale smart card and vehicle location data. Transp. Res. Part B Meth. 2017, 95, 105–125. [Google Scholar] [CrossRef]
- Yap, M.D.; van Oort, N.; van Nes, R.; van Arem, B. Identification and quantification of link vulnerability in multi-level public transport networks: A passenger perspective. Transportation 2018, 45, 1161–1180. [Google Scholar] [CrossRef]
- Chen, A.; Yang, C.; Kongsomsaksakul, S.; Lee, M. Network-based accessibility measures for vulnerability analysis of degradable transportation networks. Netw. Spat. Econ. 2007, 7, 241–256. [Google Scholar] [CrossRef]
- Adelé, S.; Tréfond-Alexandre, S.; Dionisio, C.; Hoyau, P.A. Exploring the behavior of suburban train users in the event of disruptions. Transp. Res. Part F Traffic Psychol. Behav. 2019, 65, 344–362. [Google Scholar] [CrossRef]
- Taylor, M.A.P.; Susilawati, S. Remoteness and accessibility in the vulnerability analysis of regional road networks. Transp. Res. Part A Policy Pract. 2012, 46, 761–771. [Google Scholar] [CrossRef]
- Taylor, M. Vulnerability Analysis for Transportation Networks; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Cats, O.; Jenelius, E. Dynamic vulnerability analysis of public transport networks: Mitigation effects of real-time information. Netw. Spat. Econ. 2014, 14, 435–463. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, F.; Wang, S.; Dai, Y.; Wang, Y. Structural vulnerability and intervention of high speed railway networks. Phys. A Stat. Mech. Appl. 2016, 462, 743–751. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, S.; Wang, X. Comparison analysis on vulnerability of metro networks based on complex network. Phys. A Stat. Mech. Appl. 2018, 496, 72–78. [Google Scholar] [CrossRef]
- Jenelius, E. Network structure and travel patterns: Explaining the geographical disparities of road network vulnerability. J. Transp. Geogr. 2009, 17, 234–244. [Google Scholar] [CrossRef]
- Mishra, S.; Welch, T.F.; Jha, M.K. Performance indicators for public transit connectivity in multi-modal transportation networks. Transp. Res. Part A Policy Pract. 2012, 46, 1066–1085. [Google Scholar] [CrossRef]
- Sun, D.J.; Zhao, Y.; Lu, Q.C. Vulnerability analysis of urban rail transit networks: A case study of Shanghai, China. Sustainability 2015, 7, 6919–6936. [Google Scholar] [CrossRef]
- Latora, V.; Marchiori, M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef] [PubMed]
- Vragović, I.; Louis, E.; Díaz-Guilera, A. Efficiency of informational transfer in regular and complex networks. Phys. Rev. E 2005, 71, 036122. [Google Scholar] [CrossRef]
- Shi, J.; Wen, S.; Zhao, X.; Wu, G. Sustainable development of urban rail transit networks: A vulnerability perspective. Sustainability 2019, 11, 1335. [Google Scholar] [CrossRef]
- Duan, Y.; Lu, F. Robustness of city road networks at different granularities. Phys. A Stat. Mech. Appl. 2014, 411, 21–34. [Google Scholar] [CrossRef]
- Zhang, X.; Miller-Hooks, E.; Denny, K. Assessing the role of network topology in transportation network resilience. J. Transp. Geogr. 2015, 46, 35–45. [Google Scholar] [CrossRef]
- Balijepalli, C.; Oppong, O. Measuring vulnerability of road network considering the extent of serviceability of critical road links in urban areas. J. Transp. Geogr. 2014, 39, 145–155. [Google Scholar] [CrossRef]
- Cats, O.; Jenelius, E. Beyond a complete failure: The impact of partial capacity degradation on public transport network vulnerability. Transp. B Transp. Dyn. 2018, 6, 77–96. [Google Scholar] [CrossRef]
- Leng, J.Q.; Zhai, J.; Li, Q.W.; Zhao, L. Construction of road network vulnerability evaluation index based on general travel cost. Phys. A Stat. Mech. Appl. 2018, 493, 421–429. [Google Scholar] [CrossRef]
- Jenelius, E.; Mattsson, L.G. Road network vulnerability analysis of area-covering disruptions: A grid-based approach with case study. Transp. Res. Part A Policy Pract. 2012, 46, 746–760. [Google Scholar] [CrossRef]
- Scott, D.M.; Novak, D.C.; Aultman-Hall, L.; Guo, F. Network robustness index: A new method for identifying critical links and evaluating the performance of transportation networks. J. Transp. Geogr. 2006, 14, 215–227. [Google Scholar] [CrossRef]
- Sullivan, J.L.; Novak, D.C.; Aultman-Hall, L.; Scott, D.M. Identifying critical road segments and measuring system-wide robustness in transportation networks with isolating links: A link-based capacity-reduction approach. Transp. Res. Part A Policy Pract. 2010, 44, 323–336. [Google Scholar] [CrossRef]
- Leng, N.; Corman, F. The role of information availability to passengers in public transport disruptions: An agent-based simulation approach. Transp. Res. Part A Policy Pract. 2020, 133, 214–236. [Google Scholar] [CrossRef]
- Malandri, C.; Fonzone, A.; Cats, O. Recovery time and propagation effects of passenger transport disruptions. Phys. A Stat. Mech. Appl. 2018, 505, 7–17. [Google Scholar] [CrossRef]
- Snelder, M.; Calvert, S. Quantifying the impact of adverse weather conditions on road network performance. Eur. J. Transp. Infrastruct. Res. 2016, 16, 3118. [Google Scholar]
- Dehghani, M.S.; Flintsch, G.; McNeil, S. Impact of road conditions and disruption uncertainties on network vulnerability. J. Infrastruct. Syst. 2014, 20, 04014015. [Google Scholar] [CrossRef]
- Murray-Tuite, P.M.; Mahmassani, H.S. Methodology for determining vulnerable links in a transportation network. Transp. Res. Rec. 2004, 1882, 88–96. [Google Scholar] [CrossRef]
- Connors, R.D.; Watling, D.P. Assessing the demand vulnerability of equilibrium traffic networks via network aggregation. Netw. Spat. Econ. 2015, 15, 367–395. [Google Scholar] [CrossRef]
- Chen, B.Y.; Lam, W.H.; Sumalee, A.; Li, Q.; Li, Z.C. Vulnerability analysis for large-scale and congested road networks with demand uncertainty. Transp. Res. Part A Policy Pract. 2012, 46, 501–516. [Google Scholar] [CrossRef]
- Taylor, M.; Sekhar, S.; D’Este, G. Application of accessibility based methods for vulnerability analysis of strategic road networks. Netw. Spat. Econ. 2006, 6, 267–291. [Google Scholar] [CrossRef]
- D’este, G.A.; Taylor, M.A. Network Vulnerability: An Approach to Reliability Analysis at the Level of National Strategic Transport Networks; Emerald Group Publishing Limited: Bingley, UK, 2003. [Google Scholar]
- Taylor, M.A.; D’Este, G.M. Transport network vulnerability: A method for diagnosis of critical locations in transport infrastructure systems. In Critical Infrastructure; Springer: Berlin/Heidelberg, Germany, 2007; pp. 9–30. [Google Scholar]
- Lorenz, M.O. Methods of measuring the concentration of wealth. Publ. Am. Stat. Assoc. 1905, 9, 209–219. [Google Scholar] [CrossRef]
- Delbosc, A.; Currie, G. Using Lorenz curves to assess public transport equity. J. Transp. Geogr. 2011, 19, 1252–1259. [Google Scholar] [CrossRef]
- Jang, S.; An, Y.; Yi, C.; Lee, S. Assessing the spatial equity of Seoul’s public transportation using the Gini coefficient based on its accessibility. Int. J. Urban Sci. 2017, 21, 91–107. [Google Scholar] [CrossRef]
- Lope, D.J.; Dolgun, A. Measuring the inequality of accessible trams in Melbourne. J. Transp. Geogr. 2020, 83, 102657. [Google Scholar] [CrossRef]
- Gallo, M. Assessing the equality of external benefits in public transport investments: The impact of urban railways on real estate values. Case Stud. Transp. Policy 2020, 8, 758–769. [Google Scholar] [CrossRef]
- Guzman, L.A.; Oviedo, D.; Rivera, C. Assessing equity in transport accessibility to work and study: The Bogotá region. J. Transp. Geogr. 2017, 58, 236–246. [Google Scholar] [CrossRef]
- Chen, Y.; Bouferguene, A.; Li, H.X.; Liu, H.; Shen, Y.; Al-Hussein, M. Spatial gaps in urban public transport supply and demand from the perspective of sustainability. J. Clean. Prod. 2018, 195, 1237–1248. [Google Scholar] [CrossRef]
- Pavkova, K.; Currie, G.; Delbosc, A.; Sarvi, M. Selecting tram links for priority treatments-The Lorenz Curve approach. J. Transp. Geogr. 2016, 55, 101–109. [Google Scholar] [CrossRef]
- Hörcher, D.; Graham, D.J. The Gini Index of Demand Imbalances in Public Transport; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–24. [Google Scholar] [CrossRef]
- Berche, B.; Von Ferber, C.; Holovatch, T.; Holovatch, Y. Resilience of public transport networks against attacks. Eur. Phys. J. B 2009, 71, 125–137. [Google Scholar] [CrossRef]
- Sun, D.J.; Guan, S. Measuring vulnerability of urban metro network from line operation perspective. Transp. Res. Part A Policy Pract. 2016, 94, 348–359. [Google Scholar] [CrossRef]
- Peterson, S.K.; Church, R.L. A framework for modeling rail transport vulnerability. Growth Chang. 2008, 39, 617–641. [Google Scholar] [CrossRef]
- Faturechi, R.; Miller-Hooks, E. Measuring the performance of transportation infrastructure systems in disasters: A comprehensive review. J. Infrastruct. Syst. 2015, 21, 04014025. [Google Scholar] [CrossRef]
- Jenelius, E.; Petersen, T.; Mattsson, L.G. Importance and exposure in road network vulnerability analysis. Transp. Res. Part A Policy Pract. 2006, 40, 537–560. [Google Scholar] [CrossRef]
- Wang, Z.; Chan, A.P.; Yuan, J.; Xia, B.; Skitmore, M.; Li, Q. Recent advances in modeling the vulnerability of transportation networks. J. Infrastruct. Syst. 2015, 21, 06014002. [Google Scholar] [CrossRef]
- Cats, O.; Jenelius, E. Planning for the unexpected: The value of reserve capacity for public transport network robustness. Transp. Res. Part A Policy Pract. 2015, 81, 47–61. [Google Scholar] [CrossRef]
- Cats, O.; Yap, M.; Van Oort, N. Exposing the role of exposure: Public transport network risk analysis. Transp. Res. Part A Policy Pract. 2016, 88, 1–14. [Google Scholar] [CrossRef]
- Cats, O.; West, J.; Eliasson, J. A Dynamic Stochastic Model for Evaluating Congestion and Crowding Effects in Transit Systems. Transp. Res. Part B Meth. 2016, 89, 43–57. [Google Scholar] [CrossRef]
- Malandri, C.; Mantecchini, L.; Postorino, M.N. Airport ground access reliability and resilience of transit networks: A case study. Transp. Res. Proc. 2017, 27, 1129–1136. [Google Scholar] [CrossRef]
- Gentile, G.; Nökel, K. Modelling Public Transport Passenger Flows in the Era of Intelligent Transport Systems; Springer International Publishing: New York, NY, USA, 2016; p. 10. [Google Scholar]
- Cats, O.; Burghout, W.; Toledo, T.; Koutsopoulos, H.N. Mesoscopic Modeling of Bus Public Transportation. Transp. Res. Rec. 2010, 2188, 9–18. [Google Scholar] [CrossRef]
- Toledo, T.; Cats, O.; Burghout, W.; Koutsopoulos, H.N. Mesoscopic Simulation for Transit Operations. Transp. Res. Part C Emerg. Technol. 2010, 18, 896–908. [Google Scholar] [CrossRef]
- Cats, O. Multi-agent transit operations and assignment model. Procedia Comput. Sci. 2013, 19, 809–814. [Google Scholar] [CrossRef][Green Version]
- Nuzzolo, A.; Lam, W.H. Modelling Intelligent Multi-Modal Transit Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Cats, O.; Hartl, M. Modelling public transport on-board congestion: Comparing schedule-based and agent-based assignment approaches and their implications. J. Adv. Transp. 2016, 50, 1209–1224. [Google Scholar] [CrossRef]
- Ben-Akiva, M.; Lerman, S.R. Discrete Choice Analysis; MIT Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Train, K. Discrete Choice Methods with Simulation; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Cats, O.; Koutsopoulos, H.N.; Burghout, W.; Toledo, T. Effect of real-time transit information on dynamic path choice of passengers. Transp. Res. Rec. 2011, 2217, 46–54. [Google Scholar] [CrossRef]

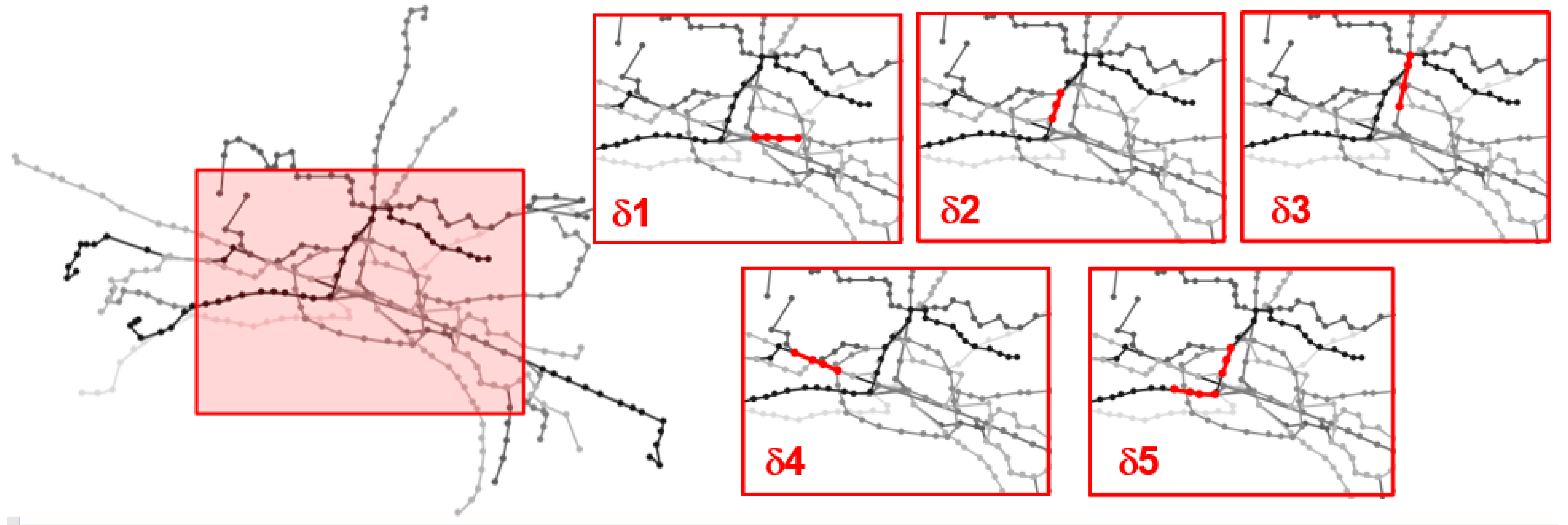


| Scenario | Disrupted Lines | Disrupted Segment Length (m) | LCe |
|---|---|---|---|
| δ1 | 14, 11, 13, 19, 20, 25, 27 | 900 | 25,382 |
| δ2 | 13, 19, 21, 25, 35, 36 | 1300 | 19,772 |
| δ3 | 11, 20, 21, 25 | 1300 | 19,603 |
| δ4 | 13, 19, 36 | 850 | 13,246 |
| δ5 | 14, 20, 21 | 1000 | 13,200 |
| Scenario | Average Travel Time (min) | Percentage of Delayed Passengers (%) |
|---|---|---|
| b | 34.19 | 0 |
| δ1 | 36.80 | 15.38 |
| δ2 | 37.80 | 20.22 |
| δ3 | 35.46 | 11.51 |
| δ4 | 35.28 | 18.14 |
| δ5 | 36.55 | 14.79 |
| Scenario | VGINIδ | LCe | (min) |
|---|---|---|---|
| δ1 | 0.40238 | 25,382 | 15.74 |
| δ2 | 0.44415 | 19,772 | 16.88 |
| δ3 | 0.38586 | 19,603 | 13.79 |
| δ4 | 0.34230 | 13,246 | 12.99 |
| δ5 | 0.34366 | 13,200 | 14.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malandri, C.; Mantecchini, L.; Paganelli, F.; Postorino, M.N. Public Transport Network Vulnerability and Delay Distribution among Travelers. Sustainability 2021, 13, 8737. https://doi.org/10.3390/su13168737
Malandri C, Mantecchini L, Paganelli F, Postorino MN. Public Transport Network Vulnerability and Delay Distribution among Travelers. Sustainability. 2021; 13(16):8737. https://doi.org/10.3390/su13168737
Chicago/Turabian StyleMalandri, Caterina, Luca Mantecchini, Filippo Paganelli, and Maria Nadia Postorino. 2021. "Public Transport Network Vulnerability and Delay Distribution among Travelers" Sustainability 13, no. 16: 8737. https://doi.org/10.3390/su13168737
APA StyleMalandri, C., Mantecchini, L., Paganelli, F., & Postorino, M. N. (2021). Public Transport Network Vulnerability and Delay Distribution among Travelers. Sustainability, 13(16), 8737. https://doi.org/10.3390/su13168737









