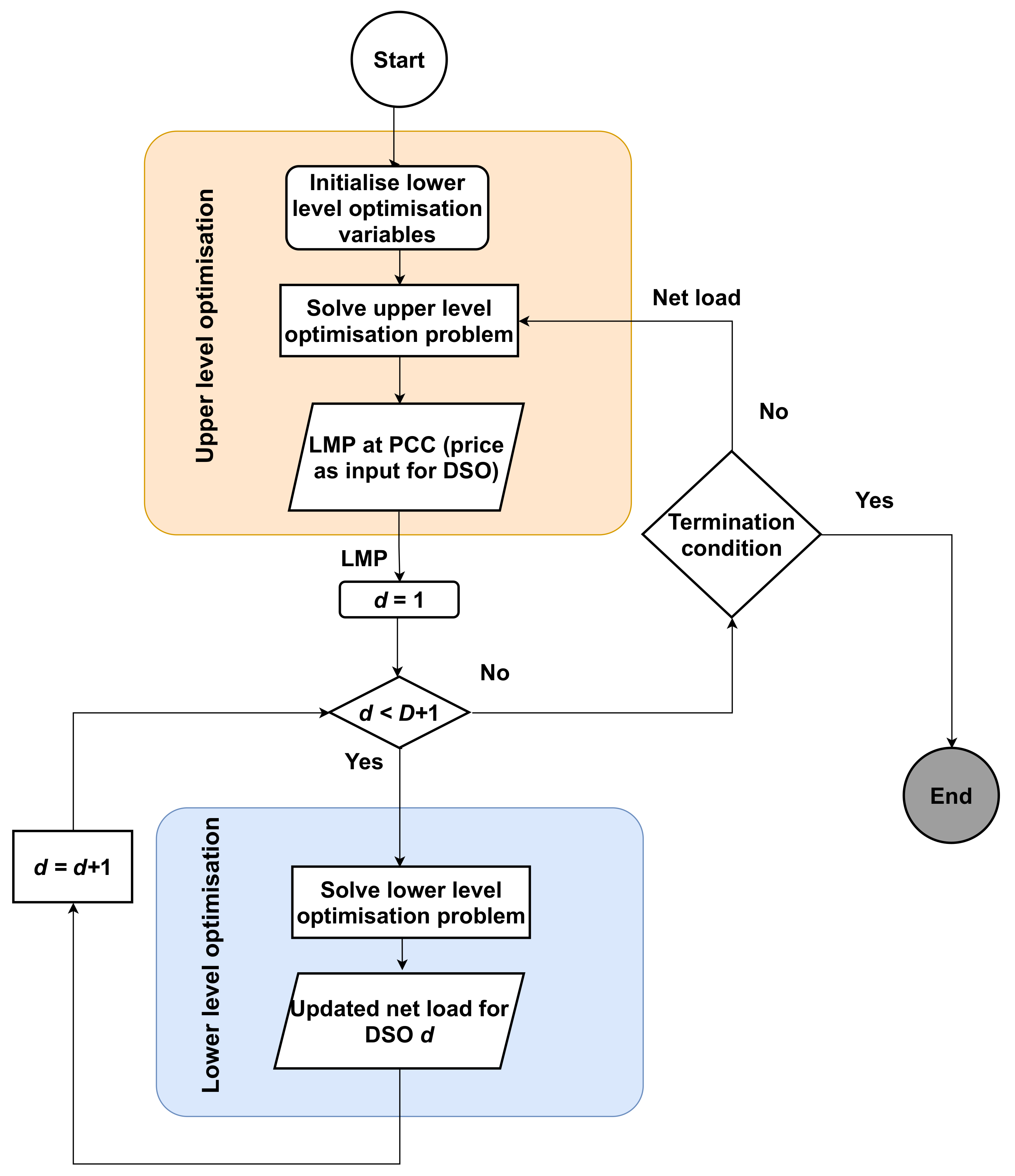
4.1. System Description
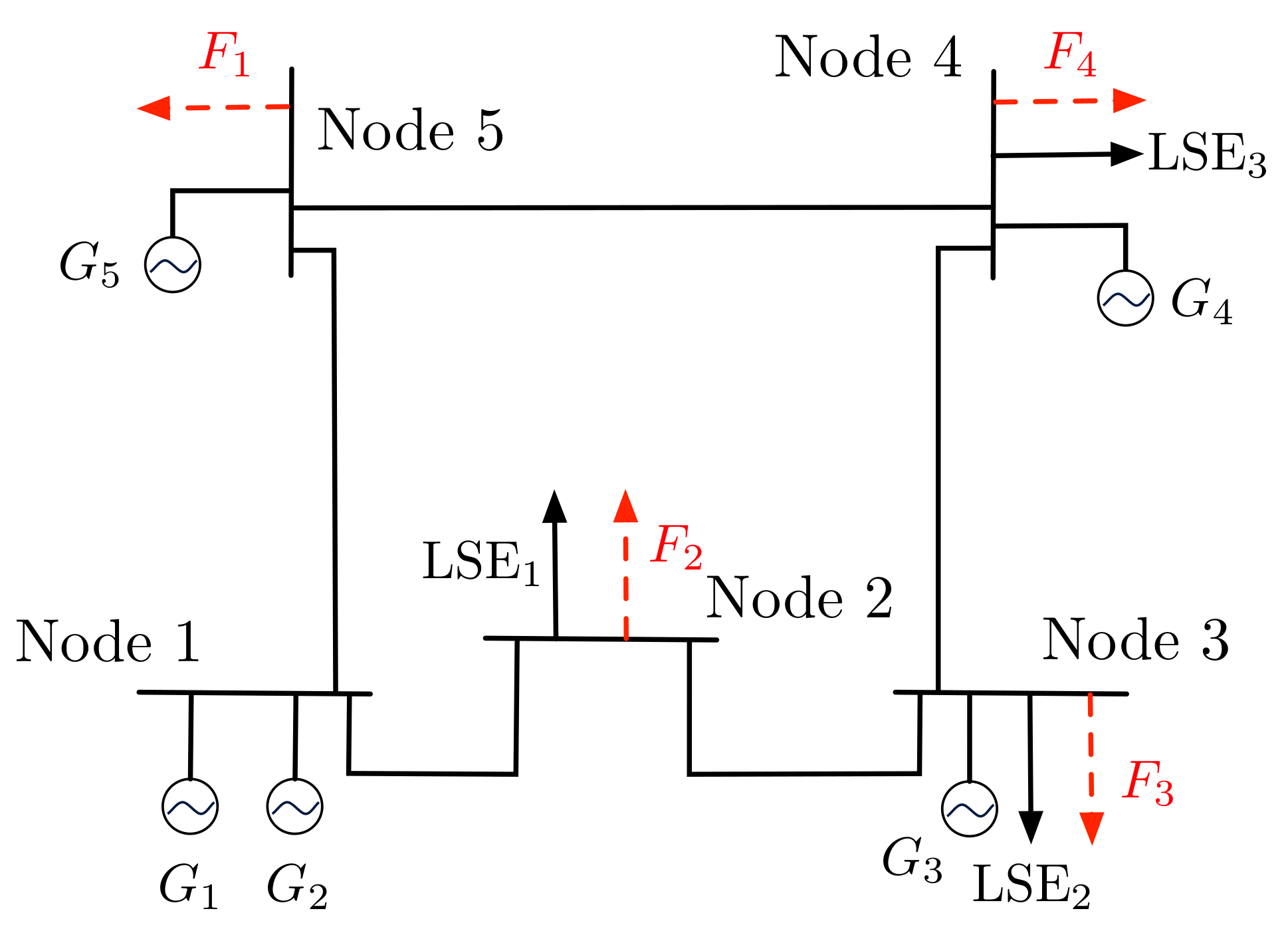
To validate the proposed framework we need to construct a power system with many voltage levels that will represent the transmission and distribution systems. As such, we select a five-node transmission system on which four distribution system feeders are connected to different nodes as depicted in
Figure 2.
We denote by
the
ith feeder connected to the transmission system. More specifically,
and
correspond to the IEEE standard 33-bus feeder and
and
to the 69-bus IEEE standard bus feeder [
44,
45,
46]. The load serving entities at a transmission node
i are denoted by
. There are five generators connected at the transmission level in nodes 1, 3, 4 and 5. The transmission system data may be found in [
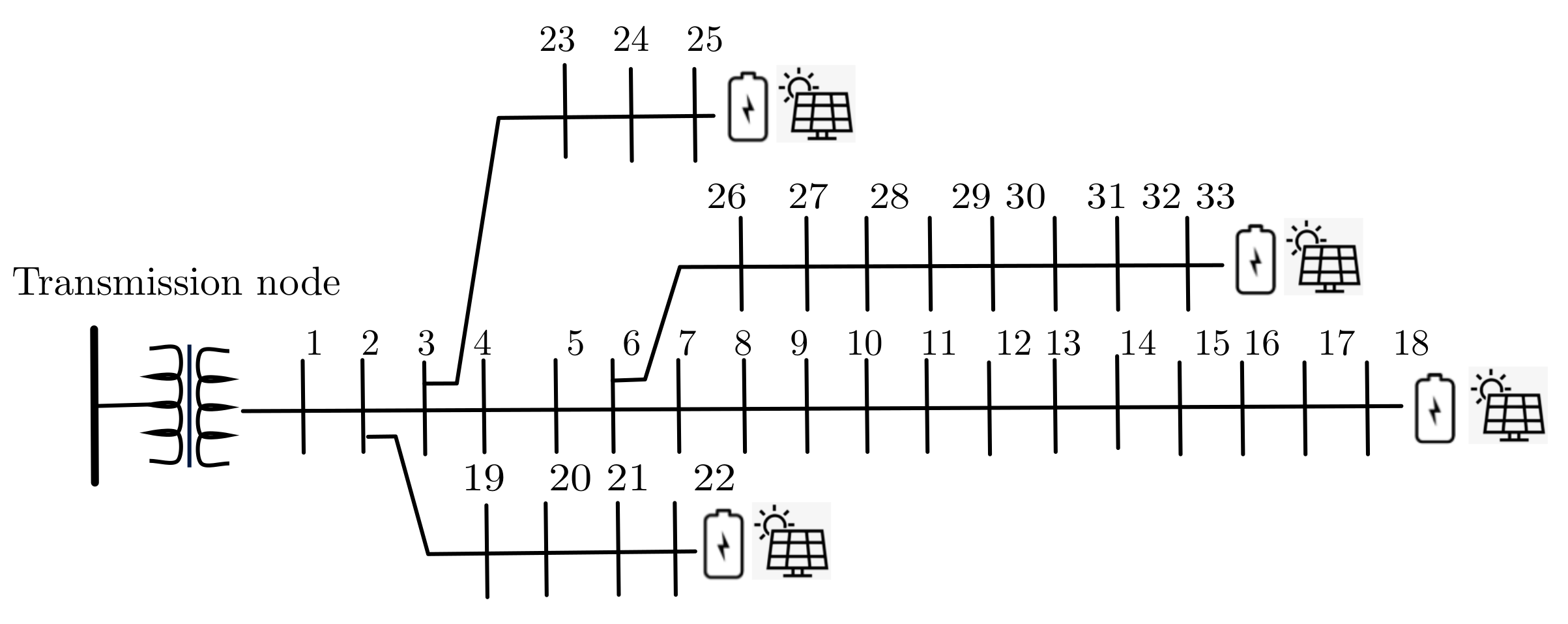
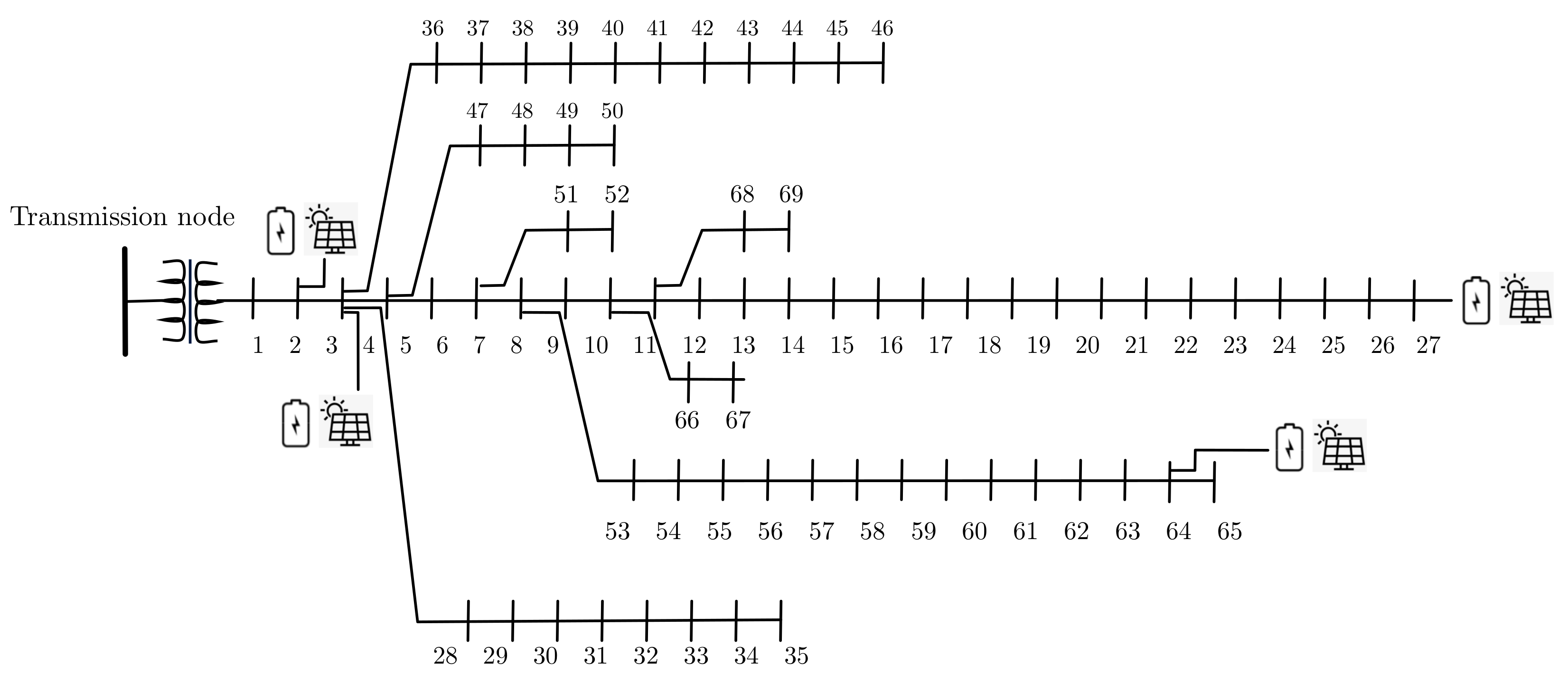
24]. To demonstrate how the TSO-DSO coordination schemes can facilitate the integration of DG we modify the standard IEEE 33- and 69-bus feeders by deploying PV and battery systems at different nodes. We assume that the distributed resources are mostly installed at end-nodes in the distribution level where the voltage drop levels are worst [
47]. The modified feeders are depicted in
Figure 3 and
Figure 4, respectively. In particular, PV and battery systems are installed in nodes 18, 22, 25 and 33 in the 33-bus feeder and in nodes 2, 3, 27, and 64 in the IEEE 69-bus feeder. The distributed resources data are presented in
Table 1. Furthermore, we assume that each node’s voltage in the distribution system is bounded between 0.95
and 1.05
.
Next, we implement both the proposed centralised and the decentralised schemes, and we compare the results with current practise, which refers to when the TSO solves its OPF and determines the LMPs at the substations. Next, the DSOs dispatch distributed DG by optimising cost and considering the LMP at the substation as a fixed parameter. In current practise, there is minimal coordination between TSOs and DSOs. The three methodologies are compared against a variety of metrics: total cost, hourly LMPs, hourly DG output, hourly generator output at the transmission level, netload; and level of congestion.
4.2. Decentralised Coordination Scheme
We apply the scheme proposed in
Section 3.1 to the system described above. In order to demonstrate how the decentralised scheme facilitates the integration of distributed energy resources we compare its optimal operation (method (ii)) against current practice (method (i)), where the current practise as discussed in the introduction section is when the TSO solves its own OPF and determines the LMPs at the substation, and the DSOs dispatch DG by optimising cost and considering the LMP at the substation as a fixed parameter. We run both cases for a one day period with hourly intervals. In
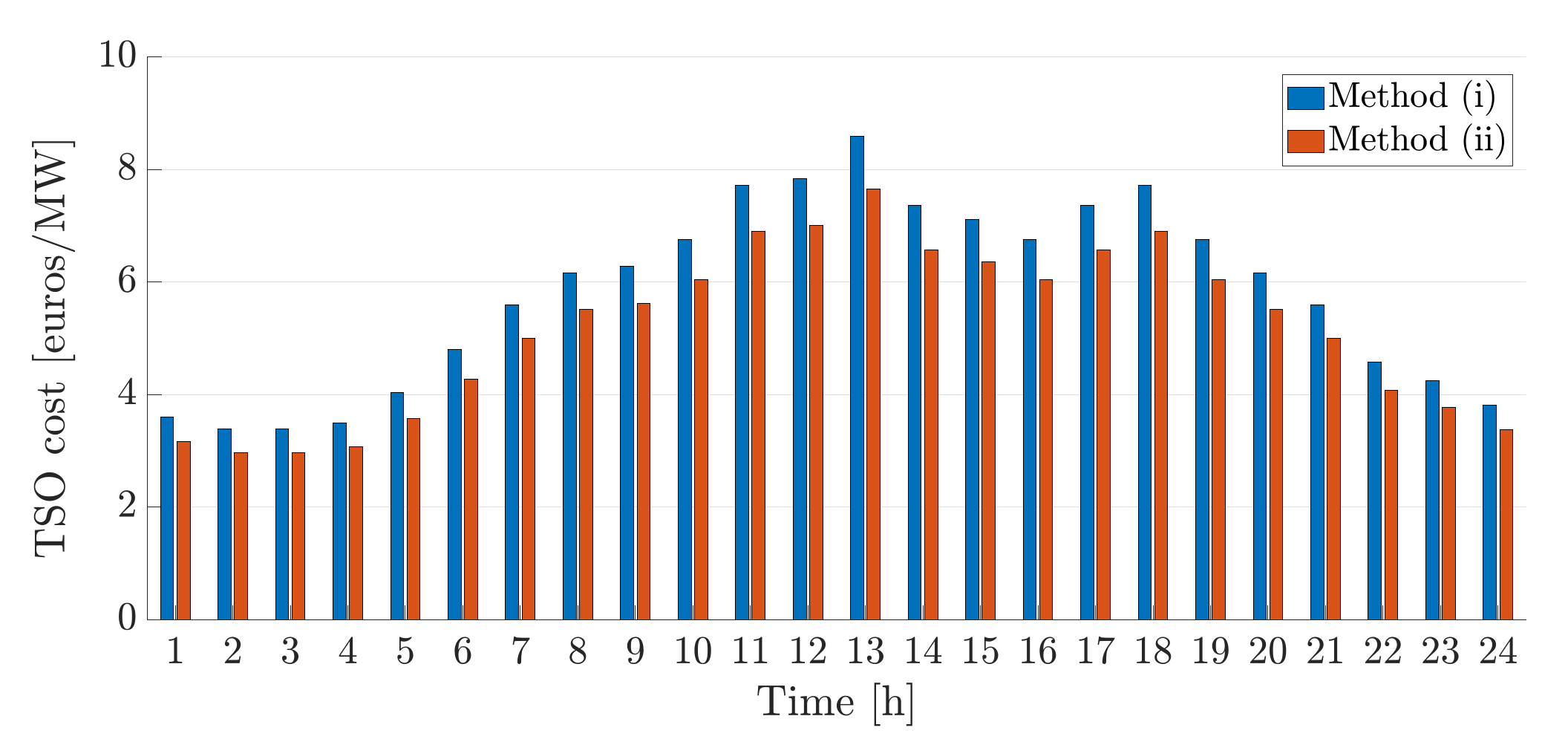
Figure 5, the TSO operation cost for both cases is depicted. We notice that the proposed decentralised coordination scheme results in a reduced transmission operation cost for all hours of the day. The reason is that distributed energy resources, which are less expensive than generators connected at the transmission level, are used to a greater extent as seen in
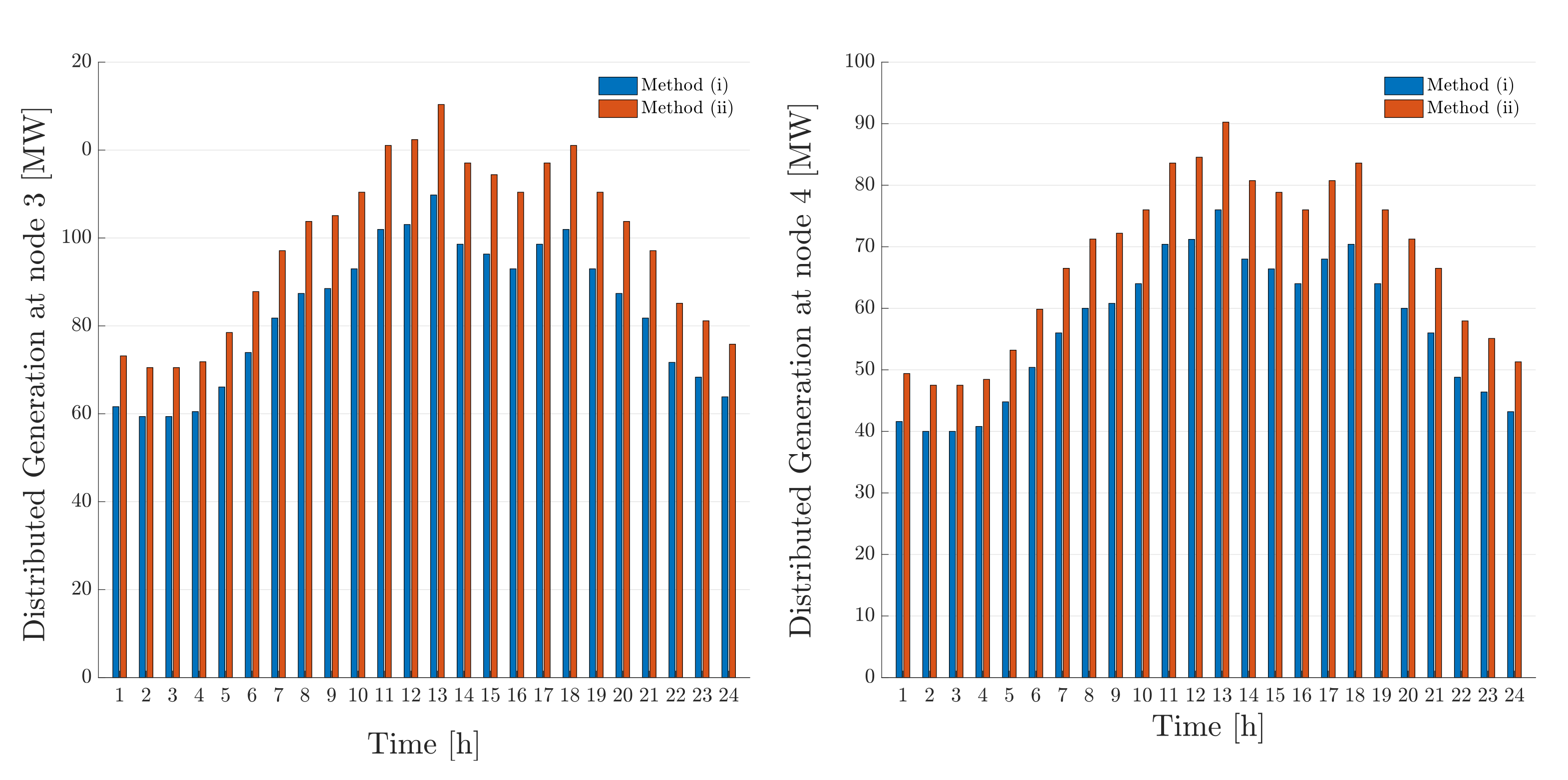
Figure 6.
Another effect of the increasing use of distributed resources is that they relieve the congestion that is present in the transmission system, which in turn reduces TSO operational costs. For method (i) the LMPs for each hour at each node may be found in
Table 2. We notice that for the same hour each node has a different LMP. This demonstrates, based on the formulation of the augmented DCOPF in (
1), that some line flows have reached their limits. The LMPs of method (ii) are shown in
Table 3. We notice that the LMP difference between hours has been reduced, reflecting the fact that there is less congestion in the transmission system. In fact the LMPs are practically the same for all nodes at every hour when the proposed decentralised scheme is implemented. Following the formulation of (
1) and using the KKT conditions of optimality, the LMP difference is expressed as a function of the congestion that can be present in the network (see, e.g., in [
48]), i.e.,:
where
is the dual variable of the power flow limits for line
ℓ;
is the subset of lines that are at their limits, i.e.,
; and
is the power transfer distribution factor of transaction with node pair
with respect to line
ℓ. We can interpret (
29) physically by considering an injection at node
k and its withdrawal at node
. We interpret
as the fraction of the transaction with node pair
of 1 MW that flows on line
ℓ. As such for every hour the LMP differences are purely a function of the transmission usage costs of the congested lines, thus showing the “level” of congestion.
In
Table 4 and
Table 5 the hourly power output of each transmission generator is shown. We notice that with method (ii) the total power used by generators at the transmission level is reduced compared to method (i). The reason is that the less expensive distributed generators at distribution level are used to satisfy the load instead. More specifically, we notice that with method (ii) the transmission level generators 2, 3, and 4 have zero output for most hours of the day as they are the most expensive ones.
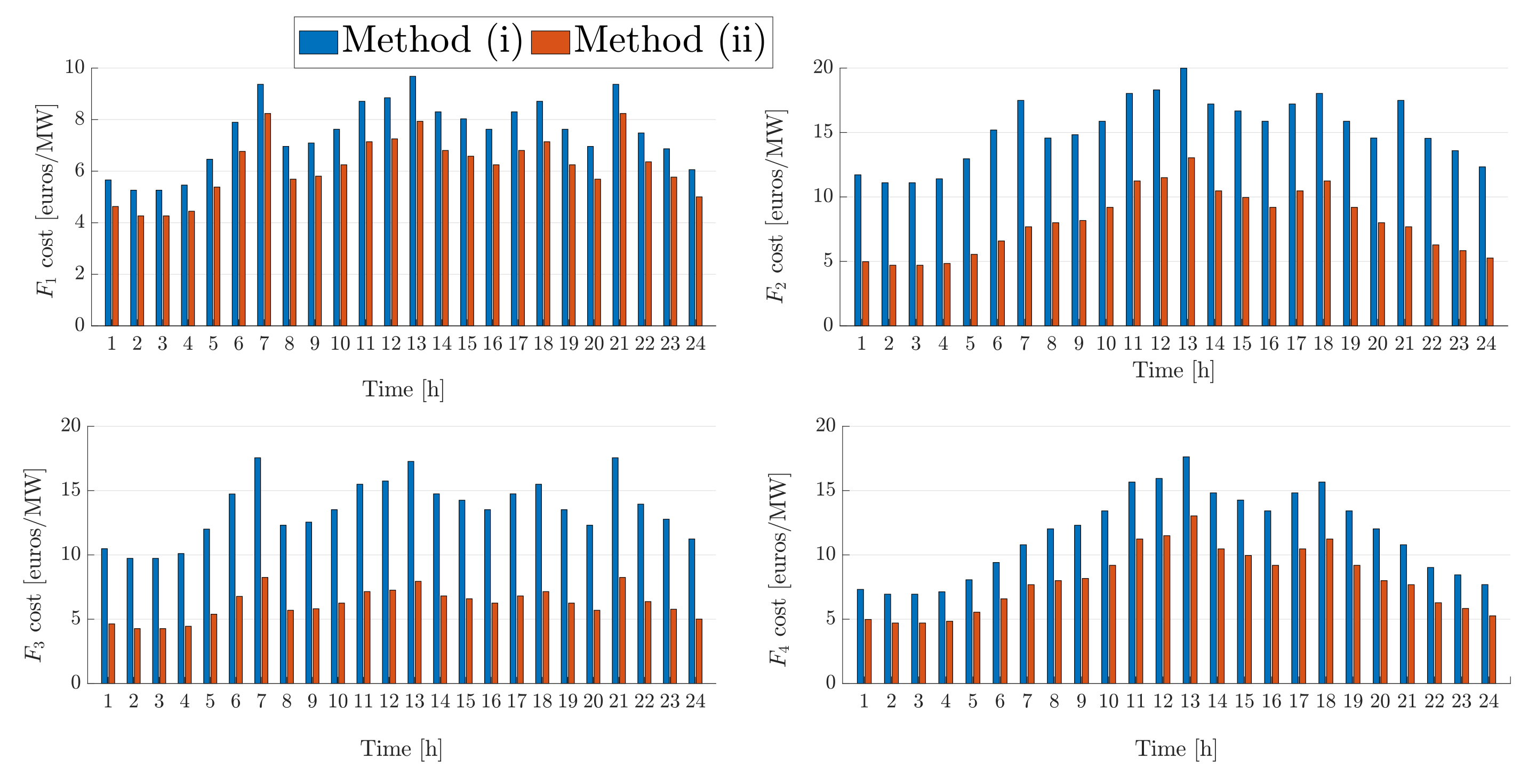
In
Figure 7 we depict the operational cost for each distribution feeder connected to different nodes of the transmission system for methods (i) and (ii). We notice that the proposed coordination scheme results in reduced costs for all DSOs as all resources were utilised in a more efficient way as discussed above.
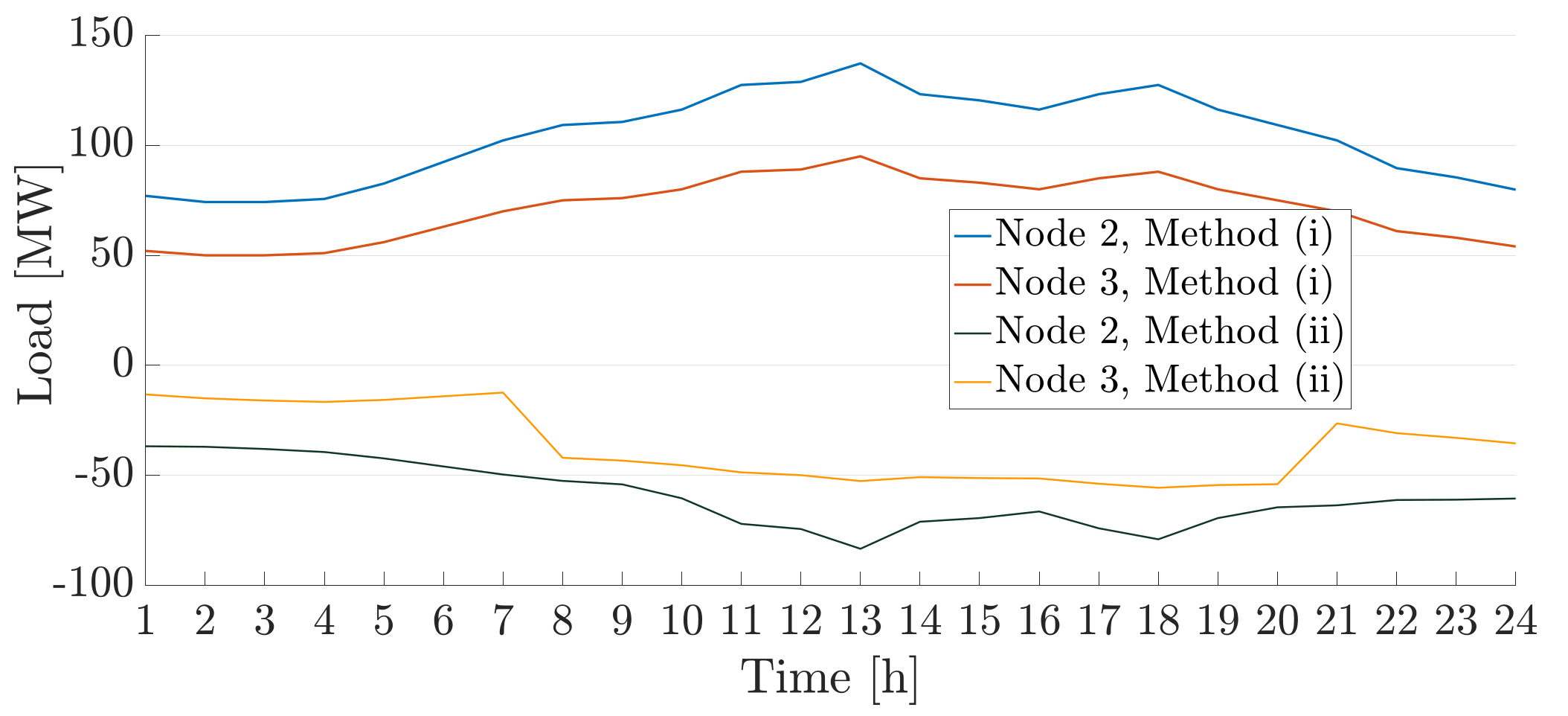
We now study the net load at the transmission nodes using both methods. We can see in
Figure 8 that the net loads at the transmission system at nodes 2 and 3 decrease, a fact that is also reflected in the OPF in the transmission system and its LMPs. We also notice that there is a sharp fall and rise in the net load, between hours 7 and 8 and 20 and 21 respectively. This is due to the fact that the power flow between nodes 1 and 2 at time 7 and 21 is 75 MW, which is equal to the line’s thermal limit. This causes the LMP divergence in these hours, as shown in
Table 3.
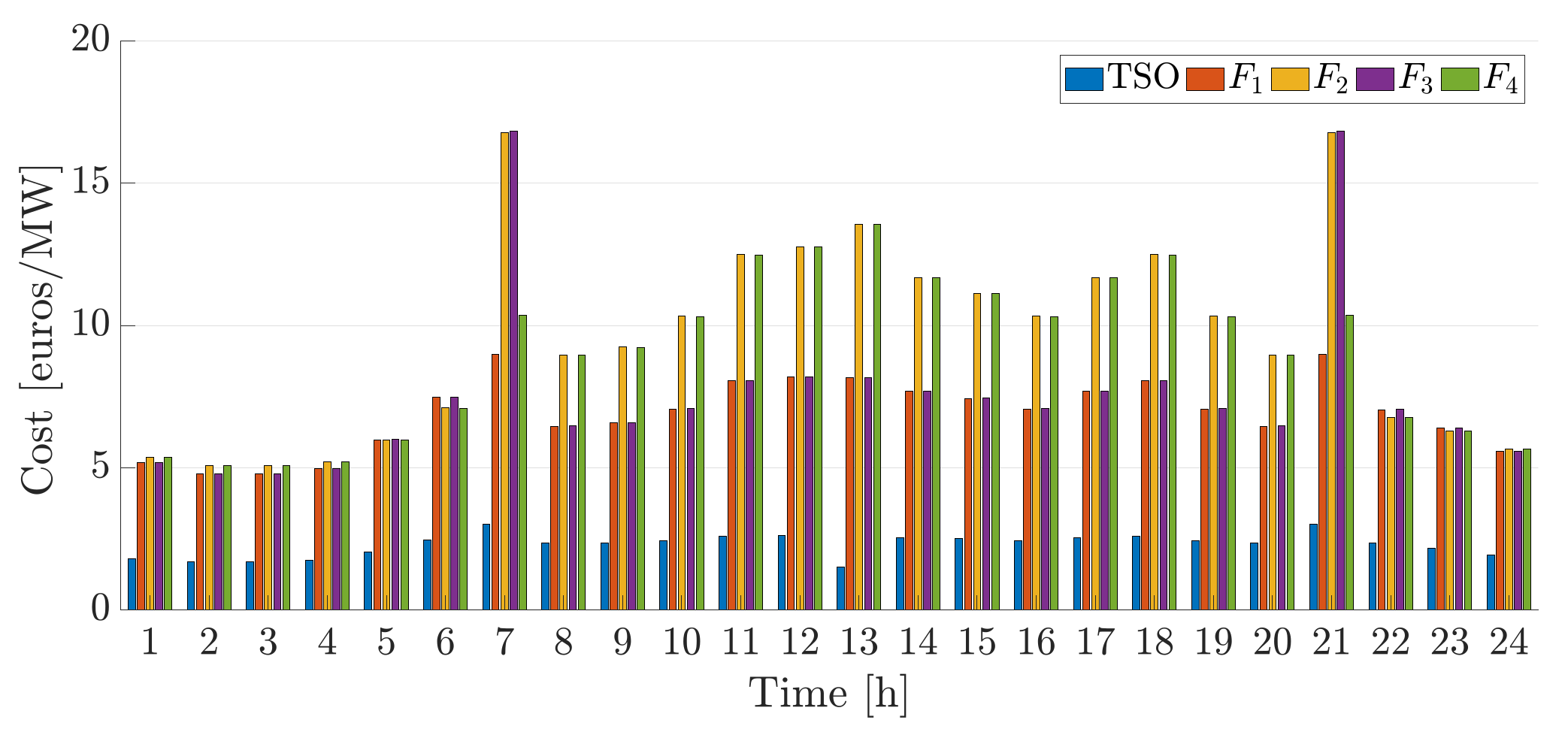
Last, we depict the hourly operational cost for the TSO and the DSOs in
Figure 9 which will be used to compare the two proposed schemes.
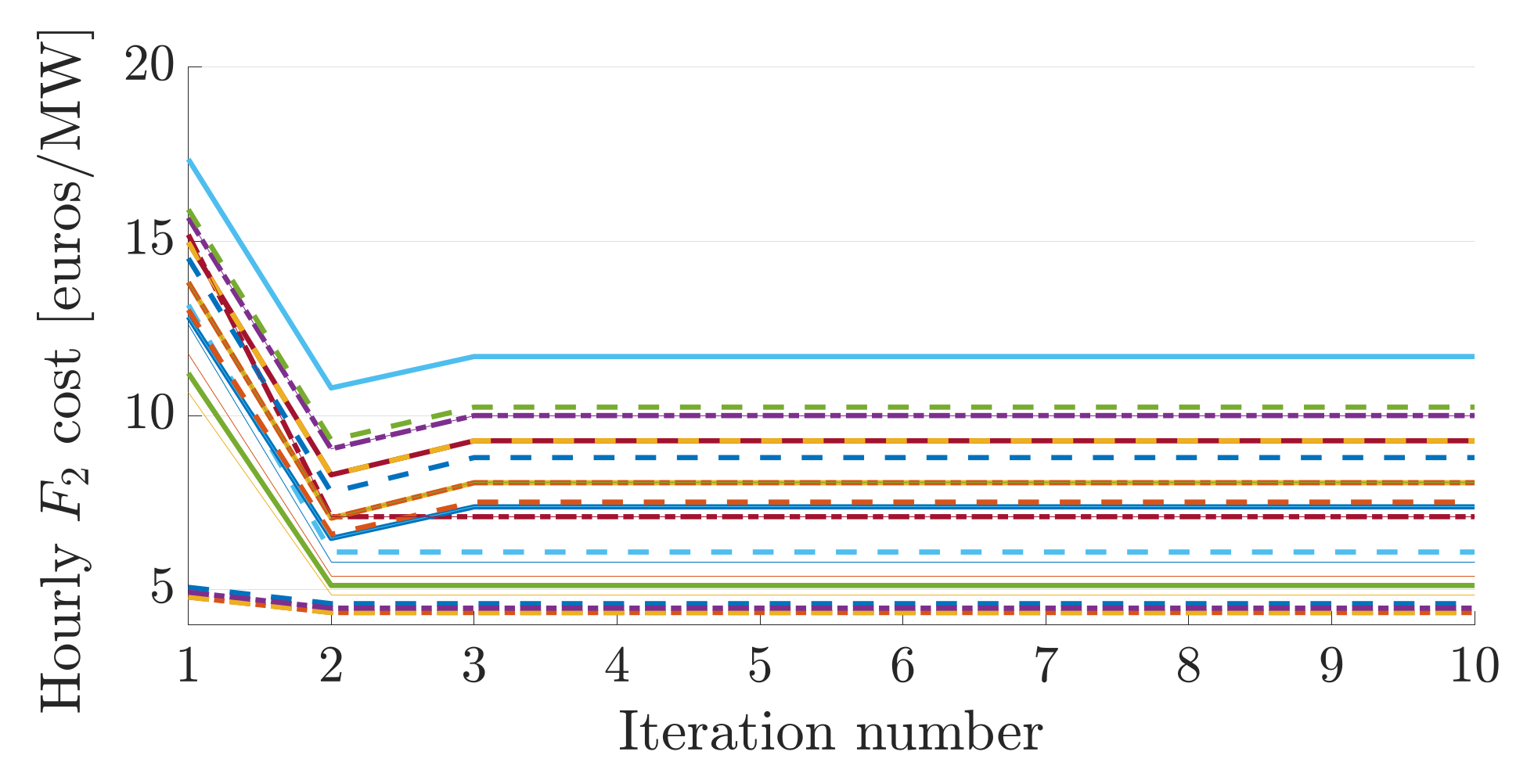
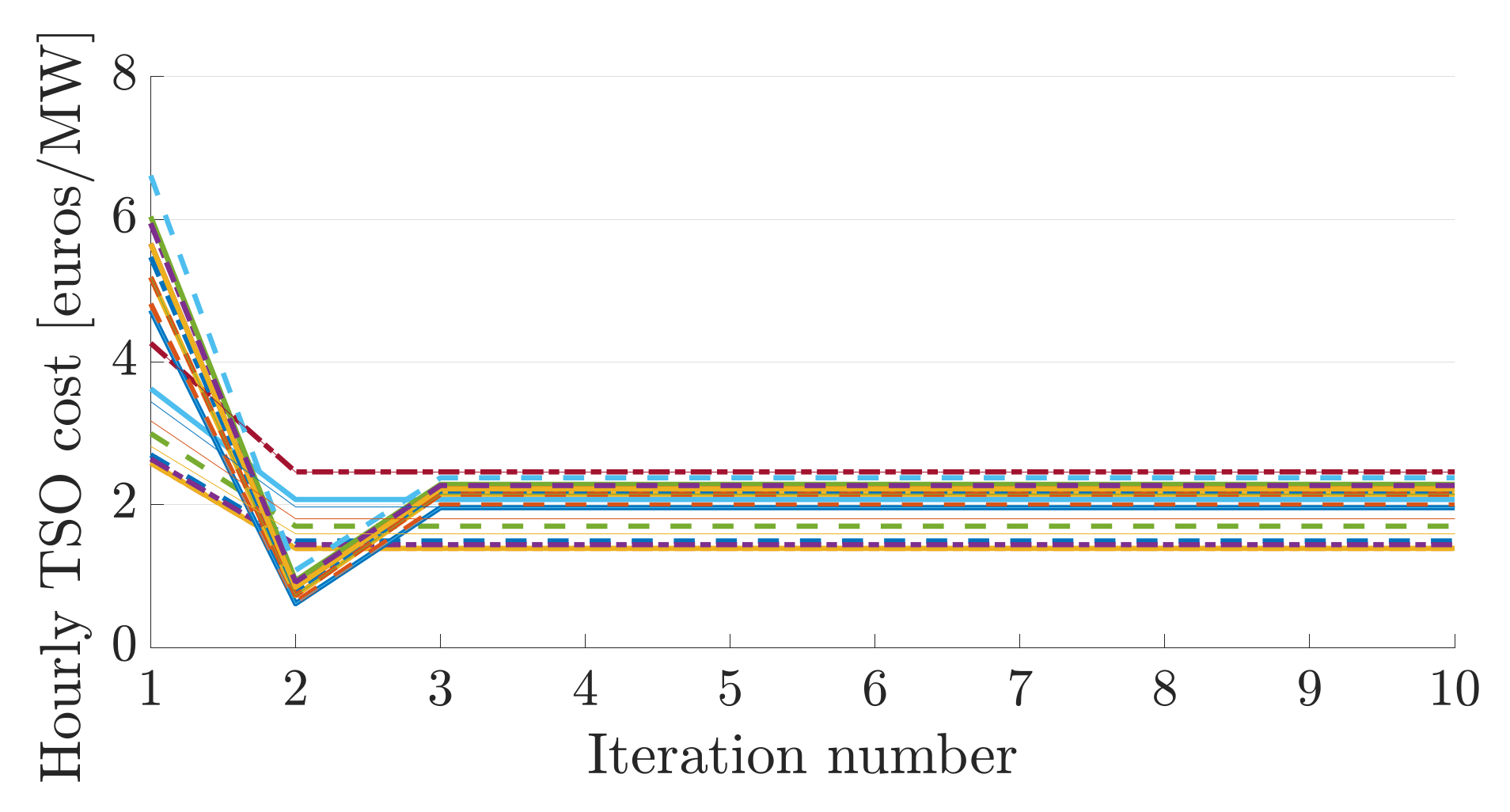
We next check the convergence properties of the proposed algorithm. In
Figure 10 and
Figure 11 we illustrate the evolution of the hourly objective functions of
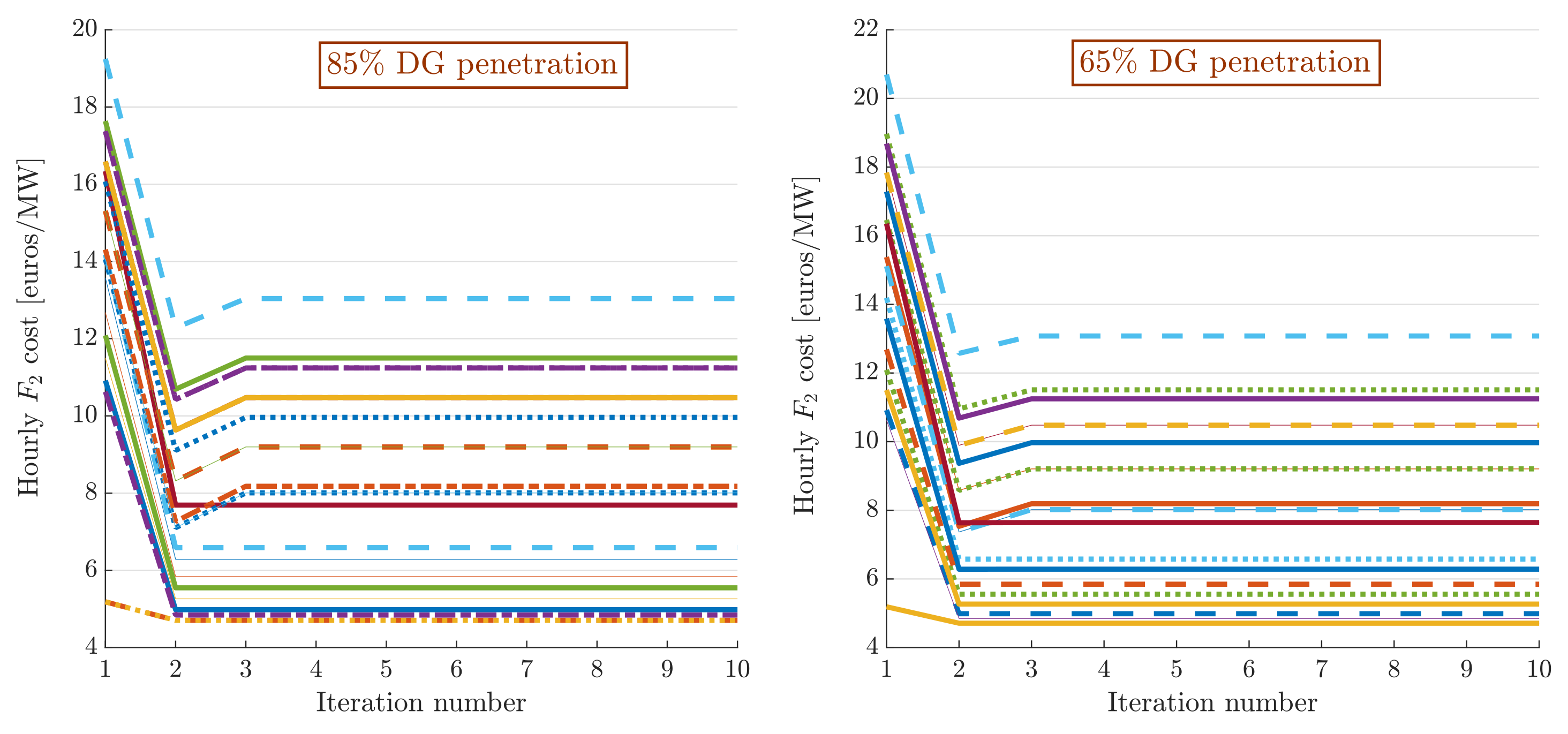
and the transmission system for a 24-h period with respect to the iteration numbers of algorithm. We notice that the algorithm converges after three iterations. To test the sensitivity of the proposed algorithm with respect to the initial point, i.e., the choice of initial load value for the distribution system, we changed the initial point to be full load, 85%, 75%, and 65% of the full load. In all cases the algorithm converges in three iterations. Next, to analyse the sensitivity of the proposed algorithm with respect to the level of distributed resources penetration we depict in
Figure 12 the evolution of
hourly cost for two different levels of penetration with the same initial point (step 3 of the algorithm) with respect to the number of iterations. The final cost is different for the two cases since there are hours where the DG price is smaller than the grid price and vice versa.
4.3. Centralised Coordination Scheme
We apply the proposed scheme developed in
Section 3.2 to the system described in
Figure 2. In order to demonstrate how the proposed centralised scheme can facilitate the integration of distributed energy resources we compare method (i), which is the optimal operation with the current practise, with method (iii), which is the proposed centralised scheme. We start the simulation by assigning the same weights to the transmission cost function and the distribution feeders’ cost functions as
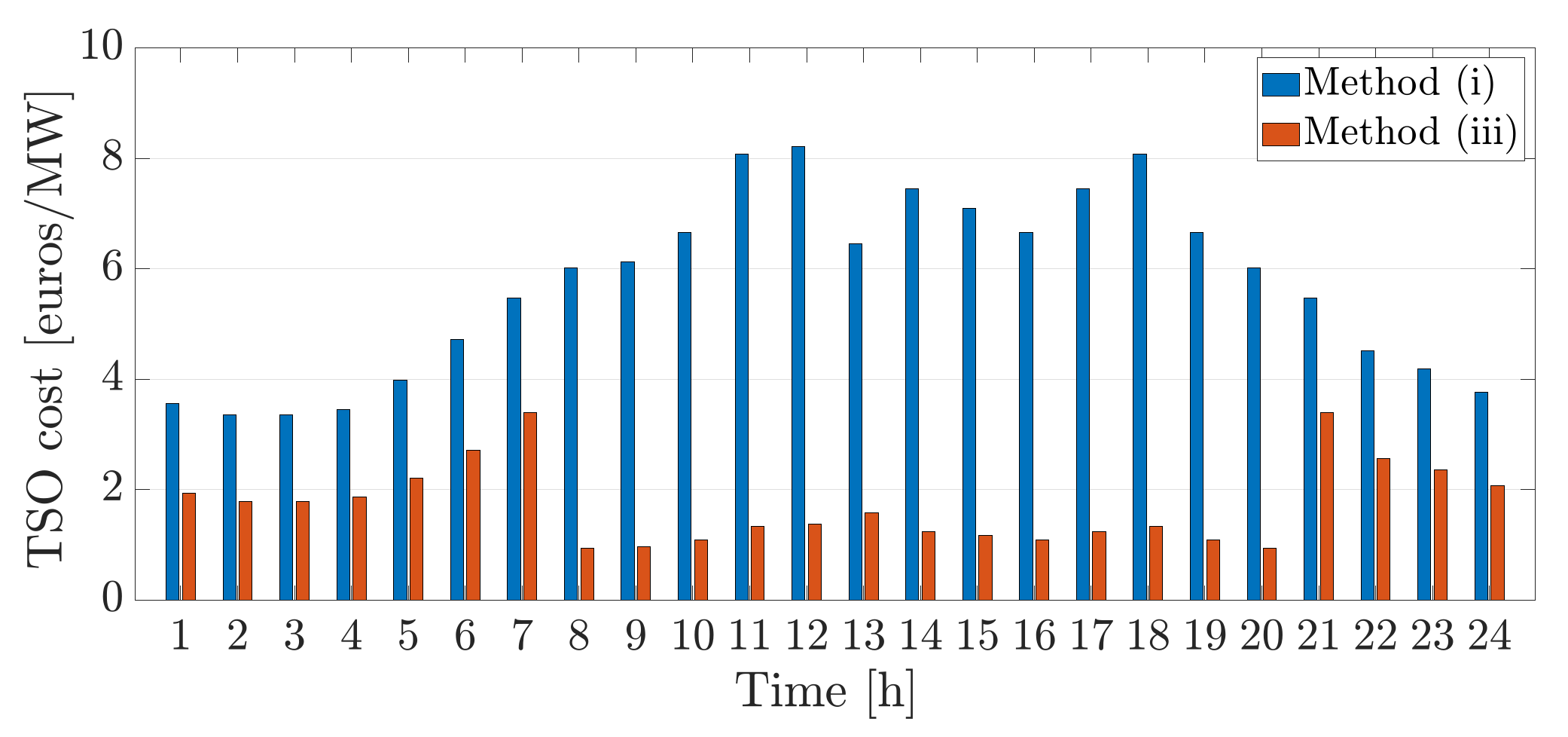
. The TSO cost as depicted in
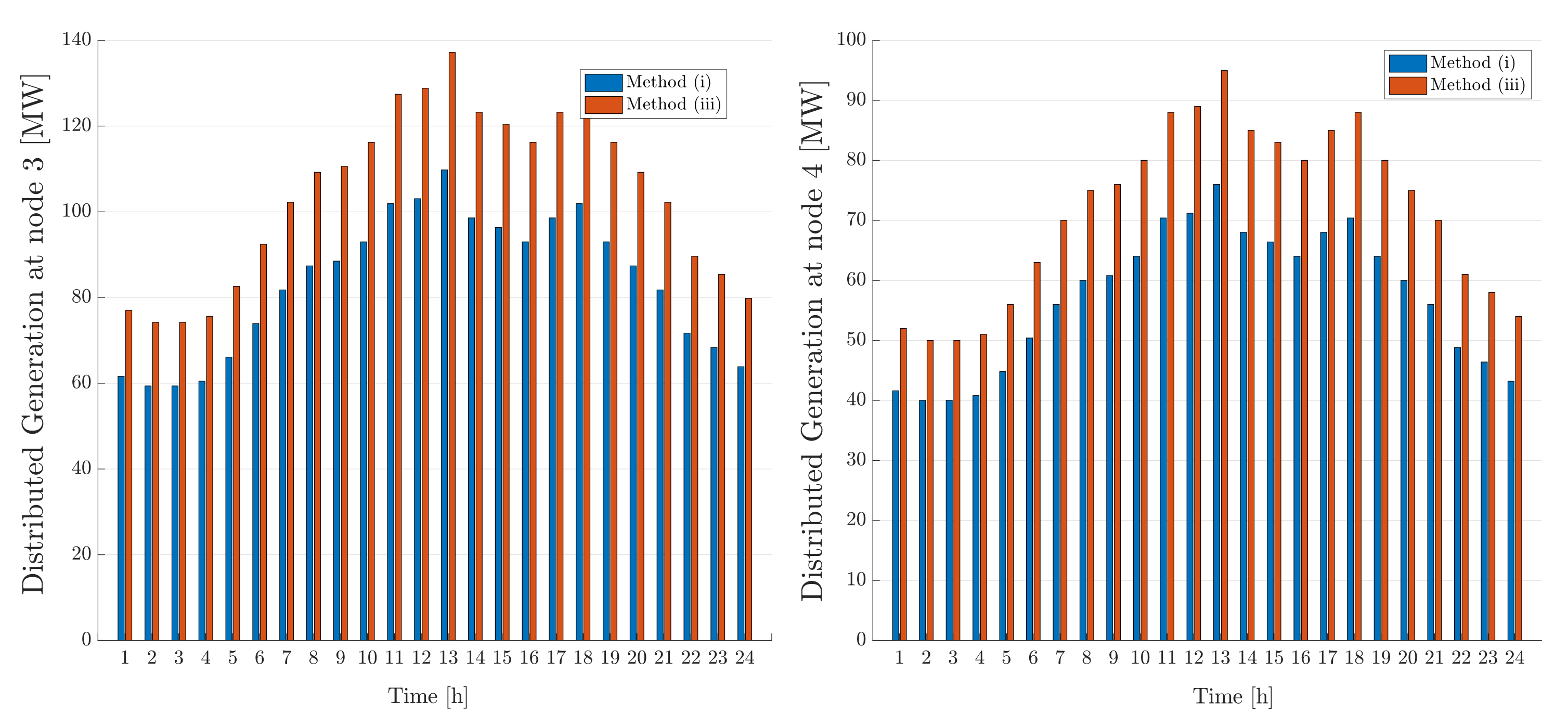
Figure 13 is reduced significantly with method (iii), i.e., the centralised scheme, in comparison to the current practise due to the increase in the integration of the distributed resources at different nodes as shown in
Figure 14.
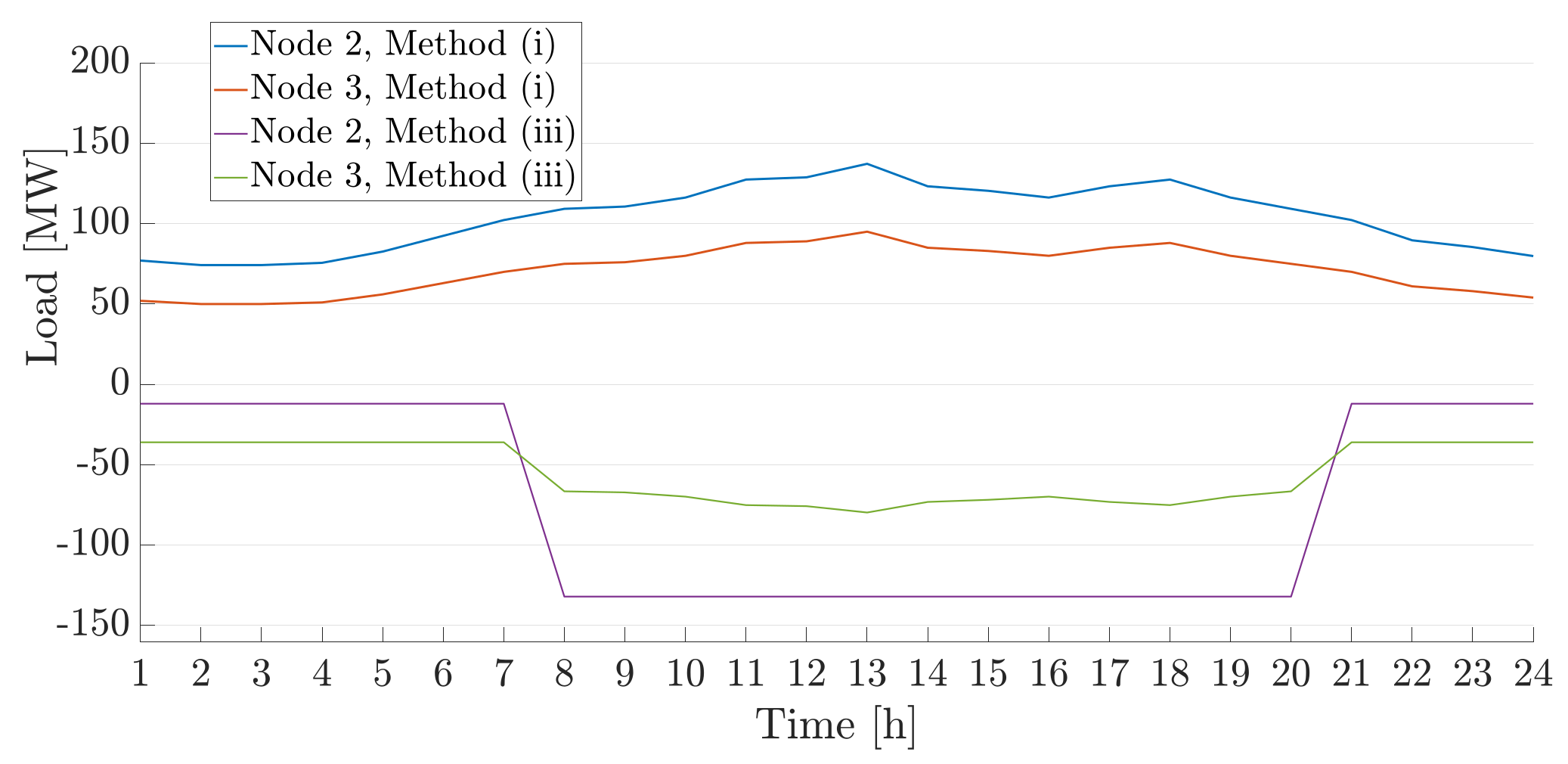
In
Figure 15 the net load at the transmission level using methods (i) and (iii) is depicted. We notice that it is more cost efficient for the TSO to purchase power from the DG that is present in the distribution systems. For instance, the negative load at node 2 means that the excess power of the distributed resources is redirected to the transmission system. DGs usually sell at a price equal to the LMP at their PCC. This results in distributed resources’ owners gaining revenue by selling power to the TSO, while the TSO also meets its load at a lower cost. In
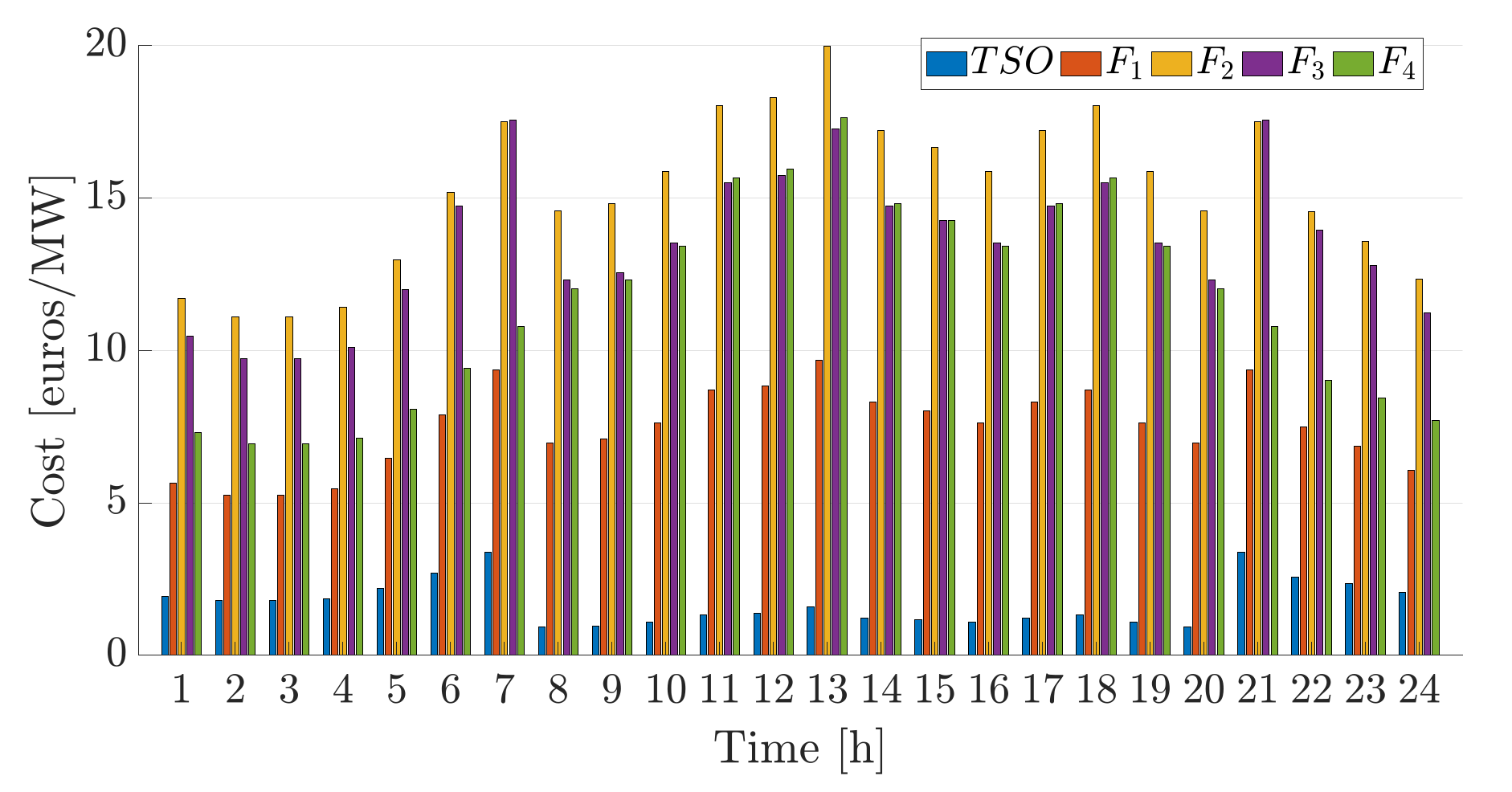
Figure 16 the operational cost for each hour for the TSO and DSOs for the proposed centralised coordination scheme is depicted.
Figure 16 shows that the transmission cost for method (iii) with
is lower than that of method (ii) as depicted in
Figure 9. The difference is that more power is being used from the DGs in method (iii) compared to that of method (ii). However, we notice that the cost of feeders in method (iii) is higher than that of method (ii). Again, this is due to the fact that more power is being used from the DGs in method (iii) compared to that of method (ii). These values can be used by DSOs and TSOs to formulate their bids and provide incentives for DG participation respectively.
The hourly power output of transmission generators for method (iii) is presented in
Table 6. We notice that between hours 8 and 20 the distributed resources located in the distribution systems satisfy the load at the transmission level, whereas at night hours mostly the TSO is responsible for supplying the load to the customers. This reverse power flow also impacts the LMP as shown in
Table 7, where we notice a marginal increase in the LMPs for the night hours is achieved. Similar to method (ii) there is congestion at hours 7 and 21 due to the congested line between nodes 1 and 2.
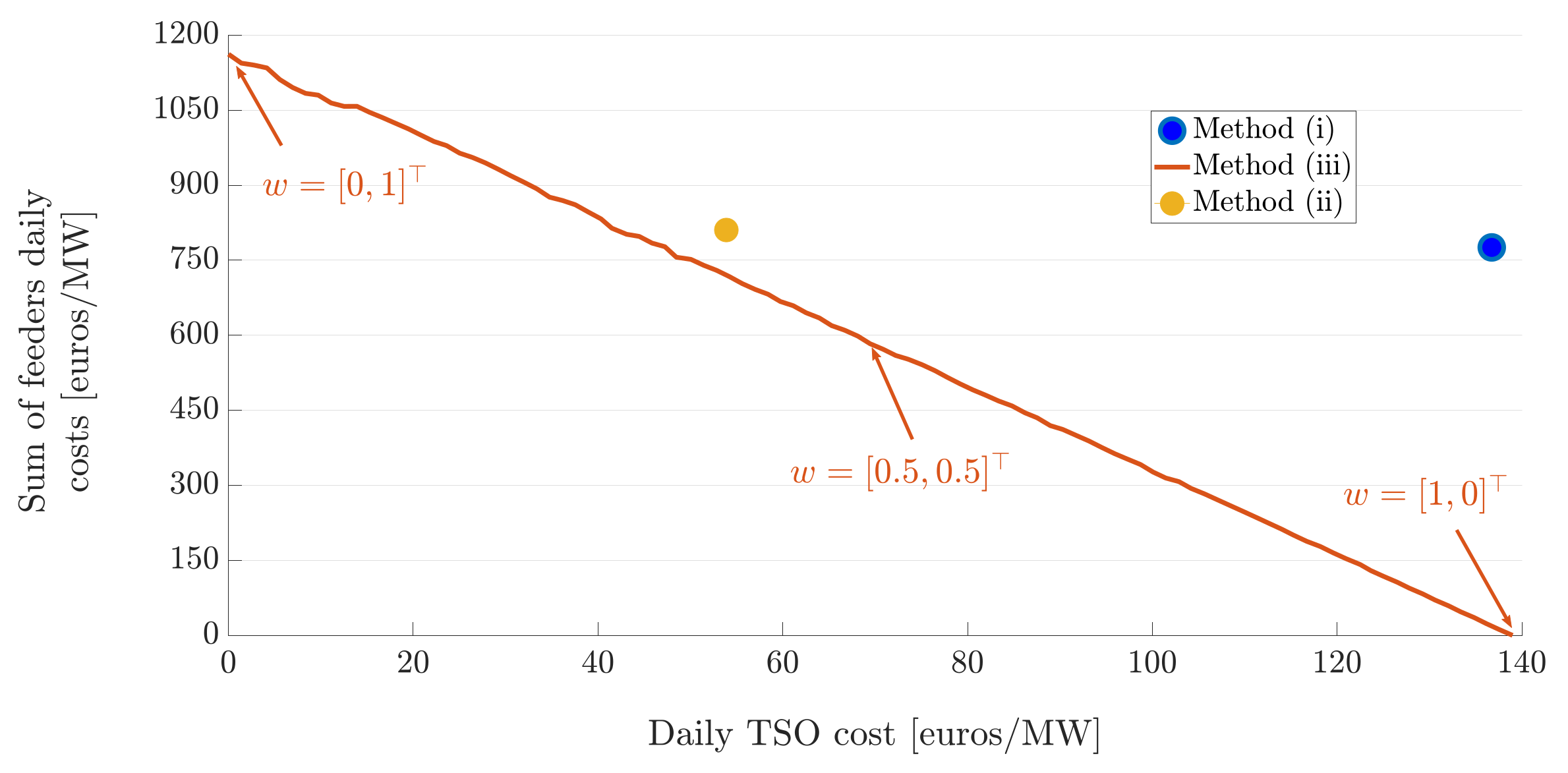
Next, we analyse the interaction between the TSO and the DSOs. For this, we modify the weights of (
28) to obtain an approximation of the Pareto front. More specifically, we start with
and
, and with increments of
we reach
and
. The Pareto front is depicted in
Figure 17. By moving along the curve, we can minimise DSOs’ objective at the expense of TSO’s objective, or minimise the TSO’s objective at the expense of DSOs’ objective. However we cannot improve both at once, i.e., there is no mathematical “best” point along the Pareto front.
To provide insights into the potential conflicts between TSOs and DSOs we discuss in greater detail the two extreme cases, i.e., and and and . The TSO and DSO costs for the first one are 0 €/MW and 500 €/MW, respectively; and for the latter they are 140 €/MW and 0 €/MW, respectively. In other words, when the objective is to only minimise the TSO cost; all costs are being incurred by the DSOs and vice versa. In both cases, all constraints, e.g., voltage and thermal limits, are met thus the power system quality is guaranteed.
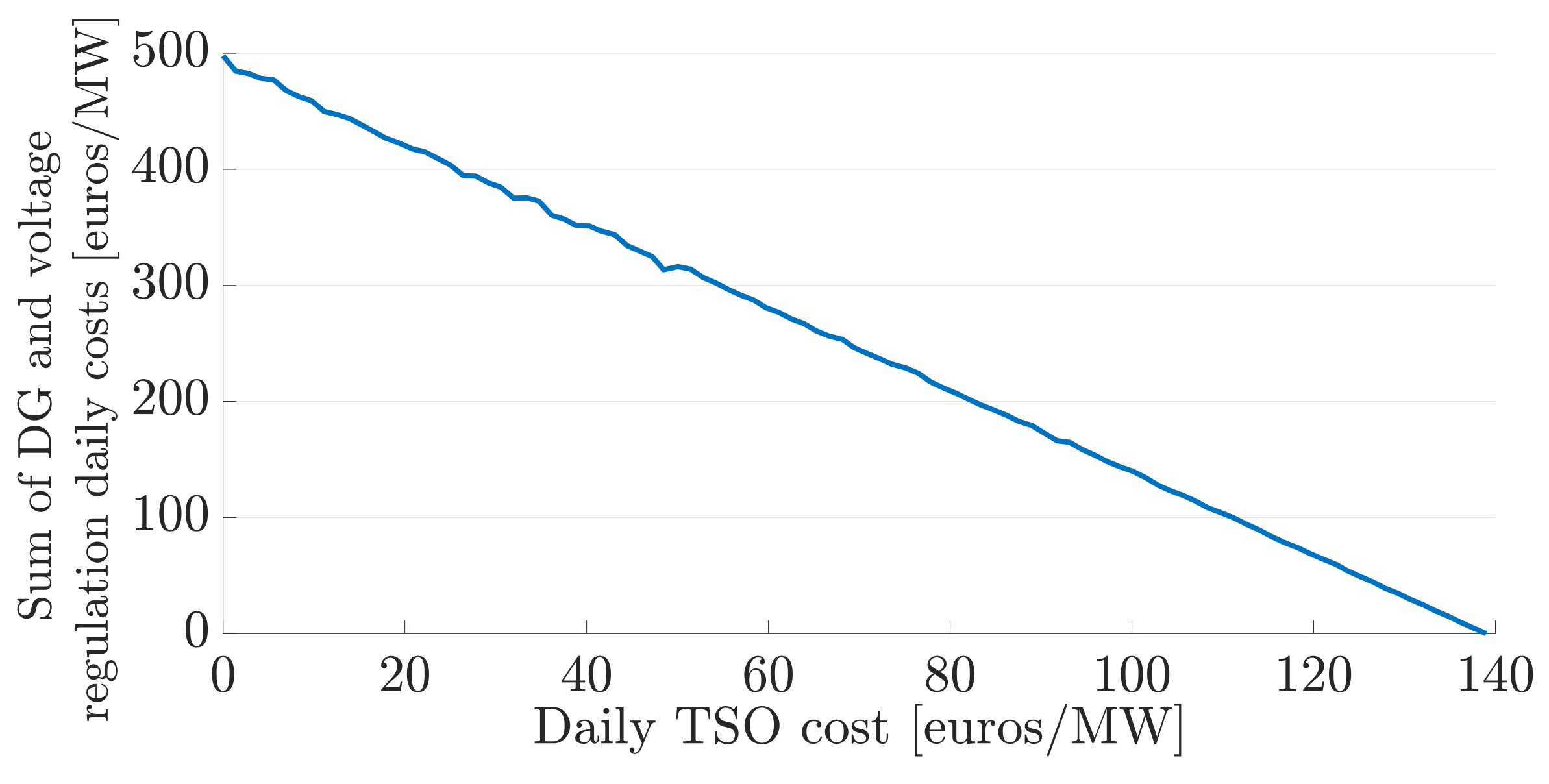
In
Figure 18, we depict the total DSO cost that includes the payments to the TSO given in (
9), DG cost given in (
10) and (
11), and voltage regulation costs given in (
12). We compare the results for different weights with methods (i) and (ii). We notice that the results of method (ii) are close to the Pareto front offering a near-optimal solution. The appropriate choice of operation for the Pareto front is a balance of priorities between TSOs and DSOs and the determination of specific incentives, which are part of future work. Another implication of the Pareto front is that any point in the feasible region that is not on the Pareto front is not considered to be a “good” solution, e.g., method (i). Either objective, or both, can be improved at no penalty to the other. This demonstrates that there are a lot of improvements to be made to current TSO-DSO coordination practise, i.e., method (i). To determine the priorities of the proposed decentralised scheme, we have to analyse where its solution lies in the Pareto front. More specifically, we notice in
Figure 18 and
Figure 19 that the proposed decentralised scheme provides a balance between the TSO and DSO objective, as it lies between the two extreme cases.
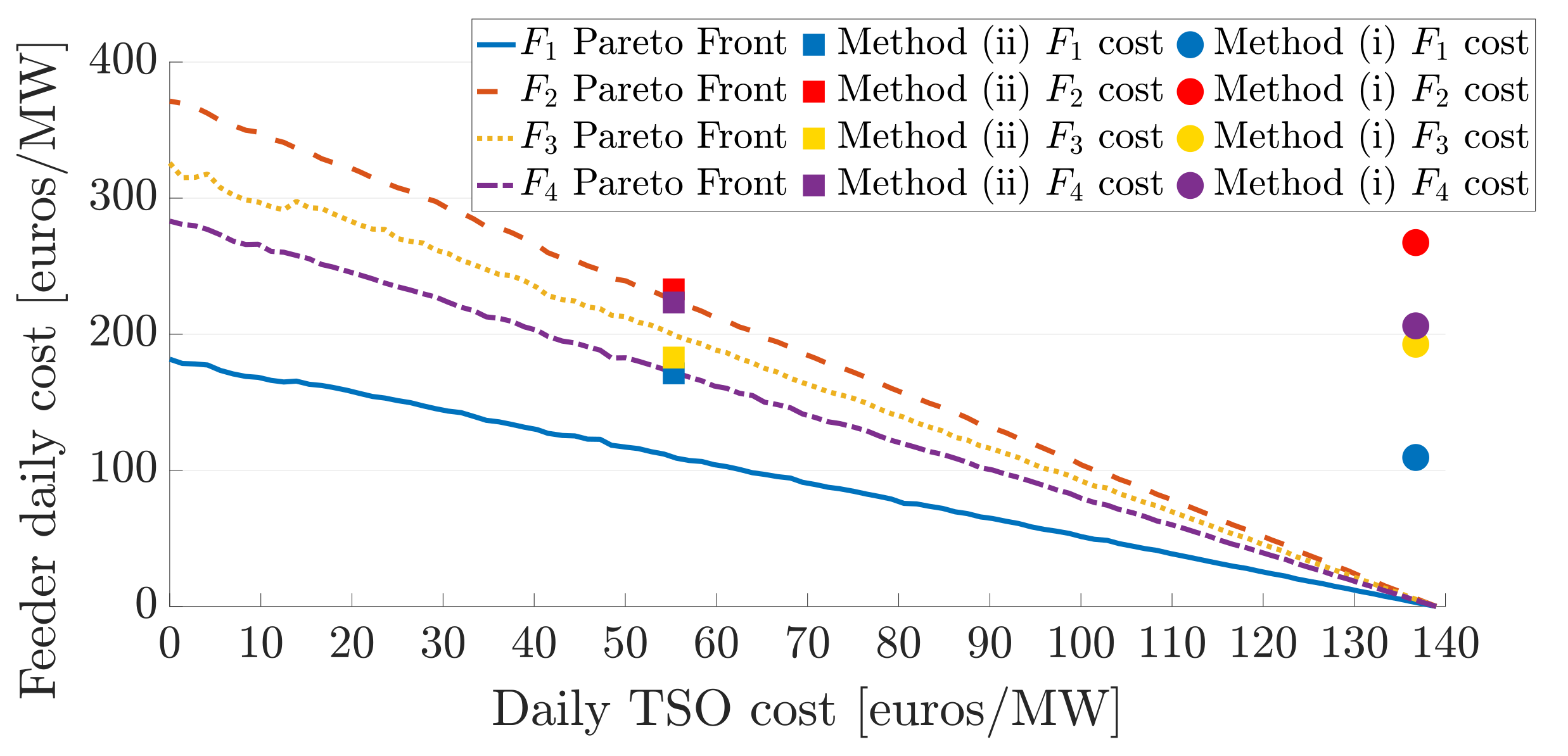
Next, we depict in
Figure 19 the daily cost of individual feeders, which includes the payments to the TSO, the cost of DG and voltage regulation, to investigate how far from the optimal solution each feeder operates for the various schemes. We notice that for method (ii),
operates at the optimum,
at a point that is at the expense of other feeders, and
and
at points further away from the optimal solutions. However, the summation of these costs corresponds to a near optimal solution as seen in
Figure 18.
In both schemes, the transmission cost decreases, while for method (iii), the transmission operation cost reduction is higher than that of method (ii). In comparison to the current practise, i.e., method (i), both schemes are more effective in terms of the share contribution of the distributed generators at each transmission node, while the utilisation rate of generation for method (iii) is higher than that of method (ii). Using method (iii), we can see that the output of each generator at the transmission level is lower than that of method (ii) and for method (ii) is lower than that of method (i). Although for method (ii) and method (iii), the congestion level is improved, the LMP for each node at each hour is higher at night hours in method (iii). This is due to the increased output of transmission generators at night hours. It should be noted that in all case studies all variables, e.g., voltage levels, transmission line flows, are kept within the limits of acceptable for power quality purposes as defined by the constraints of the OPFs. For example, voltage levels of each bus in the distribution system at every time interval are in the range of 0.95–1.05 pu. The algorithm running time for the centralised scheme is 12,387 ms and for the decentralised is 21,800 ms in a Windows machine which is equipped with AMD® FX-9830P RADEON R7 CPU with four Cores at 3.00 GHz and 16 GB of RAM. As expected the centralised scheme is approximately two times faster; however both schemes are fast enough for real-time operation purposes.