Abstract
Karst aquifers are important sources of thermal and groundwater in many parts of the world, such as the Alpine–Dinaric–Carpathian region in Europe. The Upper Triassic dolomites are regionally recognized thermal and groundwater aquifers but also hydrocarbon reservoirs. They are characterized by predominantly fractured porosity, but the actual share of depositional and diagenetic porosity is rarely investigated. In this research, we presented the geometric characterization of the measured microporosity of the Upper Triassic dolomites of the Žumberak Mts (Croatia), through thin-section image processing and particle analysis techniques. Pore parameters were analyzed on microphotographs of impregnated thin sections in scale. A total of 2267 pores were isolated and analyzed. The following parameters were analyzed: pore area, pore perimeter, circularity, aspect ratio (AR), roundness, solidity, Feret AR, compactness, and fractal dimension. Furthermore, porosity was calculated based on the pore portion in each image. The effective porosity on rock samples was determined using saturation and buoyancy techniques as an accompanying research method. We analyzed distributions of each parameter, their correlation, and most of the parameters are characterized by an asymmetric or asymmetric normal distribution. Parameters that quantify pore irregularities have similar distributions, and their values indicate the high complexity of the pore geometry, which can significantly impact permeability.
1. Introduction
Upper Triassic dolomites are a regionally widespread formation in the Alpine–Carpathian–Dinarides region. Most of this Upper Triassic dolomite succession is occupied by the Main Dolomite Formation (original name is Hauptdolomite [1]). The primary characteristics of the Upper Triassic dolomites are large lateral distribution and large thickness from 300 m up to 3000 m [2,3,4,5,6,7,8,9]. These geological conditions together with significant porosity values result in significant groundwater and geothermal water aquifer potential. Porosity is mainly represented with fracture porosity [3,10,11], but the amount and significance of depositional and diagenetic porosity have not been investigated.
Constructing an accurate reservoir or aquifer model is crucial in the sustainable management of the target resources.
The critical parameter that controls fluid flow in the subsurface rocks is porosity [12]. Porosity is a basic physical parameter that is interpreted and used for various engineering purposes. It is associated with different physical and mechanical properties of rock material [13,14,15]. Quantitative estimation of the microstructures of carbonates, irregularities of pore shapes, frequency distributions of pore sizes, and other geometrical parameters are challenging in the pore-structure analysis [16]. Understanding the geometry, size, and distribution of pores is important for the characterization of rock pore structure [17,18,19] and fluid flow characteristics of the rock matrix [20].
Knowledge of pore size distribution is critical for understanding both the mechanisms and storage [18]. The fractured rocks, aquifers, or reservoirs consist of two overlapping subsystems: one represents fractures, and the other represents the porous matrix [21,22,23]. The general flow through the rock is established by a more permeable system (fractures), while a less permeable system (matrix blocks), which have a large storage capacity, feeds fluid into the fractures [23,24]. The quantity of less permeable matrix feeding more permeable fractures has not been previously studied but is important for dual-porosity models. So, depositional and diagenetic porosity in Upper Triassic dolomites does not have a key role in the fluid flow; however, they can be very significant in feeding highly permeable fractures that indirectly influence the fluid flow.
There are a variety of different methods for pore-structure characterization: fluid invasion methods (mercury and helium porosimetry (MICP)) [25,26,27,28,29,30,31], low-temperature adsorption isotherms by adsorption of N2 or CO2 [18,20,25,27,30,31,32,33,34,35,36], nuclear magnetic resonance [37], and X-ray methods (SANS/USANS) [12,18,27,33,38] although these methods can estimate porosity values but do not give information about pore morphology. CT scans [12,30,39,40], scanning electron microscopy [16,19,25,26,29,30,33,41,42,43,44,45], and thin-section analysis [29,37,46] are methods that can quantify geometrical parameters of the rock pore structure. These methods in themselves cannot define heterogeneity and pore shape complexity of analyzed rocks [26,47,48,49]. Researchers found that fractal theory can be very effective in describing and quantifying irregular and complex pore geometry. The complexity of pore structures can be quantified by the fractal dimension’s complex fractal characteristics [16,17,25,28,39,50,51,52,53,54,55,56].
The objective of this paper is to quantify the porosity of the Upper Triassic dolomites. The two methods employed were saturation and buoyancy techniques and microphotograph image processing. Furthermore, the geometrical parameters of the pores were analyzed based on image analysis of microphotographs.
2. Study Area and Geological Setting
2.1. Study Area
The research area is located in the Žumberak Mts, in the north-west of Croatia, where the Upper Triassic dolomites are developed to a total thickness of 1590 m [2,3]. The area was selected because this is a nearly tectonically undisturbed area required for pore size analysis. Three formations have been singled out: Slapnica, with its members Vranjak and Drenovac, and the Main Dolomite with its members Kalje and the Posinak formation. Within the formations and members, cyclically alternating microfacies were determined: dolomicrite, fenestral dolomite, and stromatolitic dolomite. Sedimentary environments have been interpreted as a dynamic shallow-water system of the tidal environment from subtidal to shallow intertidal [2]. Under such precipitation conditions, mainly intergranular porosity has developed in the dolomicrite microfacies. In some places, in the facies of fenestral and stromatolite dolomites, intergranular, fenestral, and moldic and shelter porosity have developed. In all formations, the porosity of dolomicrite microfacies is negligible. Fenestral sediment porosity during rock formation was higher, probably over 30%. However, this porosity was reduced by multiphase diagenetic processes, i.e., formation of dolosparite crystals in the pores. In the Main Dolomite Formation, the facies of the fenestral dolomites have the largest number of particularly large fenestrae, which are connected by channels formed during diagenesis.
2.2. Geological Setting
The structural settings of the Žumberak area result from regional tectonic settings related to the formation of Alpine–Dinaric–Carpathian orogeny (Figure 1). The research area is in the junction zone of the Zagorje–Midtransdanubian zone [57], Internal Dinarides, a margin of the Adriatic Carbonate Platform [58], and the Sava folds [57,59,60]. The main structural features of the Žumberak Mt. result from multiphase tectonic history from the Middle Eocene to the present day. Two main phases can be distinguished [3,60]: first is Eocene to Oligocene compression, which resulted in the formation of main structural units, thrusts, and reverse faults with NW–SE striking and km scale folds being overturned in places. The second phase is represented by the change in stress orientation to approximately N–S and the change in tectonic regime from compression to transpression. By this event, existing faults were reactivated, and new NE–SW and E–W striking faults were formed [60,61,62,63]. The Upper Triassic dolomites (T3) are the most important lithological unit in the geological structure of Žumberak, with a total thickness of 1570 m [2,3] (Figure 1 and Figure 2).
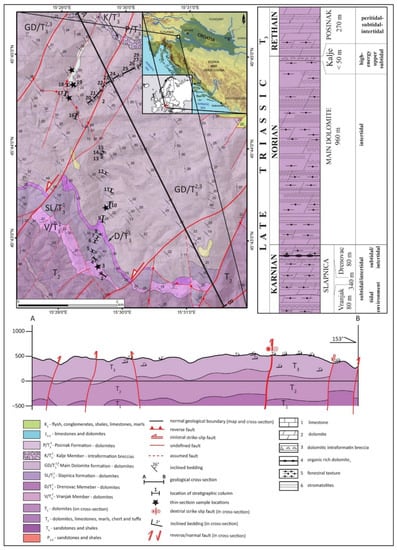
Figure 1.
Geological map (made by Croatian Geological Survey), section, and stratigraphic column of the investigated area [2,3,60].

Figure 2.
Representative outcrop and lithofacies types of the Upper Triassic dolomites from Žumberak Mts. (a) The outcrop of the Main Dolomite Formation; (b) sample of fenestral dolomite facies of the Main Dolomite Formation; (c) sample of stromatolite facies of the Main Dolomite Formation; (d) transition from peloid dolomite to fenestral dolomite lithofacies.
The Upper Triassic dolomites are mainly composed of early diagenetic dolomites, in some areas recrystallized in “saddle” dolomites. Three formations and three members are singled out in the research area (Slapnica, Main Dolomite, and Posinak) and three members (Vranjak, Drenovac, and Kalje) [2].
The oldest Slapnica formation is of the Carnian age. It is represented by more or less uniform cyclical alterations of dolomicrite, fenestral dolomicrite, and stromatolitic dolomites, deposited in a peritidal environment [2]. Bedding surfaces are differentiated. In the lower part of the formation, the member Vranjak is characterized by thin interlayers of yellowish shale, reflecting Raibl events [2]. In the upper part, the member Drenovac is characterized by a high organic matter content, interbeds of dark grey to black shale and laminite, and sporadic coal occurrence [2]. The sedimentation environments were anoxic closed lagoons [2]. The total thickness of the Slapnica formation is 340 m (Figure 1). The massive deposits of the Main Dolomite Formation of the Norian–Rhaetian age are deposited contontinuosly on the Slapnica formation (Figure 2a). The Main Dolomite Formation is characterized by more or less irregular vertical and lateral alterations of dolomicrite, fenestral dolomicrite (Figure 2b), and dark fine-laminated stromatolites (Figure 2c) [2]. The total thickness of the Main Dolomite Formation in Žumberak area is 960 m (Figure 1) [2,3]. The Posinak formation of the Rhaetian age is characterized by well-bedded dolomicrites, with intermittent horizontal stromatolite lamination and subordinated fenestral dolomicrites. The total thickness of the Posinak formation is 270 m (Figure 1). The sedimentation environment is peritidal, with pronounced deepening in comparison with underlying formations. The sedimentation continued to the Jurassic.
3. Materials and Methods
Samples were taken based on detailed stratigraphy in Žumberak area [2]. The first criterion in the research methodology was to take samples of all formations then all lithofacies from each formation. Since these dolomites are often very fractured, there were few representative locations in the area. Therefore, two major types of analysis were conducted. One was measuring the effective porosity by saturation and buoyancy techniques, and the other was thin-section analysis. A total of 27 samples were prepared (Figure 3) for porosity measurements by saturation and buoyancy techniques and 50 samples for thin-section analysis, from which 97 images were analyzed.

Figure 3.
Samples of test material: (a) field samples from which cored samples were made for testing; (b) part of the prepared samples of regular and irregular geometry.
3.1. Porosity Determination Using Saturation and Buoyancy Techniques
Effective porosity is the ratio of the volume of pores (joined so fluids can migrate within them) to the total volume. It was determined by a method recommended by the International Society for Rock Mechanics and Rock Engineering (ISRM). It measures the effective porosity, dry matter density, and rock sample properties that are irregular in geometry for geomechanical purposes but can be applied to samples with the correct geometry (Figure 3b). The method is used only for rocks that do not swell when immersed in water and do not disintegrate when dried [64].
3.2. Microphotograph Analysis
Epoxy impregnated thin sections were used where the epoxy resin was impregnated into pores [65]. Blue dye of epoxy resin is very easy to distinguish from the rock mass, so the pores are highly visible (Figure 4). Image analysis provides a relatively fast method for directly obtaining porosity measurements and various geometric parameters of pore shape [46]. Image analysis was performed in ImageJ software [66,67,68] with two plugins: Biovoxxel [69,70] and Fraclac [71]. Image process analysis begins with image preparation to emphasize differences between pores and rock mass, so the algorithms used in the next phase of image processing can have better accuracy. Image preparation consisted of manual setting up of the brightness, contrast, and color balance to enhance the contrast between pores and rock mass. The used microphotograph images are color images, so there were two possible methodologies of image segmentation: (a) converting color images to grayscale then thresholding to obtain binary images and (b) color thresholding (Figure 4).
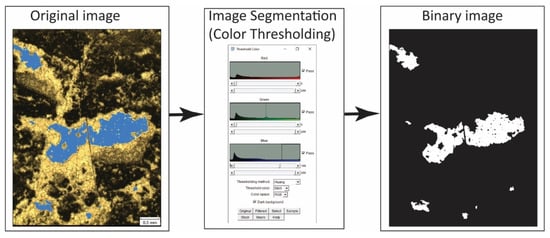
Figure 4.
Image segmentation process used for binarization of thin-section microphotographs.
Image segmentation is a process of splitting images into multiple separate segments [67]. The image segmentation and binarization process of the images converts color images to binary images where rock mass is represented by a black color (binary 0) and pores are represented by white color (binary 1). We used color thresholding because it was relatively simple to find the pores’ threshold values compared to the rest of the rock mass (Figure 4). Image thresholding is one of the most common procedures to extract features of interest from the images [72]. We used the most frequently used method to determine the threshold value by histogram analysis of intensity values (Figure 4) and the Huang thresholding algorithm [72]. The same procedure was applied to all images with manual corrections if needed.
Afterwards, images were binarized and they had to be assigned some scale. All images had scale when they were photographed with the microscope camera. Before image segmentation, we measured the scale bar in every image and defined the mm to px ratio.
After the image segmentation process was done and microphotograph images were transformed to binary, a scale was applied to each binary image so parameters could be expressed in mm.
Porosity was calculated from the binary microphotographs easily as a ratio between the number of white pixels and a total number of pixels. However, it is important to note that we could estimate only 2D porosity by this analysis.
From all parameters available for analysis, nine parameters were defined to be analyzed: pore area, pore perimeter, circularity, AR, roundness, solidity, Feret AR, compactness, and fractal dimension. More detailed descriptions of parameter determination can be found in Appendix A.
4. Results
During the fieldwork campaign, 77 rock samples (27 samples for effective porosity measurements and 50 samples for thin-section analysis) were taken from Slapnica and the Main Dolomite Formation. Few samples were taken from the area where detail stratigraphy was not taken, so these samples were characterized as T3 dolomites (without detail stratigraphy determination). The Posinak formation was not sampled due to its similarity with the Slapnica formation and representative outcrop absence comparing to Slapnica and the Main Dolomite Formation. As all formations have similar properties resulting from a similar depositional environment, we decided to present results by lithofacies.
4.1. Porosity Measurements
Effective and Microphotograph Porosity
A total of 27 samples were examined, of which 14 samples belonged to stromatolitic dolomite lithology, 7 were dolomicrite, and 6 fenestral dolomicrite. After testing the effective porosity on three types of dolomites, the results were statistically processed and presented in a box and whisker diagram (Figure 5). Stromatolitic dolomite has the highest mean value of effective porosity (3.02%), and fenestral dolomicrite the lowest (1.16%). The diagram (Figure 5) shows that the material of dolomicrite lithology has quite similar values of effective porosity as fenestral dolomicrite.
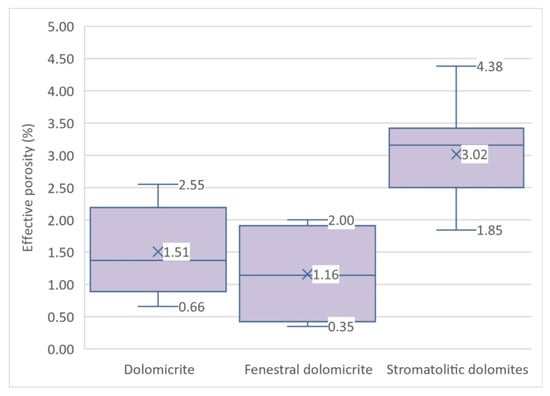
Figure 5.
Box and whisker diagrams of statistical analysis of effective porosity test results.
The results of determining 2D porosity are shown in Figure 6. Stromatolitic dolomite has the largest range of values but also the largest mean value (3.38%), followed by fenestral dolomicrite, whose mean value is 2.42%. Dolomicrite lithology has the lowest 2D porosity both in range and in the mean value of 0.74. The diagram (Figure 6) shows a certain difference between the median and the mean value for all examined lithologies, which indicates that the datasets are asymmetric.
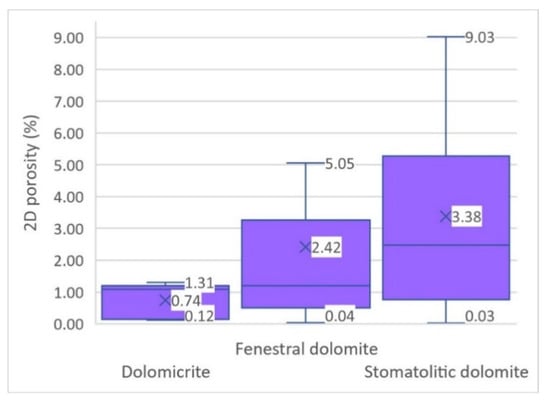
Figure 6.
Box diagrams of 2D porosity measurements from microphotographs of thin sections.
4.2. Geometrical Pore Characterization and Distribution of Pore Characteristics
A total of 2267 pores were extracted from the 97 images and evaluated. The general statistics of the calculated geometric pore parameters are shown in Table 1.

Table 1.
General statistics of calculated geometric pore parameters.
We used the Kolmogorov–Smirnov test for goodness of fit to establish the distribution that best fits each parameter. Circularity, solidity, compactness, and fractal dimension quantify pore boundary and inner irregularities. Roundness, circularity, and compactness quantify the pore’s similarity to a circle. Finally, AR and Feret AR both quantify the pore’s elongation.
- Area: minimum value is 0.001 mm2, and the maximum is 957 mm2, with a median of 0.007 mm2 and a mean of 2.46 mm2 (Table 1). Due to the limit on the image resolution, and the fact that it is proportional to the square of a very small quantity and the automatic rounding, a loss of significant digits has occurred (the data has one significant digit, and at least three are needed). Therefore, no distribution was found to fit the data sufficiently well. The histogram in Table 1 presents pores with an area less than 1 mm2 for better visibility since only 27 pores have an area between 1 and 957 mm2.
- Perimeter: minimum value is 0.015 mm, and the maximum is 242.5 mm, with a median of 0.34 mm and a mean of 1.36 mm. It is best fit by the exponential power distribution (p = 0.99), or the power log-normal distribution (p = 0.61) (Table 1).
- AR: minimum value is 1, and the maximum is 16.91, with a median of 1.75 and a mean of 2.047. It is best fit by the Laplace distribution (p = 0.4) or the exponential power distribution (p = 0.22) (Figure 7). These results mean that most of the pores have a lon axis 2–3× longer than the short axis.
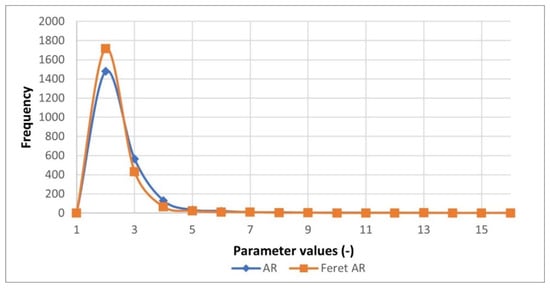 Figure 7. Frequency diagrams for AR and Feret AR.
Figure 7. Frequency diagrams for AR and Feret AR.
- Feret AR: minimum value is 1.10 and maximum is 12.50, with a median of 1.64 and a mean of 1.84. It is best fit by the chi-squared distribution (p = 0.21), or the gamma distribution (p = 0.17) (Figure 7). Feret AR results confirm AR results, and the elongation of the pores is generally between 2 and 3 in one direction.
- Circularity: minimum value is 0.03 and maximum is 1, with a median of 0.56 and a mean of 0.54. It is best fit by the generalized gamma distribution (p = 0.75), or noncentral F-distribution (p = 0.14) (Figure 8).
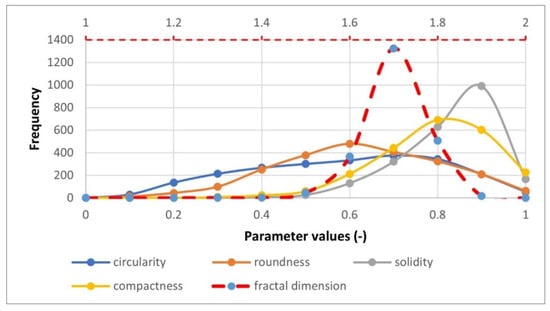 Figure 8. Frequency diagrams for circularity, roundness, solidity, compactness, and fractal dimension parameters of pores.
Figure 8. Frequency diagrams for circularity, roundness, solidity, compactness, and fractal dimension parameters of pores. - Roundness: minimum value is 0.059, and the maximum is 1, with a median of 0.57 and a mean of 0.57. It is best fit by the beta distribution (p = 0.37), or the cosine distribution (p = 0.33) (Figure 8).
- Solidity: minimum value is 0.348, and the maximum is 1, with a median of 0.80 and a mean of 0.78. It is best fit by the cosine distribution (p = 0.91), or the power-law distribution (p = 0.24) (Figure 8).
- Compactness: minimum value is 0.24, and the maximum is 1, with a median of 0.757 and a mean of 0.75. It is best fit by the hypergeometric distribution (p = 0.3), or the exponential distribution (p = 0.19) (Figure 8).
- Fractal dimension: minimum value is 1.21 and maximum is 2, with a median of 1.66 and a mean of 1.65. It is best fit by the Maxwell distribution (p = 0.98), or the normal distribution (p = 0.67) (Figure 8).
5. Discussion
Depositional and diagenetic porosity and its geometric characteristics were analyzed in 77 samples of Upper Triassic dolomites from the Žumberak area (NW Croatia). These dolomites are regionally important geothermal and groundwater aquifers in the Alpine–Dinaric–Carpathian region. The porosity in Upper Triassic dolomites is mostly represented by fracture porosity and subordinately by depositional and diagenetic porosity. In dual-porosity models, the main fluid flow would be accomplished by fractures that are partially fed from smaller fractures and cracks and partially from depositional and diagenetic pores. This paper aims to quantify how much depositional and digenetic porosity participate in the total porosity of the dolomites, and these results can be the base for further dual-porosity models of Upper Triassic dolomites.
The depositional porosity of all microfacies except dolomicrite was initially probably over 30%, but with multiphase diagenetic changes, this porosity was significantly reduced [3]. Depositional porosity was largest in fenestral and stromatolitic dolomites (intercrystal, fenestral, moldic, and shelter porosity) and smallest in dolomicrite (intercrystal porosity). Diagenesis played a major role in porosity reduction in all three facies [3]. There are visible elements of marine, meteoric, and vadose diagenetic environments, and five diagenetic phases are delineated in these dolomites, which reduced porosity to its present values [3]. By the saturation and buoyancy techniques, measurements of effective porosity on dolomite samples range from 0.35 to 4.38%. These increased values are the result of cracks and microcracks in the samples. Therefore, laboratory-measured, effective porosity does not fully correspond to depositional and diagenetic porosity but also microfracture porosity. Although Upper Triassic dolomites in our research area are relatively tectonically undisturbed but still highly fractured, it is hard to take samples without micro-cracks.
For this reason, we also made visual observations of microscopic specimens that revealed that the upper part of the interval of measured open porosities was too high for sedimentary and diagenetic porosity. 2D porosity measured in thin section images ranged from 0.8% up to 18.4% [73]. It is important to note that these are the 2D porosity estimations, so effective porosity should be smaller. The same conclusions are stated in [74]. The porosity of early diagenetic dolomites from Samoborsko gorje and Medvednica Mts (a few km east from our research area) ranges from 0.92 to 2.21% [74], correlating with our results. The porosity decrease due to diagenesis in Tarim Basin (NW China) is up to 40%, with final porosity values from 4.2 to 18.2% [75].
Furthermore, porosities of deep-buried Cambrian dolomites are in the range from 0.8 to 9.1%. Depositional and diagenetic porosity values of Upper Cretaceous dolomites in Tunisia range from 2.9 to 28.3% in two dolomite facies [76]. The amounts of depositional and diagenetic porosity in the Sella Group in the Dolomites (northern Italy) are less than 5% [7]. All mentioned values from different dolomites in the world are generally on the same scale as our results, although different dolomites from different stratigraphic ages were subdued to different diagenetic processes. Thus, porosities can be very diverse.
Pore structure geometry was quantified with nine parameters: pore area and perimeter, circularity, aspect ratio, roundness, solidity, Feret aspect ratio, compactness, and fractal dimension. The aim was to analyze how every one of these parameters quantifies the geometry of the pore. The parameters can be subdivided into four groups:
- Parameters that quantify size: area and perimeter;
- Parameters that quantify elongation: aspect ratio and Feret aspect ratio;
- Parameters that quantify the object’s overall shape without considering the roughness of the object’s surface: circularity and roundness;
- Parameters that quantify roughness or complexity of the surface (small irregularities on the object’s surface): solidity, compactness, and fractal dimension.
The pore area and perimeter quantify the size of the pores. Analysis of area and perimeter frequency plots revealed that 98.8% of pores have an area less than 1 mm2. Additionally, we were not able to quantify pores smaller than 0.001 mm2 due to image resolution limitations. We found a strong linear correlation between area and perimeter (r = 0.95), which indicates the pores’ elongation.
The analysis of the shape parameters revealed that different parameters quantify the shape of the pore in different ways. Aspect ratio and Feret aspect ratio quantify elongation of the pore in a very similar way, which is proven by the frequency plots (Figure 8 and Figure 9). The major axis is 2–3 × longer than the minor axis for most pores, so pores are slightly elongated (Figure 7 and Figure 9).
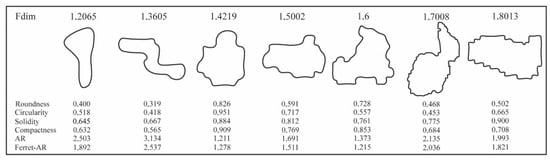
Figure 9.
Different pore shapes with their fractal dimensions and other parameter values.
Based on frequency plot analysis of circularity, roundness, solidity, compactness, and fractal dimension (all these parameters ranged from 0 to 1) we can distinguish that these parameters quantify objects’ shapes in two ways: the general shape of the object in the sense of its similarity to the sphere and roughness (or complexity) of the surface of the object. The first group of parameters quantifies the general object’s shape without considering the “small” irregularities of the object surface (i.e., roughness) (Figure 8 and Figure 9). These parameters are circularity and roundness, and correlations between them are proven by frequency plots (Figure 8). The surface roughness or complexity of the shape is an important parameter for assessing the aquifer or reservoir properties. The fractal dimension for most of the pores ranges from 1.6 to 1.8, which indicates a very complex fractal geometry of pores. Changes in pore shape complexity and associated fractal dimension (also other parameters) are visible in Figure 9. Our analysis also showed a strong linear correlation between certain parameters from different groups, such as roundness and compactness (r = 0.99) and circularity and solidity (r = 0.89).
Furthermore, AR and Feret AR changes are visible on the first and third pore examples in Figure 9. Differences of pore shape that result in smallest and largest circularity and roundness are best in the second and third pores in Figure 9. Fractal and multifractal characteristics of the pore structure in deep buried Cambrian dolomites were recognized by the authors of [73]. Fractal dimensions of these dolomites range from 1.36 to 1.680, which also indicate complex pore geometry [73].
Higher complexity, which means a more irregular surface, can decrease the permeability of the aquifer or reservoir. Measurements of pore structure geometry may be used as an auxiliary method to analyze geological controls on rock properties to estimate aquifer or reservoir properties. It is an issue when comparing the results of the effective porosity method with the results of determining 2D porosity. Both methods have advantages and disadvantages. The method of determining the effective porosity pattern is three-dimensional and better suited to in situ situations. 2D porosity is determined from a thin-section preparation but can realistically detect the shape of the pores.
Despite the sophistication of other methods, effective porosity is still irreplaceable and more realistically depicts porosity, which is essential to achieve sustainable water management [64].
6. Conclusions
Based on the results of the research and discussion, the following conclusions were reached:
- Dolomicrite microfacies had very low sedimentation and intergranular porosity reduced or remained the same in the marine diagenetic environment, recrystallization, and dolomitization processes. The effective porosity of dolomicrite facies is from 0.657 to 2.548%. 2D porosity for these facies is in the range of 0.12 to 1.31%. Increased porosity values in the dolomicrite facies result from microcrack formation that causes microcracks in the measured samples, so the upper part of the interval should be taken with caution.
- Microfacies of fenestral dolomites had a high sediment porosity, over 30%. Porosity is significantly reduced by diagenesis in the vadose, meteoric, marine environment, geopetal filling processes, crystallization, and dolomitization. The effective porosities of these facies range from 0.35 to 2% and correspond to diagenetic porosity. 2D porosity for these facies is in the range of 0.05 to 5%.
- Microfacies of stromatolite dolomites generally have the highest porosities. Depositional porosity was also quite high but was significantly reduced by diagenesis in the vadose, meteoric, and marine environments. The amounts of effective porosity range from 1.85 to 4.38% and generally correspond to diagenetic porosity. 2D porosity for these facies is in the range of 0.027 to 9.03%.
- Both porosity measurements (effective type and 2D) indicated that non-fracture porosity could not be ignored in permeability calculations, so a double-porosity model should be applied.
- Geometric parameters of pores can be subdivided into four groups: a) size quantification parameters (area, perimeter); elongation parameters (aspect ratio, Feret aspect ratio); overall shape parameters (circularity, roundness) in the sense of comparison of an object to a sphere; roughness parameters (solidity, compactness, fractal dimension).
- To quantify the pore geometry, it is necessary to use parameters from all four groups since each group and each parameter quantify the pore geometry differently. Therefore, analyzed parameters are an effective way to reflect the complexity of the pore structure. Fractured aquifers are very valuable geothermal and groundwater resources regarding quantity and quality. Hence, their sustainable management and protection are of the highest priority. Therefore, every piece of knowledge about the porosity and permeability of these systems is crucial for later modeling of fluid/contaminant flow.
Author Contributions
Conceptualization, I.P.; methodology, I.P. and Z.B.; software, I.P., Ž.D., and D.Š.; validation, I.P., Z.B., A.V., T.G., Ž.D., D.Š. and I.D.; formal analysis, I.P. and Z.B.; investigation, I.P., Z.B., T.G. and I.D.; resources, I.P., Z.B. and Ž.D.; data curation, I.P. and Z.B.; writing—original draft preparation, I.P.; writing—review and editing, I.P., Z.B., A.V., T.G., Ž.D., D.Š. and I.D.; visualization, I.P. and Z.B.; supervision, Ž.D., T.G. and I.D.; project administration, I.P.; funding acquisition, I.P. and Z.B. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by the Faculty of Mining, Geology and Petroleum Engineering, University of Zagreb.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available on request due to privacy restrictions. Data presented in this study are available on request from the first author Ivica Pavičić (ivica.pavicic@rgn.unizg.hr).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
- Pore area (mm2)—the area occupied by a two-dimensional object.
- Perimeter (mm)—the total length of the boundary of a two-dimensional object.
- Circularity (−)—the degree to which the particle is similar to a circle, regarding the curvature and the smoothness of the boundary. It takes values from [0,1], where a circle achieves the maximum of 1. Circularity is a measure of particle shape and roughness.
- AR (−)—the ratio of the particle’s circumscribed ellipse’s axes. The values of AR are greater or equal to 1.
- Roundness (−)—the inverse of aspect ratio. Measures how closely the shape of an object approaches that of a circle regarding the curvature of the object’s boundary. Its values are from [0,1], with the circle having a roundness of 1 and, for instance, an ellipse with axes a and b (a > b) has a roundness of b/a < 1.
- Solidity (−)—the fraction of the region as compared to its convex hull. It measures the convexity of an object. Objects containing all lines between any two of its points (in particular, without holes and with no boundary irregularities) have a solidity value of 1. Otherwise, the solidity value is less than 1.
- Feret AR (−)—elongation index, the values of Feret AR are greater or equal to 1.
- Compactness (−)—ratio of the area of an object to the area of a circle with same diameter. A circle is the most compact object with value 1, and all other objects have compactness less than 1.
- Fdim (−)—fractal dimension of an object. The fractal analysis represents a group of methods for quantifying complex patterns [77,78]. Fractals and fractal geometry can be applied to various geological disciplines where classical geometry is not enough to describe complex objects in nature [79,80]. We described only basic elements of fractal geometry which are necessary to understand the application in this paper. Fractals can be defined as “irregular” objects divided into segments that are equal to each other and the whole object; thus they exhibit self-similarity [81,82]. For an object to be fractal, it must have the following properties [81]:
- -
- The constituent parts of an object have the same structure as the object as a whole, except that they are slightly deformed in different scales (there are small fluctuations in the measure of fractality between scales)—self-similarity.
- -
- Objects are often irregular and fragmented and remain so in all the scales in which they exist.
- -
- Objects are created by an iterative procedure.
- -
- Objects have fractal dimensions.
Fractal analysis is based on the fractal dimension (Df) of an object. The Df is a value that quantifies the complexity of an object.
where:
- N = the number of objects fragments characterized by the linear dimension r;
- C = proportionality constant;
- Df = fractal (Hausdorff’s) dimension, which is calculated (Equation (A8)):
Fractal geometry can be applied to the statistical distribution of objects. The basic feature of fractals and fractal distributions is scale independence. Fractal dimension describes how the detail in an examined pattern changes at various scales, and this is referred to as the complexity of an object [77]. The higher the dimension is, the more complex the object is [77]. In comparison to Euclidian objects that have integer values of dimensions of 0 (point), 1 (line), 2 (surface), or 3 (body), fractal objects can have non-integer values [83].
References
- Von Gümbel, C.W. Geognostische Mittheilungen Aus Den Alpen, Das Mendel-Und Schlerngebirge. Available online: https://publikationen.badw.de/de/003899268 (accessed on 20 April 2021).
- Grgasović, T. Stratigraphy of Later Triassic Deposits in Žumberak Area; Faculty of Scinece, University of Zagreb: Zagreb, Croatia, 1998. [Google Scholar]
- Pavičić, I. Origin, Spatial Distribution and Qunatification of Porosity in Upper Triassic Dolomites in Žumberak Mts. Ph.D. Thesis, University of Zagreb, Zagreb, Croatia, 2018. [Google Scholar]
- Spanza, F.; Minelli, L. Ultra-thick Triassic dolomites control the rupture behavior of the central Apennine seismicity: Evidence from magnetic modeling of the L’Aquila fault zone. J. Geophys. Res. Solid Earth 2014, 120, 1–29. [Google Scholar] [CrossRef]
- Doglioni, C. Tectonics of the Dolomites (southern alps, northern Italy). J. Struct. Geol. 1987, 9, 181–193. [Google Scholar] [CrossRef]
- Masaryk, P.; Lintnerova, O. Diagenesis and porosity of the Upper Triassic carbonates of the pre-Neogene Vienna Basin basement. Geol. Carpathica 1997, 40, 371–386. [Google Scholar]
- Antonellini, M.; Mollema, P.N. A natural analog for a fractured and faulted reservoir in dolomite: Triassic Sella Group, northern Italy. Am. Assoc. Pet. Geol. Bull. 2000, 84, 314–344. [Google Scholar] [CrossRef]
- Haas, J.; Budai, T. Triassic Sequence Stratigraphy of the Transdanubian Range (Hungary). Geol. Carpathica 1999, 50, 459–475. [Google Scholar]
- Haas, J. Facies analysis of the cyclic Dachstein Limestone formation (Upper Triassic) in the Bakony Mountains, Hungary. Facies 2004, 50, 263–286. [Google Scholar] [CrossRef]
- Pavičić, I.; Dragičević, I.; Vlahović, T.; Grgasović, T. Fractal Analysis of Fracture Systems in Upper Triassic Dolomites in Žumberak Mountain, Croatia. Rud. Geol. Naft. Zb. 2017, 32, 1–13. [Google Scholar] [CrossRef]
- Mollema, P.N.; Antonellini, M. Development of Strike-Slip Faults in the Dolomites of the Sella Group, Northern Italy. J. Struct. Geol. 1999, 21, 273–292. [Google Scholar] [CrossRef]
- Thomson, P.R.; Jefferd, M.; Clark, B.L.; Chiarella, D.; Mitchell, T.M.; Hier-Majumder, S. Pore network analysis of Brae Formation sandstone, North Sea. Mar. Pet. Geol. 2020, 122, 104614. [Google Scholar] [CrossRef]
- Chen, L.; Wu, P.; Chen, Y.; Zhang, W. Experimental study on physical-mechanical properties and fracture behaviors of saturated yellow sandstone considering coupling effect of freeze-thaw and specimen inclination. Sustainability 2020, 12, 1029. [Google Scholar] [CrossRef]
- Briševac, Z.; Kujundžić, T.; Čajić, S. Current cognition of rock tensile strength testing by Brazilian test. Rud. Geol. Naft. Zb. 2015, 30, 101–114. [Google Scholar] [CrossRef]
- Briševac, Z.; Kujundžić, T. Models to estimate the Brazilian indirect tensile strength of limestone in saturated state. Rud. Geol. Naft. Zb. 2016, 31, 59–68. [Google Scholar] [CrossRef]
- Xie, S.; Cheng, Q.; Ling, Q.; Li, B.; Bao, Z.; Fan, P. Fractal and multifractal analysis of carbonate pore-scale digital images of petroleum reservoirs. Mar. Pet. Geol. 2010, 27, 476–485. [Google Scholar] [CrossRef]
- Shao, X.; Pang, X.; Li, Q.; Wang, P.; Chen, D.; Shen, W.; Zhao, Z. Pore structure and fractal characteristics of organic-rich shales: A case study of the lower Silurian Longmaxi shales in the Sichuan Basin, SW China. Mar. Pet. Geol. 2017, 80, 192–202. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Solano, N.; Bustin, R.M.; Bustin, A.M.M.; Chalmers, G.R.L.; He, L.; Melnichenko, Y.B.; Radliński, A.P.; Blach, T.P. Pore structure characterization of North American shale gas reservoirs using USANS/SANS, gas adsorption, and mercury intrusion. Fuel 2013, 103, 606–616. [Google Scholar] [CrossRef]
- Loucks, R.G.; Reed, R.M.; Ruppel, S.C.; Jarvie, D.M. Morphology, genesis, and distribution of nanometer-scale pores in siliceous mudstones of the mississippian barnett shale. J. Sediment. Res. 2009, 79, 848–861. [Google Scholar] [CrossRef]
- Bustin, R.M.; Bustin, A.M.M.; Cui, X.; Ross, D.J.K.; Pathi, V.S.M. Impact of Shale Properties on Pore Structure and Storage Characteristics. In Proceedings of the SPE Shale Gas Production Conference, Fort Worth, TX, USA, 16–18 November 2008; pp. 32–59. [Google Scholar] [CrossRef]
- Altinörs, A.; Önder, H. A double-porosity model for a fractured aquifer with non-Darcian flow in fractures. Hydrol. Sci. J. 2008, 53, 868–882. [Google Scholar] [CrossRef][Green Version]
- Bolshov, L.; Kondratenko, P.; Matveev, L.; Pruess, K. Elements of Fractal Generalization of Dual-Porosity Model for Solute Transport in Unsaturated Fractured Rocks. Vadose Zone J. 2008, 7, 1198–1206. [Google Scholar] [CrossRef][Green Version]
- Barenblatt, G.I.; Zheltov, I.P.; Kochina, I.N. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks [strata]. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Hamm, S.-Y.; Bidaux, P. Dual-porosity fractal models for transient flow analysis in fissured rocks. Water Resour. Res. 1996, 32, 2733–2745. [Google Scholar] [CrossRef]
- Fu, H.; Tang, D.; Xu, T.; Xu, H.; Tao, S.; Li, S.; Yin, Z.Y.; Chen, B.; Zhang, C.; Fu, H.; et al. Characteristics of pore structure and fractal dimension of low-rank coal: A case study of Lower Jurassic Xishanyao coal in the southern Junggar Basin, NW China. Fuel 2017, 193, 254–264. [Google Scholar] [CrossRef]
- Yang, R.; He, S.; Yi, J.; Hu, Q. Nano-scale pore structure and fractal dimension of organic-rich Wufeng-Longmaxi shale from Jiaoshiba area, Sichuan Basin: Investigations using FE-SEM, gas adsorption and helium pycnometry. Mar. Pet. Geol. 2016, 70, 27–45. [Google Scholar] [CrossRef]
- Mastalerz, M.; Schimmelmann, A.; Drobniak, A.; Chen, Y. Porosity of Devonian and Mississippian New Albany Shale across a maturation gradient: Insights from organic petrology’, gas adsorption, and mercury intrusion. Am. Assoc. Pet. Geol. Bull. 2013, 97, 1621–1643. [Google Scholar] [CrossRef]
- Mahamud, M.M.; Novo, M.F. The use of fractal analysis in the textural characterization of coals. Fuel 2008, 87, 222–231. [Google Scholar] [CrossRef]
- Kashif, M.; Cao, Y.; Yuan, G.; Asif, M.; Javed, K.; Mendez, J.N.; Khan, D.; Miruo, L. Pore size distribution, their geometry and connectivity in deeply buried Paleogene Es1 sandstone reservoir, Nanpu Sag, East China. Pet. Sci. 2019, 16, 981–1000. [Google Scholar] [CrossRef]
- Hall, M.R.; Mooney, S.J.; Sturrock, C.; Matelloni, P.; Rigby, S.P. An approach to characterisation of multi-scale pore geometry and correlation with moisture storage and transport coefficients in cement-stabilised soils. Acta Geotech. 2013, 8, 67–79. [Google Scholar] [CrossRef]
- Gan, H.; Nandi, S.P.; Walker, P.L. Nature of the porosity in American coals. Fuel 1972, 51, 272–277. [Google Scholar] [CrossRef]
- Ross, D.J.K.; Marc Bustin, R. The importance of shale composition and pore structure upon gas storage potential of shale gas reservoirs. Mar. Pet. Geol. 2009, 26, 916–927. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Freeman, M.; He, L.; Agamalian, M.; Melnichenko, Y.B.; Mastalerz, M.; Bustin, R.M.; Radliński, A.P.; Blach, T.P. Characterization of tight gas reservoir pore structure using USANS/SANS and gas adsorption analysis. Fuel 2012, 95, 371–385. [Google Scholar] [CrossRef]
- Schmitt, M.; Fernandes, C.P.; da Cunha Neto, J.A.B.; Wolf, F.G.; dos Santos, V.S.S. Characterization of pore systems in seal rocks using Nitrogen Gas Adsorption combined with Mercury Injection Capillary Pressure techniques. Mar. Pet. Geol. 2013, 39, 138–149. [Google Scholar] [CrossRef]
- Kuila, U.; Prasad, M. Specific surface area and pore-size distribution in clays and shales. Geophys. Prospect. 2013, 61, 341–362. [Google Scholar] [CrossRef]
- Chen, J.; Xiao, X. Evolution of nanoporosity in organic-rich shales during thermal maturation. Fuel 2014, 129, 173–181. [Google Scholar] [CrossRef]
- Carr, M.B.; Ehrlich, R.; Bowers, M.C.; Howard, J.J. Correlation of porosity types derived from NMR data and thin section image analysis in a carbonate reservoir. J. Pet. Sci. Eng. 1996, 14, 115–131. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, J.; Tang, X.; Li, W.; Li, Z. Relationship between pore type and pore size of marine shale: An example from the Sinian-Cambrian formation, upper Yangtze region, South China. Int. J. Coal Geol. 2016, 158, 13–28. [Google Scholar] [CrossRef]
- Peng, R.D.; Yang, Y.C.; Ju, Y.; Mao, L.T.; Yang, Y.M. Computation of fractal dimension of rock pores based on gray CT images. Chin. Sci. Bull. 2011, 56, 3346–3357. [Google Scholar] [CrossRef]
- Bai, B.; Zhu, R.; Wu, S.; Yang, W.; Gelb, J.; Gu, A.; Zhang, X.; Su, L. Multi-scale method of Nano(Micro)-CT study on microscopic pore structure of tight sandstone of Yanchang Formation, Ordos Basin. Pet. Explor. Dev. 2013, 40, 354–358. [Google Scholar] [CrossRef]
- Loucks, R.G.; Ruppel, S.C.; Wang, X.; Ko, L.; Peng, S.; Zhang, T.; Rowe, H.D.; Smith, P. Pore Types, Pore-Network Analysis, and Pore Quantification of the Lacustrine Shale-Hydrocarbon System in the Late Triassic Yanchang Formation in the Southeastern Ordos Basin, China. Interpretation 2017, 5, SF63–SF79. [Google Scholar] [CrossRef]
- Cao, X.; Gao, Y.; Cui, J.; Han, S.; Kang, L.; Song, S.; Wang, C. Pore characteristics of lacustrine shale oil reservoir in the Cretaceous Qingshankou Formation of the Songliao Basin, NE China. Energies 2020, 13, 2027. [Google Scholar] [CrossRef]
- Bernard, S.; Wirth, R.; Schreiber, A.; Schulz, H.M.; Horsfield, B. Formation of nanoporous pyrobitumen residues during maturation of the Barnett Shale (Fort Worth Basin). Int. J. Coal Geol. 2012, 103, 3–11. [Google Scholar] [CrossRef]
- Milliken, K.L.; Rudnicki, M.; Awwiller, D.N.; Zhang, T. Organic matter-hosted pore system, Marcellus Formation (Devonian), Pennsylvania. Am. Assoc. Pet. Geol. Bull. 2013, 97, 177–200. [Google Scholar] [CrossRef]
- Loucks, R.G.; Reed, R.M.; Ruppel, S.C.; Hammes, U. Spectrum of pore types and networks in mudrocks and a descriptive classification for matrix-related mudrock pores. Am. Assoc. Pet. Geol. Bull. 2012, 96, 1071–1098. [Google Scholar] [CrossRef]
- Ruzyla, K. Characterization of Pore Space By Quantitative Image Analysis. SPE Form. Eval. 1986, 1, 389–398. [Google Scholar] [CrossRef]
- Wang, J.; Cao, Y.; Liu, K.; Gao, Y.; Qin, Z. Fractal characteristics of the pore structures of fine-grained, mixed sedimentary rocks from the Jimsar Sag, Junggar Basin: Implications for lacustrine tight oil accumulations. J. Pet. Sci. Eng. 2019, 182, 106363. [Google Scholar] [CrossRef]
- Cao, T.; Song, Z.; Wang, S.; Xia, J. Characterization of pore structure and fractal dimension of Paleozoic shales from the northeastern Sichuan Basin, China. J. Nat. Gas Sci. Eng. 2016, 35, 882–895. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, Q.W.; Wang, S. Study of Diagenesis and Pore Evolution of Triassic Jialingjiang Formation in Southern Puguang Gasfield. J. Chem. 2016, 2016. [Google Scholar] [CrossRef]
- Orford, J.D.; Whalley, W.B. The use of the fractal dimension to quantify the morphology of irregular-shaped particles. Sedimentology 1983, 30, 655–668. [Google Scholar] [CrossRef]
- Wang, F.; Jiao, L.; Liu, Z.; Tan, X.; Wang, C.; Gao, J. Fractal Analysis of Pore Structures in Low Permeability Sandstones Using Mercury Intrusion Porosimetry. J. Porous Media 2018, 21, 1097–1119. [Google Scholar] [CrossRef]
- Schlueter, E.M.; Zimmerman, R.W.; Witherspoon, P.A.; Cook, N.G.W. The fractal dimension of pores in sedimentary rocks and its influence on permeability. Eng. Geol. 1997, 48, 199–215. [Google Scholar] [CrossRef]
- Katz, A.J.; Thompson, A.H. Fractal sandstone pores: Implications for conductivity and pore formation. Phys. Rev. Lett. 1985, 54, 1325–1328. [Google Scholar] [CrossRef]
- Cox, B.L.; Wang, J.S. Fractal Surfaces: Measurement and Applications in the Earth Sciences. Fractals 1992, 1, 87–115. [Google Scholar] [CrossRef]
- Liu, R.; Jiang, Y.; Li, B.; Wang, X. A Fractal Model for Characterizing Fluid Flow in Fractured Rock Masses Based on Randomly Distributed Rock Fracture Networks. Comput. Geotech. 2015, 65, 45–55. [Google Scholar] [CrossRef]
- Ma, J.; Qi, H.; Wong, P. Experimental Study of Multilayer Adsorption on Fractal Surfaces in Porous Media. Phys. Rev. E 1999, 59, 2049–2059. [Google Scholar] [CrossRef]
- Pamić, J.; Tomljenović, B. Basic Geologic Data from the Croatian Part of the Zagorje-Mid-Transdanubian Zone. Acta Geol. Hungarica 1998, 41. [Google Scholar]
- Tomljenović, B.; Csontos, L.; Márton, E.; Márton, P. Tectonic Evolution of the Northwestern Internal Dinarides as Constrained by Structures and Rotation of Medvednica Mountains, North Croatia. Geol. Soc. Lond. Spec. Publ. 2008, 298, 145–167. [Google Scholar] [CrossRef]
- Mioč, P. Tektonski Odnosi Savske Navlake Prema Susjednim Jedinicama u Sloveniji Te Njena Veza Sa Širim Jugoslavenskim Područjem. Nafta 1981, 32, 543–548. [Google Scholar]
- Prtoljan, B. Relationships of the Thrust-Fold and Horizontalmechanisms of the Mt. Žumberak Part of the Sava Nappe in the Northwestern Dinarides. West Croatia. Acta Geol. Hung. 2001, 44, 67–80. [Google Scholar]
- Márton, E.; Jelen, B.; Tomljenović, B.; Pavelić, D.; Poljak, M.; Márton, P.; Avanić, R.; Pamić, J. Late Neogene Counterclockwise Rotation in the SW Part of the Pannonian Basin. Geol. Carpathica 2006, 57, 41–46. [Google Scholar]
- Bada, G.; Horváth, F.; Dövényi, P.; Szafián, P.; Windhoffer, G.; Cloetingh, S. Present-Day Stress Field and Tectonic Inversion in the Pannonian Basin. Glob. Planet. Chang. 2007, 58, 165–180. [Google Scholar] [CrossRef]
- Herak, D.; Herak, M.; Tomljenović, B. Seismicity and Earthquake Focal Mechanisms in North-Western Croatia. Tectonophysics 2009, 465, 212–220. [Google Scholar] [CrossRef]
- Laboratory, I.S. for R.M.C. on S. of L. and F.T.C. on Suggested Methods for Determining Water Content, Porosity, Density Absorption and Related Properties and Swelling and Slake- Durability Index Properties. Int. J. Rock Mech. Min. Sci. 1979, 16, 141–156. [Google Scholar] [CrossRef]
- Gardner, K.L. Impregnation Technique Using Colored Epoxy To Define Porosity in Petrographic Thin Sections. Can. J. Earth Sci. 1980, 17, 1104–1107. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 Years of Image Analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Broeke, J.; Perez, J.M.M.; Pascau, J. Image Processing with ImageJ, 2nd ed.; Packt: Birmingham, UK, 2015. [Google Scholar]
- Abràmoff, M.D.; Magalhães, P.J.; Ram, S.J. Image Processing with ImageJ. Biophotonics Int. 2004, 11, 36–42. [Google Scholar]
- Brocher, J.; Wagner, T. BioVoxxel Toolbox. 2014. Available online: https://imagej.net/plugins/biovoxxel-toolbox (accessed on 13 November 2016).
- Brocher, J. The BioVoxxel Image Processing and Analysis Toolbox. In Proceedings of the European BioImage Analysis Symposium, Paris, France, 5–6 January 2015. [Google Scholar]
- Karperien, A. Fraclac for ImageJ; Charles Sturt University: Bathurst, Australia, 2013. [Google Scholar]
- Huang, L.-K.; Wang, M.-J.J. Image Thresholding by Minimizing the Measures of Fuzzines. Pattern Recognit. 1995, 28, 41–51. [Google Scholar] [CrossRef]
- Zhang, X.; Han, H.; Peng, J.; Gou, Y. Multifractal Analysis of Pore Structure and Evaluation of Deep-Buried Cambrian Dolomite Reservoir with Image Processing: A Case from Tarim Basin, NW China. Geofluids 2020, 2020, 7131573. [Google Scholar] [CrossRef]
- Maričić, A.; Starčević, K.; Barudžija, U. Physical and Mechanical Properties of Dolomites Related to Sedimentary and Diagenetic Features—Case Study of the Upper Triassic Dolomites from the Medvednica and Samobor Mts., NW Croatia. Rud. Geol. Naft. Zb. 2018, 33, 33–44. [Google Scholar] [CrossRef]
- Yang, L.; Yu, L.; Chen, D.; Liu, K.; Yang, P.; Li, X. Effects of Dolomitization on Porosity during Various Sedimentation-Diagenesis Processes in Carbonate Reservoirs. Minerals 2020, 10, 574. [Google Scholar] [CrossRef]
- Negra, M.H.; Purser, B.H.; M‘RABET, A. Permeability and porosity evolution in dolomitized Upper Cretaceous pelagic limestones of Central Tunisia. In Dolomites: A Volume in Honour of Dolomieu; Blackwell Publishing Ltd.: Oxford, UK, 1994; Volume 21, pp. 309–323. [Google Scholar]
- Karperien, A.; Ahammer, H.; Jelinek, H.F. Quantitating the Subtleties of Microglial Morphology with Fractal Analysis. Front. Cell. Neurosci. 2013, 7, 1–34. [Google Scholar] [CrossRef]
- Jelinek, H.F.; Fernandez, E. Neurons and Fractals: How Reliable and Useful Are Calculations of Of fractal Dimensions? J. Neurosci. Methods 1998, 81, 9–18. [Google Scholar] [CrossRef]
- Mace, R.E.; Marrett, R.A.; Hovorka, S.D. Fractal Scaling of Secondary Porosity in Karstic Exposures of the Edwards Aquifer. Sink. Eng. Environ. Impacts Karst 2005, 40796, 178–187. [Google Scholar] [CrossRef]
- Verbovšek, T. Extrapolation of Fractal Dimensions of Natural Fracture Networks from One to Two Dimensions in Dolomites of Slovenia. Geosci. J. 2009, 13, 343–351. [Google Scholar] [CrossRef]
- Turcotte, D. Fractals and Chaos in Geology and Geophysics, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Feder, J. Fractals (Physics of Solids and Liquids); Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Verbovšek, T. Hydrogeology and Geochemistry of Fractured Dolomites—A Case Study of Slovenia. In Aquifers: Formation, Transport, and Pollution; Laughton, R.H., Ed.; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2009. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).