Insights from an Evaluation of Nitrate Load Estimation Methods in the Midwestern United States
Abstract
:1. Introduction
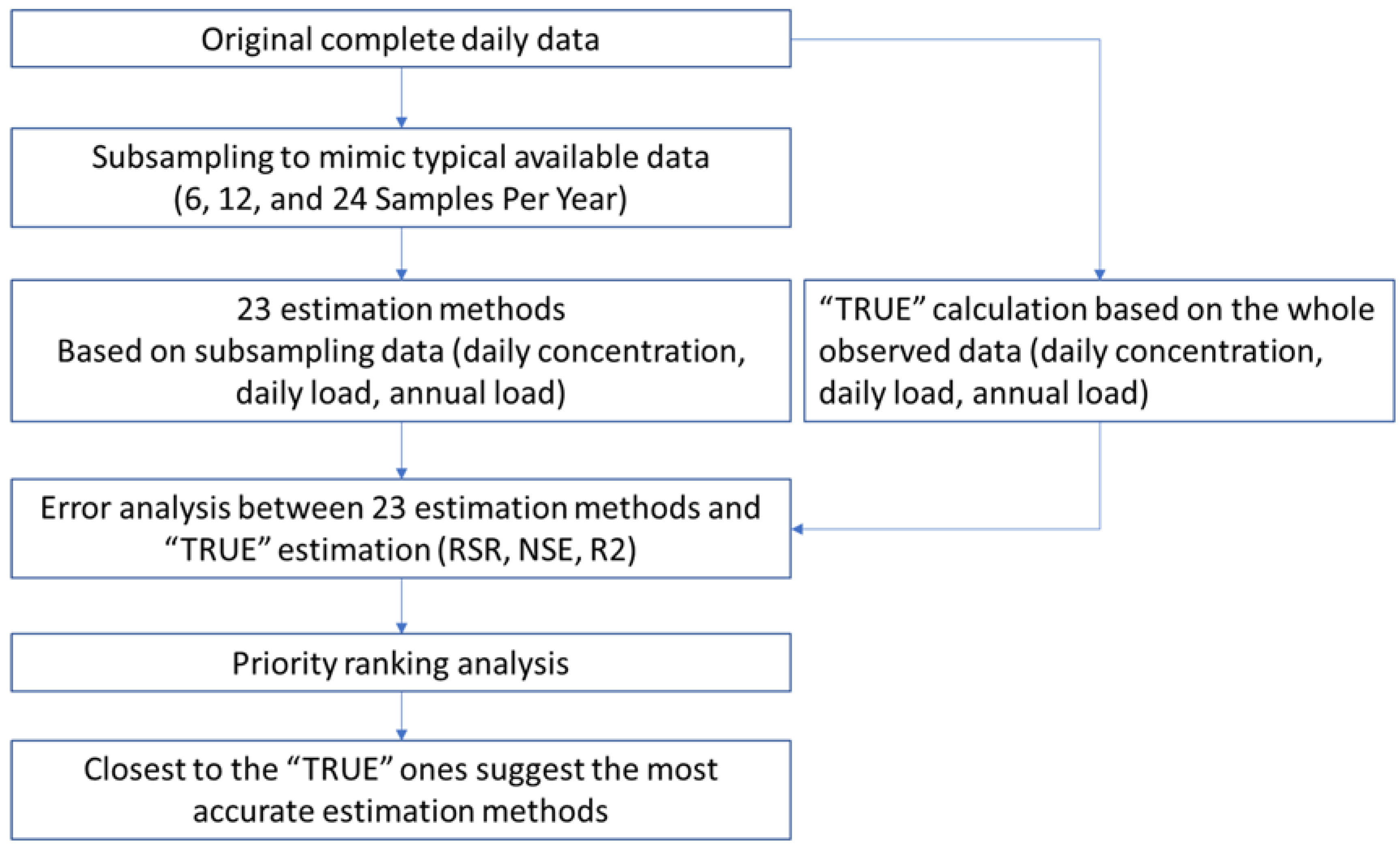
2. Methods
2.1. Study Area
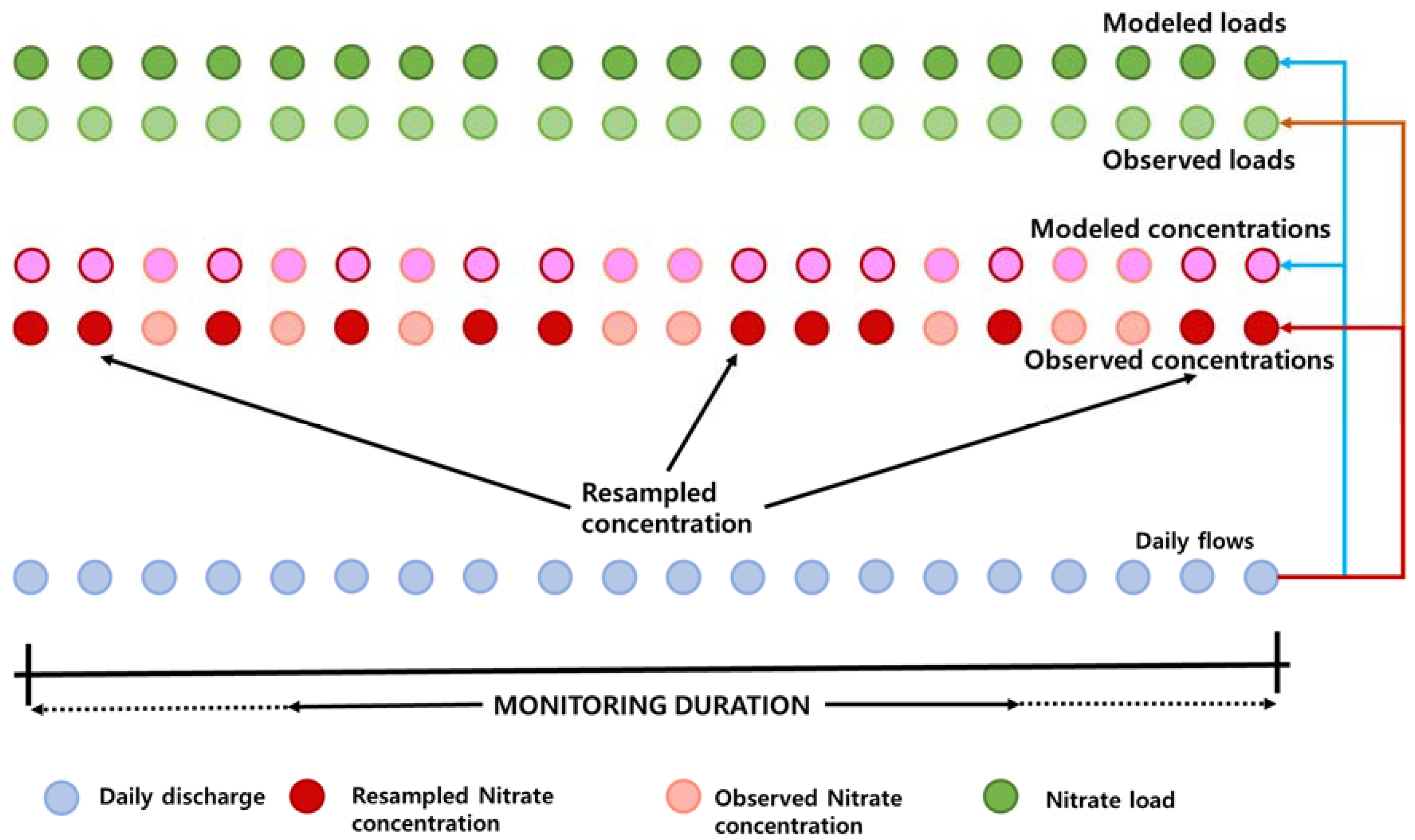
2.2. Sampling Frequency
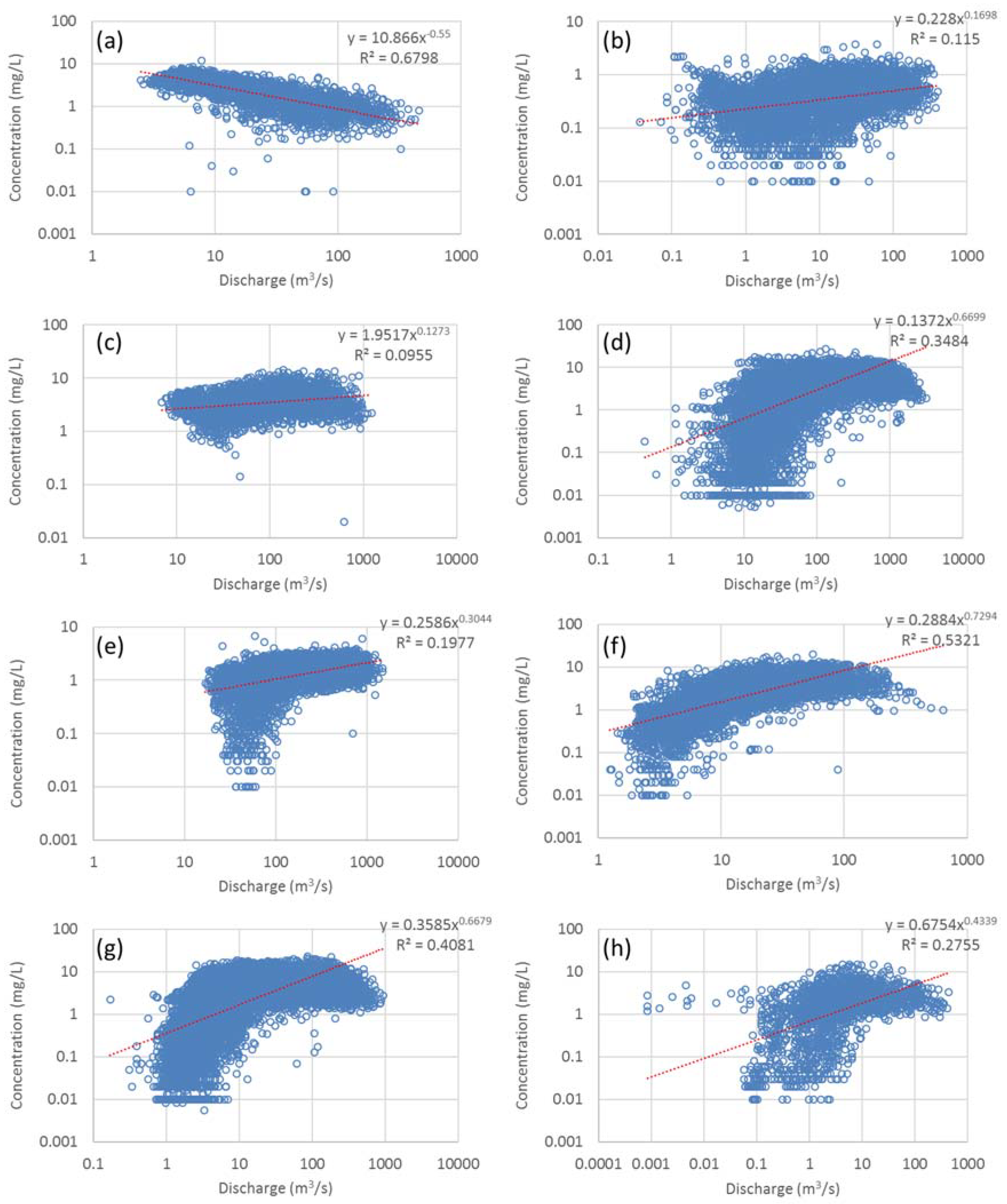
2.3. Water Quality Estimation
2.4. Regression Model with Five, Six, and Seven Parameters
2.5. Weighted Regressions on Time, Discharge, and Season (WRTDS) and Simple Linear Interpolation (SLI)
2.6. Shape of the Residual Adjustments
2.7. Residual and Proportional Adjustment Methods
2.8. Accuracy Evaluation
2.9. Priority Ranking of 23 Estimation Methods
3. Results
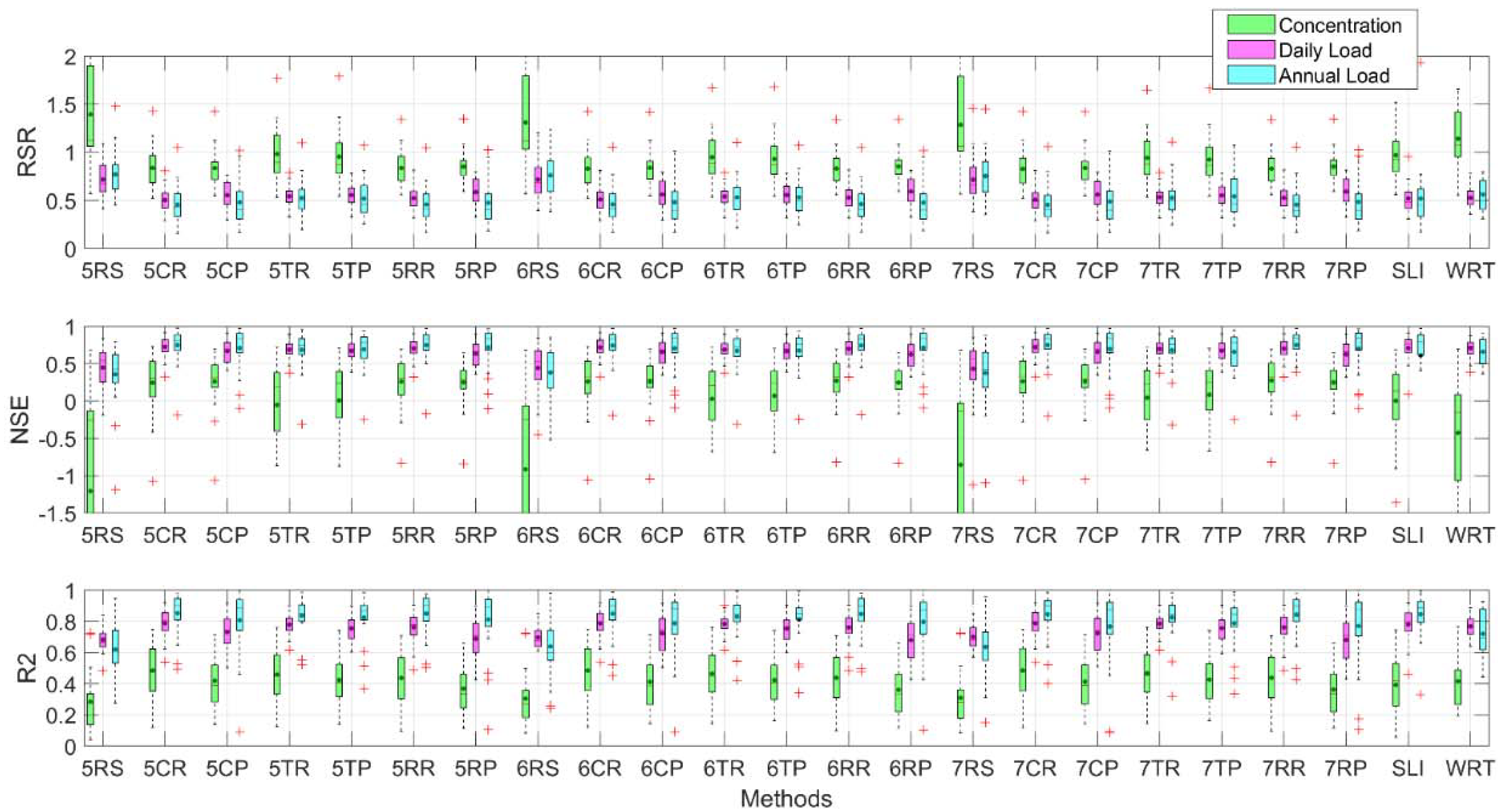
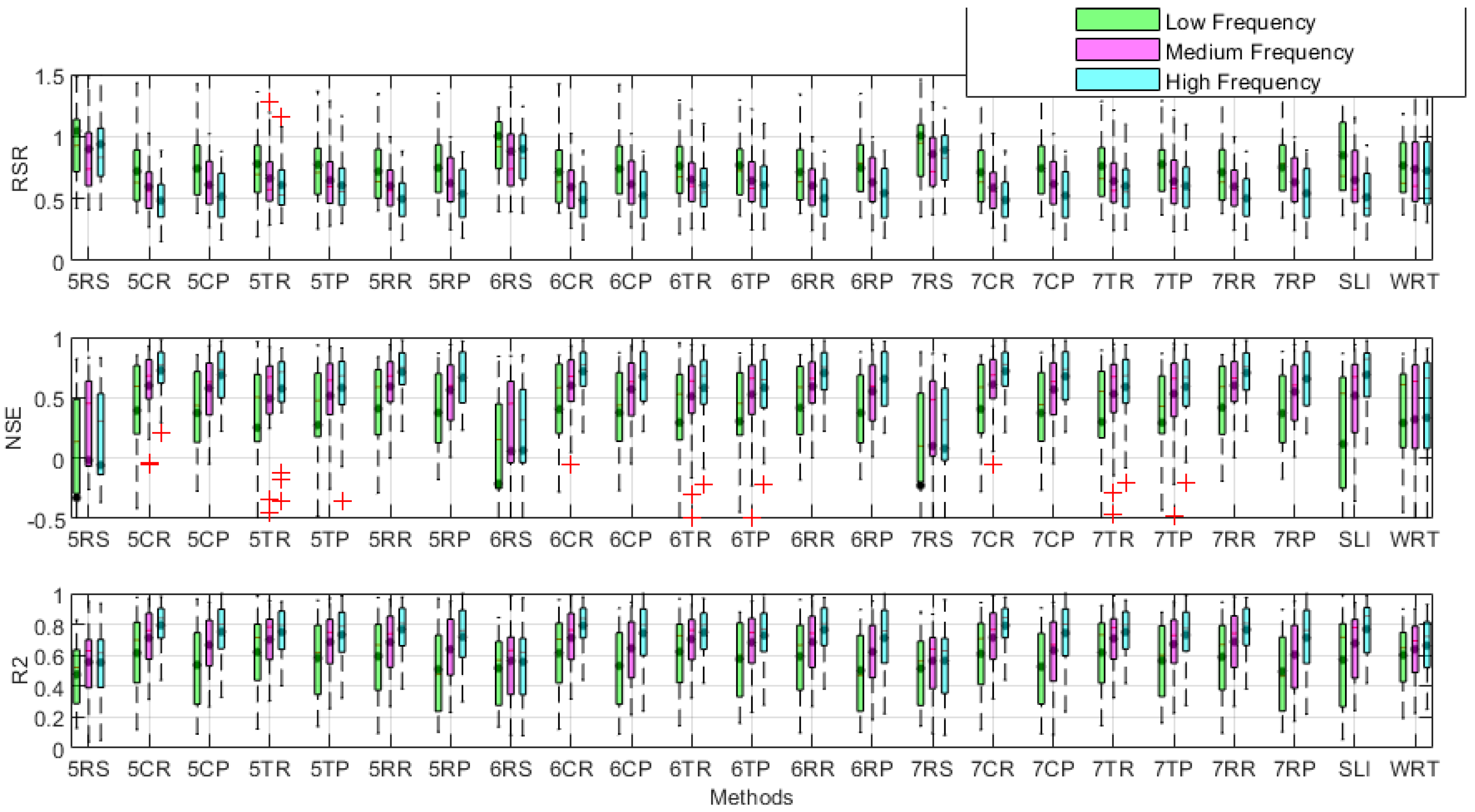
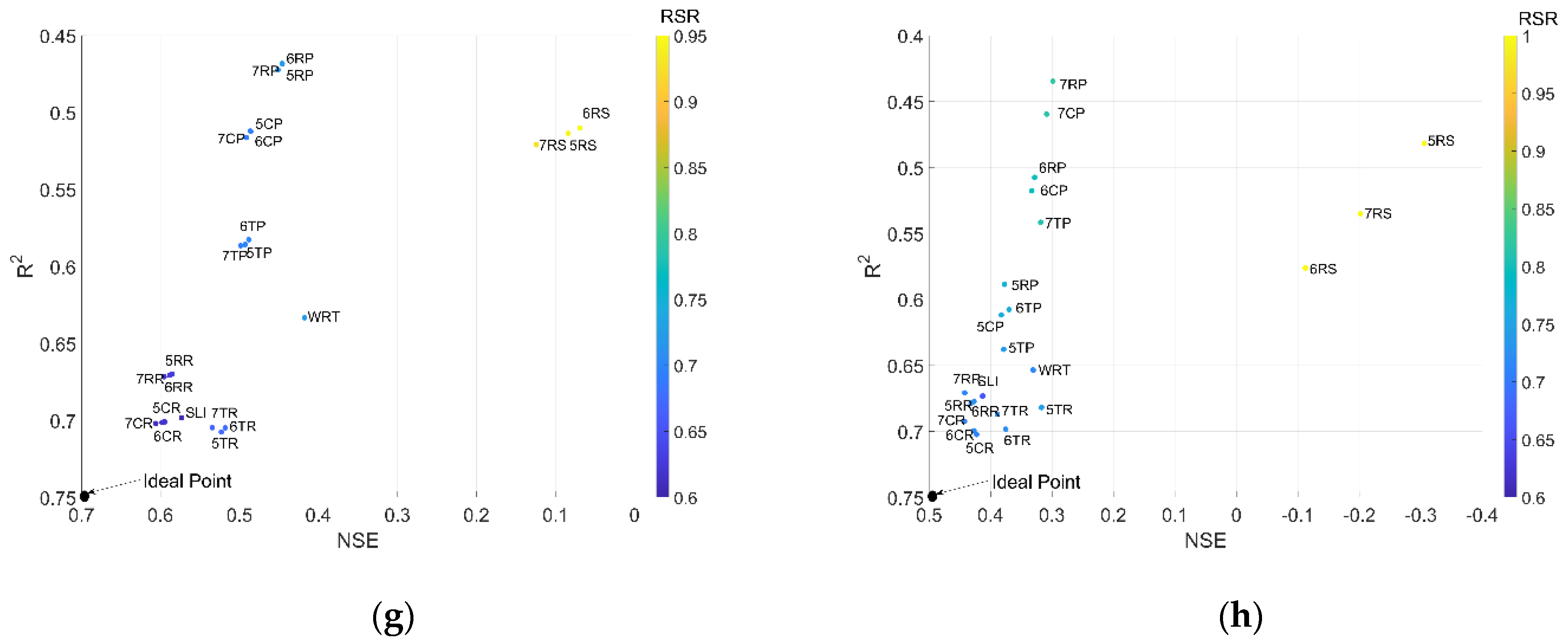
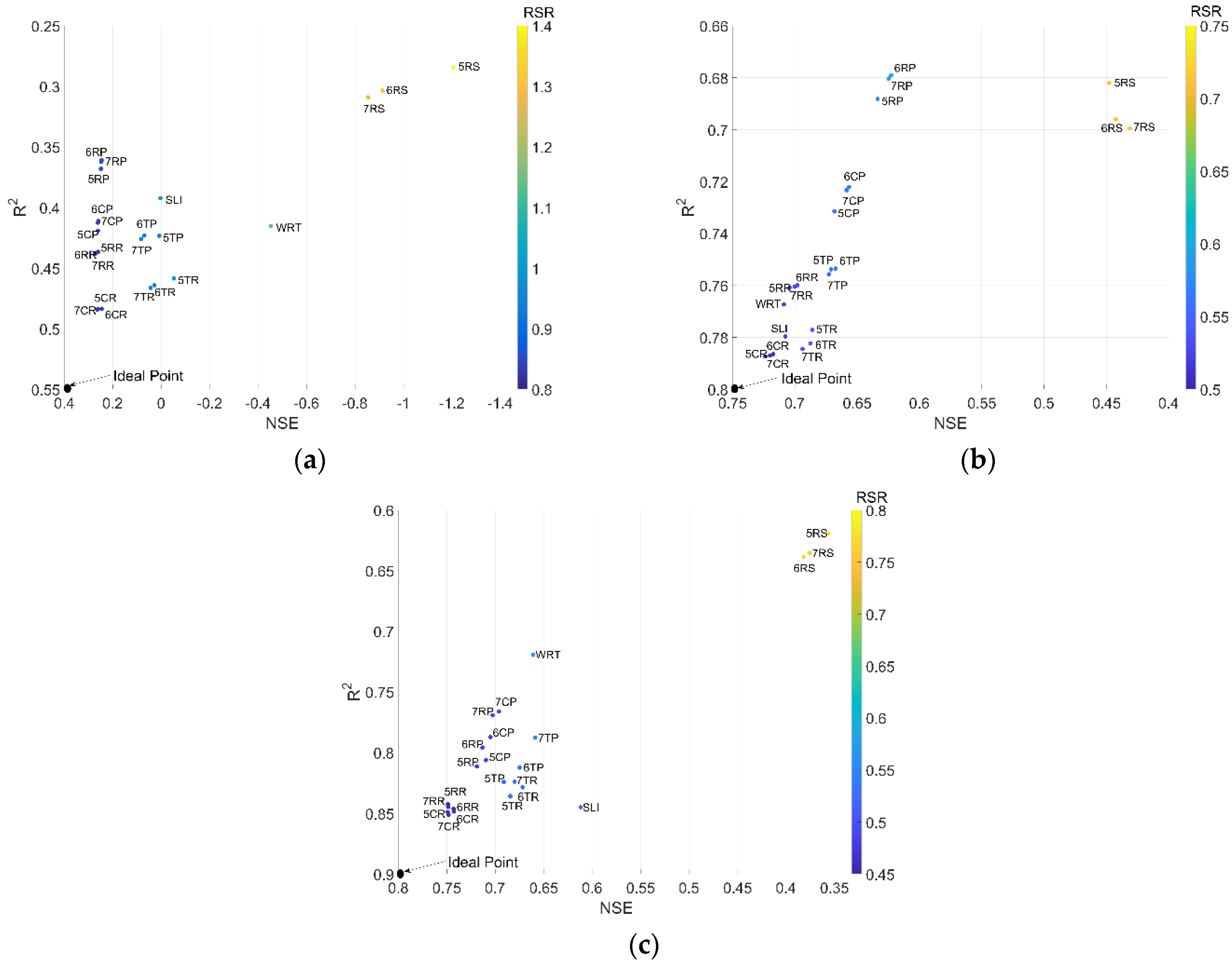
3.1. Uncertainty Analysis of the Model Estimation Performance
3.2. Priority Rankings of Estimation Methods Based on Characteristics of the Stations
4. Discussion
4.1. Suitability of the Linear Interpolation Method
4.2. Selecting the Best Estimation Method for Urbanized Watershed Stations
4.3. Regression Method with Adjustment Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barbiero, R.P.; Lesht, B.M.; Hinchey, E.K.; Nettesheim, T.G. A brief history of the US EPA Great Lakes National Program Office's water quality survey. J. Great Lakes Res. 2018, 44, 539–546. [Google Scholar] [CrossRef]
- Rodríguez, R.; Pastorini, M.; Etcheverry, L.; Chreties, C.; Fossati, M.; Castro, A.; Gorgoglione, A. Water-quality data imputation with a high percentage of missing values: A machine learning approach. Sustainability 2021, 13, 6318. [Google Scholar] [CrossRef]
- Ratolojanahary, R.; Ngouna, R.H.; Medjaher, K.; Junca-Bourié, J.; Dauriac, F.; Sebilo, M. Model selection to improve multiple imputation for handling high rate missingness in a water quality dataset. Expert Syst. Appl. 2019, 131, 299–307. [Google Scholar] [CrossRef] [Green Version]
- Stets, E.G.; Kelly, V.J.; Crawford, C.G. Regional and temporal differences in nitrate trends discerned from long-term water quality monitoring data. J. Am. Water Resour. Assoc. 2015, 51, 1394–1407. [Google Scholar] [CrossRef]
- Cohn, T.A.; Caulder, D.L.; Gilroy, E.J.; Zynjuk, L.D.; Summers, R.M. The validity of a simple statistical model for estimating fluvial constituent loads: An empirical study involving nutrient loads entering Chesapeake Bay. Water Resour. Res. 1992, 28, 2353–2363. [Google Scholar] [CrossRef]
- Runkel, R.L.; Crawford, C.G.; Cohn, T.A. Load Estimator (LOADEST): A FORTRAN program for estimating constituent loads in streams and rivers. In Techniques and Methods; US Geological Survey, U.S. Department of the Interior: Reston, VA, USA, 2004. [Google Scholar] [CrossRef] [Green Version]
- Stenback, G.A.; Crumpton, W.G.; Schilling, K.E.; Helmers, M.J. Rating curve estimation of nutrient loads in Iowa rivers. J. Hydrol. 2011, 396, 158–169. [Google Scholar] [CrossRef]
- Aulenbach, B.T.; Hooper, R.P. The composite method: An improved method for stream-water solute load estimation. Hydrol. Process. 2006, 20, 3029–3047. [Google Scholar] [CrossRef]
- Verma, S.; Markus, M.; Cooke, R.A. Development of error correction techniques for nitrate-N load estimation methods. J. Hydrol. 2012, 432, 12–25. [Google Scholar] [CrossRef]
- Park, D.; Markus, M.; Jung, K.; Um, M.-J. Uncertainty analysis of the relationship between discharge and nitrate concentration in the Lower Illinois River using a copula model. J. Clean. Prod. 2019, 222, 310–323. [Google Scholar] [CrossRef]
- Pellerin, B.A.; Bergamaschi, B.A.; Gilliom, R.J.; Crawford, C.G.; Saraceno, J.; Paul Frederick, C.; Downing, B.D.; Murphy, J.C. Mississippi River nitrate loads from high frequency sensor measurements and regression-based load estimation. Environ. Sci. Technol. 2014, 48, 12612–12619. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, C.J.; Hirsch, R.M.; Schwarz, G.E.; Holtschlag, D.J.; Preston, S.D.; Crawford, C.G.; Vecchia, A.V. An evaluation of methods for estimating decadal stream loads. J. Hydrol. 2016, 542, 185–203. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Markus, M.; Demissie, M. Uncertainty of nitrate-N load computations for agricultural watersheds. Water Resour. Res. 2002, 38, 3-1–3-12. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Moyer, D.L.; Archfield, S.A. Weighted regressions on time, discharge, and season (WRTDS), with an application to Chesapeake Bay river inputs 1. JAWRA 2010, 46, 857–880. [Google Scholar] [PubMed]
- Verma, S.; Bartosova, A.; Markus, M.; Cooke, R.; Um, M.-J.; Park, D. Quantifying the role of large floods in riverine nutrient loadings using linear regression and analysis of covariance. Sustainability 2018, 10, 2876. [Google Scholar] [CrossRef] [Green Version]
- Jung, K.; Um, M.-J.; Markus, M.; Park, D. Comparison of long short-term memory and weighted regressions on time, discharge, and season models for nitrate-N load estimation. Sustainability 2020, 12, 5942. [Google Scholar] [CrossRef]
- Verma, A.K.; Jha, M.K. Evaluation of a GIS-based watershed model for streamflow and sediment-yield simulation in the upper Baitarani river basin of Eastern India. J. Hydrol. Eng. 2015, 20, C5015001. [Google Scholar] [CrossRef]
- Government of India; Government of The Netherlands. Protocol for Water Quality Monitoring, Hydrology Project Technical Assistance Version 1.0; DHV Consultants: New Delhi, India; Delft Hydraulics: Delft, The Netherlands; HALCROW: London, UK; TAHAL: Amsterdam, The Netherlands; CES: Langley, VA, USA; ORG: New York, NY, USA; JPS: Kingston, Jamaica, 1999. [Google Scholar]
- Canadian Council of Ministers of the Environment (CCME). Guidance Manual for Optimizing Water Quality Monitoring Program Design; Canadian Council of Ministers of the Environment (CCME): Winnipeg, MB, Canada, 2015. [Google Scholar]
- El-Shaarawi, A.; Kuntz, K.; Sylvestre, A. Estimation of loading by numerical integration. In Developments in Water Science; Elsevier: Amsterdam, The Netherlands, 1986; pp. 469–478. [Google Scholar]
- Preston, S.D.; Bierman, V.J., Jr.; Silliman, S.E. An evaluation of methods for the estimation of tributary mass loads. Water Resour. Res. 1989, 25, 1379–1389. [Google Scholar] [CrossRef]
- Richards, R.P.; Baker, D.B.; Kramer, J.W.; Ewing, D.E.; Merryfield, B.J.; Miller, N.L. Storm discharge, loads, and average concentrations in Northwest Ohio rivers, 1975–1995. J. Am. Water Resour. Assoc. 2001, 37, 423–438. [Google Scholar] [CrossRef]
- Toor, G.S.; Harmel, R.D.; Haggard, B.E.; Schmidt, G. Evaluation of regression methodology with low-frequency water quality sampling to estimate constituent loads for ephemeral watersheds in Texas. J. Environ. Qual. 2008, 37, 1847–1854. [Google Scholar] [CrossRef] [PubMed]
- Cohn, T.A.; Delong, L.L.; Gilroy, E.J.; Hirsch, R.M.; Wells, D.K. Estimating constituent loads. Water Resour. Res. 1989, 25, 937–942. [Google Scholar] [CrossRef]
- Jeong, J.; Kannan, N.; Arnold, J.; Glick, R.; Gosselink, L.; Srinivasan, R. Development and integration of sub-hourly rainfall–runoff modeling capability within a watershed model. Water Resour. Manag. 2010, 24, 4505–4527. [Google Scholar] [CrossRef]
- Lamichhane, N.; Sharma, S. Effect of input data in hydraulic modeling for flood warning systems. Hydrol. Sci. J. 2018, 63, 938–956. [Google Scholar] [CrossRef]
- Meng, H.; Sexton, A.; Maddox, M.; Sood, A.; Brown, C.; Ferraro, R.; Murtugudde, R. Modeling Rappahannock River basin using SWAT-pilot for Chesapeake Bay watershed. Appl. Eng. Agric. 2010, 26, 795–805. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Sisay, E.; Halefom, A.; Khare, D.; Singh, L.; Worku, T. Hydrological modelling of ungauged urban watershed using SWAT model. Model. Earth Syst. Environ. 2017, 3, 693–702. [Google Scholar] [CrossRef]
- Jung, K.; Bae, D.H.; Um, M.J.; Kim, S.; Jeon, S.; Park, D. Evaluation of nitrate load estimations using neural networks and canonical correlation analysis with k-fold cross-validation. Sustainability 2020, 12, 400. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual model. Part 1—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar]
- Burns, D.A.; Boyer, E.W.; Elliott, E.M.; Kendall, C. Sources and transformations of nitrate from streams draining varying land uses: Evidence from dual isotope analysis. J. Environ. Qual. 2009, 38, 1149–1159. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Frankenberger, J.R.; Bowling, L.C.; Sun, Z. Quantification of uncertainty in estimated nitrate-N loads in agricultural watersheds. J. Hydrol. 2014, 519, 106–116. [Google Scholar] [CrossRef]
- Kaushal, S.S.; Groffman, P.M.; Band, L.E.; Elliott, E.M.; Shields, C.A.; Kendall, C. Tracking nonpoint source nitrogen pollution in human-impacted watersheds. Environ. Sci. Technol. 2011, 45, 8225–8232. [Google Scholar] [CrossRef] [PubMed]
- Poor, C.J.; McDonnell, J.J. The effects of land use on stream nitrate dynamics. J. Hydrol. 2007, 332, 54–68. [Google Scholar] [CrossRef]
- Adeuya, R.; Utt, N.; Frankenberger, J.; Bowling, L.; Kladivko, E.; Brouder, S.; Carter, B. Impacts of drainage water management on subsurface drain flow, nitrate concentration, and nitrate loads in Indiana. J. Soil. Water Conserv. 2012, 67, 474–484. [Google Scholar] [CrossRef]
- David, M.B.; Drinkwater, L.E.; McIsaac, G.F. Sources of nitrate yields in the Mississippi River Basin. J. Environ. Qual. 2010, 39, 1657–1667. [Google Scholar] [CrossRef]
- Lavaire, T.; Gentry, L.E.; David, M.B.; Cooke, R.A. Fate of water and nitrate using drainage water management on tile systems in east-central Illinois. Agric. Water Manag. 2017, 191, 218–228. [Google Scholar] [CrossRef]
- Hirsch, R.M. Large biases in regression-based constituent flux estimates: Causes and diagnostic tools. J. Am. Water Resour. Assoc. 2014, 50, 1401–1424. [Google Scholar] [CrossRef]
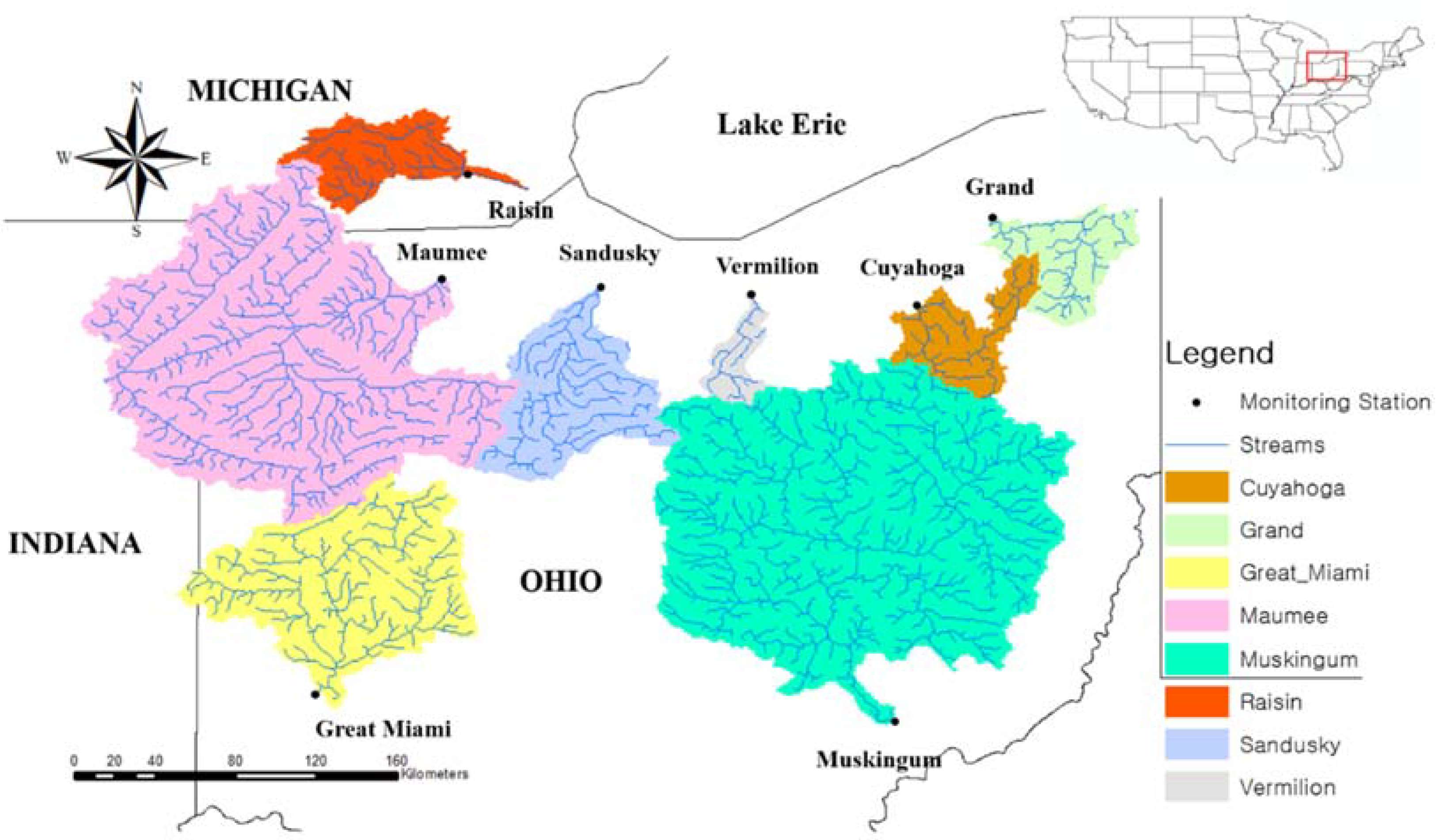

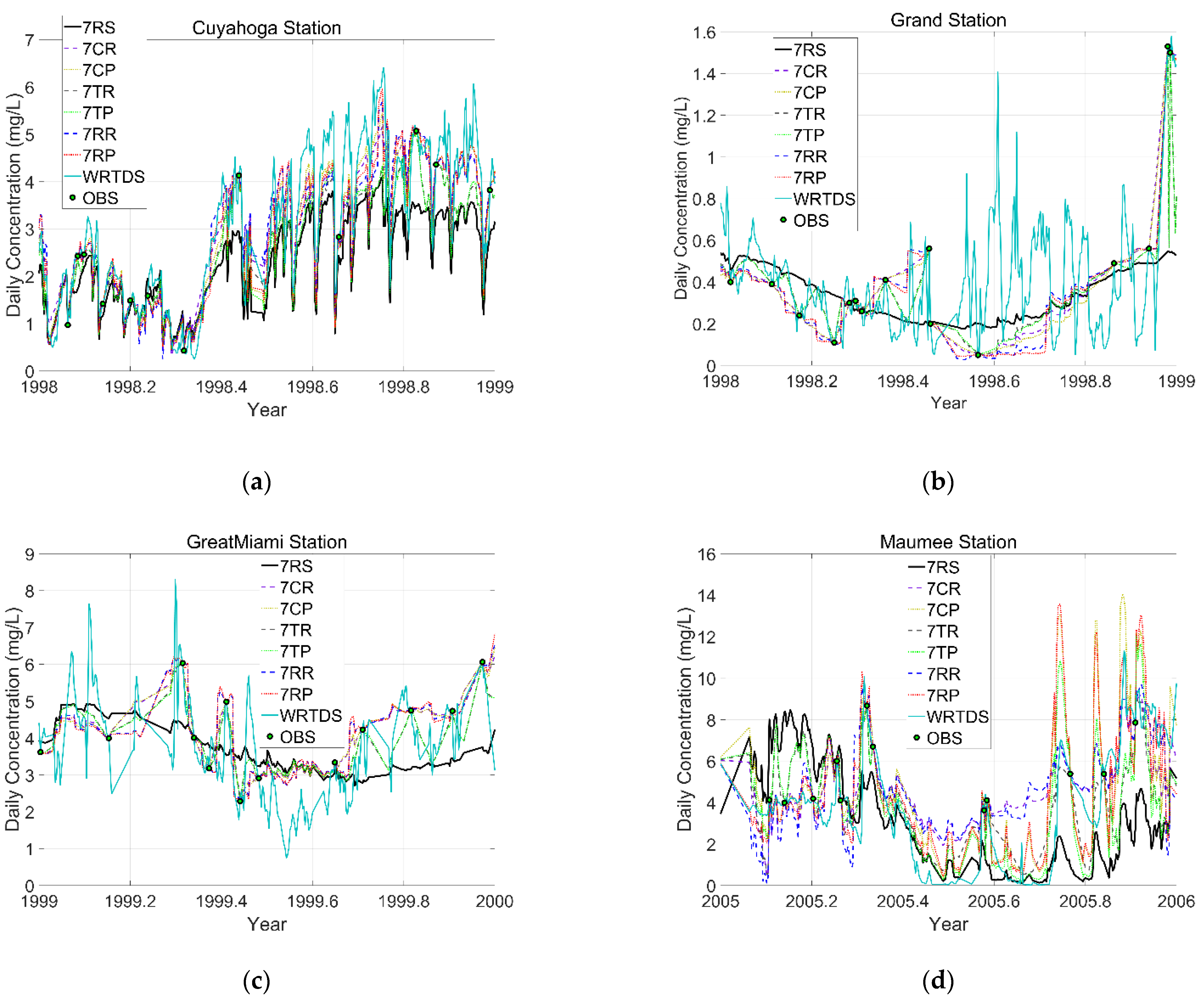


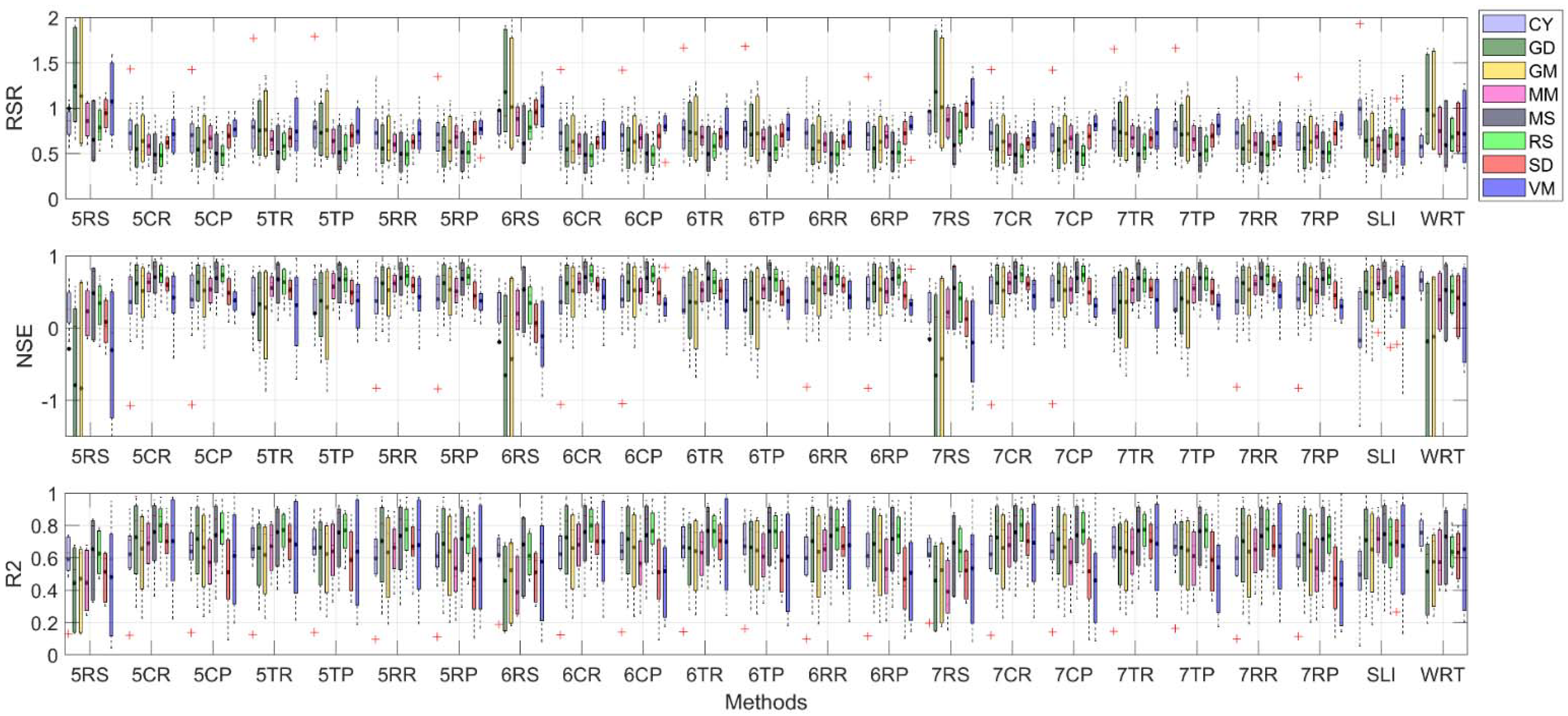





| USGS Station Number | Monitoring Period | Watershed Size (km2) | Years Selected | Land Use (%) | |||
|---|---|---|---|---|---|---|---|
| Agriculture | Urban | Wooded | |||||
| Lake Erie basin | |||||||
| Cuyahoga (CY) | 04208000 | 1982–2017 | 1843 | 36 | 17 | 47 | 35 |
| Grand (GD) | 04212100 | 1989–2006 | 1758 | 18 | 37 | 10 | 52 |
| Maumee (MM) | 04193500 | 1975–2017 | 16,427 | 43 | 81 | 11 | 8 |
| Raisin (RS) | 04176500 | 1982–2017 | 2755 | 36 | 72 | 11 | 16 |
| Sandusky (SD) | 04198000 | 1975–2017 | 3285 | 43 | 83 | 9 | 8 |
| Vermilion (VM) | 04199500 | 2001–2008 | 697 | 8 | 71 | 1 | 26 |
| Ohio River basin | |||||||
| Great Miami (GM) | 03271601 | 1996–2017 | 6953 | 22 | 82 | 5 | 10 |
| Muskingum (MS) | 03150000 | 1995–2017 | 19,208 | 23 | 52 | 2 | 43 |
| Estimation Methods | Regression (RS) | Composite Residual (CR) | Composite Proportional (CP) | Triangular Residual (TR) | Triangular Proportional (TP) | Rectangular Residual (RR) | Rectangular Proportional (RP) |
|---|---|---|---|---|---|---|---|
| 5-parameter | 5RS | 5CR | 5CP | 5TR | 5TP | 5RR | 5RP |
| 6-parameter | 6RS | 6CR | 6CP | 6TR | 6TP | 6RR | 6RP |
| 7-parameter | 7RS | 7CR | 7CP | 7TR | 7TP | 7RR | 7RP |
| Simple Linear Interpolation | SLI | ||||||
| WRTDS | WRT |
| Ranking | Cuyahoga (CY) | Grand (GD) | Great Miami (GM) | Maumee (MM) | Muskingum (MS) | Raisin (RS) | Sandusky (SD) | Vermilion (VM) |
|---|---|---|---|---|---|---|---|---|
| 1 | WRT | 7CP | 7CP | SLI | 6CR | 7CR | 7CR | SLI |
| 2 | 6CP | 6CP | 6CP | 5CR | 5CR | 6CR | 6CR | 7CR |
| 3 | 7CP | 5CP | 7RP | 6CR | 7CR | 5CR | 5CR | 7RR |
| 4 | 5CP | 7CR | 6RP | 7CR | 7TR | 7RR | SLI | 5CR |
| 5 | 5RP | 6CR | 5CP | 5RR | 7TP | 7CP | 7RR | 6CR |
| 6 | 6RP | 5CR | 7CR | 6RR | 6TR | 6CP | 6RR | 5RR |
| 7 | 7RP | 7RR | 5RP | 7RR | 6TP | 5CP | 5RR | 6RR |
| 8 | 5CR | 6RR | 6CR | 5TP | 6RR | 6RR | 7TR | 7TR |
| 9 | 6CR | 5RR | 7RR | 5TR | 5RR | 5RR | 5TR | 6TR |
| 10 | 5RR | 6RP | 6RR | 7TP | 7RR | 7RP | 6TR | 5TP |
| Ranking | Daily Concentration | Daily Load | Annual Load |
|---|---|---|---|
| 1 | 7CR | 5CR | 7CR |
| 2 | 6CR | 7CR | 5CR |
| 3 | 7RR | 6CR | 7RR |
| 4 | 5CR | SLI | 5RR |
| 5 | 6RR | EGR | 6CR |
| 6 | 5RR | 5RR | 6RR |
| 7 | 5CP | 7RR | 5RP |
| 8 | 7CP | 7TR | 6RP |
| 9 | 6CP | 6RR | 5CP |
| 10 | 5RP | 6TR | 6CP |
| Ranking | Low Frequency | Medium Frequency | High Frequency |
|---|---|---|---|
| 1 | 6CR | 7CR | SLI |
| 2 | 7CR | 6CR | 5RR |
| 3 | 5CR | 5CR | 7RR |
| 4 | 6RR | 7RR | 6RR |
| 5 | 7RR | 5RR | 5CR |
| 6 | 5RR | 6RR | 7CR |
| 7 | 6TR | 7TR | 6CR |
| 8 | 7TR | 5CP | 5CP |
| 9 | 5TR | 6TR | 7CP |
| 10 | WRT | 6TP | 6CP |
| Ranking | Low Frequency | Medium Frequency | High Frequency |
|---|---|---|---|
| 1 | 6RR | 7CR | 5RR |
| 2 | 6CR | 7RR | 5CR |
| 3 | 7RR | 5CR | 7CR |
| 4 | 7CR | 5RP | 7RR |
| 5 | 5RR | 6CR | 6RR |
| 6 | 5CR | 5RR | 6CR |
| 7 | 5TR | 6RR | 5RP |
| 8 | 6TR | 5CP | 5CP |
| 9 | WRT | 5TP | SLI |
| 10 | 5TP | 6RP | 7RP |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, D.; Um, M.-J.; Markus, M.; Jung, K.; Keefer, L.; Verma, S. Insights from an Evaluation of Nitrate Load Estimation Methods in the Midwestern United States. Sustainability 2021, 13, 7508. https://doi.org/10.3390/su13137508
Park D, Um M-J, Markus M, Jung K, Keefer L, Verma S. Insights from an Evaluation of Nitrate Load Estimation Methods in the Midwestern United States. Sustainability. 2021; 13(13):7508. https://doi.org/10.3390/su13137508
Chicago/Turabian StylePark, Daeryong, Myoung-Jin Um, Momcilo Markus, Kichul Jung, Laura Keefer, and Siddhartha Verma. 2021. "Insights from an Evaluation of Nitrate Load Estimation Methods in the Midwestern United States" Sustainability 13, no. 13: 7508. https://doi.org/10.3390/su13137508
APA StylePark, D., Um, M.-J., Markus, M., Jung, K., Keefer, L., & Verma, S. (2021). Insights from an Evaluation of Nitrate Load Estimation Methods in the Midwestern United States. Sustainability, 13(13), 7508. https://doi.org/10.3390/su13137508










