Efficient and Comprehensive Evaluation Method of Temporary Overvoltage in Distribution Systems with Inverter-Based Distributed Generations
Abstract
:1. Introduction
- This paper analyzed the TOV impacts of multiple parameters: the impedance ratio of interconnection transformers, the ratio of loads to DGs, and the distance to the fault. There have been no such works that considered various parameters at the same time.
- The proposed methodology can investigate extensive multi-parameter variations in TOV analysis, unlike time-domain, detailed simulations.
- The paper also presented TOV analysis results in a three-dimensional graph for comprehensive and simultaneous observations based on multiple parameters. This approach can facilitate the TOV analysis of multi-parameter conditions and the comparison of the fault characteristics of synchronous-machine-based and inverter-based DGs.
2. Background Theory
2.1. Voltage Formula during an SLG Fault
2.2. Voltage Rise Curve Depending on the Impedance Ratio of Transformer
3. Proposed Methodology
- The impedance ratio of the interconnection transformer ranged from 0.01 to 1000, while the ratio of load to DG ranged from 0 to 3.
- The impedance ratio of the interconnection transformer ranged from 0.01 to 1000, while the length of the fault section ranged from 0 to 5 km.
- The ratio of load to DG ranged from 0 to 3, while the length of the fault section ranged from 0 to 5 km.
4. Case Study
4.1. The Impacts of Three Specific Parameters on TOV
4.1.1. Change in x0/x1 Ratio of Interconnection Transformer
4.1.2. Change in the Ratio of Load to DG
4.1.3. Change in Fault Location
4.2. Change in Fault Resistance
4.3. The Simultaneous Impacts of Two of the Three Parameters on TOV
4.3.1. Change in x0/x1 Ratio of Interconnection Transformer and the Ratio of Load to DG
4.3.2. Change in x0/x1 Ratio of Interconnection Transformer and the Fault Location
4.3.3. Change in the Ratio of Load to DG and the Fault Location
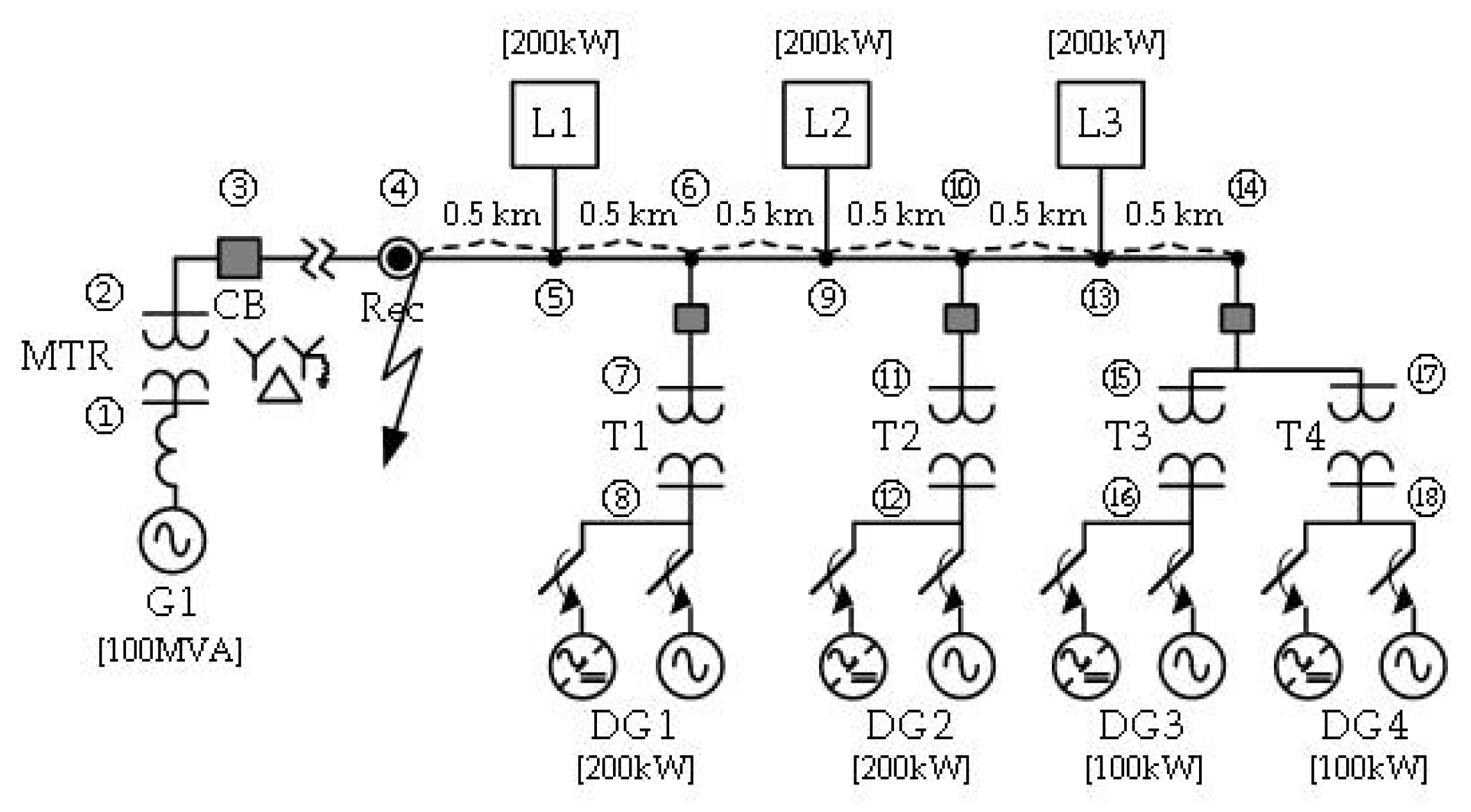
4.4. Verification in the Actual Distribution System
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Driesen, J.; Belmans, R. Distributed generation: Challenges and possible solutions. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; pp. 1–8. [Google Scholar] [CrossRef]
- Musa, H. A Review of Distributed Generation Resource Types and Their Mathematical Models for Power Flow Analysis. Int. J. Sci. Technol. Soc. 2015, 3, 204. [Google Scholar] [CrossRef] [Green Version]
- Keller, J.; Kroposki, B. Understanding Fault Characteristics of Inverter-Based Distributed Energy Resources. In Understanding Fault Characteristics of Inverter-Based Distributed Energy Resources; Technical Report; National Renewable Energy Lab (NREL): Golden, CO, USA, 2010; pp. 1–48. [Google Scholar]
- Arritt, R.F.; Dugan, R.C. Distributed generation interconnection transformer and grounding selection. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–7. [Google Scholar] [CrossRef]
- Institute of Electrical and Electronics Engineers (IEEE) Industry Applications Society. IEEE Standard for Insulation Coordination—Definitions, Principles and Rules. In IEEE Std C62.82.1-2010 (Revision of IEEE Std 1313.1-1996; IEEE: New York, NY, USA, 2011; pp. 1–22. [Google Scholar] [CrossRef]
- Institute of Electrical and Electronics Engineers (IEEE) Industry Applications Society. IEEE Recommended Practice for Grounding of Industrial and Commercial Power Systems. In IEEE Std 142-2007 (Revision of IEEE Std 142-1991; IEEE: New York, NY, USA, 2008; pp. 1–21. [Google Scholar] [CrossRef]
- Institute of Electrical and Electronics Engineers (IEEE) Industry Applications Society. IEEE Guide for the Application of Neutral Grounding in Electrical Utility Systems—Part I: Introduction. In Surge Protective Devices/High Voltage of the IEEE Power and Energy Society; IEEE: New York, NY, USA, 2017; pp. 1–37. [Google Scholar] [CrossRef]
- Grigsby, L.L. Temporary Over-Voltages and System Grounding. In Electric Power Engineering Handbook; CRC Press: Boca Raton, FL, USA, 2018; pp. 1–14. Available online: https://www.electricalengineering-book.com/pdf/chapter-754953.pdf (accessed on 29 June 2021).
- Wang, X.; Gao, J.; Wei, X.; Zeng, Z.; Wei, Y.; Kheshti, M. Single Line to Ground Fault Detection in a Non-Effectively Grounded Distribution Network. IEEE Trans. Power Deliv. 2018, 33, 3173–3186. [Google Scholar] [CrossRef]
- Ropp, M.; Hoke, A.; Chakraborty, S.; Schutz, D.; Mouw, C.; Nelson, A.; McCarty, M.; Wang, T.; Sorenson, A. Ground Fault Overvoltage with Inverter-Interfaced Distributed Energy Resources. IEEE Trans. Power Deliv. 2017, 32, 890–899. [Google Scholar] [CrossRef]
- Advanced Energy Industries Inc. Neutral Connections and Effective Grounding. Adv. Energy 2013, 1–7. Available online: https://pdf4pro.com/view/neutral-connections-and-effective-grounding-4d92e7.html (accessed on 29 June 2021).
- Bravo, R.J.; Yinger, R.; Robles, S.; Tamae, W. Solar PV inverter testing for model validation. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Detroit, MI, USA, 24–28 July 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Barker, P. Overvoltage considerations in applying distributed resources on power systems. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2003; pp. 109–114. [Google Scholar] [CrossRef]
- Balakrishnan, J.; Atputharajah, A.; Ekanayake, J. Review of the Effects of Transformer Configuration on Distributed Generator Interconnection. In Proceedings of the 2008 IEEE Region 10 and the Third international Conference on Industrial and Information Systems, Kharagpur, India, 8–10 December 2008; pp. 1–6. [Google Scholar]
- Sultan, A.; Mustafa, M.; Saini, M. Ground fault currents in unit generator-transformer at various NGR and transformer configurations. In Proceedings of the 2012 IEEE Symposium on Industrial Electronics and Applications, Bandung, Indonesia, 23–26 September 2012; pp. 136–140. [Google Scholar] [CrossRef]
- Saifi, P.; Moharana, A.; Varma, R.; Seethapathy, R. Influence of distributed generation interface transformer and DG configurations on Temporary Overvoltage (TOV). In Proceedings of the CCECE 2010, Calgary, AB, Canada, 2–5 May 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Bravo, R.J.; Salas, R.; Yinger, R.; Robles, S.; Salas, R. Solar photovoltaic inverters transient over-voltages. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Pazos, F. Power Frequency Overvoltages Generated by Solar Plants. In Proceedings of the IET International Conference on the Renewable Energies and Power Quality, Prague, Czech Republic, 8–11 June 2009; Institution of Engineering and Technology (IET): London, UK, 2009; pp. 1–8. [Google Scholar] [CrossRef] [Green Version]
- Nelson, A.; Hoke, A.; Chakraborty, S.; Ropp, M.; Chebahtah, J.; Wang, T.; Zimmerly, B. Experimental evaluation of load rejection over-voltage from grid-tied solar inverters. In Proceedings of the 2015 IEEE 42nd Photovoltaic Specialist Conference (PVSC), New Orleans, LA, USA, 14–19 June 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Philip, S.S.; Koshy, D.E. Temporary overvoltage mitigation and re-connection of inverter after fault in a grid-connected photovoltaic system. Int. J. Eng. Res. Technol. 2016, 285–288. Available online: https://www.ijert.org/research/temporary-overvoltage-mitigation-and-re-connection-of-inverter-after-fault-in-a-grid-connected-photovoltaic-system-IJERTV5IS080242.pdf (accessed on 29 June 2021).
- Ghoddami, H.; Yazdani, A. A Mitigation Strategy for Temporary Overvoltages Caused by Grid-Connected Photovoltaic Systems. IEEE Trans. Energy Convers. 2014, 30, 413–420. [Google Scholar] [CrossRef]
- Varma, R.K.; Siavashi, E.M. Enhancement of Solar Farm Connectivity with Smart PV Inverter PV-STATCOM. IEEE Trans. Sustain. Energy 2019, 10, 1161–1171. [Google Scholar] [CrossRef]
- Institute of Electrical and Electronics Engineers (IEEE). IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. In IEEE-SASB Coordinating Committees; IEEE: New York, NY, USA, 2018; pp. 1–138. [Google Scholar] [CrossRef]


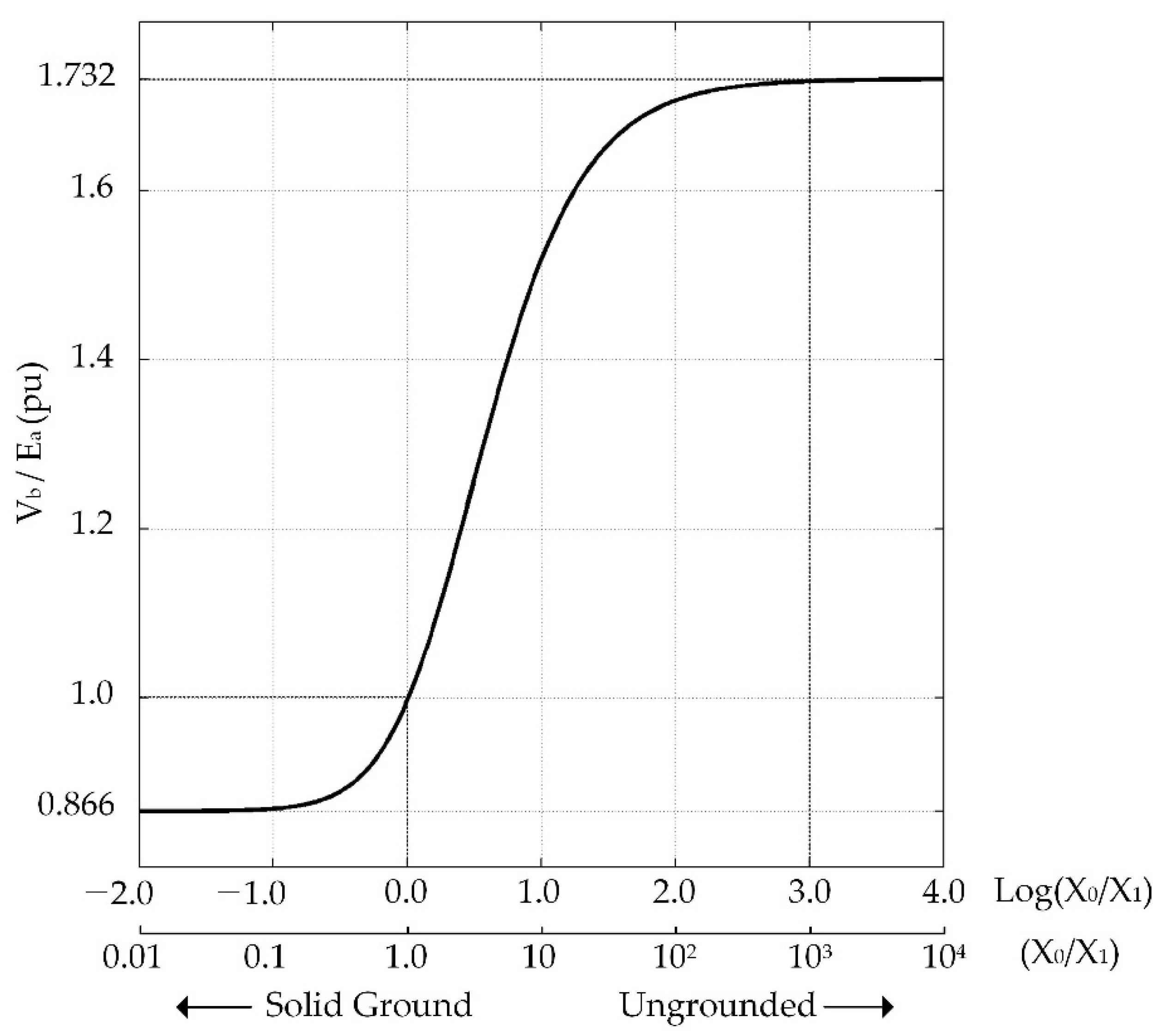


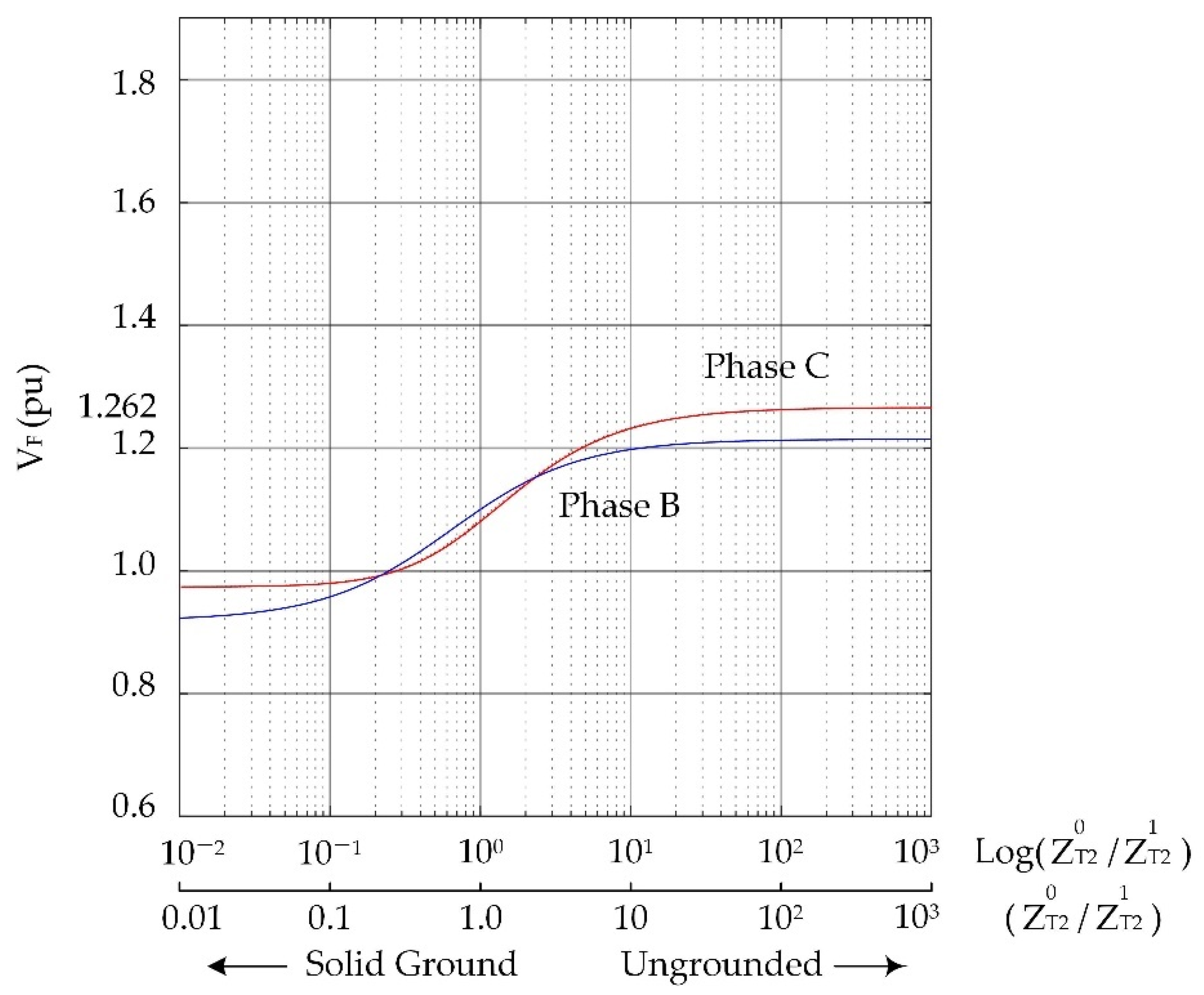













| Phase-B Voltage, Vb | Phase-C Voltage, Vc | |
|---|---|---|
| Solidly grounded systems | ||
| Ungrounded systems |
| Main Generator (G1) | MTR | Line | Interconnection Transformer (T1) | DG | |
|---|---|---|---|---|---|
| Rated power [MVA] | 100 | 45 | 100 | 3 | 3 (DG1, DG2) |
| Rated voltage [kV] | 154 | 154/22.9/6.6 | 22.9 | 22.9/0.38 | 0.38 |
| G1 | MTR | Line | Interconnection Transformer | DG | |
|---|---|---|---|---|---|
| Rated power [MVA] | 100 | 45 | 100 | 0.2 (T1, T2) | 0.2 (DG1, DG2) |
| 0.1 (T3, T4) | 0.1 (DG3, DG4) | ||||
| Rated voltage [kV] | 154 | 154/22.9/6.6 | 22.9 | 22.9/0.38 | 0.38 |
| BUS | Voltage (pu) |
|---|---|
| 5 | 1.8291 at Phase C |
| 6 | 1.8295 at Phase C |
| 7 | 1.0331 at Phase A |
| BUS | Voltage (pu) |
|---|---|
| 5 | 1.1498 at Phase B |
| 6 | 1.1498 at Phase B |
| 7 | 1.0000 at Phase C |
| BUS | Voltage (pu) |
|---|---|
| 5 | 0.9896 at Phase C |
| 6 | 0.9756 at Phase B |
| 7 | 1.0790 at Phase C |
| BUS | Voltage (pu) |
|---|---|
| 5 | 1.7888 at Phase B |
| 6 | 1.7856 at Phase B |
| 7 | 2.0023 at Phase C |
| BUS | Voltage (pu) |
|---|---|
| 5 | 0.9861 at Phase B |
| 6 | 0.9834 at Phase B |
| 7 | 1.0782 at Phase C |
| BUS | Voltage (pu) |
|---|---|
| 5 | 0.9219 at Phase B |
| 6 | 0.9191 at Phase B |
| 7 | 1.0037 at Phase C |
| Scenario | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Condition |
|
|
| |||
| DG type | Synchronous-machine-based DG | Inverter- based DG | Synchronous-machine-based DG | Inverter- based DG | Synchronous-machine-based DG | Inverter- based DG |
| Fault Resistance: 0 (Ω) | 1.8291 | 1.1494 | 0.9896 | 1.7888 | 1.0112 | 1.8001 |
| Fault Resistance: 2 (Ω) | 1.8011 | 1.1464 | 1.0080 | 1.7882 | 1.0248 | 1.8000 |
| Fault Resistance: 4 (Ω) | 1.7746 | 1.1436 | 1.0248 | 1.7876 | 1.0371 | 1.7993 |
| Fault Resistance: 6 (Ω) | 1.7497 | 1.1401 | 1.0395 | 1.7872 | 1.0476 | 1.7987 |
| Fault Resistance: 8 (Ω) | 1.7262 | 1.1382 | 1.0518 | 1.7867 | 1.0564 | 1.7982 |
| Fault Resistance: 10 (Ω) | 1.7039 | 1.1356 | 1.0618 | 1.7863 | 1.0634 | 1.7977 |
| Fault Resistance: 30 (Ω) | 1.5345 | 1.1143 | 1.0824 | 1.7844 | 1.0755 | 1.7949 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, N.; Lee, M.; Yoon, M.; Choi, S. Efficient and Comprehensive Evaluation Method of Temporary Overvoltage in Distribution Systems with Inverter-Based Distributed Generations. Sustainability 2021, 13, 7335. https://doi.org/10.3390/su13137335
Cho N, Lee M, Yoon M, Choi S. Efficient and Comprehensive Evaluation Method of Temporary Overvoltage in Distribution Systems with Inverter-Based Distributed Generations. Sustainability. 2021; 13(13):7335. https://doi.org/10.3390/su13137335
Chicago/Turabian StyleCho, Namhun, Moonjeong Lee, Myungseok Yoon, and Sungyun Choi. 2021. "Efficient and Comprehensive Evaluation Method of Temporary Overvoltage in Distribution Systems with Inverter-Based Distributed Generations" Sustainability 13, no. 13: 7335. https://doi.org/10.3390/su13137335
APA StyleCho, N., Lee, M., Yoon, M., & Choi, S. (2021). Efficient and Comprehensive Evaluation Method of Temporary Overvoltage in Distribution Systems with Inverter-Based Distributed Generations. Sustainability, 13(13), 7335. https://doi.org/10.3390/su13137335






