1. Introduction
It is well known that population aging is a global phenomenon [
1]. Additionally, one billion people, or 15% of the world’s population, experience some form of disability, and this value is expected to keep growing in the upcoming years [
2]. Thus, the European Union and its Member States are committed to improving social and economic situation of the people under these circumstances [
3]. This population, both aging and disabled, often face limitations and barriers that prevent them from participating in society. The inclusion of this population is one important aspect for many governments and organizations, and there are several initiatives and programs to promote this inclusion.
Among them, the availability and access to Assistive Technology (AT) enhances the independence of this population, enabling an improvement on their participation in all life’s activities. A significant percentage of people with disability is also elderly that require some type of equipment like wheelchairs, shower chairs, hospital beds, toileting equipment, crutches, etc., to perform daily activities or have a dignified life. We can define AT as “any item, piece of equipment or software that is used to increase, maintain, or improve an individual’s ability to perform daily tasks or to communicate, learn, and live independent, fulfilling and productive lives” [
4].
Despite the enormous need for these type of equipment and their recognized benefits, the access to them is still limited in many regions and countries. These equipment is essential to provide a good quality of life for users and also to help the caregivers of Home Health and Social Care Programs to provide a good service. These equipment can be expensive to purchase, and, in some countries, the AT programs are provided by non-governmental organization (NGO) or by local governments. These organizations are frequently based on Circular Economy principles that can help reduce the costs and meet the needs of the population in a faster and more effective way. Additionally, they can help reduce waste by having a reuse program for the AT equipment, considering that, in many cases, there is no need to ownership the equipment since it is used in a reduced time period.
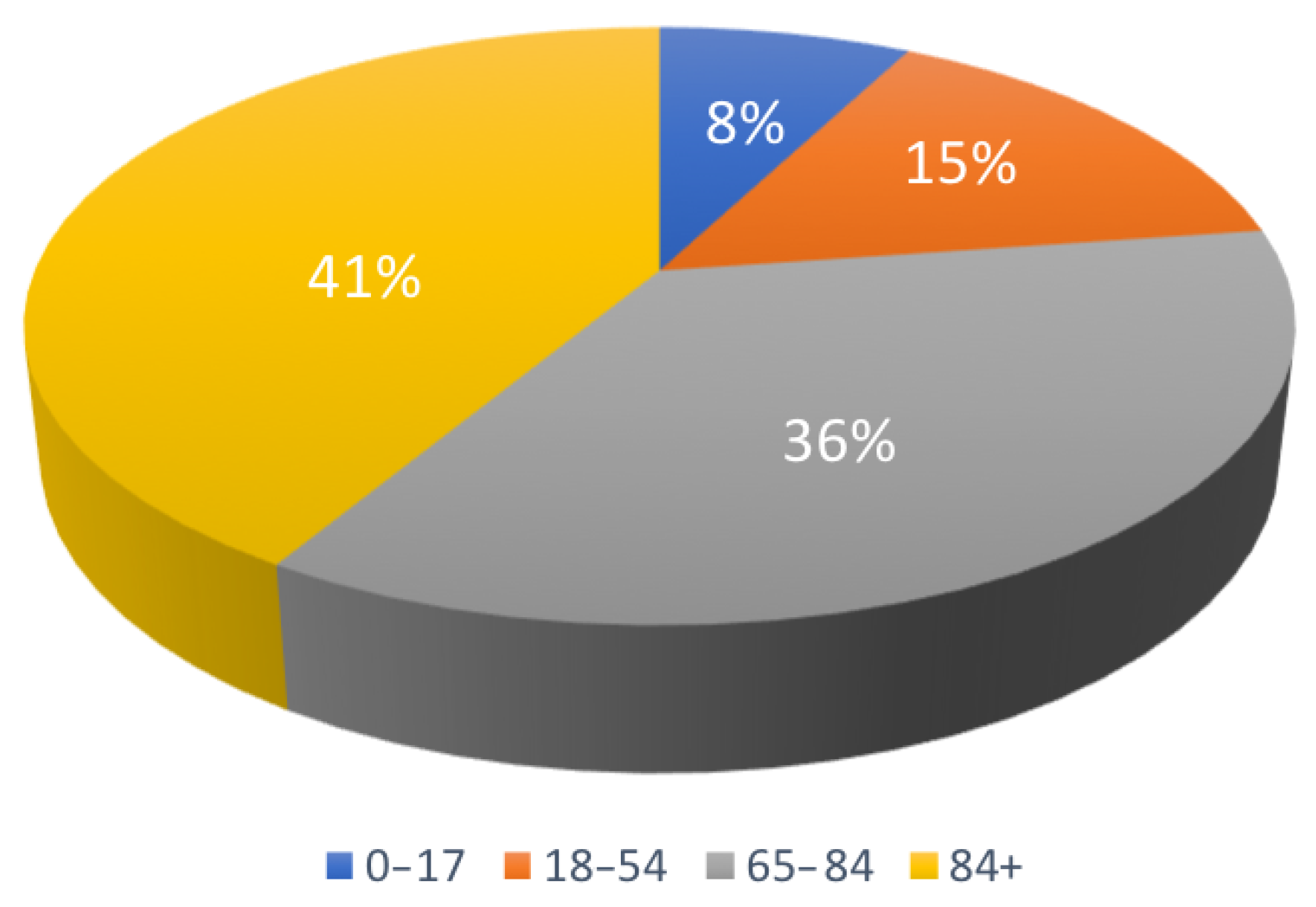
The main motivation of this research is to evaluate and optimize relevant logistics operations of an AT program, with the aim of giving access to this type of equipment to a larger population, consequently improving their quality of life. The operations related to the AT programs present distinct features when compared with other type of services, which raises the need for innovative decision support methods. The research work described in this paper has been done in close collaboration with the AT program in Barcelona, known as Banc del Moviment (BM). In 2020, BM loaned about 750 products to users, among which about 77% are people over 65 years of age (see
Figure 1), and collected around 250 products in donations. From the user’s perspective, the main factors entailing an increased need for these type of services are the age and the reduction in individual mobility (see
Table 1).
Therefore, the objective of this research is to study and provide efficient solutions for the management of the operations in an AT program, based on mathematical models and efficient algorithms that have been developed considering the specificities and particular characteristics of this social program. We focus on three main aspects: the location of warehouses and customer service points, inventory management of the different types of equipment, and the optimization of the home delivery and collection routes. As far as we know, no previous work using the optimization methodology has been applied to similar services. We apply the mathematical models and algorithms in an AT program in Barcelona that provided us with all data and necessary explanations of their organization and logistical systems. We have also validated the reliability of our results in conjunction with the BM managers. It is important to mention that a similar methodology can be applied to other similar programs around the world.
To provide decision support systems and solutions to assist in the management of AT operations, we have developed and applied mathematical models and algorithms from the Operations Research field. Some of the proposed models present innovative aspects specific to the area, others are well-known models but the context of the application is original. It is also important to mention that simplicity is an important factor for these target organizations. In most of these programs, the daily operations, and even the managers, can be volunteers from different backgrounds and frequently they have short linking period with the organization. Therefore, the main challenge here is to develop optimization systems that represent adequately the problems and provide efficient solutions that can, at the same time, be easy to understand and use. For these reasons, we have decided to create our optimization tools using Microsoft Excel software [
5].
The remainder of this paper is structured as follows.
Section 2 presents a literature review on logistics operations in similar fields and the main differences regarding their application to the industry. In
Section 3, we describe the AT operations in the BM organization. In
Section 4,
Section 5 and
Section 6, a detailed description of the each studied problem and the proposed solutions are presented followed by a presentation of the Decision Support Systems developed and provided to the organization. In
Section 7, an analysis of the results is discussed, and, finally, we present some possible future work.
2. Related Literature
In the literature, we can find an increased interest in research studies of the Logistics and Operations problems in Nonprofit Organizations (NPOs) and NGOs. However, actually, there is only a few references. In Reference [
6], the authors present several operational challenges in the management of NPOs and a literature review on this topic. Sinuany-Stern and Sherman [
7] mention the importance of applying Operations Research and Optimization to the management of NPOs with the aim of improving the operations and achievements. Most studies of applying Operations Research to NPOs/NGOs are on the area of Humanitarian Logistics [
8,
9,
10,
11].
Within the NGOs, we can find the AT organizations with the need to manage several operations to collect and delivery the mobility equipment. This organization can be classified in the area of Health and Social organizations, and present different AT delivery models as explained in Reference [
12]. These authors mention the charity-based model, which are programs that provide individuals with products that they could not access due to socioeconomic conditions. This is the kind of model that best fit the BM. Authors comment that this model usually experiences difficulties and can offer low quality solutions. However, there is a clear lack of literature on the modeling and management of decision problems in the context of AT operations, volunteering and charity.
Operations optimization, including Location, Inventory, and Routing, has been extensive applied to Healthcare with excellent results, as shown in several surveys [
13,
14,
15,
16]. In the case of social care, there are much fewer publications, although it is considered an emerging research area. Most of the work done focused on home social care [
17,
18] or mobility services offered to elderly or reduced mobility population [
19,
20,
21].
The location, inventory, and routing literature is very extensive in terms of theoretical work and applications to several industries. However, we are not aware of any application to AT organizations or similar NGOs. In terms of location, the main difference between AT environments or private companies lies on the objectives of the decision-makers. In AT services, decision-makers are more focused on ensuring access and equity, or cost minimization, instead of maximizing profits. Despite the growing literature on public sector facility location planning, to the best of our knowledge, there is no research related to facility location in AT organizations. Some of the trends topics in public facility locations are emergency/disaster management [
22,
23] and healthcare facility location [
24]. However, there are also other topics as location of electric vehicle charging stations, bike sharing systems design, or waste disposal, as pointed in the survey on the location of service facilities in urban areas [
25].
In inventory management, the demand [
26] and supply [
27] uncertainty has been widely investigated in the literature, and several models have been proposed to help solve inventory problems in practice [
28]. In fact, there are a number of applications for inventory management under (demand and supply) uncertainty in many different fields. Demand uncertainty has been considered, for instance, in the forest industry [
29], aircraft parts management [
30], or the storage of platelets in hospitals [
31], while uncertainty in supply has been in the blood transshipment [
32,
33] field. Nevertheless, a deeper look at the literature shows that there are no papers devoted to inventory planning and management in the context of AT services. Given the particular characteristics regarding product flows found in AT services, there is a need for adapting current inventory models to their specific operations.
Finally, regarding routing decisions, there is an extensive literature about the different versions of these problems and their applications to the industry, as shown by the number of recent surveys in this topic [
34,
35,
36,
37]. However, to the best of our knowledge, there is not any application in the context of AT organizations. Some fields that present similarities with the AT routing problems are health [
13,
38] and humanitarian logistics [
39,
40,
41], where budget constraints are relevant, although the social welfare and benefits are the priority. There are some tools that are being proposed recently to cover routing issues in the context COVID-19 and vaccine distribution in low income countries, such as the one detailed in Reference [
42]. Authors also use Excel to create the tool, although the features of the problem are different from needs of the BM.
From the above, we can observe that the present work contributes to the knowledge by applying optimization models and algorithm to solve logistics problems in AT organizations, and can be easily extended to similar NGOs. The proposed methodology and tools adapt optimization models and methods well-known and extensive applied to several industries to the AT organization, considering particularities and specific aspect of these organizations.
3. Assistive Technology Operations
BM is a service provided by the Barcelona City Council that offers customized equipment loans and other resources to people with reduced mobility, which include a large percentage of older adults [
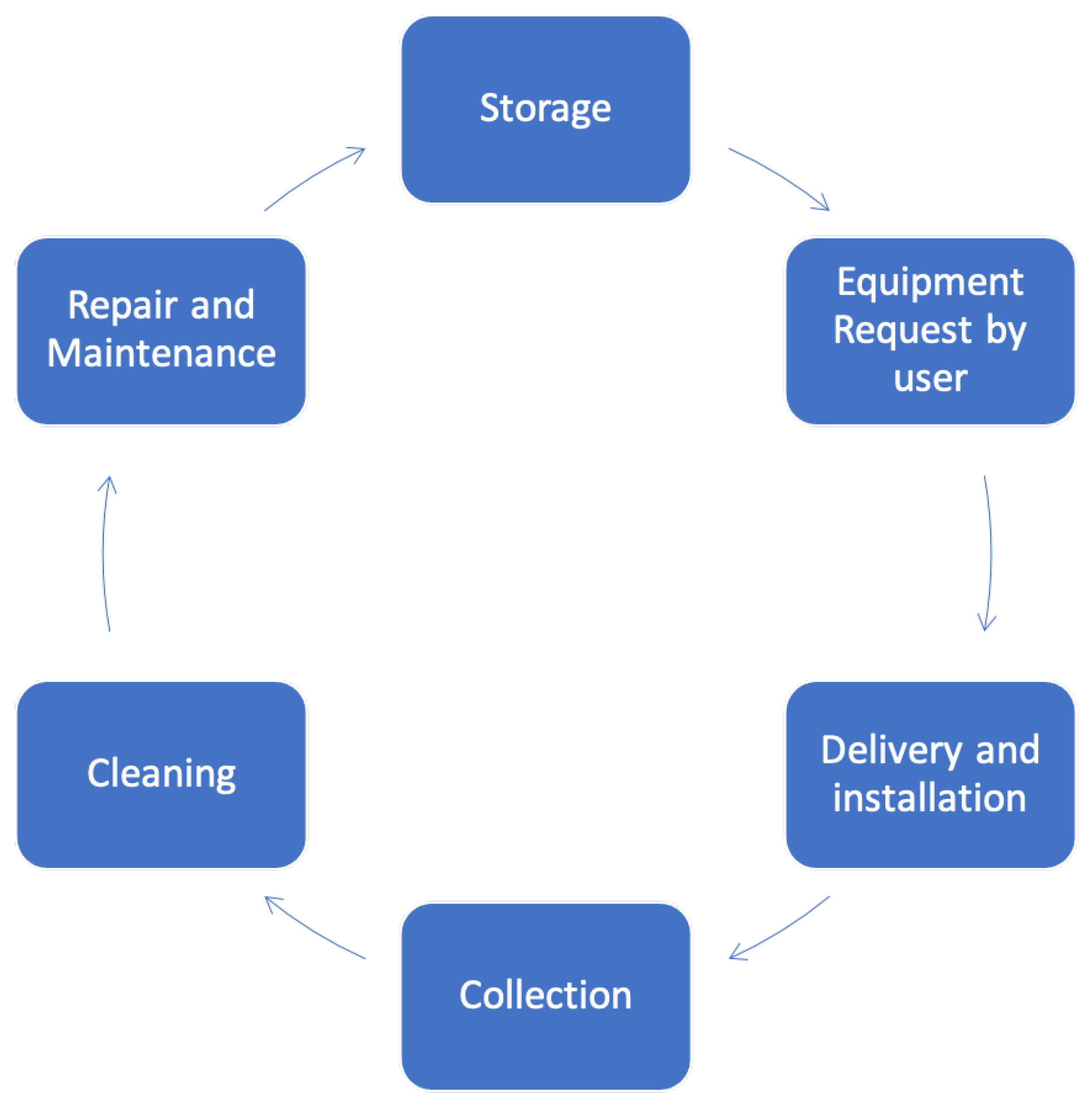
43]. This institution provides free medical and mobility equipment on a long-term loan basis to people with all types of disabilities, ages and income in the city of Barcelona. The AT equipment provided by BM includes equipment for adults and children as crutches, walkers, manual and electric wheelchairs, scooters, lifts, hospital beds, bathroom equipment, etc. Most of the material comes from donations, but it can also include newly purchased items. All incoming materials are revised, cleaned, labeled, and stored with the help of volunteer technicians and specialists. The main goal of the BM is to provide AT items to the population with limited temporally or permanently mobility conditions so that they have a more independent live, enabling this population to have an equal participation in all of life’s activities. BM bases its service in Circular Economy principles and their system can be resumed in
Figure 2.
Currently, BM has two facilities that work both as warehouse (a small and large warehouse) and pick-up/drop-off point. Currently, they are open to the public for 2.5 h per day on alternative days. The users can come to these facilities to collect or deliver material, or they can request a home delivery or pick-up service offered by the BM. The collecting and delivery service is usually requested for large equipment, such as, for example, hospital beds. If necessary, they also offer training on the use of the equipment (e.g., cranes). This also takes place in the facilities when a person goes to the BM to pick up the equipment. Thus, the BM has the following main activities:
Collection or delivery of equipment by users in their facilities.
Home delivery of loaned equipment.
Home pick-up of returned or donated equipment.
Inventory management of the equipment.
Repair of the equipment at their facilities.
Training in the use of the equipment.
The last two services are performed by technical personnel that can be volunteers to the program. The four first points are undertaken by the managers, who make decisions on planing the level of inventory needed and the design of the routes to deliver and collect the equipment.
Lately, the demand of AT equipment has been growing significantly in the city of Barcelona. To respond to this growth, the organization is considering is considering the possibilities of opening new facilities working as both, warehouse and pick-up/drop-off point, or to re-structure the whole supply chain.
To help the decision-making process of the BM’ managers, we focus on three main operational problems in the AT programs: the location of warehouses and customer service points, the inventory management of the different types of equipment, and the optimization of the pick-up and delivery routes. In the next subsections, we will describe the operational problems in each of these areas in more detail. In
Section 4,
Section 5 and
Section 6, we present the proposed solutions to improve and optimize the operations of the BM so they are able to provide a better service.
3.1. Location
The management of logistic systems has become crucial for the efficient organization of any public institution, industrial companies or service delivery business. In that sense, and due to the inter-relationships between logistics decisions, the location of facilities is a critical aspect to be considered in any organization. Operational decisions, although dependent on the nature of the company, are generally secondary to facility location decisions, as in the case of materials management, production planning, inventory management, or vehicle routing. Furthermore, unlike other logistics decisions that can be fluently re-optimized and adapted to changes in the future conditions, location decisions are likely to hold for several years or decades due to their great impact, complexity of implementation, and generally high costs (facilities are expensive to construct and difficult to modify). Hence, location decisions are usually consider as strategic decisions involving a long term financial impact. A proper facility location decision leads to a greater degree of efficiency and competitive advantage, by reducing costs, saving operational time, and optimizing the use of resources and processes. In its turn, such savings imply a positive impact on the quality of the customer services, brand image, and corporate reputation.
Location decisions consist of determining the physical facility network design that is most advantageous for the entity in order to achieve its strategic planning goals. These decisions imply resolving the structure of the network and determining the physical characteristics of the facilities. Some of the essential decisions in the location field are: deciding the type and number of facilities (e.g., warehouses, terminals, distributions centers, customer services points), defining the degree of hierarchy between facilities, identifying the type of services offered in each of them, and deciding the specific physical location of each facility. Decisions vary according to the nature of the business strategy and depend on the particular constraints and objectives considered. For more detail on the topic, we refer to References [
44,
45].
3.2. Inventory
The management of the inventory in any organization can make a great impact on the customer and user satisfaction and on the cost of the operations, and this is also true in the AT organizations. One of the major challenges for AT organizations is about monitoring and predicting the entry and exit of products from their warehouses in order to estimate appropriate target inventory levels to avoid stock-outs and waiting lists.
For an AT organization, managing the flow of products is not straightforward. A major hurdle is that there are several uncertain variables that need to be considered when modeling the expected output of products. Unlike most profit-seeking organizations, products are not consumed or bought at a certain rate, which is then used as a basis to plan orders and replace inventory levels accordingly. First, the amount and location of requests for AT products are highly uncertain. It is not uncommon to go several days without a single request for a given product, and suddenly experiencing several units of that same product being requested on the same day. Second, the time at which a certain product will break down and become unusable, usually ending up being discarded, is unknown. Third, the returns of products are unpredictable. Although a loan is initially set-up with an agreed return date, most products have their return date eventually extended, or the product may break down and become unusable at the end of the loan period. All these variables need to be taken into account when calculating the expected product output to set inventory target levels accordingly.
Another characteristic of AT services is the diversity in supply. Since these are usually non-profit organizations relying mostly on donations and giveaways, products cannot simply be purchased to meet target inventory levels as seen in common enterprises. Due to the fact that there are strict budget limitations, product supply mostly comes from donations from nearby hospitals, other governmental organizations, or individual donors. Moreover, the majority of the picking-up, setting-up, and labeling of the “new” products are done manually by volunteers with restricted time availability. Therefore, the lead time, defined as time between the moment a certain product is deemed as “needed” (and, therefore, a certain action for replacement is taken) and the time it arrives to the warehouse can vary substantially between different product types depending on the action taken. For instance, while crutches and walkers may be relatively easy to obtain from supply sources or easily acquired due to their easy transportation and low price, larger products, such as beds, cranes, or electric wheelchairs, may be more difficult to obtain to re-fill inventories.
3.3. Routing
One of the most relevant decisions for a supply company is related to the transportation of products. Usually, this part of the activity involves a high cost, since vehicles are required for the transport, either purchased or rented, and should comply with requirements specific to the products that are to be transported.
Much of the daily cost associated with the vehicles corresponds to maintenance and fuel. The latter depends, to a large extent, on the distances traveled to serve customers. Therefore, a proper routing is fundamental. Currently, BM rents vehicles to carry out the movements of equipment, paying a fixed amount per vehicle and a variable amount which depends on the distance traveled. They usually rent the same kind of vehicle, since the use of a lifting platform is essential when managing the BM’s equipment (such as beds, cranes, or large wheelchairs). The size of the smallest vehicle with a lifting platform is usually enough to ensure the proper transportation within their size routes.
There are four types of routes that can be considered in the BM: delivery route, pick-up route, mixed delivery and pick-up route, and backhauling route. In a delivery route, the vehicle only makes equipment deliveries to users who have requested a loan. In a pick-up route, the vehicle only makes pick-ups belonging to both returned and donated equipment. In a mixed delivery and pick-up route, deliveries and pick-ups may occur in any order. Finally, a backhauling route is a special case built on the premise that all deliveries must be served before pick-ups can begin. The motivation behind this last kind of route comes from the COVID-19 pandemic, that has forced a proper equipment cleaning and disinfection. Once some equipment has been cleaned and disinfected they should not be mixed with other equipment that have not undergone this process. Accordingly, a suitable route should consider the delivery of cleaned equipment first, and pick-ups of other material later. Otherwise, an extra visit to a warehouse for disinfection of the vehicle is required, impairing the efficient execution of the route. Any of these routes should be planned to serve as many users as possible at a minimum cost.
Many commercial software packages are available to solve VRPs [
46,
47,
48,
49]. However, if managers of a company decide to use any of these tools, they need to integrate them with the existing software infrastructure, which is not trivial. Additionally, the staff in charge of planning would need to learn how to use it. On the other hand, there are some optimization tools in the literature that overcome the problems about the familiarity with the user interface using Excel. One of the most famous optimizations tools based on Excel was proposed in Reference [
50]. The authors use a heuristic optimization algorithm, which allows to obtain efficient solutions in a short computation time. Nevertheless, these commercial software packages and optimization tools do not fit the needs and peculiarities of an AT organization. For example, the possibility of creating backhauling routes, obtaining open routes that can start at one warehouse and finish in a customer (and vice versa), and making decisions about the specific group of customers that must served in a specific week. In this work, we provide these routing functionalities for AT managers via a user-friendly Excel-based tool.
Next, we present and describe in detail the mathematical models, solving methods and results for each of the tools developed: Location, Inventory, and Routing.
4. Location Module
The recent increase in the volume of activity carried out by the BM, together with its nature of a public service based on an acceptable proximity to their users, raises the need to increase the number of facilities open to the public. To respond to this need, the organization contemplates the opening of new facilities in the city. However, finding a spacious location in the city center, close to citizens, can be very expensive. For this reason, the organization also considers the alternative of restructuring the entire supply chain by establishing a two-echelon network, where a main warehouse on the outskirts provides customer access points. Concentrating the volume of equipment in a suburban facility has multiple advantages. Broadly, rental costs in the peripheral area of the city are lower, reducing the associated rental costs or allowing larger installations to be available for a lower price. This makes it possible to reduce the number and/or of the inner city facilities, which can be converted exclusively into customer service points without storage (or with minimal storage) to pick-up or drop-off the equipment. In turn, this eases the storage of material since more space is available, especially for those equipment that, due to their features, may require more space available (e.g., beds or lifting cranes).
The purpose of the location module in this research is to provide decision-makers with a tool that allows them to evaluate and compare different alternatives in terms of their growing network of facilities. Because the BM is a municipal service, they can benefit from municipal facilities with very competitive costs. The location module also intends to be useful to study possible re-locations of the current facilities, helping to identify possible location changes with a clear added value. Therefore, if there is a new municipal facility available, the module can be used to determine whether moving to this facility favors the service and, if so, which of the current facilities should be closed.
In this section, we describe in detail the definition and guidelines of the Excel-based tool developed to support location decisions in the BM context. Our optimization tool includes two types of location options: one-level or two-level network. We describe how these problem types are modeled and made available through a user interface using a real-world example from the BM.
4.1. Location Models and Methods
Identifying where to open a given number of facilities from a list of candidates, in a way that minimizes the sum of the fixed facility cost and the cost of supplying the customer demand, is the goal of the
p-median location problem. This can be formally defined as follows: Let
I denote the set of potential facilities with an associated fixed cost
. Let
J be the set of users to be supplied with an associated demand
. For each pairwise
and
, we denote by
as the unit cost in terms of distance traveled for serving user
j from a potential facility
i. The parameter
p refers to the number of locations to be chosen. In the case of BM, the set of facilities is composed of the list of identified possible buildings or areas where a warehouse or an access points can be open. Due to the uncertainty on the demand, in the BM framework, the set of users usually considers districts or small region within the planning area where the demand is aggregated and set as the target population. Hence, the demand can be asses as the number of older adults or the level of required service in a given district or region. The demand and its geographic distribution play a key role in the location model, making its collection process important. In that sense, accessible past data is a valuable source, but can be influenced by the current location of the facilities and it is desirable to also consider demographic demand studies, such as References [
51,
52]
For each
, let
be a binary variable indicating whether the potential location
i is chosen. For each
and
, let
be a binary variable equal to 1 if customer
j is assigned to a potential facility
i. The classical integer linear programming formulation for the
p-median problem is presented below.
subject to
The objective Function (
1) refers to the sum of the cost of supplying the customer demand and the fixed facility cost, with the aim of minimizing the total cost. Assignment Constraints (
2) specify that each customer
j should be assigned to exactly one potential facility. Constraints (3) guarantee that if a potential facility
i is not open, customer
j cannot be assigned to it. Constraints (4) ensure that exactly
p facilities are chosen. Finally, Constraints (5) and (6) define the domain of the variables.
When considering a multiple echelon in the supply chain, the problem can be modeled as a double p-median, where to open a given number of facilities in each level, and to allocate users to the 2-level facilities and these to 1-level facilities. The aim is to minimize the sum of the fixed facility cost and of the cost of supplying the customer demand through the 2-level network.
Let K and I denote the set of potential facilities in each level, respectively, with an associated fixed cost . Let J remain the set of users with a demand . For each triplet , , and , we denote by the unit cost of supplying demand to user j from 1-level facility k, through 2-level facility i. We now differentiate between parameters and to refer to the number of locations to be chosen in each level.
Similarly, for each
, we let
be a binary variable indicating whether the potential location
k is chosen, and for each triplet
,
, and
,
is a binary variable equal to 1 if customer
j is assigned to first-level facility
k through facility
i.
subject to
The objective Function (
7) is the sum of the cost of supplying the customer demand through the 2-level network and the fixed facility cost. Assignment Constraints (
8) specify that each customer
j should be assigned to exactly one pair of 1-level and 2- level facilities. Constraints (9) and (10) guarantee that customer
j can only be assigned to a pair of open facilities. Constraints (11) and (12) ensure exactly
and
facilities are chosen on first and second level, respectively. Finally, Constraints (13) and (14) define the domain of the variables.
A natural extension of the p-median problem within the framework of the BM is to differentiate between services and/or products. This can be easily handled by the previous models, but distinguishing the demand that each user has for each service and ensuring the user is assigned to a facility that offers all services or to as many facilities as needed to be covered for all services.
4.2. User Interface
We have developed a location decision support tool that consists of an Excel-based user interface, where network parameters and data regarding potential locations, demand and cost are specified in order to provide the best locations to open for maximal user comfort. To ensure the ease-of-use feature, we have divided the decision process into several sequenced steps.
Figure 3 depicts the ribbon tab of the Location module, where the steps are sorted and classified according to whether they belong to the input (Data) or the output (Solution).
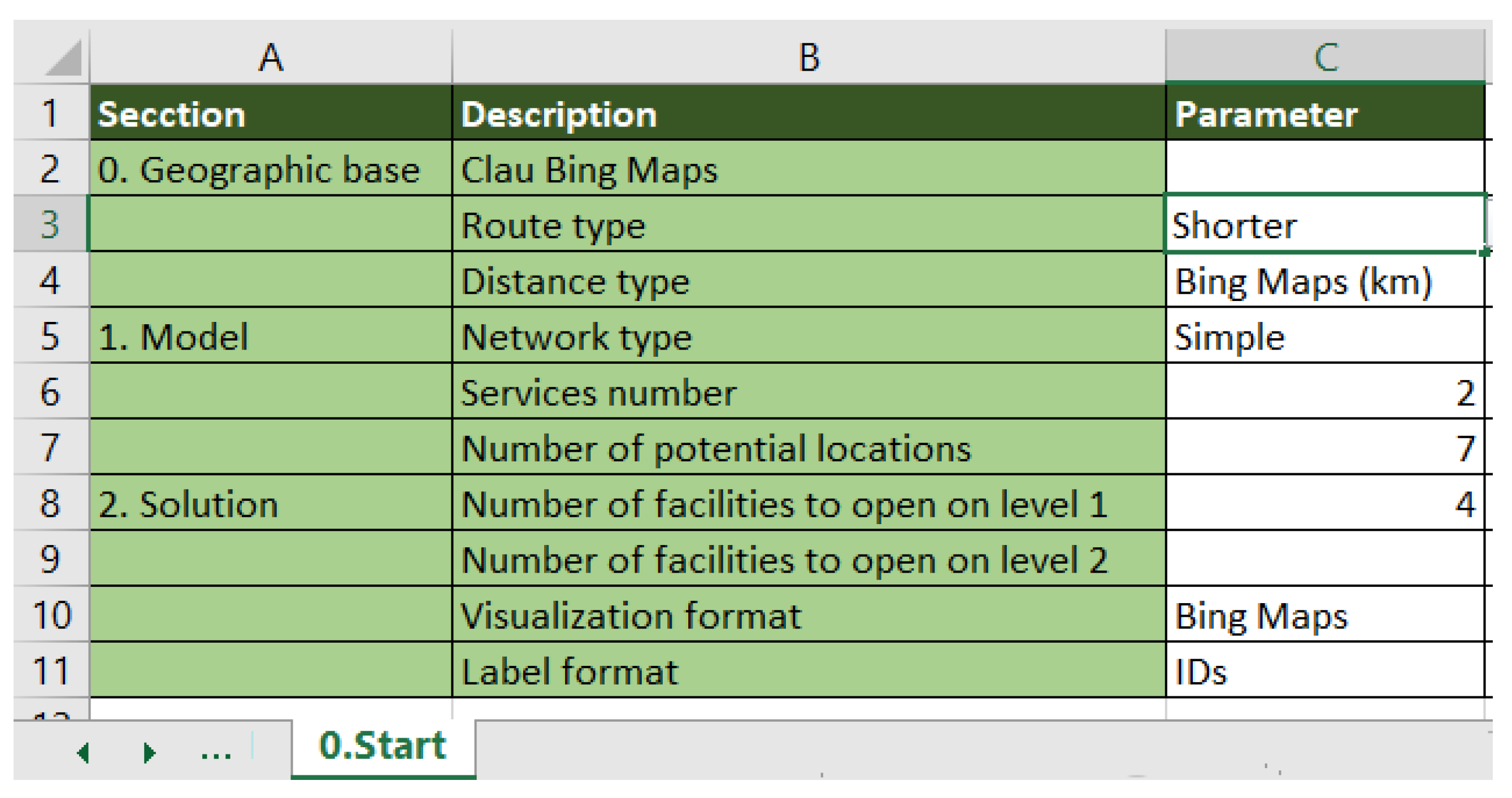
Before starting, step zero generates a new spreadsheet to collect basic parameters that will be key for the subsequent steps. In particular, the initial spreadsheet contains geographic parameters needed for distance computation, network parameters that together with the output parameters determine its configuration and visualization parameters (see
Figure 4). Note that, in each worksheet, the white color identify cells where data must be introduced by the decision-maker, while light green color is used to identify system cells with description or automatic computations.
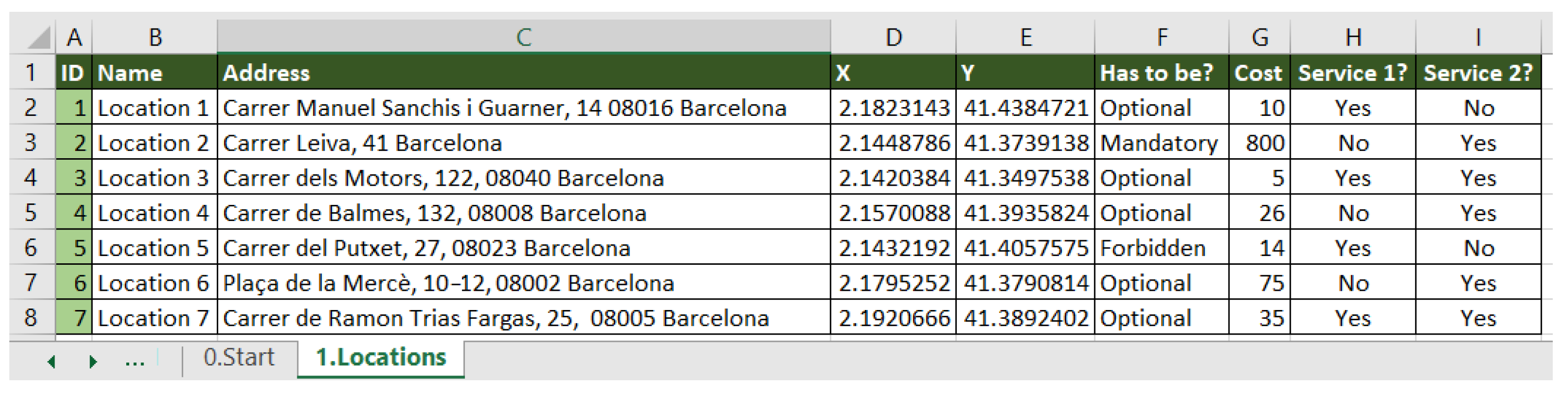
The first step originates the potential location spreadsheet (see
Figure 5) which gathers the name, address, coordinates, whether a location must obligatorily be open or not, the cost, and whether a location provides a specific service or not. Coordinates may be introduced by the user or calculated from a web GIS server. The option of choosing if a potential location has to be compulsorily open or forbidden is helpful to study potential facility re-locations.
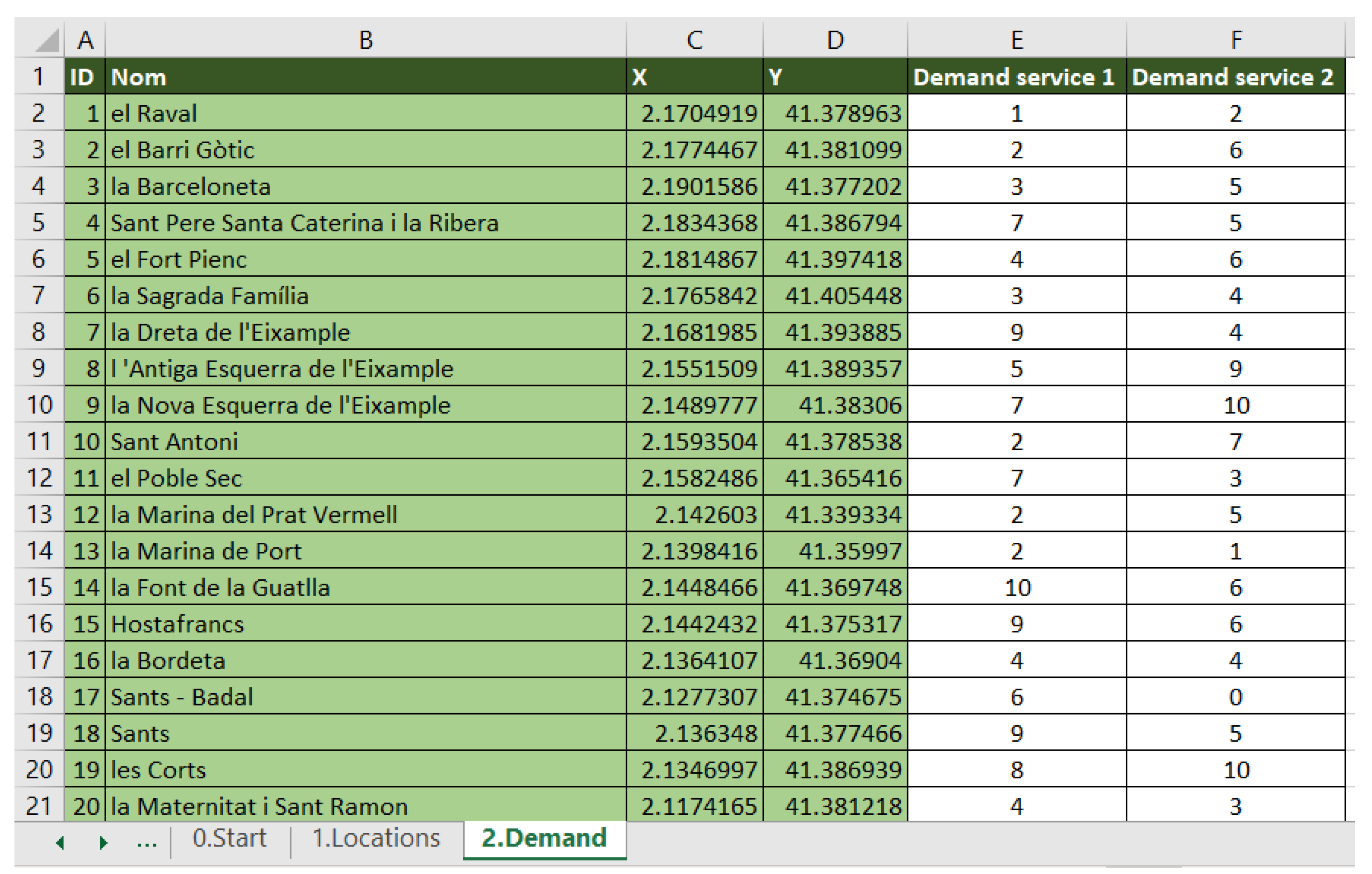
The second step captures the users’ demand for each service (see
Figure 6). For location purposes, BM considers their users demand on an aggregated level at the neighborhood centroid.
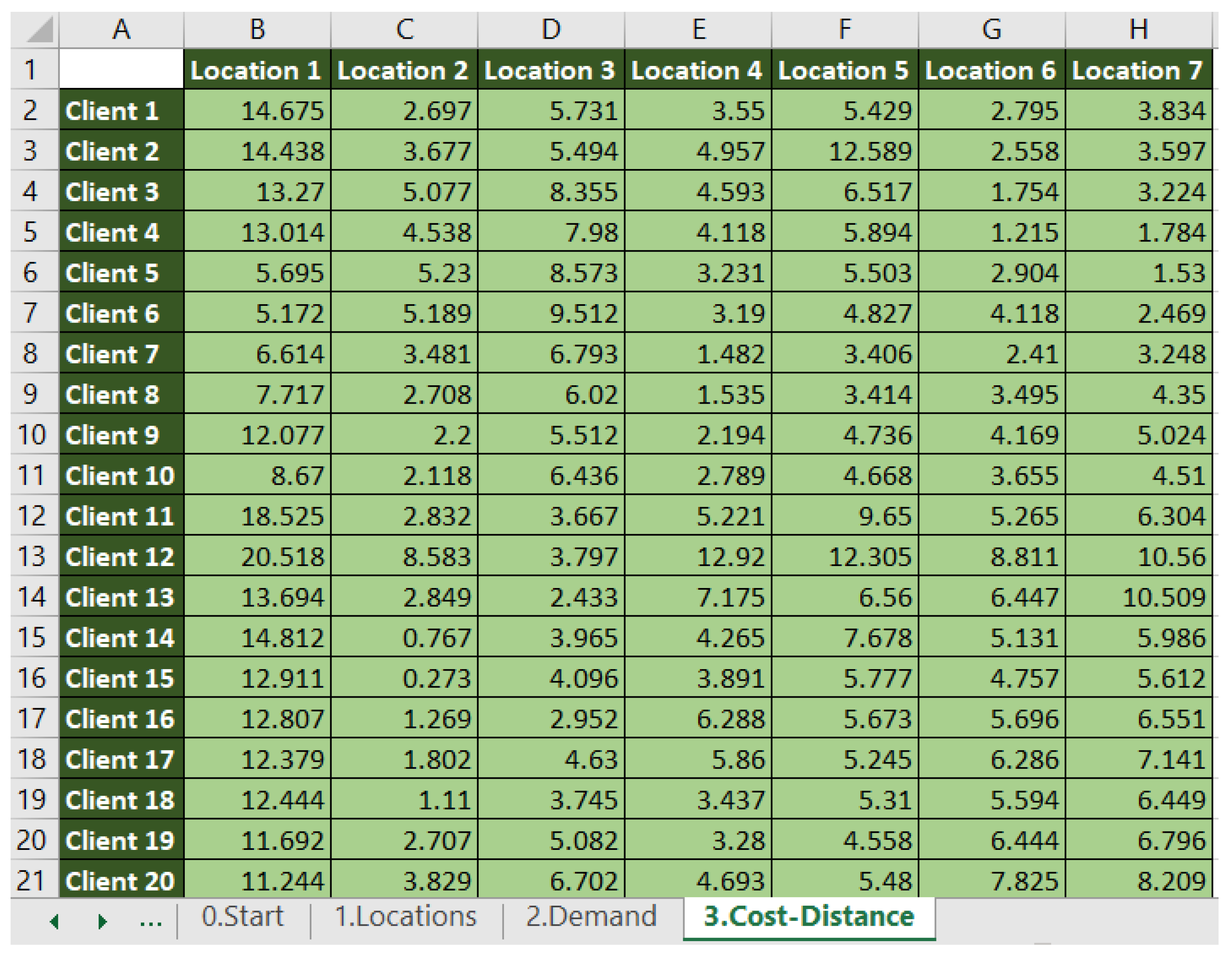
Step three computes the cost distances between users and potential locations according to the fixed parameters (see
Figure 7).
Once all data is gathered, step four solves the problem to optimality by using the the Open Solver add-in. The solution obtained can be visualized in step five.
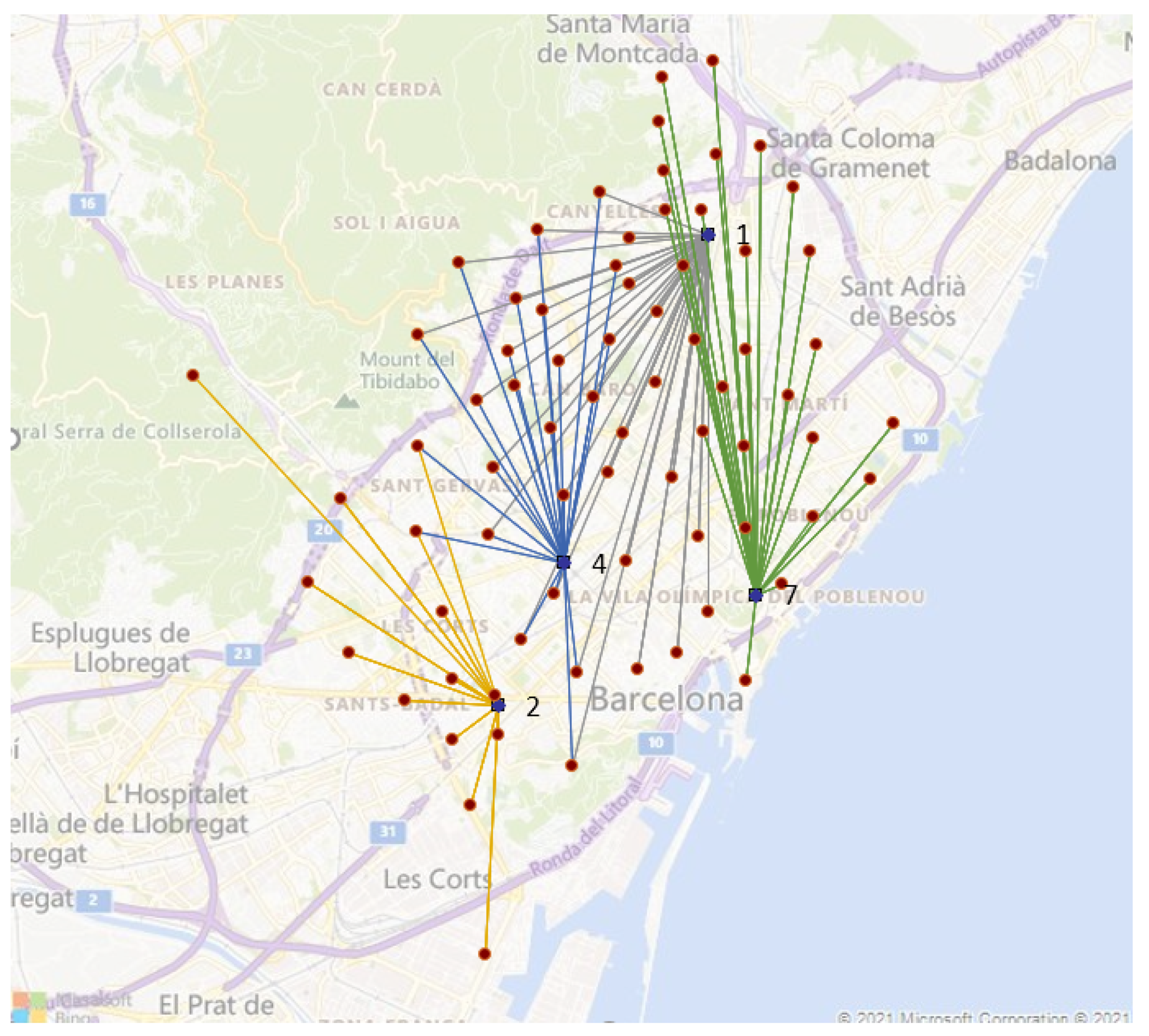
Figure 8 shows a visualization example for a
p-median problem with two services, where the the number of facilities to be potentially open is
.
5. Inventory Module
In this section, we describe the framework developed to support the BM, and other similar organizations, in managing their inventory levels more efficiently. In our tool, we propose a way of calculating the lower and upper bounds of a range of inventory levels that are deemed as adequate considering the dynamics of both the supply and demand of an AT organization. The target inventory range is bounded by a minimum stock level, inspired by the reorder point model commonly used in continuous inventory review models, and a maximum recommended stock level calculated based on periodic review modeling [
28]. In this section, we explain these models and an ABC categorization in detail, and present the contents of the inventory management tool developed for the BM case that can be easily adapted for use by similar organizations.
For ease of reference, we provide
Table 2 containing a brief description of all the variables considered in this section.
5.1. Inventory Methods
5.1.1. Minimum Recommended Stock Level (Reorder Point)
The minimum recommended stock level is calculated based on the Re-Order Point (ROP) model with uncertain demand (and known lead-time). This level is recommended when inventory is monitored continuously, i.e., every single item entry or exit is updated on the inventory dashboard. Demand follows a normal distribution with known mean and standard deviation (
), and the lead time (
l), defined as the time between taking an inventory replenishing action and the arrival of the products, is variable amongst different product families. For the BM case, orders to refill inventory can include, for instance, the acquisition of new products (subject to budget limitations), or the planning of a pick-up trip for collecting products at standing donors or at users waiting to return their products. In both cases, order sizes are limited. With this model, when inventory is reduced to a level below the pre-defined target ROP, an order of size
Q must be placed to replenish provisions. This trigger can be launched whenever a product is loaned, which happens during volunteers working hours. The order quantity
Q, which should be equal to or larger than the difference between ROP and the current stock level, arrives at a time offset by the lead time
l. For each product, the minimum recommended stock level is calculated as follows:
with the first component
corresponding to the expected (average) demand during the lead time. Due to the variability inherent to the movement of products in which spikes in demand may occur, a second component
, referred to as Safety Stock (SS), is added:
This additional stock provision reduces the probability of hitting a stock-out during the lead time period for a certain pre-defined service level
z considering the variability of the demand (
). The value of
z is obtained from the normal distribution function as a factor of the number of the standard deviations that the safety stock must cover (for instance, for a service level of 99.73%, additional inventory levels must cover three times the standard deviation; thus,
). In the context of the operations of an AT organization, such as the BM, demand (
d) cannot merely include the number of products being borrowed by users, but it must also include the products being returned, as well those which are eventually discarded. Therefore, we define demand
in a certain period
t, as the summation of loaned products (
) and discarded products (
), discounted by the product returns (
), as stated in Equation (
17). All of the variables defining demand are variable and outside the control of the BM; thus, they are included altogether when calculating demand over a certain time frame
t.
5.1.2. Maximum Recommended Stock Level
Monitoring inventory continuously according to the ROP model presents some disadvantages worth considering from a BM’s viewpoint. First, every product type needs to be replenished separately as its ROP level is achieved, which means that orders for product types are made at different times, potentially missing on joint buying or transportation deals. This may also be a hurdle when BMs’ actions to reestablish inventory are mostly about raising campaigns or collecting products at donors. Besides, ROP control requires constant monitoring of the inventory levels which, depending on the specific BM workflow and infrastructure(s), may be hard to execute, especially in the case of multiple locations operating simultaneously with the help of volunteer workers. A more realistic alternative is, in those cases, to use the Periodic Review (PR) model to define a higher target inventory level. In this model, the inventory level of each product type is revised at a certain interval (
T), and actions to reestablish inventory can be taken for many items simultaneously. The order quantity
Q, in this case, is equal to the difference between the theoretical maximum stock level
and the current level of inventory (
I) for that product, i.e.,
. The maximum recommended stock level, using this model, reduces the probability of a stock-out for the period until the next revision plus the lead time for a certain service level, as follows:
where
corresponds to the standard deviation during
, and
is computed as
. Similar to the ROP model,
z is defined as a multiplier of the standard deviation to provide a certain service level; thus, the SS is given by
. With the proposed tool, decision-makers can observe the effect of different
T values on the required levels of inventory to decide upon the best
T value that fits their needs and resource availability. The shorter the interval between inventory reviews (
T), the lower levels of inventory are needed to cover demand during the period
. However, a shorter
T increases the number of orders, collections, or campaigns that potentially need to be planned, substantially increasing the associated costs. A longer
T, on the other hand, saves the burden of having to acquire “new” products, often while reducing inventory review costs, at the expense of requiring an increased number of existences available for loans, i.e., higher storage and maintenance costs. Thus, in our view, AT organizations should aim at the highest
T value possible within the storage capacity of their warehouses to save inventory replenishing costs (assuming that maintenance costs are low, which is the case for the BM). Although this target often results in slightly more inventory levels, the aforementioned benefits of joint inventory management may offset these costs given that storage space is not an issue.
Table 3 shows the data obtained from 868 daily demand points over the period between 3 July 2018 and 16 November 2020 for the BM operations in Barcelona. The service level, for the purpose of these calculations, was defined at 99.9% (
). Note that although the average daily demand, in the case of the BM, is rather low, the high variability (standard deviation) associated with the movement of products on a daily basis requires a certain safety stock that leads to the need of having higher levels of inventory to avoid stock-outs. If inventory levels are aimed at the lower bound (ROP) level, then inventory must be monitored continuously and new re-fill initiatives must be undertaken when the stock level has gone below the recommended threshold. In case inventory levels are at or above the upper bound
, then a periodic inventory review will most likely suffice.
5.1.3. ABC Classification
Inventory monitoring policies and targets can vary between product families based on their particular characteristics. A way to categorize products in relative terms of importance is the ABC classification. This process can help an organization find the most critical families in terms of their products’ input and output dynamics, and use different inventory management strategies accordingly. For product types where the outflow is several-fold higher than the number of donations, a constant inventory monitoring policy may be more adequate to avoid stock-outs. On the other hand, for products that are easy to obtain and move, revising inventory at a certain frequency (e.g., once every month or every trimester) may suffice, saving inventory monitoring and review costs. Selecting inventory policies on a product basis instead of a single, global policy, may help AT organizations achieve their service level goals with overall lower inventory and transportation costs. For instance, since beds, mobile cranes and large wheelchairs are difficult to obtain when compared to the number of times they are requested, an ROP model with a constant inventory monitoring policy may be more adequate. On the other hand, since crutches or bathroom chairs usually run on a surplus and do not require too much storage space, a periodic review model may suffice, saving inventory monitoring and review costs. Hypothetically,
C products may be made available at multiple locations with higher stock availability and lower inventory review frequency, while products
A can be made available at a single, central warehouse with their inventory levels being constantly monitored. The main point is that product categories can be subject to different inventory strategies and stock levels. In this work, we categorize products based on their relative importance (
R) using the ratio between loans (
L) and donations (
D), i.e.,
, according to
Table 4. The ratio
R of each family of products is normalized using the minimum (1.4) and maximum (7.0) ration values within the range of products, as follows
. Moreover, we use the following ranges to define categories in this hypothetical example:
Results for the loan-donation ratio analysis showed that large products, such as beds and large wheelchairs, which are more difficult to acquire, store, and transport, should have a tighter control of inventory and greater focus on replenishing options, while smaller products, such as crutches and walkers, can be managed with a looser inventory policy as they can be easily obtained and stored, if needed.
5.2. User Interface
In order to make the proposed inventory management system available for AT organizations in a user-friendly manner, we have developed an Excel-based user interface spreadsheet in which parameters and data can be handled and visualized with little effort. In the proposed tool (see
Figure 9), products are categorized in families, which are identified by a code number and description (e.g., 0-Beds). The purpose of the tool is to monitor inventory levels and get a visual warning when the inventory level of some product type falls below the minimum recommended threshold. The recommended range of inventory level is defined by a reorder point (lower bound), and a maximum stock level (upper bound), as described above. Likewise, an ABC classification is used to assess the relative importance between product families to help on a certain inventory target that minimizes the possibility of a stock-out. The user can also define the relevant parameters used in the back-end calculations, such as a global desired service level (90.0–99.9%), and the lead time and time between inventory reviews for each product type.
The top row contains information about the total number of products available and the current date, as well as the service level, defined as the expected probability of not hitting a stock-out for each family of products. The main table of the dashboard is composed by the following components:
Status—Current stock level status. There are two possible statuses:
- −
OK—The stock level is equal to or above the minimum recommended level.
- −
REPLACE—The stock level has fallen below the minimum recommended level and must be restored.
Family—Code of the family of products.
Product—Description of the type of product belonging to each family.
Current stock level—Current level of inventory. This field should be updated every time there is an exit/entry of a product, or by the time a periodic inventory review is performed.
Lead time—Time, in days, between the moment a replace order is made and the arrival of the product to the warehouse.
Time between reviews—(Average) time, in days, between two consecutive inventory reviews.
Reorder Point—Stock level below which there is an increased risk of not fulfilling demand for the corresponding product type, which triggers the “REPLACE” warning.
Maximum stock level—Maximum stock level above which there is no added value in storing more products in terms of the risk of missing demand.
Relative importance—Normalized relative importance of each product in relation to the others based on the loan-donation ratio.
ABC classification—Classification of the family based on their relative importance.
Note that products classified in the C category are assigned a longer time between reviews than products of class B or A, since they tend to have lower loan-to-donation ratio and, therefore, more products available. We can also observe that products with a greater dimension and weight are generally more scarce and have greater lead times; thus, a more frequent control of inventory is recommended, especially those belonging to class A.
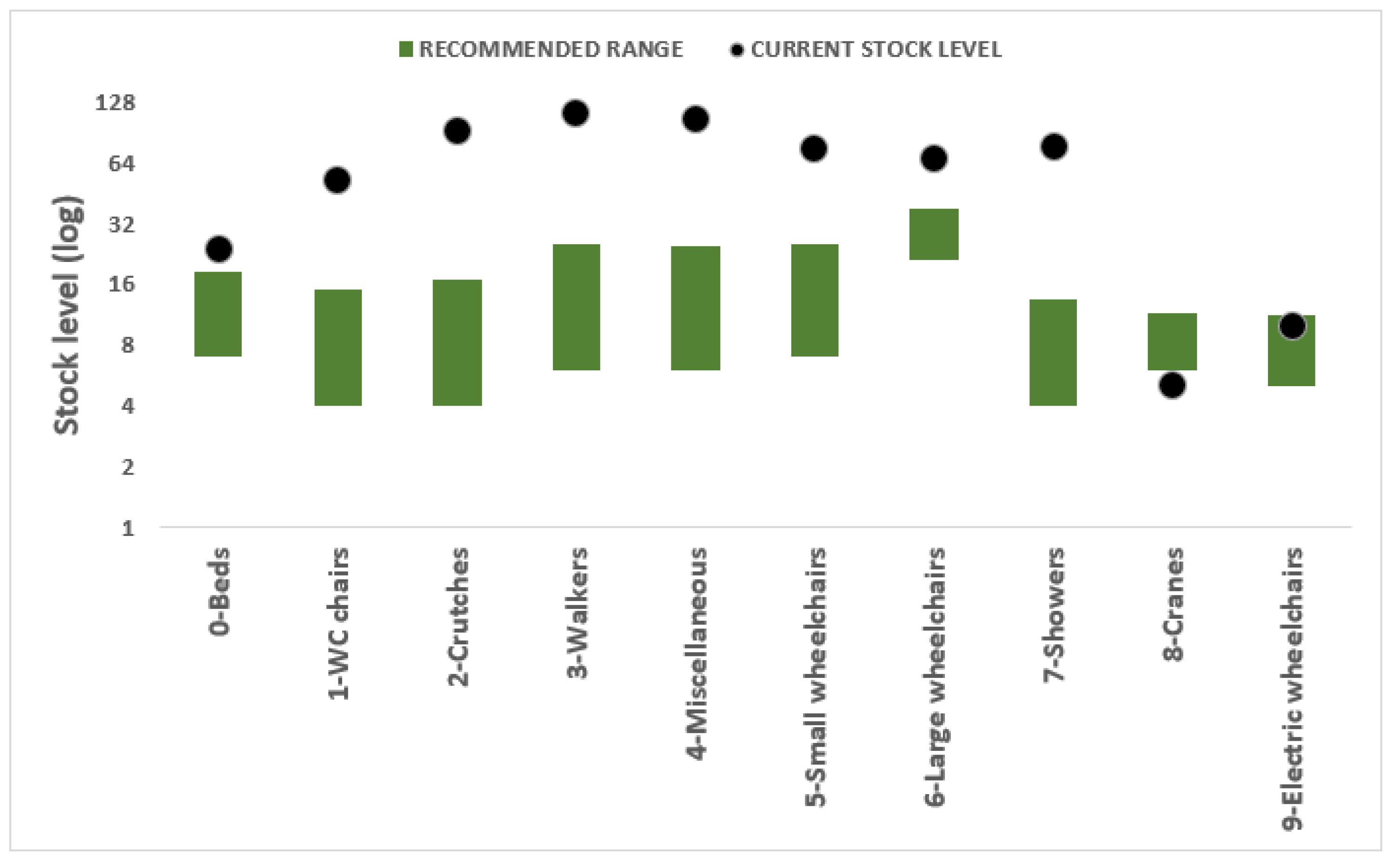
Figure 10, which is shown and automatically updated in our spreadsheet, allows the user to visualize the recommended range (in green) for the stock level of each product family, and compare it with the current stock level (black dots) at the time of this study (16 November 2020). As we can observe, the BM was provided with a large surplus of inventory for most product types, especially the smaller products; thus, the logarithmic scale is used on the y-axis. On the other hand, larger products, such as cranes, large wheelchairs, beds, and electric wheelchairs, seem to be the most critical in terms of availability. In fact, the figure revels a risk of not having enough cranes in stock to fulfill demand levels, effectively pointing out the need of acquiring or collecting cranes that are expected to be requested. The tool allows AT organizations to experiment with several values of service level, lead time, and time between reviews for each single product, allowing to visually analyze how far the current inventory levels would be from the recommended range in each scenario. The black dots move up and down along with the changes in inventory levels, while the green ranges are widened or thickened along with the changes in (previous) demand, and the manual definition of the lead time, time between reviews, and the service level.
6. Routing Module
Due to the kind of actions developed by the BM and their characteristics, the way that routes are designed to deliver (loaned equipment) and pick-up (returned and donated equipment) plays an important role in this organization. Since they open 2.5 h per day and the material must be collected from and carried to one of the warehouses considering this time frame, routes should be planned carefully to serve as many customers as possible. Additionally, customers change every day, making transportation points the most dynamic part of the system.
In this section, we detail the definition and guidelines of the Excel-based tool developed to support routing decisions in the BM context. First, the problem modeling is described, and last the user interface is explained with the help of an example.
6.1. Routing Models and Methods
Depending on the type of route to consider, the problem can be modeled as a different optimization problem. Nevertheless, all of them are variants of the Vehicle Routing Problem (VRP), which has been deeply studied in the literature [
34,
53,
54].
If delivery routes and pick-up routes are developed independently, both kinds of routes can be planned separately and modeled as two multi-depot VRPs. This VRP variant is defined by a directed graph , where is the vertex set and the edge set. The vertex set V is partitioned into two subsets and representing, respectively, the set of n places to visit and the set of m warehouses.
Sets:
: set of vertex;
: set of warehouses;
: set of customers;
: edge set;
K: set of homogeneous vehicles;
Q: capacity of each vehicle.
Parameters:
: demand of customer which is associated to warehouse ;
: 1 if customer has demand associated to warehouse ;
: distance between i and j, ;
: time (minutes) to travel from i to j, ;
p: penalty for not serving a customer;
c: cost by km.
Decision variables:
: binary variable representing the routing solution. 1, if customer is visited immediately after customer , by vehicle ; 0, otherwise;
: a binary variable assigning vehicles to customers. 1, if customer is visited by vehicle ; 0, otherwise;
: total demand of nodes on the route until node (including node i), by vehicle .
The objective Function (
19) focuses on minimizing the total cost. Additionally, considering that it is important to serve as many costumers as possible, a penalty is incurred to each not-served customer, increasing the total cost. Constraints (20) state that every customer is served exactly once. Constraints (21) and (22) are flow constraints, so that if a vehicle visit a customer or warehouse then it must leave it. Constraints (23) guarantee that every vehicle visit only one warehouse. Constraints (24) ensure that the route demand do not exceed the vehicle capacity. Constraints (25)–(27) state that a route only contains customers with demands associated with the same warehouse. Constraints (
28) guarantee that each route duration (including travel and service times) does not exceed a preset limit. The maximum time the BM hires a vehicle per day is four hours and a half due to budget limitations. Constraints (29) and (30) are Miller–Tucker–Zemlin (MTZ) [
55] formulation of subtours elimination. Variables’ domains are given at Constraints (31) and (32).
Notice that delivery routes start at a warehouse and end at the last customer in that route. Conversely, pick-up routes start at the first customer and end at a warehouse. Therefore, distances from customers to warehouses are considered zero for delivery routes, while distances from warehouses to customers are zero for the pick-up routes.
When mixed delivery and pick-up routes are possible, they are planned using the same model instead of two independent models. Then, it is necessary to specify the kind of demand (delivery or pick-up) associated to each customer. For this reason, the original parameter has been replaced by:
Additionally, decision variables
are not necessary, and two new decision variables are required to model this problem variant [
56]:
: the amount of delivery equipment on board on edge , vehicle ;
: the amount of pick-up equipment on board on edge , vehicle .
Finally, Constraints (
28) must be modified such that the right-hand side is not 270 but 150, since routes start and end at one warehouse and they open 2.5 h during the day. Besides, the following constraints replace Constraints (24), (29), (30), and (31):
Constraints (
33) and (34) are the flow conservation and subtour elimination constraints. Constraints (35) guarantee that the total load does not exceed the vehicle capacity during the route. Constraints (36) and (37) ensure that vehicles start with zero pick-up load and finish with zero delivery load. The new variables’ domains are given at Constraints (38). It is worth noting that distances from and to warehouses are not necessary zero when mixed delivery and pick-up routes are allowed. If it is deemed necessary to serve deliveries before pick-ups (backhauling model) then an extra parameter is required indicating the number of delivery customers:
Delivery customers must be at the beginning of set
C, and the following constraints must be included to avoid any other order of deliveries and pick-ups:
Depending on the size of the problem to solve, these models may require too much computation time to obtain a solution. In order to provide a tool that can be used in useful time, these models can be simplified if decisions about vehicles-warehouses assignments are made before. We distribute the total number of vehicles proportionally to the number of customers with demand associated to each warehouse, and solve the problem associated to each warehouse independently. Thus, parameter and Constraints (25)–(27) can be omitted, reducing the complexity of the problem.
6.2. User Interface
We have developed an additional Excel-based user interface to specify parameters and data about home deliveries, home pick-ups and donations, and to obtain the corresponding routes to be carried out during a one week planning horizon. The sequence of steps required to this end is described next.
Once the routing package for AT organizations is enabled, a new Excel tag appears, and a set of options are available clicking on it. These options are shown in
Figure 11. Additionally, an initial worksheet similar to
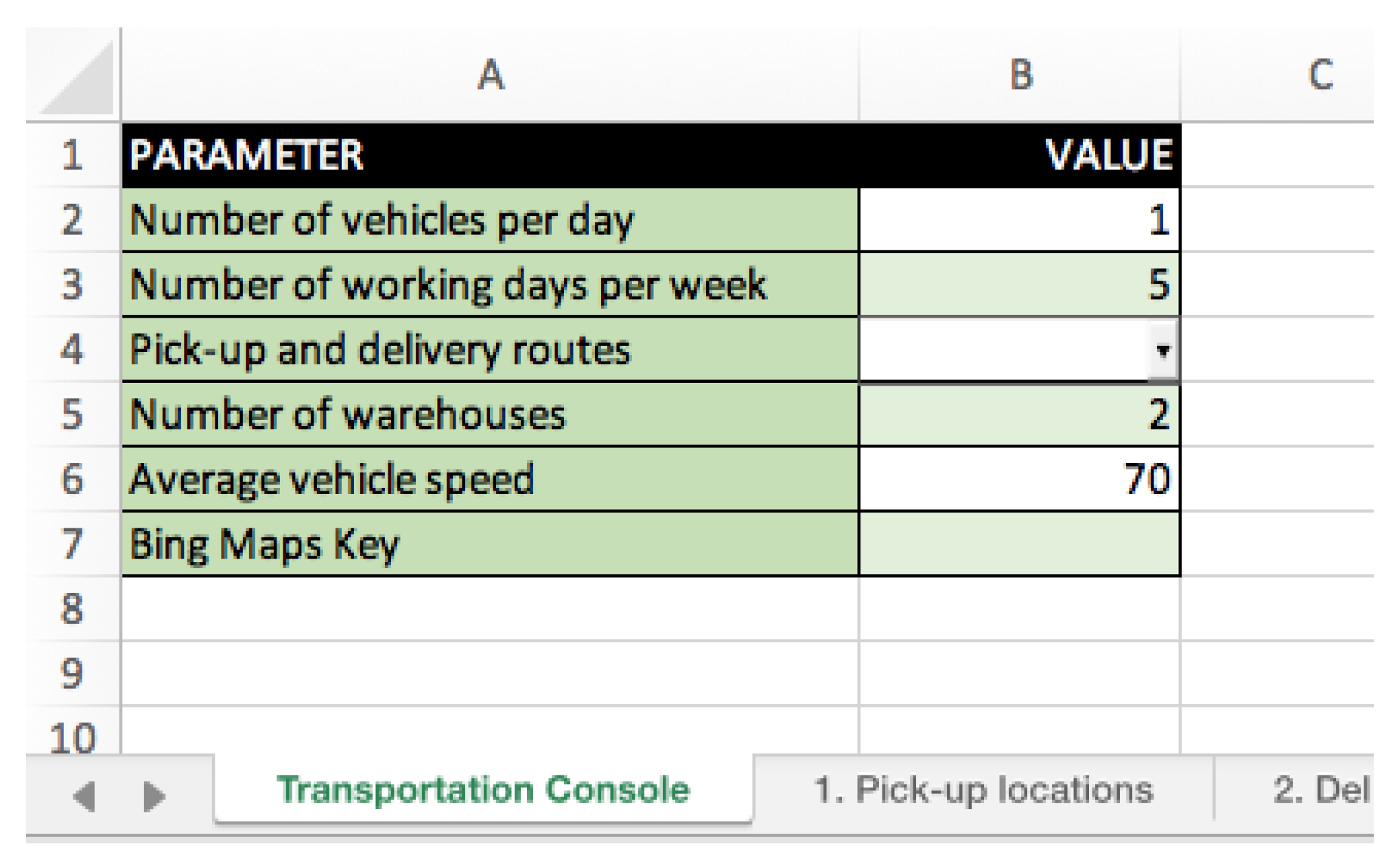
Figure 12 emerges to specify the routing parameters, such as the number of vehicles available per day, the number of working days per week, the kind of routes required (separated pick-ups and deliveries, mixed pick-ups and deliveries, backhauling routes), the number of warehouses, the average vehicle speed, and the Bing Maps add-in key.
Regarding the routing options in
Figure 11, the first option allows to reset the content of the workbook. By clicking on the second and third buttons, two new worksheets appear (
Figure 13 and
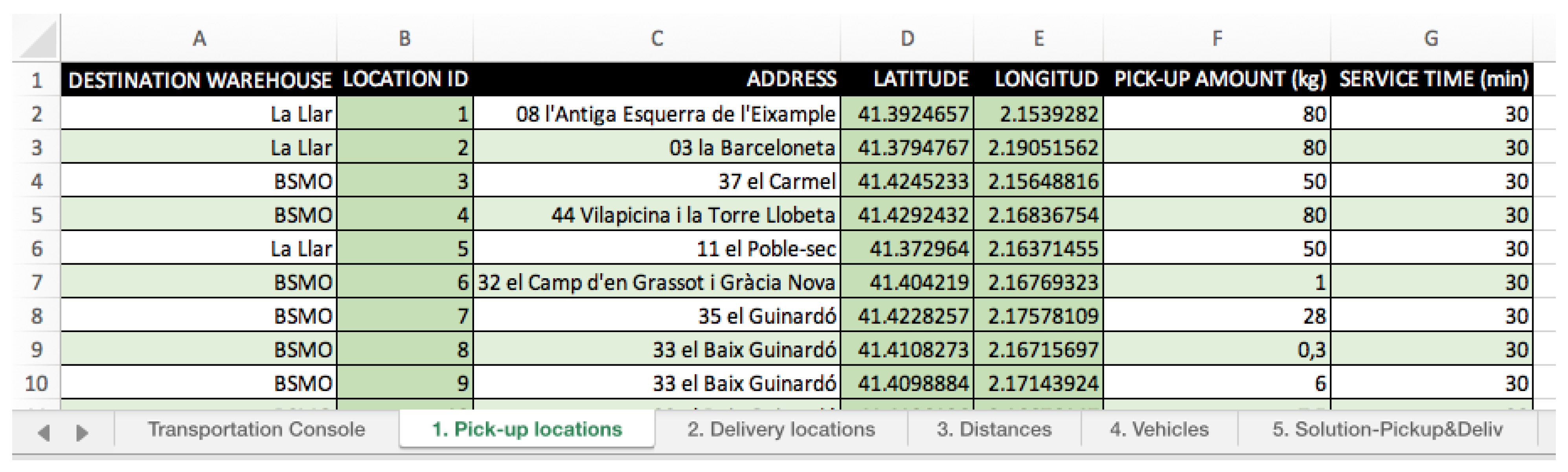
Figure 14) to introduce details about the pick-up locations corresponding to customers returning equipment or making donations, and delivery locations corresponding to customers requiring some equipment. These details include the origin or destination warehouse, address, amount to pick-up or deliver and service times. Location identifiers, and latitude and longitude coordinates, are assigned automatically.
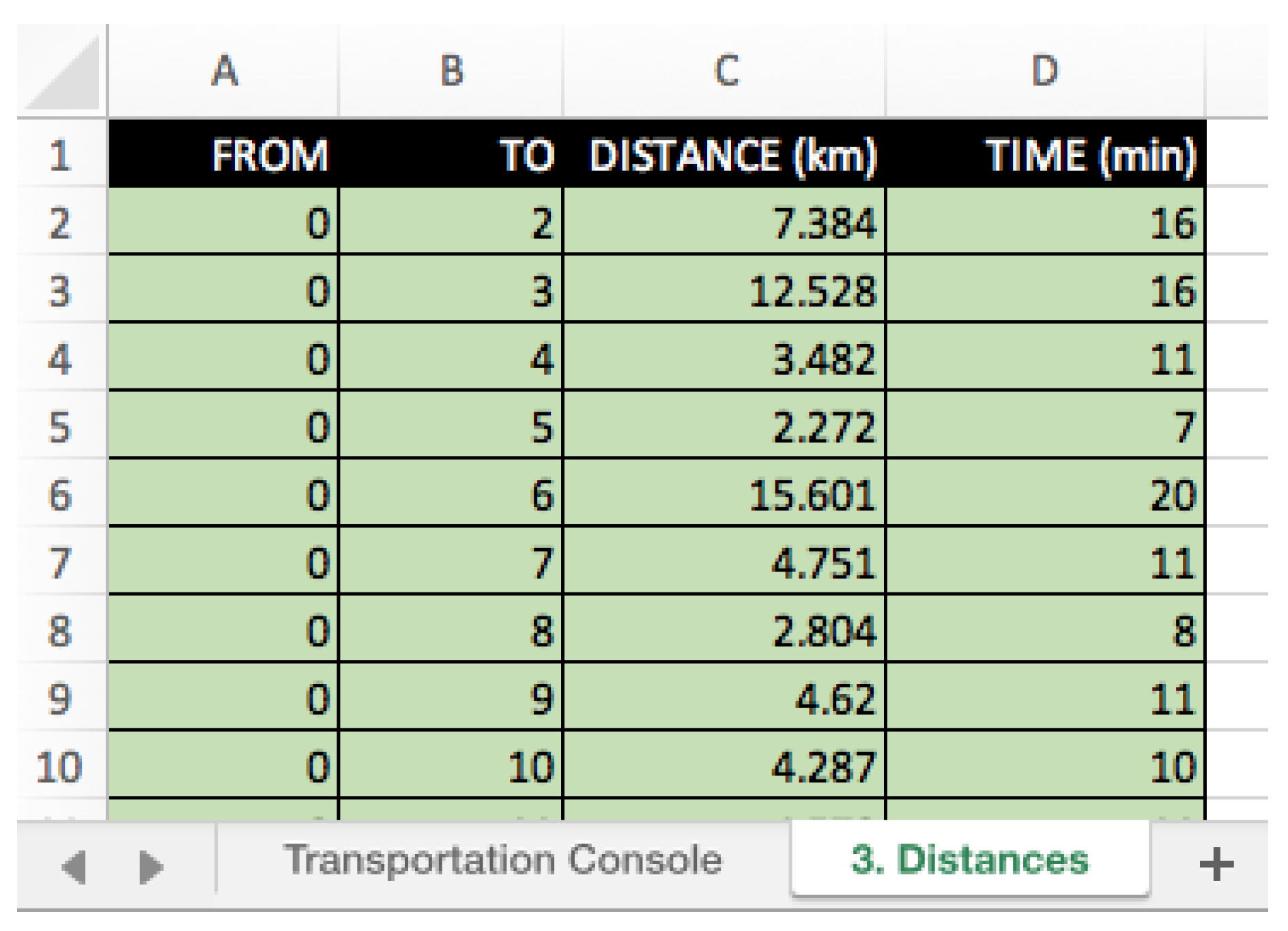
The fourth option (“3. Distances”) allows to create a new worksheet (
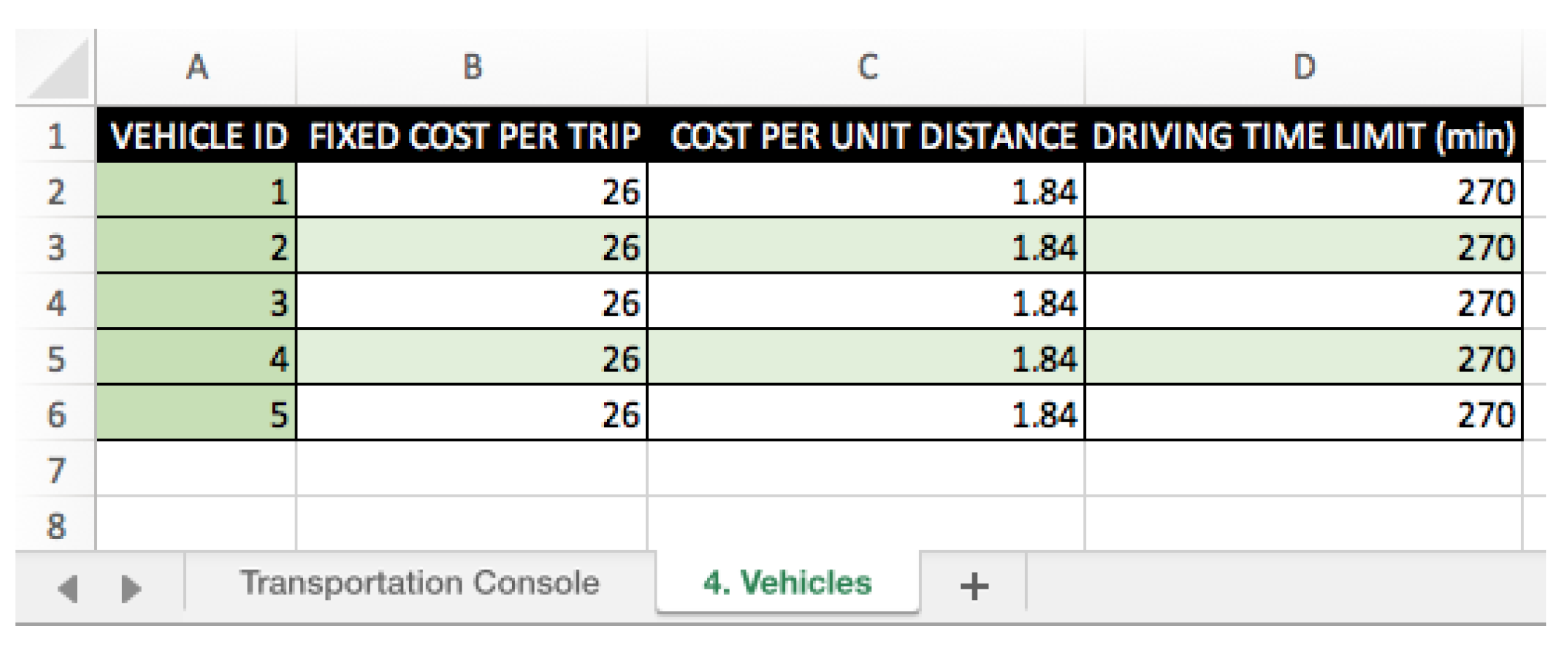
Figure 15) where distances and times between each pair of locations can be automatically calculated. The fifth button (“4. Vehicles”) creates a new worksheet to include details about vehicles (
Figure 16), such as the fixed cost per trip, the cost per unit distance, and driving time limit. Vehicles identifiers are assigned automatically.
The “5. Solution” option enables a working sheet with tables that include information about the solution when the problem is solved. Each table corresponds to one route to be carried out by one vehicle. As shown in
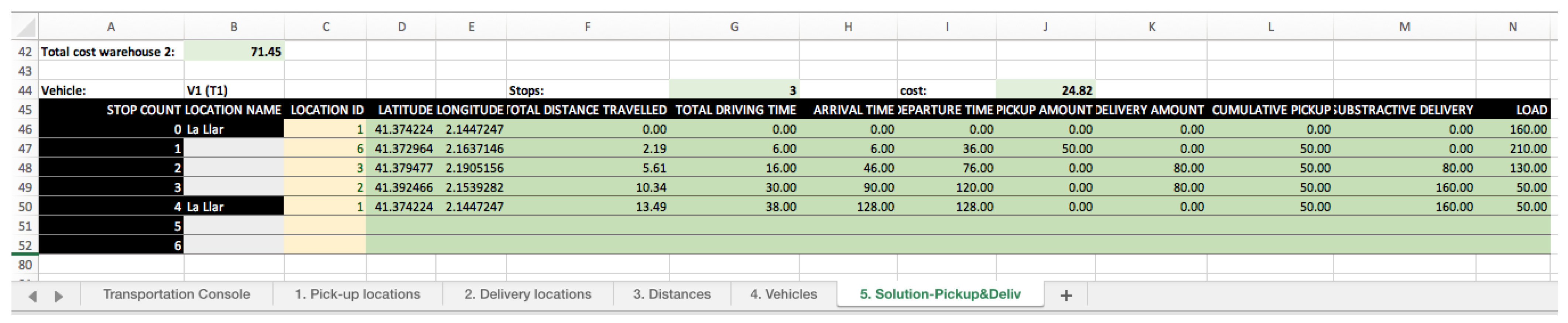
Figure 17, information presented in each table includes the number of stops required, the cost associated to that route, and several details about each stop: the total distance traveled, the total driving time, the arrival time, the departure time, the pick-up amount, the delivery amount, the cumulative pick-up, the subtractive delivery, and the vehicle load after that stop.
Routes starting or ending in a warehouse are shown in tables placed in the same row in this worksheet. If there is more than one warehouse, tables corresponding to other warehouses will be placed below. Additionally, the total cost associated to each warehouse is shown in this same spreadsheet.
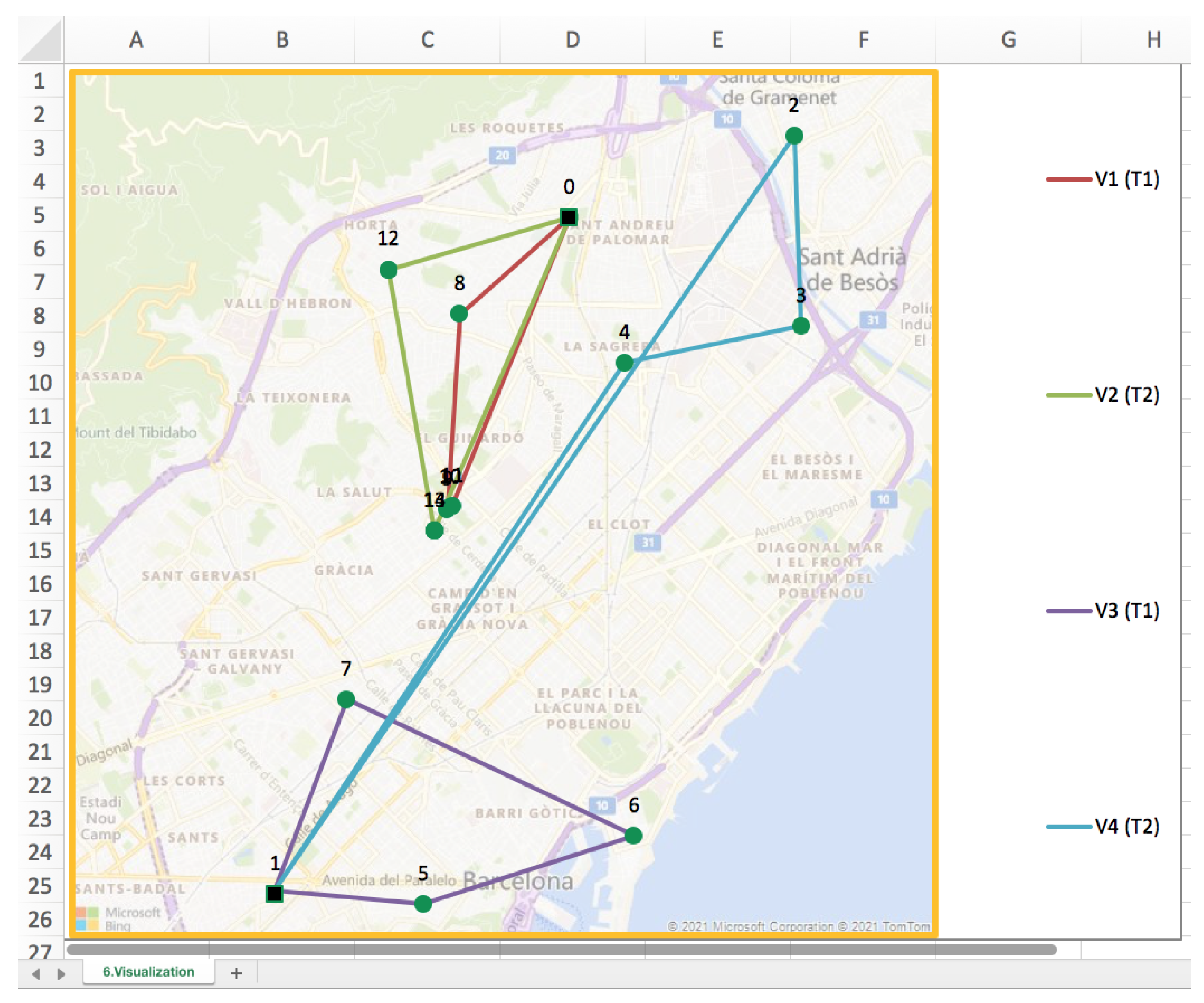
The next button (“6. Visualization”) allows to create a new tag which is going to contain the visual representation of the routes in a map, as shown in
Figure 18. Finally, the last option (“7. Solver”) solves the problem to obtain the content of the solution worksheet together with a visual representation. In this regard, the OpenSolver add-in is required to solve the “back-end” models. Depending on the dimension of the problem, the solution search process could take several seconds or minutes.
Notice that a dark green color is used in each worksheet to highlight the information that is automatically set and, thus, does not need action from the user.
7. Discussion
AT programs are growing in many countries, and, due their particular characteristics, budget limitations, and usage of the equipment, AT organizations are adopting a Circular Economy model. In this research, we provide several tools to help the AT services’ managers improve and optimize their operations, consequently allowing them to provide a better service to the users and increase the number of people with access to this equipment. We focus on three main logistic problems for this type of organizations: the location of warehouses and customer service points, inventory management of the different types of equipment, and the optimization of the pick-up and delivery routes.
Regarding location, we have developed a tool for AT organizations that allows them to analyze and evaluate their growing logistical system. A well defined network of warehouses and customer service points will reduce the logistics cost and improve the efficiency of transport flows contributing to the harmonious development of the economy, environment, and society. Furthermore, the location of the facilities plays a key role in the quality of the service. A comprehensive coverage of the service area implies an increase of access to AT equipment that will not only improve the quality of life of people living with disability but will also provide benefits in terms of health, social inclusion and lower socio-economic burden.
The management of inventory by AT organizations also introduces several challenges, such as the high variability in product flows, the (budget and transport) limitations regarding the supply of products, and the diversity in the specific characteristics of each family of products. An efficient way of planning inventory is by leveraging existing data regarding product flows to calculate a range of values in which the inventory level of each product type must fall. By estimating a lead time and a time between reviews depending on a product’s characteristics and ease of access, AT organizations can use ROP and/or PR models to define target inventory levels that ensure a desired service level while complying with their operational and financial restrictions. The inventory management tool that we have developed facilitates the monitoring of inventory levels and provides a visual representation of the current inventory levels in comparison with the target ranges.
The routing optimization tool allows the decision-maker to plan the collection and delivery routes of the equipment from several warehouses. The main benefits of this tool are related to saving time during the planning operation; it can provide economic savings by producing an optimized route, and, at the same time, it increases the users satisfaction by helping to collect and deliver the equipment in a more efficient way and able to reach more users in short time. The system incorporates a variety of Vehicle Routing Problem version: delivery routes, pick-up routes, mixed delivery, and backhauling routes; therefore, it can be used and extended to other AT organizations with similar logistic systems. The tool also allows to incorporate last minute collection points if needed since it only takes a few minutes to re-plan the routes. Another main advantage, in comparison with other routing tools, is that it allows making decisions about users that should be served in further time periods (weeks) if it is impossible to fulfill all the requests for the desired week.
Overall, the developed tools can help AT managers make strategical decisions as the location of new facilities, and operational decisions, such as routing and inventory. All tools are based on data analysis and have behind advanced mathematical models that provide evidence-based decisions. At the same time, due their simplicity and flexibility, the proposed methods allow managers to evaluate several possible scenarios for decision-making by simply playing with input parameters. The tools are developed in VBA for Excel, so the organizations do not need to make large investments in an information system infrastructure. Although joint optimization between AT departments are outside the scope of our work, by not having dependencies between modules, there is an increased flexibility for applying the proposed methodologies in practice. Thus, an AT organization may opt to apply the approaches of only one or two modules in their operations without the need for additional data or information.
The development of this research was done in straight collaboration with the AT of Barcelona City Council, Banc del Moviment, that provided all data and context of the reality of their AT program, and participated in a proof-of-context of the systems developed. They commented: “The Institut Municipal de Persones amb Discapacitat, as other local governments, are under pressure to improve public sector performance and at the same time contain expenditure growth. Sometimes public organizations cannot go too far in innovating and optimizing, but projects like this one lead to savings in operational costs that could be reinvested in the BM and lead to a higher impact on society, improve quality service and easy the access to AT to a larger population.”.
We would like to remark the challenge of developing a tool that needs to be simple enough to be used by volunteers and other personnel of these types of organizations but, at the same time, provide efficient and state-of-the art solutions based on mathematical models and algorithms of the Operations Research area to help to make quality decisions. These tools are available to other NGO organization on request to the authors. While we have focused on the BM, we strongly believe that the proposed methodologies can be used by other AT organizations as they often operate in a similar manner. According to the interviewed managers and planners from the BM, who are aware of the functioning of other AT organizations, the process often has more similarities than differences, even between different countries. Unfortunately, there is no comprehensive survey or review pointing the differences between the logistic processes of different AT organizations. Nevertheless, while we acknowledge that differences can exist, the models and tools proposed can be easily adapted to address additional constraints or objectives that other AT organizations may have.
One limitation of our approach may appear when very large logistic problems need to be solved, since mathematical models could require long time to run. Although very large problems are not common in AT organizations due to the nature of the service, one of our future research lines includes the development of heuristics and metaheuristics that will enable AT organizations to solve more complex problems in this field, as for example stochastic problems including demand and supply uncertainty for this type of equipment. Furthermore, Microsoft Excel have been chosen due to its flexibility and extended use. Actually, BM staff use this software for other purposes. Nevertheless, our approach can be extended to other similar spreadsheets that are free and open source, such as OpenOffice. The main drawback is that these open spreadsheets are not fully developed for some of our requirements. Linear Programming Models behind our proposal need a mathematical solver, and the ones proposed by the “open” community are not as evolved as those for Excel. Anyway, due to the kind of institutions that provide AT, this is one of our future works.