An Improved Residential Electricity Load Forecasting Using a Machine-Learning-Based Feature Selection Approach and a Proposed Integration Strategy

Abstract

Load forecasting (LF) has become the main concern in decentralized power generation systems with the smart grid revolution in the 21st century. As an intriguing research topic, it facilitates generation systems by providing essential information for load scheduling, demand-side integration, and energy market pricing and reducing cost. An intelligent LF model of residential loads using a novel machine learning (ML)-based approach, achieved by assembling an integration strategy model in a smart grid context, is proposed. The proposed model improves the LF by optimizing the mean absolute percentage error (MAPE). The time-series-based autoregression schemes were carried out to collect historical data and set the objective functions of the proposed model. An algorithm consisting of seven different autoregression models was also developed and validated through a feedforward adaptive-network-based fuzzy inference system (ANFIS) model, based on the ML approach. Moreover, a binary genetic algorithm (BGA) was deployed for the best feature selection, and the best fitness score of the features was obtained with principal component analysis (PCA). A unique decision integration strategy is presented that led to a remarkably improved transformation in reducing MAPE. The model was tested using a one-year Pakistan Residential Electricity Consumption (PRECON) dataset, and the attained results verify that the proposed model obtained the best feature selection and achieved very promising values of MAPE of 1.70%, 1.77%, 1.80%, and 1.67% for summer, fall, winter, and spring seasons, respectively. The overall improvement percentage is 17%, which represents a substantial increase for small-scale decentralized generation units.

1. Introduction

The growing global need for electricity has given rise to a smart solution termed a smart grid. A smart grid system is an intelligent system that can sense and control loads to avoid power outages and is flexible enough to incorporate other energy resources and loads. End users can alter their energy consumption according to their preference of time, price, and significance in various aspects. This approach also enables the customers to minimize their bills, and the grid is capable of rapid outage detection. The smart grid covers a variety of functionalities, including two-way secure communication of information between the electric suppliers and users, and provides measurements via smart meters [1,2,3,4]. Controllable power generation groups include biomass and hydropower, while wind and solar are categorized in the variable and intermittent power generation groups. Load forecasting (LF) is especially required when both groups of energy resources are integrated into the utility grid. In the conventional power management system, only the supply side is managed, while it is required to conduct demand-side management via LF and demand response management. Smart appliances assist in reducing the residential peaks by alerting consumers to shift the load to low peak periods or by shedding the load automatically [5]. Currently, LF and implementation of demand response are used to improve efficiency, ensure system reliability, and achieve the balance of load and supply. This approach is much better than conventional schemes as it offers improved response time, reduced cost, and fewer environmental hazards and runs smoothly if integrated with distributed systems [6]. It also increases energy efficiency and helps national electricity markets to grow by incorporating control and communication systems to maintain reliable power systems. However, the physical implementation of the smart grid is facing both technical and financial challenges.

Household load variation occurs at different times of the day, and careful examination is required to assure flexibility. An aggregator can be used for this examination [7,8]. The aggregator depends upon enabling technologies such as controllable loads, micro-generators, and distributed energy resources [9]. Smart meters act as a gateway between the household and the outside world. A community storage system can store excess energy while the owners of the community and their cooperatives manage the generators and batteries. The aggregator assists in signaling and scheduling demand response to maintain the balance between demand and supply [10]. Numerous hybrid approaches that integrate the expert system of load prediction with many other LF designs have been proposed. For instance, Dash [11] blended fuzzy logic and an expert method. A Korean electric power company’s convolutional neural network with a fuzzy export system was also used to forecast load [12]. Integration of a neural network and a distribution method to predict load for the Egyptian Electricity Holding Company [13] was employed to form an hourly forecasting model.

LF will become an important part of the power system soon. In addition to the smart grid, which faces the technical and financial challenges as described above, LF also needs to ensure accurate predictions with minimal MAPE. In the existing LF model, there are two types of concerns, and the model we propose is better than other models due to the following reasons:

• The first concern of existing models is that the feature selection approach is not employed for analysis as shown in Table 1. Furthermore, the mentioned methods have the problems of high computational time, complex data, repeated data, and issues with extracting relevant data from a huge quantity of data. In our proposed model (BGA-PCA), historical data of four seasons based on different inputs for 10 houses were exploited, whereas the duplicated, irrelevant, and unimportant data were removed without affecting the information. This contribution reduces the computational time and makes it less complex as compared to the other existing models that do not employ the feature selection approach.
• The second concern is that the different models existing in the literature have their drawbacks under diverse conditions as demonstrated in Table 1. Our proposed integration strategy aims to improve the success rate by using a combined strategy of time series autoregression, the ANFIS model, and the BGA-PCA model in a single collaborative method. In our model, the final decision is not made by considering all algorithms in an autonomous way; only the best model is considered, based on the historical data for MAPE calculation of each season.

We investigated that some researchers have worked on a GA-based feature selection approach for reducing the complexity and computational time. To the best of our knowledge, the proposed hybrid model of BGA-PCA for feature selection purposes has never been deployed yet in electricity LF. Further improvement in MAPE calculation is made by an integration strategy where the optimistic integration model takes maximum inputs compared with other models that have limitations (demonstrated in Table 1) of fewer inputs. It is a novel attempt to integrate a time series autoregression algorithm, ANFIS based algorithm, and BGA-PCA algorithms for optimal MAPE calculation in LF.

In this paper, data are collected from Pakistan Residential Electricity Consumption (PRECON), for the load forecasting model where 10 houses out of 42 are used for data collection [14]. A load of each building shows variation when the different loads with different seasons are attached to the system. The system proposed in this research is based on residential houses with four seasons: Summer, Fall, Winter, and Spring, whereas the data of weekdays and weekends have also been taken into account. The consumers respond to the power system with the sudden event where power consumption varied. In this regard, the proposed system is based on the four seasons as events where LF is optimized and tries to reduce the Mean Absolute Percentage Error (MAPE). The time-series approach is firstly adopted for collecting the data and optimizing LF; then, a blend of the BGA-PCA feature selection technique is proposed.

Paper contributions are accomplished well and summarized as:

• Data of 10 houses from PRECON have considered where the LF has optimized by reducing the MAPE.
• Time series and autoregression algorithms have been developed to fetch the data set and to set the objective function, while proposed equations set the base for further validation, which is verified by improved results.
• Feedforward ANFIS based on the ML approach is proposed which is better as compared to the previous one.
• BGA-PCA approach for attaining the best feature selection is evaluated for further improvement.
• MAPE calculations for the integration strategy are formulated for individual building and obtained remarkable improvement.
• Our results validate the proposed model by providing 17% in the overall system improvement compared to past work. Moreover, the most optimized value of MAPE is obtained for the four seasons.

The rest of the article is organized as follows: Section 2 summarized the latest related research work as given in Table 1. Section 3 is based on the framework where time series and autoregression algorithms are proposed in the first part. The model is further validated by machine learning (ML) in the second part. The third part is a novel feature selection model based on BGA-PCA algorithms. The fourth part validates the model by the proposed integration strategy. Section 4, Section 5 and Section 6 are the model validation, results discussion, and conclusions, respectively.

2. Related Work

The introduction of a smart grid requires a more detailed load modeling in which the behavior of individual appliances should also be considered [15]. Household electricity consumption in the US was analyzed, and it is found that air-conditioning, water and space heating comprise 66% of energy consumption [16,17]. Residential modeling of load profiles can be top-down, bottom-up, or hybrid [18]. The top-down model considers the residential load as a large energy pool in which individual household consumption is not taken into account. In a bottom-up approach, data from each appliance is taken into consideration while the hybrid model combines both the features of top-down and bottom-up [19]. It is investigated in [20] that the top-down model uses past measures and does not take future changes in load; therefore, it is suitable for finding the supply side requirements. Load modeling is done by taking aggregated data from the meters of residential, commercial, and industrial users [21]. Responses of the customers and grid reliability are the key factors to achieve advantages of a smart grid, which results in spurring the effective decision by the supply providers and end-users. Users can effectively utilize and save electricity with the use of demand-side management [22].

To forecast energy consumption data, several methods have been proposed such as engineering methods, statistical methods, and artificial intelligence (AI). AI applications permeate our lives and become a dominant force in both fundamental approaches and technological advancement by being used in large-scale machine learning, deep learning, reinforcement learning, robotics, computer vision, natural language processing, collaborative systems, crowdsourcing and human computation, algorithmic game theory, computational social choice, internet of things (IoT), and neuromorphic computing [23]. Many researchers are working on AI applications such as ANN, SVM, evolutionary programming, expert system, fuzzy logic, and LF-related problems. In this regard, many hybrid AI models have been developed to LF include neural networks, fuzzy expert systems, fuzzy neural networks, neural expert systems, neural-genetic algorithm, and fuzzy expert, etc. On the other hand, the primary attention has been made to ANN undoubtedly as the LF application of ANN was published in the 1980s, and, eventually, the applications started growing steadily [24]. AI is a part of many techniques through Artificial Neural Networks (ANN) and Support Vector Machine (SVM) [25,26]. The other two methods, including engineering and statistical approaches, are also applied and used, although they have deficiencies such as complexity, accuracy, and non-flexibility [27]. ANNs have also gained popularity for their simplicity and heftiness. Mainly, it focuses on the backpropagation method, while it is a slow learning process and there is no exact rule for over and underfitting [28]. Fuzzy logic is applied to collect historical load data updating the current load by necessary compensation. Later, self-organizing feature mapping (SOFM) is applied to load profiling. The memory of ANN forecasts variables such as holidays, day type, and weather [29].

A hybrid model can distribute the electrical load into two parts where the first is a scaled curve load having five ANNs and the second is a day maxima and minima having both the fuzzy logic and ANNs for LF. The benefit of the proposed hybrid structure was to use both fuzzy logic and ANNs for uncertainty handling [30]. In [31], a hybrid approach is proposed for daily LF using Neural Fuzzy Network (NFN) and an improved Genetic Algorithm (GA). The GA has been used to compute the optimal policy of fuzzy rules, and fuzzy logic here has been used to deal with variable linguistic information in LF. This approach has reduced the common problems of convergence in maxima and minima methods to initial values. An expert system known as LoFy was developed for short time load forecasting (STLF), and it has three models including daily, weekly and special days for forecasting. Moreover, it was concluded that no technique can be evaluated for all types of days [32]. Another AI technique multilayer perceptron (MLP) has also been implemented for STLF. It includes a data mining methodology to construct rules for STLF. The optimal tree regression is also helpful in defining a relation between input and output variables. It is also useful for the classification of input data into clusters for pre-filtering. Hence, MLP is easy to handle because of the similarity of classified input data [33]. ANN models can also be merged with time-series models for better policy development of hourly loads for all types of days. Two parts are included in this approach. One technique is based on correlation techniques for the selection of input variables and training sets. Moreover, the second technique was used once for weekdays and once for the weekend and obtained an improved MAPE [34].

Support Vector Machines (SVM) are the most recent techniques for regression and classification problem analysis. In [35], the Statistical Learning theory approach has been used to solve the same problem. It is different from neural networks in their nonlinear mapping of data and uses simple linear functions to develop linear decision boundaries in the new space. Therefore, due to its advancements, SVMs are also implemented for short-term scheduling [36]. Its performance compared with the autoregressive methods indicates that SVM has better forecasting as it gives the result by considering past and current data points while ignoring other influential elements. The daily load demand of the month can also be computed using SVM. This idea was also encouraged by the EU-NITE network [37].

A Multi-Layer Neural Network (MLNN) model is presented in [38] for load forecasting while the computational time is very high. A model of Long Short-Term Memory (LSTM) and Recurrent Neural Network (RNN) in [39] evaluated the accuracy rate by labeling the model’s name of Gated Recurrent Units (GRU). The load is forecasted in [40] by a hybrid technique of three different schemes such as Cuckoo Search, Singular Spectrum Analysis, and SVM to increase the accuracy in forecasting. Despite the hybrid model, it cannot also reduce the computational time as well.

The models mentioned earlier forecast the load in an optimized manner but originated a problem of reducing the computational time, data storage setup, and irrelevant data. In this regard, feature selection and feature extraction techniques have been presented in recent years. The authors in [41] computed the accuracy by data preprocessing through feature selection and feature extraction while the authors removed the irrelevant data to predict accurate forecasting.

GA is a commonly used algorithm for feature selection as a hybrid model of Ant Colony Optimization (ACO), and GA for LF is presented in [42], and ANFIS is used for the best prediction. In [43], a combination of GA and support vector regression (SVR) is proposed for the LF of hotels, while GA is deployed for feature selection and SVR for the optimization of LF. Similarly, some other GA-based schemes [44] for LF of industries and health care centers are also carried out where the feature selection approach shows accuracy in the prediction of LF. The trend of integration strategy becomes more valuable due to its high accuracy rate of LF. The authors proposed an integrated strategy to forecast the power consumption and the model hybridized with GA-ANFIS for LF. Similarly, there are also the integration methods proposed for the combined decision of different schemes together and finalized the final decision [45]. The highlights of the related work are summarized in Table 1 and symbolic representations of different parameters and objective functions are presented in

Table 2. Symbolic representations.

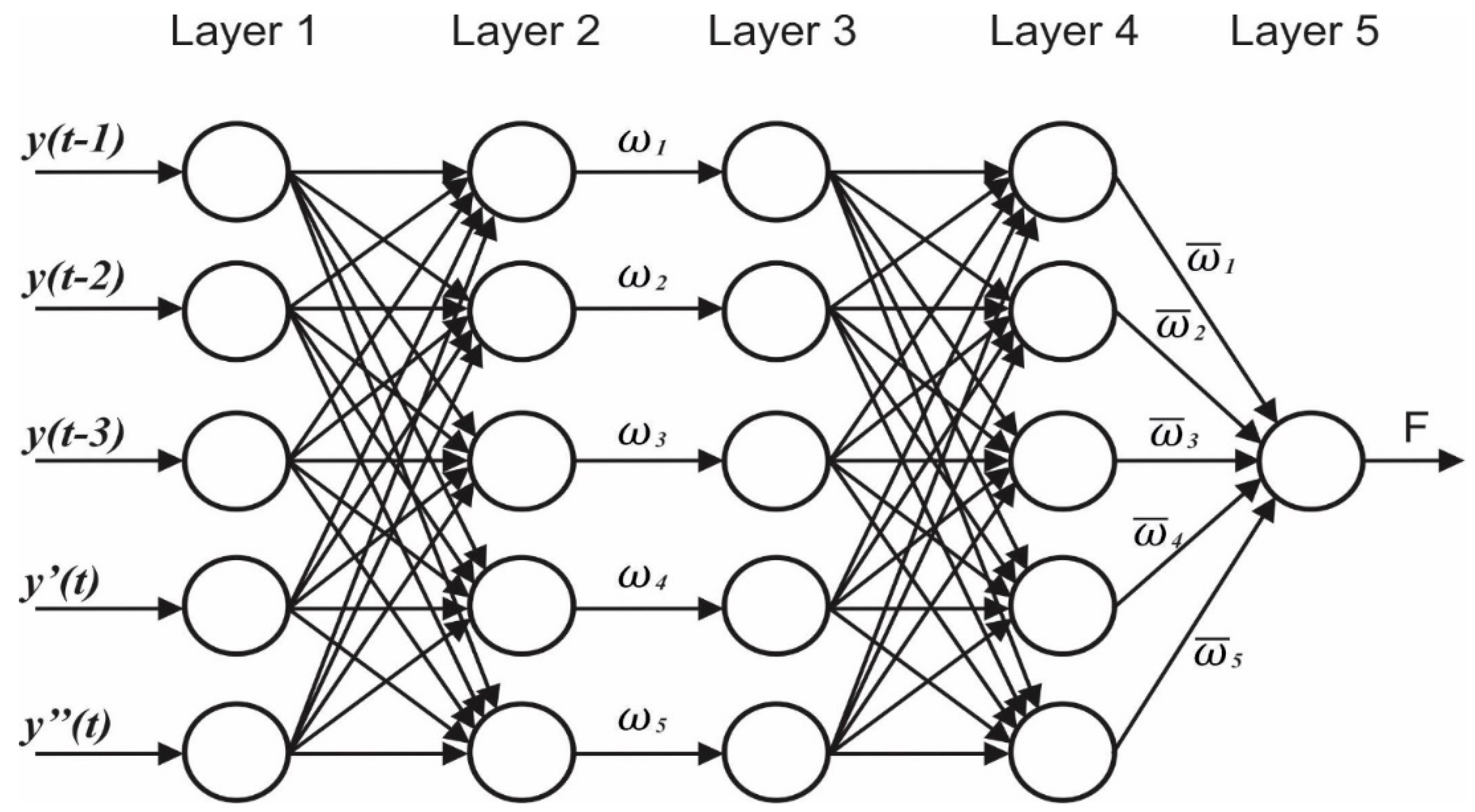
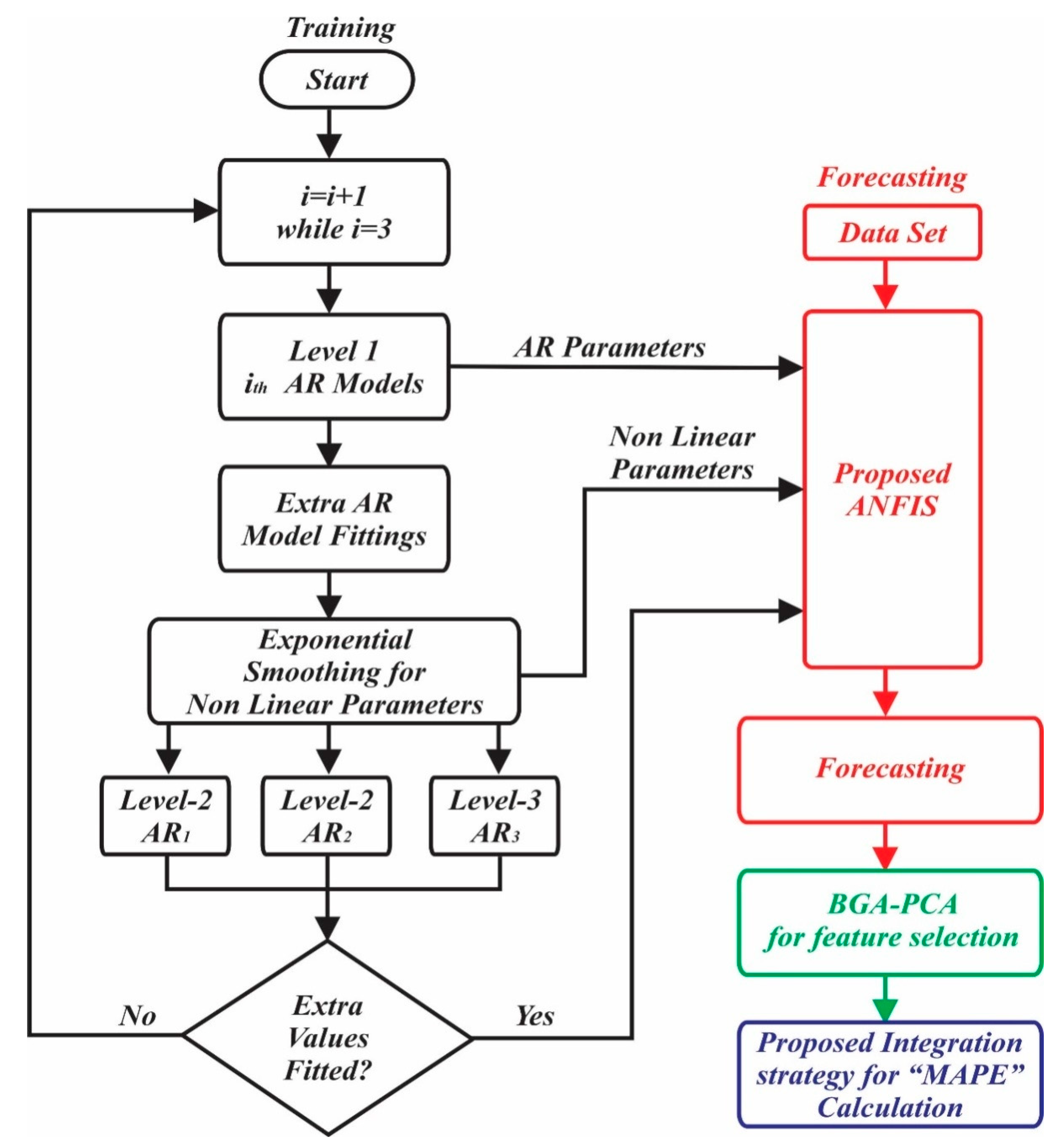
Symbols	Description
$y\left(t\right)$	Autoregression objective function
$y^{\prime }\left(t\right) \& y^{″}\left(t\right)$	Level-11 Autoregression objective function
$P_{t-1}$	Previous period load demand
$F_{t-1}$	LF demand
${\gamma }_k{Y}_{k,t}$	Extra autoregression term for a year of 4 season
$fi{t}_{fun}$	Feature selection function
$a_i\&c_i$	Set of premise parameters

.

Table 1. A comparison of related work of load forecasting.

Work	Key Contribution	AI Approach	FS	Limitations
[27]	Load Forecasting	Fuzzy logic and ANNs	NO	They have deficiencies including complexity and non-flexibility
[28]	Peak LF	Adaptive backpropagation learning-based ANN	NO	The slow learning process and no exact rule for over and underfitting
[30]	Load Forecasting	Fuzzy logic and ANNs	NO	It mainly focuses on the load curve, not on MAPE calculation
[31]	Genetic Algorithm based daily LF	NFN	NO	Only deals with variable linguistic information in LF
[32]	Short time LF one for weekdays and weekend	ANNs	NO	No technique can be evaluated for all types of days
[33]	Time-series models for policy development of hourly loads	ANN	NO	Very complex as no technique was used for eliminating irrelevant data
[35]	Regression and classification problem analysis for LF	SVM	NO	Only computed short time load forecasting
[37]	Daily LF of the month	EU-NITE network	NO	Only the daily load demand of the month is computed
[38]	LF of Wind Power	MLNN	NO	Computational time is very high.
[39]	Price Forecast by GRU	RNN	NO	Not reduced the irrelevant data.
[40]	STLF	SVM	NO	Computational time is very high
[41]	Load and Price Forecast	NO	Yes	Low computational time but fewer inputs are taken into account.
[42]	Hourly LF	ANFIS	Yes	Comparatively high MAPE
[43]	Hotel room LF	SVM	Yes	Less complex but fewer inputs taken into account.
[44]	Industrial LF	Radius Basis Function Neural Network	Yes	Not work well for large datasets
[45]	Survey on an integrated strategy to LF	ANFIS	Yes	Only suitable of the given scenario
Proposed Work	Residential Electricity LF with a novel Proposed Integration Strategy	ANFIS	Novel BGA-PCA	A new variety of data input and complex autoregression methods are not analyzed.

Table 1. A comparison of related work of load forecasting.

Work	Key Contribution	AI Approach	FS	Limitations
[27]	Load Forecasting	Fuzzy logic and ANNs	NO	They have deficiencies including complexity and non-flexibility
[28]	Peak LF	Adaptive backpropagation learning-based ANN	NO	The slow learning process and no exact rule for over and underfitting
[30]	Load Forecasting	Fuzzy logic and ANNs	NO	It mainly focuses on the load curve, not on MAPE calculation
[31]	Genetic Algorithm based daily LF	NFN	NO	Only deals with variable linguistic information in LF
[32]	Short time LF one for weekdays and weekend	ANNs	NO	No technique can be evaluated for all types of days
[33]	Time-series models for policy development of hourly loads	ANN	NO	Very complex as no technique was used for eliminating irrelevant data
[35]	Regression and classification problem analysis for LF	SVM	NO	Only computed short time load forecasting
[37]	Daily LF of the month	EU-NITE network	NO	Only the daily load demand of the month is computed
[38]	LF of Wind Power	MLNN	NO	Computational time is very high.
[39]	Price Forecast by GRU	RNN	NO	Not reduced the irrelevant data.
[40]	STLF	SVM	NO	Computational time is very high
[41]	Load and Price Forecast	NO	Yes	Low computational time but fewer inputs are taken into account.
[42]	Hourly LF	ANFIS	Yes	Comparatively high MAPE
[43]	Hotel room LF	SVM	Yes	Less complex but fewer inputs taken into account.
[44]	Industrial LF	Radius Basis Function Neural Network	Yes	Not work well for large datasets
[45]	Survey on an integrated strategy to LF	ANFIS	Yes	Only suitable of the given scenario
Proposed Work	Residential Electricity LF with a novel Proposed Integration Strategy	ANFIS	Novel BGA-PCA	A new variety of data input and complex autoregression methods are not analyzed.

In this research work, we presented a novel approach for residential LF using a machine learning-based feature selection approach and proposed integration strategy. Most of the articles in the literature have improved the accuracy rate of MAPE using AI approaches including ANN, SVM, ANFIS, evolutionary programming, expert system, fuzzy logic, LF-related problems, etc. These approaches have the limitation of high computational time and complexity as it includes a high amount of data. Therefore, the reduction of irrelevant and repeated data without affecting the essential information is a vital step in LF. On the other hand, the research work on feature selection-based GA algorithm has become the latest trend in LF. In this regard, we proposed a hybrid model of BGA-PCA for feature selection purposes, and it has never been deployed in electricity LF. The other novelty of our research work is an integration of a time series autoregression algorithm, ANFIS based algorithm, and BGA-PCA algorithm for optimal MAPE calculation in LF. This model not only reduces the unnecessary inputs through machine learning-based feature selection (BGA-PCA) and also improved a remarkable transformation in reducing MAPE.

3. Proposed Framework

This section is based on the proposed LF techniques and framework such as:

3.1. Time Series and Autoregression Method

The time series forecasting models have a standard approach of collecting historical data for predicting load, and nine different regression algorithms are taken in [46]. In our model, we have computed seven estimation models and three autoregression models with one exponential smoothing. The autoregression models are further estimated at level-II with exponential smoothing, and the algorithm with parameters that have been taken into account is defined in

Table 3. Time series and autoregression algorithm.

Models	Formulations	Description of Variable
Level I Autoregression Model (AR1)	${\mathrm{y}}_{\mathrm{t}}={\mathsf{\beta }}_0+{\mathsf{\beta }}_1{\mathrm{y}}_{\mathrm{t}-1}+{\mathsf{\beta }}_2{\mathrm{y}}_{\mathrm{t}-2}+{\mathrm{u}}_{\mathrm{t}}$	Variation in Weekly load demand: Special holidays or weekend $\mathrm{y}\left(\mathrm{t}-1\right)$, peak hour$\mathrm{y}\left(\mathrm{t}-2\right)$, off-peak hour $\mathrm{y}\left(\mathrm{t}-3\right)$
Level I Autoregression Model (AR2)	${\mathrm{y}}_{\mathrm{t}}={\mathsf{\beta }}_0+{\mathsf{\beta }}_1{\mathrm{y}}_{\mathrm{t}-1}+{\mathsf{\beta }}_2{\mathrm{y}}_{\mathrm{t}-2}+{\mathsf{\beta }}_3{\mathrm{y}}_{\mathrm{t}-3}+{\displaystyle {\displaystyle \sum }_{\mathrm{k}=1}^4}{\mathsf{\alpha }}_{\mathrm{k}}{\mathrm{S}}_{\mathrm{k},\mathrm{t}}+{\mathrm{u}}_{\mathrm{t}}$	AR2 is modeled by adding season autoregression term ${\mathrm{S}}_{\mathrm{k},\mathrm{t}}$, where k = 1,…,4. Pakistan has four seasons such as summer, winter, fall, and spring.
Level I Autoregression Model (AR3)	${\mathrm{y}}_{\mathrm{t}}={\mathsf{\beta }}_0+{\mathsf{\beta }}_1{\mathrm{y}}_{\mathrm{t}-1}+{\mathsf{\beta }}_2{\mathrm{y}}_{\mathrm{t}-2}+{\mathsf{\beta }}_3{\mathrm{y}}_{\mathrm{t}-3}+{\mathsf{\gamma }}_k{Y}_{k,\mathrm{t}}+{\displaystyle {\displaystyle \sum }_{\mathrm{k}=1}^4}{\mathsf{\alpha }}_{\mathrm{k}}{ \overline{\mathrm{S}} }_{\mathrm{k},\mathrm{t}}+u_{\mathrm{t}}$	AR3 model has an extra autoregression term for a year ${\mathsf{\gamma }}_k{Y}_{k,\mathrm{t}}$ and for the seasons of the year ${ \overline{\mathrm{S}} }_{\mathrm{k},\mathrm{t}}$, where k = 1,…,4.
Exponential Smoothing Method	${\mathrm{y}}_{\mathrm{t}}=\mathsf{\alpha }{P}_{\mathrm{t}-1}+\left(1-\mathsf{\alpha }\right)F_{\mathrm{t}-1}+u_{\mathrm{t}}$	This model is used for the purpose where there is no seasonality in the load. Where $\mathsf{\alpha }$= smooth constant, $P_{\mathrm{t}-1}$= previous period load demand, and $F_{\mathrm{t}-1}$= previous period LF demand
Level II Autoregression Model (AR1)	${\mathrm{y}}_{\mathrm{t}}^{\prime }=\mathsf{\alpha }{P}_{\mathrm{t}-1}+\left(1-\mathsf{\alpha }\right)F_{\mathrm{t}-1}+u_{\mathrm{t}}$ ${\mathrm{y}}_{\mathrm{t}}^{″}={\mathrm{y}}_{\mathrm{t}}={\mathsf{\beta }}_0+{\mathsf{\beta }}_1{\mathrm{y}}_{\mathrm{t}-1}+{\mathsf{\beta }}_2{\mathrm{y}}_{\mathrm{t}-2}+{\mathrm{u}}_{\mathrm{t}}$ ${\mathrm{y}}_{\mathrm{t}}={\mathrm{y}}_{\mathrm{t}}^{\prime }-{\mathrm{y}}_{\mathrm{t}}^{″}+{\mathrm{u}}_{\mathrm{t}}$	In level-II, the model is applied on the data of the same series in AR1, but the demand values and residential values from customer demand modeled in the Exponential Smoothing Method are added.
Level II Autoregression Model (AR2)	${\mathrm{y}}_{\mathrm{t}}^{\prime }=\mathsf{\alpha }{P}_{\mathrm{t}-1}+\left(1-\mathsf{\alpha }\right)F_{\mathrm{t}-1}+u_{\mathrm{t}}$ ${\mathrm{y}}_{\mathrm{t}}^{″}={\mathsf{\beta }}_0+{\mathsf{\beta }}_1{\mathrm{y}}_{\mathrm{t}-1}+{\mathsf{\beta }}_2{\mathrm{y}}_{\mathrm{t}-2}+{\mathsf{\beta }}_3{\mathrm{y}}_{\mathrm{t}-3}+{\displaystyle {\displaystyle \sum }_{\mathrm{k}=1}^4}{\mathsf{\alpha }}_{\mathrm{k}}{\mathrm{S}}_{\mathrm{k},\mathrm{t}}+{\mathrm{u}}_{\mathrm{t}}$ ${\mathrm{y}}_{\mathrm{t}}={\mathrm{y}}_{\mathrm{t}}^{\prime }-{\mathrm{y}}_{\mathrm{t}}^{″}+{\mathrm{u}}_{\mathrm{t}}$	In level-II, the model is applied on the data of the same series in AR2, but the demand values and residential values from customer demand modeled in the Exponential Smoothing Method are added.
Level II Autoregression Model (AR3)	${\mathrm{y}}_{\mathrm{t}}^{\prime }=\mathsf{\alpha }{P}_{\mathrm{t}-1}+\left(1-\mathsf{\alpha }\right)F_{\mathrm{t}-1}+u_{\mathrm{t}}$ ${\mathrm{y}}_{\mathrm{t}}^{″}={\mathsf{\beta }}_0+{\mathsf{\beta }}_1{\mathrm{y}}_{\mathrm{t}-1}+{\mathsf{\beta }}_2{\mathrm{y}}_{\mathrm{t}-2}+{\mathsf{\beta }}_3{\mathrm{y}}_{\mathrm{t}-3}+{\mathsf{\gamma }}_k{Y}_{k,\mathrm{t}}+{\displaystyle {\displaystyle \sum }_{\mathrm{k}=1}^4}{\mathsf{\alpha }}_{\mathrm{k}}{ \overline{\mathrm{S}} }_{\mathrm{k},\mathrm{t}}+u_{\mathrm{t}}$ ${\mathrm{y}}_{\mathrm{t}}={\mathrm{y}}_{\mathrm{t}}^{\prime }-{\mathrm{y}}_{\mathrm{t}}^{″}+{\mathrm{u}}_{\mathrm{t}}$	In level-II, the model is applied on the data of the same series in AR3, but the demand values and residential values from customer demand modeled in the Exponential Smoothing Method are added.

.

3.2. Machine Learning Approach of Proposed Feedforward ANFIS

The model is further validated by the ML approach for implementing ANN, while it is a computer model influenced by the brain and nervous system in animals or humans. Each network is a “neuron” integration that can generate values from sources that feed data across to the network. It provides a systematic analysis of neural networks. The majority of the research articles indicated that ANNs can be divided into two categories. Thirty US power companies used a software-based ML platform in 1998 [47]. The radial base feature network, self-organizing maps, grouping, and recursive cognitive network are a few of the neural forecasting models used by LF. The ANFIS model is presented in [48] to forecast the potential load, and we have modified it according to our requirement as five stages computed in this section. An algorithm uses an unmonitored training data principle to construct a load–temperature relationship to forecast 24 h of load [48]. This method uses real-time data as error-correcting function input, and simulation findings reveal that acceptable percent mean absolute error percentage is better than the conventional method. In this regard, the proposed system validates the Feedforward Artificial Neural Network of one-year LF data. The proposed Feedforward ANFIS model consists of five stages where Random Forest training schemes are taken into account, and the training process is given as follows:

Stage 1: This layer is known as the fuzzy fiction layer. At this layer, the received signal of any node will transmit to the other layer. Each node in this layer produces a membership function of the linguistic variable. The outputs are given in the equations where the linear data containing weekly, seasonally, and per year demand are illustrated in Table 3 and considered in Equation (1). The nonlinear data include ambient temperature, dew pony, solar irradiation, peak loads time, off-peak loads time, energy price, sunshine duration, fog duration in winter, and robust weather conditions. Table 3 defines it with the exponential method and level-2 AR methods considered in Equations (2) and (3):

$$O_i^1=\mu A_i\left(Y_{y-i}\right) \mathrm{for} \mathrm{I}=1,2,3$$

(1)

$$O_2^1=\mu A_2\left(Y^{\prime }t\right)$$

(2)

$$O_3^1=\mu A_3\left(Y^{″}t\right)$$

(3)

where $Y{\left(t-1\right)}_{}, y_t^{\prime }, \mathrm{and} Y_t^{″}$ are the inputs to the nodes as shown in Figure 1.

$\mu A_i$ is a Member Function.

A is a linguistic variable that is linked with the node function.

The μA in the model is chosen based on Equation (4):

$$\mu A_i\left(x\right)=exp{\left[-\frac{Y_t-c_i}{2a_i}\right]}^2$$

(4)

where $a_i\mathrm{and} c_i$ are the set of premise parameters.

Stage 2: This layer 2 is the rule layer. It is used as a simplification of the predicter training scheme and minimizes the burden. The output of each node demonstrates the firing strength of each rule obtained by the membership functions given in Equation (5):

$$w_n=\mu A_i\left(Y_{t-i}\right)\times \mu A_2\left(Y^{\prime }t\right)\times \mu A_3\left(Y^{″}t\right) \mathrm{for} n=1,2,3,4,5$$

(5)

Stage 3: Each node at this stage is a fixed node and is named N. This layer is known as the normalization layer because it calculates a ratio of firing strength of the rule relative and the sum of firing strengths of previous rules. The output is given by Equation (6):

$${\overline{w}}_n=\frac{w}{w_1+w_2+w_3+w_4+w_5} n=1, 2, 3, 4, 5$$

(6)

Stage 4: The nodes at this stage depend on adaptive nodes. The output for each rule is calculated by taking the product of normalized firing strength from the previous phase and the first-order Sugeno Model. This layer is known as the defuzzification layer:

$${\theta }_n^4={\overline{w}}_n{f}_{n }={\overline{w}}_n\left(p_n+q_n+r_n\right)$$

(7)

where ${\overline{w}}_n$ is the output of stage 3, and $p_i, q_i, r_i$ are the parametric set.

Stage 5: The total output for the proposed model is calculated at this layer. The calculation is done based on the output values of each rule. This is why this layer is called the sum layer. There is a single node here that computes the overall output. The overall output is computed in a single node as illustrated in Figure 1 and given in Equation (8):

$${\theta }_n^5={\displaystyle \sum }_n{\overline{w}}_n{f}_{n }=\frac{{{\displaystyle \sum }}_n{\overline{w}}_n{f}_{n }}{{{\displaystyle \sum }}_n{\overline{w}}_n}$$

(8)

Using the ANFIS model, the final output for given premise parameters can be represented as a linear combination of consequent parameters:

$$f={\overline{w}}_1(p_1+q_1+r_1) + {\overline{w}}_2 (p_2+q_2+r_3) + {\overline{w}}_3(p_3+q_3+r_3) + {\overline{w}}_4(p_4+q_4+r_4) + {\overline{w}}_5(p_5+q_5+r_5)$$

(9)

3.3. BGA-PCA for Feature Selection

Feature selection is used in this research for eliminating the extraneous and redundant data that can improve accuracy and reduce computation time as applied to ML in [49]. In this regard, the BGA is based on the evolutionary perception of genetics and natural selection as it is considered a global solution for optimization problems. In this proposed model, the feature selection is based on BGA along with the blend of PCA as shown by the flowchart in Figure 2. The best feature selection is evaluated in five key steps. The steps are:

3.3.1. Initialization of Data Inputs and Model Paraments

The model is started with objective functions as BGA works on a binary data set of special values for variables (chromosomes) as a genetic algorithm starts with these variables for indicating the optimal variables for the problem [50]. The model parameters of this section are “1” and “0”, where “1” means that the feature selected for the fitness evaluation and “0” is for the feature that is going to be not selected. After defining the objective functions and model parameters, the next step is the creation of the initial population.

3.3.2. Initial Population

As this feature selection is a GA-based solution, there is a need for two matrices for creating the initial population that is “k” matrix and “l” matrix, where k defines the number of chromosomes and l indicates the length. Quantity and length of chromosomes are computed by population size and the number of genes, respectively. The suggestion for every population is given [51].

3.3.3. Determining Fitness from PCA

Although the time series and autoregression method are used in this research for assessing the deployed fitness function, the objective functions are linked with parameters in Table 3 to evaluate the means square error of the autoregression method. After MSE evaluation and for each subset, there is a need for data reduction. All forecasting work consists of a massive amount of data and facing difficulties of a lot of computational work. PCA has been used to overcome the computational complexity by reducing the number of features and processing time for intrusion detection [52]. The autoregression methods are a function of $y\left(t\right),$and two matrices $k$ and $l$ are proposed. Then, the PCA of the linear combination for required value forms as:

$$P{C}_1={\varnothing }_1{y}_1+{\varnothing }_2{y}_2+{\varnothing }_3{y}_3+\dots +{\varnothing }_k{y}_l$$

(10)

In addition, the large sample variance is reduced by:

$${\displaystyle \sum }_{j=1}^l{\varnothing }_{j1}^2=1$$

(11)

It indicates and optimizes the problem that is needed as a maximize function formed as:

$$\frac{1}{n}{\displaystyle \sum }_{j=1}^k{\left({\displaystyle \sum }_{j=1}^l{\varnothing }_k{y}_l\right)}^2$$

(12)

The data are further minimized by:

$$\frac{1}{n}{\displaystyle \sum }_{j=1}^n{\varnothing }_{j1}^2=0$$

(13)

On the other hand, the main objective of BGA is a minimization of MSE as a loss function for ML approach that is formulated by:

$$fi{t}_{fun}=\frac{i}{n}{\displaystyle \sum }_{i=1}^n{\left(Ti-yt\right)}^2$$

(14)

where T is a vector function of load demand and n is a training sample or assumptions for forecasting. As earlier mentioned, the term 1 defines the selected values, while 0 defines the non-selected values for the assessment of chromosomes. Each irritation of the BGA-PCA feature selection method decreases the MSE and finds the best objective function value.

3.3.4. Selection or Reproduction

The parameters considered for BGA are given in

Table 4. The parameters considered for BGA.

Sr. No	Model Parameters	Considered Values
1.	Population Size	48
2.	Selection probability	1
3.	Selection Mechanism	Tournament selection
4.	Crossover probability	0.95
5.	Mutation Probability	0.20
6.	Maximum iteration	50
7.	Stopping criteria	1. When reached max no. of iteration 2. If fitness values are not better than the previous

. The chromosome length is 48, and the number of iterations is set to be 50. The new population is further produced by crossover and mutation sections. The crossover and mutation functions use two chromosomes as parent-1 and parent-2 in this model, while the crossover function is the child selection.

In the parents’ chromosomes, the child must be better than the parent. The XOR function is applied for the binary form where the crossover probability is 0.95. Here are two options, one is yes for the violation of any constraints, and the second is no for the evaluation of the new population. This crossover function can operate a single time or multiple times based on the maximum length of chromosomes. In the mutation process, each bit is checked individually for searching for the best possible solution where its operating function single/multiple times is the same as the crossover function. The mutation probability is 0.20 as it is a genetic disorder of chromosomes, and it creates a random number which uniformly distributed with a maximum length of chromosome size. The proposed BGA-PCA model is chosen by setting the initial population, various probability values for mutation and crossover, maximum iterations, and the stopping criteria. It helps in the selection of a new population ultimately for the best feature subset.

3.3.5. Convergence Condition and Final Feature Subset

The new population is further tested in one step if it succeeds in finding the best chromosome within the iteration limit, decoding it, and considering the best feature subset. On the other hand, the new population might not be better than the previous one. Then, it is suggested to keep the initial value as new. The convergence limits are as follows:

• When a maximum number of iterations is reached;
• If fitness values are not better than the previous.

After finding the best chromosome, encode the best fitness score, and finally, choose the best feature subset. This flowchart of this complete process is shown in Figure 2 and is ready for further validation.

3.4. Proposed Integration Strategy

The LF approach is based on a time series and autoregression model, ML method, and the proposed feature selection scheme. In this section, the forecasting is further optimized by reducing MAPE. In this regard, this section integrates all approaches, where data fetching and modeling of time series and autoregression model are considered. One-year data having four seasons with the transformation of per week data, ML, and feature selection are not considered as a final decision because the integration strategy looks toward the best algorithm of the related week of each season. Moreover, the MAPE calculations are modified as computed for the integration strategy in [46] for individual buildings as follows:

$$MAP{E}_i=\frac{1}{W_s}{\displaystyle \sum }_{t=1}^{W_s}\frac{\left|fi{t}_{fun}\left(t\right)-D\left(t\right)\right|}{D\left(t\right)}$$

(15)

where $fi{t}_{fun}$ $(t$) is a function taking from feature selection concerning time $t$, $D$ is actual data, and $w_s$ is weeks per season. The average MAPE is then further calculated as:

$$MAP{E}_{avg}={\displaystyle \sum }_{i=1}^{W_s}{C}_i\ast MAP{E}_i$$

(16)

The PRECON data are modeled by the proposed time series and autoregression system, where it has seven different estimation models. These consist of three AR models, one exponential smoothing, and three AR models with exponential smoothing. The algorithm is elaborated in Table 3 and validated with a Feedforward Artificial Neural Network of one-year LF data. The proposed feedback ANFIS model consists of five stages and uses real-time data as error-correcting function input. The simulation findings reveal that an acceptable mean absolute error percentage is better than the conventional method. The next step for the model evaluation starts from the feature selection, and a novel BGA-PCA model is presented in the article for the best fitness score. Finally, the best feature subset is chosen as indicated in Equation (13). Moreover, the MAPE calculation for the integration strategy is formulated for an individual building in Equations (14) and (15). This complete sequence of simulations is shown in

Table 5. The sequence of simulation.

Proposed Algorithm
Step 1:	According to Table 3, adjust the simulation parameters.
Step 2:	Compute y(t) and $y^{\prime }\left(t\right)$ and $y^{″}\left(t\right)$ for different objective functions.
Step 3:	Generate random estimation for feedback ANFIS model consists of five stages.
Step 4:	Evaluate feature selection with BGA-PCA
Step 5:	Compute $fi{t}_{fun}=\frac{i}{n}{\displaystyle \sum }_{i=1}^n{\left(Ti-yt\right)}^2$ for the different objective function of $y\left(t\right).$
Step 6:	Compute $MAP{E}_i$ for 10 houses
Step 7:	Compute $MAP{E}_{avg}$
Step 8	Plot of figures for MAPE of four seasons

.

4. Model Evaluation

In this article, the time series and autoregression models are considered for an ML-based feature selection named BGA-PCA. It is further validated using the integration strategy technique. For this purpose, 10 residential houses are taken into consideration where building area in square feet, number of floors, building year, the ceiling height in feet, total number of rooms, bedrooms, living rooms, drawing rooms, kitchen, connection type, number of people, number of adults (14 to 60), number of children (0–13), permanent residents, temporary residents, number of ACs, number of refrigerators, number of washing machines, number of electronic devices, number of fans, number of water dispensers, number of water pumps, number of electric heaters, number of irons, number of lighting devices, and number of UPS are the parts of data set.

As earlier discussed, the data of 10 houses from PRECON are considered for the LF. The proposed work and Random Forest training scheme are shown in Figure 3 systematized as follows:

Time series and autoregression algorithms are developed to fetch the data set and set the objective function, while the proposed equations in Table 3 set the base for further validation as improved results validate it. In Table 3, the data set fetching with seven AR methods are computed by different linear and nonlinear data.

The preprocessing of the AR method is illustrated in Figure 3, where the three types of data are fed to feedback ANFIS. It contains linear data of Level-1 AR models, nonlinear data of exponential smooth method, and Level-II AR models as computed in Table 3.

The time series AR data have been considered the inputs of proposed Feedforward ANFIS as formulated in Equations (1)–(3). The overall output of Feedforward ANFIS is computed in Equations (8) and (9).${\overline{ w}}_1$, ${\overline{w}}_2$, ${\overline{w}}_3$, ${\overline{w}}_4$, ${\overline{w}}_5$ are the five best weights obtained from the ANFIS model. For example, weights are ${\overline{w}}_1=50\%$, ${\overline{w}}_2=40\%$, ${\overline{w}}_3=30\%$, ${\overline{w}}_4=20\%$, ${\overline{w}}_5=10\%,$ respectively. Then, the new weights according to Equation (6) could be: ${\overline{w}}_1=\frac{50}{150}=33.3\%$, ${\overline{w}}_2=\frac{40}{150}=26.6\%$, ${\overline{w}}_3=\frac{30}{150} =20\%$, ${\overline{w}}_4=\frac{20}{150}=13.3\%$, and ${\overline{w}}_5=\frac{10}{150}=6.6\%$. The forecasted weight according to Equations (8) and (9), where $f_n$ is the forecasting parameter of each weight according to week, weekend, month, season, and year as parameters defined in Table 3. Assume that $f_n$ are 30, 25, 20, 15, 10. Then, the forecast weights are computed as: $f=$ 0.33 × 30+ 0.26 × 25+ 0.2 × 20 + 0.13 × 15+ 0.06 × 10 ≈ 23.

BGA-PCA for the proposed feature selection used in this work eliminates the extraneous and redundant data that can improve accuracy and reduce computation time. The main objective of BGA is to minimize the loss function as computed in Equation (14). The extra parameters, repeated terms, and irrelevant data have been removed by the BGA-PCA algorithms, as shown in the flowchart of the algorithm in Figure 2 and simulation parameters in Table 4. It also shows that the child’s chromosomes are better than the parent’s. In the next step, the XOR function is applied where the crossover probability is 0.95. Whereas there are two possibilities, the first one is yes if the violation of any constraints is found, and the second one is no when the new population is evaluated. This crossover function can operate a single time or multiple times based on the maximum length of chromosomes. In the mutation process, each bit is checked individually for searching for the best possible solution where it is an operating function single/multiple times is the same as the crossover function. The mutation probability is 0.20 as it is a genetic disorder of chromosomes, and it creates a random number that is distributed uniformly with a maximum length of chromosome size. The proposed BGA-PCA model is chosen by setting the initial population, various probability values for mutation and crossover, maximum iterations, and the stopping criteria that help in the selection of new population ultimately for the best feature subset.

MAPE calculation for the integration strategy is formulated for an individual building, and average MAPE calculation is done in Equations (15) and (16), respectively. As per MAPE calculation in

Table 6. LF improvement per building.

Customer Type.	Without Proposed Integration $$\begin{gathered} {\mathit{M}}_1 \\ \mathbf{MAPE} \mathbf{Percentage} \end{gathered}$$				With Proposed Integration $$\begin{gathered} {\mathit{M}}_2 \\ \mathbf{MAPE} \mathbf{Percentage} \end{gathered}$$				With Proposed Integration & BGA-PCA feature selection $$\begin{gathered} {\mathit{M}}_3 \\ \mathbf{MAPE} \mathbf{Percentage} \end{gathered}$$				With Proposed Integration Improvement Percentage	With Proposed Integration & Machine Learning Improvement Percentage	Over All Improvement Percentage
	Summer MAPE %	Fall MAPE %	Winter MAPE %	Spring MAPE %	Summer MAPE %	Fall MAPE %	Winter MAPE %	Spring MAPE %	Summer MAPE %	Fall MAPE %	Winter MAPE %	Spring MAPE %	${\mathit{E}}_1=\frac{({\mathit{M}}_1-{\mathit{M}}_{2)}}{{\mathit{M}}_2}$	${\mathit{E}}_2=\frac{({\mathit{M}}_2-{\mathit{M}}_{3)}}{{\mathit{M}}_3}$	$\mathit{E}={\mathit{E}}_1-{\mathit{E}}_2$
House 1	2.97	3.01	3.07	2.83	2.08	2.19	2.23	2.06	1.72	1.79	1.76	1.71	39%	23%	16%
House 2	2.88	3.02	3.06	2.67	2.10	2.19	2.20	2.02	1.69	1.67	1.84	1.67	37%	24%	13%
House 3	2.87	2.98	3.08	2.84	2.16	2.17	2.29	2.02	1.82	1.75	1.81	1.71	36%	22%	14%
House 4	2.84	2.94	3.09	2.89	2.10	2.19	2.18	2.08	1.73	1.80	1.84	1.69	38%	21%	16%
House 5	2.91	2.96	3.09	3.01	2.20	2.14	2.16	2.07	1.72	1.72	1.77	1.75	40%	23%	17%
House 6	2.81	2.94	2.99	2.98	2.19	2.11	2.16	2.02	1.81	1.78	1.81	1.64	38%	20%	18%
House 7	2.88	3.08	2.98	2.94	2.06	2.13	2.17	2.06	1.66	1.77	1.82	1.60	41%	23%	18%
House 8	2.9	3.04	2.97	2.85	2.01	2.12	2.15	2.06	1.67	1.85	1.76	1.65	41%	20%	21%
House 9	2.94	3.06	3.06	2.84	2.10	2.16	2.11	2.07	1.60	1.76	1.79	1.69	41%	23%	18%
House 10	2.95	2.99	3.08	2.83	2.04	2.14	2.30	2.04	1.60	1.83	1.82	1.61	39%	24%	15%
Average	2.90	3.00	3.05	2.87	2.10	2.15	2.20	2.05	1.70	1.77	1.80	1.67	39%	22%	17%

, the average MAPE of house 1 for the summer season is 1.72 as calculated from Equation (16). The weekly coefficient from different algorithms $C_i$ are 30%, 25%, 20%, 15%, 10%, and $MAP{E}_i$ of house 1 according to different algorithms are 1.70, 1,77,1.68,1.78, 1.69 as per Equation (15). The integration strategy computed the minimum MAPE as per Equation (16) is $MAPE of house 1=0.30\times 1.70+0.25\times 1.77+0.20\times 1.68+0.15\times 1.78+0.10\times 1.69=1.72$. Similarly, the MAPE of each house for four seasons is calculated, and the average is computed as given in Table 6.

The MAPE improvements are discussed in Equations (17)–(19), and the calculated results are demonstrated in Table 6, and Figure 4, Figure 5, Figure 6 and Figure 7 validate the proposed model. The MAPE has improved the system by 0.89, for the summer seasons of house 1, as its value was 2.97 with MAPE and 2.08 without MAPE, taking the MAPE value equal to 1.72. Then, $E_1$ according to Equation (17) is $\frac{2.97-2.08}{2.97}$= 29.99%, and, after four seasons, the house 1 MAPE average becomes 39% as shown in Table 6. The further improvement is calculated in Equation (18) as $\frac{2.08-1.72}{2.08}$ = 17%, where after four seasons, the house 1 MAPE average becomes 23% as shown in Table 6. The overall MAPE improvement of house 1 is calculated using Equation (19) as $39\%-23\%=16\%,$ and the average of 10 houses is 17%.

The highest load is in the summer season, in which July and August were at their peak, and the minimum load is in the winter season, in which January and February were on their minimum value. In addition, the feature selection approach has the following features: day hours, day of the week, weekend, holidays, weeks in a month, months of a season, seasons in a year, ambient temperature, dew pony, solar irradiation, peak loads time, off-peak loads time, energy price, sunshine duration, fog duration in winter, and robust weather conditions. One year of data from July 2018 to June 2019 is taken into account. After deploying the complete model modeled in Section 3 and the complete sequence of simulation illustrated in Table 5, the MAPE for the LF improvement and the MAPE of each house are calculated, where the average MAPE without proposed integration strategy is $\left(M_1\right)$. The average MAPE with only the proposed integrated approach without feature selection is ($M_2$). This improvement percentage is calculated by:

$$E_1=\frac{\left(M_1-M_2\right)}{M_2}$$

(17)

The average MAPE of 10 houses computed by our proposed model is ($M_3$). Then, the improvement is formulated by:

$$E_2=\frac{\left(M_2-M_3\right)}{M_3}$$

(18)

The overall improvement percentage can be calculated by:

$$E=E_1-E_2$$

(19)

This complete model is simulated in a MATLAB simulation environment on a research workstation with an Intel Core i5-4300CU, 8 GB RAM, 64-bit operating system, and 2.50 GHz Processor. The proposed model of 10 houses with a one-year hourly database is simulated in 50 min.

5. Results and Discussion

LF improvement for the MAPE of each house is calculated in Table 6. The results of $M_1$ without proposed integration strategy is 2.90, 3.00, 3.05, and 2.87 percentage for Summer, Fall, Winter, and Spring, respectively. The results are improved with only the proposed integrated approach without feature selection, which is: 2.10, 2.15, 2.20, and 2.05 percentage for Summer, Fall, Winter, and Spring, respectively. The results are more improved with the proposed model illustrated in Table 6, and the average MAPE of 10 houses $M_3$ is calculated with help of proposed equations and sequence simulation.

The proposed model attained 1.70, 1.77, 1.80, and 1.67 percentage for Summer, Fall, Winter, and Spring, respectively. The overall improvement based on 10 buildings is 17% computed in Table 6.

Randomly, eight weeks of each season are selected to illustrate the forecasting results, where Sunday is considered a weekend and the seasons are: Summer (July–August 2018), Fall (October–November 2018), Winter (January–February 2019), and Spring (March–April 2019). The actual and forecasted results of electricity demand with minimum MAPE are depicted in Figure 4, Figure 5, Figure 6 and Figure 7 for the Summer, Fall, Winter, and Spring seasons, respectively. Besides the overall improvement with our proposed model, being 17% computed in Table 6, the proposed model has some better results of LF as compared with LF models that are given in [53,54], illustrated in

Table 7. Comparison: Results in Figure 4, Figure 5, Figure 6 and Figure 7 with past works.

Results [53] Novel Hybrid STLF Model Five Regions in Australia		Results [54] Second Learning of Error Trend Model on Different Regions		Results (Proposed Model) 10 Residential Buildings
Season	Min MAPE %	Season	Min MAPE %	Season	Min MAPE %
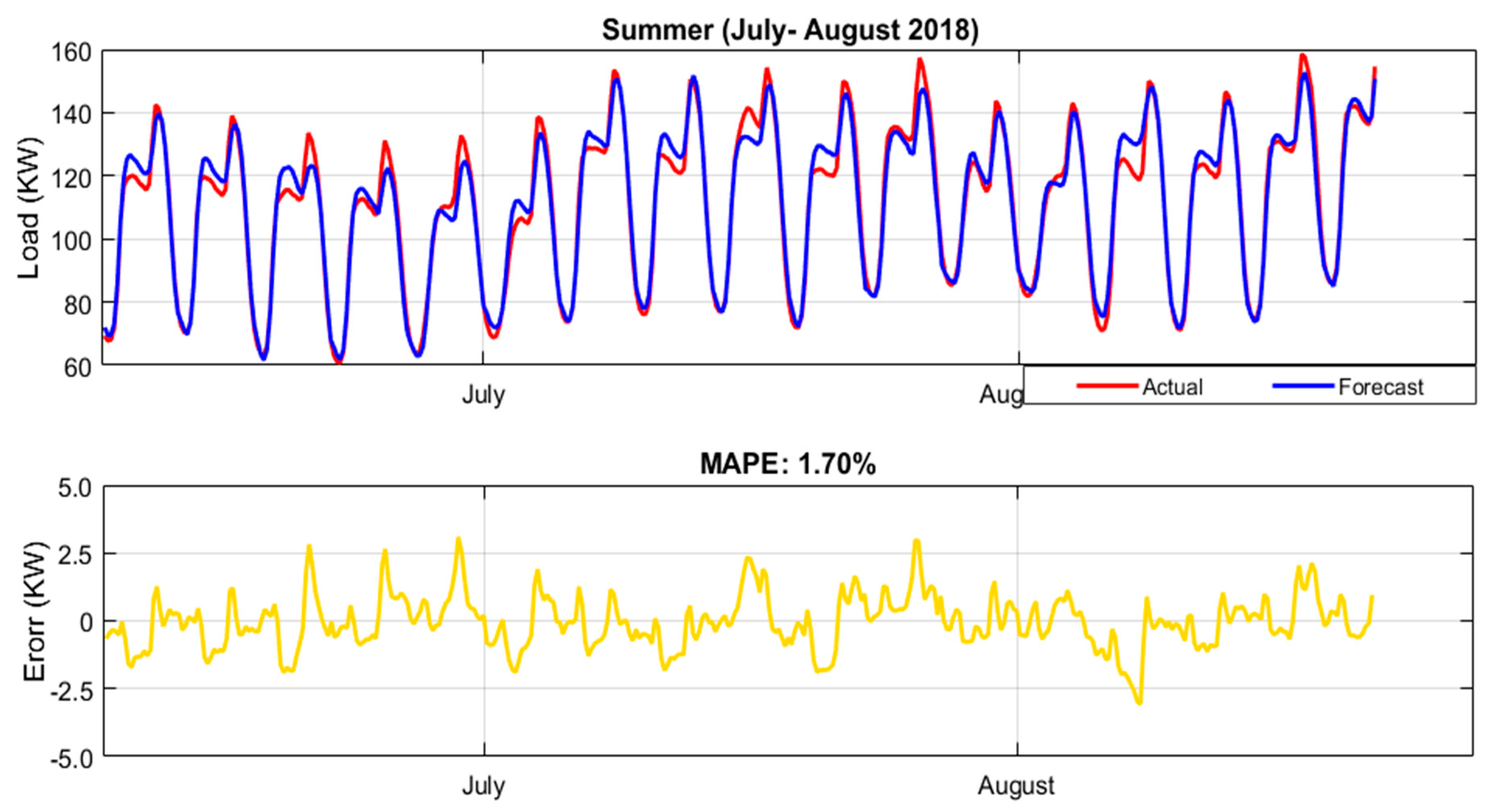
Summer (July–Sep)	1.68	Summer	1.84	Summer (July–August)	1.70
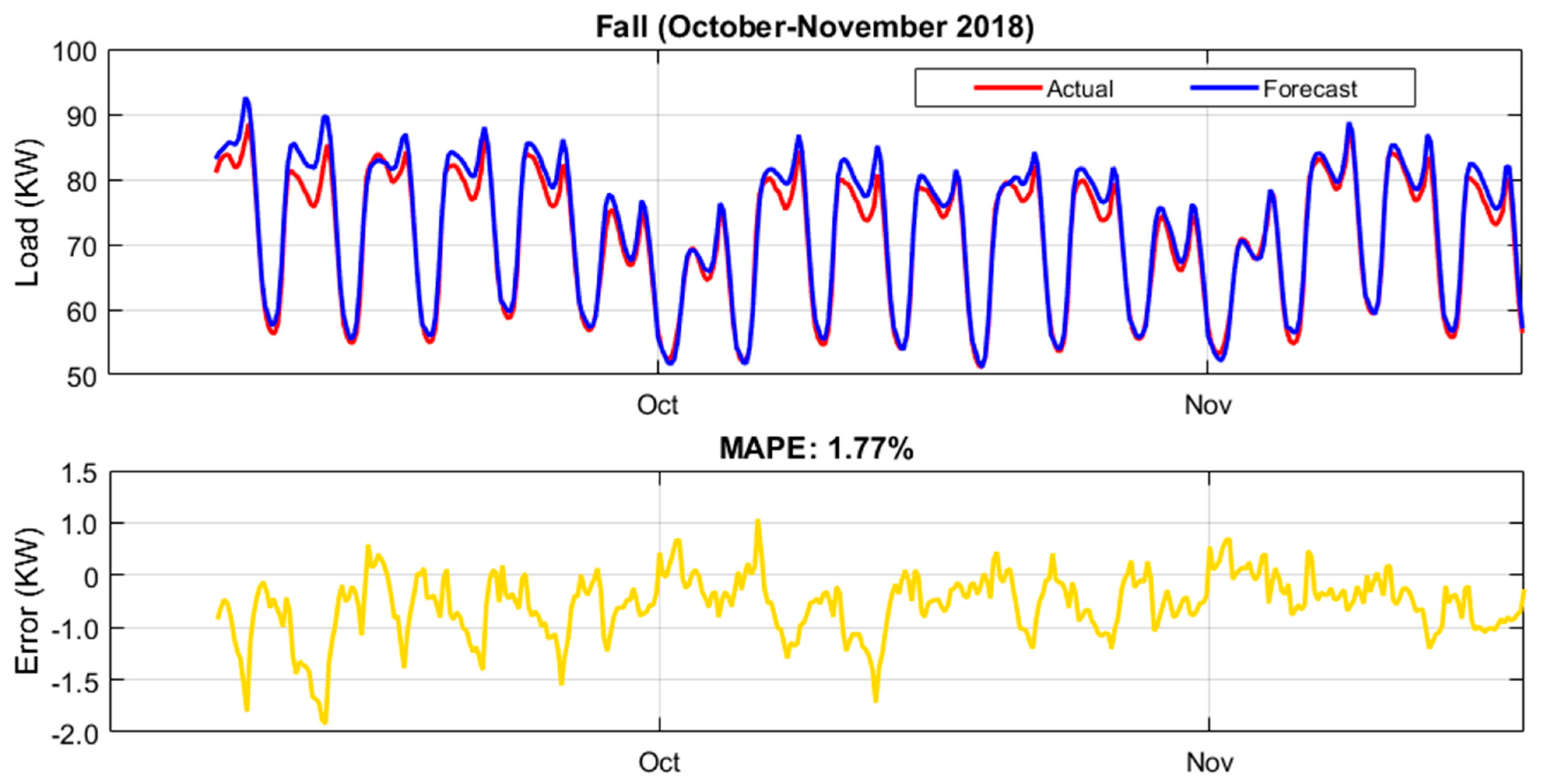
Fall (Oct–Dec)	2.71	Fall	1.87	Fall (Oct–Nov)	1.77
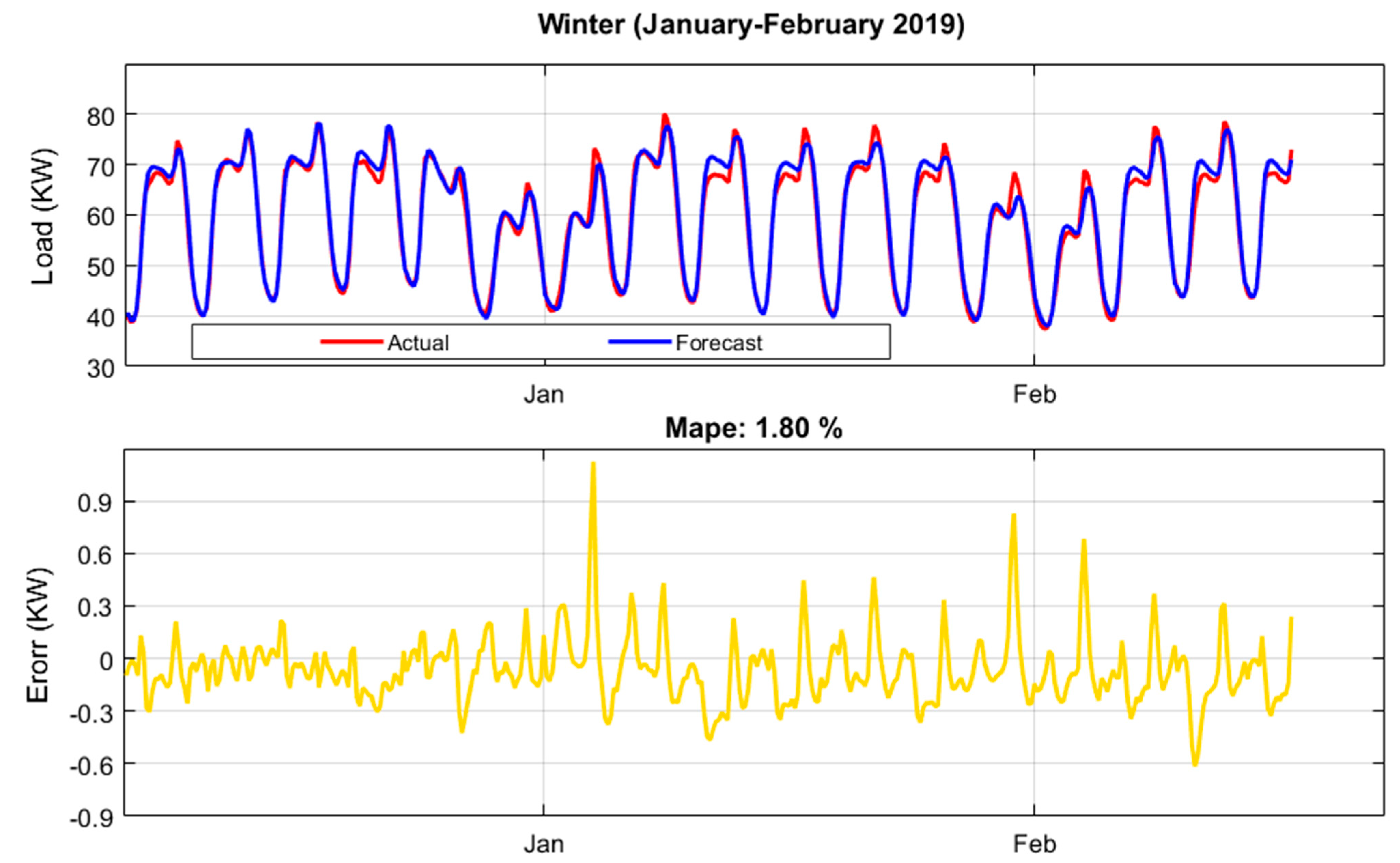
Winter (Jan–Mar)	2.28	Winter	1.66	Winter (Jan–Feb)	1.80
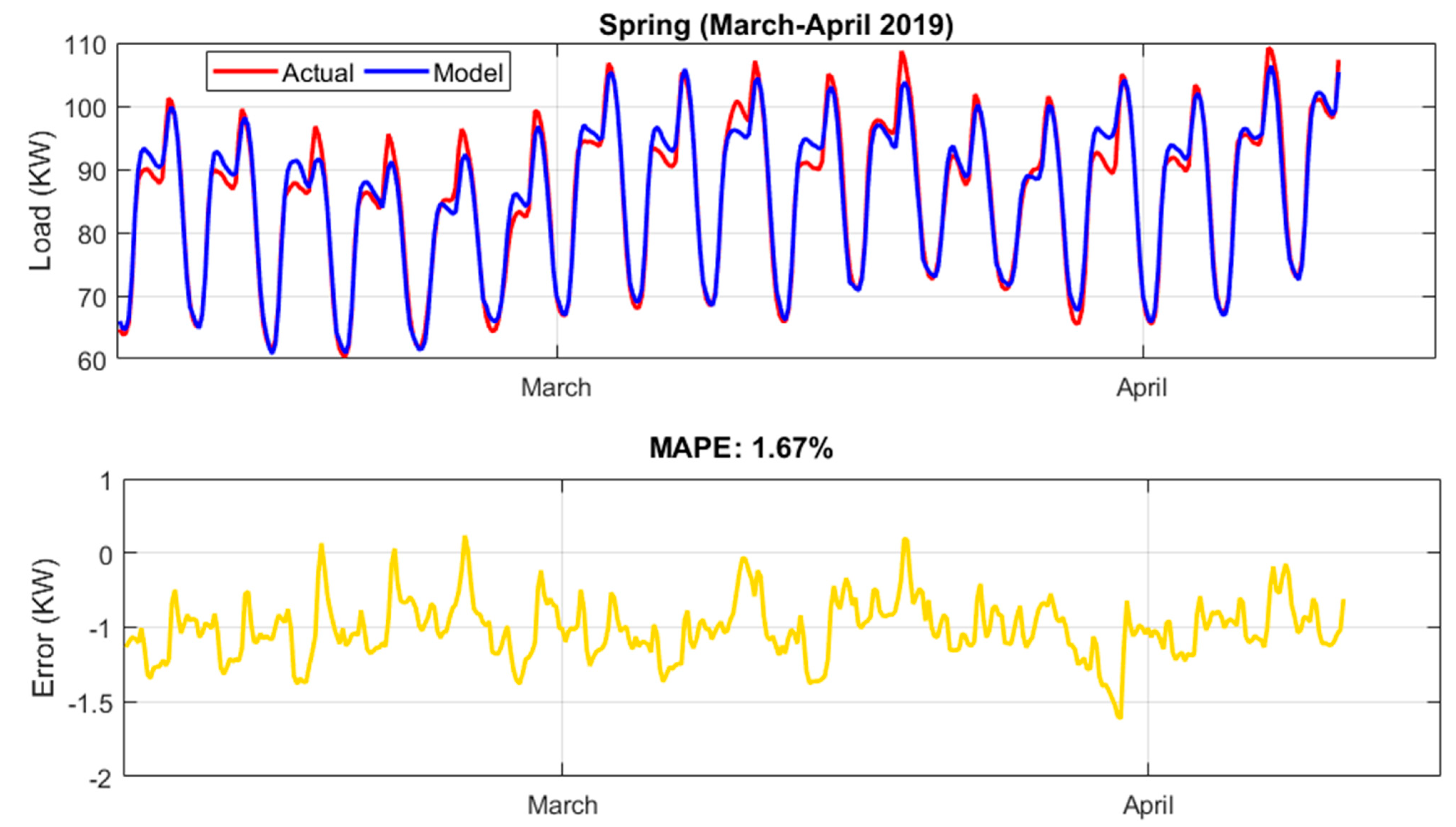
Spring (April–June)	2.29	Spring	1.80	Spring	1.67

.

Although the results of our research work are promising and desirable, some limitations of this study are that a new variety of data input like the probability of load shedding, faults occurring, and power failure of the region can also be considered. In addition, seven regression methods are adopted in time series and autoregression algorithms, but this model can consider more AR methods for accurate data preprocessing. Despite these trivial limitations, our trial with a large dataset is sped up and beneficial for the researchers, as it obtained a MAPE of less than 2%.

6. Conclusions and Future Studies

LF is a key tool for better planning and operation of power generation systems in smart grid applications. This paper proposes a new combinational forecasting model based on the following: time series and autoregression algorithm for data fetching, ML-based feedback ANFIS, BGA-PCA algorithm for best feature selection, and a proposed integration strategy for MAPE calculation. We presented a new time series and autoregression algorithm for analyzing the more complex and massive historical data. The time series AR model is further validated using the ML-based feedback ANFIS model where five stages are computed. The BGA-PCA approach for attaining the best feature selection is evaluated and attained more optimized results. A remarkable improvement in MAPE and average MAPE have been achieved by a proposed integration strategy, which gives a 17% better annual improvement compared to previous ones. Mainly, the attained MAPE are as follows: 1.70, 1.77, 1.80, and 1.67 percentage for Summer, Fall, Winter, and Spring, respectively. This model can optimize the performance of power grids by predicting the optimized LF and can overcome the problems related to the planning and operation of the smart grid.

In the future, this proposed model can be implemented for LF with various time horizon locations to validate its effectiveness. Moreover, by taking a new variety of data input for economic studies, the model can be implemented for price forecasting in financial applications. Lastly, we plan to do stability analysis to check the stability of our model through various data sizes of statistically significant data.