Spatial–Temporal Heterogeneity and the Related Influencing Factors of Tourism Efficiency in China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Super-Efficiency SBM Model
2.2. Malmquist Index Model
2.3. Exploratory Spatial Data Analysis (ESDA) Method
2.4. Geographically Weighted Regression (GWR) Model
3. Methods and Data Source
3.1. Selection of Tourism Indexes
3.2. Indexes in Geographic Weighted Regression (GWR) Model
3.3. Data Sources
4. Analysis of Results
4.1. Static Analysis of Tourism Efficiency
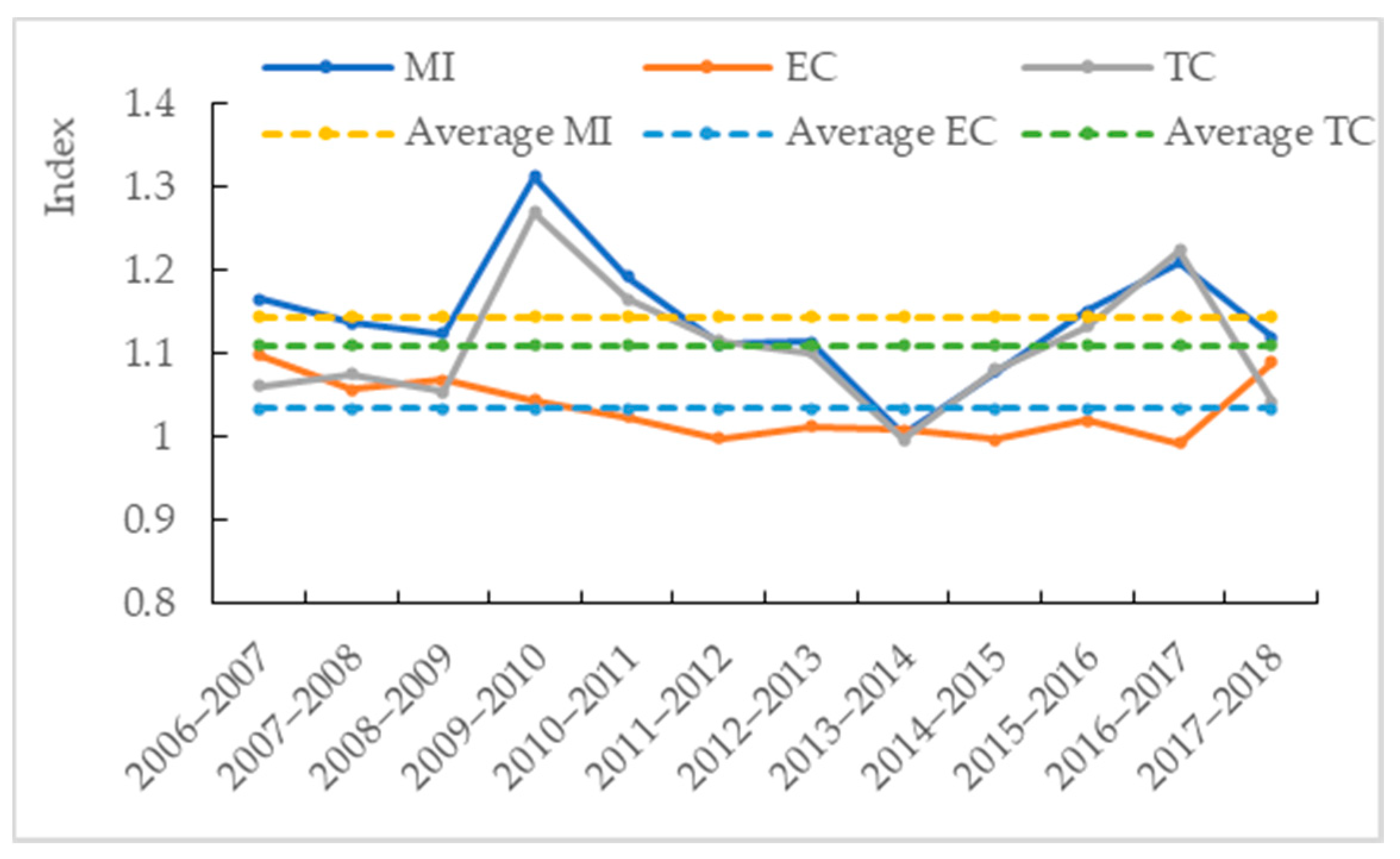
4.2. Dynamic Variation Tendency of Tourism Efficiency
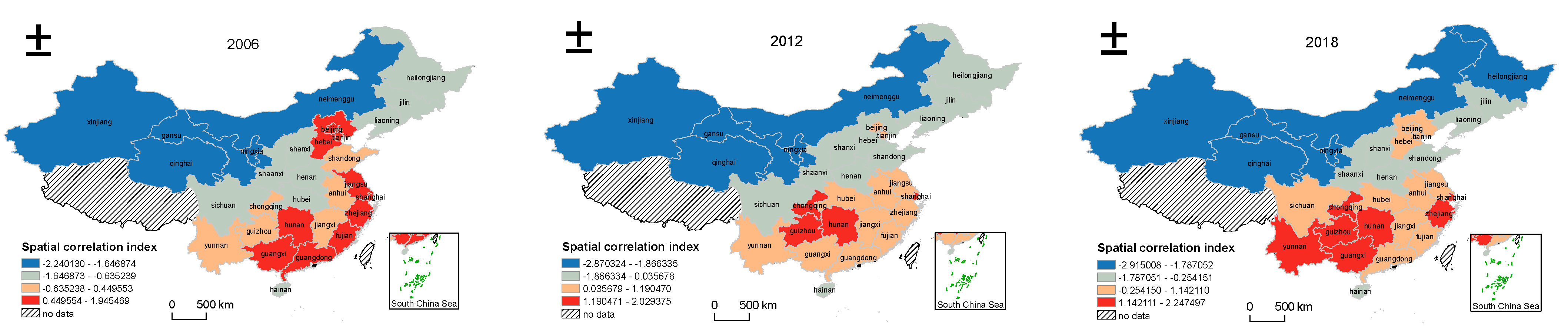
4.3. Spatial–Temporal Differentiation Characteristics of Tourism Efficiency in China
4.4. Analysis of the Influencing Factors of Tourism Efficiency
4.4.1. Validation of GWR Model
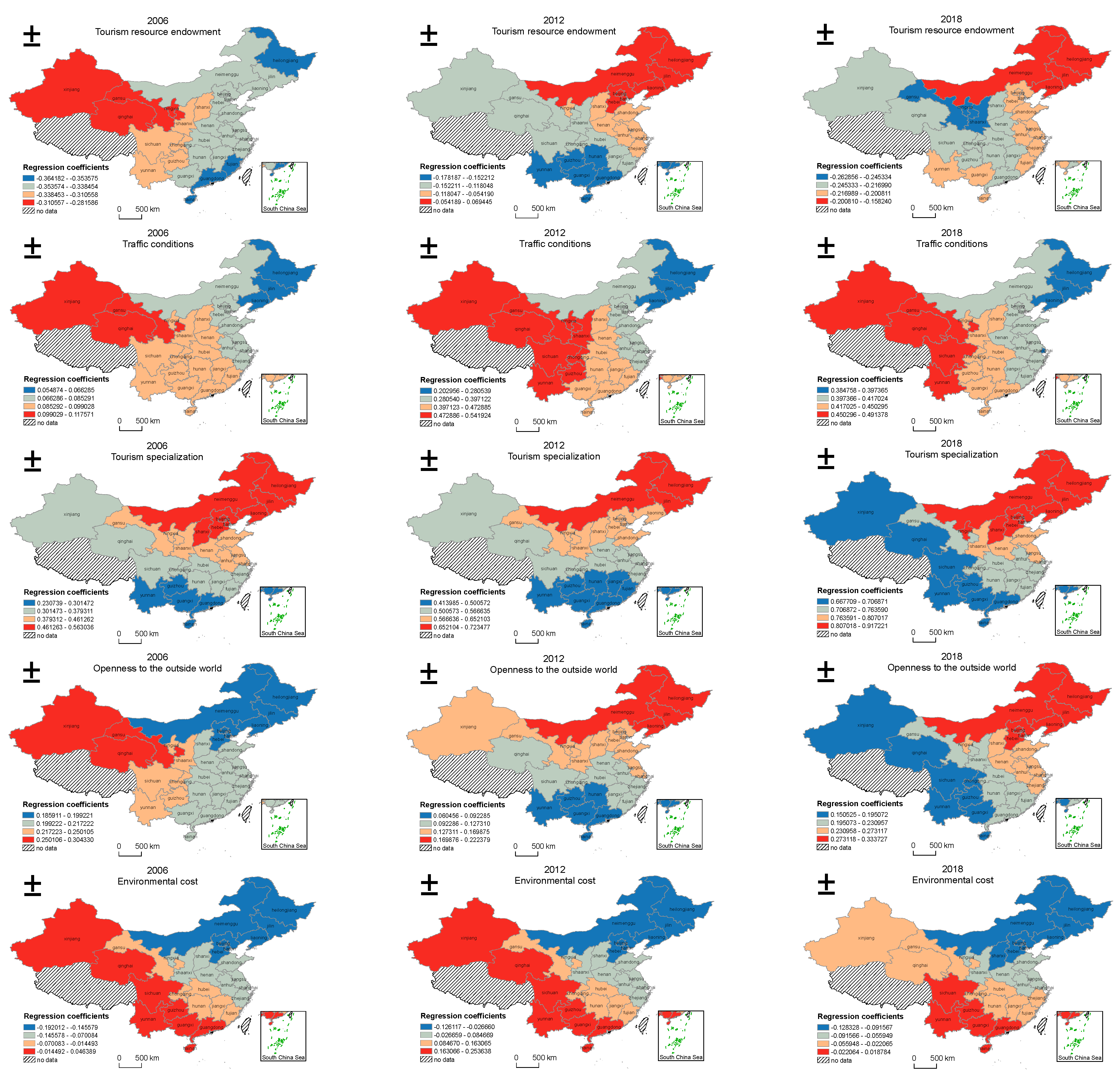
4.4.2. Analysis of the Spatial Heterogeneity of the Influencing Factors
5. Conclusions and Discussion
5.1. Conclusions
5.2. Policy Suggestions
5.3. Limitations and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Organiztion, W.T. UNWTO Annual Report 2019; UNWTO: Madrid, Spain, 2019. [Google Scholar]
- Ministry of Culture and Tourism of the People’s Republic of China; Statistical Bulletin of Culture and Tourism Development in 2018; Ministry of Culture and Tourism: Beijing, China, 2019.
- Hadad, S.; Hadad, Y.; Malul, M.; Rosenboim, M. The economic efficiency of the tourism industry: A global comparison. Tour. Econ. 2012, 18, 931–940. [Google Scholar] [CrossRef]
- Ma, X. Progress and trends of tourism efficiency research home and abroad. Hum. Geogr. 2012, 27, 11–17. [Google Scholar]
- Köksal, C.D.; Aksu, A.A. Efficiency evaluation of A-group travel agencies with data envelopment analysis (DEA): A case study in the Antalya region, Turkey. Tour. Manag. 2007, 28, 830–834. [Google Scholar] [CrossRef]
- Barros, C.P. Airports in Argentina: Technical efficiency in the context of an economic crisis. J. Air Transp. Manag. 2008, 14, 315–319. [Google Scholar] [CrossRef]
- Sarkis, J.; Talluri, S. Performance based clustering for benchmarking of US airports. Transp. Res. Part A Policy Pract. 2004, 38, 329–346. [Google Scholar] [CrossRef]
- Fuentes, R. Efficiency of travel agencies: A case study of Alicante, Spain. Tour. Manag. 2011, 32, 75–87. [Google Scholar] [CrossRef]
- Assaf, A.; Barros, C.P.; Josiassen, A. Hotel efficiency: A bootstrapped metafrontier approach. Int. J. Hosp. Manag. 2010, 29, 468–475. [Google Scholar] [CrossRef]
- Barros, C.P. Analysing the rate of technical change in the Portuguese hotel industry. Tour. Econ. 2006, 12, 325–346. [Google Scholar] [CrossRef]
- Aurélie, C. Benchmarking and tourism efficiency in France. Tour. Econ. 2015, 51, 91–95. [Google Scholar]
- Ane, E.R.; Josep, M.R. Tourism indicators and airports’ technical efficiency. Ann. Tour. Res. 2020, 80, 102819. [Google Scholar]
- lo Storto, C. The analysis of the cost-revenue production cycle efficiency of the Italian airports: A NSBM DEA approach. J. Air Transp. Manag. 2018, 72, 77–85. [Google Scholar] [CrossRef]
- Assaf, A.G.; Dwyer, L. Benchmarking international tourism destinations. Tour. Econ. 2013, 19, 1233–1247. [Google Scholar] [CrossRef] [Green Version]
- Bosetti, V.; Locatelli, G. A data envelopment analysis approach to the assessment of natural park s economic efficiency and sustainability: The case of Italian natural parks. Sustain. Dev. 2006, 14, 277–286. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.K.; Han, S.H. Estimating the use and preservation values of national parks’ tourism resources using a contingent valuation method. Tour. Manag. 2002, 23, 531–540. [Google Scholar] [CrossRef]
- Baggio, R.; Micera, R.; Del Chiappa, G. Smart tourism destinations: A critical reflection. J. Hosp. Tour. Technol. 2020, 11, 407–423. [Google Scholar] [CrossRef]
- Cuccia, T.; Guccio, C.; Rizzo, I. The effects of UNESCO World Heritage List inscription on tourism destinations performance in talian regions. Econ. Model. 2016, 53, 494–508. [Google Scholar] [CrossRef]
- Peypoch, N.; Solonandrasana, B. Aggregate efficiency and productivity analysis in the tourism industry. Tour. Econ. 2008, 14, 45–56. [Google Scholar] [CrossRef]
- Goncalves, O. Efficiency and productivity of French ski resorts. Tour. Manag. 2013, 36, 650–657. [Google Scholar] [CrossRef]
- Assaf, A.; Agbola, F.W. Total productivity in the Australian hotel industry: Estimating and bootstrapping Malmquist indices. Tour. Anal. 2011, 16, 295–304. [Google Scholar] [CrossRef] [Green Version]
- Barros, C.P.; Alves, F.P. Productivity in the tourism industry. Int. Adv. Econ. Res. 2004, 10, 215–225. [Google Scholar] [CrossRef]
- Jiang, L.; Shao, H.; Wang, K. A research on space-time heterogeneity of tourism efficiency and influencing factors in China. Tour. Res. 2018, 10, 20–30. [Google Scholar]
- Zhang, Y. Spatial and temporal evolution of star-rated hotels’ efficiency in China based on DEA-Malmquist model. Sci. Geogr. Sin. 2017, 37, 406–415. [Google Scholar]
- Sun, J.; Zhang, J.; Zhang, J.; Ma, J.; Li, L. Spatial differentiation of efficiency of Chinese regional travel service industry. Sci. Geogr. Sin. 2014, 34, 430–437. [Google Scholar]
- Wang, S.; Qiao, H.; Feng, J.; Xie, S. The spatio-temporal evolution of tourism eco-efficiency in the Yellow River Basin and its interactive response with tourism economy development level. Econ. Geogr. 2020, 40, 81–89. [Google Scholar]
- Wang, Z.; Liu, Q. The spatio-temporal evolution of tourism eco-efficiency in the Yangtze River Economic Belt and its interactive response with tourism economy. J. Nat. Resour. 2019, 34, 1945–1961. [Google Scholar]
- Jiang, Y.; Pan, Z.; Pan, M. Spatial variation and strategic pattern optimization of operation efficiency of rural tourism in Chongqing. Resour. Sci. 2016, 38, 2181–2191. [Google Scholar]
- Long, Z.; Du, Q.; Zhou, T. The evolution of time and space differentiation of Wuling Mountain area tourism poverty alleviation efficiency. Econ. Geogr. 2015, 35, 210–217. [Google Scholar]
- Wang, H. A research on China’s tourism efficiency: A managerial and environmental perspective. Tour. Sci. 2014, 28, 31–40+53. [Google Scholar]
- Fang, Y.; Huang, Z.; Lu, W.; Peng, Q. Spatial differentiation of tourism economy and its mechanism in Chinese cities. Geogr. Geo-Inf. Sci. 2013, 29, 100–104, 110, 129. [Google Scholar]
- Wang, Z.; Zhao, S. Temporal and spatial dynamic evolution and influencing factors of tourism efficiency in Hunan Province based on DEA-Malmquist model. Resour. Environ. Yangtze Basin 2019, 28, 1886–1897. [Google Scholar]
- Lin, C.; Wen, J. Review and prospect of tourism efficiency research in China. J. Cent. South Univ. For. Technol. (Soc. Sci.) 2017, 11, 61–64, 70. [Google Scholar]
- Ji, X.; Qin, W.; Li, S.; Liu, X.; Wang, Q. Development efficiency of tourism and influencing factors in China’s prefectural-level administrative units. Resour. Sci. 2021, 43, 185–196. [Google Scholar]
- Gong, Y.; Guo, Z. A study on efficiency and countermeasures of tourism development in Jiangsu Province—Analyses based on super-efficiency DEA and Malmquist index. East China Econ. Manag. 2014, 28, 7–12, 17. [Google Scholar]
- Cao, Y.; Ma, L. Evaluation on the efficiency of tourism poverty alleviation in China’s ethnic regions based on the three-stage DEA. East China Econ. Manag. 2017, 31, 91–97. [Google Scholar]
- Zhu, C.; Yue, H.; Yan, H.; Li, T. Study on the efficiency of regional tourism industry in China based on stochastic frontline production and cost function estimation. Tour. Trib. 2009, 24, 18–22. [Google Scholar]
- You, S.; Lin, Z.; Han, Z. Spatial-temporal characteristics and growth mechanism of urban tourism efficiency in Guangdong Province. Resour. Sci. 2017, 39, 1545–1559. [Google Scholar]
- Wang, R.; Xia, B.; Dong, S.; Li, Y. Research on the Spatial Differentiation and Driving Forces of Eco-Efficiency of Regional Tourism in China. Sustainability 2021, 13, 280. [Google Scholar] [CrossRef]
- Kaoru, T. A Slacks-Based Measure of Super-Efficiency in Data Envelopment Analysis; Elsevier B.V.: Amsterdam, The Netherlands, 2002; Volume 143. [Google Scholar]
- Färe, R.; Grosskopf, S.; Lindgren, B.; Roos, P. Productivity Changes in Swedish Pharamacies 1980-1989: A Non-Parametric Malmquist Approach. Kluwer Acad. Publ. 1992, 3, 85–101. [Google Scholar]
- Li, J.; Zhou, C.; Zhang, C.; Liu, F.; Wang, J. Total-factor ecological efficiency of Dongting Lake Ecological and Economic Zone in Hunan Province on the basis of ecological footprint. Econ. Geogr. 2019, 39, 199–206. [Google Scholar]
- Ma, X.; Bao, J. Study on the evolution of Chinese primary cities’ tourism efficiency influence factors. Econ. Geogr. 2009, 29, 1203–1208. [Google Scholar]
- Han, Y.; Shi, Q.; Feng, W.; Zhou, X.; Li, X. Temporal spatial differences of tourism industry efficiency and the influencing factors in Shanxi province. J. Arid. Land Resour. Environ. 2019, 33, 187–194. [Google Scholar]
- Guo, X.; Mu, X.; Ming, Q. Spatial differences and driving factors of tourism efficiency in border regions—A case of Yunnan Province. World Reg. Stud. 2020, 29, 416–427. [Google Scholar]
- Deng, H.; Lu, L. The urban tourism efficiencies of cities in Anhui Province based on DEA model. J. Nat. Resour. 2014, 29, 313–323. [Google Scholar]
- Xie, Y.; Zhao, Y. Measuring carbon dioxide emissions from energy consumption by tourism in Yangtze River Delta. Geogr. Res. 2012, 31, 429–438. [Google Scholar]
- Wu, Y.; Song, Y. Spatio-temporal pattern evolution and driving factors of tourism efficiency in Northeast China. Areal Res. Dev. 2019, 38, 85–90. [Google Scholar]

| Year | Mean | Coefficient of Variation | ρ ≥ 1 | 0.8 ≤ ρ < 1 | 0.6 ≤ ρ < 0.8 | ρ ≤ 0.6 |
|---|---|---|---|---|---|---|
| 2006 | 0.609 | 0.486 | 5 | 0 | 5 | 20 |
| 2007 | 0.665 | 0.472 | 7 | 1 | 4 | 18 |
| 2008 | 0.701 | 0.474 | 9 | 0 | 6 | 15 |
| 2009 | 0.741 | 0.451 | 10 | 0 | 9 | 11 |
| 2010 | 0.751 | 0.418 | 11 | 0 | 9 | 10 |
| 2011 | 0.766 | 0.408 | 10 | 4 | 6 | 10 |
| 2012 | 0.758 | 0.391 | 10 | 3 | 8 | 9 |
| 2013 | 0.766 | 0.390 | 9 | 4 | 8 | 9 |
| 2014 | 0.760 | 0.386 | 9 | 3 | 10 | 8 |
| 2015 | 0.761 | 0.403 | 10 | 2 | 10 | 8 |
| 2016 | 0.767 | 0.393 | 9 | 3 | 11 | 7 |
| 2017 | 0.771 | 0.432 | 12 | 2 | 6 | 10 |
| 2018 | 0.807 | 0.416 | 12 | 2 | 6 | 10 |
| DMU | 2006 | 2012 | 2018 | Mean | DMU | 2006 | 2012 | 2018 | Mean |
|---|---|---|---|---|---|---|---|---|---|
| Beijing | 1.035 | 1.045 | 1.068 | 1.059 | Henan | 0.685 | 0.838 | 0.821 | 0.896 |
| Tianjin | 1.279 | 1.182 | 1.155 | 1.253 | Hubei | 0.474 | 0.816 | 0.844 | 0.728 |
| Hebei | 0.459 | 0.507 | 0.522 | 0.510 | Hunan | 0.500 | 0.756 | 0.851 | 0.739 |
| Liaoning | 0.543 | 0.850 | 1.018 | 0.765 | Central region mean | 0.522 | 0.822 | 0.814 | 0.757 |
| Shanghai | 1.125 | 1.171 | 1.329 | 1.175 | Chongqing | 0.658 | 1.102 | 1.144 | 1.046 |
| Jiangsu | 1.007 | 1.014 | 1.015 | 0.963 | Sichuan | 0.706 | 1.076 | 1.059 | 0.970 |
| Zhejiang | 0.529 | 0.705 | 0.764 | 0.687 | Guizhou | 0.606 | 1.121 | 1.594 | 1.170 |
| Fujian | 0.684 | 0.609 | 1.003 | 0.711 | Yunnan | 0.438 | 0.575 | 0.685 | 0.602 |
| Shandong | 0.562 | 0.678 | 0.589 | 0.628 | Shaanxi | 0.590 | 0.750 | 0.770 | 0.715 |
| Guangdong | 1.465 | 1.111 | 1.075 | 1.234 | Gansu | 0.301 | 0.374 | 0.519 | 0.386 |
| Hainan | 0.405 | 0.415 | 0.502 | 0.436 | Qinghai | 0.292 | 0.277 | 0.249 | 0.273 |
| Eastern region mean | 0.827 | 0.844 | 0.913 | 0.856 | Ningxia | 0.275 | 0.267 | 0.246 | 0.273 |
| Shanxi | 0.546 | 0.639 | 1.062 | 0.752 | Xinjiang | 0.229 | 0.276 | 0.285 | 0.257 |
| Jilin | 0.474 | 0.585 | 0.591 | 0.587 | Guangxi | 0.568 | 0.744 | 0.858 | 0.722 |
| Heilongjiang | 0.582 | 1.117 | 0.466 | 0.794 | Inner Mongolia | 0.333 | 0.317 | 0.257 | 0.319 |
| Anhui | 0.469 | 0.774 | 0.846 | 0.730 | Western region mean | 0.454 | 0.625 | 0.697 | 0.612 |
| Jiangxi | 0.450 | 1.047 | 1.031 | 0.826 |
| Year | Eastern China | Central China | Western China | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MI | EC | TC | MI | EC | TC | MI | EC | TC | |
| 2006–2007 | 1.102 | 1.038 | 1.060 | 1.268 | 1.176 | 1.074 | 1.156 | 1.101 | 1.052 |
| 2007–2008 | 1.073 | 1.000 | 1.077 | 1.203 | 1.107 | 1.085 | 1.151 | 1.079 | 1.067 |
| 2008–2009 | 1.112 | 1.030 | 1.080 | 1.142 | 1.115 | 1.025 | 1.123 | 1.072 | 1.048 |
| 2009–2010 | 1.341 | 1.059 | 1.263 | 1.379 | 1.071 | 1.330 | 1.236 | 1.009 | 1.232 |
| 2010–2011 | 1.127 | 0.989 | 1.139 | 1.293 | 1.075 | 1.203 | 1.187 | 1.021 | 1.163 |
| 2011–2012 | 1.076 | 0.978 | 1.104 | 1.158 | 1.023 | 1.134 | 1.114 | 1.001 | 1.114 |
| 2012–2013 | 1.096 | 0.992 | 1.111 | 1.162 | 1.042 | 1.116 | 1.096 | 1.013 | 1.082 |
| 2013–2014 | 1.037 | 1.017 | 1.020 | 0.951 | 0.976 | 0.978 | 1.010 | 1.024 | 0.987 |
| 2014–2015 | 1.084 | 1.014 | 1.069 | 1.139 | 0.997 | 1.143 | 1.028 | 0.981 | 1.049 |
| 2015–2016 | 1.149 | 1.029 | 1.124 | 1.145 | 0.979 | 1.170 | 1.158 | 1.040 | 1.113 |
| 2016–2017 | 1.130 | 0.964 | 1.173 | 1.364 | 1.083 | 1.271 | 1.178 | 0.958 | 1.242 |
| 2017–2018 | 1.143 | 1.146 | 1.009 | 1.050 | 1.007 | 1.061 | 1.147 | 1.094 | 1.065 |
| Mean value | 1.123 | 1.021 | 1.102 | 1.188 | 1.054 | 1.132 | 1.132 | 1.033 | 1.101 |
| Variation coefficient | 0.065 | 0.045 | 0.060 | 0.100 | 0.056 | 0.085 | 0.054 | 0.042 | 0.067 |
| Year | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Moran’s I | 0.2407 | 0.2104 | 0.1277 | 0.1526 | 0.1879 | 0.2450 | 0.2286 | 0.2261 | 0.3192 | 0.3155 | 0.2771 | 0.3725 | 0.3170 |
| Z-score | 2.3424 | 2.0346 | 1.3339 | 1.5296 | 1.8022 | 2.2671 | 2.1342 | 2.1202 | 2.8806 | 2.8472 | 2.5392 | 3.3153 | 2.8901 |
| p-value | 0.0192 | 0.0419 | 0.1822 | 0.1261 | 0.0715 | 0.0234 | 0.0328 | 0.0340 | 0.0040 | 0.0044 | 0.0111 | 0.0009 | 0.0039 |
| Year | Variance Inflation Factor (VIF) | Number of Conditions | |||||
|---|---|---|---|---|---|---|---|
| ED | TRE | TC | TS | OD | EC | ||
| 2006 | 9.27 | 3.45 | 2.16 | 2.95 | 3.15 | 5.3 | 17.18–19.88 |
| 2012 | — | 2.26 | 2.05 | 1.74 | 1.58 | 2.59 | 11.81–13.09 |
| 2018 | 4.26 | 2.42 | 1.6 | 2.5 | 2.18 | 2.71 | 12.65–14.91 |
| Test Items | 2006 | 2012 | 2018 |
|---|---|---|---|
| R2 | 0.854 | 0.673 | 0.782 |
| Adjusted R2 | 0.777 | 0.527 | 0.67 |
| Local R2 | 0.794–0.854 | 0.524–0.756 | 0.674–0.804 |
| Residual sum of squares | 0.14 | 0.172 | 0.193 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Lu, C.; Mao, J.; Sun, D.; Li, H.; Lu, C. Spatial–Temporal Heterogeneity and the Related Influencing Factors of Tourism Efficiency in China. Sustainability 2021, 13, 5825. https://doi.org/10.3390/su13115825
Liu Z, Lu C, Mao J, Sun D, Li H, Lu C. Spatial–Temporal Heterogeneity and the Related Influencing Factors of Tourism Efficiency in China. Sustainability. 2021; 13(11):5825. https://doi.org/10.3390/su13115825
Chicago/Turabian StyleLiu, Zhiliang, Chengpeng Lu, Jinhuang Mao, Dongqi Sun, Hengji Li, and Chenyu Lu. 2021. "Spatial–Temporal Heterogeneity and the Related Influencing Factors of Tourism Efficiency in China" Sustainability 13, no. 11: 5825. https://doi.org/10.3390/su13115825
APA StyleLiu, Z., Lu, C., Mao, J., Sun, D., Li, H., & Lu, C. (2021). Spatial–Temporal Heterogeneity and the Related Influencing Factors of Tourism Efficiency in China. Sustainability, 13(11), 5825. https://doi.org/10.3390/su13115825







