Evaluation of Rural Dwellings’ Energy-Saving Retrofit with Adaptive Thermal Comfort Theory
Abstract
1. Introduction
2. Methods
2.1. Modeling
2.2. Building Energy-Saving Retrofit Methods
2.3. Energy-Saving Evaluation Method
2.4. Thermal Comfort Evaluation Method
2.5. Entropy Weight Decision-Making Method
- Data normalization: Assuming that the original matrix of entropy evaluation is X, X = (xij) n × k (I = 1, 2, …, n; j = 1, 2, …, k); the normalized matrix is Y, and the elements of Y are calculated in Equations (10) and (11) [67]:
- Calculation of index entropy Ej [68]:where, in order to make lnPij meaningful, when Pij = 0, assume that Pij × lnPij = 0. However, when Pij = 1, Pij × lnPij = 0, which is inconsistent with reality and will introduce errors to the analysis results. Therefore, Pij needs to be corrected, as shown in Equation (13) [68]:
- Calculation of proximity Ti: The judgment matrix A after considering the entropy weight is as follows [68]:
3. Results
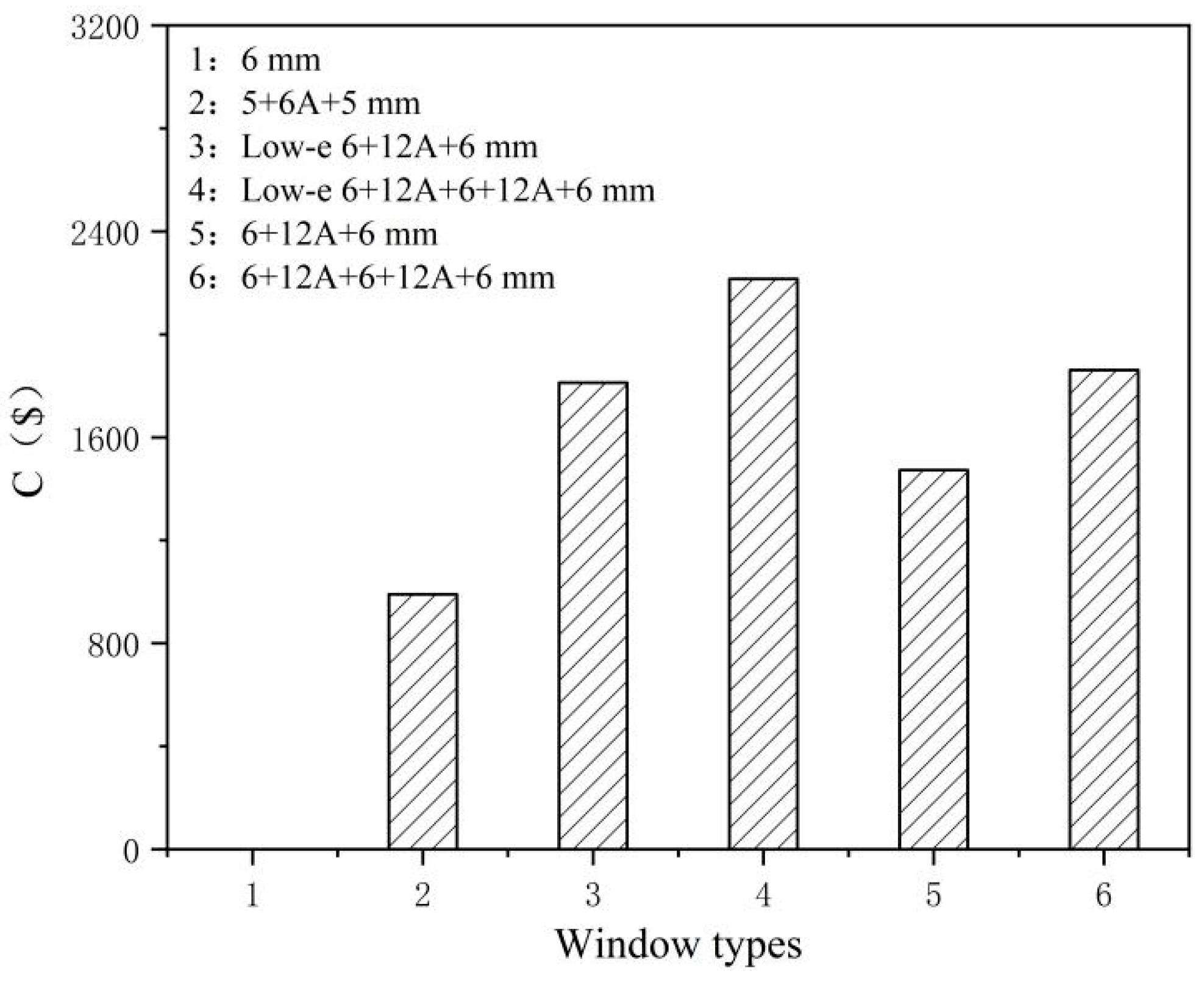
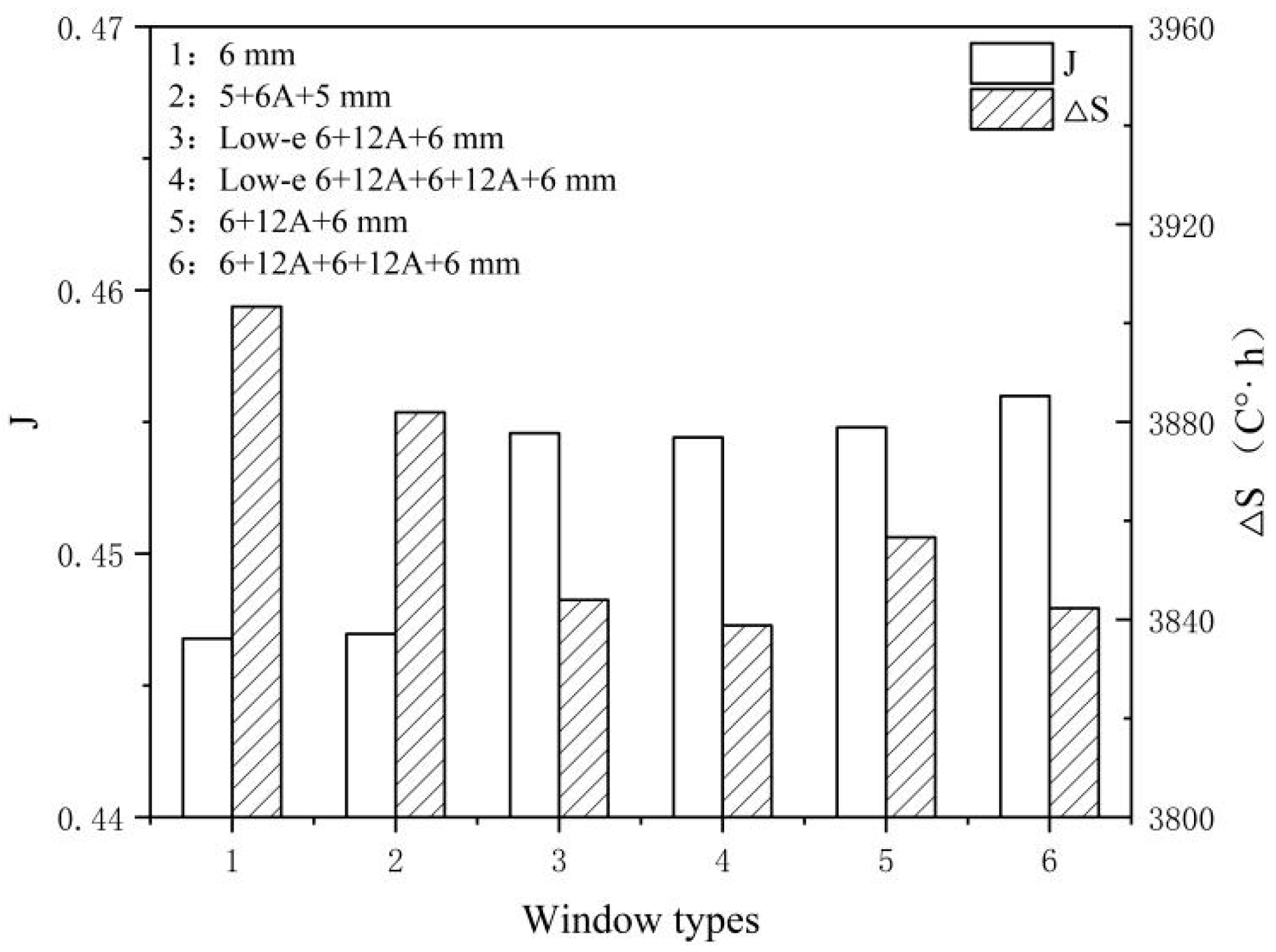
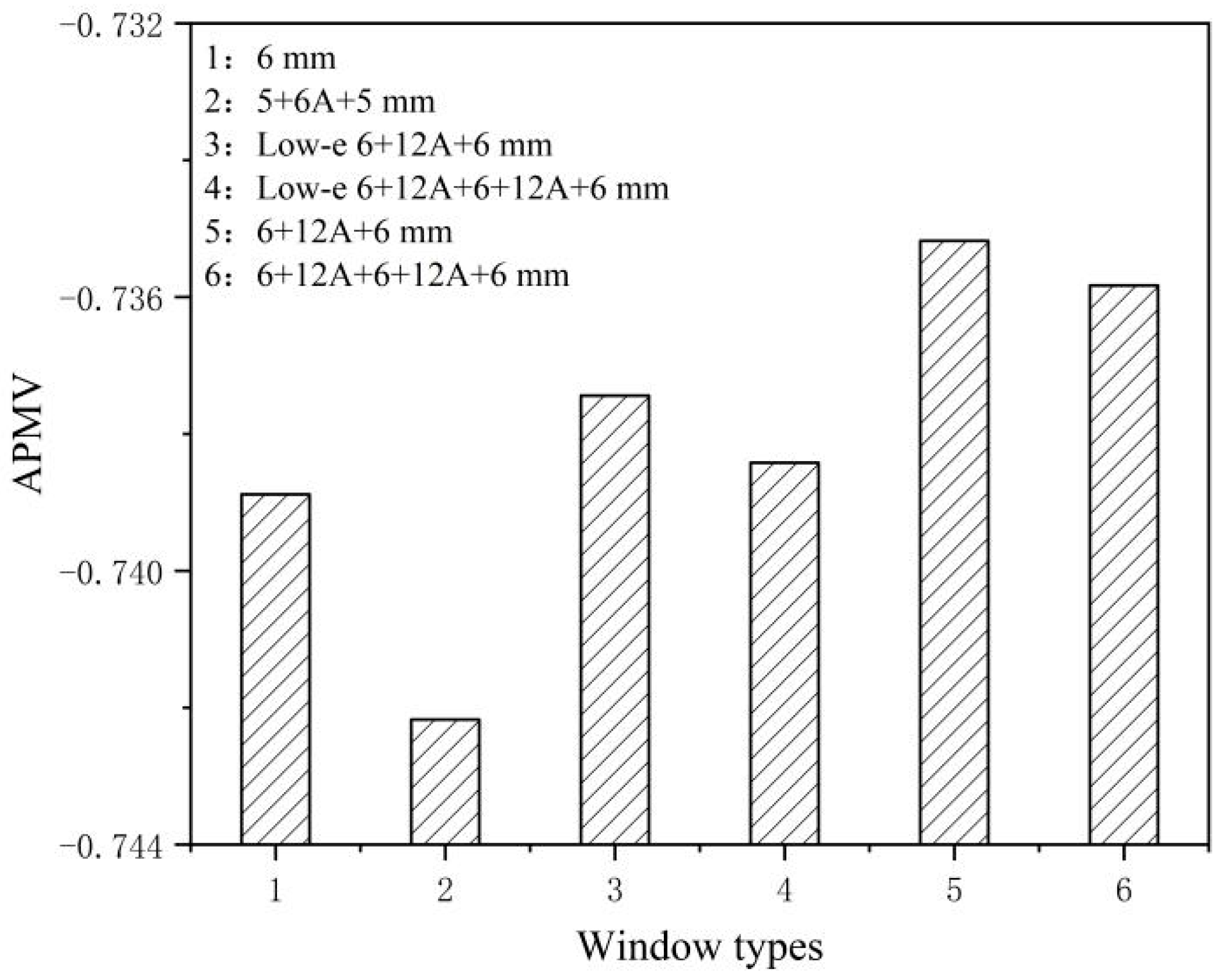
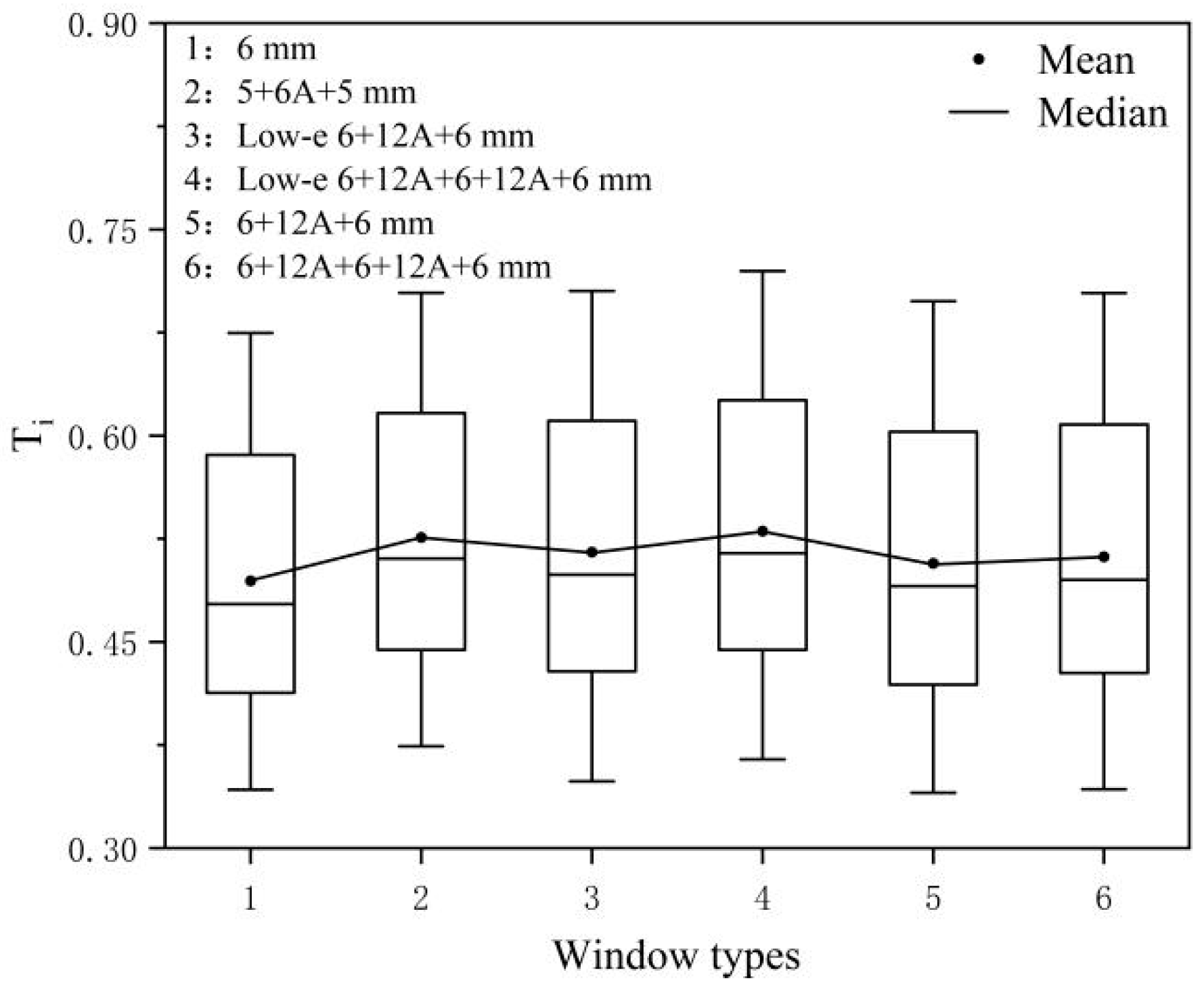
3.1. Energy-Saving Retrofit of External Windows
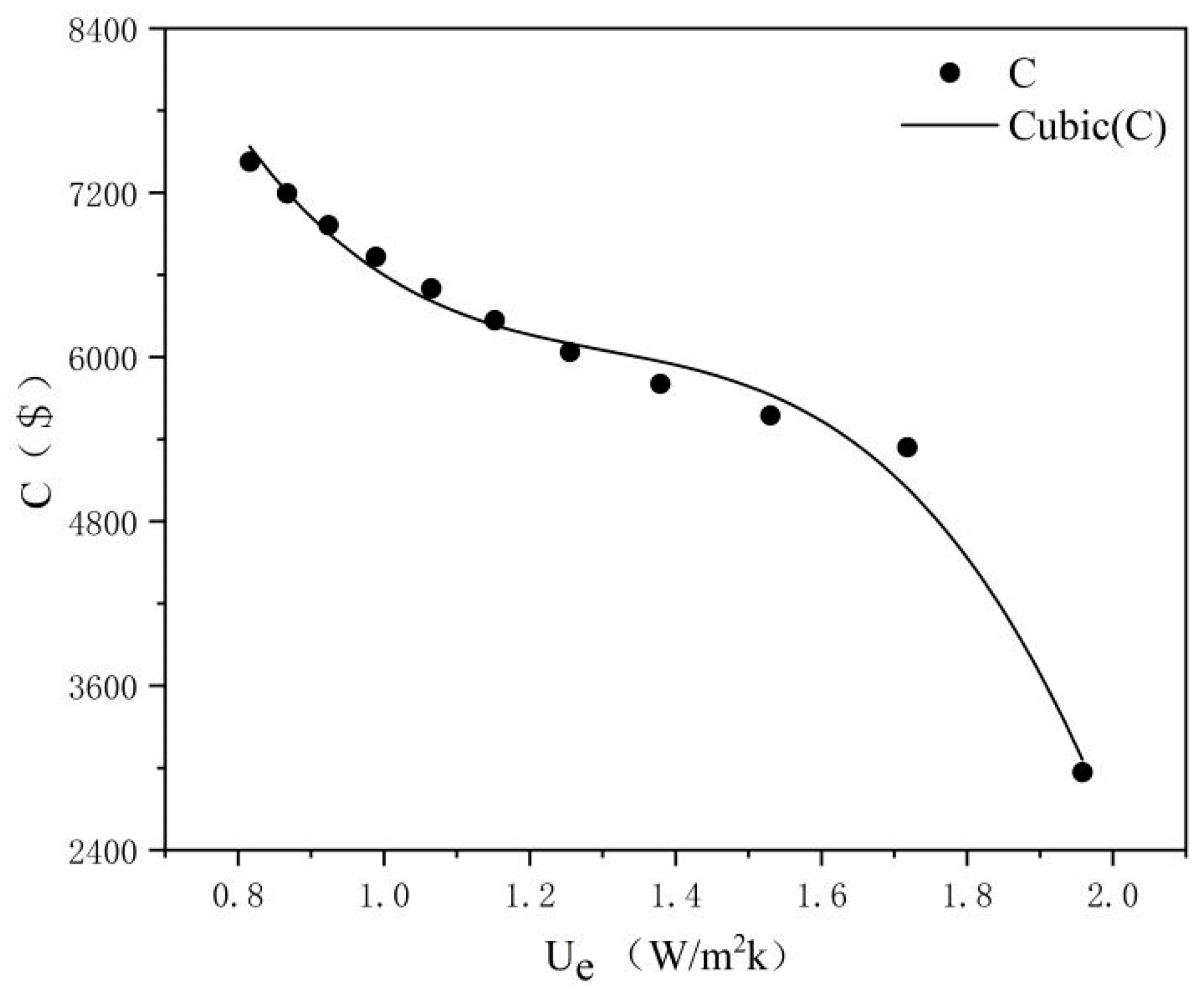
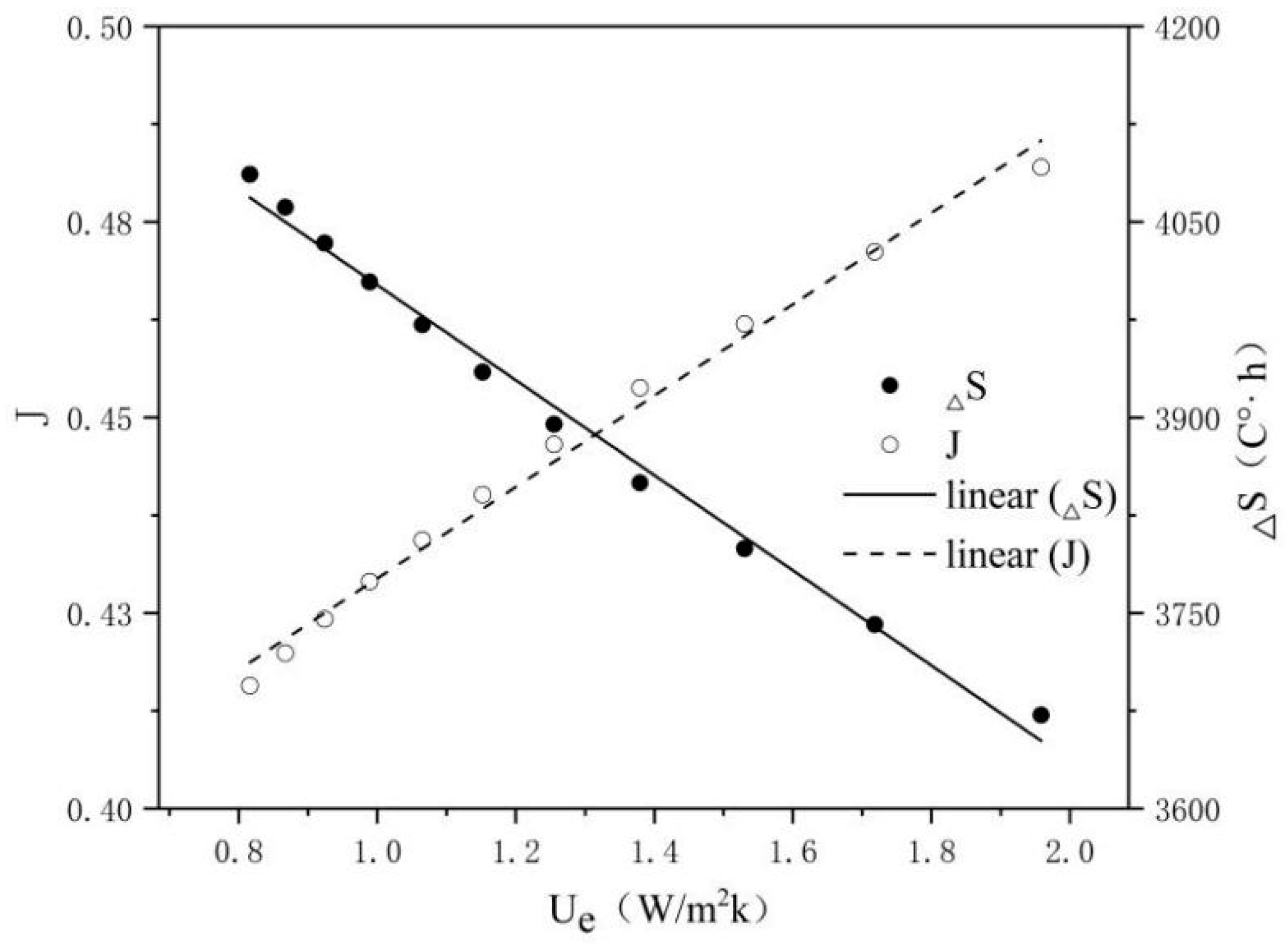
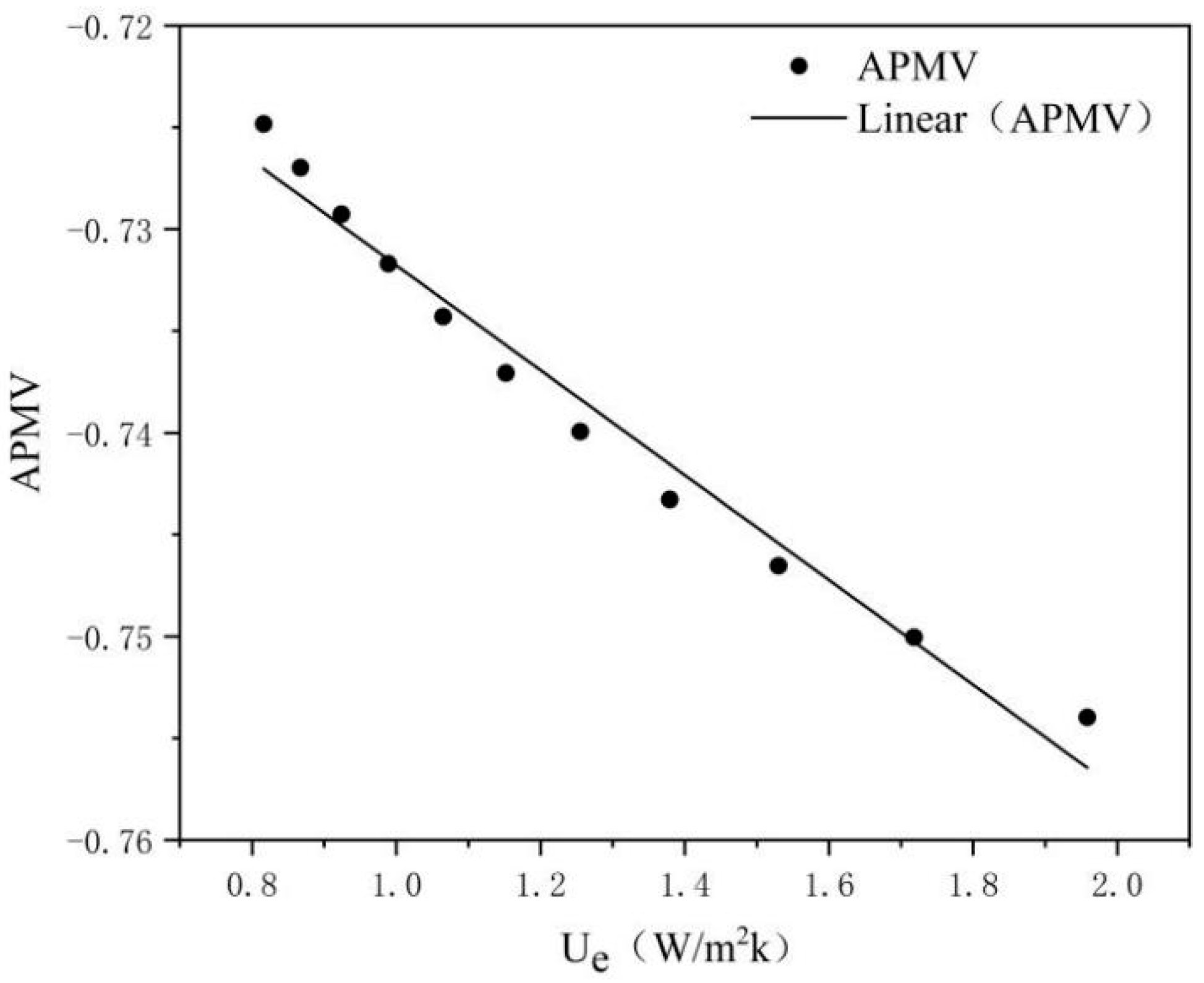
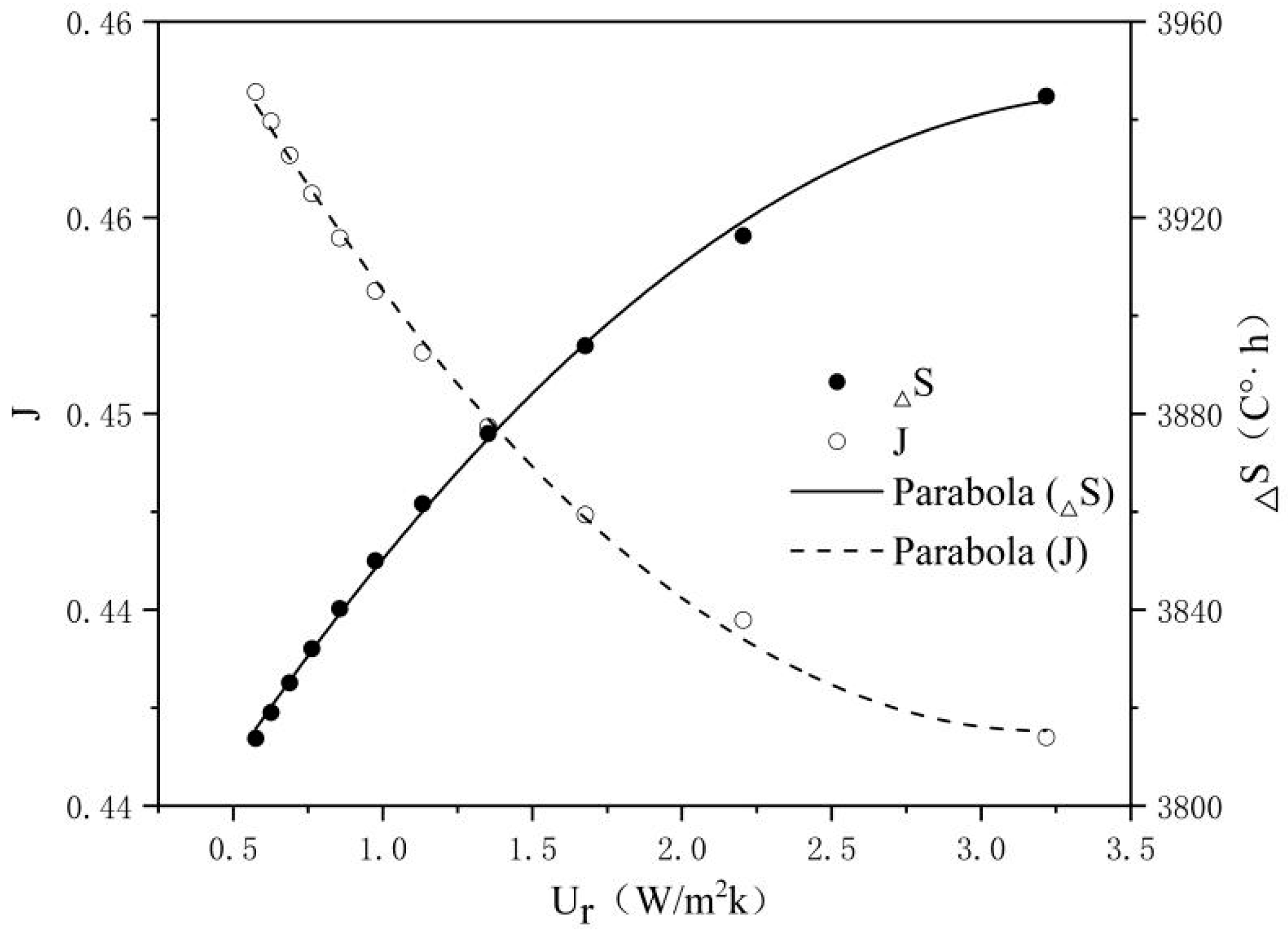
3.2. Energy-Saving Retrofit of the External Wall
3.3. Energy-Saving Retrofit of the Roof
4. Discussion
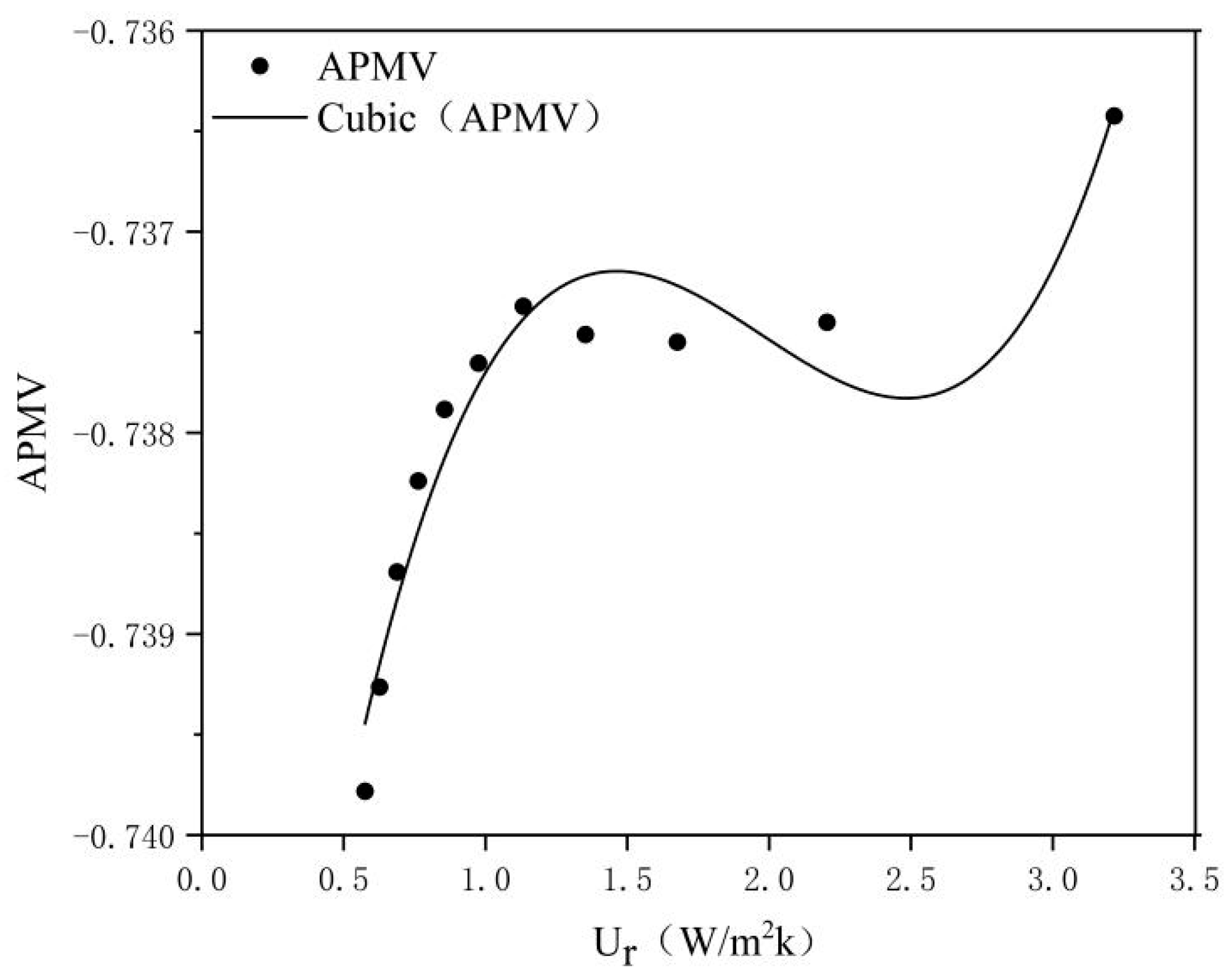
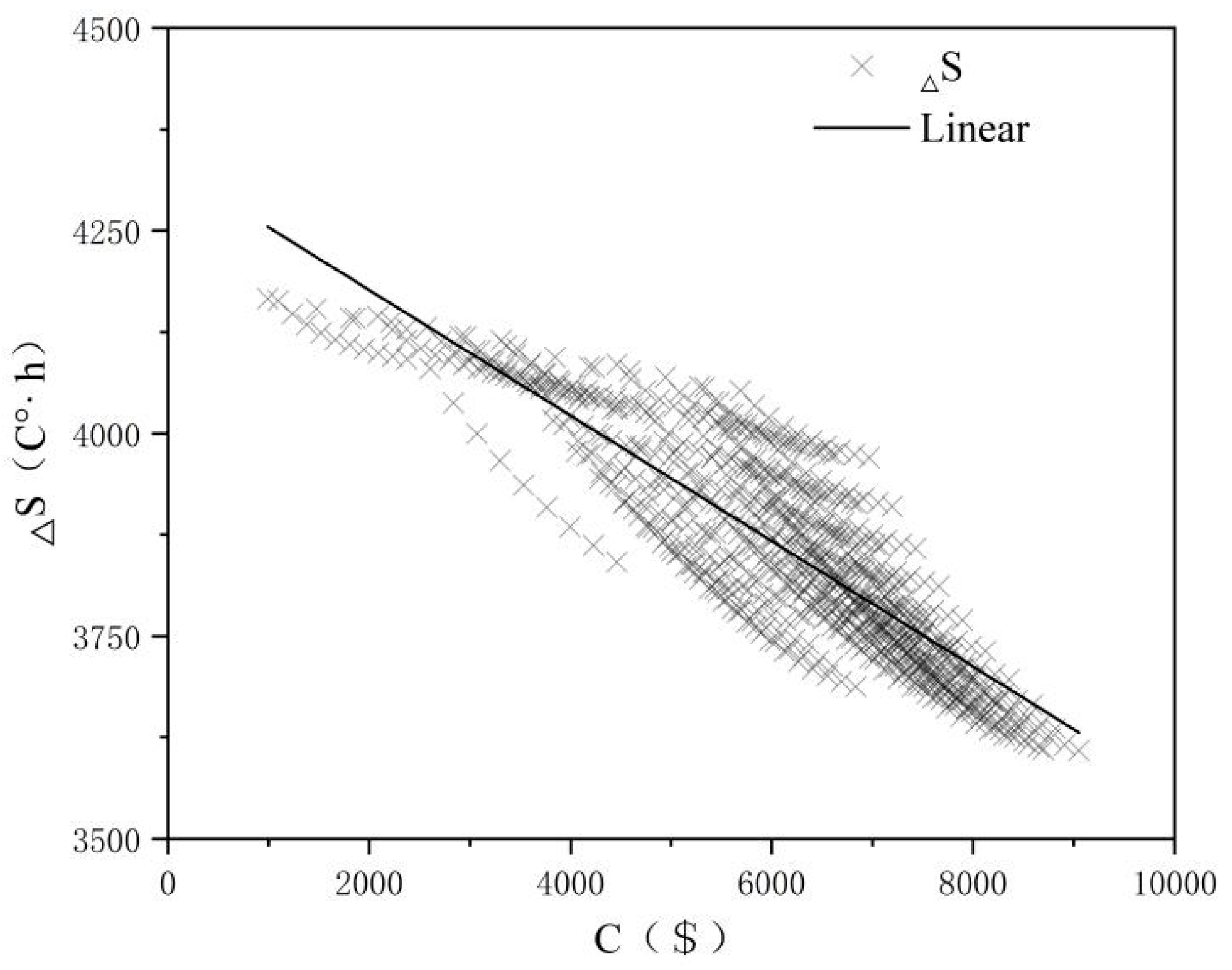
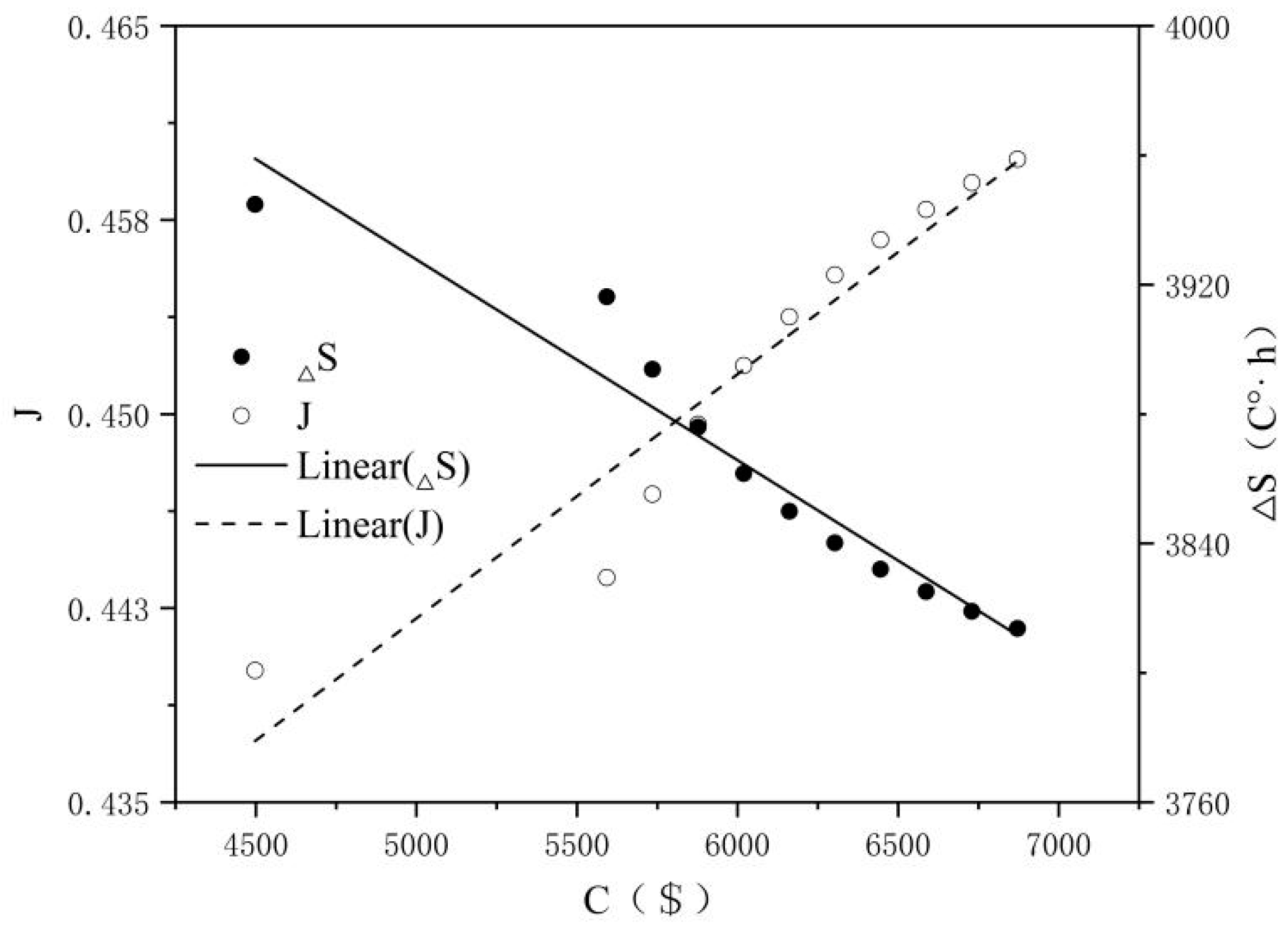
4.1. The Impact of Costs on the Energy Saving Rate and Thermal Comfort
4.2. The Impact of Costs on Different Retrofit Measures
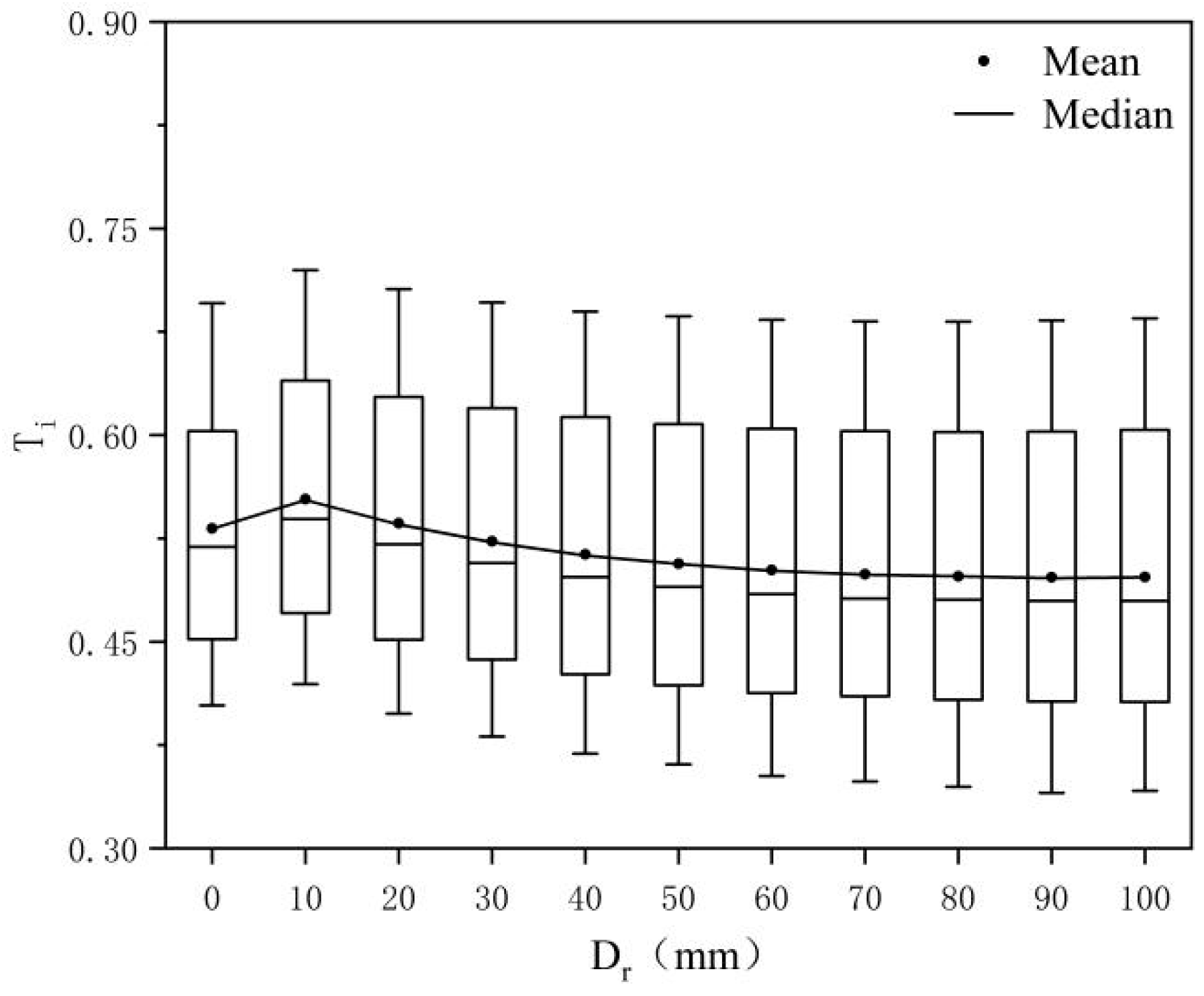
4.3. Entropy Weight Optimization Analysis
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Uw | external window heat transfer coefficient (W/m2K) |
| Ue | external wall heat transfer coefficient (W/m2K) |
| Ur | roof heat transfer coefficient (W/m2K) |
| De | external wall insulation thickness (mm) |
| Dr | roof insulation thickness (mm) |
| C | retrofit costs ($) |
| J | energy-saving contribution rate of envelope structure (referred to as the “energy-saving rate”) [19] |
| Tout | outdoor air temperature (°C) |
| Tin | mean indoor operative temperature (°C) |
| Tn | indoor comfortable temperature (°C) |
| H | reference degree-hours (C°·h) |
| H1 | design degree-hours (C°·h) |
| ti | indoor operative temperature in a room (°C) |
| si | room floor area (m2) |
| N | the total number of rooms in the building model |
| PMV | predicted mean vote |
| APMV | adaptive predicted mean vote [64] |
| λ | adaptive coefficient [62] |
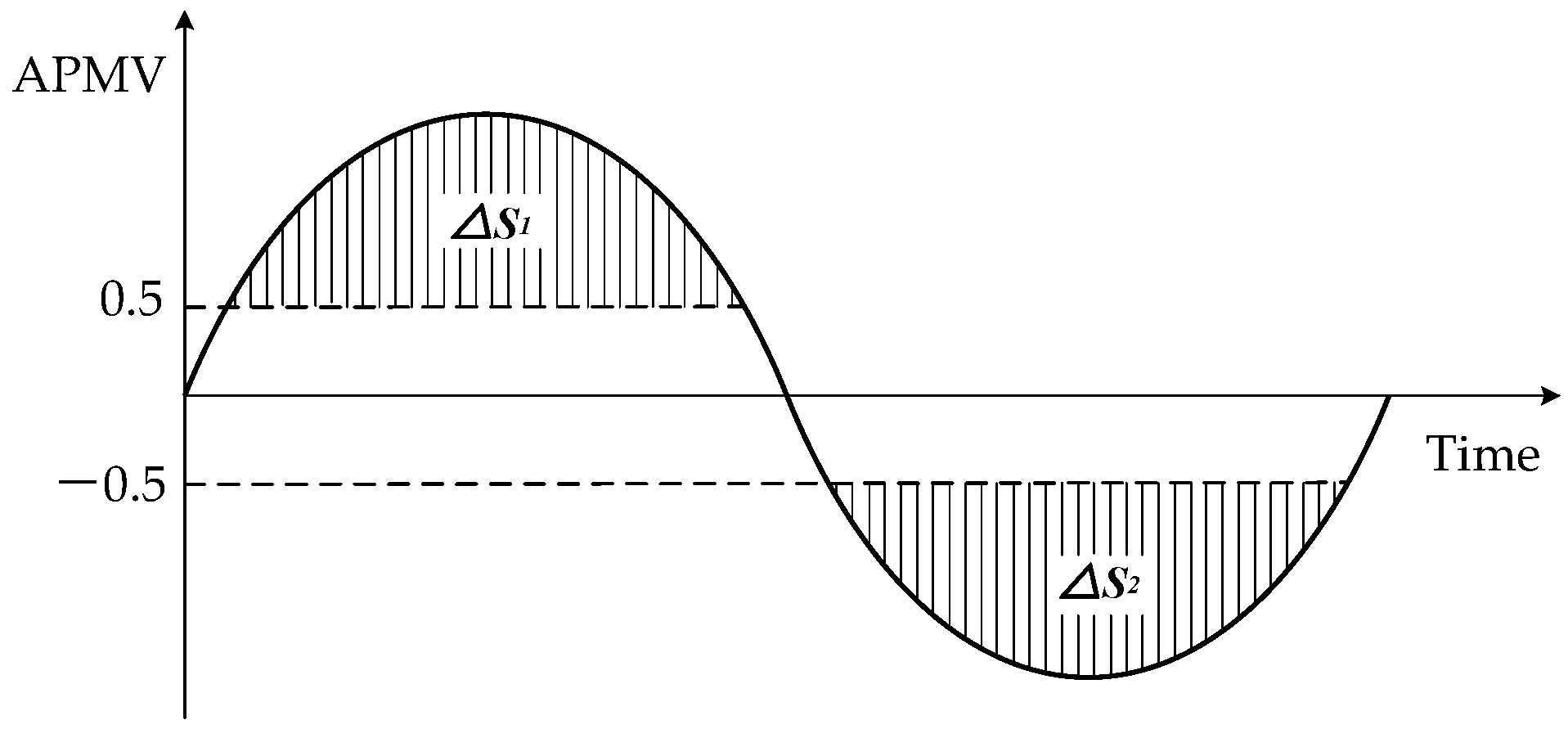
| ΔS | annual adaptive thermal discomfort degree-hours (C°·h) |
| ΔS1 | annual hot adaptive thermal discomfort degree-hours (C°·h) |
| ΔS2 | annual cold adaptive thermal discomfort degree-hours (C°·h) |
| ΔAPMV | degree of adaptive thermal discomfort |
| Ej | entropy |
| Wj | entropy weight |
| Ti | proximity [31] |
| mean proximity |
References
- 2020 Annual Report on China Building Energy Efficiency; Building Energy Efficiency Research Center of Tsinghua University: Beijing, China, 2020.
- Houkai, W.; Zhixiong, D. China Rural Development Report, 3rd ed.; China Social Sciences Press: Beijing, China, 2020; pp. 480–503. [Google Scholar]
- Ekici, B.B.; Gulten, A.A.; Aksoy, U.T. A study on the optimum insulation thicknesses of various types of external walls with respect to different materials, fuels and climate zones in Turkey. Appl. Energy 2012, 92, 211–217. [Google Scholar] [CrossRef]
- Guven, S. Calculation of optimum insulation thickness of external walls in residential buildings by using exergetic life cycle cost assessment method: Case study for Turkey. Environ. Prog. Sustain. Energy 2019, 38, e13232. [Google Scholar] [CrossRef]
- Kurekci, N.A. Determination of optimum insulation thickness for building walls by using heating and cooling degree-day values of all Turkey’s provincial centers. Energy Build. 2016, 118, 197–213. [Google Scholar] [CrossRef]
- Yang, Z.; Zhao, Y.; Xu, X.; Zhai, B. Analysis and comparison of building energy saving reconstruction in hot summer and warm winter regions of South China and cold regions of North China. Energy Build. 2012, 54, 192–195. [Google Scholar] [CrossRef]
- Solvang, W.D.; Zhang, C.Y. Benefit Analysis of the Energy Saving Reconstruction of the Office Building in Chagan Hada; Trans Tech Publications: Zurich, Switzerland, 2011; pp. 4976–4980. [Google Scholar]
- Sheina, S.G.; Zilberova, I.Y.; Vongay, A.O. Energy-Saving Processes Simulation in Reconstruction of Educational Institutions Edifices; EDP Sciences: Les Ulis, France, 2017; p. 00153. [Google Scholar]
- Domínguez, S.; Sendra, J.J.; León, A.L.; Esquivias, P.M. Towards energy demand reduction in social housing buildings: Envelope system optimization strategies. Energies 2012, 5, 2263–2287. [Google Scholar] [CrossRef]
- Dominguez-Delgado, A.; Domínguez-Torres, H.; Domínguez-Torres, C.-A. Energy and Economic Life Cycle Assessment of Cool Roofs Applied to the Refurbishment of Social Housing in Southern Spain. Sustainability 2020, 12, 5602. [Google Scholar] [CrossRef]
- Xinhui, Z.; Zhicong, M.; Chenhui, G.; Zhao, L. Analysis on energy consumption of rural residential buildings in Shanxi. J. Xi’an Univ. Architect. Technol. (Nat. Sci. Ed.) 2020, 52, 667–673. [Google Scholar]
- Zhe, L. Analysis on the Suitability of Energy Saving Retrofit and Clean Heating for Rural Buildings in Shandong. Master’s Thesis, Shandong Jianzhu University, Jinan, China, 2019. [Google Scholar]
- Sheng, X.; Lin, D. Energy saving analyses on the reconstruction project in district heating system with distributed variable speed pumps. Appl. Therm. Eng. 2016, 101, 432–445. [Google Scholar] [CrossRef]
- He, Q.; Ng, S.T.; Hossain, M.; Skitmore, M. Energy-efficient window retrofit for high-rise residential buildings in different climatic zones of China. Sustainability 2019, 11, 6473. [Google Scholar] [CrossRef]
- Liu, C.; Mohammadpourkarbasi, H.; Sharples, S. Evaluating the potential energy savings of retrofitting low-rise suburban dwellings towards the Passivhaus EnerPHit standard in a hot summer/cold winter region of China. Energy Build. 2021, 231, 110555. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; Mauro, G.M.; Napolitano, D.F. Villas on Islands: Cost-effective energy refurbishment in Mediterranean coastline houses. Energy Procedia 2019, 159, 192–200. [Google Scholar] [CrossRef]
- Liu, Y.; Wuxing, W.; Lei, Z. A Calculation Method of Building Energy Saving Rate. Patent ZL201510072207, 2015. [Google Scholar]
- Liu, Y.; Yufan, L.; Lei, Z. Calculation Method of Building Energy Saving Rate Based on Human Thermal Adaptation Model. Patent ZL201510070484, 2015. [Google Scholar]
- Liu, Y.; Yang, L.; Zheng, W.; Liu, T.; Zhang, X.; Liu, J. A novel building energy efficiency evaluation index: Establishment of calculation model and application. Energy Convers. Manag. 2018, 166, 522–533. [Google Scholar] [CrossRef]
- Albatayneh, A.; Alterman, D.; Page, A.; Moghtaderi, B. The impact of the thermal comfort models on the prediction of building energy consumption. Sustainability 2018, 10, 3609. [Google Scholar] [CrossRef]
- Nicol, J.F.; Humphreys, M.A. Adaptive thermal comfort and sustainable thermal standards for buildings. Energy Build. 2002, 34, 563–572. [Google Scholar] [CrossRef]
- Shi, X. Multi-Objective Optimization of Building Design Based on Performance. In Proceedings of the 13th National Conference on Building Technology, Beijing, China, 24–26 September 2010; pp. 162–165. [Google Scholar]
- Gero, J.S.; D’Cruz, N.; Radford, A.D. Energy in context: A multicriteria model for building design. Build. Sci. 1983, 18, 99–107. [Google Scholar] [CrossRef]
- Juan, Y.-K.; Kim, J.H.; Roper, K.; Castro-Lacouture, D. GA-based decision support system for housing condition assessment and refurbishment strategies. Autom. Constr. 2009, 18, 394–401. [Google Scholar] [CrossRef]
- Kaklauskas, A.; Zavadskas, E.K.; Raslanas, S. Multivariant design and multiple criteria analysis of building refurbishments. Energy Build. 2005, 37, 361–372. [Google Scholar] [CrossRef]
- Flourentzou, F.; Roulet, C.A. Elaboration of retrofit scenarios. Energy Build. 2002, 34, 185–192. [Google Scholar] [CrossRef]
- Asadi, E.; da Silva, M.G.; Antunes, C.H.; Dias, L.; Glicksman, L. Multi-objective optimization for building retrofit: A model using genetic algorithm and artificial neural network and an application. Energy Build. 2014, 81, 444–456. [Google Scholar] [CrossRef]
- Deb, C.; Lee, S.E.; Santamouris, M. Using artificial neural networks to assess HVAC related energy saving in retrofitted office buildings. Sol. Energy 2018, 163, 32–44. [Google Scholar] [CrossRef]
- Asadi, E.; da Silva, M.G.; Antunes, C.H.; Dias, L. A multi-objective optimization model for building retrofit strategies using TRNSYS simulations, GenOpt and MATLAB. Build. Sci. 2012, 56, 370–378. [Google Scholar] [CrossRef]
- Han, Y.; Fan, C.; Geng, Z.; Ma, B.; Cong, D.; Chen, K.; Yu, B. Energy efficient building envelope using novel RBF neural network integrated affinity propagation. Energy 2020, 209, 118414. [Google Scholar] [CrossRef]
- Weidong, W.; Duan, Q.; Feng, Y.; Lv, Y.; Wang, J.; Meng, Q. Constructing prototypical building models based on the similarity theory coupled with entropy weight method. Sci. Technol. 2020, 26, 90–100. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mobile Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Yan, X.; Gong, J.; He, J.; Zhang, H.; Zhang, C.; Liu, Z. Integrated Data Mining and TOPSIS Entropy Weight Method to Evaluate Logistics Supply and Demand Efficiency of a 3PL Company. Math. Probl. Eng. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Feng, J.; Gong, Z. Integrated linguistic entropy weight method and multi-objective programming model for supplier selection and order allocation in a circular economy: A case study. J. Clean. Prod. 2020, 277, 122597. [Google Scholar] [CrossRef]
- Lin, H.; Du, L.; Liu, Y. Soft Decision Cooperative Spectrum Sensing with Entropy Weight Method for Cognitive Radio Sensor Networks. IEEE Access 2020, 8, 109000–109008. [Google Scholar] [CrossRef]
- Gong, W.; Wang, N.; Zhang, N.; Han, W.; Qiao, H. Water resistance and a comprehensive evaluation model of magnesium oxychloride cement concrete based on Taguchi and entropy weight method. Constr. Build. Mater. 2020, 260, 119817. [Google Scholar] [CrossRef]
- Wang, C.; Xu, M.; Olsson, G.; Liu, Y. Characterizing of water-energy-emission nexus of coal-fired power industry using entropy weighting method. Resour. Conserv. Recycl. 2020, 161, 104991. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, Y.; Yu, Y.; Xu, Y.; Xu, M.; Zhang, R.; De Dieu, G.J.; Yin, D.; Liu, Z. Historical data-driven risk assessment of railway dangerous goods transportation system: Comparisons between Entropy Weight Method and Scatter Degree Method. Reliab. Eng. Syst. 2021, 205, 107236. [Google Scholar] [CrossRef]
- Zhu, Q.; Liu, L. Ranking Factors of Infant Formula Milk Powder Using Improved Entropy Weight Based on HDT Method and Its Application of Food Safety. Processes 2020, 8, 740. [Google Scholar] [CrossRef]
- Mehdi, S.; Hossein, M.; Seyed, Z.H.; Ali, R.I. Assessment of food hazard mapping in urban areas using entropy weighting method: A case study in Hamadan city, Iran. Acta Geophys. 2019, 8, 21. [Google Scholar]
- Bai, H.; Feng, F.; Wang, J.; Wu, T. A Combination Prediction Model of Long-Term Ionospheric foF2 Based on Entropy Weight Method. Entropy 2020, 22, 442. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Sun, H.; Singh, V.P.; Zhou, Y.; Ma, M. Agricultural Water Resources Management Using Maximum Entropy and Entropy-Weight-Based TOPSIS Methods. Entropy 2020, 21, 364. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of entropy weight method in decision-making. Math. Probl. Eng. 2020, 2020, 1–5. [Google Scholar] [CrossRef]
- Qian, B.; Zhu, Y.; Wang, Y.; Yan, F. Can Entropy Weight Method Correctly Reflect the Distinction of Water Quality Indices? Water Resour. Manag. 2020, 8, 4. [Google Scholar]
- Chinese Standard JGJ/T129-2012, Technical Specification for Energy Efficiency Retrofitting of Existing Residential Buildings; China Academy of Building Research: Beijing, China, 2012.
- Zhang, H.; Wang, L. Building Energy Saving Technology; Higher Education Press: Beijing, China, 2016. [Google Scholar]
- Chinese Standard GB/T 50824-2013, Design Standard for Energy Efficiency of Rural Residental Building; China Academy of Building Research: Beijing, China, 2012.
- Chinese Standard JGJ 253-2011, Technical Specification for Themal Insulating Systems of Inorgania Lightweight Aggregate Mortar; Guangsha Construction Group Co. Ltd. and Ningbo Rongshan New Material Co. Ltd.: Beijing, China, 2011.
- Chinese Standard DBT 279-2010, Inorganic Insulation Mortar Wall Insulation System; Anhui Institute of Product Quality Supervision and Inspection: Hefei, China, 2010.
- Anhui Provincial Construction Engineering Cost Management Station. Anhui Provincial Construction Engineering Cost Management Station, Anhui Province Construction Engineering Valuation Quota; Anhui Province Construction Engineering Valuation Quota; China Building Materials Industry Press: Beijing, China, 2018. [Google Scholar]
- Carlos, E.; Naghelli, O.; Norma, A.R. Energy Savings on an Industrial Building in Different Climate Zones: Envelope Analysis and PV System Implementation. Sustainability 2020, 12, 1391. [Google Scholar]
- Yu, D.; Tongyu, Q.; Siyuan, Z.; Lu, H.; Rui, B.; Haibo, G.; Xunzhi, Y. Comparative Whole Building Life Cycle Assessment of Energy Saving and Carbon Reduction Performance of Reinforced Concrete and Timber Stadiums—A Case Study in China. Sustainability 2020, 12, 1566. [Google Scholar]
- Andrey, A.; Ben, C. Numerical simulation of thermal mass enhanced envelopes for office buildings in subtropical climate zones. Energy Build. 2016, 118, 214–225. [Google Scholar]
- Chinese Standard JGJ/T 346-2014, Standard for Weather Data of Building Energy Efficiency; China Academy of Building Research: Beijing, China, 2014.
- Ryu, J.; Kim, J.; Hong, W.; de Dear, R. Defining the thermal sensitivity (Griffiths constant) of building occupants in the Korean residential context. Energy Build. 2020, 208, 109648. [Google Scholar] [CrossRef]
- Zhou, L.; Li, N.; He, Y.; Peng, J.; Wang, C.; Yongga, A. A field survey on thermal comfort and energy consumption of raditional electric heating devices (Huo Xiang) for residents in regions without central heating systems in China. Energy Build. 2019, 196, 134–144. [Google Scholar] [CrossRef]
- ASHRAE-55:2017, Thermal Environmental Conditions for Human Occupancy; American Society of Heating, Refrigerating and Air-Conditioning Engineering: Atlanta, GA, USA, 2013.
- Chinese Standard JGJ 26-2018, Design Standard for Energy Efficiency of Residential Buildings in Severe Cold and Cold Zones; China Academy of Building Research: Beijing, China, 2018.
- Xu, J.; Lu, Z.; Gao, W.; Yang, M.; Su, M. The comparative study on the climate adaptability based on indoor physical environment of traditional dwelling in Qinba mountainous areas, China. Energy Build. 2019, 197, 140–155. [Google Scholar]
- Liu, T.; Liu, J.; Qiao, Y.; Yang, L.; Liu, Y. Energy-Saving Performance Evaluation Method of Phase Change Heat Storage Wall Room Based on Human Thermal Adaptation. Build. Sci. 2020, 36, 133–139. [Google Scholar]
- Liu, Y.; Yan, H.; Yan, M. The Basis of Climate Adaptation for Human Thermal Comfort; Science Press: Beijing, China, 2017. [Google Scholar]
- Yao, R.; Li, B.; Liu, J. A theoretical adaptive model of thermal comfort-Adaptive Predicted Mean Vote (aPMV). Build. Environ. 2009, 44, 2089–2096. [Google Scholar] [CrossRef]
- Ming, R.; Yu, W.; Zhao, X.; Liu, Y.; Li, B.; Essah, E.; Yao, R. Assessing energy saving potentials of office buildings based on adaptive thermal comfort using a tracking-based method. Energy Build. 2020, 208, 109611. [Google Scholar] [CrossRef]
- Chinese Standard GB/T 50785-2012, Evaluation Standard for Indoor Thermal Environment in Civil Buildings; China Academy of Building Research: Beijing, China, 2012.
- ISO 7730, Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria; International Standardization Organization: Geneva, Switzerland, 2005; p. 48.
- DIN EN 15251, Indoor Environmental Input Parameters for Design and Assessment of Energy Performance of Buildings Addressing Indoor Air Quality, Thermal Environment, Lighting and Acoustics. 2007. Available online: http://www.cres.gr/greenbuilding/PDF/prend/set4/WI_31_Pre-FV_version_prEN_15251_Indoor_Environment.pdf (accessed on 20 September 2019).
- Tian, X.; Meie, W.; Chao, S.; Weiping, C. Evaluation of the natural attenuation capacity of urban residential soils with ecosystem-service performance index (EPX) and entropy-weight methods. Environ. Pollut. 2018, 238, 222–229. [Google Scholar]
- Yan, W.; Gu, L. Application of the method of Entropy proportion in the engineering mark. J. Xi’an Univ. Architect. Technol. (Nat. Sci. Ed.) 2004, 36, 98–100. [Google Scholar]
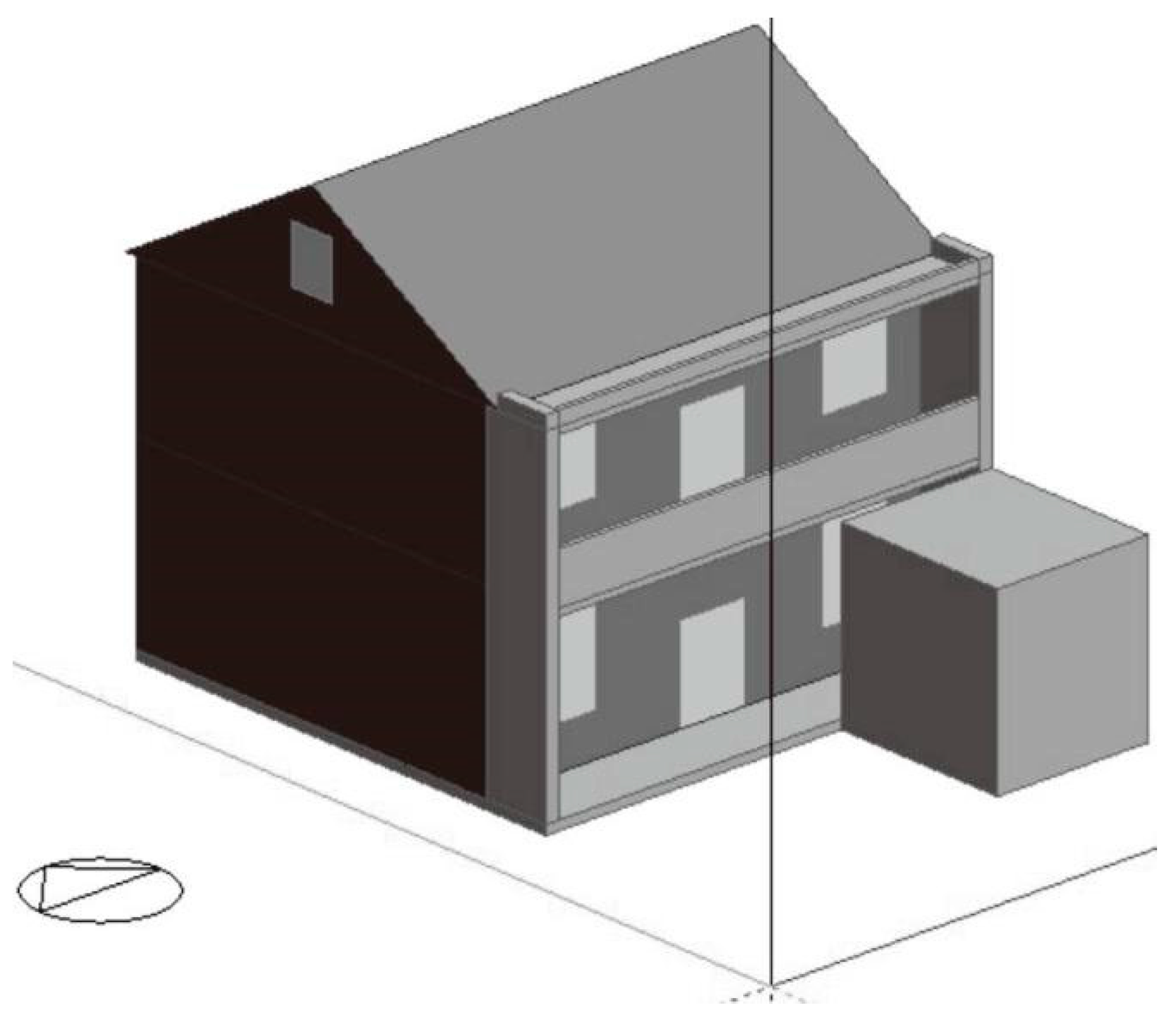

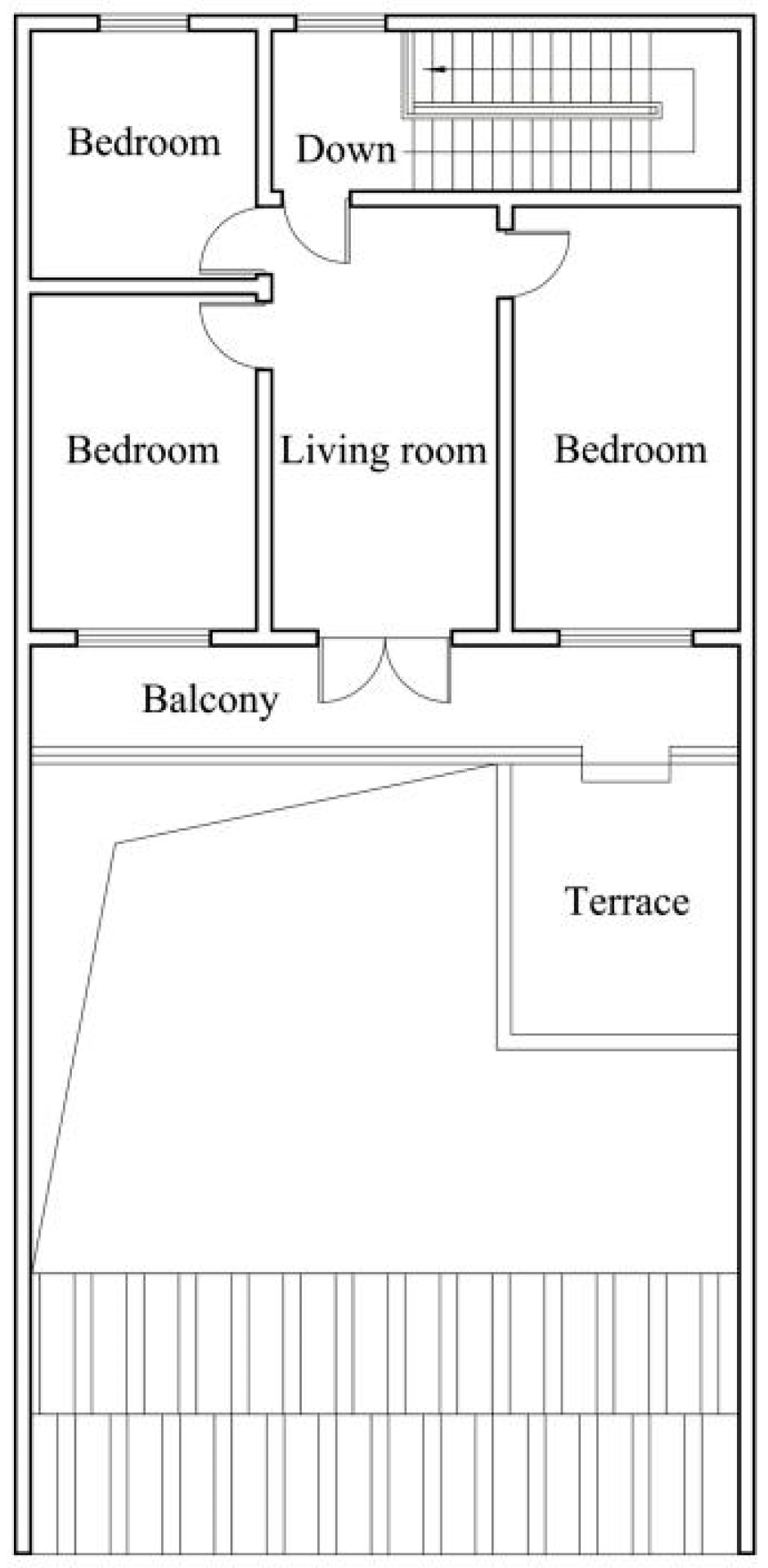
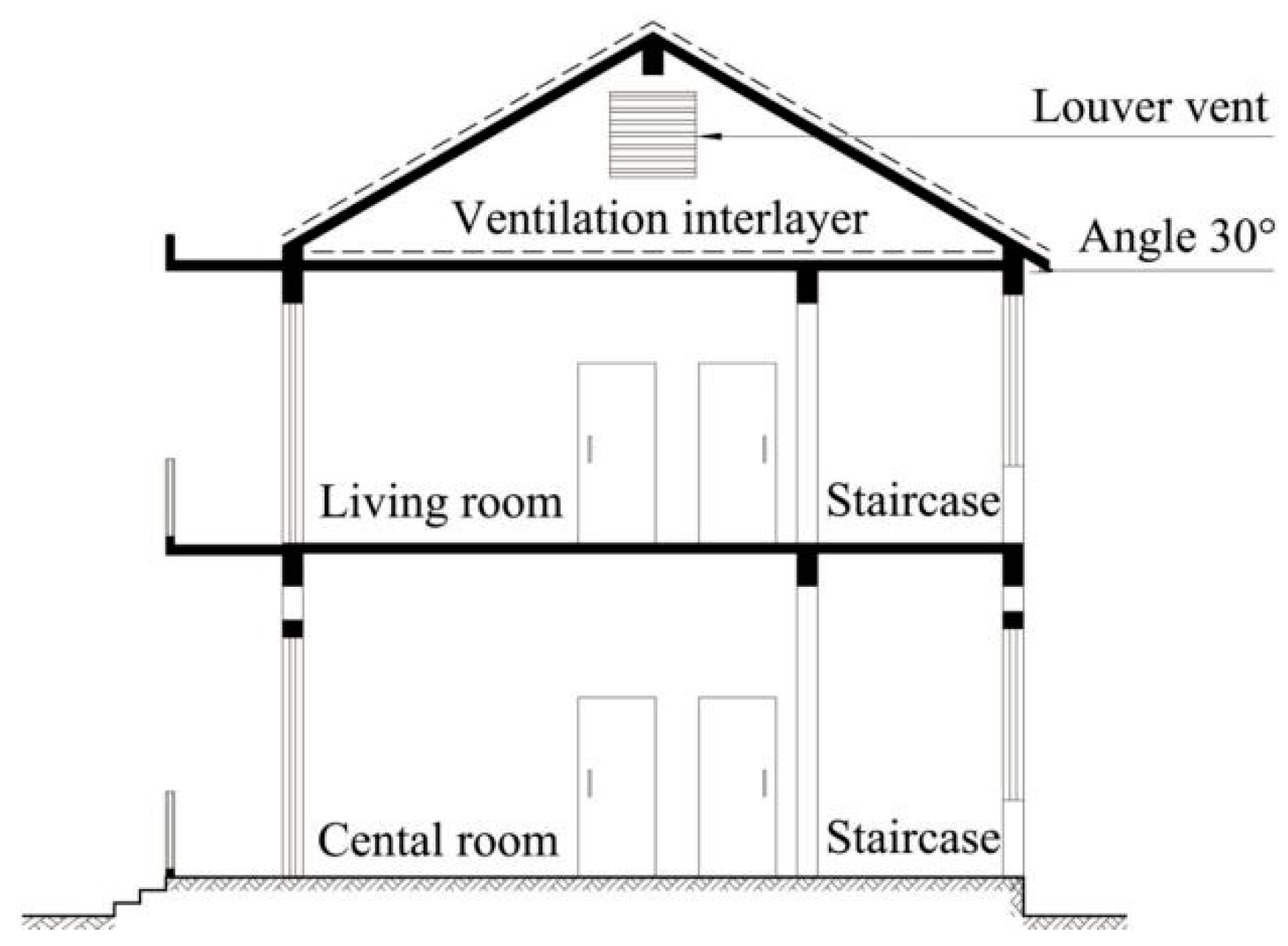
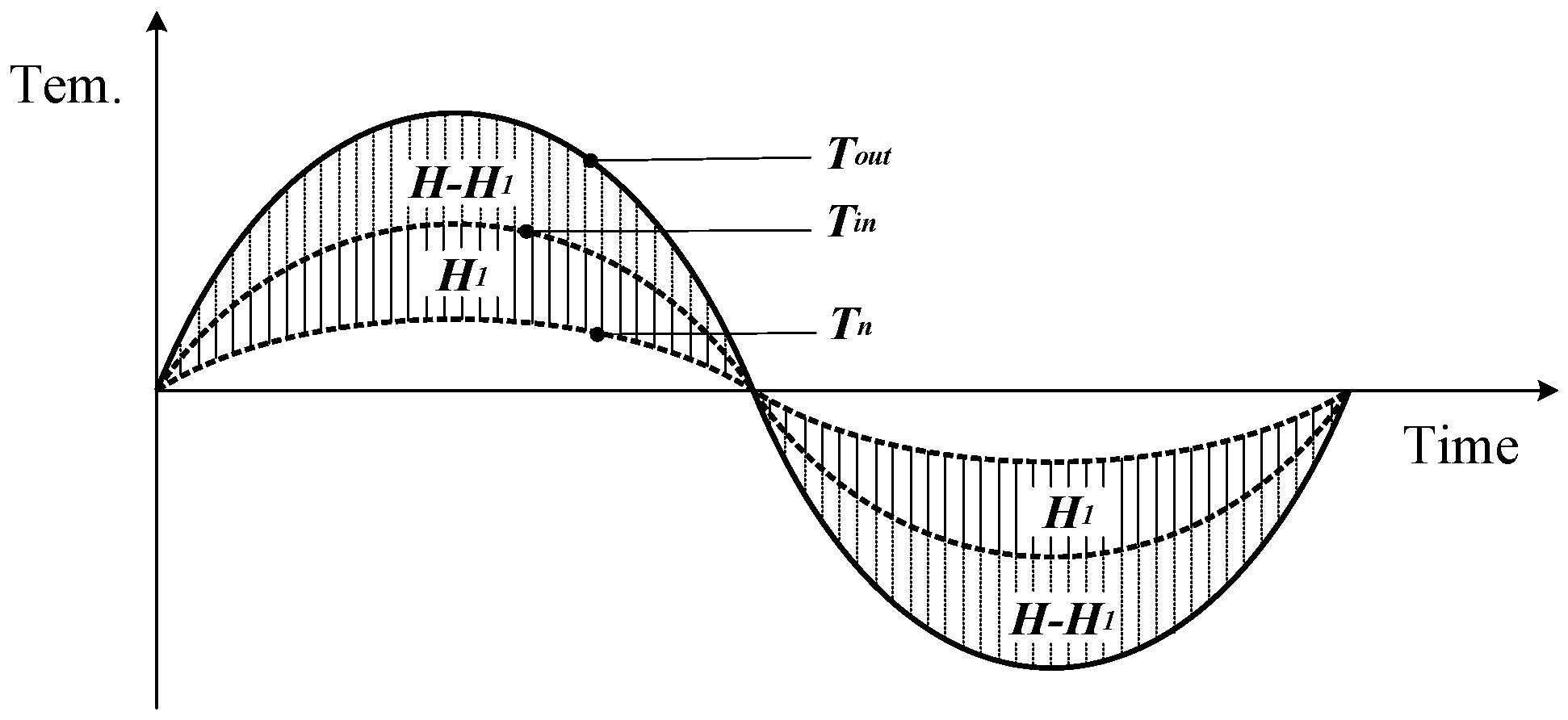





| External Wall (Outside-To-In) | Roof (Outside-To-In) | External Window |
|---|---|---|
| 20 mm lime cement mortar 240 mm clay brick 20 mm cement mortar | 20 mm concrete tile 35 mm lime cement mortar 5 mm SBS waterproof membrane 120 mm reinforced concrete slab 20 mm cement mortar | 6 mm single-layer glass and aluminum window frame |
| Window Types 1 | Uw (W/m2K) | C ($/m2) 2 |
|---|---|---|
| 6 mm single layer glass (no break) | 5.778 | 0 |
| 5+6A+5 double insulating glass (no break) | 3.115 | 41.265 |
| Low-e 6+12A+6 double insulating glass (with thermal break) | 1.771 | 75.529 |
| 6+12A+6 double insulating glass (with thermal break) | 2.685 | 61.402 |
| 6+12A+6+12A+6 three-layer insulating glass (with thermal break) | 1.754 | 77.574 |
| Low-e 6+12A+6+12A+6 three-layer insulating glass (with thermal break) | 1.307 | 92.320 |
| Insulation Thickness (mm) | Ue (W/m2K) | Ur (W/m2K) | Costs of External Wall ($/m2) 1 | Costs of Roof ($/m2) 1 | |
|---|---|---|---|---|---|
| External Wall | Roof | ||||
| 0 | 0 | 1.958 | 3.217 | 0.000 | 0.000 |
| 5 | 10 | 1.718 | 2.204 | 9.001 | 10.546 |
| 10 | 20 | 1.53 | 1.676 | 9.889 | 11.913 |
| 15 | 30 | 1.379 | 1.352 | 10.769 | 13.281 |
| 20 | 40 | 1.255 | 1.133 | 11.648 | 14.649 |
| 25 | 50 | 1.152 | 0.975 | 12.528 | 16.017 |
| 30 | 60 | 1.065 | 0.856 | 13.408 | 17.384 |
| 35 | 70 | 0.989 | 0.763 | 14.288 | 18.752 |
| 40 | 80 | 0.924 | 0.688 | 15.168 | 20.120 |
| 45 | 90 | 0.867 | 0.626 | 16.048 | 21.488 |
| 50 | 100 | 0.816 | 0.575 | 16.927 | 22.855 |
| Indicator | Size | Min. | Max. | Mean | S.D. |
|---|---|---|---|---|---|
| J | 725 | 0.399 | 0.495 | 0.452 | 0.023 |
| ΔS | 725 | 3608.851 | 4166.266 | 3860.717 | 132.569 |
| C | 725 | 990.369 | 9047.716 | 6082.652 | 1500.802 |
| Position | Fitting Equation |
|---|---|
| External window | |
| External wall | |
| Roof |
| Position | Fitting Equation |
|---|---|
| External window | |
| External wall | |
| Roof |
| Indicator | J | ΔS (C°·h) | C ($) |
|---|---|---|---|
| E | 0.9892 | 0.9888 | 0.9884 |
| W | 0.3218 | 0.3328 | 0.3454 |
| Comparison Object | J | ΔS (C°·h) | C ($) |
|---|---|---|---|
| Benchmark building | 0.3979 | 4185.8340 | 0.0000 |
| Optimal scheme | 0.4926 | 3634.5740 | 8163.6541 |
| Window Types | |
|---|---|
| 6 mm single-layer glass (no break) | 0.4944 |
| 5+6A+5 double insulating glass (no break) | 0.5260 |
| Low-e 6+12A+6 double insulating glass (with thermal break) | 0.5153 |
| 6+12A+6 double insulating glass (with thermal break) | 0.5071 |
| 6+12A+6+12A+6 three-layer insulating glass (with thermal break) | 0.5119 |
| Low-e 6+12A+6+12A+6 three-layer insulating glass (with thermal break) | 0.5306 |
| Insulation Thickness (mm) | |||
|---|---|---|---|
| External Wall | Roof | ||
| 0 | 0 | 0.6444 | 0.5322 |
| 5 | 10 | 0.6733 | 0.5535 |
| 10 | 20 | 0.6193 | 0.5360 |
| 15 | 30 | 0.6193 | 0.5230 |
| 20 | 40 | 0.5337 | 0.5134 |
| 25 | 50 | 0.4993 | 0.5067 |
| 30 | 60 | 0.4694 | 0.5020 |
| 35 | 70 | 0.4432 | 0.4990 |
| 40 | 80 | 0.4202 | 0.4974 |
| 45 | 90 | 0.4002 | 0.4967 |
| 50 | 100 | 0.3821 | 0.4970 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, W.; Yang, L.; Zhang, Q.; Chen, L.; Wu, W. Evaluation of Rural Dwellings’ Energy-Saving Retrofit with Adaptive Thermal Comfort Theory. Sustainability 2021, 13, 5350. https://doi.org/10.3390/su13105350
Cao W, Yang L, Zhang Q, Chen L, Wu W. Evaluation of Rural Dwellings’ Energy-Saving Retrofit with Adaptive Thermal Comfort Theory. Sustainability. 2021; 13(10):5350. https://doi.org/10.3390/su13105350
Chicago/Turabian StyleCao, Wen, Lin Yang, Qinyi Zhang, Lihua Chen, and Weidong Wu. 2021. "Evaluation of Rural Dwellings’ Energy-Saving Retrofit with Adaptive Thermal Comfort Theory" Sustainability 13, no. 10: 5350. https://doi.org/10.3390/su13105350
APA StyleCao, W., Yang, L., Zhang, Q., Chen, L., & Wu, W. (2021). Evaluation of Rural Dwellings’ Energy-Saving Retrofit with Adaptive Thermal Comfort Theory. Sustainability, 13(10), 5350. https://doi.org/10.3390/su13105350







