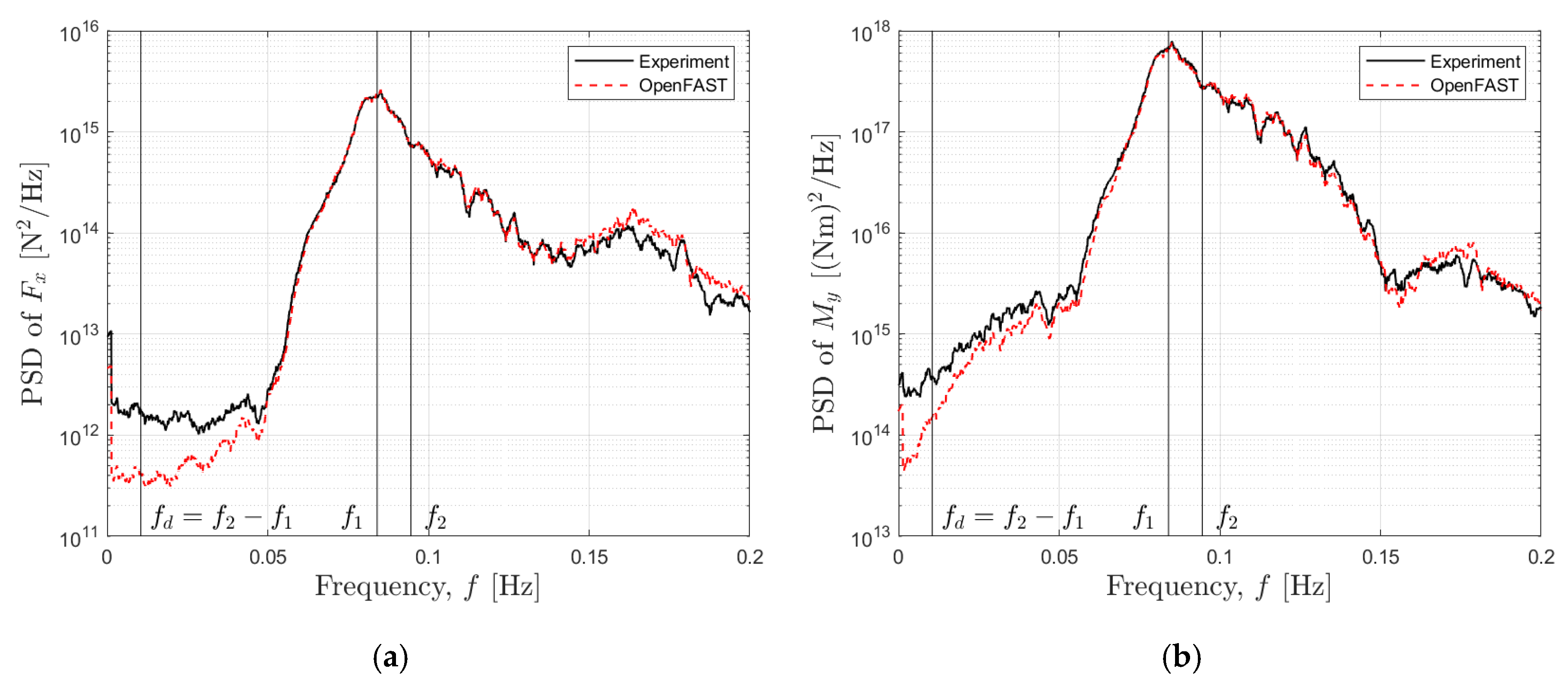
Figure 1.
Power spectral density of wave-exciting (
a) surge force and (
b) pitch moment on a fixed OC5-DeepCwind semisubmersible FOWT platform in irregular incident waves [
2,
3,
9].
Figure 1.
Power spectral density of wave-exciting (
a) surge force and (
b) pitch moment on a fixed OC5-DeepCwind semisubmersible FOWT platform in irregular incident waves [
2,
3,
9].
Figure 2.
Geometry of the semisubmersible platform and the adopted coordinate system.
Figure 2.
Geometry of the semisubmersible platform and the adopted coordinate system.
Figure 3.
The numerical domain for the CFD simulation with bichromatic incident waves and a fixed floater.
Figure 3.
The numerical domain for the CFD simulation with bichromatic incident waves and a fixed floater.
Figure 4.
Mesh refinement zones/boxes. See
Table 4.
Figure 4.
Mesh refinement zones/boxes. See
Table 4.
Figure 5.
Incident wave-elevation time series at the center position of the floater .
Figure 5.
Incident wave-elevation time series at the center position of the floater .
Figure 6.
Variation of wave amplitudes (magnitude) at the two wave frequencies, and , and the difference frequency, , over the length of the numerical domain.
Figure 6.
Variation of wave amplitudes (magnitude) at the two wave frequencies, and , and the difference frequency, , over the length of the numerical domain.
Figure 7.
Comparison of the difference-frequency wave amplitudes evaluated directly from the CFD solution (symbols) to those reconstructed from , , and using Equation (7) (lines). The real and imaginary parts of the wave amplitude are compared separately.
Figure 7.
Comparison of the difference-frequency wave amplitudes evaluated directly from the CFD solution (symbols) to those reconstructed from , , and using Equation (7) (lines). The real and imaginary parts of the wave amplitude are compared separately.
Figure 8.
Amplitude (magnitude) spectra of (a) wave-exciting force in surge, , and (b) moment in pitch, , computed from the time window The difference-frequency component at and the two wave-frequency components at and are highlighted in red with a filled symbol.
Figure 8.
Amplitude (magnitude) spectra of (a) wave-exciting force in surge, , and (b) moment in pitch, , computed from the time window The difference-frequency component at and the two wave-frequency components at and are highlighted in red with a filled symbol.
Figure 9.
Fluctuation of (a) surge-force and (b) pitch-moment amplitudes (magnitude) at the difference frequency and the two wave frequencies with the time window for the FFT analysis.
Figure 9.
Fluctuation of (a) surge-force and (b) pitch-moment amplitudes (magnitude) at the difference frequency and the two wave frequencies with the time window for the FFT analysis.
Figure 10.
Maximum residual of the -momentum equation at the end of the outer iterations during the time window .
Figure 10.
Maximum residual of the -momentum equation at the end of the outer iterations during the time window .
Figure 11.
Estimation of iterative errors and uncertainties in the normalized wave-load amplitudes (magnitude). The red crosses correspond to the results from different convergence runs, and the red uncertainty bands represent the estimated iterative uncertainty. The fitted error estimators are included as blue lines. The top (a–c), middle (d–f), and bottom (g–i) rows correspond to the amplitudes of surge force, heave force, and pitch moment, respectively. The left (a,d,g), center (b,e,h), and right (c,f,i) columns correspond to the difference frequency, first wave frequency, and second wave frequency, respectively. The residual is normalized by that of the baseline solution with 40 iterations per time step.
Figure 11.
Estimation of iterative errors and uncertainties in the normalized wave-load amplitudes (magnitude). The red crosses correspond to the results from different convergence runs, and the red uncertainty bands represent the estimated iterative uncertainty. The fitted error estimators are included as blue lines. The top (a–c), middle (d–f), and bottom (g–i) rows correspond to the amplitudes of surge force, heave force, and pitch moment, respectively. The left (a,d,g), center (b,e,h), and right (c,f,i) columns correspond to the difference frequency, first wave frequency, and second wave frequency, respectively. The residual is normalized by that of the baseline solution with 40 iterations per time step.
Figure 12.
Estimation of spatial discretization errors and uncertainties in the normalized wave-load amplitudes (magnitude). The red crosses correspond to results from different convergence runs, and the red uncertainty bands represent the estimated spatial-discretization uncertainty. The fitted error estimators, when available, are included as blue lines. If no error estimator is shown, the range-based uncertainty estimate was used. The top (a–c), middle (d–f), and bottom (g–i) rows correspond to the amplitudes of surge force, heave force, and pitch moment, respectively. The left (a,d,g), center (b,e,h), and right (c,f,i) columns correspond to the difference frequency, first wave frequency, and second wave frequency, respectively. The reference cell size is normalized by the baseline value of .
Figure 12.
Estimation of spatial discretization errors and uncertainties in the normalized wave-load amplitudes (magnitude). The red crosses correspond to results from different convergence runs, and the red uncertainty bands represent the estimated spatial-discretization uncertainty. The fitted error estimators, when available, are included as blue lines. If no error estimator is shown, the range-based uncertainty estimate was used. The top (a–c), middle (d–f), and bottom (g–i) rows correspond to the amplitudes of surge force, heave force, and pitch moment, respectively. The left (a,d,g), center (b,e,h), and right (c,f,i) columns correspond to the difference frequency, first wave frequency, and second wave frequency, respectively. The reference cell size is normalized by the baseline value of .
Figure 13.
Estimation of temporal discretization errors and uncertainties in the normalized wave-load amplitudes (magnitude). The red crosses correspond to results from different convergence runs, and the red uncertainty bands represent the estimated temporal-discretization uncertainty. The time step is normalized by the baseline value of
. The top (
a–
c), middle (
d–
f), and bottom (
g–
i) rows correspond to the amplitudes of surge force, heave force, and pitch moment, respectively. The left (
a,
d,
g), center (
b,
e,
h), and right (
c,
f,
i) columns correspond to the difference frequency, first wave frequency, and second wave frequency, respectively. See caption of
Figure 12 for more information.
Figure 13.
Estimation of temporal discretization errors and uncertainties in the normalized wave-load amplitudes (magnitude). The red crosses correspond to results from different convergence runs, and the red uncertainty bands represent the estimated temporal-discretization uncertainty. The time step is normalized by the baseline value of
. The top (
a–
c), middle (
d–
f), and bottom (
g–
i) rows correspond to the amplitudes of surge force, heave force, and pitch moment, respectively. The left (
a,
d,
g), center (
b,
e,
h), and right (
c,
f,
i) columns correspond to the difference frequency, first wave frequency, and second wave frequency, respectively. See caption of
Figure 12 for more information.
Figure 14.
Amplitudes (magnitude) of wave-induced surge force, , heave force, , and pitch moment, , on the floater at the difference () and the two wave frequencies ( and ). The red (narrow) and black (wide) uncertainty bands represent the numerical uncertainty, , and the total uncertainty, , respectively. The hatched areas represent the prediction from potential-flow theory. All quantities associated with the difference-frequency heave force are scaled by a factor of 0.2.
Figure 14.
Amplitudes (magnitude) of wave-induced surge force, , heave force, , and pitch moment, , on the floater at the difference () and the two wave frequencies ( and ). The red (narrow) and black (wide) uncertainty bands represent the numerical uncertainty, , and the total uncertainty, , respectively. The hatched areas represent the prediction from potential-flow theory. All quantities associated with the difference-frequency heave force are scaled by a factor of 0.2.
Table 1.
Linear-wave properties of the bichromatic incident waves.
Table 1.
Linear-wave properties of the bichromatic incident waves.
| Wave | Period, T | Frequency, f | Wavelength, λ | Wave Height, H | Repeat Period, TR |
|---|
| 1 | 11.9000 s | 0.08403 Hz | 221.1 m | 3.569 m | 190.4 s |
| 2 | 10.5778 s | 0.09454 Hz | 174.7 m | 3.703 m |
Table 2.
Boundary conditions.
Table 2.
Boundary conditions.
| Boundary | Type | Velocity | Pressure | Phase Fraction |
|---|
| Floater | Wall | No slip | N/A | N/A |
| Upstream | Velocity inlet | Linear incident wave field | N/A | Incident wave |
| Downstream * | Pressure outlet | Extrapolated backflow dir. | Hydrostatic | Calm water |
| Top | Pressure outlet | Extrapolated backflow dir. | Hydrostatic | Air only |
| Bottom | Velocity inlet | Linear incident wave field | N/A | Water only |
| Sides | Symmetry planes | N/A | N/A | N/A |
Table 3.
Spatial and temporal discretization schemes.
Table 3.
Spatial and temporal discretization schemes.
| Terms | Methods |
|---|
| Momentum advection | Second-order upwinding |
| Gradient | Second-order hybrid Gauss-LSQ with Venkatakrishnan’s limiter |
| Phase fraction advection | High-resolution interface-capturing scheme |
| Time integration | Second-order implicit scheme based on backward differentiation |
Table 4.
Mesh refinement zones for the baseline setup.
Table 4.
Mesh refinement zones for the baseline setup.
| Box No. | x [m] | y [m] | z [m] | | | |
|---|
| 1 | Full length * | [0, 100] | [−4, 4.5] | 2 | 8 | 0.5 |
| 2 | Full length * | [0, 100] | [−10, −4] | 4 | 8 | 1 |
| 3 | Full length * | [0, 100] | [−25, −10] | 4 | 8 | 2 |
| 4 | Full length * | [100, 225] | [−4, 4.5] | 2 | 16 | 0.5 |
| 5 | Full length * | [100, 225] | [−10, −4] | 4 | 16 | 1 |
| 6 | Full length * | [100, 225] | [−25, −10] | 4 | 16 | 2 |
| 7 | [−47.5, 35] | [0, 45] | [−4, 4.5] | 2 | 2 | 0.5 |
| 8 | [−45.0, 30] | [0, 40] | [−25, −4] | 2 | 2 | 2 |
Table 5.
Normalization factors for the wave-load amplitudes at the frequencies of interest.
Table 5.
Normalization factors for the wave-load amplitudes at the frequencies of interest.
| | | | |
|---|
| | | |
| | | |
| | | |
Table 6.
Normalized amplitudes (magnitude) of wave excitation at the frequencies of interest.
Table 6.
Normalized amplitudes (magnitude) of wave excitation at the frequencies of interest.
| | | | |
|---|
| | Before Correction | After Correction | % Change |
|---|
| 1.65 | 1.57 | −4.7% | 0.544 | 0.559 |
| 6.51 | 4.63 | −29% | 0.447 | 0.533 |
| 1.20 | 1.18 | −1.8% | 0.389 | 0.450 |
Table 7.
Iterative uncertainties, , in the magnitudes of the wave-load amplitudes.
Table 7.
Iterative uncertainties, , in the magnitudes of the wave-load amplitudes.
| | | | |
|---|
| ±0.5% | ±2.2% | ±0.9% |
| ±1.4% | ±0.7% | ±2.1% |
| ±1.2% | ±2.0% | ±2.0% |
Table 8.
Spatial discretization uncertainties, , in the magnitudes of wave-load amplitudes.
Table 8.
Spatial discretization uncertainties, , in the magnitudes of wave-load amplitudes.
| | | | |
|---|
| ±18% | ±0.9% | ±1.1% |
| ±31% | ±6.0% | ±8.6% |
| ±9.8% | ±3.8% | ±2.9% |
Table 9.
Temporal discretization uncertainties, , in the magnitudes of the wave-load amplitudes.
Table 9.
Temporal discretization uncertainties, , in the magnitudes of the wave-load amplitudes.
| | | | |
|---|
| ±1.3% | ±0.2% | ±0.8% |
| ±2.0% | ±3.1% | ±0.9% |
| ±1.2% | ±1.0% | ±0.5% |
Table 10.
Statistical uncertainties, , in the magnitudes of the wave-load amplitudes.
Table 10.
Statistical uncertainties, , in the magnitudes of the wave-load amplitudes.
| | | | |
|---|
| ±4.0% | ±0.3% | ±0.3% |
| ±37% | ±0.6% | ±0.3% |
| ±2.6% | ±0.3% | ±0.3% |
Table 11.
Total uncertainties, , in the magnitudes of the wave-load amplitudes.
Table 11.
Total uncertainties, , in the magnitudes of the wave-load amplitudes.
| | | | |
|---|
| ±20% | ±3.3% | ±2.8% |
| ±51% | ±9.7% | ±12% |
| ±13% | ±6.7% | ±5.3% |