Exploring EU’s Regional Potential in Low-Carbon Technologies
Abstract
1. Introduction
2. Methodology and Data
2.1. Estimating Potential Advantage in Green Technologies
- xil is the number of patents of technology i in region l
- xil is the sum of patents of technology i across all regions
- xil is the sum of all patents across all regions
2.2. Dimensionality Reduction: A Data-Driven Selection of Variables that Associate with RTA
- r = 258 (NUTS2 regions)
- i = Low-carbon technology
- t = 3 years non overlapping time-stack
3. Results
3.1. The Geographical Dimension of Potential Advantage
3.2. Unpacking Network Proximity Measures
3.3. Socio-Economic Variables and Low-Carbon Innovation
4. Discussion
4.1. Limitations and Further Research
4.2. Implications for Policy
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Green Technologies Definition
| Technology | CPC-Y Codes (Patents) |
|---|---|
| Solar PV | Y02E1050, Y02E1052, Y02E1054, Y02E10541, Y02E10542, Y02E10543, Y02E10544, Y02E10545, Y02E10546, Y02E10547, Y02E10548, Y02E10549, Y02E1056, Y02E10563, Y02E10566, Y02E1058 |
| Solar Thermal | Y02E1040, Y02E1041, Y02E1042, Y02E1043, Y02E1044, Y02E1045, Y02E1046, Y02E10465, Y02E1047 |
| Wind | Y02E1070, Y02E1072, Y02E10721, Y02E10722, Y02E10723, Y02E10725, Y02E10726, Y02E10727, Y02E10728, Y02E1074, Y02E1076, Y02E10763, Y02E10766 |
| Hydro | Y02E1020, Y02E1022, Y02E10223, Y02E10226, Y02E1028 |
| Energy management | Y02B7030, Y02B7032, Y02B703208, Y02B703216, Y02B703225, Y02B703233, Y02B703241, Y02B70325, Y02B703258, Y02B703266, Y02B703275, Y02B703283, Y02B703291, Y02B7034, Y02B70343, Y02B70346 |
| Lighting | Y02B2010, Y02B2012, Y02B20125, Y02B2014, Y02B20142, Y02B20144, Y02B20146, Y02B20148, Y02B2016, Y02B2018, Y02B20181, Y02B20183, Y02B20185, Y02B20186, Y02B20188, Y02B2019, Y02B2020, Y02B20202, Y02B20204, Y02B20206, Y02B20208, Y02B2022, Y02B2030, Y02B2032, Y02B20325, Y02B2034, Y02B20341, Y02B20342, Y02B20343, Y02B20345, Y02B20346, Y02B20347, Y02B20348, Y02B2036, Y02B2038, Y02B20383, Y02B20386, Y02B2040, Y02B2042, Y02B2044, Y02B20445, Y02B2046, Y02B2048, Y02B2070, Y02B2072 |
| Heating and cooling | Y02B3008, Y02B3010, Y02B30102, Y02B30104, Y02B30106, Y02B30108, Y02B3012, Y02B30123, Y02B30126, Y02B3014, Y02B3016, Y02B3018, Y02B3020, Y02B3022, Y02B3024, Y02B3026, Y02B3028, Y02B3050, Y02B3052, Y02B3054, Y02B30542, Y02B30545, Y02B30547, Y02B3056, Y02B30563, Y02B30566, Y02B3060, Y02B3062, Y02B30625, Y02B3064, Y02B3066, Y02B3070, Y02B3072, Y02B3074, Y02B30741, Y02B30743, Y02B30745, Y02B30746, Y02B30748, Y02B3076, Y02B30762, Y02B30765, Y02B30767, Y02B3078, Y02B3080, Y02B3090, Y02B3092, Y02B3094 |
| Combustion | Y02B8010, Y02B8012, Y02B8014, Y02B8020, Y02B8022, Y02B8024, Y02B8026, Y02B8028, Y02B8030, Y02B8032, Y02B8034, Y02B8040, Y02B8050 |
| Residential insulation | Y02E2010, Y02E2012, Y02E2014, Y02E2016, Y02E2018, Y02E2030, Y02E2032, Y02E20322, Y02E20324, Y02E20326, Y02E20328, Y02E2034, Y02E20342, Y02E20346, Y02E20348, Y02E2036, Y02E20363, Y02E20366, Y02E20185, Y02E20344 |
| Biofuels | Y02E5010, Y02E5011, Y02E5012, Y02E5013, Y02E5014, Y02E5015, Y02E5016, Y02E5017, Y02E5018, Y02E5030, Y02E5032, Y02E5034, Y02E50343, Y02E50346 |
| Batteries | Y02E6012, Y02E60122, Y02E60124, Y02E60126, Y02E60128, Y02T1070, Y02T107005, Y02T107011, Y02T107016, Y02T107022, Y02T107027, Y02T107033, Y02T107038, Y02T107044, Y02T10705, Y02T107055, Y02T107061, Y02T107066, Y02T107072, Y02T107077, Y02T107083, Y02T107088, Y02T107094, Y02T1072, Y02T107208, Y02T107216, Y02T107225, Y02T107233, Y02T107241, Y02T10725, Y02T107258, Y02T107266, Y02T107275, Y02T107283, Y02T107291 |
| Electric cars | Y02T1064, Y02T10641, Y02T10642, Y02T10643, Y02T10644, Y02T10645, Y02T10646, Y02T10647, Y02T10648, Y02T10649, Y02T1062, Y02T106204, Y02T106208, Y02T106213, Y02T106217, Y02T106221, Y02T106226, Y02T10623, Y02T106234, Y02T106239, Y02T106243, Y02T106247, Y02T106252, Y02T106256, Y02T10626, Y02T106265, Y02T106269, Y02T106273, Y02T106278, Y02T106282, Y02T106286, Y02T106291, Y02T106295 |
| Rail transport | Y02T3000, Y02T3010, Y02T3012, Y02T3014, Y02T3016, Y02T3018, Y02T3030, Y02T3032, Y02T3034, Y02T3036, Y02T3038, Y02T3040, Y02T3042 |
| Nuclear | Y02E3030, Y02E3031, Y02E3032, Y02E3033, Y02E3034, Y02E3035, Y02E3037, Y02E3038, Y02E3039, Y02E3040 |
Appendix B. Imputation Methodology

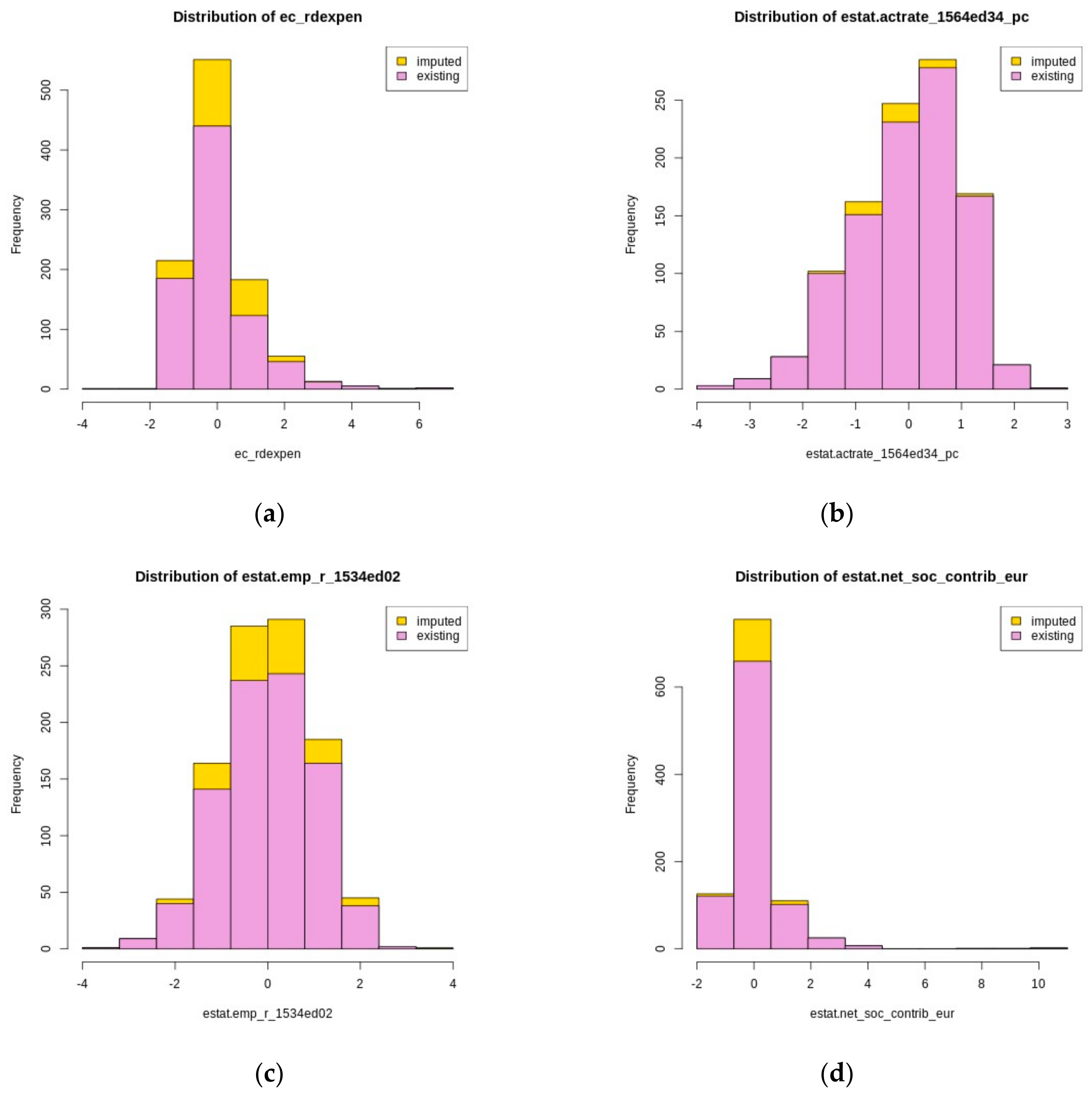
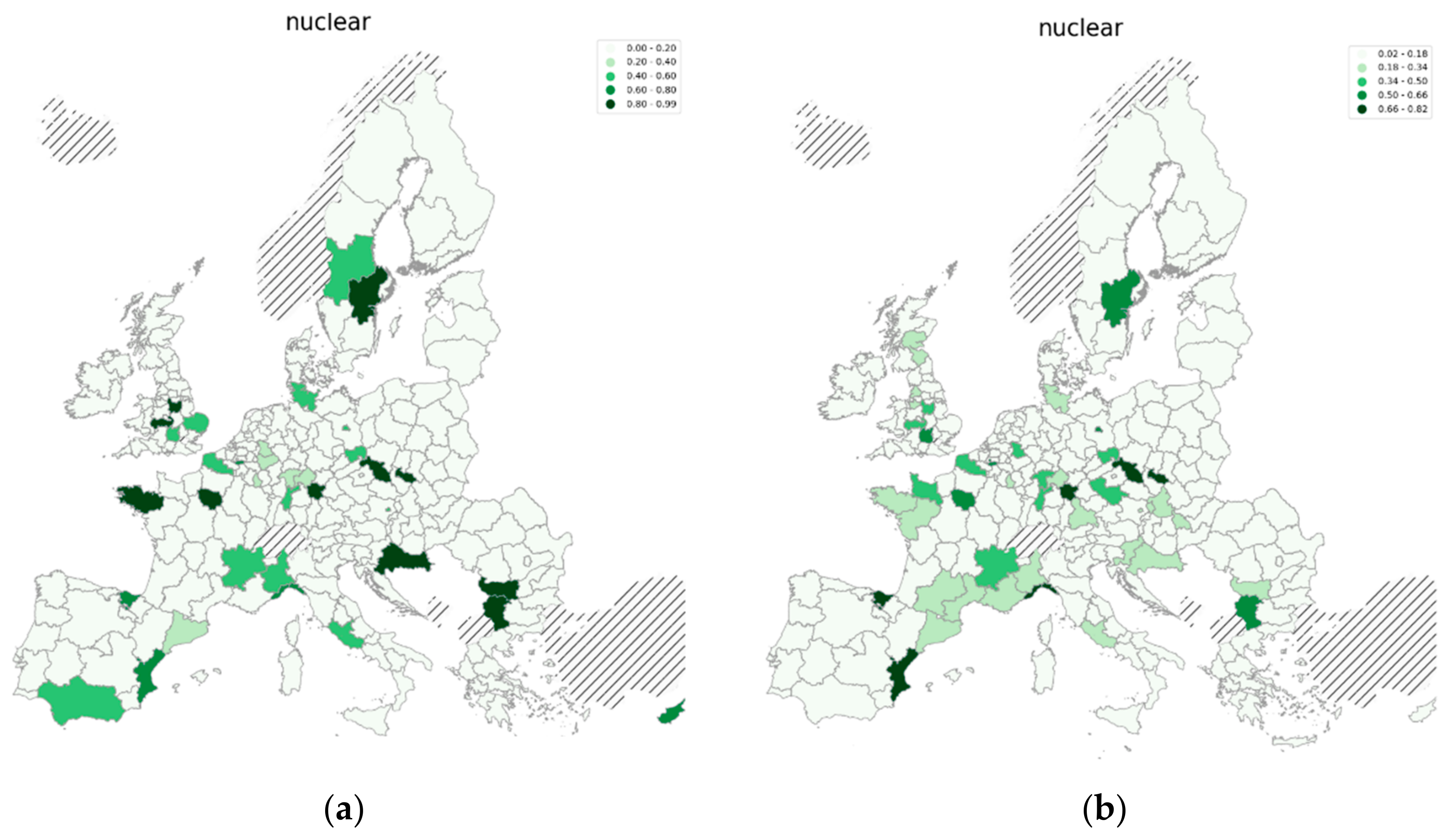
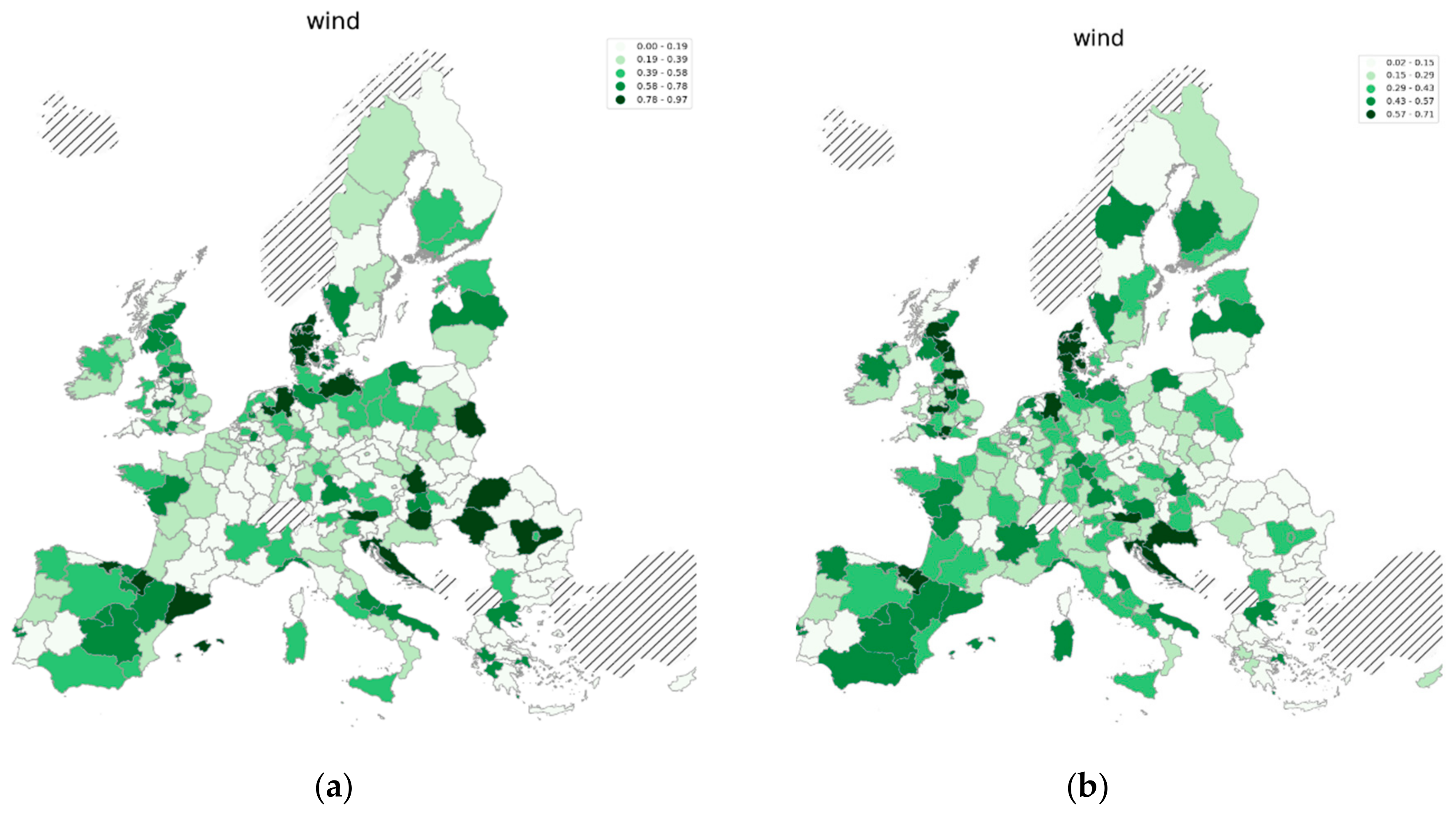
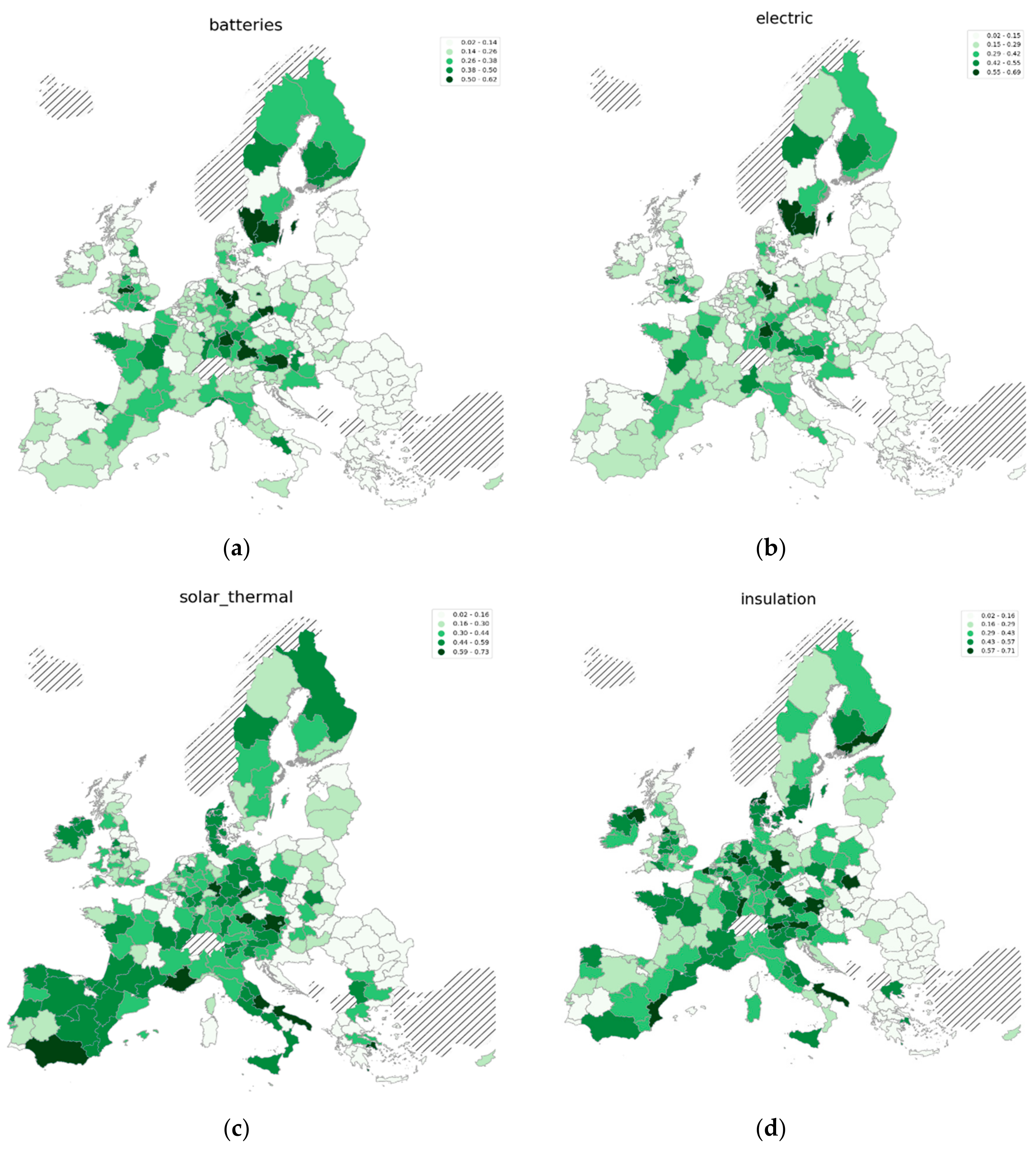
Appendix C. Regional Potential in Low-Carbon Technologies
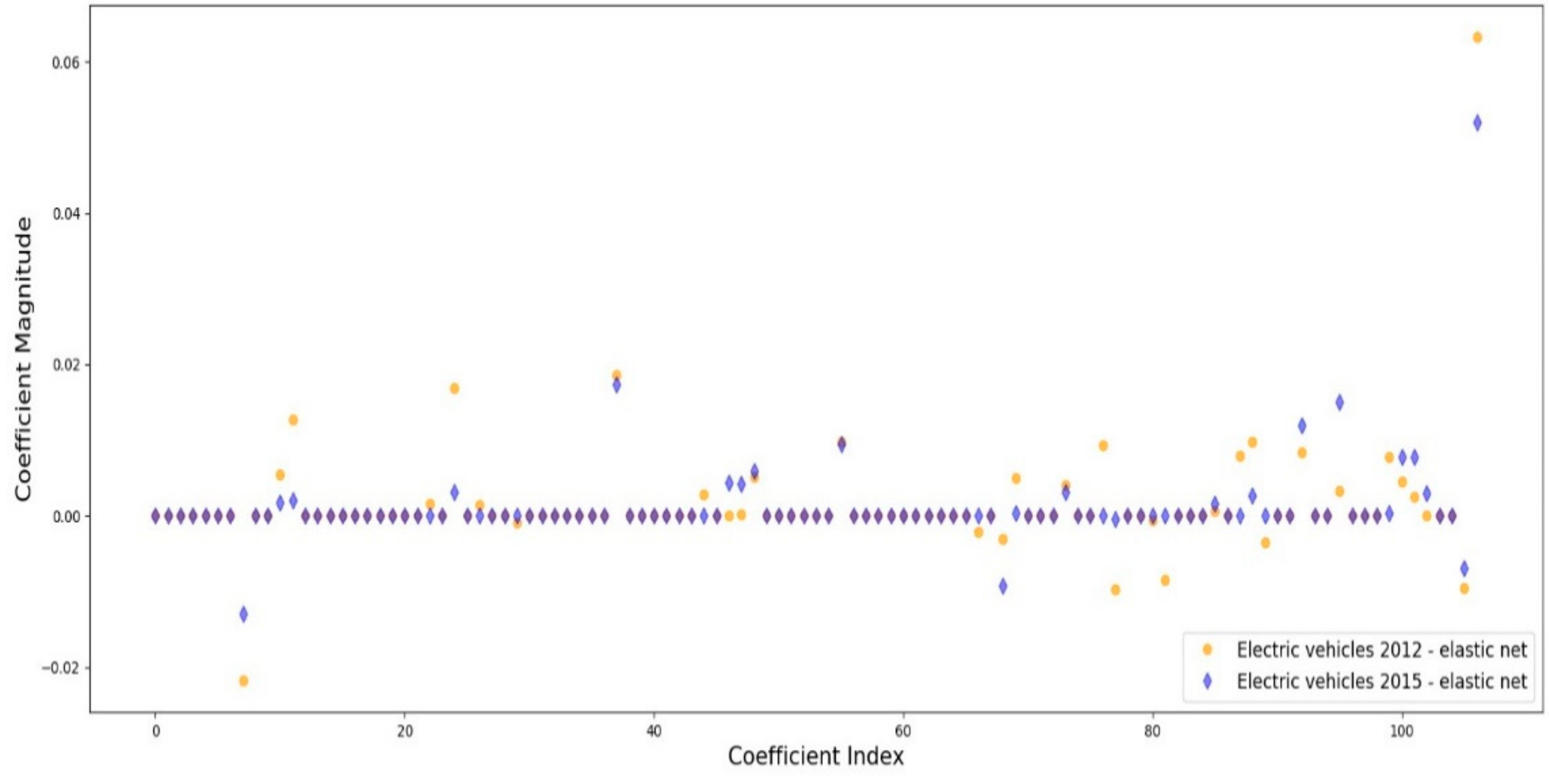
Appendix D. Regularisation Results
| t | t − 1 | t − 2 | All | |
|---|---|---|---|---|
| Activity rates by age education attainment level and citizenship | 15 | 16 | 21 | 52 |
| Total duration | 13 | 21 | 14 | 48 |
| Scientists and engineers | 4 | 7 | 7 | 18 |
| HH Paid current taxes on income wealth etc. mil EUR | 5 | 6 | 5 | 16 |
| HH Social benefits other than social transfers in kind received mil EUR | 5 | 8 | 3 | 16 |
| Persons employed in science and technology | 8 | 2 | 4 | 14 |
| Long term unemployment (12 months or longer) in thousands | 6 | 3 | 5 | 14 |
| Unemployment rate by age | 4 | 5 | 5 | 14 |
| Average number of usual weekly hours in the main job by age in hours | 6 | 1 | 5 | 12 |
| Participation rate in education and training (last 4 weeks) total age 25–64 | 0 | 6 | 5 | 11 |
| Gross domestic expenditure on R&D million EUR government | 5 | 6 | 0 | 11 |
| Self-employed persons | 2 | 4 | 5 | 11 |
| HH Net social contributions mil EUR | 3 | 4 | 4 | 11 |
| Gross domestic expenditure on R&D million EUR business enterprise sector | 6 | 4 | 0 | 10 |
| t | t − 1 | t − 2 | All | |
|---|---|---|---|---|
| Activity rates by age education attainment level and citizenship | 12 | 14 | 13 | 39 |
| Total duration | 11 | 12 | 10 | 33 |
| Scientists and engineers | 6 | 7 | 5 | 18 |
| Average number of usual weekly hours in the main job by age in hours | 7 | 4 | 5 | 16 |
| Persons employed in science and technology | 8 | 4 | 4 | 16 |
| HH Paid current taxes on income wealth etc. mil EUR | 4 | 6 | 4 | 14 |
| Long term unemployment (12 months or longer) in thousands | 7 | 2 | 4 | 13 |
| Self-employed persons | 3 | 2 | 6 | 11 |
| Proportion of population aged 20–39 | 4 | 2 | 5 | 11 |
| Participation rate in education and training (last 4 weeks) total age 25–64 | 0 | 6 | 5 | 11 |
| HH Social benefits other than social transfers in kind received mil EUR | 4 | 7 | 0 | 11 |
| Gross domestic expenditure on R&D million EUR government | 8 | 3 | 0 | 11 |
| Persons with tertiary education (ISCED) and/or employed in science and technology % of the active population | 2 | 4 | 3 | 9 |
| Unemployment rate by age | 2 | 5 | 2 | 9 |
| t | t − 1 | t − 2 | All | |
|---|---|---|---|---|
| Total duration | 12 | 12 | 17 | 41 |
| Activity rates ISCED > 3 | 11 | 12 | 13 | 36 |
| Age dependency ratio (0–19 and over 60 to pop. aged 20–59) | 4 | 5 | 5 | 14 |
| Scientists and engineers | 6 | 4 | 4 | 14 |
| Long term unemployment (12 months or longer) in thousands | 6 | 2 | 6 | 14 |
| Students (ISCED 5–6) at regional level—as % of total country level students (ISCED 5–6) | 0 | 6 | 7 | 13 |
| Persons employed in science and technology | 8 | 3 | 2 | 13 |
| Gross domestic expenditure on R&D million EUR business enterprise sector | 6 | 4 | 3 | 13 |
| t | t − 1 | t − 1 | All | |
|---|---|---|---|---|
| Total duration of employment | 0 | 2 | 3 | 5 |
| Activity rates ISCED > 3 | 2 | 1 | 1 | 4 |
| HH Net social contributions mil EUR | 0 | 1 | 1 | 2 |
| Self-employed persons | 0 | 2 | 0 | 2 |
| Total R&D personnel bussiness enterprise sector full time equivalent (FTE) | 1 | 1 | 0 | 2 |
| Unemployment Rate (Females) | 2 | 0 | 0 | 2 |
References
- Huberty, M.; Zachmann, G. Green exports and the global product space: Prospects for EU industrial policy (No. 2011/07). In Bruegel Working Paper; Bruegel: Brussels, Belgium, 2011. [Google Scholar]
- Hidalgo, C.A.; Klinger, B.; Barabasi, A.L.; Hausmann, R. The product space conditions the development of nations. Science 2007, 317, 482–487. [Google Scholar] [CrossRef] [PubMed]
- Hamwey, R.; Pacini, H.; Assunção, L. Mapping green product spaces of nations. J. Environ. Dev. 2013, 22, 155–168. [Google Scholar] [CrossRef]
- Hidalgo, C.A.; Hausmann, R. The building blocks of economic complexity. Proc. Natl. Acad. Sci. USA 2009, 106, 10570–10575. [Google Scholar] [CrossRef] [PubMed]
- Fraccascia, L.; Giannoccaro, I.; Albino, V. Green product development: What does the country product space imply? J. Clean. Prod. 2018, 170, 1076–1088. [Google Scholar] [CrossRef]
- Foray, D.; David, P.A.; Hall, B.H. Smart Specialisation from Academic Idea to Political Instrument, the Surprising Career of a Concept and the Difficulties Involved in Its Implementation (No. REP_WORK); EPFL: Lusanne, Switzerland, 2011. [Google Scholar]
- Balland, P.A.; Boschma, R.; Crespo, J.; Rigby, L.D. Smart specialization policy in the European Union: Relatedness, knowledge complexity and regional diversification. Reg. Stud. 2019, 53, 1252–1268. [Google Scholar] [CrossRef]
- Crespo, J.; Balland, P.A.; Boschma, R.; Rigby, D. Regional Diversification Opportunities and Smart Specialization Strategies; European Commission: Brussels, Belgium, 2017; Available online: https://ec.europa.eu/research/openvision/pdf/rise/crespo-balland-boschma-rigby_regional_diversification.pdf (accessed on 20 December 2020).
- Zachmann, G.; Roth, A. Report on Assessing the Technology Innovation Implications of NDCs, Technology Portfolio Choices, and International Competitiveness in Clean Technologies V2.0–Final–01/08/2018. Available online: https://www.cop21ripples.eu/wp-content/uploads/2018/08/RIPPLES_D3.3.pdf (accessed on 20 December 2020).
- Mealy, P.; Teytelboym, A. Economic complexity and the green economy. Res. Policy 2020, 103948. [Google Scholar] [CrossRef]
- Van Den Berge, M.; Weterings, A. Relatedness in eco-technological development in European regions. Pap. Evol. Econ. Geogr. 2014, 14, 1–30. [Google Scholar]
- Montresor, S.; Quatraro, F. Green technologies and Smart Specialisation Strategies: A European patent-based analysis of the intertwining of technological relatedness and key enabling technologies. Reg. Stud. 2020, 54, 1354–1365. [Google Scholar] [CrossRef]
- Boschma, R.; Frenken, K. The emerging empirics of evolutionary economic geography. J. Econ. Geogr. 2011, 11, 295–307. [Google Scholar] [CrossRef]
- Hausmann, R.; Hidalgo, C.; Stock, D.; Yildirim, M.A. Implied Comparative Advantage; Center for International Development, Harvard University: Cambridge, MA, USA, 2019. [Google Scholar]
- Boschma, R.; Gianelle, C. Regional Branching and Smart Specialization Policy; JRC Technical Reports; 06/2104; Publications Office of the European Union: Luxembourg, 2013. [Google Scholar]
- Santoalha, A.; Boschma, R. Diversifying in green technologies in European regions: Does political support matter? Reg. Stud. 2020, 1–14. [Google Scholar] [CrossRef]
- Dordmond, G.; de Oliveira, H.C.; Silva, I.R.; Swart, J. The complexity of green job creation: An analysis of green job development in Brazil. Environ. Dev. Sustain. 2020, 1–24. [Google Scholar] [CrossRef]
- Shutters, S.T.; Muneepeerakul, R.; Lobo, J. How hard is it for urban economies to become ‘green’? Environ. Plan. B Plan. Des. 2016, 43, 198–209. [Google Scholar] [CrossRef]
- Fiorini, A.; Georgakaki, A.; Pasimeni, F.; Tzimas, E. Monitoring R&I in Low-Carbon Energy Technologies; Publications Office of the European Union: Luxembourg, 2017. [Google Scholar]
- Yan, B.; Luo, J. Measuring technological distance for patent mapping. J. Assoc. Inf. Sci. Technol. 2017, 68, 423–437. [Google Scholar] [CrossRef]
- Stellner, F. Technological distance measures: Theoretical foundation and empirics. In Proceedings of the DRUID Society Conference, Copenhagen, Denmark, 16–18 June 2014. [Google Scholar]
- Ospina, R.; Ferrari, S.L. A general class of zero-or-one inflated beta regression models. Comput. Stat. Data Anal. 2012, 56, 1609–1623. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Imai, K.; Kim, I.S. On the Use of Two-Way Fixed Effects Regression Models for Causal Inference with Panel Data; Harvard University: Cambridge, MA, USA, 2018. [Google Scholar]
- Giesselmann, M.; Schmidt-Catran, A. Interactions in Fixed Effects Regression Models. Sociol. Methods Res. 2018. [Google Scholar] [CrossRef]
- Ghisetti, C.; Marzucchi, A.; Montresor, S. The open eco-innovation mode. An empirical investigation of eleven European countries. Res. Policy 2015, 44, 1080–1093. [Google Scholar] [CrossRef]
- Barbieri, N.; Marzucchi, A.; Rizzo, U. Knowledge sources and impacts on subsequent inventions: Do green technologies differ from non-green ones? Res. Policy 2020, 49, 103901. [Google Scholar] [CrossRef]
- Mariani, M.S.; Medo, M.; Lafond, F. Early identification of important patents: Design and validation of citation network metrics. Technol. Forecast. Soc. Chang. 2019, 146, 644–654. [Google Scholar] [CrossRef]
- Wu, C.C.; Yao, C.B. Constructing an intelligent patent network analysis method. Data Sci. J. 2012, 11, 110–125. [Google Scholar] [CrossRef][Green Version]
- Song, B.; Triulzi, G.; Alstott, J.; Yan, B.; Luo, J. Overlay patent network to analyze the design space of a technology domain: The case of hybrid electrical vehicles. In Proceedings of the DESIGN 2016 14th International Design Conference, Dubrovnik, Croatia, 16–19 May 2016; pp. 1145–1154. [Google Scholar]
- Martin, S.; Brown, W.M.; Klavans, R.; Boyack, K.W. OpenOrd: An open-source toolbox for large graph layout. In Proceedings Volume 7868, Visualization and Data Analysis 2011; International Society for Optics and Photonics: Bellingham, WA, USA, 2011. [Google Scholar]
- Calignano, G.; Trippl, M. Innovation-Driven or Challenge-Driven Participation in International Energy Innovation Networks? Empirical Evidence from the H2020 Programme. Sustainability 2020, 12, 4696. [Google Scholar] [CrossRef]
- Barca, F. Agenda for a Reformed Cohesion Policy; European Communities: Brussels, Belgium, 2009. [Google Scholar]
- Capasso, M.; Hansen, T.; Heiberg, J.; Klitkou, A.; Steen, M. Green growth–A synthesis of scientific findings. Technol. Forecast. Soc. Chang. 2019, 146, 390–402. [Google Scholar] [CrossRef]
- Fankhauser, S.; Bowen, A.; Calel, R.; Dechezleprêtre, A.; Grover, D.; Rydge, J.; Sato, M. Who will win the green race? In search of environmental competitiveness and innovation. Glob. Environ. Chang. 2013, 23, 902–913. [Google Scholar] [CrossRef]
- Cosbey, A.; Wooders, P.; Bridle, R.; Casier, L. In with the good, out with the bad: Phasing out polluting sectors as green industrial policy. In Green Industrial Policy. Concept, Policies, Country Experiences; UN Environment: Geneva, Switzerland; Bonn, Germany, 2017. [Google Scholar]
- Pahle, M.; Pachauri, S.; Steinbacher, K. Can the Green Economy deliver it all? Experiences of renewable energy policies with socio-economic objectives. Appl. Energy 2016, 179, 1331–1341. [Google Scholar] [CrossRef]
- Aiginger, K.; Rodrik, D. Rebirth of Industrial Policy and an Agenda for the Twenty-First Century. J Ind Compet Trade 2020, 189–207. [Google Scholar] [CrossRef]
- Rodrik, D. Green industrial policy. Oxf. Rev. Econ. Policy 2014, 30, 469–491. [Google Scholar] [CrossRef]
- Pegels, A.; Vidican-Auktor, G.; Lütkenhorst, W.; Altenburg, T. Politics of green energy policy. J. Environ. Dev. 2018, 27, 26–45. [Google Scholar] [CrossRef]
- Lane, N. The new empirics of industrial policy. J. Ind. Compet. Trade 2020, 20, 209–234. [Google Scholar] [CrossRef]
- Addo, E.D. . Performance Comparison of Imputation Algorithms on Missing at Random Data. Master’s Thesis. Electronic Theses and Dissertations, 2018; Paper 3422. Department of Mathematics East Tennessee State University. Available online: https://dc.etsu.edu/etd/3422 (accessed on 20 December 2020).
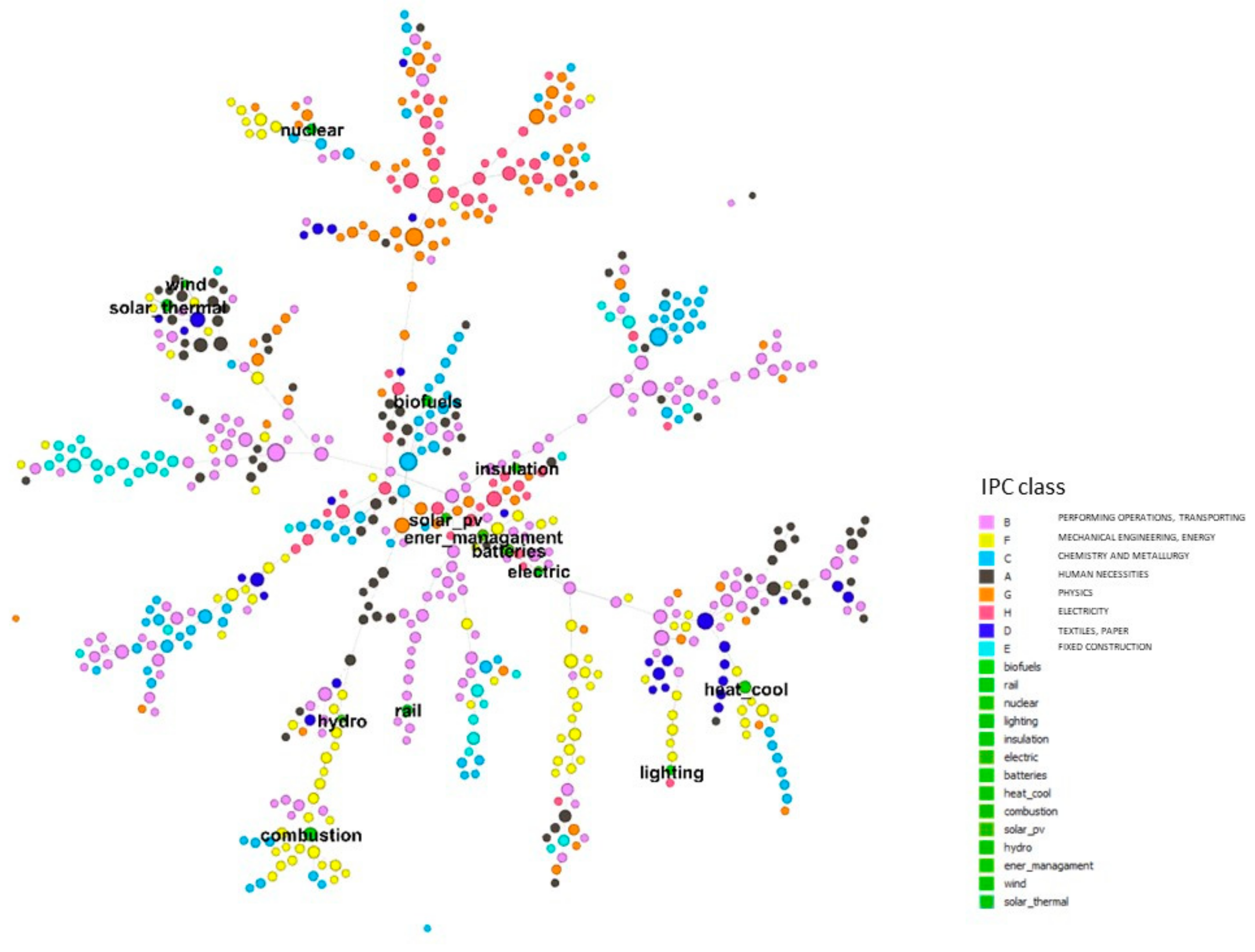
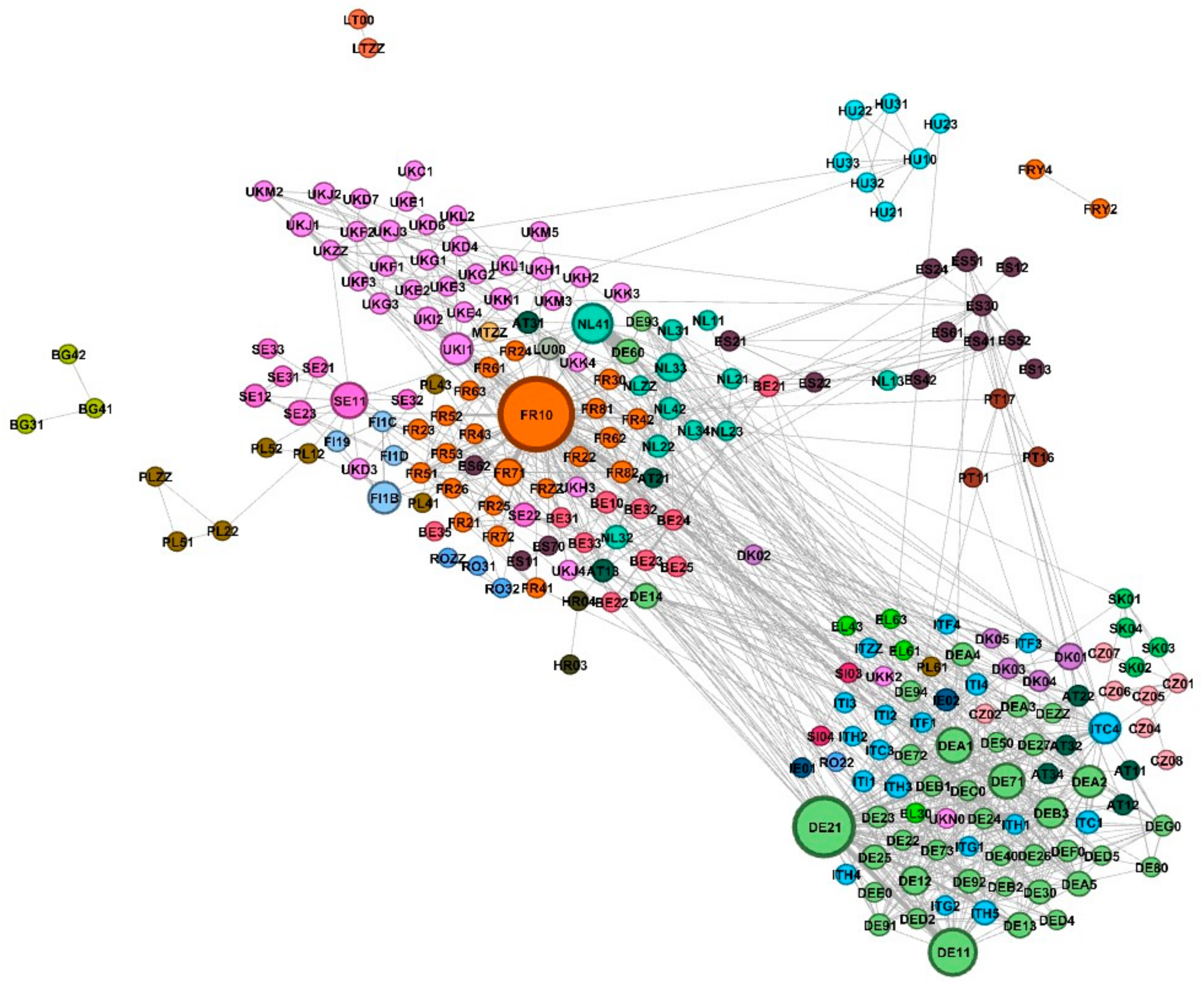

| Technology | pRTA (2019) | RTA (2015) |
|---|---|---|
| Energy Management | 0.67 | 0.28 |
| Solar Panels | 0.62 | 0.37 |
| Batteries | 0.60 | 0.27 |
| Electric vehicles | 0.59 | 0.34 |
| Lighting | 0.59 | 0.21 |
| Biofuels | 0.58 | 0.46 |
| Heating andcooling | 0.54 | 0.32 |
| Combustion | 0.53 | 0.38 |
| Insulation | 0.49 | 0.30 |
| Rail | 0.39 | 0.28 |
| Solar Thermal | 0.34 | 0.27 |
| Wind | 0.29 | 0.24 |
| Nuclear | 0.24 | 0.25 |
| Hydro | 0.10 | 0.18 |
| t | t − 1 | t − 2 | All | |
|---|---|---|---|---|
| Activity rate of population | 15 | 16 | 21 | 52 |
| Total duration of employment | 13 | 21 | 14 | 48 |
| Scientists and engineers | 4 | 7 | 7 | 18 |
| HH Paid current taxes on income wealth etc. mil EUR | 5 | 6 | 5 | 16 |
| HH Social benefits other than social transfers in kind received mil EUR | 5 | 8 | 3 | 16 |
| Persons employed in science and technology | 8 | 2 | 4 | 14 |
| Long term unemployment (12 months or longer) in thousands | 6 | 3 | 5 | 14 |
| Unemployment rate by age | 4 | 5 | 5 | 14 |
| t | t − 1 | t − 2 | All | |
|---|---|---|---|---|
| Activity rates of population | 12 | 14 | 13 | 39 |
| Total duration of employment | 11 | 12 | 10 | 33 |
| Scientists and engineers | 6 | 7 | 5 | 18 |
| Average number of usual weekly hours in the main job by age in hours | 7 | 4 | 5 | 16 |
| Persons employed in science and technology | 8 | 4 | 4 | 16 |
| HH Paid current taxes on income wealth etc. mil EUR | 4 | 6 | 4 | 14 |
| Long term unemployment (12 months or longer) in thousands | 7 | 2 | 4 | 13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bergamini, E.; Zachmann, G. Exploring EU’s Regional Potential in Low-Carbon Technologies. Sustainability 2021, 13, 32. https://doi.org/10.3390/su13010032
Bergamini E, Zachmann G. Exploring EU’s Regional Potential in Low-Carbon Technologies. Sustainability. 2021; 13(1):32. https://doi.org/10.3390/su13010032
Chicago/Turabian StyleBergamini, Enrico, and Georg Zachmann. 2021. "Exploring EU’s Regional Potential in Low-Carbon Technologies" Sustainability 13, no. 1: 32. https://doi.org/10.3390/su13010032
APA StyleBergamini, E., & Zachmann, G. (2021). Exploring EU’s Regional Potential in Low-Carbon Technologies. Sustainability, 13(1), 32. https://doi.org/10.3390/su13010032




