Conceptual Model of Drainage-Sub Irrigation System Functioning-First Results from a Case Study of a Lowland Valley Area in Central Poland
Abstract
1. Introduction
2. Materials and Methods
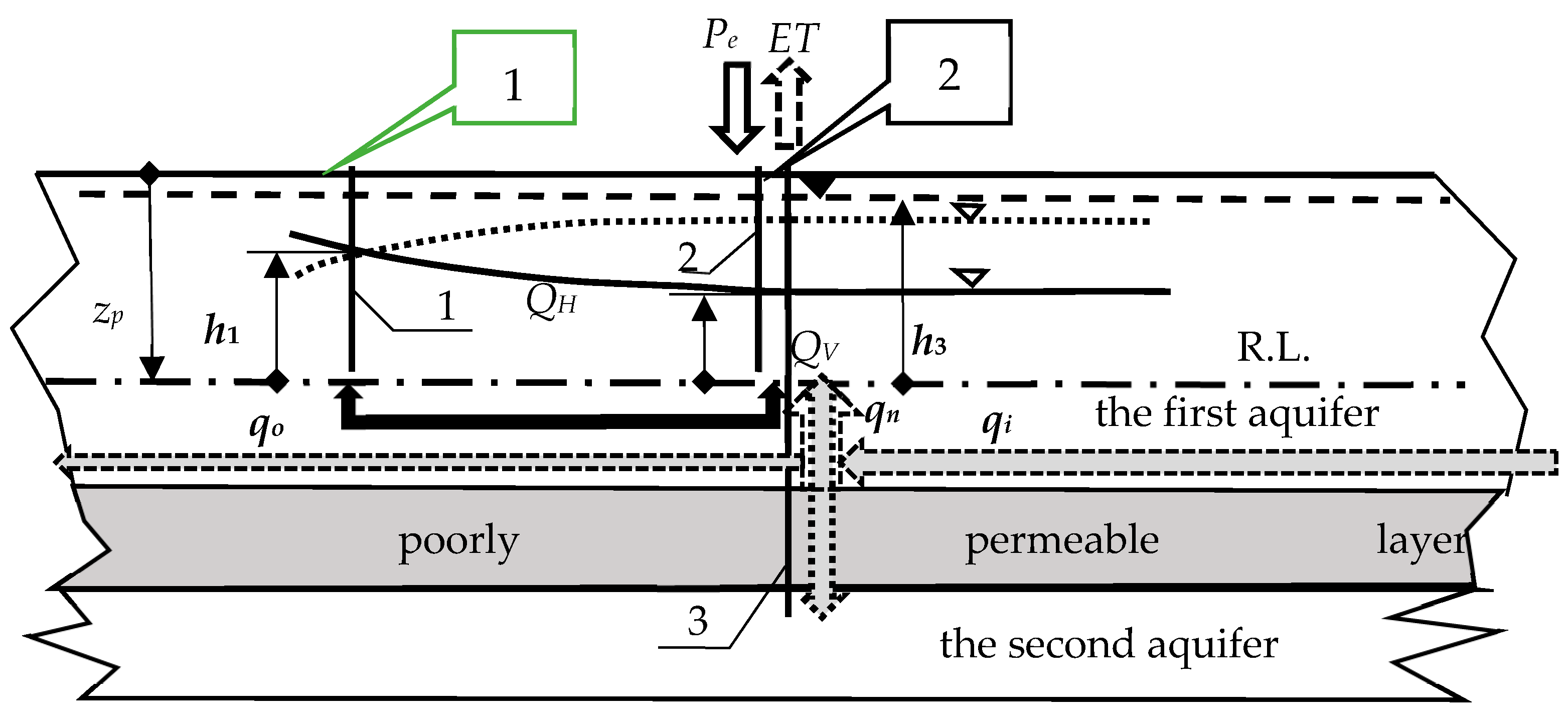
2.1. Study Site
2.2. Meteorological Indicators
- ETo—reference evapotranspiration [mm day−1],
- Rn—net radiation at the crop surface [MJ m−2 day−1],
- G—soil heat flux density [MJ m−2 day−1],
- T—mean daily air temperature at 2 m height [°C],
- u2—wind speed at 2 m height [m s−1],
- es—saturation vapor pressure [kPa],
- es − ea—saturation vapor pressure deficit [kPa],
- ∆—slope vapor pressure curve [kPa °C−1],
- γ—psychrometric constant [kPa °C−1].
2.3. Model Description
- j = number of the current moment of calculation,
- = the computation interval of time, e.g., day
- n = natural number and zero; τ = n · Δt = time-lag of irrigation or drainage [T],
- T = the time constant of drainage/irrigation [T],
- = the specific yield in soil profile [-],
- = groundwater table level midspacing between the ditches/drain pipes without taking into account deep percolation of soil water, at the moment j + 1 [L],
- = initial condition-groundwater table level midspacing between the ditches/drain pipes after taking into account deep percolation of soil water, at the moment j [L],
- = inducing factors–the water table level in the ditches/in the soil at the lines of the drain pipes in moment j + 1 − n and j − n, respectively.
- = the average level of groundwater at any given time without taking into account deep percolation of soil water [L],
- = the water level in the ditches/in the line of the drain pipes and the groundwater level midspacing between the ditches/drain pipes, respectively, at the cross-section without taking into account deep percolation of soil water [L],
- = coefficient of the shape of the groundwater table curve between the ditches/drain pipes [-],
- ET = flux density of evapotranspiration at the cross-section [LT−1],
- = flux density of effective precipitation and effective sprinkler irrigation rate (infiltration into the unsaturated zone) [LT−1],
- = depth beneath the land surface to the reference level [L],
- = the depth of the root zone of plants in the soil profile [L],
- = water exchange coefficient between the aquifers [T−1],
- = the net lateral flux density of water in horizontal subsurface flow exchanged with adjacent areas (released from or taken into soil storage) [LT−1].
- = coefficient of the additional water storage capacity of the root zone and soil surface [-],
- = corrected (after soil water deep percolation) water equivalent of transient porosity in the soil profile at j + 1 moment,
- = drainable porosity; ; = maximum value of specific yield [-].
- = water equivalent of transient porosity in the soil profile at j + 1 moment-corrected (after soil water deep percolation),
- = total specific yield of the soil [L].
- = average soil moisture of the root layer of thickness za [L3 L−3],
- = average saturated soil moisture of the root layer of thickness za [L3 L−3],
- = transient porosity below the layer of the main mass of plant roots about thickness za.
2.4. Model Calibration and Validation
- N = the number of results of measurements and the number of results of calculations taken for comparisons,
- = calculated and measured values, respectively.
3. Results and Discussion
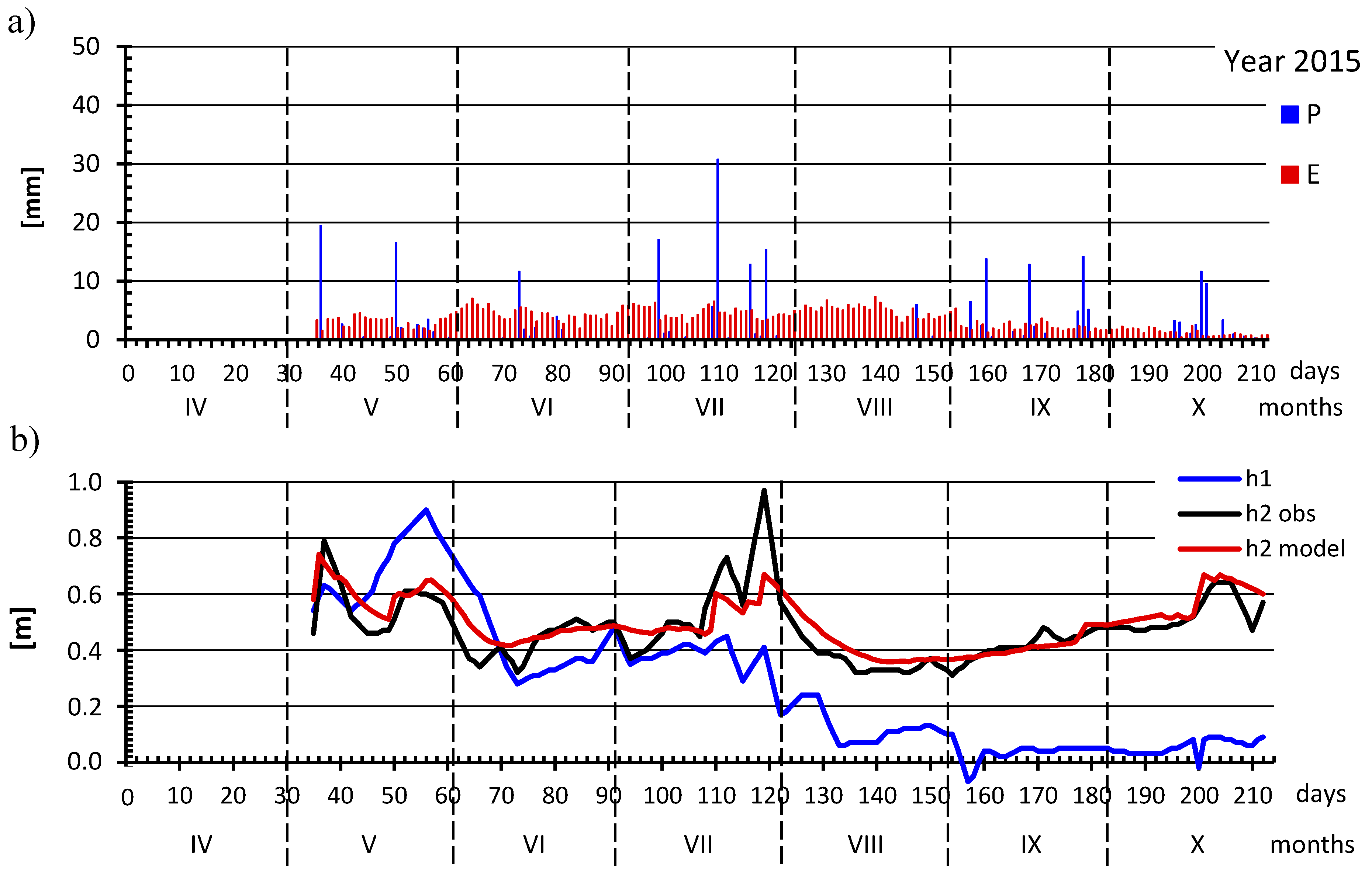
3.1. Estimation of Model Performance
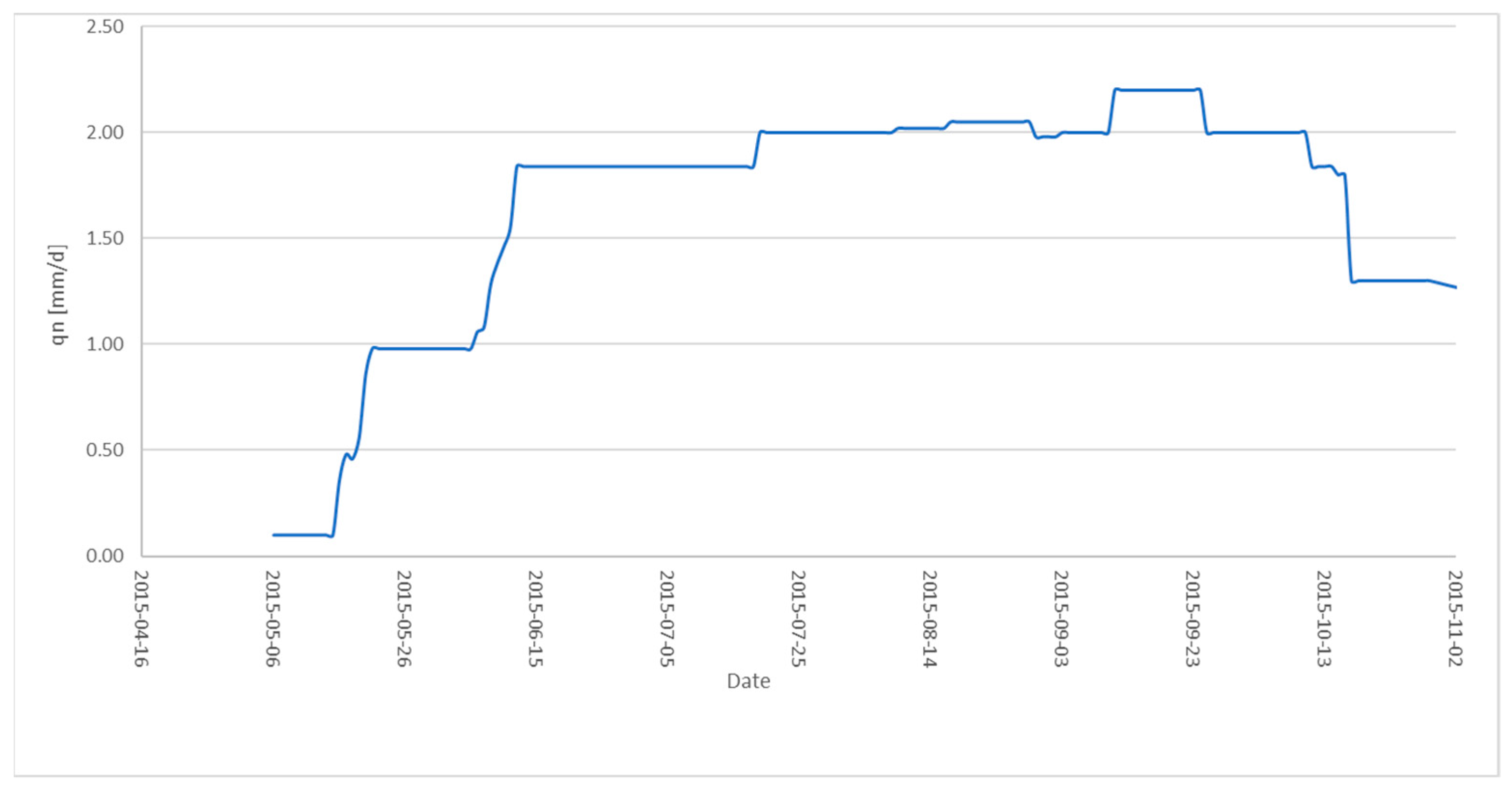
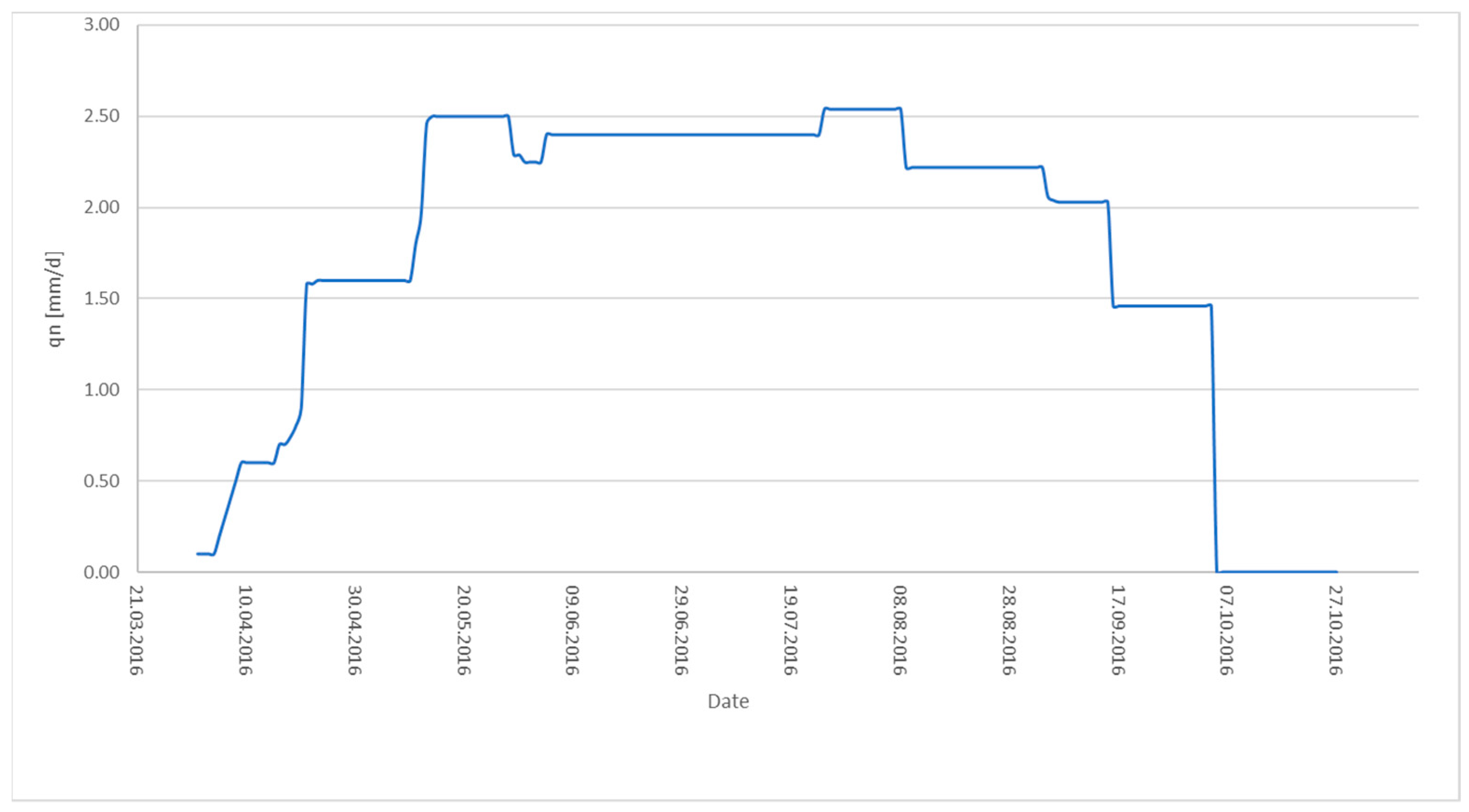
3.2. Lateral Inflows (qn)
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Van Keulen, H.; Van Beek, C.G. Water movement in layered soils—A simulation model. Neth. J. Agric. Sci. 1971, 19, 138–153. [Google Scholar] [CrossRef]
- Wierenga, P.J.; De Wit, C.T. Simulation of heat transfer in soils. Soil Sci. Soc. Am. Proc. 1970, 34, 845–848. [Google Scholar] [CrossRef]
- Gerke, H.H.; van Genuchten, M.T. A dual-porosity model for simulating the preferential movement of water and solutes in structured porous-media. Water Resour. Res. 1993, 29, 305–319. [Google Scholar] [CrossRef]
- Van Veen, J.A.; Paul, E.A. Organic-carbon dynamics in grassland soils. 1. Background information and computer-simulation. Can. J. Soil Sci. 1981, 61, 185–201. [Google Scholar] [CrossRef]
- Cole, C.V.; Innis, G.S.; Stewart, J.W. Simulations of phosphorus cycling in semi arid grasslands. In Grassland Simulation Model; Innis, G.S., Ed.; Springer: New York, NY, USA, 1978; Volume 26, pp. 205–230. [Google Scholar] [CrossRef]
- Hunt, H.W.; Wall, D.H. Modelling the effects of loss of soil biodiversity on ecosystem function. Glob. Chang. Biol. 2002, 8, 33–50. [Google Scholar] [CrossRef]
- Hopmans, J.W.; Bristow, K.L. Current Capabilities and Future Needs of Root Water and Nutrient Uptake Modeling. Adv. Agron. 2002, 77, 103–183. [Google Scholar]
- Javaux, M.V.; Couvreur, J.; Borght, V.; Vereecken, H. Root water uptake: From three-dimensional biophysical processes to macroscopic modeling approaches. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Schnepf, A.; Roose, T.; Schweiger, P. Impact of growth and uptake patterns of arbuscular mycorrhizal fungi on plant phosphorus uptake—A modelling study. Plant. Soil 2008, 312, 85–99. [Google Scholar] [CrossRef]
- Leitner, D.; Klepsch, S.; Ptashnyk, M.; Marchant, A.; Kirk, G.J.; Schnepf, A.; Roose, T. A dynamic model of nutrient uptake by root hairs. New Phytol. 2010, 185, 792–802. [Google Scholar] [CrossRef]
- Kaca, E. Modeling of Subirrigation; Wydawnictwo IMUZ: Falenty, Poland, 1999; p. 115, (In Polish with English Summary). [Google Scholar]
- Vogel, H.J.; Roth, K. Moving through scales of flow and transport in soil. J. Hydrol. 2003, 272, 95–106. [Google Scholar] [CrossRef]
- Brandyk, T.; Leeds-Harrison, P.; Skapski, K. A simple flow resistance model for the management of drainage/sub-irrigation systems. Agric. Water Manag. 1992, 21, 67–77. [Google Scholar] [CrossRef]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014, Update 2015: International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; Fao: Rome, Italy, 2015. [Google Scholar]
- Gurley Kahn, K.; Ge, S.; Saul Caine, J.; Manning, A. Characterization of the shallow groundwater system in an alpine watershed: Handcart Gulch, Colorado, USA. Hydrogeol. J. 2008, 16, 103–121. [Google Scholar] [CrossRef]
- Eijkelkamp. Laboratory Permeameters. User Manual. 2020 [WWW Document]. Available online: https://en.eijkelkamp.com/products/laboratory-equipment/ (accessed on 17 November 2020).
- Brandyk, A.; Kiczko, A.; Majewski, G.; Kleniewska, M.; Krukowski, M. Uncertainty of Derdorff’s soil moisture model based on continuous TDR measurements for sandy loam soil. J. Hydrol. Hydromech. 2016, 64, 23–29. [Google Scholar] [CrossRef]
- Łabędzki, L. Agricultural Droughts an Outline of Problems and Methods of Monitoring and Classification; Wydawnictwo IMUZ: Falenty, Poland, 2006; 107p, (In polish with English summary). [Google Scholar]
- Bąk, B.; Łabędzki, L. Assessing drought severity with the relative precipitation index (RPI) and the standardized precipitation index (SPI). J. Water Land Dev. 2002, 6, 29–49. [Google Scholar]
- Kalyanmoy, D. Optimization for Engineering Design; Prentice Hall: New Delhi, India, 1988. [Google Scholar]
- Calderon-Palma, H.; Bentley, L. A regional scale groundwater flow model for the Leon- Chinandega aquifer, Nicaragua. Hydrogeol. J. 2007, 15, 1457–1472. [Google Scholar] [CrossRef]
- Copty, N.; Sarioglu, M.; Findikakis, A. Equivalent transmissivity of heterogeneous leaky aquifers for steady state radial flow. Water Resour. Res. 2006, 42, W04416. [Google Scholar] [CrossRef]
- Brandyk, T.; Szatylowicz, J.; Oleszczuk, R.; Gnatowski, T. Water-related physical attributes of organic soils. In Organic Soils and Peat Materials for Sustainable Agriculture, 1st ed.; Parent, L.E., Ilnicki, P., Eds.; CRC Press and International Peat Society: Boca Raton, FL, USA, 2002. [Google Scholar]
- Khadri, S.; Pande, C. Ground water flow modeling for calibrating steady state using MODFLOW software: A case study of Mahesh River basin, India. Modeling Earth Syst. Environ. 2016, 2, 39. [Google Scholar] [CrossRef]



| Monthly Sums of Precipitation (mm) | |||||||
|---|---|---|---|---|---|---|---|
| Year/Month | April | May | June | July | August | September | October |
| 2015 | 32.5 | 55.9 | 22.2 | 87.8 | 7.4 | 66.4 | 37.5 |
| 2016 | 43.2 | 24.9 | 46.6 | 24.6 | 62.8 | 16.9 | 115.7 |
| 2017 | 62.8 | 61.0 | 85.8 | 89.0 | 52.6 | 124.7 | 89.0 |
| Average sum for period of 1960 to 2017 | 36.7 | 59.4 | 68.7 | 78.6 | 64.6 | 48.9 | 39.8 |
| Relative precipitation index (%) | |||||||
| 2015 | 88.5 average | 94.1 average | 32.3 Very dry | 111.7 average | 11.4 Extremely dry | 135.8 wet | 94.2 Average |
| 2016 | 117.7 average | 41.9 Very dry | 67.8 dry | 31.3 Very dry | 97.2 average | 34.5 Very dry | 290.7 Wet |
| 2017 | 171.1 wet | 102.7 average | 124.9 average | 113.2 average | 81.4 average | 255.0 wet | 223.6 wet |
| RPI classes on the basis of monthly sum of precipitation [19]: (1) extremely dry 0–24.9; (2) very dry 25–49.9; (3) dry 50–74.98; (4) average (75–125.9) | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brandyk, A.; Kaca, E.; Oleszczuk, R.; Urbański, J.; Jadczyszyn, J. Conceptual Model of Drainage-Sub Irrigation System Functioning-First Results from a Case Study of a Lowland Valley Area in Central Poland. Sustainability 2021, 13, 107. https://doi.org/10.3390/su13010107
Brandyk A, Kaca E, Oleszczuk R, Urbański J, Jadczyszyn J. Conceptual Model of Drainage-Sub Irrigation System Functioning-First Results from a Case Study of a Lowland Valley Area in Central Poland. Sustainability. 2021; 13(1):107. https://doi.org/10.3390/su13010107
Chicago/Turabian StyleBrandyk, Andrzej, Edmund Kaca, Ryszard Oleszczuk, Janusz Urbański, and Jan Jadczyszyn. 2021. "Conceptual Model of Drainage-Sub Irrigation System Functioning-First Results from a Case Study of a Lowland Valley Area in Central Poland" Sustainability 13, no. 1: 107. https://doi.org/10.3390/su13010107
APA StyleBrandyk, A., Kaca, E., Oleszczuk, R., Urbański, J., & Jadczyszyn, J. (2021). Conceptual Model of Drainage-Sub Irrigation System Functioning-First Results from a Case Study of a Lowland Valley Area in Central Poland. Sustainability, 13(1), 107. https://doi.org/10.3390/su13010107





