Identification of the Relationship between Rainfall and the CN Parameter in Western Carpathian Mountain Catchments in Poland
Abstract
1. Introduction
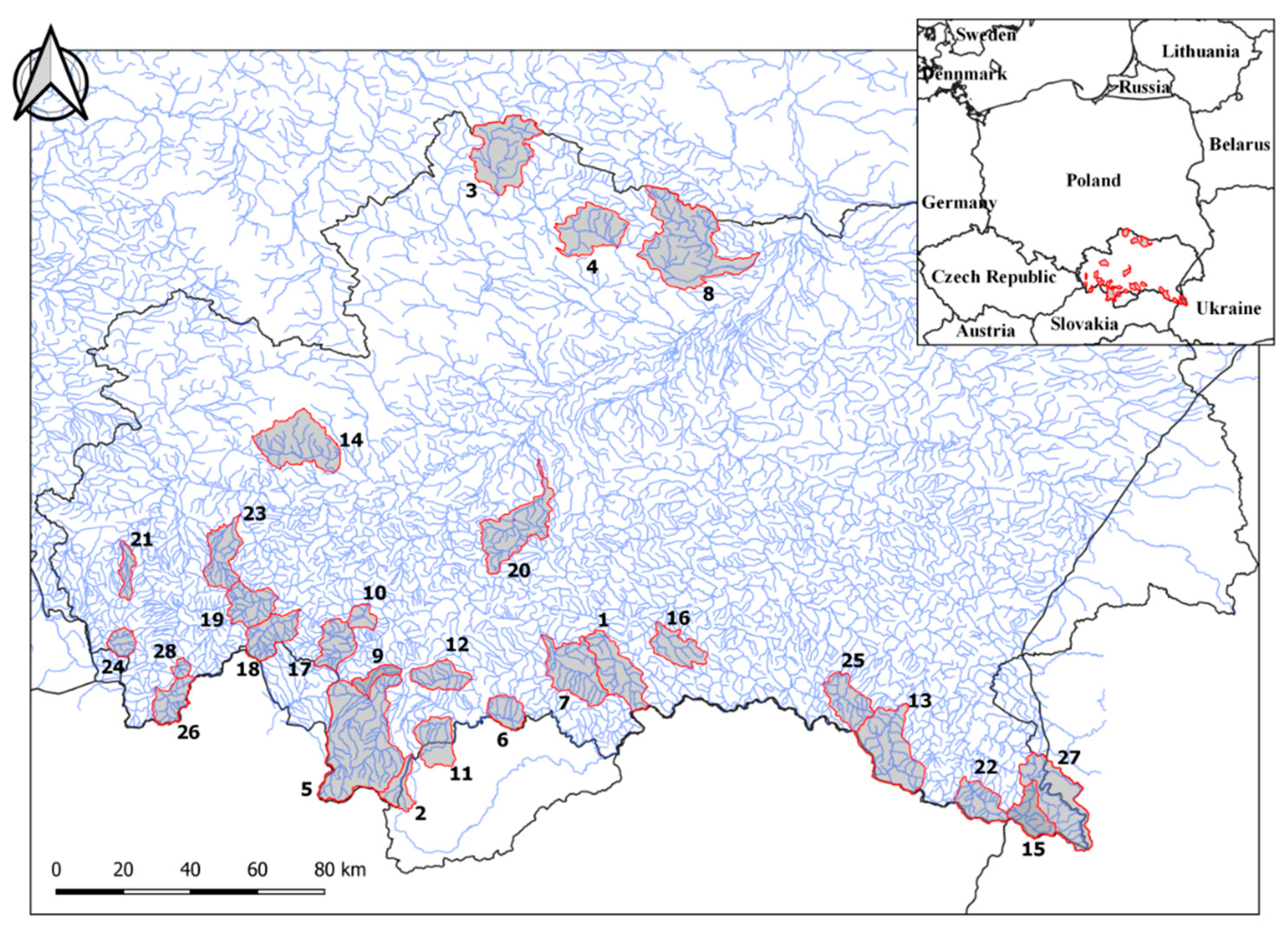
2. Study Area
3. Materials and Methods
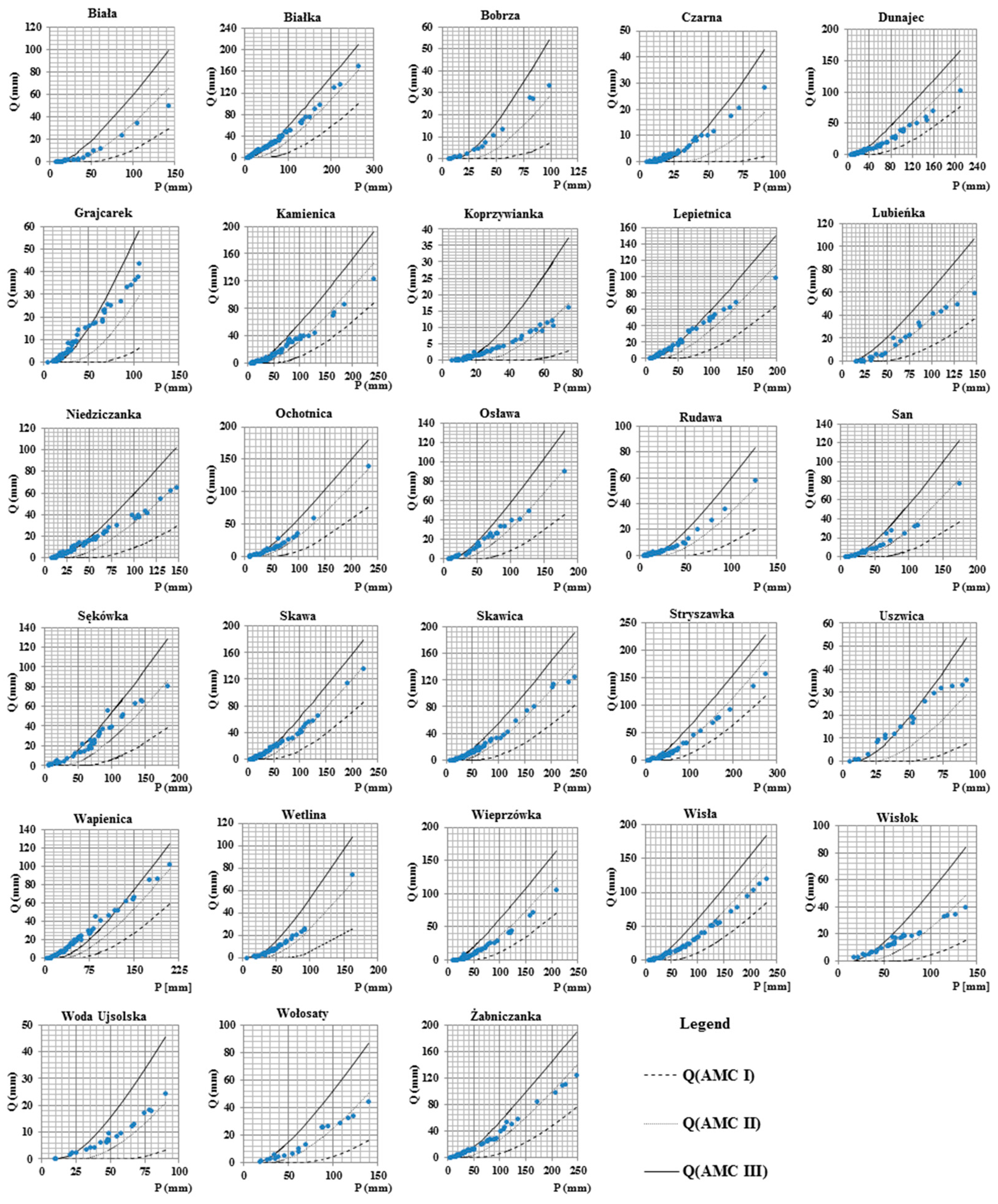
3.1. Determination of the Volume of Runoff Using the NRCS-CN Method
- Q—direct drain (mm);
- P—total rainfall (mm);
- S—maximum potential catchment retention (mm).
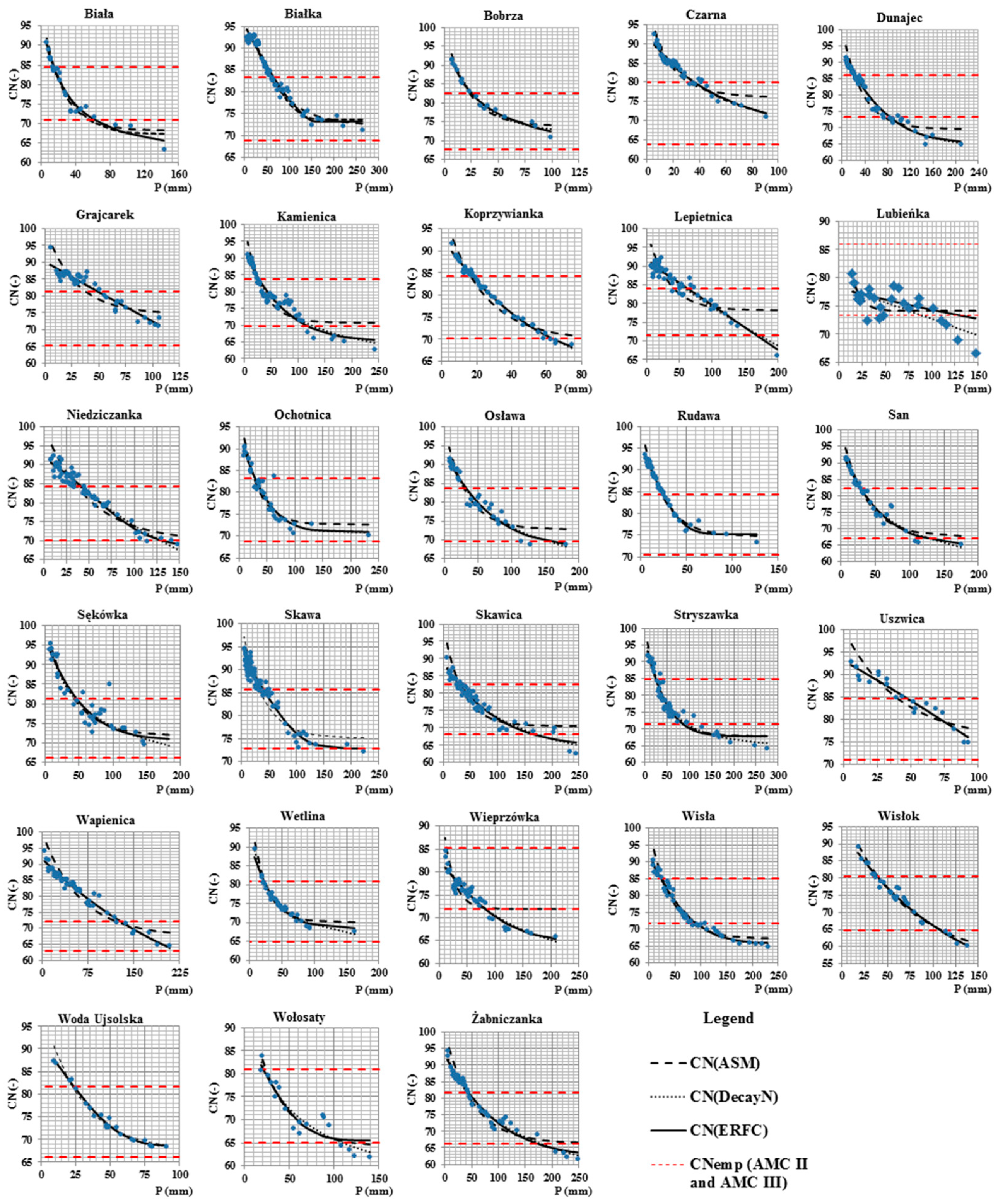
3.2. Determining the Rainfall–CN Parameter Relationship
- Si—episode retention height (mm);
- Pi—rainfall for the episode (mm);
- Qi—direct runoff in an episode (mm).
- CN∞—constant for P→∞;
- k—matching constant;
- P—rainfall (mm).
- CNL—number of the curve for the highest rainfall;
- b, c, d—parameters of the equation.
- CN∞—constant for P→∞;
- b—amplitude of the density function;
- c—location parameter;
- d—scale parameter;
- P—rainfall (mm).
- CN90—the value of the curve number determined for the 90th rainfall percentile in the distribution series of observations;
- CN∞, L—constant for P→∞ or number of the curve for the highest rainfall.
3.3. Determining the Value of the CN Parameter Taking into Account the Correction for Decrease
- CNII, CNIII—empirical values of the CN parameter for the average and moist moisture level;
- a, b, c—equation parameters;
- α—catchment decline (m/m).
- Qo—observed direct runoff (mm);
- Qcal—direct runoff calculated (mm).
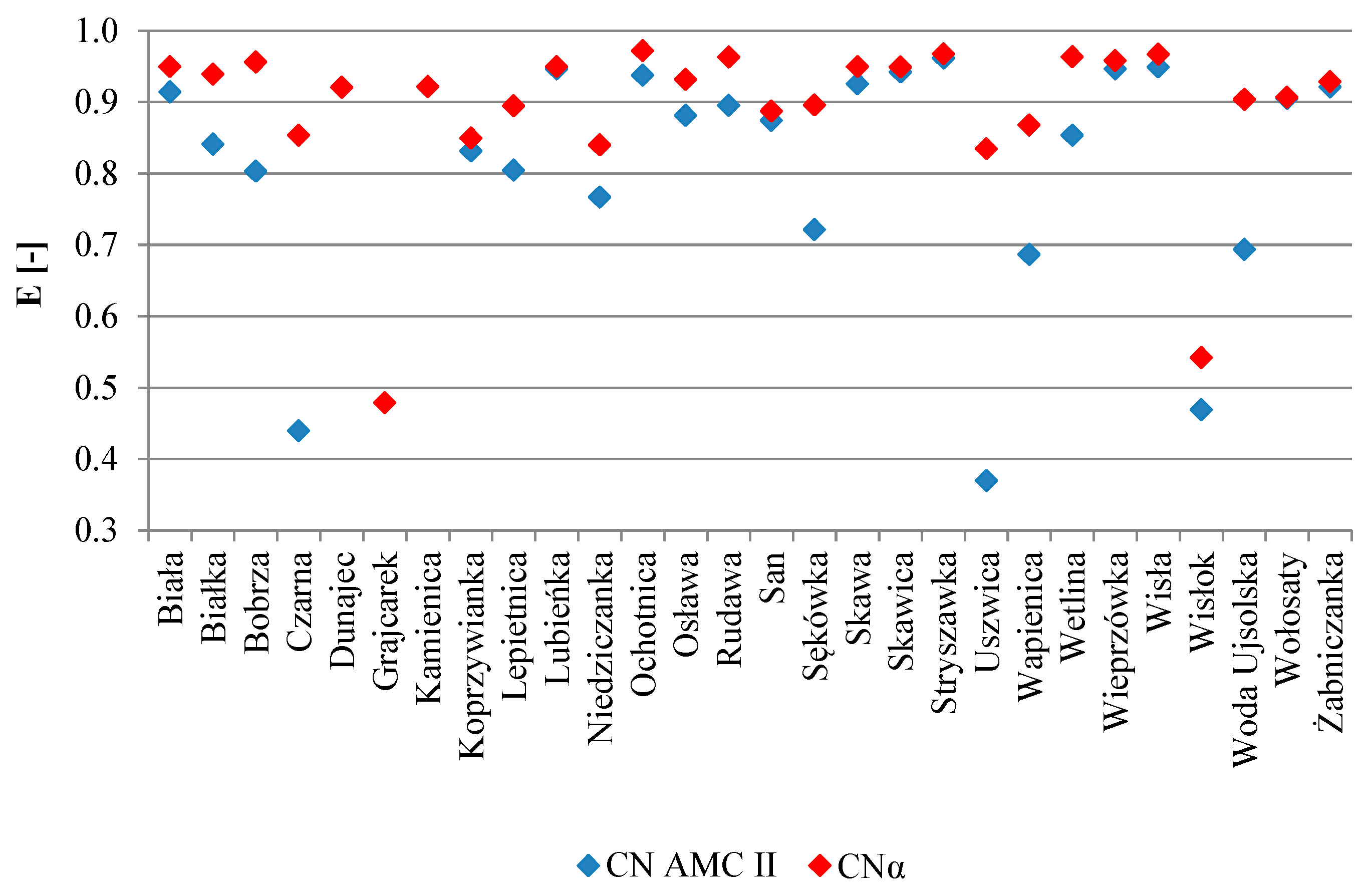
3.4. Assessment of the Work Quality of the Analysed Models
- yo—values from observations;
- ycal—values calculated using the analysed models;
- ym—mean value from the observation.
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schneiderman, E.M.; Steenhuis, T.S.; Thongs, D.J.; Easton, Z.M.; Zion, M.S.; Neal, A.L.; Mendoza, G.F.; Walter, M.T. Incorporating variable source area hydrology into a Curve-Number-based watershed model. Hydrol. Process. 2007, 21, 3420–3430. [Google Scholar] [CrossRef]
- Gaál, L.; Szolgay, J.; Lapin, M.; Faško, P. Hybrid approach to delineation of homogeneous regions for regional precipitation frequency analysis. J. Hydrol. Hydromech. 2009, 57, 226–249. [Google Scholar] [CrossRef]
- Zhang, W.Y. Application of NRCS-CN method for estimation of watershed runoff and disaster risk. Geomat. Nat. Hazards Risk 2019, 10, 2220–2238. [Google Scholar] [CrossRef]
- Amatya, D.M.; Wałęga, A. Long-term Data–the Key for Evaluating Runoff Peak Discharge Estimation Tools and Parameters for Watersheds on Forest Lands. Adv. Civ. Eng. Technol. 2020, 4, 1–5. [Google Scholar]
- Fan, F.; Deng, Y.; Hu, X.; Weng, Q. Estimating composite curve number using an improved SCS-CN method with remotely sensed variables in Guangzhou, China. Remote Sens. 2013, 5, 1425–1438. [Google Scholar] [CrossRef]
- Wałęga, A.; Rutkowska, A. Usefulness of the Modified NRCS-CN Method for the Assessment of Direct Runoff in a Mountain Catchment. Acta Geophys. 2015, 63, 1423–1446. [Google Scholar] [CrossRef][Green Version]
- Jung, J.W.; Yoon, K.S.; Choi, D.H.; Lim, S.S.; Choi, W.J.; Choi, S.M.; Lim, B.J. Water management practices and SCS curve numbers of paddy fields equipped with surface drainage pipes. Agric. Water Manag. 2012, 110, 78–83. [Google Scholar] [CrossRef]
- Ozdemir, H.; Elbaşi, E. Benchmarking land use change impacts on direct runoff in ungauged urban watersheds. Phys. Chem. Earth A/B/C 2015, 79–82, 100–107. [Google Scholar] [CrossRef]
- Babu, P.S.; Mishra, S.K. Improved SCS-CN–inspired model. J. Hydrol. Eng. 2012, 17, 1164–1172. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Romano, N. Green-Ampt Curve-Number mixed procedure as an empirical tool for rainfall-runoff modelling in small and ungauged basins. Hydrol. Process. 2013, 27, 1253–1264. [Google Scholar] [CrossRef]
- Singh, P.K.; Mishra, S.K.; Berndtsson, R.; Jain, M.K.; Pandey, R.P. Development of a modified SMA based MSCS-CN model for runoff estimation. Water Resour. Manag. 2015, 29, 4111–4127. [Google Scholar] [CrossRef]
- Ogden, F.L.; Hawkins, R.; Walter, M.T.; Goodrich, D.C. Comment on “Beyond the SCS-CN method: A theoretical framework for spatially lumped rainfall-runoff response” by M. S. Bartlett et al. Water Resour. Res. 2017, 53, 6345–6350. [Google Scholar] [CrossRef]
- Petroselli, A. A generalization of the EBA4SUB rainfall–runoff model considering surface and subsurface flow. Hydrol. Sci. J. 2020, 66, 2390–2401. [Google Scholar] [CrossRef]
- Szymczak, T.; Krężałek, K. Prognostic model of total runoff and its components from a partially urbanized small lowland catchment. Acta Sci. Pol. Form. Circumiectus 2018, 18, 185–203. [Google Scholar] [CrossRef]
- Wałęga, A.; Amatya, D.M. Modification of the SME-CN method for predicting event runoff and peak discharge from a drained forest watershed on the North Carolina tlantic coastal plain. Trans. ASABE 2020, 63, 275–278. [Google Scholar] [CrossRef]
- Caletka, M.; Šulc Michalková, M.; Karásek, P.; Fučík, P. Improvement of SCS-CN Initial Abstraction Coefficient in the Czech Republic: A Study of Five Catchments. Water 2020, 12, 1964. [Google Scholar] [CrossRef]
- Moon, G.; Ajmal, M.; Ahn, J.; Kim, T.W. Investigating practical alternatives to the NRCS-CN method for direct runoff estimation using slope-adjusted curve numbers. KSCE J. Civ. Eng. 2016, 20, 3022–3030. [Google Scholar] [CrossRef]
- Ebrahimian, M.; Nuruddin, A.A.B.; Soom, M.A.; Neng, L.J. Runoff estimation in steep slope catchment with standard and slope-adjustment Curve Number Method. Pol. J. Environ. Stud. 2012, 21, 1191–1202. [Google Scholar]
- Shi, W.; Wang, N. An Improved SCS-CN Method Incorporating Slope, Soil Moisture, and Storm Duration Factors for Runoff Prediction. Water 2020, 12, 1335. [Google Scholar] [CrossRef]
- Hawkins, R.H. Asymptotic determination of Curve Numbers from data. J. Irrig. Drain. Eng. 1993, 119, 334–345. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D. SCS-CN parameter determination using rainfall-runoff data inheterogeneous watersheds–the two-CN system approach. Hydrol. Earth Syst. Sci. 2012, 16, 1001–1015. [Google Scholar] [CrossRef]
- Wałęga, A.; Devendra, D.M.; Caldwell, P.; Marion, D.; Panda, S. Assessment of storm direct runoff and peak flow rates using improved SCS-CN models for selected forested watersheds in the Southeastern United States. J. Hydrol. Reg. Stud. 2020, 27, 100645. [Google Scholar] [CrossRef]
- Ebrahimian, A.; Gulliver, J.S.; Wilson, B.N. Estimating effective impervious area in urban watersheds using land cover, soil character and asymptotic curve number. Hydrol. Sci. J. 2018, 63, 513–526. [Google Scholar] [CrossRef]
- Ryu, J.; Jang, W.S.; Kim, J.; Choi, J.D.; Engel, B.A.; Yang, J.E.; Lim, K.J. Development of a Watershed-Scale Long-Term Hydrologic Impact Assessment Model with the Asymptotic Curve Number Regression Equation. Water 2016, 8, 153. [Google Scholar] [CrossRef]
- Velásquez-Valle, M.A.; Sánchez-Cohen, I.; Hawkins, R.H.; Serna-Pérez, A.; Gutiérrez-Luna, R.; Pedroza-Sandoval, A. Rainfall-runoff relationships in a semiarid rangeland watershed in central Mexico, based on the CN-NRCS approach. Model. Earth Syst. Environ. 2017, 3, 1263–1272. [Google Scholar] [CrossRef]
- Santikari, V.P.; Murdoch, L.C. Including effects of watershed heterogeneity in the curve number method using variable initial abstraction. Hydrol. Earth Syst. Sci. 2018, 22, 4725–4743. [Google Scholar] [CrossRef]
- Krajewski, A.; Sikorska-Senoner, A.E.; Hejduk, A.; Hejduk, L. Variability of the Initial Abstraction Ratio in an Urban and an Agroforested Catchment. Water 2020, 12, 415. [Google Scholar] [CrossRef]
- Młyński, D.; Wałęga, A.; Książek, L.; Florek, J.; Petroselli, A. Possibility of Using Selected Rainfall-Runoff Models for Determining the Design Hydrograph in Mountainous Catchments: A Case Study in Poland. Water 2020, 12, 1450. [Google Scholar] [CrossRef]
- Wałęga, A.; Cupak, A.; Amatya, D.M.; Drożdżal, E. Comparison of direct outflow calculated by modified scs-cn methods for mountainous and highland catchments in upper Vistula basin, Poland and lowland catchment in South Carolina, USA. Acta Sci. Pol. Form. Circumiectus 2017, 16, 187–207. [Google Scholar] [CrossRef]
- Kohnová, S.; Rutkowska, A.; Banasik, K.; Hlavčová, K. The L-moment based regional approach to curve numbers for Slovak and Polish Carpathian catchments. J. Hydrol. Hydromech. 2020, 68, 170–179. [Google Scholar] [CrossRef]
- Rutkowska, A.; Kohnová, S.; Banasik, K.; Szolgay, J.; Karabová, B. Probabilistic properties of a curve number: A case study for small Polish and Slovak Carpathian Basins. J. Mt. Sci. 2015, 12, 533–548. [Google Scholar] [CrossRef]
- Młyński, D.; Cebulska, M.; Wałęga, A. Trends, Variability, and Seasonality of Maximum Annual Daily Precipitation in the Upper Vistula Basin, Poland. Atmosphere 2018, 9, 313. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, Q.; Fan, J.; Han, F.; Dai, Q. Application of the SCS-CN Model to Runo_ Estimation in a Small Watershed with High Spatial Heterogeneity. Pedosphere 2011, 26, 738–749. [Google Scholar] [CrossRef]
- Soulis, K.X. Estimation of SCS Curve Number variation following forest fires. Hydrol. Sci. J. 2018, 63, 1332–1346. [Google Scholar] [CrossRef]
- NRCS (Natural Resources Conservation Service). National Engineering Handbook Section-4, Part 630, Hydrology; NRCS: Washington, DC, USA, 2001.
- Wałęga, A.; Salata, T. Influence of land cover data sources on estimation of direct runoff according to SCS-CN and modified SME methods. Catena 2019, 172, 232–242. [Google Scholar] [CrossRef]
- Gajbhiye, S.; Mishra, S.K.; Pandey, A. Relationship between SCS-CN and Sediment Yield. Appl. Water Sci. 2014, 4, 363–370. [Google Scholar] [CrossRef]
- Ajmal, M.; Kim, T.W.; Ahn, J.H. Stability assessment of the curve number methodology used to estimate excess rainfall in forest-dominated watersheds. Arab. J. Geosci. 2016, 9, 402. [Google Scholar] [CrossRef]
- Ryu, J.; Jung, Y.; Kong, D.S.; Park, B.K.; Kim, Y.S.; Engel, B.A.; Lim, K.J. Approach of Land Cover Based Asymptotic Curve Number Regression Equation to Estimate Runoff. Irrig. Drain. 2016, 65, 94–104. [Google Scholar] [CrossRef]
- Singh, P.; Mishra, S.K. Determination of curve number and estimation of runoff using Indian experimental rainfall and runoff data. J. Spat. Hydrol. 2017, 13, 1–26. [Google Scholar]
- Wałęga, A.; Michalec, B.; Cupak, A.; Grzebinoga, M. Comparison of SCS-CN determination methodologies in a heterogeneous catchment. J. Mt. Sci. 2015, 12, 1084–1094. [Google Scholar] [CrossRef]
- Banasik, K.; Krajewski, A.; Sikorska, A.; Hejduk, L. Curve Number estimation for a small urban catchment from recorded rainfall-runoff events. Arch. Environ. Prot. 2014, 40, 75–86. [Google Scholar] [CrossRef]
- Mishra, S.K.; Chaudhary, A.; Shrestha, R.K.; Pandey, A.; Lal, M. Experimental verification of the effect of slope and land use on scs runoff curve number. Water Res. Manag. 2014, 28, 3407–3416. [Google Scholar] [CrossRef]
- Sharpley, A.; Williams, J. Epic—Erosion/Productivity Impact Calculator: I. Model Documentation. II: User Manual; Technical Bulletin, No. 1768 1990; United State Department of Agriculture: Washington, DC, USA, 1990.
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Dunne, T.; Black, R.D. An Experimental Investigation of Runoff Production in Permeable Soils. Water Resour. Res. 1970, 6, 478–490. [Google Scholar] [CrossRef]
- Kowalik, T.; Wałęga, A. Estimation of CN Parameter for Small Agricultural Watersheds Using Asymptotic Functions. Water 2015, 7, 939–955. [Google Scholar] [CrossRef]
- Młyński, D. Analysis of Problems Related to the Calculation of Flood Frequency Using Rainfall-Runoff Models: A Case Study in Poland. Sustainability 2020, 12, 7187. [Google Scholar] [CrossRef]
- De Paola, F.; Ranucci, A.; Feo, A. Antecedent moisture condition (SCS) frequency assessment: A case study in southern Italy. Irrig. Drain. 2013, 62, 61–71. [Google Scholar] [CrossRef]
- Randusová, B.; Marková, R.; Kohnová, S.; Hlavčová, K. Comparison of cn estimation approaches. Int. J. Eng. Res. Sci. 2015, 1, 34–40. [Google Scholar]
- Lal, M.; Mishra, S.K.; Pandey, A.; Pandey, R.P.; Meena, P.K.; Chaudhary, A.; Kumar, J.R.; Shreevastava, A.K.; Kumar, Y. Evaluation of the Soil Conservation Service curve number methodology using data from agricultural plots. Hydrogeol. J. 2017, 25, 151–167. [Google Scholar] [CrossRef]
- Oliveira, P.T.S.; Nearing, M.A.; Hawkins, R.H.; Stone, J.J.; Rodrigues, D.B.B.; Panachuki, E.; Wendland, E.J. Curve num-ber estimation from Brazilian Cerrado rainfall and runoff data. Soil Water Conserv. 2016, 71, 420–429. [Google Scholar] [CrossRef]
- Deshmukh, D.S.; Chaube, U.C.; Hailu, A.E.; Gudeta, D.A.; Kassa, M.T. Estimation and comparision of curve numbers based on dynamic land use land cover change, observed rainfall-runoff data and land slope. J. Hydrol. 2013, 492, 89–101. [Google Scholar] [CrossRef]
- Muche, M.E.; Hutchinson, S.L.; Hutchinson, J.M.; Johnston, J.M. Phenology-adjusted dynamic curve number for improved hydrologic modeling. J. Environ. Manag. 2019, 1, 403–413. [Google Scholar] [CrossRef] [PubMed]
- D’Asaro, F.; Grillone, G. Empirical Investigation of Curve Number Method Parameters in the Mediterranean Area. J. Hydrol. Eng. 2012, 17, 1141–1152. [Google Scholar] [CrossRef]
- D’Asaro, F.; Grillone, G.; Hawkins, R.H. Curve Number: Empirical evaluation andcomparison with Curve Number handbook tables in Sicily. J. Hydrol. Eng. 2014, 19, 04014035. [Google Scholar] [CrossRef]
- Wałęga, A.; Młyński, D.; Wachulec, K. The use of asymptotic functions for determining empirical values of CN parameter in selected catchments of variable land cover. Stud. Geotech. Mech. 2017, 39, 111–120. [Google Scholar] [CrossRef]
- Ajmal, M.; Wassem, M.; Kim, D.; Kim, T.W. A Pragmatic Slope-Adjusted Curve Number Model to Reduce Uncertainty in Predicting Flood Runoff from Steep Watersheds. Water 2020, 12, 1469. [Google Scholar] [CrossRef]
- Huang, M.; Gallichand, J.; Wang, Z.; Goulet, M. A modification to the soil conservation service curve number method for steep slopes in the Loess Plateau of China. Hydrol. Process. 2006, 20, 579–589. [Google Scholar] [CrossRef]
- Fang, H.; Cai, Q.; Chen, H.; Li, Q. Effect of rainfall regime and slope on runo_ in a gullied loess region on the Loess Plateau in China. Environ. Manag. 2008, 42, 402–411. [Google Scholar] [CrossRef]
- Mah, M.; Douglas, L.; Ringrose-Voase, A. Effects of crust development and surface slope on erosion by rainfall. Soil Sci. 1992, 154, 37–43. [Google Scholar] [CrossRef]
| Code | River | A (km2) | L (km) | Ψ (–) | D (km·km−2) | N (–) | Land Use (%) | Pave (mm) | tave (°C) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| URB | AGR | FOR | WET | WAT | |||||||||
| 1 | Biała | 212.2 | 31.7 | 0.039 | 1.8 | 0.85 | 2 | 45 | 53 | 0 | 0 | 890 | 6.9 |
| 2 | Białka | 78.0 | 19.9 | 0.159 | 1.3 | 0.48 | 0 | 0 | 98 | 0 | 2 | 1539 | 2.6 |
| 3 | Bobrza | 311.6 | 40.2 | 0.046 | 1.1 | 0.52 | 17 | 44 | 39 | 0 | 0 | 649 | 7.8 |
| 4 | Czarna | 221.2 | 22.1 | 0.016 | 0.9 | 0.46 | 1 | 45 | 54 | 0 | 0 | 629 | 7.8 |
| 5 | Dunajec | 685.1 | 50.5 | 0.062 | 2.1 | 0.82 | 6 | 52 | 42 | 1 | 0 | 1023 | 5.4 |
| 6 | Grajcarek | 86.0 | 15.6 | 0.084 | 1.4 | 0.80 | 4 | 21 | 74 | 0 | 0 | 765 | 7.3 |
| 7 | Kamienica | 237.7 | 34.5 | 0.055 | 1.9 | 0.82 | 5 | 36 | 59 | 0 | 0 | 901 | 7.8 |
| 8 | Koprzywianka | 518.6 | 70.3 | 0.013 | 1.1 | 0.64 | 3 | 74 | 23 | 0 | 0 | 613 | 7.6 |
| 9 | Lepietnica | 50.3 | 19.5 | 0.087 | 2.6 | 0.78 | 28 | 27 | 45 | 0 | 0 | 873 | 6.0 |
| 10 | Lubieńka | 48.1 | 4.7 | 0.074 | 2.2 | 0.80 | 0 | 56 | 44 | 0 | 0 | 902 | 7.0 |
| 11 | Niedziczanka | 137.8 | 22.0 | 0.059 | 1.4 | 0.80 | 3 | 52 | 45 | 0 | 0 | 978 | 5.5 |
| 12 | Ochotnica | 109.0 | 22.8 | 0.084 | 2.1 | 0.79 | 1 | 27 | 72 | 0 | 0 | 830 | 8.7 |
| 13 | Osława | 307.0 | 38.9 | 0.034 | 2.3 | 0.86 | 1 | 23 | 76 | 0 | 0 | 911 | 6.6 |
| 14 | Rudawa | 294.1 | 30.0 | 0.016 | 1.2 | 0.62 | 8 | 65 | 26 | 0 | 0 | 705 | 8.0 |
| 15 | San | 418.0 | 75.9 | 0.038 | 1.9 | 0.61 | 14 | 1 | 84 | 0 | 0 | 992 | 7.1 |
| 16 | Sękówka | 122.7 | 24.0 | 0.049 | 1.8 | 0.84 | 2 | 29 | 69 | 0 | 0 | 791 | 7.9 |
| 17 | Skawa | 123.7 | 36.8 | 0.037 | 2.4 | 0.77 | 2 | 66 | 32 | 0 | 0 | 840 | 7.0 |
| 18 | Skawica | 143.8 | 19.5 | 0.104 | 2.6 | 0.79 | 1 | 32 | 67 | 0 | 0 | 1207 | 6.5 |
| 19 | Stryszawka | 140.4 | 17.5 | 0.067 | 1.4 | 0.80 | 3 | 45 | 52 | 0 | 0 | 1023 | 6.8 |
| 20 | Uszwica | 268.5 | 55.3 | 0.021 | 1.8 | 0.79 | 4 | 67 | 29 | 0 | 0 | 749 | 8.4 |
| 21 | Wapienica | 52.7 | 18.5 | 0.110 | 1.8 | 0.83 | 9 | 56 | 33 | 0 | 2 | 939 | 8.5 |
| 22 | Wetlina | 131.2 | 17.7 | 0.062 | 2.2 | 0.89 | 0 | 8 | 92 | 0 | 0 | 1115 | 7.2 |
| 23 | Wieprzówka | 151.8 | 29.4 | 0.054 | 2.0 | 0.78 | 7 | 64 | 28 | 0 | 1 | 885 | 7.3 |
| 24 | Wisła | 53.4 | 12.1 | 0.101 | 2.0 | 0.78 | 3 | 14 | 83 | 0 | 1 | 1190 | 7.7 |
| 25 | Wisłok | 143.6 | 27.8 | 0.040 | 1.8 | 0.87 | 0 | 21 | 78 | 0 | 0 | 910 | 7.1 |
| 26 | Woda Ujsolska | 106.6 | 13.8 | 0.079 | 1.3 | 0.72 | 1 | 28 | 70 | 0 | 0 | 1005 | 7.7 |
| 27 | Wołosaty | 118.9 | 28.2 | 0.074 | 1.5 | 0.67 | 0 | 8 | 92 | 0 | 0 | 1033 | 7.1 |
| 28 | Żabniczanka | 23.4 | 4.6 | 0.156 | 2.0 | 0.72 | 0 | 20 | 80 | 0 | 0 | 1094 | 7.8 |
| Code | Catchment | Rainfall (mm) | Runoff (mm) | CNobs (–) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Minimum | Average | Maximum | Minimum | Average | Maximum | Minimum | Average | Maximum | ||
| 1 | Biała | 6.7 | 33.3 | 142.5 | 0.1 | 5.9 | 49.4 | 63.5 | 79.8 | 90.8 |
| 2 | Białka | 5.3 | 53.3 | 262.7 | 0.1 | 24.6 | 170.5 | 71.3 | 86.6 | 93.1 |
| 3 | Bobrza | 6.4 | 34.4 | 98.6 | 0.1 | 8.0 | 33.4 | 71.0 | 82.6 | 91.5 |
| 4 | Czarna | 5.3 | 21.4 | 90.7 | 0.1 | 2.9 | 28.3 | 71.1 | 84.5 | 84.5 |
| 5 | Dunajec | 6.0 | 41.2 | 209.0 | 0.1 | 12.1 | 103.3 | 64.9 | 82.8 | 91.6 |
| 6 | Grajcarek | 4.7 | 38.2 | 106.1 | 0.2 | 10.6 | 43.4 | 71.2 | 83.3 | 94.4 |
| 7 | Kamienica | 6.1 | 52.0 | 241.5 | 0.1 | 16.1 | 123.5 | 62.8 | 80.1 | 91.2 |
| 8 | Koprzywianka | 5.6 | 23.7 | 74.4 | 0.1 | 2.7 | 16.1 | 69.0 | 82.4 | 91.8 |
| 9 | Lepietnica | 6.9 | 45.4 | 198.2 | 0.1 | 18.6 | 98.4 | 66.2 | 86.0 | 91.4 |
| 10 | Lubieńka | 14.3 | 55.4 | 146.9 | 0.1 | 15.6 | 59.4 | 66.7 | 75.3 | 80.8 |
| 11 | Niedziczanka | 7.6 | 45.0 | 146.9 | 0.3 | 14.9 | 65.1 | 69.2 | 83.9 | 91.5 |
| 12 | Ochotnica | 8.3 | 50.5 | 231.3 | 0.1 | 15.6 | 139.1 | 70.4 | 80.3 | 90.4 |
| 13 | Osława | 7.0 | 52.0 | 180.2 | 0.2 | 16.9 | 91.0 | 68.9 | 81.2 | 91.7 |
| 14 | Rudawa | 4.4 | 26.1 | 126.1 | 0.1 | 5.7 | 58.3 | 73.5 | 85.6 | 93.7 |
| 15 | San | 6.4 | 43.5 | 174.1 | 0.1 | 10.5 | 77.2 | 65.5 | 79.9 | 91.7 |
| 16 | Sękówka | 5.8 | 63.5 | 182.8 | 0.3 | 23.5 | 80.5 | 64.2 | 80.6 | 95.5 |
| 17 | Skawa | 4.4 | 40.3 | 222.3 | 0.1 | 15.4 | 136.7 | 72.2 | 86.4 | 94.4 |
| 18 | Skawica | 6.9 | 62.4 | 244.4 | 0.1 | 21.8 | 125.2 | 62.6 | 78.7 | 90.4 |
| 19 | Stryszawka | 5.6 | 63.3 | 274.1 | 0.1 | 21.4 | 156.7 | 64.4 | 78.3 | 92.1 |
| 20 | Uszwica | 5.2 | 43.8 | 92.2 | 0.1 | 15.8 | 35.3 | 74.9 | 85.2 | 93.0 |
| 21 | Wapienica | 4.1 | 62.4 | 208.2 | 0.1 | 24.4 | 101.9 | 64.6 | 81.7 | 94.4 |
| 22 | Wetlina | 7.3 | 50.1 | 162.3 | 0.1 | 10.4 | 73.8 | 67.8 | 75.2 | 89.5 |
| 23 | Wieprzówka | 10.8 | 56.4 | 208.2 | 0.1 | 14.9 | 106.0 | 66.1 | 75.4 | 84.7 |
| 24 | Wisła | 6.8 | 74.2 | 229.7 | 0.1 | 26.7 | 120.9 | 65.0 | 77.0 | 90.6 |
| 25 | Wisłok | 17.1 | 63.2 | 137.8 | 2.9 | 15.5 | 40.1 | 60.3 | 74.7 | 89.2 |
| 26 | Woda Ujsolska | 9.2 | 47.5 | 90.0 | 0.1 | 8.3 | 24.3 | 68.5 | 75.1 | 87.5 |
| 27 | Wołosaty | 18.7 | 65.7 | 139.5 | 0.7 | 14.9 | 44.4 | 61.9 | 71.7 | 83.9 |
| 28 | Żabniczanka | 4.4 | 64.5 | 247.0 | 0.1 | 23.6 | 125.0 | 61.9 | 80.0 | 94.5 |
| Code | Catchment | CN∞ | CNL | E (–) | R2 (–) | A(90) (–) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 7 | 6 | 5 | 6 | 7 | 5 | 6 | 7 | 5 | 6 | 7 | ||
| 1 | Biała | 68.2 | 67.3 | 61.0 | 0.938 | 0.957 | 0.950 | 0.942 | 0.957 | 0.950 | 0.958 | 0.856 | 0.945 |
| 2 | Białka | 72.3 | 73.7 | 73.2 | 0.906 | 0.963 | 0.906 | 0.930 | 0.963 | 0.968 | 0.949 | 0.961 | 0.967 |
| 3 | Bobrza | 73.8 | 72.7 | 58.8 | 0.964 | 0.988 | 0.981 | 0.969 | 0.988 | 0.981 | 0.989 | 0.787 | 0.974 |
| 4 | Czarna | 76.3 | 69.8 | 52.5 | 0.842 | 0.947 | 0.943 | 0.861 | 0.947 | 0.943 | 0.954 | 0.657 | 0.873 |
| 5 | Dunajec | 69.5 | 65.2 | 63.9 | 0.909 | 0.980 | 0.979 | 0.929 | 0.980 | 0.979 | 0.962 | 0.885 | 0.903 |
| 6 | Grajcarek | 74.6 | 41.8 | 25.9 | 0.726 | 0.914 | 0.914 | 0.755 | 0.910 | 0.910 | 0.997 | 0.346 | 0.558 |
| 7 | Kamienica | 70.7 | 65.3 | 52.0 | 0.862 | 0.940 | 0.923 | 0.879 | 0.940 | 0.923 | 0.986 | 0.735 | 0.923 |
| 8 | Koprzywianka | 69.8 | 64.0 | 51.6 | 0.951 | 0.989 | 0.989 | 0.952 | 0.988 | 0.988 | 0.953 | 0.705 | 0.874 |
| 9 | Lepietnica | 78.1 | 29.8 | 27.7 | 0.624 | 0.944 | 0.950 | 0.698 | 0.944 | 0.952 | 0.988 | 0.351 | 0.377 |
| 10 | Lubieńka | 74.0 | 62.1 | 37.8 | 0.302 | 0.535 | 0.395 | 0.302 | 0.535 | 0.519 | 0.974 | 0.510 | 0.839 |
| 11 | Niedziczanka | 69.9 | 68.7 | 43.5 | 0.883 | 0.979 | 0.984 | 0.914 | 0.979 | 0.984 | 0.964 | 0.601 | 0.948 |
| 12 | Ochotnica | 72.7 | 71.0 | 70.8 | 0.919 | 0.963 | 0.963 | 0.934 | 0.963 | 0.963 | 0.996 | 0.971 | 0.973 |
| 13 | Osława | 72.8 | 68.0 | 49.5 | 0.884 | 0.948 | 0.943 | 0.902 | 0.948 | 0.943 | 0.985 | 0.670 | 0.920 |
| 14 | Rudawa | 74.7 | 75.3 | 75.1 | 0.964 | 0.983 | 0.985 | 0.970 | 0.983 | 0.985 | 0.971 | 0.976 | 0.978 |
| 15 | San | 67.6 | 65.1 | 56.6 | 0.918 | 0.955 | 0.952 | 0.931 | 0.955 | 0.952 | 0.956 | 0.800 | 0.920 |
| 16 | Sękówka | 71.8 | 70.8 | 43.0 | 0.856 | 0.878 | 0.857 | 0.859 | 0.878 | 0.857 | 0.985 | 0.589 | 0.971 |
| 17 | Skawa | 75.1 | 72.8 | 73.3 | 0.846 | 0.970 | 0.970 | 0.893 | 0.970 | 0.970 | 0.990 | 0.967 | 0.961 |
| 18 | Skawica | 70.5 | 64.9 | 51.5 | 0.762 | 0.953 | 0.949 | 0.820 | 0.953 | 0.949 | 0.992 | 0.736 | 0.928 |
| 19 | Stryszawka | 67.8 | 67.8 | 63.8 | 0.959 | 0.970 | 0.962 | 0.962 | 0.970 | 0.962 | 0.983 | 0.925 | 0.983 |
| 20 | Uszwica | 75.6 | -47.7 | 14.2 | 0.743 | 0.926 | 0.930 | 0.921 | 0.926 | 0.930 | 0.973 | 0.182 | -0.613 |
| 21 | Wapienica | 67.6 | 50.3 | 30.4 | 0.832 | 0.967 | 0.967 | 0.853 | 0.967 | 0.967 | 0.962 | 0.433 | 0.716 |
| 22 | Wetlina | 70.1 | 68.5 | 59.9 | 0.938 | 0.981 | 0.969 | 0.946 | 0.981 | 0.969 | 0.999 | 0.854 | 0.976 |
| 23 | Wieprzówka | 71.9 | 64.9 | 58.3 | 0.592 | 0.899 | 0.900 | 0.625 | 0.899 | 0.900 | 0.946 | 0.857 | 0.955 |
| 24 | Wisła | 67.2 | 65.7 | 65.6 | 0.917 | 0.973 | 0.973 | 0.939 | 0.973 | 0.973 | 0.998 | 0.978 | 0.980 |
| 25 | Wisłok | 56.1 | 48.3 | 19.9 | 0.959 | 0.973 | 0.973 | 0.959 | 0.971 | 0.988 | 0.870 | 0.309 | 0.749 |
| 26 | Woda Ujsolska | 67.5 | 68.5 | 68.6 | 0.959 | 0.987 | 0.988 | 0.967 | 0.987 | 0.988 | 0.980 | 0.995 | 0.993 |
| 27 | Wołosaty | 64.2 | 65.5 | 45.6 | 0.875 | 0.895 | 0.863 | 0.877 | 0.916 | 0.865 | 0.985 | 0.965 | 0.721 |
| 28 | Żabniczanka | 66.3 | 62.4 | 42.2 | 0.917 | 0.973 | 0.969 | 0.935 | 0.973 | 0.935 | 0.940 | 0.599 | 0.885 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Młyński, D.; Wałęga, A. Identification of the Relationship between Rainfall and the CN Parameter in Western Carpathian Mountain Catchments in Poland. Sustainability 2020, 12, 9317. https://doi.org/10.3390/su12229317
Młyński D, Wałęga A. Identification of the Relationship between Rainfall and the CN Parameter in Western Carpathian Mountain Catchments in Poland. Sustainability. 2020; 12(22):9317. https://doi.org/10.3390/su12229317
Chicago/Turabian StyleMłyński, Dariusz, and Andrzej Wałęga. 2020. "Identification of the Relationship between Rainfall and the CN Parameter in Western Carpathian Mountain Catchments in Poland" Sustainability 12, no. 22: 9317. https://doi.org/10.3390/su12229317
APA StyleMłyński, D., & Wałęga, A. (2020). Identification of the Relationship between Rainfall and the CN Parameter in Western Carpathian Mountain Catchments in Poland. Sustainability, 12(22), 9317. https://doi.org/10.3390/su12229317






