Anomaly Detection System for Water Networks in Northern Ethiopia Using Bayesian Inference
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Model of Water Usage
2.3. Inference and Parameter Estimation
2.4. Anomaly Detection
2.4.1. Observation-Level Score
2.4.2. Pump-Level Score
3. Results and Discussion
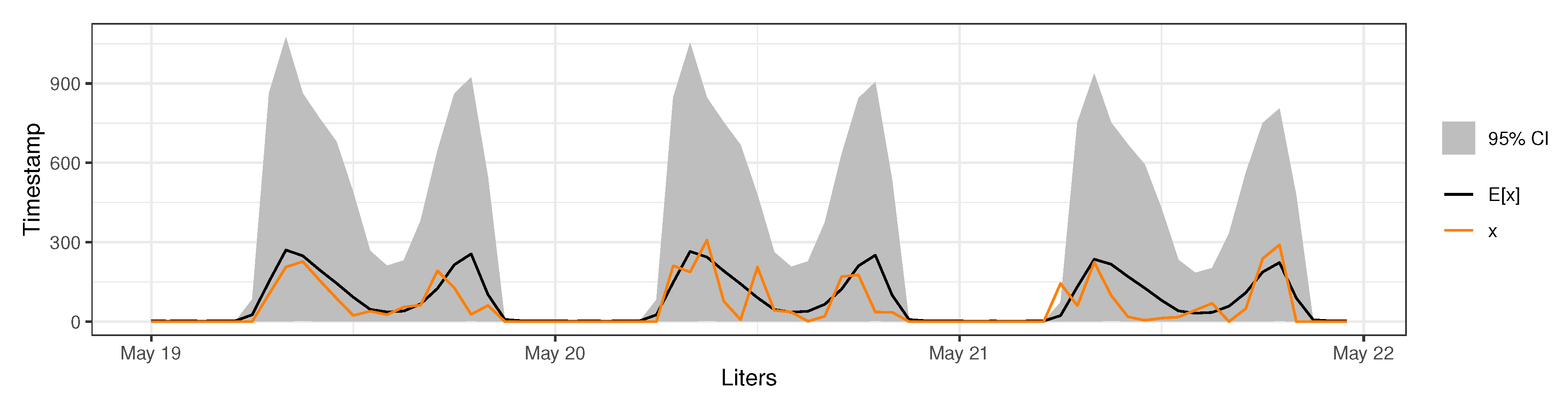
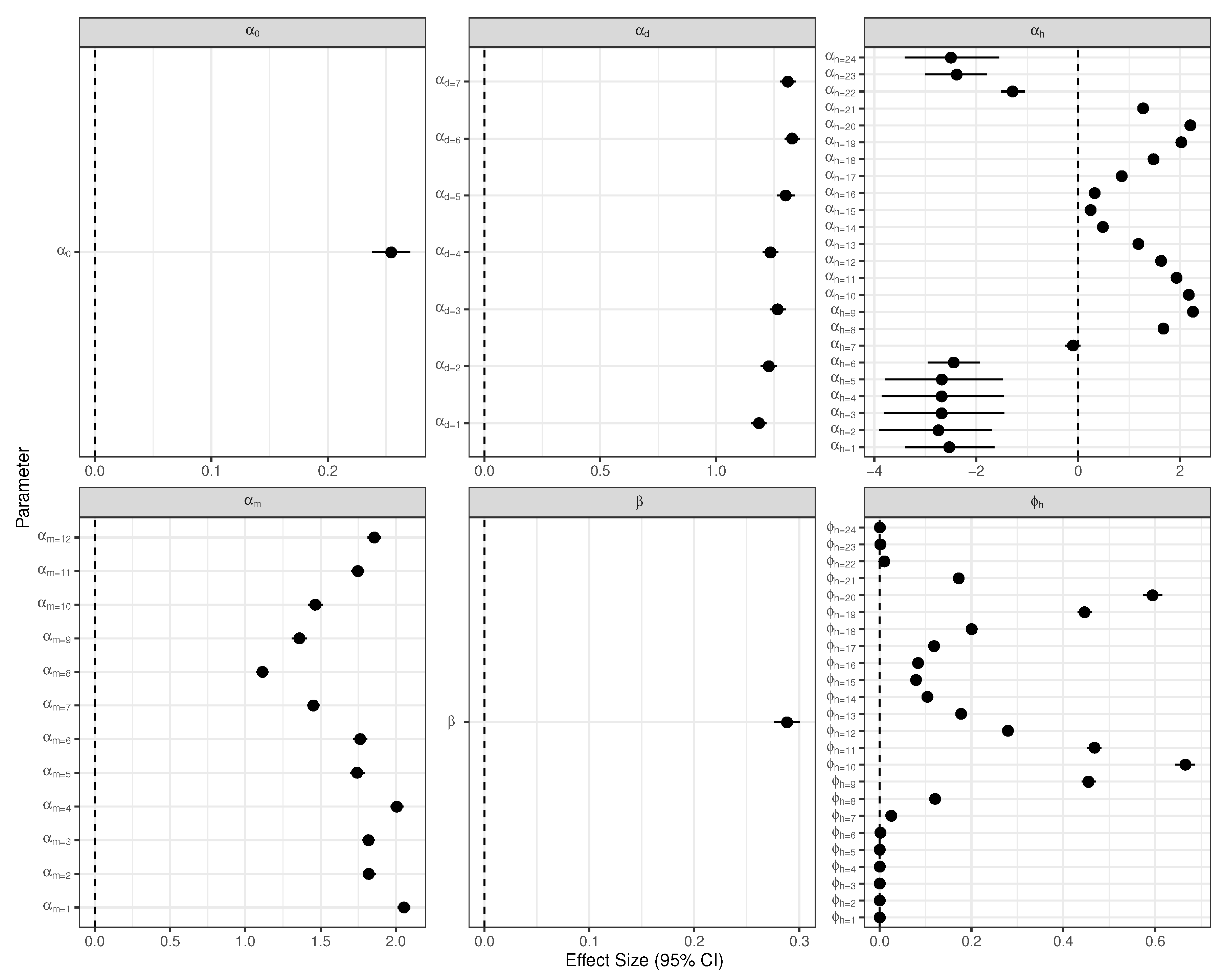
3.1. Model of Water Usage
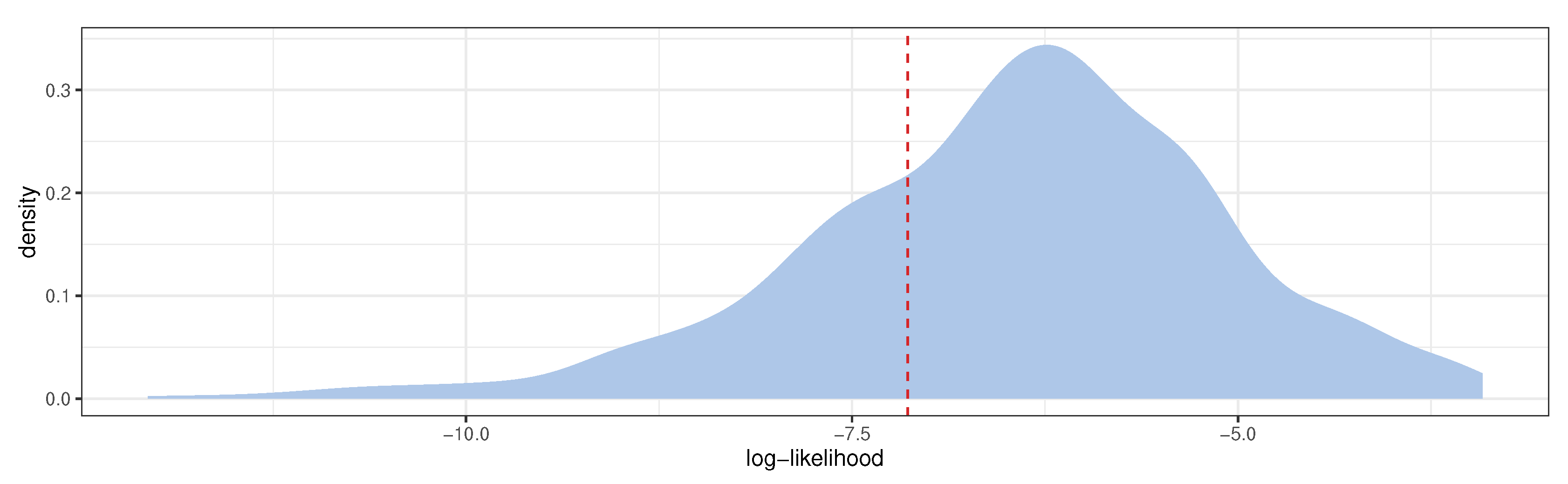
3.2. Model Predictive Checking
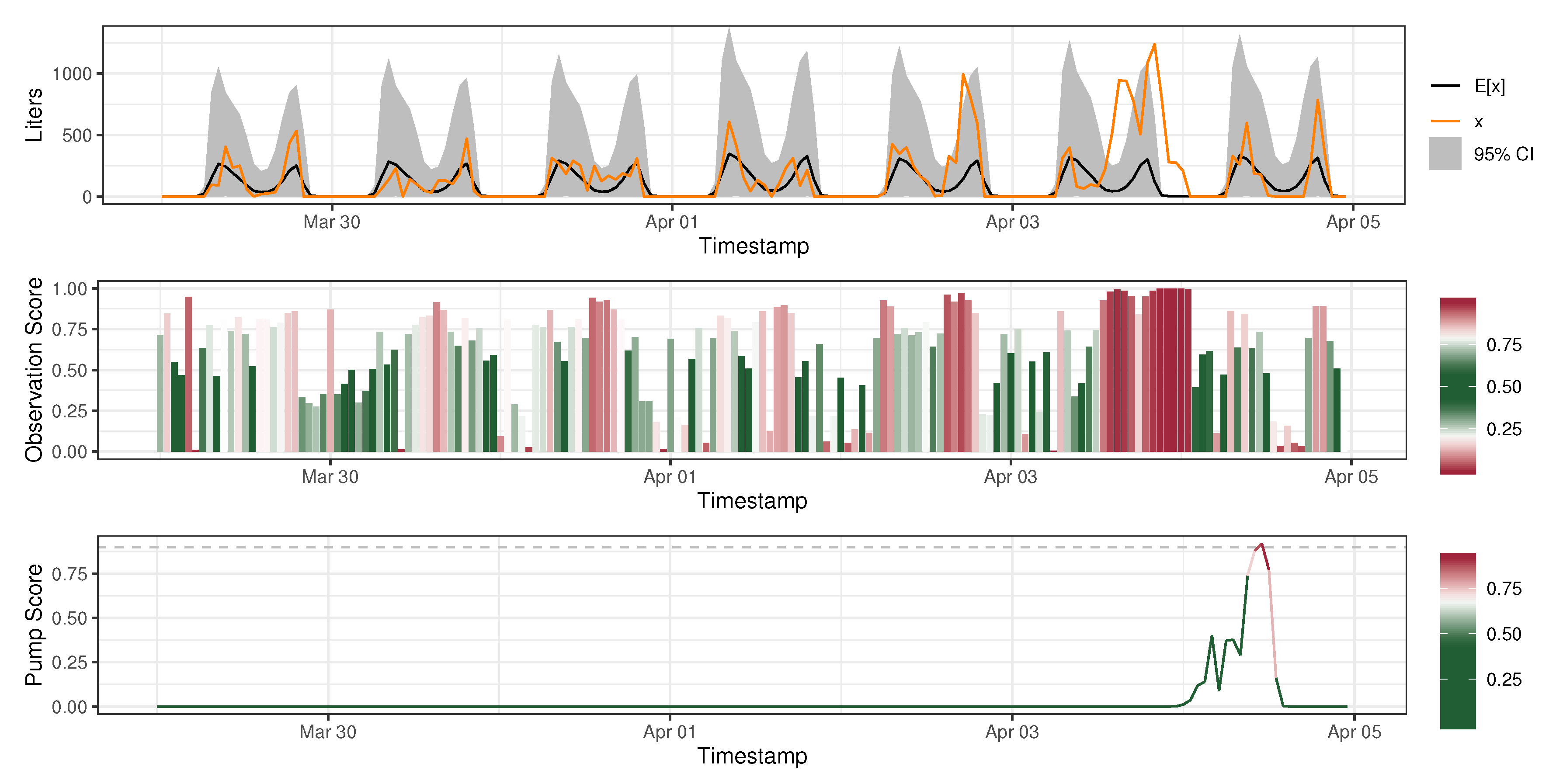
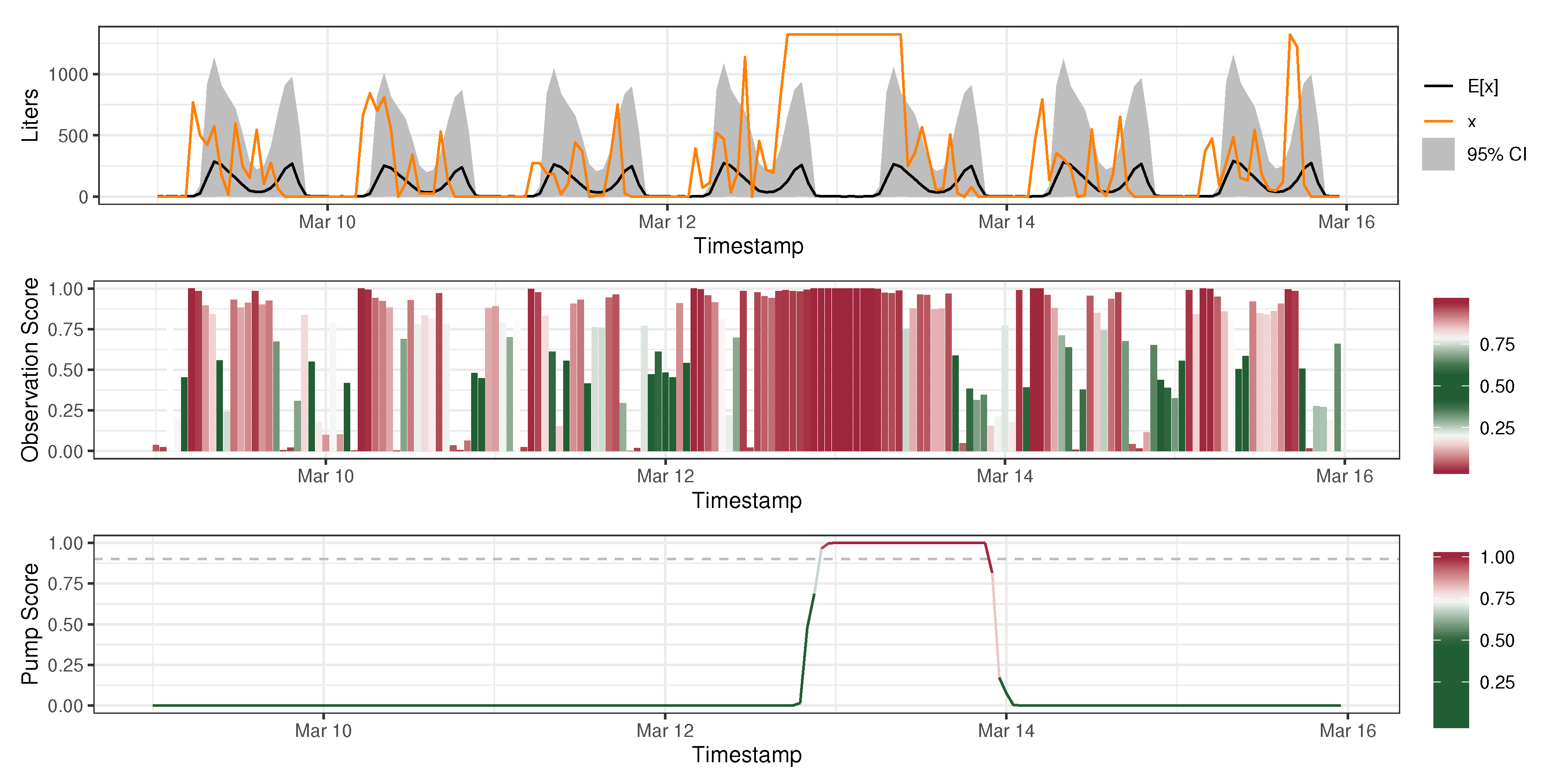
3.3. Anomaly Detection
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- United Nations. Available online: https://www.un.org/press/en/2003/sgsm8707.doc.htm (accessed on 22 February 2020).
- World Health Organization UNICEF. Available online: https://washdata.org/data/household#!/dashboard/2805 (accessed on 22 February 2020).
- Sansom, K.; Koestler, L. African Handpump Market Mapping Study; UNICEF: New York, NY, USA, 2009. [Google Scholar]
- Foster, T. Predictors of sustainability for community-managed handpumps in sub-Saharan Africa: Evidence from Liberia, Sierra Leone, and Uganda. Environ. Sci. Technol. 2013, 47, 12037–12046. [Google Scholar] [CrossRef]
- Fisher, M.B.; Shields, K.F.; Chan, T.U.; Christenson, E.; Cronk, R.D.; Leker, H.; Samani, D.; Apoya, P.; Lutz, A.; Bartram, J. Understanding handpump sustainability: Determinants of rural water source functionality in the G reater A fram P lains region of G hana. Water Resour. Res. 2015, 51, 8431–8449. [Google Scholar] [CrossRef] [PubMed]
- Foster, T.; Furey, S.; Banks, B.; Willetts, J. Functionality of handpump water supplies: A review of data from sub-Saharan Africa and the Asia-Pacific region. Int. J. Water Resour. Dev. 2019, 1–15. [Google Scholar] [CrossRef]
- Baguma, A.; Bizoza, A.; Carter, R.; Cavill, S.; Foster, S.; Foster, T.; Jobbins, G.; Hope, R.; Katuva, J.; Koehler, J.; et al. Groundwater and Poverty in Sub-Saharan Africa. 2017. Available online: https://upgro.files.wordpress.com/2017/06/groundwater-and-poverty-report_0004.pdf (accessed on 22 February 2020).
- Hunter, P.R.; Zmirou-Navier, D.; Hartemann, P. Estimating the impact on health of poor reliability of drinking water interventions in developing countries. Sci. Total Environ. 2009, 407, 2621–2624. [Google Scholar] [CrossRef] [PubMed]
- Charity: Water. Available online: https://my.charitywater.org/about (accessed on 26 February 2020).
- Charity: Water. Available online: https://blog.charitywater.org/post/143492619882/new-technology-supported-by-google (accessed on 26 February 2020).
- Schwab, K. The Fourth Industrial Revolution; Currency: Redfern, New South Wales, Australia, 2017. [Google Scholar]
- Dickinson, N.; Knipschild, F.; Magara, P.; Kwizera, G. Harnessing Water Point Data to Improve Drinking Water Services; The Hague, WASHNote: Rotterdam, The Netherlands, 2017. [Google Scholar]
- Charity: Water. Available online: https://github.com/charitywater/afridev-sensor (accessed on 22 February 2020).
- Hodge, V.; Austin, J. A survey of outlier detection methodologies. Artif. Intell. Rev. 2004, 22, 85–126. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Leroy, A.M. Robust Regression and Outlier Detection; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 589. [Google Scholar]
- Barnett, V.; Lewis, T. Outliers in Statistical Data; John Wiley and Sons: New York, NY, USA, 1994. [Google Scholar]
- Hawkins, D.M. Identification of Outliers; Springer: Dordrecht, The Netherlands, 1980; Volume 11. [Google Scholar]
- Bakar, Z.A.; Mohemad, R.; Ahmad, A.; Deris, M.M. A comparative study for outlier detection techniques in data mining. In Proceedings of the 2006 IEEE Conference on Cybernetics and Intelligent Systems, Bangkok, Thailand, 7–9 June 2006; pp. 1–6. [Google Scholar]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. (CSUR) 2009, 41, 15. [Google Scholar] [CrossRef]
- Duan, H.; Lee, P. Transient-based frequency domain method for dead-end side branch detection in reservoir pipeline-valve systems. J. Hydraul. Eng. 2016, 142, 04015042. [Google Scholar] [CrossRef]
- Duan, H.; Lee, P.; Che, T.; Ghidaoui, M.; Karney, B.; Kolyshkin, A. The influence of non-uniform blockages on transient wave behavior and blockage detection in pressurized water pipelines. J. Hydro-Environ. Res. 2017, 17, 1–7. [Google Scholar] [CrossRef]
- Islam, M.S.; Sadiq, R.; Rodriguez, M.J.; Najjaran, H.; Hoorfar, M. Integrated decision support system for prognostic and diagnostic analyses of water distribution system failures. Water Resour. Manag. 2016, 30, 2831–2850. [Google Scholar] [CrossRef]
- Duan, H.F.; Tung, Y.K.; Ghidaoui, M.S. Probabilistic analysis of transient design for water supply systems. J. Water Resour. Plan. Manag. 2010, 136, 678–687. [Google Scholar] [CrossRef]
- Rougier, J.; Goldstein, M. A Bayesian analysis of fluid flow in pipe-lines. J. R. Stat. Soc. Ser. C (Applied Stat.) 2001, 50, 77–93. [Google Scholar] [CrossRef]
- Wang, C.W.; Niu, Z.G.; Jia, H.; Zhang, H.W. An assessment model of water pipe condition using Bayesian inference. J. Zhejiang Univ.-SCIENCE A 2010, 11, 495–504. [Google Scholar] [CrossRef]
- Wilson, D.L.; Coyle, J.R.; Thomas, E.A. Ensemble machine learning and forecasting can achieve 99% uptime for rural handpumps. PLoS ONE 2017, 12, e0188808. [Google Scholar] [CrossRef]
- Greeff, H.; Manandhar, A.; Thomson, P.; Hope, R.; Clifton, D.A. Distributed inference condition monitoring system for rural infrastructure in the developing world. IEEE Sens. J. 2018, 19, 1820–1828. [Google Scholar] [CrossRef]
- Mounce, S.R.; Mounce, R.B.; Boxall, J.B. Novelty detection for time series data analysis in water distribution systems using support vector machines. J. Hydroinf. 2011, 13, 672–686. [Google Scholar] [CrossRef]
- Candelieri, A. Clustering and support vector regression for water demand forecasting and anomaly detection. Water 2017, 9, 224. [Google Scholar] [CrossRef]
- Zohrevand, Z.; Glasser, U.; Shahir, H.Y.; Tayebi, M.A.; Costanzo, R. Hidden Markov based anomaly detection for water supply systems. In Proceedings of the 2016 IEEE International Conference on Big Data (Big Data), Washington, DC, USA, 5–8 December 2016; pp. 1551–1560. [Google Scholar]
- Charity: Water. Available online: https://my.charitywater.org/projects/sensors (accessed on 22 February 2020).
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC: London, UK, 2013. [Google Scholar]
- Gelman, A.; Hill, J. Data Analysis Using Regression and Multilevel/Hierarchical Models; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Jordan, M.I.; Ghahramani, Z.; Jaakkola, T.S.; Saul, L.K. An introduction to variational methods for graphical models. Mach. Learn. 1999, 37, 183–233. [Google Scholar] [CrossRef]
- Wainwright, M.J.; Jordan, M.I. Graphical models, exponential families, and variational inference. Found. Trends® Mach. Learn. 2008, 1, 1–305. [Google Scholar]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational Inference: A Review for Statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Hoffman, M.D.; Blei, D.M.; Wang, C.; Paisley, J. Stochastic variational inference. J. Mach. Learn. Res. 2013, 14, 1303–1347. [Google Scholar]
- Kucukelbir, A.; Tran, D.; Ranganath, R.; Gelman, A.; Blei, D.M. Automatic differentiation variational inference. J. Mach. Learn. Res. 2017, 18, 430–474. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Chen, X.; Liu, S.; Sun, R.; Hong, M. On the convergence of a class of adam-type algorithms for non-convex optimization. arXiv 2018, arXiv:1808.02941. [Google Scholar]
- Carpenter, B.; Gelman, A.; Hoffman, M.D.; Lee, D.; Goodrich, B.; Betancourt, M.; Brubaker, M.; Guo, J.; Li, P.; Riddell, A. Stan: A probabilistic programming language. J. Stat. Softw. 2017, 76, 1–32. [Google Scholar] [CrossRef]
- Stan Development Team. RStan: The R interface to Stan; R Package Version 2.19.2; Stan Development Team: Portland, ON, USA, 2019. [Google Scholar]
- Kucukelbir, A.; Ranganath, R.; Gelman, A.; Blei, D. Automatic variational inference in Stan. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2015; pp. 568–576. [Google Scholar]
- Van de Meent, J.W.; Paige, B.; Yang, H.; Wood, F. An introduction to probabilistic programming. arXiv 2018, arXiv:1809.10756. [Google Scholar]
- Gordon, A.D.; Henzinger, T.A.; Nori, A.V.; Rajamani, S.K. Probabilistic programming. In Proceedings of the on Future of Software Engineering; Association for Computing Machinery: New York, NY, USA, 2014; pp. 167–181. [Google Scholar]
- Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 2015, 521, 452–459. [Google Scholar] [CrossRef]
- WORLD BANK GROUP. Available online: https://data.worldbank.org/country/ethiopia (accessed on 17 January 2020).
- climatemps.com. Available online: http://www.addis-ababa.climatemps.com/precipitation.php (accessed on 17 January 2020).
- Gelman, A.; Meng, X.L.; Stern, H. Posterior predictive assessment of model fitness via realized discrepancies. Stat. Sin. 1996, 6, 733–760. [Google Scholar]
- Wang, Y.; Blei, D.M. The blessings of multiple causes. J. Am. Stat. Assoc. 2019, 114, 1–71. [Google Scholar] [CrossRef]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tashman, Z.; Gorder, C.; Parthasarathy, S.; Nasr-Azadani, M.M.; Webre, R. Anomaly Detection System for Water Networks in Northern Ethiopia Using Bayesian Inference. Sustainability 2020, 12, 2897. https://doi.org/10.3390/su12072897
Tashman Z, Gorder C, Parthasarathy S, Nasr-Azadani MM, Webre R. Anomaly Detection System for Water Networks in Northern Ethiopia Using Bayesian Inference. Sustainability. 2020; 12(7):2897. https://doi.org/10.3390/su12072897
Chicago/Turabian StyleTashman, Zaid, Christoph Gorder, Sonali Parthasarathy, Mohamad M. Nasr-Azadani, and Rachel Webre. 2020. "Anomaly Detection System for Water Networks in Northern Ethiopia Using Bayesian Inference" Sustainability 12, no. 7: 2897. https://doi.org/10.3390/su12072897
APA StyleTashman, Z., Gorder, C., Parthasarathy, S., Nasr-Azadani, M. M., & Webre, R. (2020). Anomaly Detection System for Water Networks in Northern Ethiopia Using Bayesian Inference. Sustainability, 12(7), 2897. https://doi.org/10.3390/su12072897




