A Novel Hybrid Soft Computing Model Using Random Forest and Particle Swarm Optimization for Estimation of Undrained Shear Strength of Soil
Abstract
1. Introduction
2. Case Study and Data Collection
2.1. Description of the Study Area
2.2. Data Used
2.2.1. Output (Undrained Shear Strength of Soil)
2.2.2. Input Variables
3. Methods Used
3.1. Random Forest
3.2. Particle Swarm Optimization (PSO)
3.3. Dataset Splitting
3.4. Modeling and Hyperparameters Tuning
3.5. RF Model Assessment
4. Results and Discussion
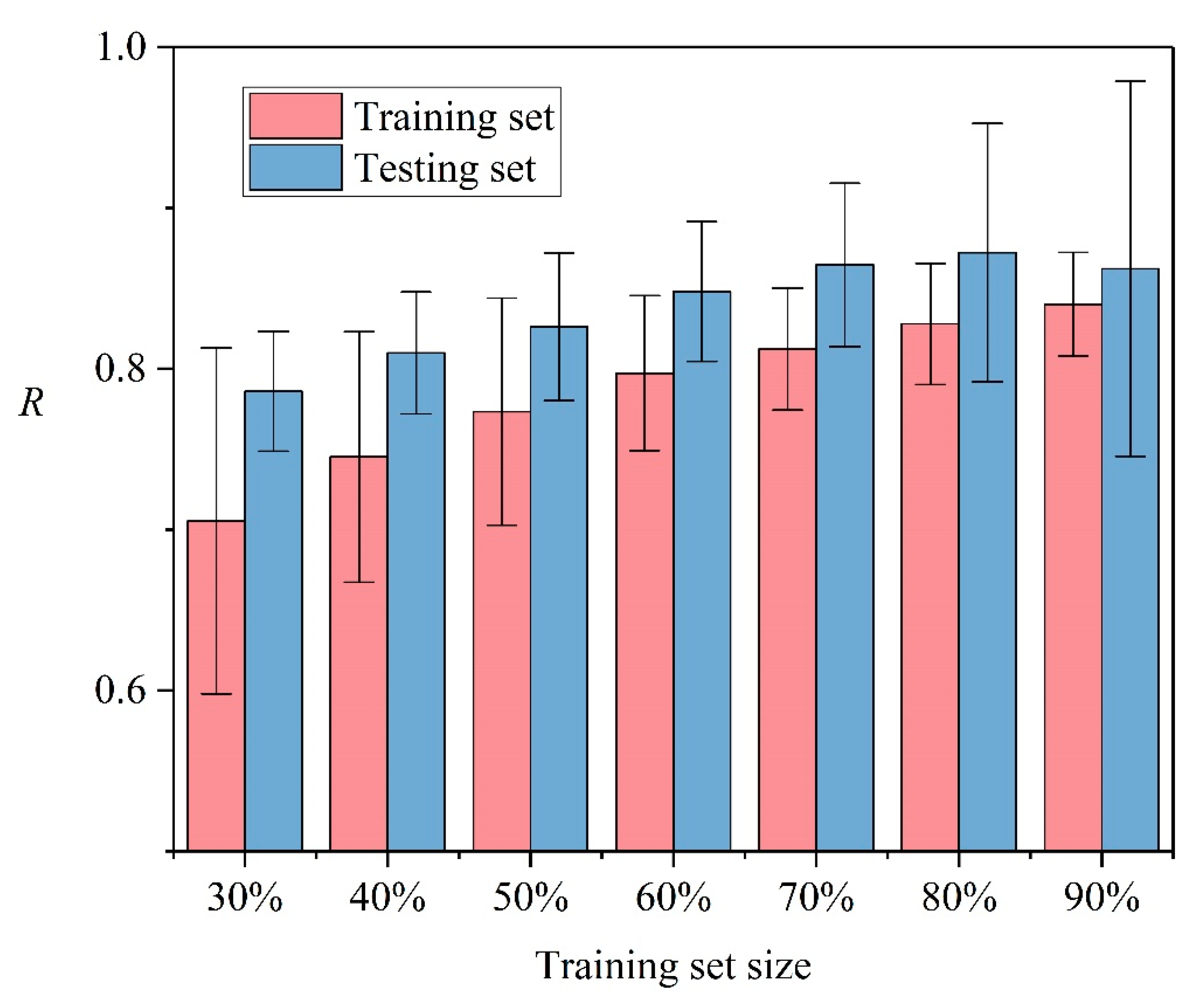
4.1. Influence of Training Set Size (TSS)
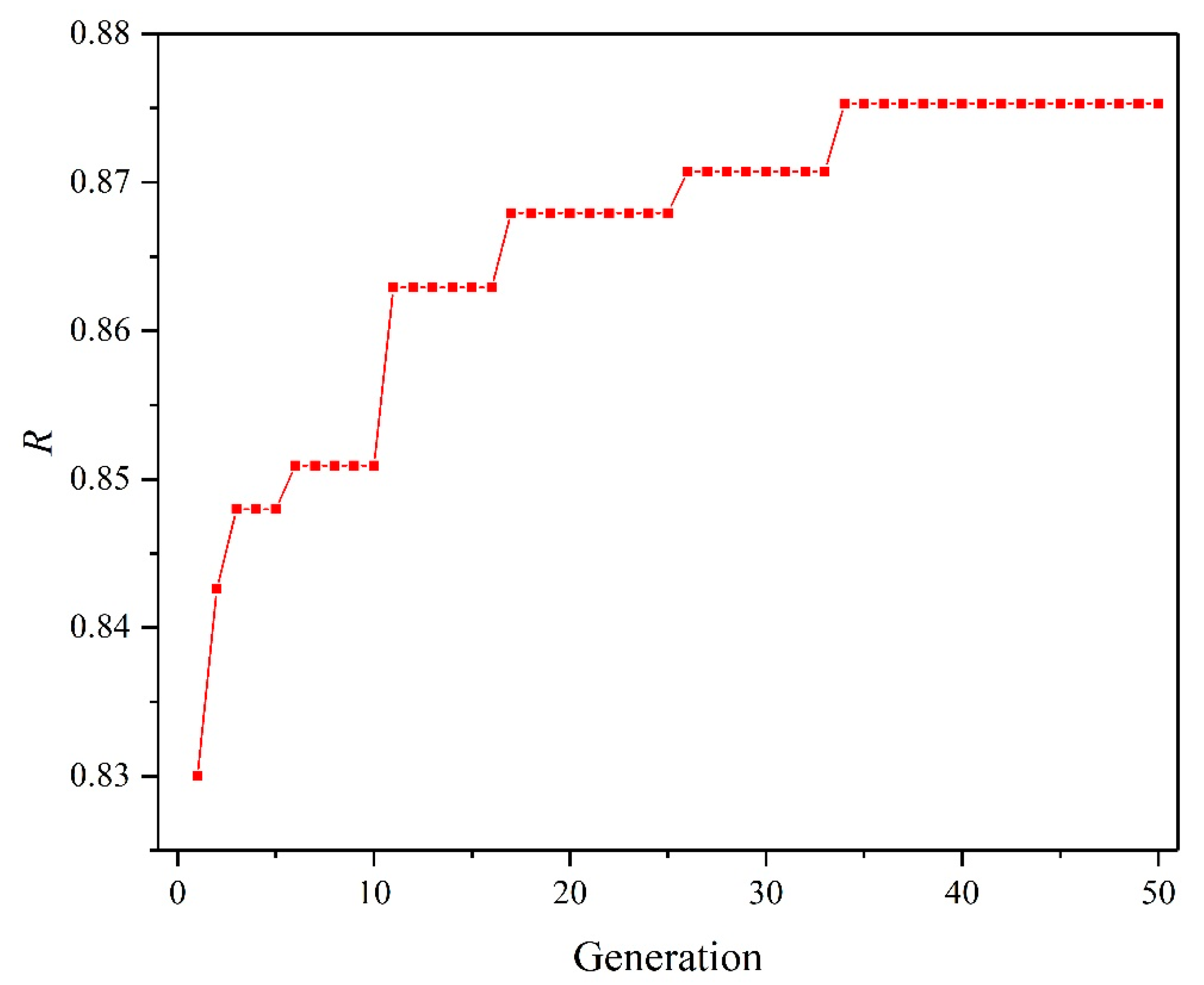
4.2. Hyperparameters Tuning
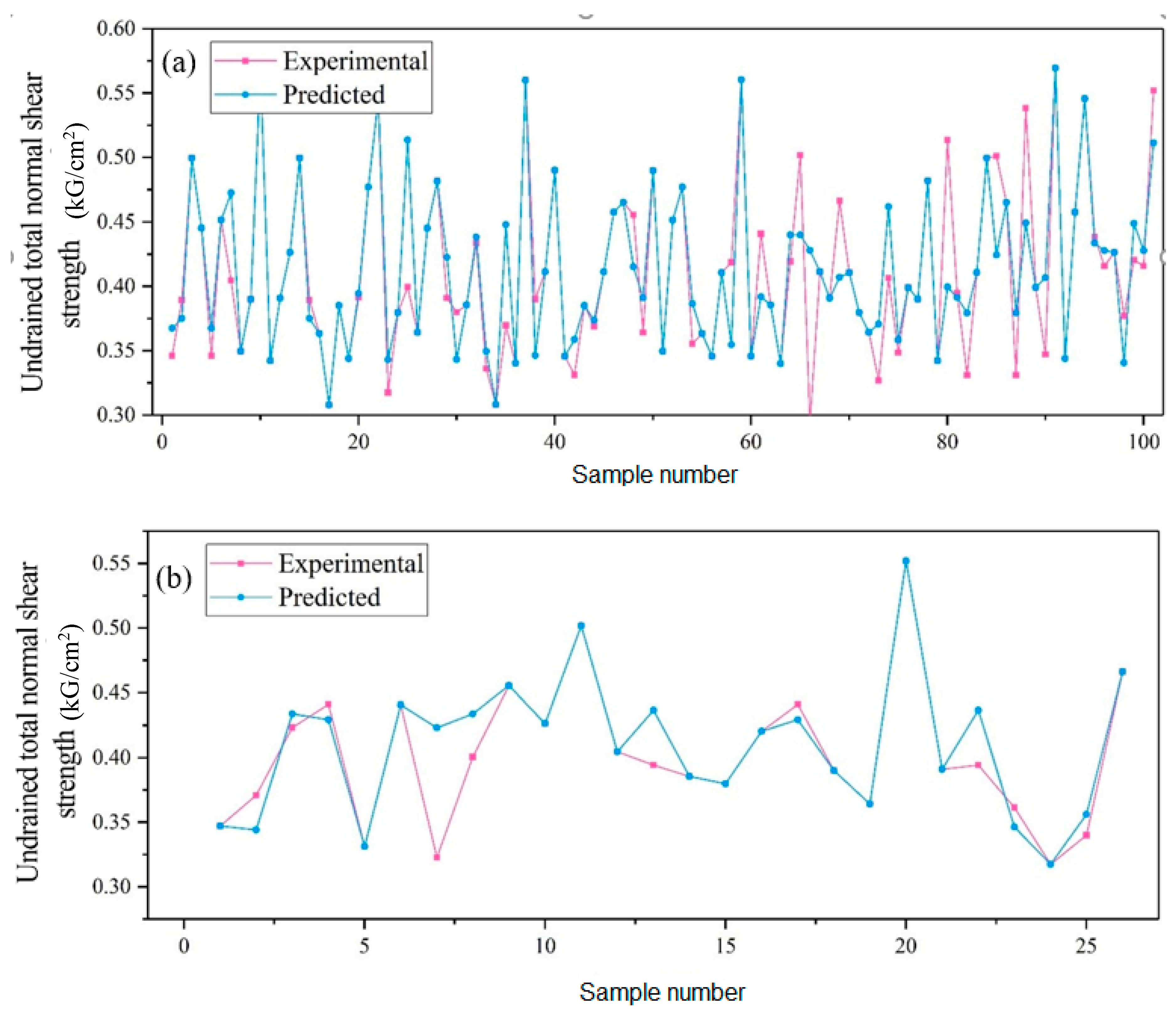
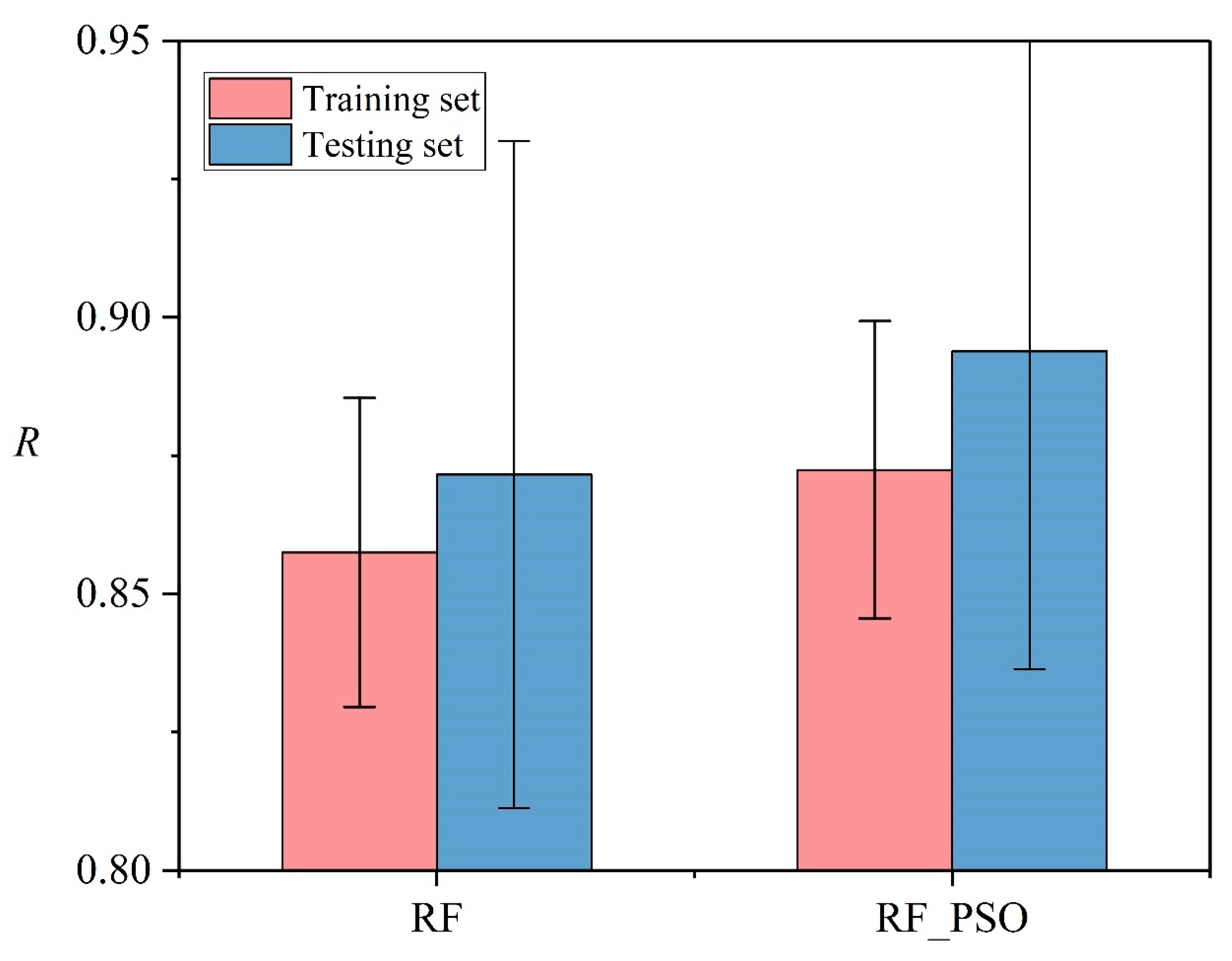
4.3. Predictive Capability of the Models
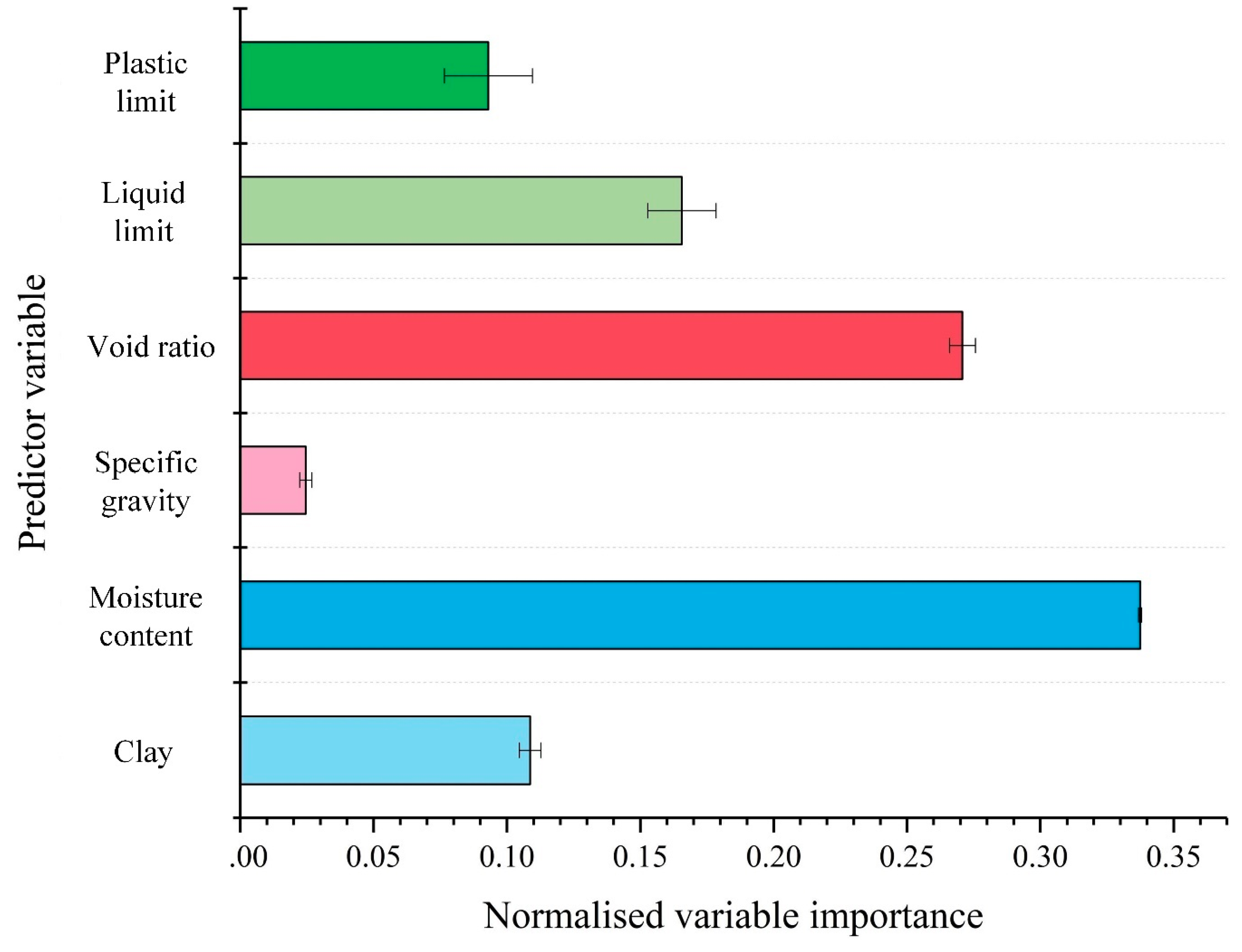
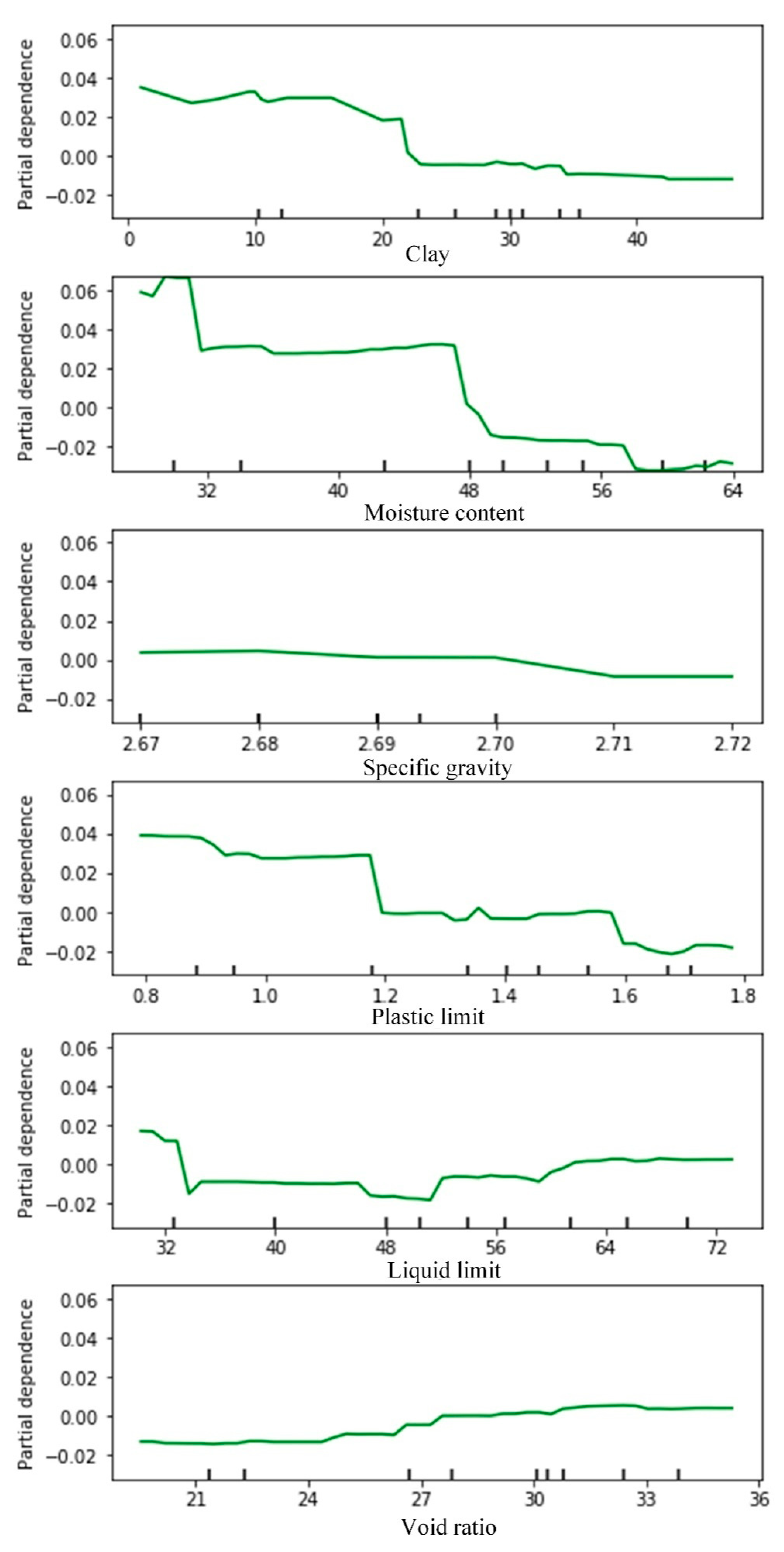
4.4. Sensitivity Analysis of Input Parameters
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Poulos, H.G. Design of reinforcing piles to increase slope stability. Can. Geotech. J. 1995, 32, 808–818. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Wang, T.-W.; Cai, C.-F.; Li, Z.-X.; Cheng, D.-B. Effects of vegetation on runoff generation, sediment yield and soil shear strength on road-side slopes under a simulation rainfall test in the Three Gorges Reservoir Area, China. Sci. Total Environ. 2014, 485, 93–102. [Google Scholar] [CrossRef] [PubMed]
- Hettiarachchi, H.; Brown, T. Use of SPT blow counts to estimate shear strength properties of soils: Energy balance approach. J. Geotech. Geoenviron. Eng. 2009, 135, 830–834. [Google Scholar] [CrossRef]
- Motaghedi, H.; Eslami, A. Analytical approach for determination of soil shear strength parameters from CPT and CPTu data. Arab. J. Sci. Eng. 2014, 39, 4363–4376. [Google Scholar] [CrossRef]
- Cha, M.; Cho, G.-C. Shear strength estimation of sandy soils using shear wave velocity. Geotech. Test. J. 2007, 30, 484–495. [Google Scholar]
- Garven, E.; Vanapalli, S. Evaluation of empirical procedures for predicting the shear strength of unsaturated soils. In Unsaturated Soils 2006, Fourth International Conference on Unsaturated Soils, Carefree, AZ, USA, 2–6 April 2006; American Society of Civil Engineers: Reston, VA, USA, 2006; pp. 2570–2592. [Google Scholar]
- Kim, B.-S.; Shibuya, S.; Park, S.-W.; Kato, S. Application of suction stress for estimating unsaturated shear strength of soils using direct shear testing under low confining pressure. Can. Geotech. J. 2010, 47, 955–970. [Google Scholar] [CrossRef]
- Ohu, J.O.; Raghavan, G.; McKyes, E.; Mehuys, G. Shear strength prediction of compacted soils with varying added organic matter contents. Trans. ASAE 1986, 29, 351–355. [Google Scholar] [CrossRef]
- Tiwari, B.; Marui, H. A new method for the correlation of residual shear strength of the soil with mineralogical composition. J. Geotech. Geoenviron. Eng. 2005, 131, 1139–1150. [Google Scholar] [CrossRef]
- Vilar, O.M. A simplified procedure to estimate the shear strength envelope of unsaturated soils. Can. Geotech. J. 2006, 43, 1088–1095. [Google Scholar] [CrossRef]
- Huang, B.; Qiu, M.; Lin, J.; Chen, J.; Jiang, F.; Wang, M.-K.; Ge, H.; Huang, Y. Correlation between shear strength and soil physicochemical properties of different weathering profiles of the non-eroded and collapsing gully soils in southern China. J. Soils Sediments 2019, 19, 3832–3846. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A.; Dai, G. Estimation of unsaturated shear strength from soil–water characteristic curve. Acta Geotech. 2019, 14, 1977–1990. [Google Scholar] [CrossRef]
- Leong, E.-C. Soil-water characteristic curves-Determination, estimation and application. Jpn. Geotech. Soc. Spec. Publ. 2019, 7, 21–30. [Google Scholar] [CrossRef]
- Bui, D.T.; Nhu, V.-H.; Hoang, N.-D. Prediction of soil compression coefficient for urban housing project using novel integration machine learning approach of swarm intelligence and multi-layer perceptron neural network. Adv. Eng. Inform. 2018, 38, 593–604. [Google Scholar]
- Chen, W.; Wang, Y.; Cao, G.; Chen, G.; Gu, Q. A random forest model based classification scheme for neonatal amplitude-integrated EEG. Biomed. Eng. Online 2014, 13, S4. [Google Scholar] [CrossRef]
- Chou, J.-S.; Pham, A.-D. Enhanced artificial intelligence for ensemble approach to predicting high performance concrete compressive strength. Constr. Build. Mater. 2013, 49, 554–563. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Fallah, A.; Armaghani, D.J.; Azizi, A.; Mohamad, E.T. Three hybrid intelligent models in estimating flyrock distance resulting from blasting. Eng. Comput. 2019, 35, 243–256. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Ghaleini, E.N.; Tootoonchi, H.; Armaghani, D.J.; Haghighi, M.; Hedayat, A. Developing a new intelligent technique to predict overbreak in tunnels using an artificial bee colony-based ANN. Environ. Earth Sci. 2019, 78, 165. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Prakash, I.; Dholakia, M. Hybrid integration of Multilayer Perceptron Neural Networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. Catena 2017, 149, 52–63. [Google Scholar] [CrossRef]
- Samui, P. Prediction of friction capacity of driven piles in clay using the support vector machine. Can. Geotech. J. 2008, 45, 288–295. [Google Scholar] [CrossRef]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. Recent advances and future challenges for artificial neural systems in geotechnical engineering applications. Adv. Artif. Neural Syst. 2009, 2009, 5. [Google Scholar] [CrossRef]
- Dao, D.V.; Adeli, H.; Ly, H.-B.; Le, L.M.; Le, V.M.; Le, T.-T.; Pham, B.T. A Sensitivity and Robustness Analysis of GPR and ANN for High-Performance Concrete Compressive Strength Prediction Using a Monte Carlo Simulation. Sustainability 2020, 12, 830. [Google Scholar] [CrossRef]
- Pham, B.T.; Avand, M.; Janizadeh, S.; Phong, T.V.; Al-Ansari, N.; Ho, L.S.; Das, S.; Le, H.V.; Amini, A.; Bozchaloei, S.K. GIS Based Hybrid Computational Approaches for Flash Flood Susceptibility Assessment. Water 2020, 12, 683. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Dou, J.; Singh, S.K.; Trinh, P.T.; Tran, H.T.; Le, T.M.; Van Phong, T.; Khoi, D.K.; Shirzadi, A. A novel hybrid approach of landslide susceptibility modelling using rotation forest ensemble and different base classifiers. Geocarto Int. 2019, 1–25. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Prakash, I.; Nguyen, L.H.; Dholakia, M. A comparative study of sequential minimal optimization-based support vector machines, vote feature intervals, and logistic regression in landslide susceptibility assessment using GIS. Environ. Earth Sci. 2017, 76, 371. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Pham, H.V.; Le, H.Q.; Prakash, I.; Dholakia, M. Landslide hazard assessment using random subspace fuzzy rules based classifier ensemble and probability analysis of rainfall data: A case study at Mu Cang Chai District, Yen Bai Province (Viet Nam). J. Indian Soc. Remote Sens. 2017, 45, 673–683. [Google Scholar] [CrossRef]
- Sharma, L.; Singh, R.; Umrao, R.; Sharma, K.; Singh, T. Evaluating the modulus of elasticity of soil using soft computing system. Eng. Comput. 2017, 33, 497–507. [Google Scholar] [CrossRef]
- Kalkan, E.; Akbulut, S.; Tortum, A.; Celik, S. Prediction of the unconfined compressive strength of compacted granular soils by using inference systems. Environ. Geol. 2009, 58, 1429–1440. [Google Scholar] [CrossRef]
- Nhu, V.H.; Hoang, N.D.; Duong, V.B.; Vu, H.D.; Bui, D.T. A hybrid computational intelligence approach for predicting soil shear strength for urban housing construction: a case study at Vinhomes Imperia project, Hai Phong City (Vietnam). Eng. Comput. 2019, 1–14. [Google Scholar] [CrossRef]
- Moavenian, M.; Nazem, M.; Carter, J.; Randolph, M. Numerical analysis of penetrometers free-falling into soil with shear strength increasing linearly with depth. Comput. Geotech. 2016, 72, 57–66. [Google Scholar] [CrossRef]
- Pham, B.T.; Hoang, T.-A.; Nguyen, D.-M.; Bui, D.T. Prediction of shear strength of soft soil using machine learning methods. Catena 2018, 166, 181–191. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Jahed Armaghani, D.; Hajihassani, M.; Yazdani Bejarbaneh, B.; Marto, A.; Tonnizam Mohamad, E. Indirect measure of shale shear strength parameters by means of rock index tests through an optimized artificial neural network. Measurement 2014, 55, 487–498. [Google Scholar] [CrossRef]
- Hajihassani, M.; Armaghani, D.J.; Kalatehjari, R. Applications of particle swarm optimization in geotechnical engineering: a comprehensive review. Geotech. Geol. Eng. 2018, 36, 705–722. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Noorian-Bidgoli, M.; Armaghani, D.J.; Khamesi, H. Feasibility of PSO-ANN model for predicting surface settlement caused by tunneling. Eng. Comput. 2016, 32, 705–715. [Google Scholar] [CrossRef]
- Kalatehjari, R.; Ali, N.; Kholghifard, M.; Hajihassani, M. The effects of method of generating circular slip surfaces on determining the critical slip surface by particle swarm optimization. Arab. J. Geosci. 2014, 7, 1529–1539. [Google Scholar] [CrossRef]
- Das, B.M.; Sobhan, K. Principles of Geotechnical Engineering; Cengage Learning: Stamford, CT, USA, 2013. [Google Scholar]
- Terzaghi, K.; Peck, R.B.; Mesri, G. Soil Mechanics; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Hong, H.; Pourghasemi, H.R.; Pourtaghi, Z.S. Landslide susceptibility assessment in Lianhua County (China): a comparison between a random forest data mining technique and bivariate and multivariate statistical models. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
- Stumpf, A.; Kerle, N. Object-oriented mapping of landslides using Random Forests. Remote Sens. Environ. 2011, 115, 2564–2577. [Google Scholar] [CrossRef]
- Archer, K.J.; Kimes, R.V. Empirical characterization of random forest variable importance measures. Comput. Stat. Data Anal. 2008, 52, 2249–2260. [Google Scholar] [CrossRef]
- Biau, G.; Devroye, L.; Lugosi, G. Consistency of random forests and other averaging classifiers. J. Mach. Learn. Res. 2008, 9, 2015–2033. [Google Scholar]
- Trigila, A.; Iadanza, C.; Esposito, C.; Scarascia-Mugnozza, G. Comparison of Logistic Regression and Random Forests techniques for shallow landslide susceptibility assessment in Giampilieri (NE Sicily, Italy). Geomorphology 2015, 249, 119–136. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Cheng, Y.; Li, L.; Chi, S.-C.; Wei, W. Particle swarm optimization algorithm for the location of the critical non-circular failure surface in two-dimensional slope stability analysis. Comput. Geotech. 2007, 34, 92–103. [Google Scholar] [CrossRef]
- Awad, Z.K.; Aravinthan, T.; Zhuge, Y.; Gonzalez, F. A review of optimization techniques used in the design of fibre composite structures for civil engineering applications. Mater. Des. 2012, 33, 534–544. [Google Scholar] [CrossRef]
- Chen, W.; Panahi, M.; Pourghasemi, H.R. Performance evaluation of GIS-based new ensemble data mining techniques of adaptive neuro-fuzzy inference system (ANFIS) with genetic algorithm (GA), differential evolution (DE), and particle swarm optimization (PSO) for landslide spatial modelling. Catena 2017, 157, 310–324. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Chen, Q.; Zhang, Q. A strength prediction model using artificial intelligence for recycling waste tailings as cemented paste backfill. J. Clean. Prod. 2018, 183, 566–578. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Qi, C.; Chen, Q.; Fourie, A.; Zhang, Q. An intelligent modelling framework for mechanical properties of cemented paste backfill. Miner. Eng. 2018, 123, 16–27. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y. Comparing inertia weights and constriction factors in particle swarm optimization. In Proceedings of the 2000 Congress on Evolutionary Computation, CEC00 (Cat. No.00TH8512), La Jolla, CA, USA, 16–19 July 2000; Volume 81, pp. 84–88. [Google Scholar]
- Van den Bergh, F.; Engelbrecht, A.P. A study of particle swarm optimization particle trajectories. Inf. Sci. 2006, 176, 937–971. [Google Scholar] [CrossRef]
- Li-ping, Z.; Huan-jun, Y.; Shang-xu, H. Optimal choice of parameters for particle swarm optimization. J. Zhejiang Univ. Sci. A 2005, 6, 528–534. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Chen, Q.; Tang, X.; Zhang, Q.; Gao, R. Data-driven modelling of the flocculation process on mineral processing tailings treatment. J. Clean. Prod. 2018, 196, 505–516. [Google Scholar] [CrossRef]
- Qi, C.; Ly, H.-B.; Chen, Q.; Le, T.-T.; Le, V.M.; Pham, B.T. Flocculation-dewatering prediction of fine mineral tailings using a hybrid machine learning approach. Chemosphere 2020, 244, 125450. [Google Scholar] [CrossRef] [PubMed]
- Pham, B.T.; Le, L.M.; Le, T.-T.; Bui, K.-T.T.; Le, V.M.; Ly, H.-B.; Prakash, I. Development of advanced artificial intelligence models for daily rainfall prediction. Atmos. Res. 2020, 237, 104845. [Google Scholar] [CrossRef]
- Dao, D.V.; Ly, H.-B.; Vu, H.-L.T.; Le, T.-T.; Pham, B.T. Investigation and Optimization of the C-ANN Structure in Predicting the Compressive Strength of Foamed Concrete. Materials 2020, 13, 1072. [Google Scholar] [CrossRef] [PubMed]
- Van Dao, D.; Jaafari, A.; Bayat, M.; Mafi-Gholami, D.; Qi, C.; Moayedi, H.; Van Phong, T.; Ly, H.-B.; Le, T.-T.; Trinh, P.T. A spatially explicit deep learning neural network model for the prediction of landslide susceptibility. Catena 2020, 188, 104451. [Google Scholar]
- Pham, B.T.; Phong, T.V.; Nguyen, H.D.; Qi, C.; Al-Ansari, N.; Amini, A.; Ho, L.S.; Tuyen, T.T.; Yen, H.P.H.; Ly, H.-B. A Comparative Study of Kernel Logistic Regression, Radial Basis Function Classifier, Multinomial Naïve Bayes, and Logistic Model Tree for Flash Flood Susceptibility Mapping. Water 2020, 12, 239. [Google Scholar] [CrossRef]
- Nguyen, V.V.; Pham, B.T.; Vu, B.T.; Prakash, I.; Jha, S.; Shahabi, H.; Shirzadi, A.; Ba, D.N.; Kumar, R.; Chatterjee, J.M. Hybrid machine learning approaches for landslide susceptibility modeling. Forests 2019, 10, 157. [Google Scholar] [CrossRef]
- Nguyen, M.D.; Pham, B.T.; Tuyen, T.T.; Yen, H.; Phan, H.; Prakash, I.; Vu, T.T.; Chapi, K.; Shirzadi, A.; Shahabi, H. Development of an Artificial Intelligence Approach for Prediction of Consolidation Coefficient of Soft Soil: A Sensitivity Analysis. Open Constr. Build. Technol. J. 2019, 13, 178–188. [Google Scholar] [CrossRef]
- Dao, D.V.; Ly, H.-B.; Trinh, S.H.; Le, T.-T.; Pham, B.T. Artificial intelligence approaches for prediction of compressive strength of geopolymer concrete. Materials 2019, 12, 983. [Google Scholar] [CrossRef]
- Dao, D.V.; Trinh, S.H.; Ly, H.-B.; Pham, B.T. Prediction of compressive strength of geopolymer concrete using entirely steel slag aggregates: Novel hybrid artificial intelligence approaches. Appl. Sci. 2019, 9, 1113. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen, M.D.; Van Dao, D.; Prakash, I.; Ly, H.-B.; Le, T.-T.; Ho, L.S.; Nguyen, K.T.; Ngo, T.Q.; Hoang, V. Development of artificial intelligence models for the prediction of Compression Coefficient of soil: An application of Monte Carlo sensitivity analysis. Sci. Total Environ. 2019, 679, 172–184. [Google Scholar] [CrossRef]
- Nguyen, H.-L.; Pham, B.T.; Son, L.H.; Thang, N.T.; Ly, H.-B.; Le, T.-T.; Ho, L.S.; Le, T.-H.; Tien Bui, D. Adaptive network based fuzzy inference system with meta-heuristic optimizations for international roughness index prediction. Appl. Sci. 2019, 9, 4715. [Google Scholar] [CrossRef]
- Janizadeh, S.; Avand, M.; Jaafari, A.; Phong, T.V.; Bayat, M.; Ahmadisharaf, E.; Prakash, I.; Pham, B.T.; Lee, S. Prediction Success of Machine Learning Methods for Flash Flood Susceptibility Mapping in the Tafresh Watershed, Iran. Sustainability 2019, 11, 5426. [Google Scholar] [CrossRef]
- Kohestani, V.; Hassanlourad, M.; Ardakani, A. Evaluation of liquefaction potential based on CPT data using random forest. Nat. Hazards 2015, 79, 1079–1089. [Google Scholar] [CrossRef]
- Wan, S. Entropy-based particle swarm optimization with clustering analysis on landslide susceptibility mapping. Environ. Earth Sci. 2012, 68. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Chen, Q. Neural network and particle swarm optimization for predicting the unconfined compressive strength of cemented paste backfill. Constr. Build. Mater. 2018, 159, 473–478. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen, M.D.; Bui, K.-T.T.; Prakash, I.; Chapi, K.; Bui, D.T. A novel artificial intelligence approach based on Multi-layer Perceptron Neural Network and Biogeography-based Optimization for predicting coefficient of consolidation of soil. Catena 2019, 173, 302–311. [Google Scholar] [CrossRef]
| No | Parameters | Min Values | Max Values | Mean Values | Standard Deviation |
|---|---|---|---|---|---|
| 1 | Clay content (%) | 1.00 | 47.5 | 25.72 | 10.172 |
| 2 | Water content (%) | 23.04 | 70.74 | 48.3 | 11.73 |
| 3 | Specific gravity | 2.67 | 2.72 | 2.69 | 0.01 |
| 4 | Void ratio | 0.63 | 1.92 | 1.36 | 0.31 |
| 5 | Liquid limit (%) | 26.08 | 79.76 | 53.34 | 13.39 |
| 6 | Plastic limit (%) | 15.36 | 40.48 | 28.38 | 5.01 |
| 7 | Undrained total normal shear strength (kG/cm2) | 0.29 | 0.57 | 0.41 | 0.06 |
| No | Hyperparameters | Explanation | Range |
|---|---|---|---|
| 1 | Max_depth | The maximum depth of DTs. | 1–20 |
| 2 | Min_samples_split | The minimum number of samples for the split. | 2–10 |
| 3 | Min_samples_leaf | The minimum number of samples at the leaf node. | 1–10 |
| 4 | Max_DT | The maximum number of RT models in the ensemble | 1–1000 |
| 5 | Max_features | The number of features considered during the selection of the best splitting | 0.4–1 |
| No | Models | RMSE | |
|---|---|---|---|
| Training | Testing | ||
| 1 | RF | 0.517 | 0.480 |
| 2 | RF-PSO | 0.487 | 0.453 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, B.T.; Qi, C.; Ho, L.S.; Nguyen-Thoi, T.; Al-Ansari, N.; Nguyen, M.D.; Nguyen, H.D.; Ly, H.-B.; Le, H.V.; Prakash, I. A Novel Hybrid Soft Computing Model Using Random Forest and Particle Swarm Optimization for Estimation of Undrained Shear Strength of Soil. Sustainability 2020, 12, 2218. https://doi.org/10.3390/su12062218
Pham BT, Qi C, Ho LS, Nguyen-Thoi T, Al-Ansari N, Nguyen MD, Nguyen HD, Ly H-B, Le HV, Prakash I. A Novel Hybrid Soft Computing Model Using Random Forest and Particle Swarm Optimization for Estimation of Undrained Shear Strength of Soil. Sustainability. 2020; 12(6):2218. https://doi.org/10.3390/su12062218
Chicago/Turabian StylePham, Binh Thai, Chongchong Qi, Lanh Si Ho, Trung Nguyen-Thoi, Nadhir Al-Ansari, Manh Duc Nguyen, Huu Duy Nguyen, Hai-Bang Ly, Hiep Van Le, and Indra Prakash. 2020. "A Novel Hybrid Soft Computing Model Using Random Forest and Particle Swarm Optimization for Estimation of Undrained Shear Strength of Soil" Sustainability 12, no. 6: 2218. https://doi.org/10.3390/su12062218
APA StylePham, B. T., Qi, C., Ho, L. S., Nguyen-Thoi, T., Al-Ansari, N., Nguyen, M. D., Nguyen, H. D., Ly, H.-B., Le, H. V., & Prakash, I. (2020). A Novel Hybrid Soft Computing Model Using Random Forest and Particle Swarm Optimization for Estimation of Undrained Shear Strength of Soil. Sustainability, 12(6), 2218. https://doi.org/10.3390/su12062218









