Mixed Logit Model Based on Improved Nonlinear Utility Functions: A Market Shares Solution Method of Different Railway Traffic Modes
Abstract
1. Introduction
1.1. Literature Review
1.2. The Focus of This Paper
2. Mathematical Formulation
2.1. Problem Description
- (A1)
- According to the utility theory proposed by Fishburn [24], based on the usual mentality of passengers for making choices, passengers will evaluate the utility values of different available railway traffic modes and always choose the most reasonable mode which has maximum utility value.
- (A2)
- Under the condition of assumption (A1) and in order to the convenience of research, we will take the same income passenger group as a whole.
2.2. Mathematical Model
2.2.1. Mixed Logit Model
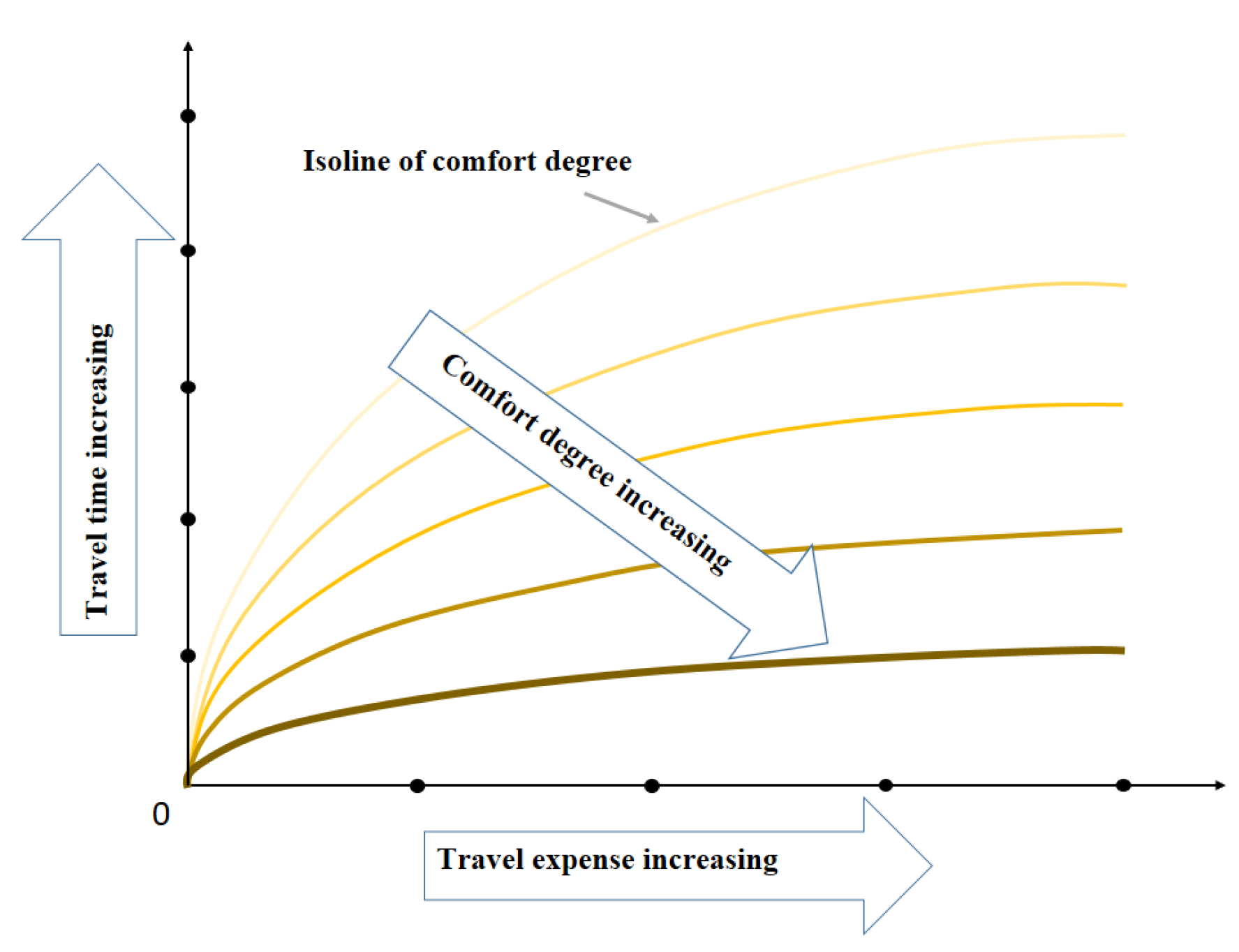
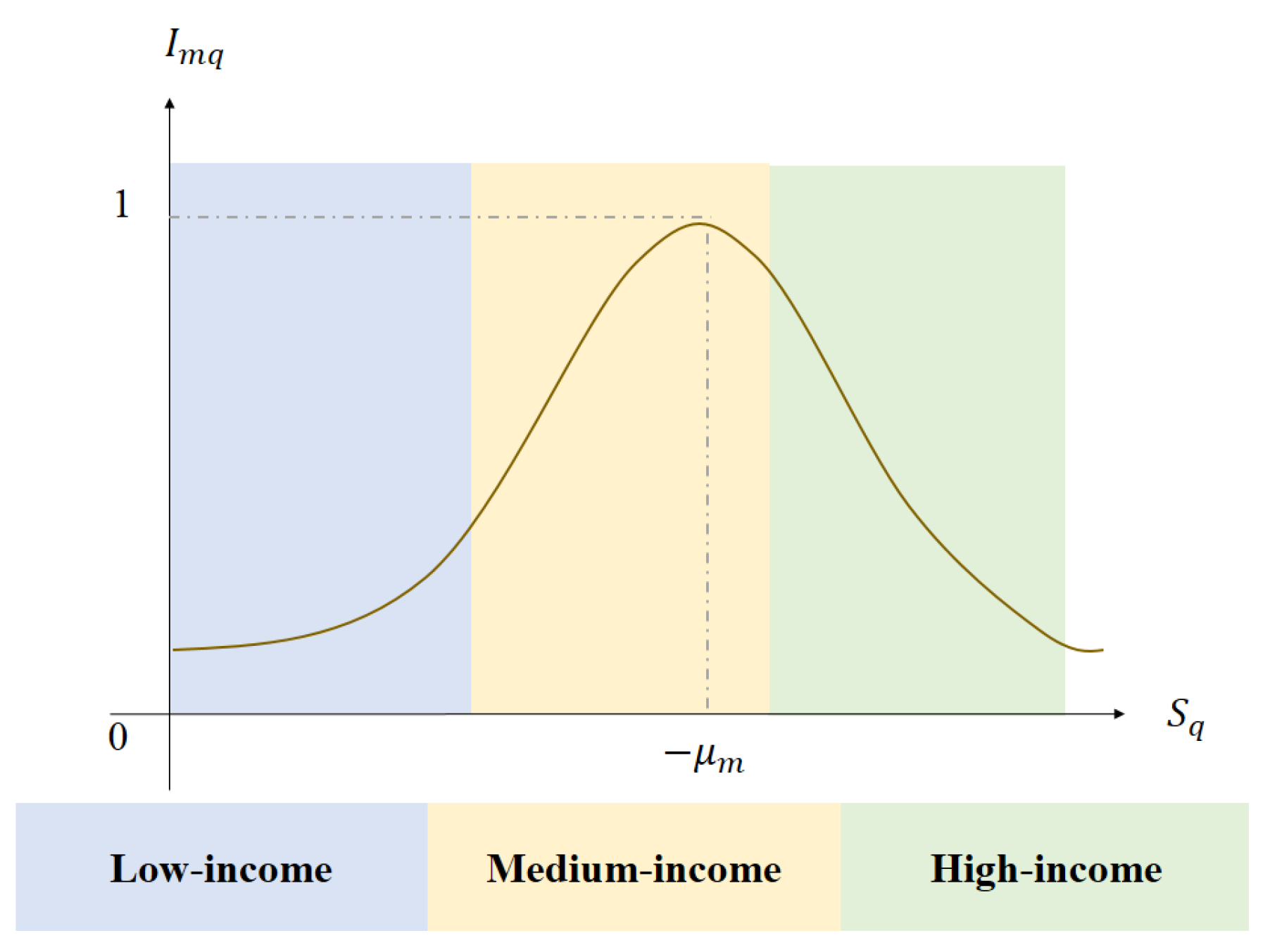
2.2.2. Improved Nonlinear Utility Functions
2.2.3. Maximum Likelihood Estimation
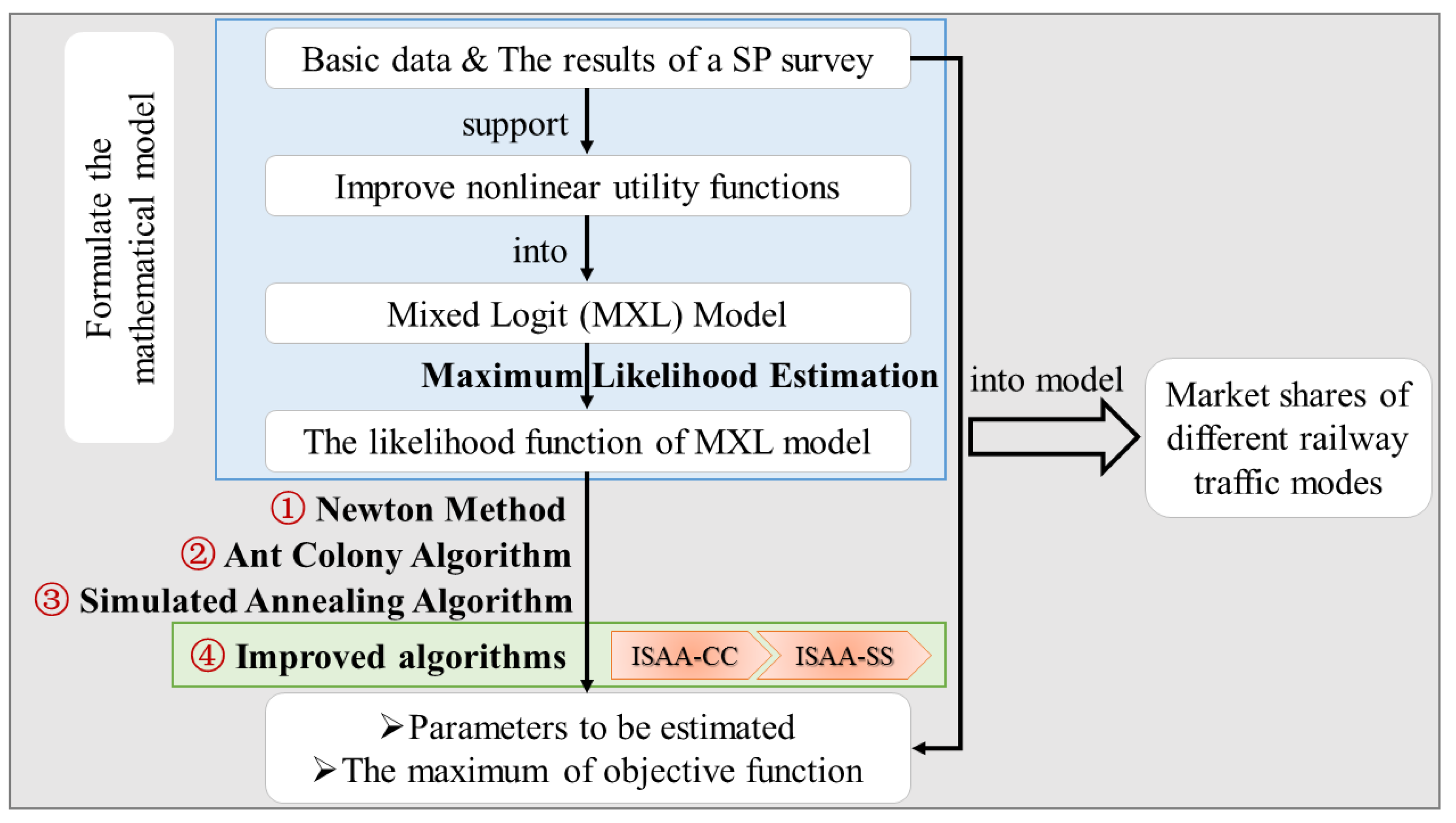
3. Solution Approaches
| Algorithm 1: A heuristic bionic evolutionary algorithm based on swarm intelligence. |
| Step 1. The relevant parameters need to be initialized, including ant colony size (the total number of ants) , the pheromones volatilization coefficient , total pheromones released by ants for one iteration Q (constant), a constant of transfer probability , maximum number of iterations . Initial pheromones . Step 2. Do for i = 1, 2, ⋯, , Step 2.1. Do for t = 1, 2, ⋯, , Step 2.1.1. Each ant is randomly placed in different positions, and the next position of ant t, namely next feasible solution, is determined according to transfer probability , i.e., pheromones in the current population (i.e. the current maximum of the function), the transfer probability is smaller, and variable value tends to be fine-tuning, i.e., where is a 0-1 random number, and is heuristic function (degree of expectation) and it gradually decreases as the iteration progresses. (b) Global Search: The farther away the ant t is from the position with the highest concentration of pheromones in the current population, the greater of transfer probability , the more the algorithm tends to search for the optimal value in a wider range, i.e., , where is upper bound and is lower bound of . Step 3. Calculate the pheromones of each path, and update the concentration of pheromones by the iteration formula as follows, i.e., . At the same time, the optimal solution of the current iteration is recorded. |
| Algorithm 2: An optimization algorithm based on probability. |
| Step 1. The relevant parameters need to be initialized, including an initial temperature ,
termination temperature , an initial state , maximum number of disturbance and maximum number of iterations . Let current temperature be and current state be . Step 2. Do for i = 1, 2, ⋯, , Step 2.1. Do for t = 1, 2, ⋯, , Step 2.1.1. Calculate the internal energy of the current state (objective function value) . Transform the current state to a new one by exchanging certain elements; and internal energy of this new state is calculated. Step 2.1.2. Calculate increment . If , the new state is accepted. Otherwise, the new state is accepted when a random number , (0 1) is greater than . Step 2.1.3. Let be the current state, i.e., . Step 2.2. Exit the loop until . Step 3. Let where is used to control the speed of cooling and its value ranges from 0.01 to 0.99. The larger the value of is, the slower temperature will drop. If the value of is too large, the possibility of searching the global optimal solution is higher, but the searching process is also longer. |
3.1. Ant Colony Algorithm
3.2. Simulated Annealing Algorithm
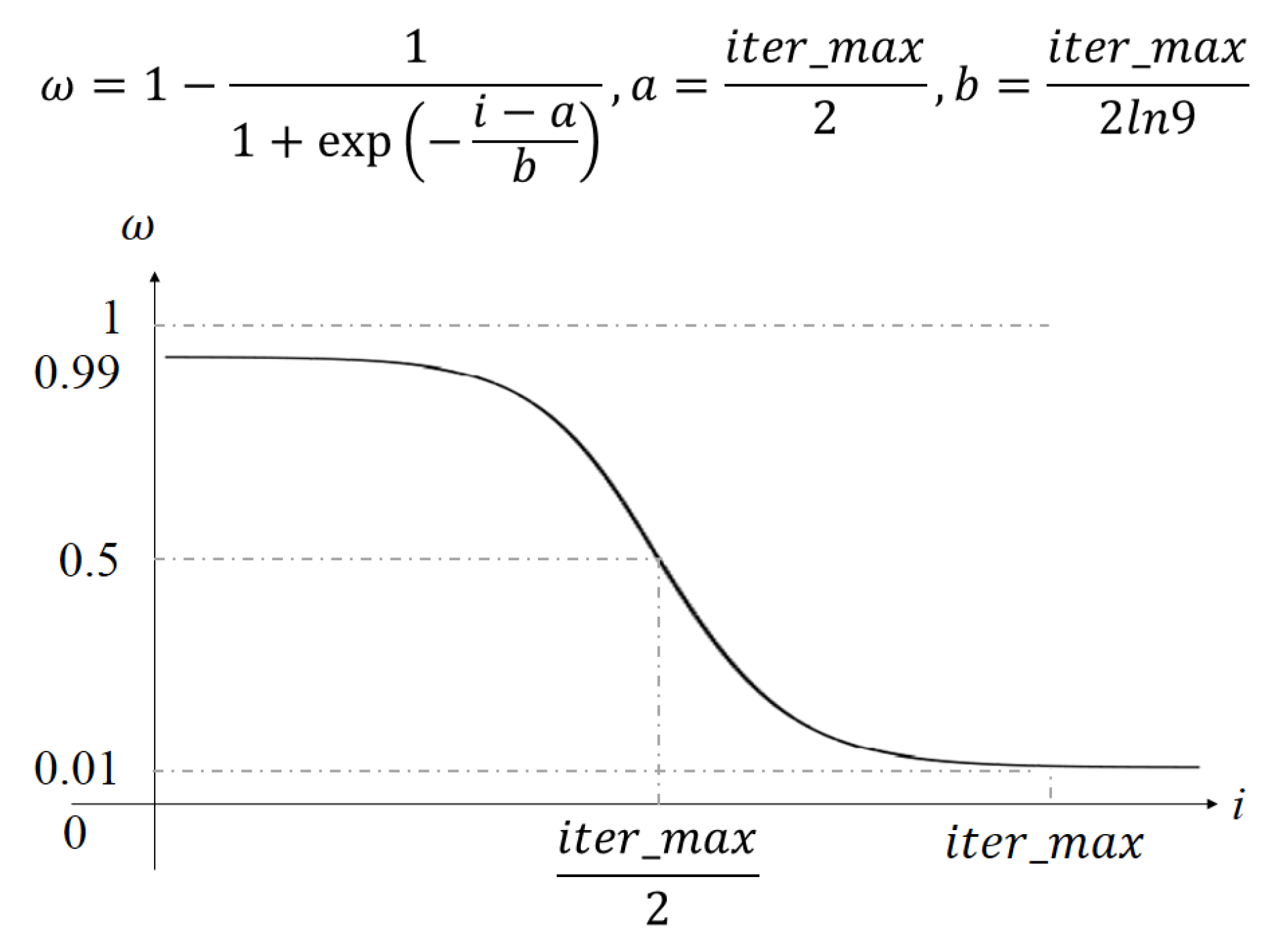
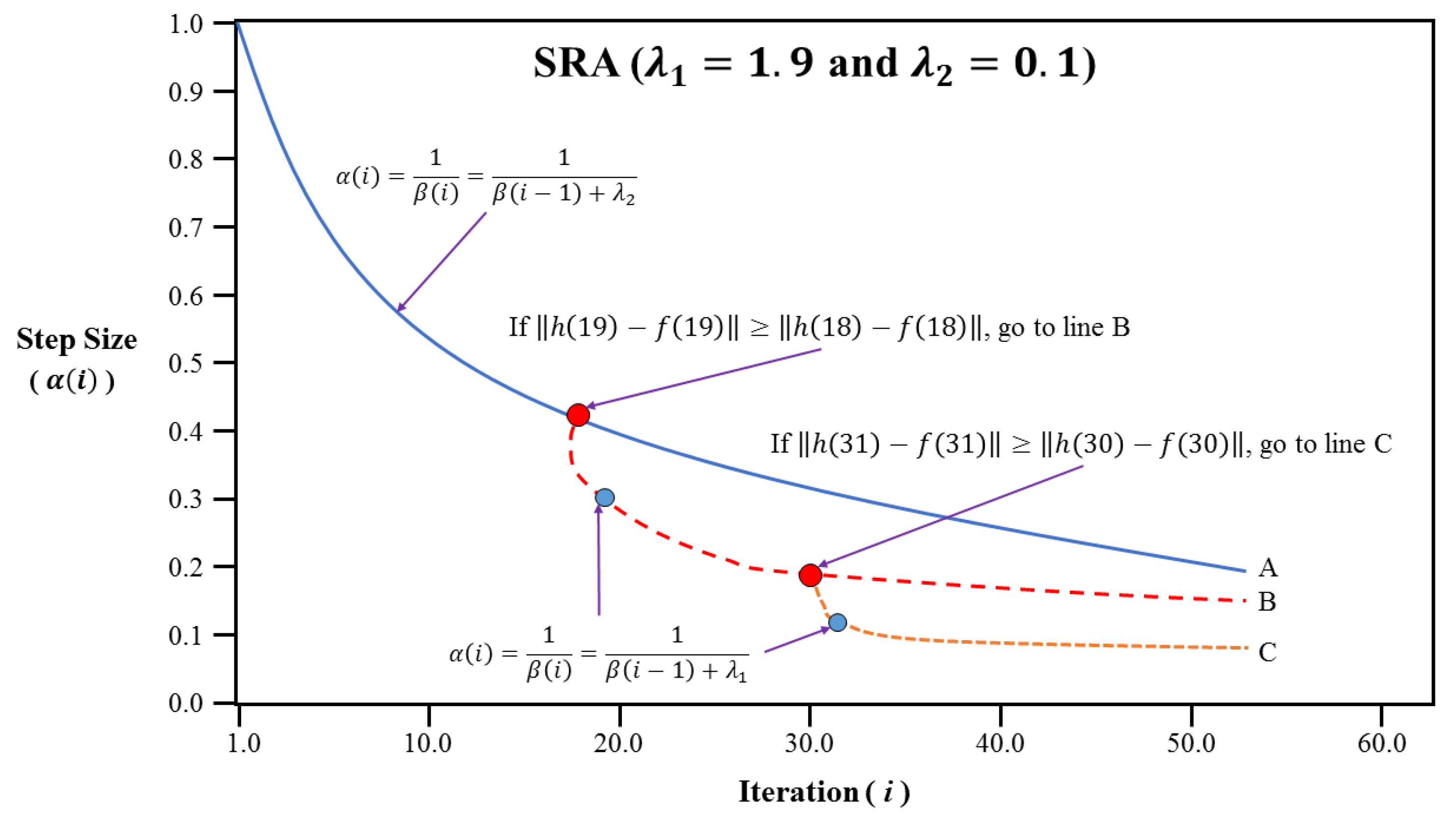
3.3. Improved Algorithms Based on Simulated Annealing Algorithm
4. Numerical Experiment
4.1. Computations of Five Algorithms
4.1.1. Results of Ant Colony Algorithm
4.1.2. Computation of Simulated Annealing Algorithm
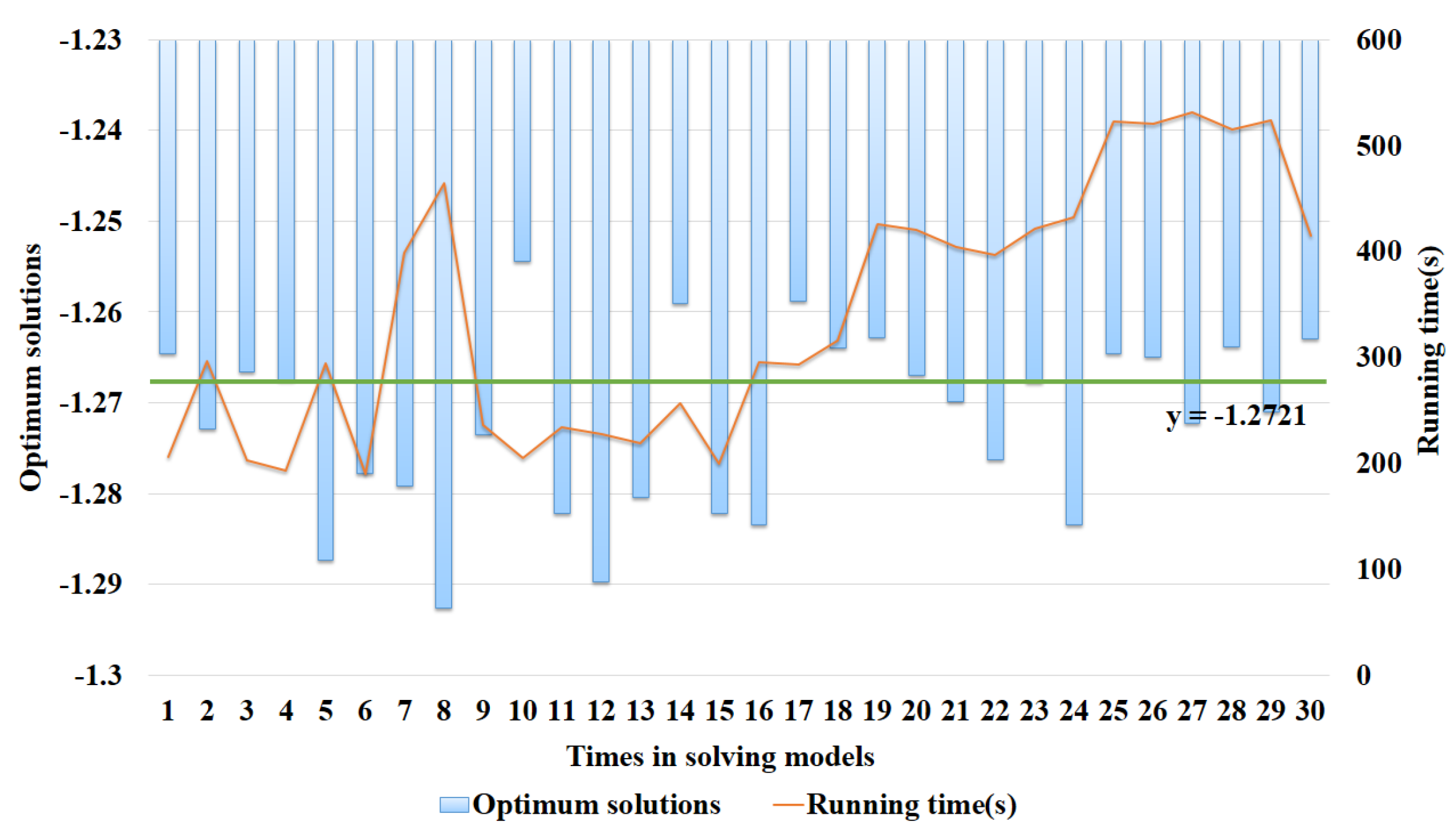
4.1.3. Computation of ISAA-CC
4.1.4. Computation of ISAA-SS
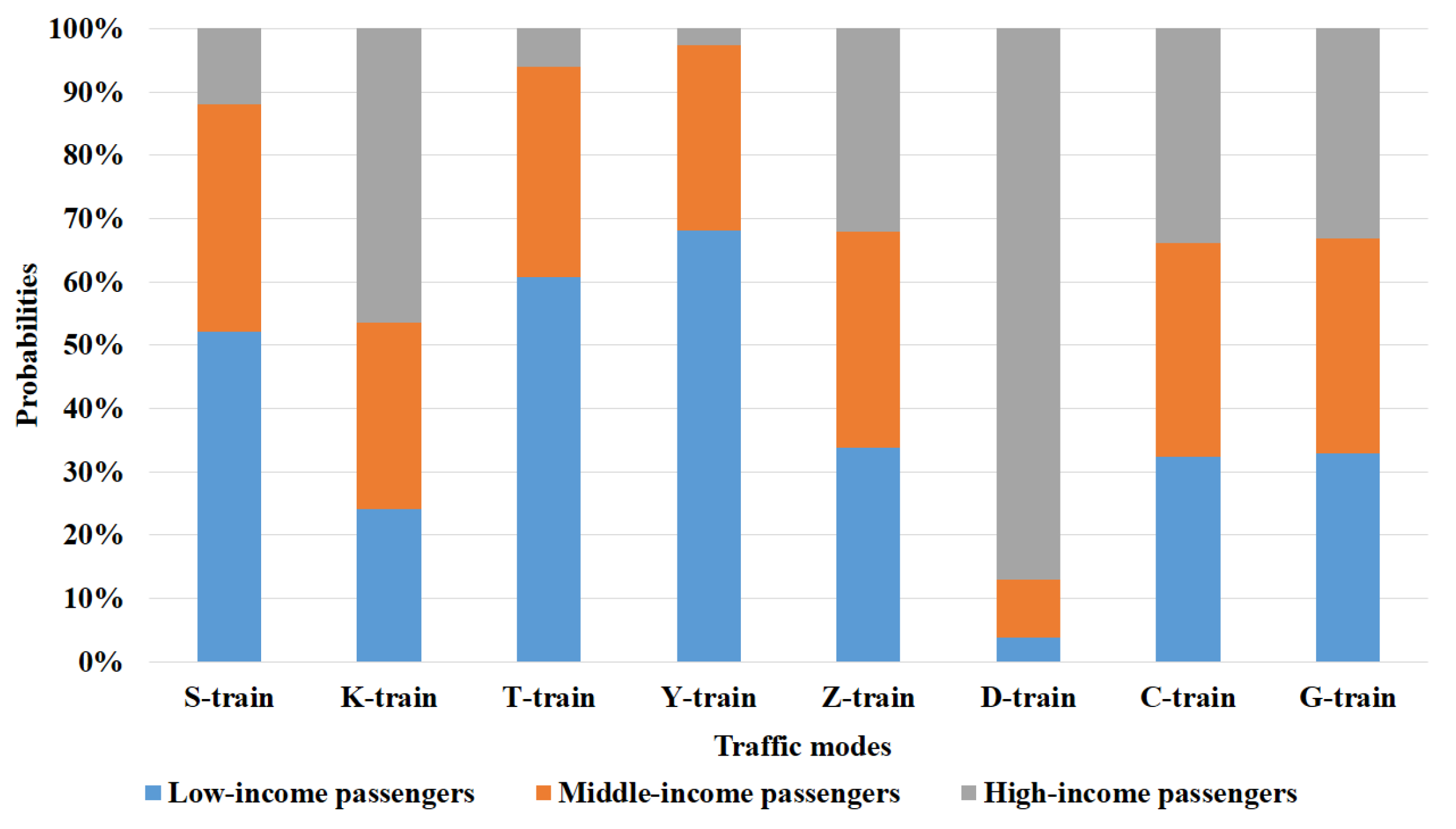
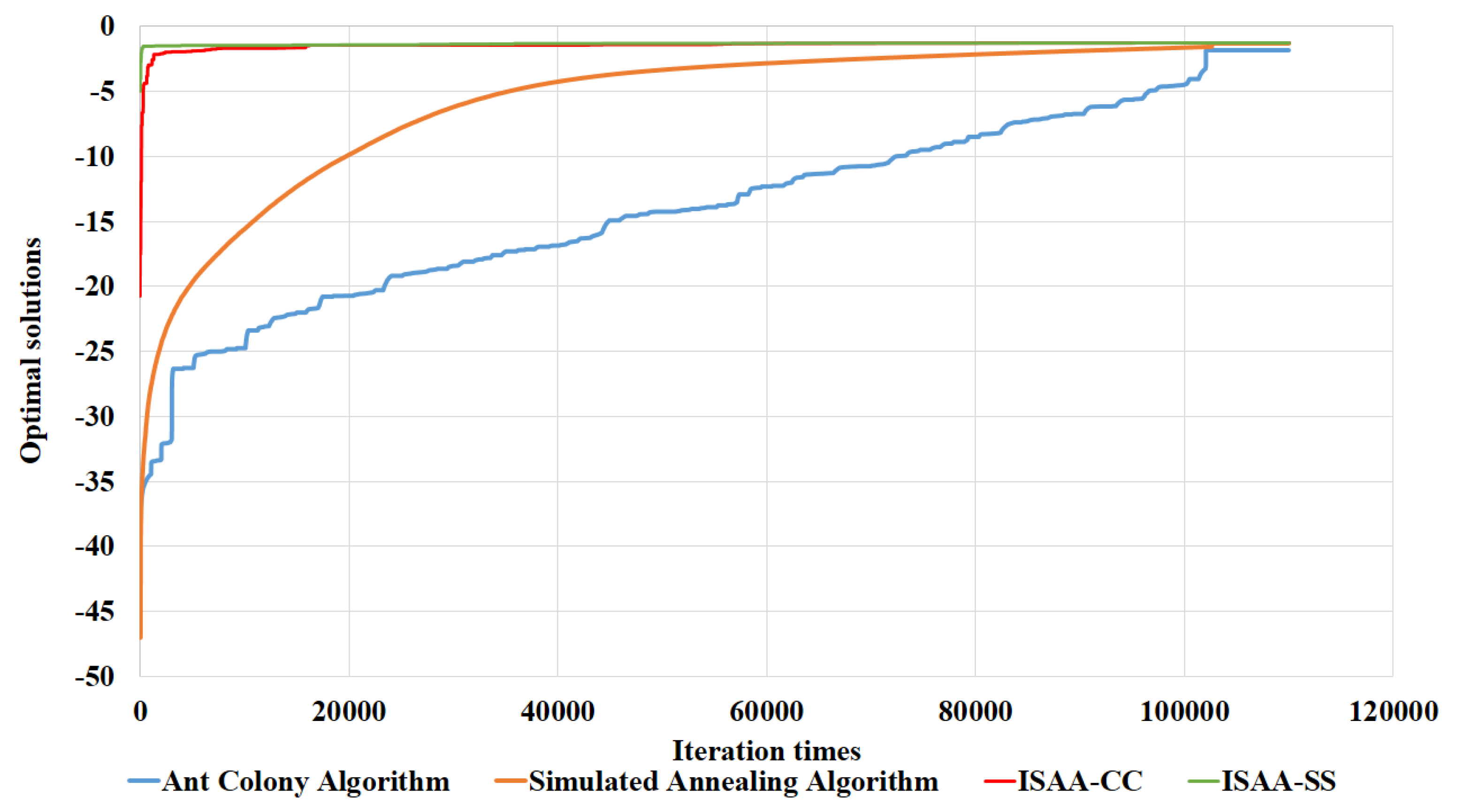
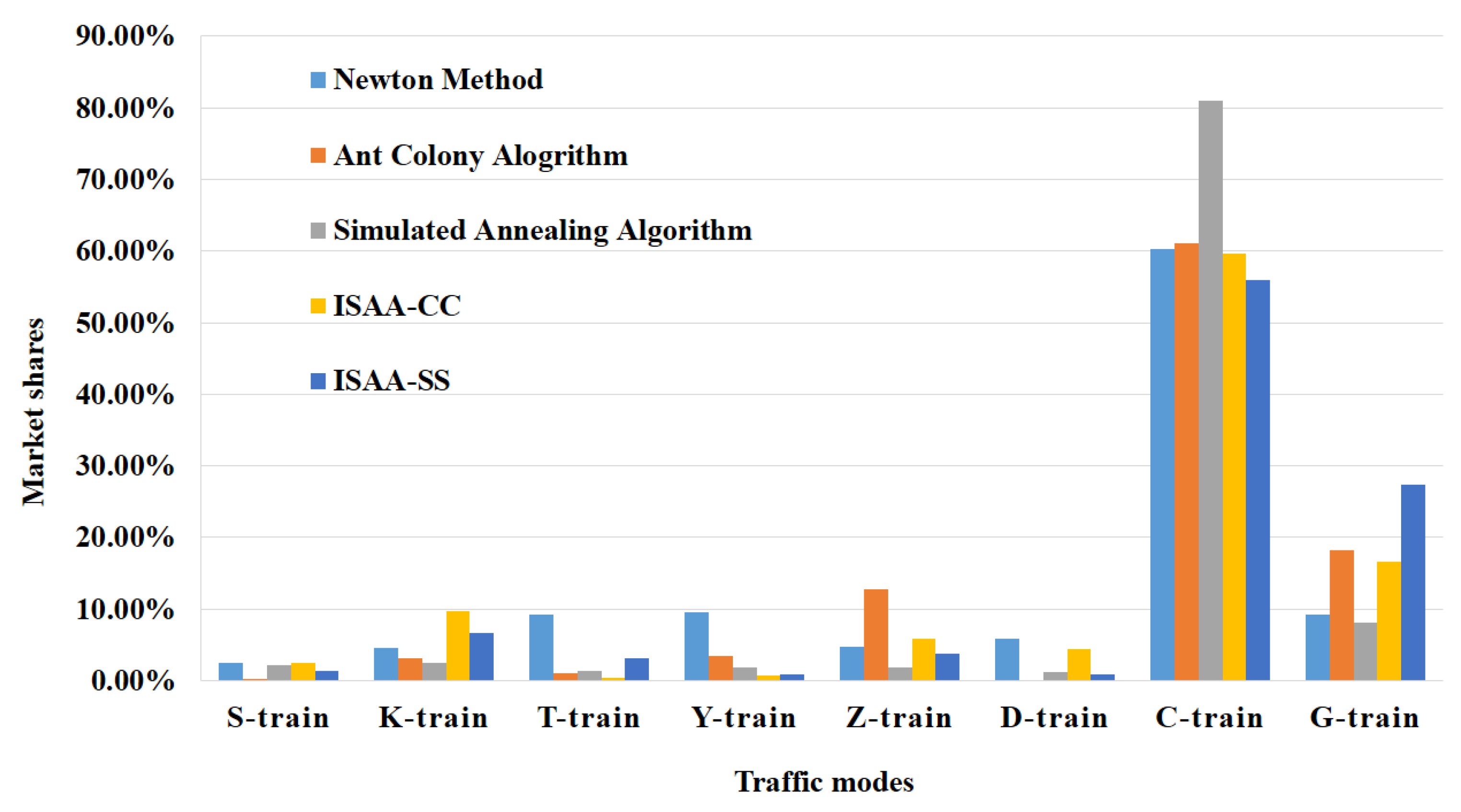
4.2. Contrast of Five Algorithms
5. Conclusions and Future Researches
Author Contributions
Funding
Conflicts of Interest
Appendix A. Newton Method
| Algorithm A1: A traditional algorithm. |
|
| (Unit: %) | Probabilities of Different Passenger Groups | Market Shares | ||
|---|---|---|---|---|
| Low-Income Passengers | Medium-Income Passengers | High-Income Passengers | ||
| S-train | 1.95566 | 0.51933 | 0.01213 | 2.48712 |
| K-train | 3.61539 | 0.94379 | 0.02108 | 4.58026 |
| T-train | 4.26496 | 2.69122 | 2.25409 | 9.21027 |
| Y-train | 2.97179 | 3.23895 | 3.33122 | 9.54196 |
| Z-train | 2.39705 | 0.89547 | 1.39025 | 4.68277 |
| D-train | 1.49488 | 2.83946 | 1.56699 | 5.90133 |
| C-train | 25.25601 | 8.35767 | 26.70956 | 60.32324 |
| G-train | 0.62972 | 1.29245 | 7.25221 | 9.17438 |
References
- Train, K.E. Properties of discrete choice models. In Discrete Choice Methods with Simulation; Cambridge University Press: Cambridge, UK, 2003; pp. 15–37. [Google Scholar]
- Train, K.E. Properties of discrete choice models. In Discrete Choice Methods with Simulation, Second Edition; Cambridge University Press: Cambridge, UK, 2009; pp. 9–33. [Google Scholar]
- Marschak, J. Binary choice constraints on random utility indications. In Economic Information, Decision, and Prediction; Stanford University Press: Stanford, CA, USA, 1960; pp. 312–329. [Google Scholar]
- Train, K.E.; McFadden, D.; Ben-Akiva, M. The demand for local telephone service: A fully discrete model of residential calling patterns and service choice. Rand J. Econ. 1987, 18, 109–123. [Google Scholar] [CrossRef]
- McFadden, D. Conditional logit analysis of qualitative choice behavior. In Frontiers in Econometrics; Academic Press: New York, NY, USA, 1973; pp. 105–142. [Google Scholar]
- McFadden, D. Modelling the choice of residential location. In Cowles Foundation Discussion Papers; Yale University Press: New Haven, CT, USA, 1977; p. 673. [Google Scholar]
- Hensher, D.A.; Rose, J.M.; Greene, W.H. Getting started modeling: The workhorse—Multinomial logit. In Applied Choice Analysis; Cambridge University Press: Cambridge, UK, 2015; p. 1188. [Google Scholar]
- McFadden, D.; Train, K.E. Mixed MNL models for discrete response. J. Appl. Econom. 2000, 15, 447–470. [Google Scholar] [CrossRef]
- Hess, S.; Polak, J.W. Development and Application of a Model for Airport Choice in Multi-Airport Regions; CTS Working Paper; Centre for Transport Studies, Imperial College London: London, UK, 2004. [Google Scholar]
- Hensher, D.; Greene, W.H. The mixed logit model: the state of practice. Transportation 2003, 30, 133–176. [Google Scholar] [CrossRef]
- Hess, S.; Polak, J.W. On the use of discrete choice models for airport competition with applications to the San Francisco Bay area Airports. Paper presented at the 10th Triennial World Conference on Transport Research, Istanbul, Turkey, 4–8 July 2004. [Google Scholar]
- Hess, S.; Polak, J.W. Mixed logit estimation of parking type choice. In Proceedings of the 83rd Annual Meeting of the Transportation Research Board, Washington, DC, USA, 11–15 January 2004. [Google Scholar]
- Ma, B.T.; Zhang, Y.X.; Zhao, C.X. Estimation of the distributing rates of high-speed passenger flows with the logit model. J. North. Jiaotong Univ. 2003, 27, 67–69. [Google Scholar]
- Hess, S.; Polak, J.W. Mixed logit modeling of airport choice in multi-airport regions. J. Air Transp. Manag. 2005, 11, 59–68. [Google Scholar] [CrossRef]
- He, Y.Q.; Mao, B.H.; Chen, T.S.; Yang, J. The mode share model of the high-speed passenger railway line and its application. J. China Railw. Soc. 2006, 28, 18–21. [Google Scholar]
- Park, Y.; Ha, H.K. Analysis of the impact of high-speed railroad service on air transport demand. Transp. Res. Part E Logist. Transp. Rev. 2006, 42, 95–105. [Google Scholar] [CrossRef]
- Feng, H.H.; Zhu, C.K. Application of rough set theory in the Inter-city passenger traffic sharing. J. Univ. Sci. Technol. Suzhou Eng. Technol. 2007, 20, 30–33, 38. [Google Scholar]
- Ge, D.S.; Liu, Z.K. Research on mixed logit model improved by value engineering method. Value Eng. 2008, 1, 78–80. [Google Scholar]
- Jou, R.C.; Hensher, D.A.; Hsu, T.L. Airport ground access mode choice behavior after the introduction of a new mode: A case study of Taoyuan International Airport in Taiwan. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 371–381. [Google Scholar] [CrossRef]
- Huang, D.M.; Qin, S.H.; Zhao, C.C. Application of logit model in passenger flow sharing forecast of Nan-Guang high-speed railway. Railw. Eng. 2012, 11, 45–48. [Google Scholar]
- Chen, J.; Yan, Q.P.; Yang, F.; Hu, J. SEM-logit integration model of travel mode choice behaviors. J. South China Univ. Technol. Nat. Sci. Ed. 2013, 41, 51–57, 65. [Google Scholar]
- Hensher, D.; Greene, W.H. Passenger airline choice behavior for domestic short haul travel in South Korea. J. Air Transp. Manag. 2014, 38, 43–47. [Google Scholar]
- Lee, J.K.; Yoo, K.E.; Son, K.H. A study on travelers’ railway traffic mode choice behavior using the mixed logit model: A case study of the Seoul-Jeju route. J. Air Transp. Manag. 2016, 56, 131–137. [Google Scholar] [CrossRef]
- Fishburn, P.C. Utility Theory. Manag. Sci. 1968, 14, 335–378. [Google Scholar] [CrossRef]
- Wardman, M. The value of travel time a review of British evidence. J. Transp. Econ. Policy 1998, 32, 285–316. [Google Scholar]
- Dorigo, M. Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 1992. [Google Scholar]
- Dorigo, M.; Member, S.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1996, 1, 53–66. [Google Scholar] [CrossRef]
- Metropolis, N. Algorithms in unnormalized arithmetic. Numer. Math. 1953, 7, 104–112. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Ant Colony System: A cooperative learning approach to the traveling salesman problem. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Chen, A.; Ryu, S.; Xu, X.D.; Choi, K. Computation and application of the paired combinatorial logit stochastic user equilibrium problem. Comput. Oper. Res. 2014, 43, 68–77. [Google Scholar] [CrossRef]
- Liu, H.; He, X.; He, B.S. Method of successive weighted averages (MSWA) and self-regulated averaging schemes for solving stochastic user equilibrium problem. Netw. Spat. Econ. 2009, 9, 485–503. [Google Scholar] [CrossRef]
- Robbins, H.; Monro, S. A stochastic approximation method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Blum, J.R. Multidimensional stochastic approximation methods. Ann. Math. Stat. 1954, 25, 737–744. [Google Scholar] [CrossRef]
| Publication | Traffic modes | Variables | Models |
|---|---|---|---|
| Ma, et al. [13] | Airport, Coach, Railway | Safety, rapidity, economy, comfort, environmental impact, services | Conditional logit model |
| Hess, et al. [14] | Airport | Access time, fare, frequency | Mixed logit model |
| He, et al. [15] | Airport, Coach, High Speed Passenger dedicated line | Fare, time value | Conditional logit model |
| Park, et al. [16] | Airport, High Speed Railway (KTX), Conventional railroad | Access time, fare, operational frequency, distance | Binomial logit model and SP/RP model |
| Feng, et al. [17] | Airport, Coach, Train | Fare, time value | Logit model based on Rough Set Theory |
| Ge, et al. [18] | Airport, Coach, Railway | Safety, rapidity, economy, choice preference, comfort, accessibility | Mixed logit model |
| Jou, et al. [19] | High Speed Railway, Hyper-speed Transportation | In-vehicle travel time, travel cost, out-of-vehicle travel time | Mixed logit model |
| Huang, et al. [20] | Airport, Coach, High Speed Railway | Fare, time value | Multinomial logit model |
| Chen, et al. [21] | Bus | Service environment, comfort, safety, convenience | SEM-Multinomial logit integration model |
| Jung, et al. [22] | Korea Train Express | Access time, journey time, air fare, operational frequency | Multinomial and nested logit model |
| Lee, et al. [23] | High Speed Railway | Travel cost, travel time, operational frequency, safety, duty free shopping availability | Mixed logit model |
| This paper | Different railway traffic modes | Passenger income, rapidity (travel time), Economy (travel expense), comfort (operational frequency, degree of seat) | Mixed logit model based on improved nonlinear utility functions |
| Passenger Groups | Rapidity | Economy | Comfort | Total Number |
|---|---|---|---|---|
| Low-income passengers | 76 | 29 | 12 | 117 |
| Medium-income passengers | 214 | 55 | 73 | 342 |
| High-income passengers | 163 | 27 | 68 | 258 |
| Total number | 453 | 111 | 153 | 717 |
| Model Parameters | |
|---|---|
| M | A set of railway traffic modes, i.e., M = {1, 2, ⋯, 8}. There are eight (M = 8) kinds of railway trains for passengers to choose in this study, including Common slow train named S-train, i.e., m = 1, Fast train named K-train, i.e., m = 2, Express train named T-train, i.e., m = 3, Tourist train named Y-train, i.e., m = 4, Direct special express train named Z-train, i.e., m = 5, EMU train named D-train, i.e., m = 6, Inter-city train named C-train, i.e., m = 7 and High-speed train named G-train, i.e., m = 8. |
| S | A set of train seats grades, i.e., S = {1, 2, ⋯, 9}. There are twenty-one kinds of train seats for passengers to choose in this study which are classified into nine grades (S = 9), including business seat of C-train \ G-train, i.e., s = 1, Soft sleeper of D-train, i.e., s = 2, Hard sleeper of D-train, i.e., s = 3, Soft sleeper of S-train \ K-train \ T-train \ Z-train, i.e., s = 4, First seat of C-train \ G-train, i.e., s = 5, First seat of S-train \ K-train \ T-train, i.e., s = 6, Second seat of C-train \ G-train \ D-train, i.e., s = 7, Soft seat of Y-train, i.e., s = 8 and Hard seat of S-train \ K-train \ T-train \ Y-train, i.e., s = 9. |
| Q | A set of passenger groups, i.e., Q = {1, 2, 3}. There are three passenger groups, including the low-income passenger group where q = 1, the medium-income passenger group where q = 2 and the high-income passenger group where q = 3. |
| The travel time of passengers choosing railway traffic mode m. | |
| The travel expense of passengers choosing railway traffic mode m. | |
| The monthly average income of passenger group q. | |
| A parameter of maximum time required to fatigue recovery which equals to 14 or 15 hours under normal conditions. | |
| Dimensionless parameter of seat degree s for passengers choosing railway traffic mode m. | |
| The intensity factor of fatigue recovery time in per unit travel time (Unit: ). The greater its value is, the longer fatigue recovery time will be; and there is 0 1. | |
| Model Variables | |
| The variable vector to be estimated of choosing railway traffic modes m, i.e., , , where denotes the weight of rapidity, denotes the weight of economy, denotes the weight of comfort, denotes the weight of passenger income, denotes a position parameter and denotes a scale parameter. There are = 1, 0 1, 0 1, 0 1, 0 1. | |
| Algorithm | Advantages | Disadvantages |
|---|---|---|
| Newton method | The simple principle Second order convergence | (a) It is quite computationally expensive because it requires calculating both the objective function and derivatives. (b) It is highly correlated with initial parameters because the improper selections of them will lead to local convergence or non-convergence of function. (c) Gradient explosion or gradient disappearance also occurs easily. |
| Ant colony algorithm | parallel computation Robustness Positive feedback mechanism Low time complexity | The setting of parameters has a great influence on the results. In the initial stage, the pheromones are basically the same, which requires a long search time and is easily trapped in local optimum. |
| Simulated annealing algorithm | parallel computation Low time complexity Independent of the initial solution | It is easy to be affected by the setting of parameters, especially the cooling coefficient. |
| Line Search Methods | Type | Objective Function Evaluation | Derivative Evaluation |
|---|---|---|---|
| MSA | exact | No | No |
| SRA | inexact | No | No |
| Bisection | exact | No | Yes |
| Quadratic interpolation | inexact | No | Yes |
| Armijo | inexact | Yes | Yes |
| Type | Traffic Modes | Frequency | Running Time | Ticket Price | ||
|---|---|---|---|---|---|---|
| S-train | Common slow train | 3 | 2 h 10 min | Soft sleeper | Hard sleeper | Hard seat |
| RMB 99.5 | RMB 64.5 | RMB 18.5 | ||||
| K-train | Fast train | 13 | 2 h | Soft sleeper | Hard sleeper | Hard seat |
| RMB 102.5 | RMB 67.5 | RMB 21.5 | ||||
| T-train | Express train | 5 | 1 h 40 min | Soft sleeper | Hard sleeper | Hard seat |
| RMB 99.5 | RMB 65.5 | RMB 19.5 | ||||
| Y-train | Tourist train | 1 | 1 h 30 min | Soft seat | Hard seat | - |
| RMB 33.5 | RMB 21.5 | - | ||||
| Z-train | Direct special | 6 | 1 h 20 min | Soft sleeper | - | - |
| express train | RMB 102.5 | - | - | |||
| D-train | EMU train | 3 | 1 h 10 min | Second seat | Soft sleeper | Hard sleeper |
| RMB 24 | RMB 141 | RMB 102 | ||||
| C-train | Inter-city train | 100 | 30 min | Business seat | First seat | Second seat |
| RMB 174 | RMB 88 | RMB 54.5 | ||||
| G-train | High-speed train | 53 | 30 min | Business seat | First seat | Second seat |
| RMB 174.5 | RMB 94.5 | RMB 54.5 | ||||
| Seat Grades | Grades | |||
|---|---|---|---|---|
| Business seat of C-train and G-train | First | 99 | 0.15 | 0.1 |
| Soft sleeper of D-train | Second | 89 | 0.17 | 0.2 |
| Hard sleeper of D-train | Third | 79 | 0.19 | 0.3 |
| Soft sleeper of Z-train, T-train, K-train and S-train | Fourth | 69 | 0.21 | 0.4 |
| First seat of C-train and G-train | Fifth | 59 | 0.25 | 0.5 |
| Hard sleeper of T-train, K-train and S-train | Sixth | 49 | 0.3 | 0.6 |
| Second seat of C-train, G-train and D-train | Seventh | 39 | 0.38 | 0.7 |
| Soft seat of Y-train | Eight | 29 | 0.5 | 0.8 |
| Hard seat of Y-train, T-train, K-train and S-train | Ninth | 19 | 0.75 | 0.9 |
| (Unit: %) | Probabilities of Different Passenger Groups | Market Shares | ||
|---|---|---|---|---|
| Low-Income Passengers | Medium-Income Passengers | High-Income Passengers | ||
| S-train | 0.19493 | 0.04319 | 0.00031 | 0.23843 |
| K-train | 1.79652 | 1.15837 | 0.14346 | 3.09835 |
| T-train | 0.09347 | 0.20911 | 0.72672 | 1.02929 |
| Y-train | 0.50415 | 0.94739 | 2.06373 | 3.51527 |
| Z-train | 9.21536 | 3.45605 | 0.10014 | 12.77155 |
| D-train | 0.00084 | 0.00194 | 0.00761 | 0.01039 |
| C-train | 20.31588 | 24.48429 | 16.23912 | 61.03929 |
| G-train | 1.21302 | 3.02454 | 14.05987 | 18.29743 |
| (Unit: %) | Probabilities of Different Passenger Groups | Market Shares | ||
|---|---|---|---|---|
| Low-Income Passengers | Medium-Income Passengers | High-Income Passengers | ||
| S-train | 1.12259 | 0.77471 | 0.25678 | 2.15408 |
| K-train | 0.61782 | 0.76154 | 1.19499 | 2.57435 |
| T-train | 0.81984 | 0.44944 | 0.08037 | 1.34965 |
| Y-train | 1.23649 | 0.52862 | 0.04854 | 1.81365 |
| Z-train | 0.61727 | 0.62685 | 0.58522 | 1.82934 |
| D-train | 0.04823 | 0.11632 | 1.10444 | 1.26899 |
| C-train | 26.21268 | 27.33246 | 27.38921 | 80.93435 |
| G-train | 2.65841 | 2.74341 | 2.67377 | 8.07559 |
| (Unit: %) | Probabilities of Different Passenger Groups | Market Shares | ||
|---|---|---|---|---|
| Low-Income Passengers | Medium-Income Passengers | High-Income Passengers | ||
| S-train | 0.65306 | 0.53241 | 0.30614 | 1.49161 |
| K-train | 2.22391 | 2.15581 | 1.97175 | 6.35147 |
| T-train | 0.89405 | 0.97312 | 1.21411 | 3.08128 |
| Y-train | 0.29216 | 0.26248 | 0.19584 | 0.75048 |
| Z-train | 0.80645 | 0.75232 | 0.62084 | 2.17961 |
| D-train | 0.61448 | 0.61119 | 0.59892 | 1.82459 |
| C-train | 17.78366 | 18.03989 | 18.63512 | 54.45867 |
| G-train | 10.06556 | 10.00609 | 9.79064 | 29.86229 |
| (Unit: %) | Probabilities of Different Passenger Groups | Market Shares | ||
|---|---|---|---|---|
| Low-Income Passengers | Medium-Income Passengers | High-Income Passengers | ||
| S-train | 0.47426 | 0.45893 | 0.41196 | 1.34515 |
| K-train | 2.28111 | 2.23759 | 2.08312 | 6.60182 |
| T-train | 0.79375 | 0.93598 | 1.42719 | 3.15692 |
| Y-train | 0.09546 | 0.15845 | 0.60417 | 0.85808 |
| Z-train | 1.13772 | 1.22099 | 1.44641 | 3.80512 |
| D-train | 0.43591 | 0.32485 | 0.14478 | 0.90554 |
| C-train | 18.39575 | 18.64658 | 18.95445 | 55.99678 |
| G-train | 9.71939 | 9.34995 | 8.26125 | 27.33059 |
| NM | ACA | SAA | ISAA-CC | ISAA-SS | |
|---|---|---|---|---|---|
| Optimum solutions | −2.39049 | −1.82703 | −1.29297 | −1.25441 | −1.25924 |
| Running time | 60,904 s | 1927 s | 518 s | 205 s | 858 s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, B.; Ren, S.; Bao, J. Mixed Logit Model Based on Improved Nonlinear Utility Functions: A Market Shares Solution Method of Different Railway Traffic Modes. Sustainability 2020, 12, 1406. https://doi.org/10.3390/su12041406
Han B, Ren S, Bao J. Mixed Logit Model Based on Improved Nonlinear Utility Functions: A Market Shares Solution Method of Different Railway Traffic Modes. Sustainability. 2020; 12(4):1406. https://doi.org/10.3390/su12041406
Chicago/Turabian StyleHan, Bing, Shuang Ren, and Jingjing Bao. 2020. "Mixed Logit Model Based on Improved Nonlinear Utility Functions: A Market Shares Solution Method of Different Railway Traffic Modes" Sustainability 12, no. 4: 1406. https://doi.org/10.3390/su12041406
APA StyleHan, B., Ren, S., & Bao, J. (2020). Mixed Logit Model Based on Improved Nonlinear Utility Functions: A Market Shares Solution Method of Different Railway Traffic Modes. Sustainability, 12(4), 1406. https://doi.org/10.3390/su12041406




