Abstract
Climate change caused by greenhouse gas emissions is of critical concern to international shipping. A large portfolio of mitigation measures has been developed to mitigate ship gas emissions by reducing ship energy consumption but is constrained by practical considerations, especially cost. There are difficulties in ranking the priority of mitigation measures, due to the uncertainty of ship information and data gathered from onboard instruments and other sources. In response, a neural network model is proposed to evaluate the cost-effectiveness of mitigation measures based on decarbonization. The neural network is further enhanced with a Bayesian method to consider the uncertainties of model parameters. Three of the key advantages of the proposed approach are (i) its ability to simultaneously consider a wide range of sources of information and data that can help improve the robustness of the modeling results; (ii) the ability to take into account the input uncertainties in ranking and selection; (iii) the ability to include marginal costs in evaluating the cost-effectiveness of mitigation measures to facilitate decision making. In brief, a negative “marginal cost-effectiveness” would indicate a priority consideration for a given mitigation measure. In the case study, it was found that weather routing and draft optimization could have negative marginal cost-effectiveness, signaling the importance of prioritizing these measures.
1. Introduction
With the global economy’s continuous growth, global seaborne trade is forecasted to grow by 3.8% between 2018 and 2023 by the United Nations Conference on Trade and Development [1]. Shipping is becoming a significant contributor to global carbon emissions that affect climate change. The Marine Environment Protection Committee (MEPC 72), meeting at the International Maritime Organization (IMO), has published a preliminary strategy to reduce carbon emissions by half by 2050 [2,3]. To help achieve this goal, the IMO has proposed some indicators, such as the Energy Efficiency Design Index (EEDI), to improve ship energy efficiency [4]. For instance, newly built ships need to comply with the hull design index, including the EEDI. IMO has also proposed some emission reduction measures to reduce ship gas emissions, such as the vessel speed reduction imposed on ships [5]. Some mitigation measures have been implemented for most existing ships to save energy and reduce emissions [4].
To reduce ship gas emissions, the IMO has proposed more than 50 mitigation measures, which can be grouped into technical measures and operational measures [6]. The technical measures are related to the marine vessel and equipment for reducing ship fuel consumption. The operational measures include route optimization, speed reduction, and others that do not require engineering improvements to the ship. In order to evaluate the performance of these mitigation measures, it is necessary to evaluate the impact of the corresponding factors for these mitigation measures on ship energy consumption. For this reason, most studies are focused on predicting and estimating the impact of these factors on energy consumption either from a top-down approach or a bottom-up approach. The top-down approach generally relies on the statistics of fuel consumption data, such as those published in [7], to estimate carbon emissions. The bottom-up approach employs detailed contributing factors, such as ship speed, ship size, and other metered data from different data sources, such as the Automatic Identification System (AIS) and the Noon Report, to estimate carbon emissions [8].
The bottom-up approach is usually preferred due to its accuracy and the availability of various data sources. Several models have been developed in the bottom-up approach, such as dynamic regression [9], the LASSO (Least Absolute Shrinkage and Selection Operator) [10], the linear regression model [11], the artificial neural network (ANN) [12], and the Gaussian process (GP) [13]. Studies in [12,14] show that the ANN has better prediction performance when dealing with nonlinear relationships compared with the dynamic regression, linear regression, and LASSO models. The GP and ANN models have comparable performance in prediction and have been applied to evaluate ships’ mitigation measures [15].
GP models are generally flexible and can account for various uncertainties associated with input data and variables used in the model [16]. However, the GP’s performance deteriorates when the input data dimension or the data size is increased [15,16]. In comparison, ANN models are more suitable for handling high dimensional problems and a large amount of data [15,16]. Due to the high volume of shipping data from various sources, an ANN model is proposed in this paper to evaluate mitigation measures.
ANNs have been widely used to predict energy consumption, such as natural gas consumption [17], thermal energy consumption [18], and ship energy consumption [12]. Particularly in shipping, several ANN models have been developed, such as the recurrent neural network [19], and backpropagation neural network (BPNN) [20,21]. Among the various models, BPNN has demonstrated a better performance in predicting ship energy consumptions. With more detailed environmental data becoming available from many sources [9], more factors (such as weather and marine factors) can be selected to evaluate mitigation measures based on the BPNN.
Despite the fact that the information and data are recorded, very often in a non-duplicative manner, in different databases or sources, most of the studies in the literature tend to focus on the use of a single data source, mainly due to concern over data consistency. The data used for model development might inevitably contain noise or errors. For instance, Aldous (2013) highlighted that the Noon Report is a low-resolution database with data recorded by the crew at 24-h intervals and a high risk of incorrect 24-h average values being recorded [22]. Such errors and noise in data may cause uncertainty when developing the model. Some erroneous and missing data in the Noon Report can be processed by data mining methods, such as k-means and outlier score base [23]. It is also possible to combine AIS and Noon Report data (i.e., multiple data sources) for improving the quality of shipping data [24]. Nevertheless, the uncertainties associated with error data and noise data cannot be eliminated and should be considered in the modeling. Some uncertainty quantification techniques can be used to consider the impact of uncertainty [25]. One of the most commonly used techniques for quantifying uncertainty in data-driven regression models is through the Bayesian framework. Wright proposed to consider the input uncertainty in BPNN using a Bayesian method [26]. However, their work only provided the general framework to account for the input uncertainty when using the BPNN. The evaluation of ship mitigation measures usually has different data sources and heterogeneous uncertainties. The use of BPNN to evaluate ship mitigation measures, taking into account the uncertainties of different data sources and parameters, still needs a comprehensive study.
In this paper, a Bayesian neural network approach is proposed to predict ship energy savings and mitigation potentials of operational measures through a combined BPNN and Bayesian method. Furthermore, the predicted results are incorporated into the mitigation measures’ ranking and selection, based on the marginal cost-effectiveness. The advantages of the proposed approach over existing methods are threefold. First, multiple available data sources are combined to develop the proposed neural network model to improve the robustness of the model when handling different data sources. Next, the proposed approach is able to consider the heterogeneous uncertainties in the model variables and input data based on the Bayesian framework. The evaluation results are more reliable by accounting for these input uncertainties. Last, the proposed approach is able to evaluate the “marginal cost-effectiveness” of mitigation measures based on cost and emissions, which can provide an important reference for decision making.
2. Ship Energy System
Using a typical chemical tanker as an example, a ship can be represented as a complex energy system, as shown in Figure 1. In this energy system, the ultimate source of energy is from the chemical energy released through the combustion of fuel. The main engine, auxiliary engine, and boiler are three fuel-related devices that interact with the other shipboard equipment to provide various energies for the entire ship. The daily driving of the ship mainly depends on the power provided by the main engine. It transmits the power to the propeller through a gearbox. The power generated by the auxiliary engine drives the generator set; the electricity generated by the generator set is used throughout the ship. The boiler is mainly responsible for providing thermal energy [27].
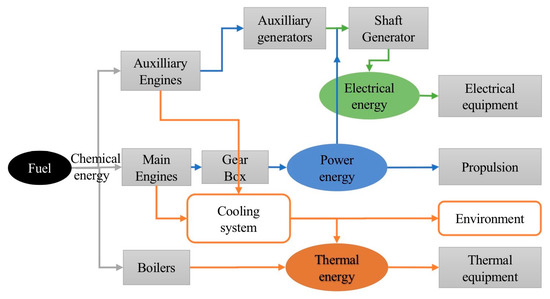
Figure 1.
Chemical tanker energy system and relevant equipment.
The complexity of the energy system lies in the many devices involved in maintaining the energy required by the ship. The equipment may be affected by certain factors during operation to affect fuel consumption. Mitigation measures are usually proposed for some marine equipment based on these influencing factors to reduce energy consumption. Sometimes there are also interactions between ship equipment, which may affect the potential of mitigation measures [28]. From a system perspective, selecting more influencing factors can help evaluate the impact of mitigation measures on fuel consumption more comprehensively.
According to the analysis of IMO and the availability of the factors, four operational mitigation measures are considered in this article, including speed reduction (10%), draft optimization, trim optimization, and weather routing. Among these measures, the main engine’s fuel consumption is directly related to vessel speed, which is considered an influencing factor. The draft is defined as the ship’s depth entering the water, which affects the ship’s resistance and thus, the energy consumption. The difference between the ship’s aft and forward drafts leads to the existence of trim. The trim has different effects on the maneuverability and the vessel speed under different ship states. Therefore, the drafts and trim are considered as two influencing factors. In addition to the above factors, the conditions of wind speed, wind direction, wave height, and wave direction are considered as four influencing factors on the energy consumption of weather routing. This paper aims to develop a model to study the impact of the seven influencing factors on ship fuel consumption under uncertainty, so as to estimate the potential of corresponding mitigation measures.
3. Materials and Methods
3.1. Data Sources
A chemical tanker was used as the reference ship for this study. The tanker had two main engines and two auxiliary engines. The length and width of the tanker were 181 and 31.3 m, respectively. The maximum capacity was 51,000 m3. The maximum draft was 12.4 m. The data of seven factors and fuel consumption used for estimating mitigation measures were recorded in multiple data sources. The AIS, the Noon Report, the weather report, and onboard measurement data of this tanker were collected from January 2017 to March 2018. The way of recording data for different data sources is different. Some data sources may have a certain degree of uncertainty. For instance, the Noon Report contains the data record of ship working conditions during ship navigation by crews, manually. Human error is inevitable in the Noon Report [22]. The AIS records a real-time record of static and dynamic data during the ship navigation through a global positioning system. The accuracy of AIS data is slightly higher than Noon Report data [29]. However, they both have data uncertainty, as do the weather reports and onboard measurements.
This paper combines shipping data of the same ship and the same period from multiple data sources and extracts the parameters required by neural networks to evaluate mitigation measures. On the one hand, the quality of the data can be improved. On the other hand, the neural network model trained by multiple data sources is more effective. However, the uncertainty remains in the merged data and parameters not required by the model to be filtered out. For the combined data, each data source recorded the data at different intervals. The average of daily data from multiple data sources was used as the model parameters.
3.2. Model Frameworks
3.2.1. BPNN Modeling Without Uncertainty Analysis
BPNN is a multi-layer feedforward neural network trained according to the error backpropagation algorithm, which includes forward and backpropagation, and a simple topology can adapt to almost any nonlinear relationship [30,31]. It has good parallelism and can map the relationship between multiple inputs and outputs at the same time. Neural networks are also suitable for processing large amounts of data. For the evaluation of mitigation measures, there is usually a large amount of data from different data sources. The goal was to develop a BPNN to represent the relationship between mitigation measures and ship energy consumption. Therefore, the corresponding factors of four mitigation measures were taken as inputs to the model, and the ship fuel consumption was the output of interest. Let denote the dimensional corresponding factors of the considered mitigation measures, such as the vessel speed of the mitigation measure speed reduction, and denote the output of interest.
BPNN consists of an input layer, some hidden layers, and an output layer. Every layer has some neurons. Here, the input layer has neurons that represent dimensional input factors, and the output layer has one neuron that represents the output of interest. The number of neurons in hidden layers has to be determined. There are weights between neurons in adjacent layers, and each layer has a bias to improve the network’s fitting capabilities. During the forward propagation of neural networks, each hidden layer has inputs and outputs. The weighted sum of the previous layer’s outputs is taken as the input of the next layer. For the input layer, the weighted sum of the input factors is taken as the first hidden layer’s inputs. Let denote the output of the th neuron in the th layer, and denote the input of theth neuron in the th layer. Then, the relationship between the output of the th layer and the input of theth layer can be represented as follows:
Here, and , where denotes the number of neurons in the th layer; denotes the bias of the th neuron of the th layer, which can improve the fit of the data [32]; is the weight connecting the th neuron in the th layer and theth neuron in the th layer [33]. The weights represent the importance of different factors. The weighted sum of is taken as the input of the next layer. When , , which denotes the -th input factor of the input layer.
Each neuron in the hidden layers contains an activation function to ensure that the BPNN can approximate nonlinear relationships. The input to the th neuron in the th layer is activated by the activation function , which is the output of the th neuron in the th layer . There are currently three most commonly used activation functions in neural networks: sigmoid, rectified linear unit (ReLU), and tansig [21], where the ReLU is suitable for processing big data and deep neural networks, and the tansig and sigmoid functions may lead to the existence of gradient disappearance. However, the study in [21] found that when using the BPNN to predict the relationship between seven influencing factors and energy consumption, a simple three-layer neural network model is enough to ensure prediction performance. Moreover, the activation functions using sigmoid and tansig have a higher prediction performance than that of using the ReLU. Since tansig has a faster convergence speed than sigmoid, it was selected as the activation function in this study to save computing time. The formula of tansig is expressed as Equation (2).
It should be noted that the output of th layer can be taken as the input of the next layer. However, there is no activation function in the output layer of the neural network for the regression problem. When is the output layer, . It denotes the predicted output value. The propagation of the BPNN is to predict the output value of the output layer, that is, the predicted ship energy consumption. Here, a three-layer neural network topology in Figure 2 was simply drawn from MATLAB software to show the process of neural network forward propagation. The number of hidden layer neurons needs to be further determined by input layer neurons and output layer neurons , usually as shown in Equation (3). The constant is 1 minus 10.
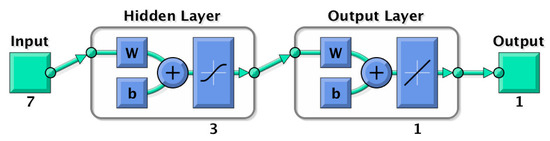
Figure 2.
Forward propagation of a three-layer neural network.
With the predicted value , obtained from the output layer, a loss function is defined to calculate the error value between the predicted output and the observed output . Suppose the error value is not within the expected range; in that case, the BPNN performs the backpropagation algorithm by the gradient descent method to readjust weights and biases until the minimum error value is obtained [34]. There are various loss functions, such as the mean square error (MSE) and the root mean square error, that have been used to represent the error indicators of the BPNN prediction model [20]. Here, the most widely used loss function, MSE, was used, which can be represented as Equation (4):
where denotes the number of observations. The backpropagation algorithm corrects the weights from the output layer to the input layer until it finds a weight vector that minimizes the loss function . Sometimes it is necessary to adjust multiple times to obtain the minimum error or fail to find the minimum error. When creating a neural network in a program, the iteration parameter is added as a stopping criterion after the backpropagation algorithm. It is used to indicate the number of weight adjustments from the output layer to the input layer. The goal error is another stopping criterion. Generally, the goal error value and the maximum number of iterations is set in the program. If the value of is found within the goal error range, or the maximum number of iterations is reached, the program will stop, and running information, such as iterations, error, and gradient, can be shown. In a neural network model, gradient and error can indicate the model’s prediction performance, and iterations can display the model’s computing performance.
3.2.2. Bayesian Neural Network Modeling with Uncertainty Analysis
The Bayesian neural network (BNN) is a Bayesian method for neural network modeling. Compared with the BPNN, the BNN takes into account the uncertainty in the model. Wright [35] proposed a Bayesian approach that considered the uncertainty of the model and input data by analyzing the posterior of the prediction. For the evaluation of mitigation measures, there was uncertainty in both inputs and outputs. For instance, the vessel speed was taken as an input factor to the model. The average speed is usually taken as the input value for a specific voyage corresponding to the observed fuel consumption. However, the speed during this voyage changed frequently, and there may be uncertainty for the average speed. Besides, the observed fuel consumption can also be uncertain due to the observation error. The uncertainty of both inputs and outputs may influence the prediction accuracy. Therefore, it was essential to consider these uncertainties in the evaluation of mitigation measures. Furthermore, the estimated parameters in the BPNN have uncertainties, such as weights and biases. These uncertainties may also have an impact on prediction performance. Therefore, the uncertainty of parameters also had to be considered. Here, the BNN model was proposed to take into account the uncertainty in the developed model.
Let and denote the observed input values (e.g., vessel speed) and the observed output values (e.g., fuel consumption). The total observed data set is . Due to the uncertainty of inputs and outputs, the observed data can be further expressed as Equation (5).
where represents the actual fuel consumption for specific input sets, and represents the observation error for the outputs; represents the expected input values, and represents the noise of the inputs. The distributions of and can be assessed from the observed data. In most cases, it is reasonable to assume that and follow normal distributions with zero means [22]. Specifically, and .
The developed BPNN was used to predict fuel consumption, given the input sets (Section 3.2.1). Let denote the predicted output at input with weight . Then, the expected prediction concerning can be obtained by Equation (6).
The expectation of the output is characterized by the prediction distribution of BPNN . It is also required for noisy inputs to obtain the distribution of the noise process and the prior over the noisy input . With this, the expected prediction at any new noisy input can be expressed as Equation (7).
is the prediction distribution of the output, given new noisy input . Let denote the expected input. Then, the posterior of the output can be rewritten as Equation (8).
The prediction distribution of the output, given new expected input . Using the Bayes’ rule, the posterior of the weight . Therefore, the posterior distribution can be denoted as Equation (9).
It can be seen that three items are integrated out in Equation (9), including , , and . The integration over is to consider the uncertainty in the weights. The integration over is to consider the training of the network using uncertain input data. The integration over indicates that the model allows new input data to be noisy [26].
In case the input data are noiseless, the expected output can be obtained directly by calculating the expectation of output.
Therefore, the expected output can be obtained, no matter if the input data are noisy or noiseless. However, it is difficult to integrate with all these parameters to get the close form. The numerical integration method is often used to solve complicated computational problems [36]. In this paper, the Markov Chain Monte Carlo method was used for numerical integration [37].
3.3. Mitigation Potential Evaluation Using BPNN and BNN
The models in this article were realized by MATLAB software using in-house made codes. Before developing neural networks to assess the impact of input factors on ship fuel consumption, the performance of the BPNN and BNN had to be compared to obtain a better model architecture for the evaluation of mitigation measures. Generally, the models have some parameters that need to be set first. These models’ parameters were trained through the training set, which was the obtained data from 2017. The models were further validated using the validation set, which was the remaining data from 2018. The validated models were used for prediction. The parameters were set as follows:
The activation function and loss function are mentioned in Section 3.2.1, which were the tansig and the MSE, respectively. The weights and biases were optimized by the conjugate gradient method. The study in [38] indicated that initializing the weights and the biases to some small values can help neural networks to learn nonlinear relationships. It was randomly initialized to a Gaussian distribution with a mean and variance of 0 and 0.1, respectively. The maximum number of iterations for the network was set to 1000. The goal error value was set to 0.01. Then the BPNN and BNN models were developed, including an input layer, a hidden layer, and an output layer. The input layer had seven neurons corresponding to seven input factors. The output layer had one neuron, which represented the output of interest. The number of neurons for the hidden layer had to be determined. According to Equation (3), the hidden layer, with the number of neurons from 1 to 12, was evaluated. Based on Equation (5), the input factors and the output in the data sets were assumed to be the normal distribution, where the mean and the variance were estimated from the observed data. To improve the computing performance of models, the input parameters were scaled in the MATLAB software by the mean and standard deviation method. The corresponding output values were unscaled.
The performance of the BPNN and BNN with different numbers of neurons could be compared by MSE values to find the best model structure. Also, the performance of the BPNN and BNN with the best structure was further compared with the GP model, which made it easy to account for various uncertainties [16]. The GP model proposed by [39] was applied here. The 95% confidence interval of prediction for three models was also computed, and the probability that the observed fuel consumption was within the 95% confidence interval of predicted fuel consumption could be obtained. Finally, an optimal model accounting for the uncertainties was developed to evaluate the impact of selected factors on fuel consumption. It predicted the energy savings and emission reductions of different measures to estimate the mitigation potential of each measure.
3.4. Cost-Effectiveness Evaluation
The marginal cost-effectiveness (MCE) criterion proposed in [40] was applied to analyze the cost-effectiveness of the mitigation measures. Although the mitigation measures were considered to save energy and reduce emissions, it was necessary to evaluate the corresponding scenarios’ costs to ensure that the mitigation measures can achieve positive benefits. The core idea of the MCE is to compare the increased implementation costs and emission reductions of different measures to rank the mitigation measures. The implementation costs were considered to be the ship’s investment costs, the operational costs, the opportunity costs, and the fuel consumption costs. An in-house made code was applied to complete the cost-effectiveness evaluation with MATLAB software, where the code’s calculation cost and design cost were ignored.
4. Results and Discussion
The performance of different neurons in the hidden layer was first evaluated by MATLAB. The MSE values to the convergence of the BPNN and BNN models with different network structures were obtained, as shown in Table 1 and Table 2. Three numbers in the network structure represent the number of neurons from the input layer to the output layer. The results show that for both the BPNN and BNN, the network structure with three neurons in the hidden layer had the minimum MSE value. The corresponding running information includes the following: iterations and gradient show that the structure also has good computing performance and does not trap in local optima. Therefore, the network with the structure of 7–3–1 was used for further analysis.

Table 1.
Mean square error (MSE) values for the backpropagation neural network (BPNN) model.

Table 2.
MSE values for the Bayesian neural network (BNN) model.
Given the network with the best structure, the performance of the BPNN, without taking into uncertainty, and the BNN, considering uncertainty, were compared with the GP model proposed in [39]. Figure 3, Figure 4 and Figure 5 show the fit of predicted and observed fuel consumption for three models, using training data and validation data. It can be seen that the predicted values were close to the observed values in most cases for all three models.
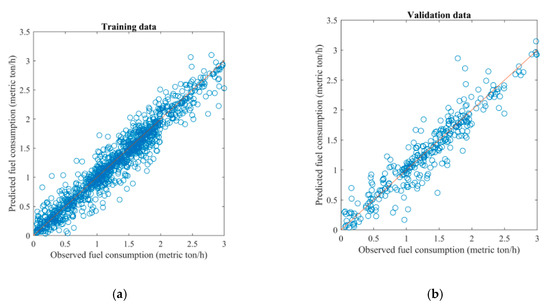
Figure 3.
The fit of observed and predicted fuel consumption using backpropagation neural network BPNN for training data (a) and validation data (b).
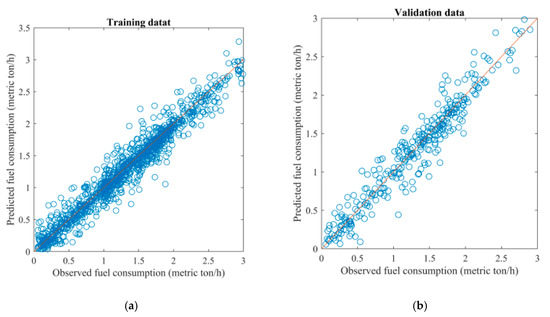
Figure 4.
The fit of observed and predicted fuel consumption using Bayesian neural network (BNN) for training data (a) and validation data (b).
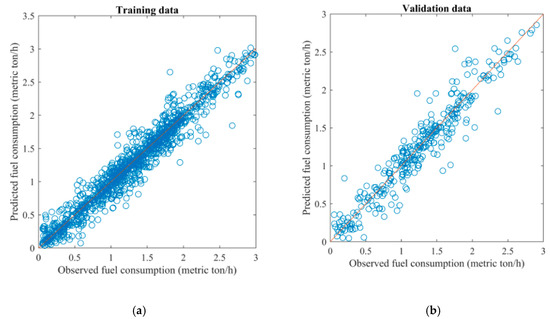
Figure 5.
The fit of observed and predicted fuel consumption using Gaussian process (GP) for training data (a) and validation data (b).
The average MSE values over 100 replications for three models, using both training and validation data, were further computed. The results are given in Table 3. It can be seen that the BNN has the smallest MSE, followed by the GP. The BPNN has the largest MSE. The two-sample t-test showed no significant difference between the BNN and the GP, while the MSEs of both the BNN and GP are significantly smaller than BPNN. As the smaller MSE means better prediction performance, the BNN and the GP, which take into account uncertainty, have significantly better prediction performance than the BPNN, which does not take into account uncertainty. The BNN has the best prediction performance with the smallest MSE. However, the difference between the BNN and the GP is not significant, which indicates that both models have similar prediction performance.

Table 3.
Average MSE values, using BPNN, BNN and Gaussian process (GP) models for training data and validation data.
The probabilities that the observed fuel consumption was within a 95% confidence interval of the predicted fuel consumption using the BPNN, BNN, and GP were then computed: 0.714, 0.925, and 0.953, respectively. The results indicate that the GP has the most considerable probability of covering the observed fuel consumption, and the BNN has a larger probability than the BPNN. This is because the prediction using the GP not only accounts for data uncertainty and parameter uncertainty; it also accounts for spatial uncertainty. The prediction variance of the GP is usually larger than the BNN. It is expected that the BPNN has the smallest probability to cover the observed fuel consumption, as the uncertainties were not taken into account. The developed BNN was further used to assess the mitigation measures.
The annual energy saving of four measures was then evaluated using the BNN, of which the predicted average values are given in Table 4. The corresponding emission reduction was also computed, where the emission factor was 3.114 g/g, which was adopted from [8]. The results show that the four mitigation measures selected can effectively save ship fuel consumption. Each measure’s mitigation potential was also computed based on the annual total fuel consumption, which was 2845 metric tons (MT) in 2017. As a decisive factor affecting ship energy consumption, speed reduction has the largest abatement potential, at 18.47%. Weather routing is also an essential factor in ship energy consumption. The abatement potential for weather routing is 2.42%. The abatement potentials for draft optimization and trim optimization are 1.68% and 1.61%, respectively. Therefore, draft optimization and trim optimization also have an individual impact on ship energy consumption.

Table 4.
Annual energy saving and emission reduction of four mitigation measures.
Furthermore, the cost-effectiveness of the four mitigation measures was also estimated. The increased implementation costs of four measures were adopted from [28], shown in Table 5. Negative costs mean that the costs can be reduced by implementing the mitigation measure. The marginal cost-effectiveness values (MCEs) of different measures were then calculated to rank the mitigation measures, given in Table 5. The MCEs in Table 5 represent the additional implementation costs per unit of energy saved by the measure, compared with its next measure. Here, the carbon price of US$57/metric ton adopted from [41] was taken as the threshold for the ranking of mitigation measures. It was found that the MCE between speed reduction and weather routing is 12.55. This indicates that compared with weather routing, the implementation of speed reduction will add a US$2.55 cost, with an additional metric ton of carbon emission. This additional cost is accepted, as it is smaller than the carbon price compared with the given carbon price.

Table 5.
Ranking of different mitigation measures.
Therefore, speed reduction is still the optimal mitigation measure, although the costs saved for this mitigation measure are the smallest. The MCEs between weather routing and draft optimization, as well as draft optimization and trim optimization, are both negative. That is, compared with draft optimization, weather routing can not only reduce more emissions but can also save more costs. A similar result can be found between draft optimization and trim optimization. No other measures need to be further compared in this paper, so there is no MCE value for trimming optimization.
5. Conclusions
In this paper, the BNN model, a Bayesian method to neural network modeling, was built to evaluate four mitigation measures from multiple data sources. Different from the common BPNN model, the BNN considers the input uncertainty, parameter uncertainty, and output uncertainty in the developed model. Its performance of considering these uncertainties was compared to the developed BPNN and validated GP models. The results show that, although the probability of the BNN covering the observed values is slightly lower than that of GP, it is significantly higher than the BPNN, and the BNN has the smallest MSE among the three models. This means that the BNN has the best prediction performance. At the same time, different iterations of the three models show that the models have good prediction performance. Therefore, a developed BNN model, considering the uncertainty of data and parameters, is valid and useful to evaluate mitigation measures. This summary provides a more convincing explanation for the previous research about using neural network modeling to evaluate ship energy consumption.
Based on the BNN model, the energy savings and emission reductions of different measures were computed to estimate their mitigation potential from an energy perspective. From an economic perspective, the increased costs and marginal cost-effectiveness were computed to evaluate each measure’s cost-effectiveness. Finally, the ranking of the different measures through the two perspectives was obtained. A chemical tanker was used as an example of a complex chemical system to evaluate the mitigation measures. The results show that all four measures are beneficial in the implementation costs while saving energy consumption. A consistent ranking in mitigation potential and cost-effectiveness was obtained, which can further prioritize different mitigation measures.
Evaluating the proposed mitigation measures from economic and energy perspectives can provide directions for policymakers to develop new mitigation measures. It could also be suitable for promoting the formulation of national policies and international treaties to realize sustainable development. Ultimately, it can effectively help mitigate climate change and environmental pollution caused by ship gas emissions. However, there are still some areas for improvement in further research. For example, the presented developed model only considers the chemical tanker, and the adaptability of this method to other types of ships needs to be further verified. Additionally, due to the availability of data sources, four mitigation measures were considered. More relevant mitigation measures and corresponding influencing factors can be collected as the model’s parameters in future research. It can also consider using some lower-cost simulation databases to reduce evaluation costs.
Author Contributions
Conceptualization, J.Y. and V.N.; methodology, J.Y. and J.Z.; software, J.Y and J.Z.; validation, J.Y. and V.N.; formal analysis, J.Y.; investigation, J.Z.; resources, J.Y.; data curation, J.Y. and J.Z.; writing—original draft preparation, J.Y. and J.Z.; writing—review and editing, J.Y. and V.N.; visualization, J.Z.; supervision, J.Y.; project administration, J.Y.; funding acquisition, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China grant number 71804108.
Conflicts of Interest
The authors declare no conflict of interest.
References
- UNCTAD. Review of Maritime Transport 2018; United Nations Conference on Trade and Development (UNCTAD): New York, NY, USA, 2018; ISBN 978-92-1-112928-1. [Google Scholar]
- IMO. Report of the Marine Environment Protection Committee on Its Seventy-second Session; International Maritime Organization (IMO): London, UK, 2018. [Google Scholar]
- Julià, E.; Tillig, F.; Ringsberg, J.W. Concept Design and Performance Evaluation of a Fossil-Free Operated Cargo Ship with Unlimited Range. Sustainability 2020, 12, 6609. [Google Scholar] [CrossRef]
- IMO. Energy Saving Potentials for Existing Ships and Candidate Measures Submitted by CESA; Reduction of GHG Emissions from Ships; International Maritime Organization (IMO): London, UK, 2018. [Google Scholar]
- Nian, V.; Yuan, J. A method for analysis of maritime transportation systems in the life cycle approach—The oil tanker example. Appl. Energy 2017, 206, 1579–1589. [Google Scholar] [CrossRef]
- IMO. Marginal Abatement Costs and Cost-Effectiveness of Energy-Efficiency Measures; Reduction of GHG Emissions from Ships; International Maritime Organization (IMO): London, UK, 2011. [Google Scholar]
- IMO. Further Technical and Operational Measures for Enhancing the Energy Efficiency of International Shipping; International Maritime Organization (IMO): London, UK, 2018. [Google Scholar]
- Smith, T.; Jalkanen, J.; Anderson, B.; Corbett, J.; Faber, J.; Hanayama, S. Third IMO GHG Study; International Maritime Organization (IMO): London, UK, 2014. [Google Scholar]
- Kim, K.-I.; Lee, K.M. Dynamic Programming-Based Vessel Speed Adjustment for Energy Saving and Emission Reduction. Energies 2018, 11, 1273. [Google Scholar] [CrossRef]
- Wang, S.; Ji, B.; Zhao, J.; Liu, W.; Xu, T. Predicting ship fuel consumption based on LASSO regression. Transp. Res. Part D Transp. Environ. 2018, 65, 817–824. [Google Scholar] [CrossRef]
- Kee, K.-K.; Simon, B.-Y.L.; Renco, K.-H. Artificial Neural Network Back-Propagation Based Decision Support System for Ship Fuel Consumption Prediction; Institution of Engineering and Technology: Kuala Lumpur, Malaysia, 2018; 13p. [Google Scholar]
- Gkerekos, C.; Lazakis, I.; Theotokatos, G. Machine learning models for predicting ship main engine Fuel Oil Consumption: A comparative study. Ocean Eng. 2019, 188, 106282. [Google Scholar] [CrossRef]
- Yuan, J.; Nian, V. Ship Energy Consumption Prediction with Gaussian Process Metamodel. Energy Procedia 2018, 152, 655–660. [Google Scholar] [CrossRef]
- Lago, J.; De Ridder, F.; De Schutter, B. Forecasting spot electricity prices: Deep learning approaches and empirical comparison of traditional algorithms. Appl. Energy 2018, 221, 386–405. [Google Scholar] [CrossRef]
- Yuan, J.; Wei, S. Comparison of Using Artificial Neural Network and Gaussian Process in Ship Energy Consumption Evaluation. DEStech Trans. Environ. Energy Earth Sci. 2019. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, H.; Ng, S.H.; Nian, V. Ship Emission Mitigation Strategies Choice Under Uncertainty. Energies 2020, 13, 2213. [Google Scholar] [CrossRef]
- Anagnostis, A.; Papageorgiou, E.I.; Bochtis, D. Application of Artificial Neural Networks for Natural Gas Consumption Forecasting. Sustainability 2020, 12, 6409. [Google Scholar] [CrossRef]
- Golzar, F.; Nilsson, D.; Martin, V. Forecasting Wastewater Temperature Based on Artificial Neural Network (ANN) Technique and Monte Carlo Sensitivity Analysis. Sustainability 2020, 12, 6386. [Google Scholar] [CrossRef]
- Mandal, S.; Prabaharan, N. Ocean wave forecasting using recurrent neural networks. Ocean Eng. 2006, 33, 1401–1410. [Google Scholar] [CrossRef]
- Beşikçi, E.B.; Arslan, O.; Turan, O.; Ölçer, A. An artificial neural network based decision support system for energy efficient ship operations. Comput. Oper. Res. 2016, 66, 393–401. [Google Scholar] [CrossRef]
- Jeon, M.; Noh, Y.; Shin, Y.; Lim, O.-K.; Lee, I.; Cho, D. Prediction of ship fuel consumption by using an artificial neural network. J. Mech. Sci. Technol. 2018, 32, 5785–5796. [Google Scholar] [CrossRef]
- Aldous, L.; Smith, T.; Bucknall, R. Noon Report Data Uncertainty. In Proceedings of the Low Carbon Shipping Conference, London, UK, 9–10 September 2013; p. 13. [Google Scholar]
- Safaei, A.A.; Ghassemi, H.; Ghiasi, M. Correcting and Enriching Vessel’s Noon Report Data Using Statistical and Data Mining Methods. Eur. Trans. 2018, 14, 1–13. [Google Scholar]
- Safaei, A.A.; Ghassemi, H.; Ghiasi, M. Methodology of Acquiring Valid Data by Combining Oil Tankers’ Noon Report and Automatic Identification System Satellite Data. Promet–Traffic Transp. 2019, 31, 299–309. [Google Scholar] [CrossRef]
- Deo, R.; Chandra, R. Multi-step-ahead Cyclone Intensity Prediction with Bayesian Neural Networks. In PRICAI 2019: Trends in Artificial Intelligence; Nayak, A.C., Sharma, A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 11671, pp. 282–295. ISBN 978-3-030-29910-1. [Google Scholar]
- Wright, W. Bayesian approach to neural-network modeling with input uncertainty. IEEE Trans. Neural Netw. 1999, 10, 1261–1270. [Google Scholar] [CrossRef]
- Baldi, F. Modelling, Analysis and Optimisation of Ship Energy Systems; Doktorsavhandlingar vid Chalmers Tekniska Högskola; Chalmers University of Technology: Gothenburg, Sweden, 2016; ISBN 978-91-7597-359-3. [Google Scholar]
- Yuan, J.; Nian, V.; He, J.; Yan, W. Cost-effectiveness analysis of energy efficiency measures for maritime shipping using a metamodel based approach with different data sources. Energy 2019, 189, 116205. [Google Scholar] [CrossRef]
- Mao, S.; Tu, E.; Zhang, G.; Rachmawati, L.; Rajabally, E.; Huang, G.-B. An Automatic Identification System (AIS) Database for Maritime Trajectory Prediction and Data Mining. In Proceedings of ELM-2016; Cao, J., Cambria, E., Lendasse, A., Miche, Y., Vong, C.M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 9, pp. 241–257. ISBN 978-3-319-57420-2. [Google Scholar]
- Zhao, Z.; Xin, H.; Ren, Y.; Guo, X. Application and Comparison of BP Neural Network Algorithm in MATLAB. In Proceedings of the 2010 International Conference on Measuring Technology and Mechatronics Automation, Changsha, China, 13–14 March 2010; IEEE: Piscataway, NJ, USA, 2010; Volume 1, pp. 590–593. [Google Scholar]
- Ding, S.; Su, C.; Yu, J. An optimizing BP neural network algorithm based on genetic algorithm. Artif. Intell. Rev. 2011, 36, 153–162. [Google Scholar] [CrossRef]
- Meng, F.H.; Sun, L.P.; Zhu, L.K. The Intelligent Controller Design of Parallel Online Mixing and Supplying Glue System. Appl. Mech. Mater. 2010, 44, 4089–4093. [Google Scholar] [CrossRef]
- Nan, X.; Li, Q.; Qiu, D.; Zhao, Y.; Guo, X. Short-term wind speed syntheses correcting forecasting model and its application. Int. J. Electr. Power Energy Syst. 2013, 49, 264–268. [Google Scholar] [CrossRef]
- Lin, H.; Chen, S.; Luo, L.; Wang, Z.; Zeng, Y. Research on the Speed Optimization Model Based on BP Neural Network and Genetic Algorithm (GA). In Proceedings of the 29th International Ocean and Polar Engineering Conference, Honolulu, HI, USA, 16–21 June 2019. [Google Scholar]
- Wright, W. Neural Network Regression with Input Uncertainty. In Neural Networks for Signal Processing VIII, Proceedings of the 1998 IEEE Signal Processing Society Workshop (Cat. No.98TH8378), Cambridge, UK, 2 September 1998; IEEE: Piscataway, NJ, USA, 2002; pp. 284–293. [Google Scholar] [CrossRef]
- Taimre, T.; Kroese, D.P.; Botev, Z.I. Monte Carlo methods. In Wiley StatsRef: Statistics Reference Online; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2019; p. 10. [Google Scholar]
- Buyukada, M. Uncertainty estimation by Bayesian approach in thermochemical conversion of walnut hull and lignite coal blends. Bioresour. Technol. 2017, 232, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Vahidinasab, V.; Jadid, S. Bayesian neural network model to predict day-ahead electricity prices. Eur. Trans. Electr. Power 2008, 20. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, J.; Ng, S.H. Gaussian process based optimization algorithms with input uncertainty. IISE Trans. 2019, 52, 377–393. [Google Scholar] [CrossRef]
- Yuan, J.; Ng, S.H. Emission reduction measures ranking under uncertainty. Appl. Energy 2017, 188, 270–279. [Google Scholar] [CrossRef]
- Reflections on the International Coordination of Carbon Pricing. Glob. Carbon Pricing 2017, 13. [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).