Scale-Up of Physics-Based Models for Predicting Degradation of Large Lithium Ion Batteries
Abstract
1. Introduction
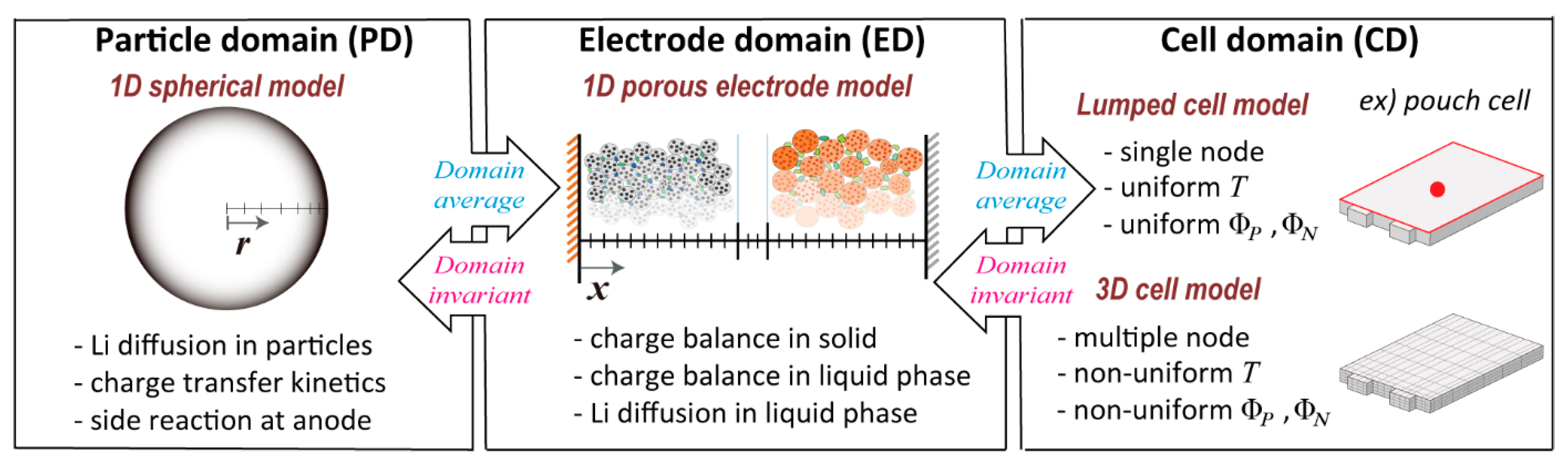
2. Selection of Domain Models
2.1. Cell Domain Models
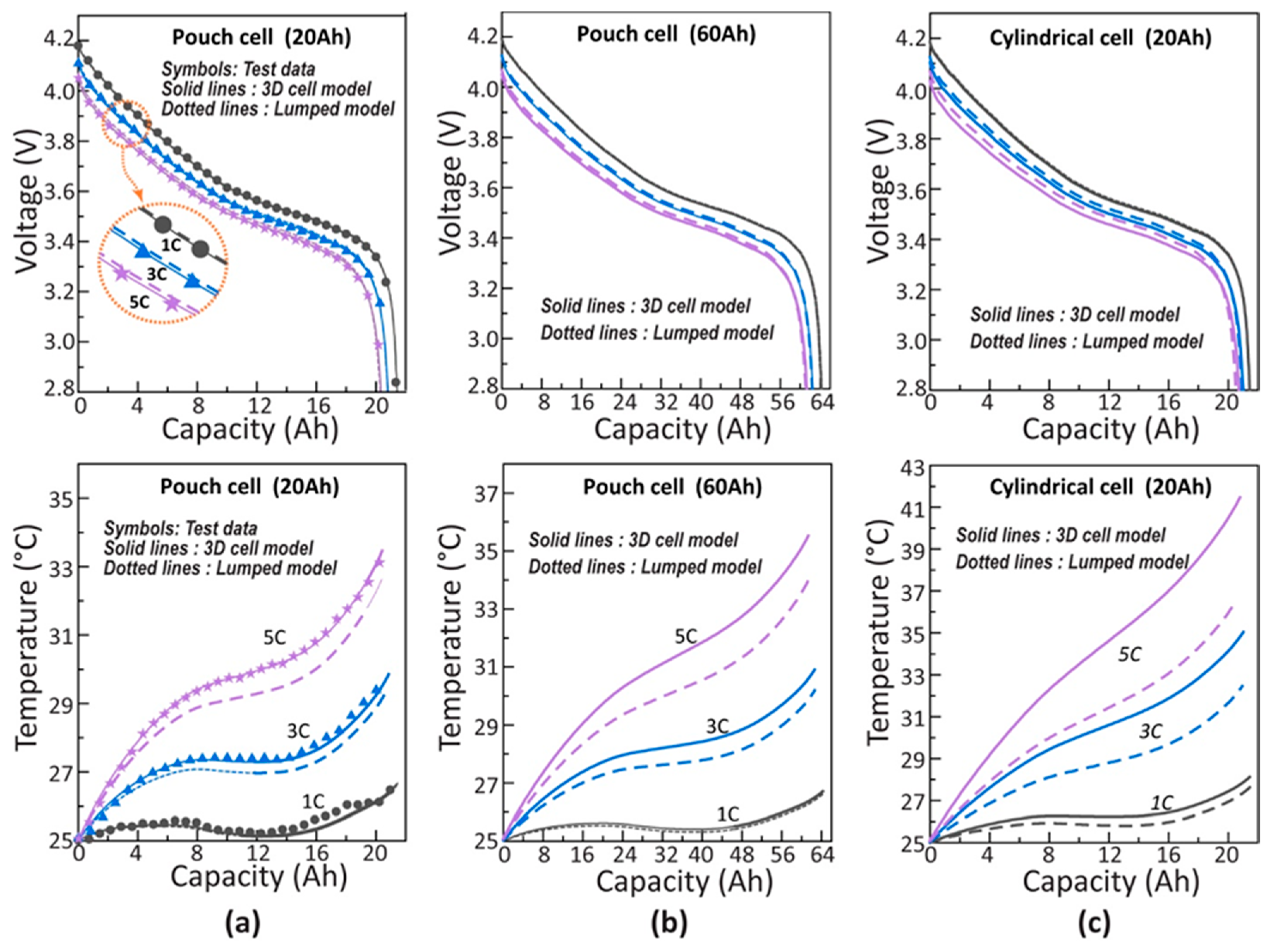
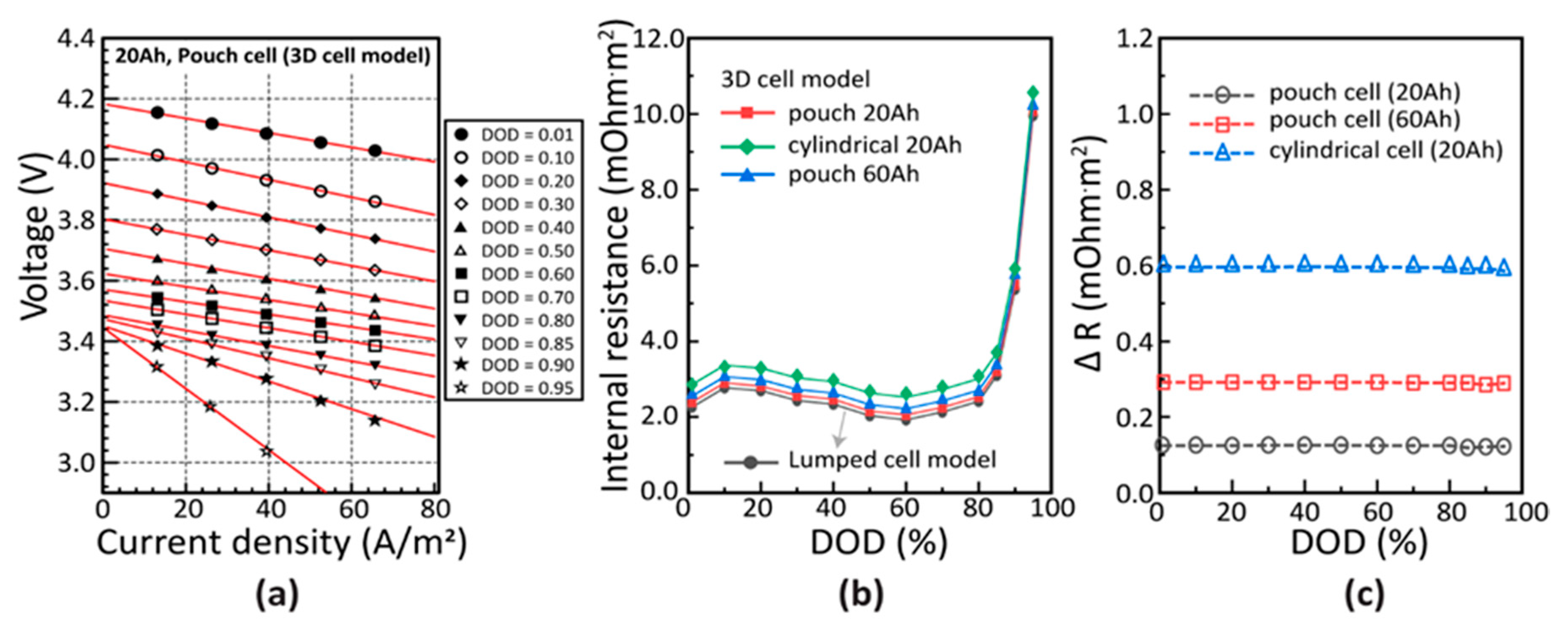
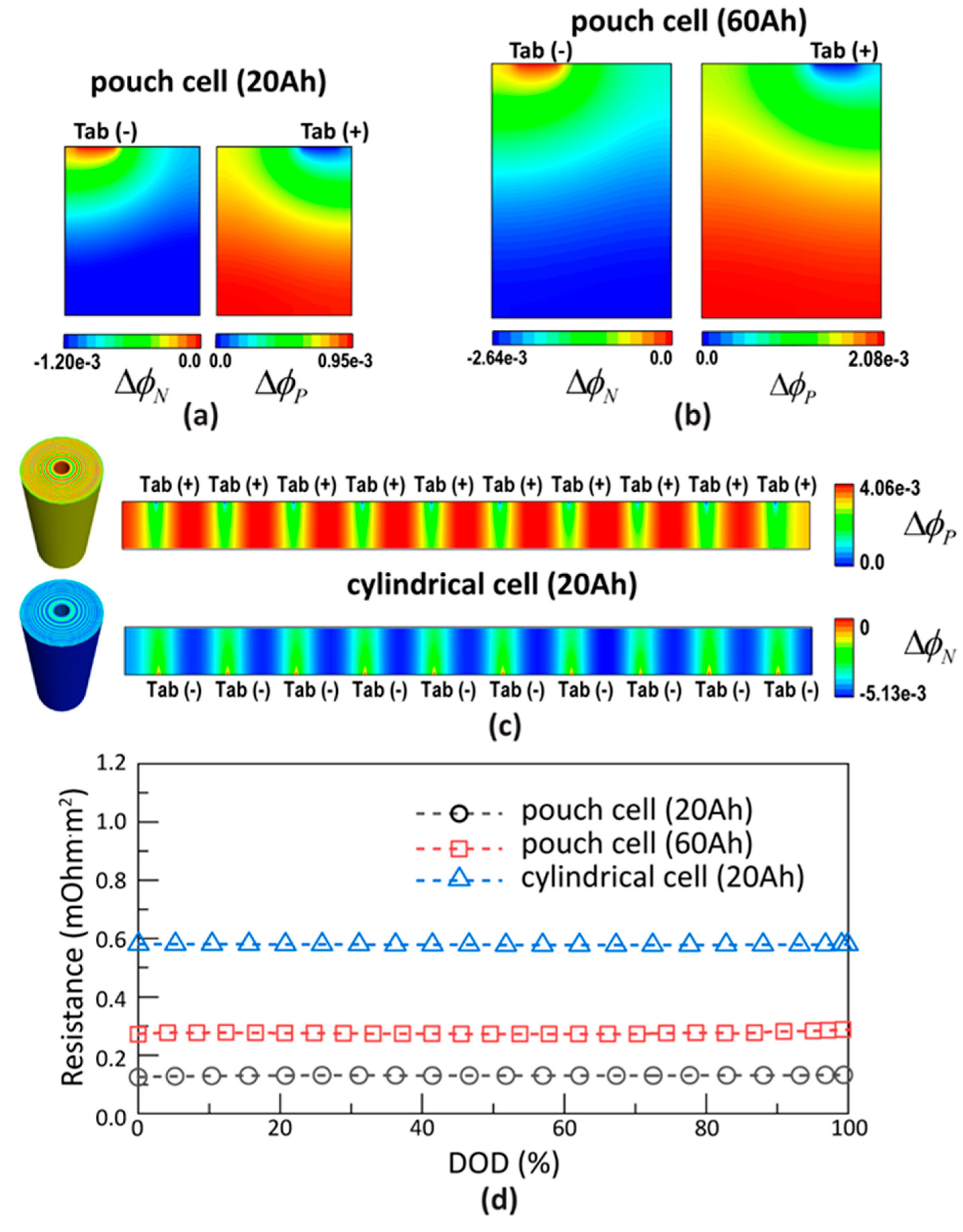
2.2. Comparisons of Lumped Cell and 3D Cell Models
3. Lumped Cell Model with Equivalent Resistances (LER Cell Model)
4. Results and Discussion
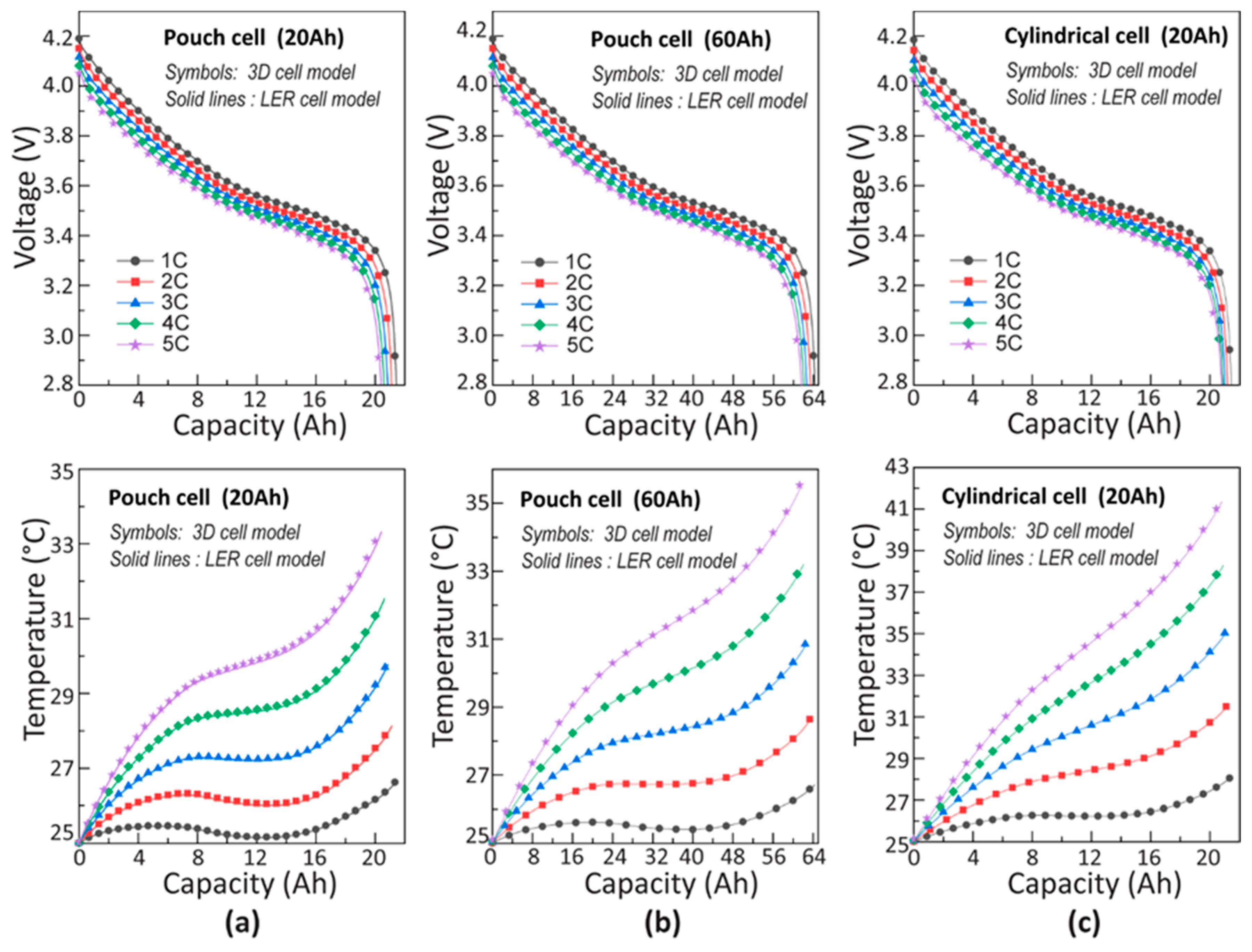
4.1. Constant Current Discharge Simulation
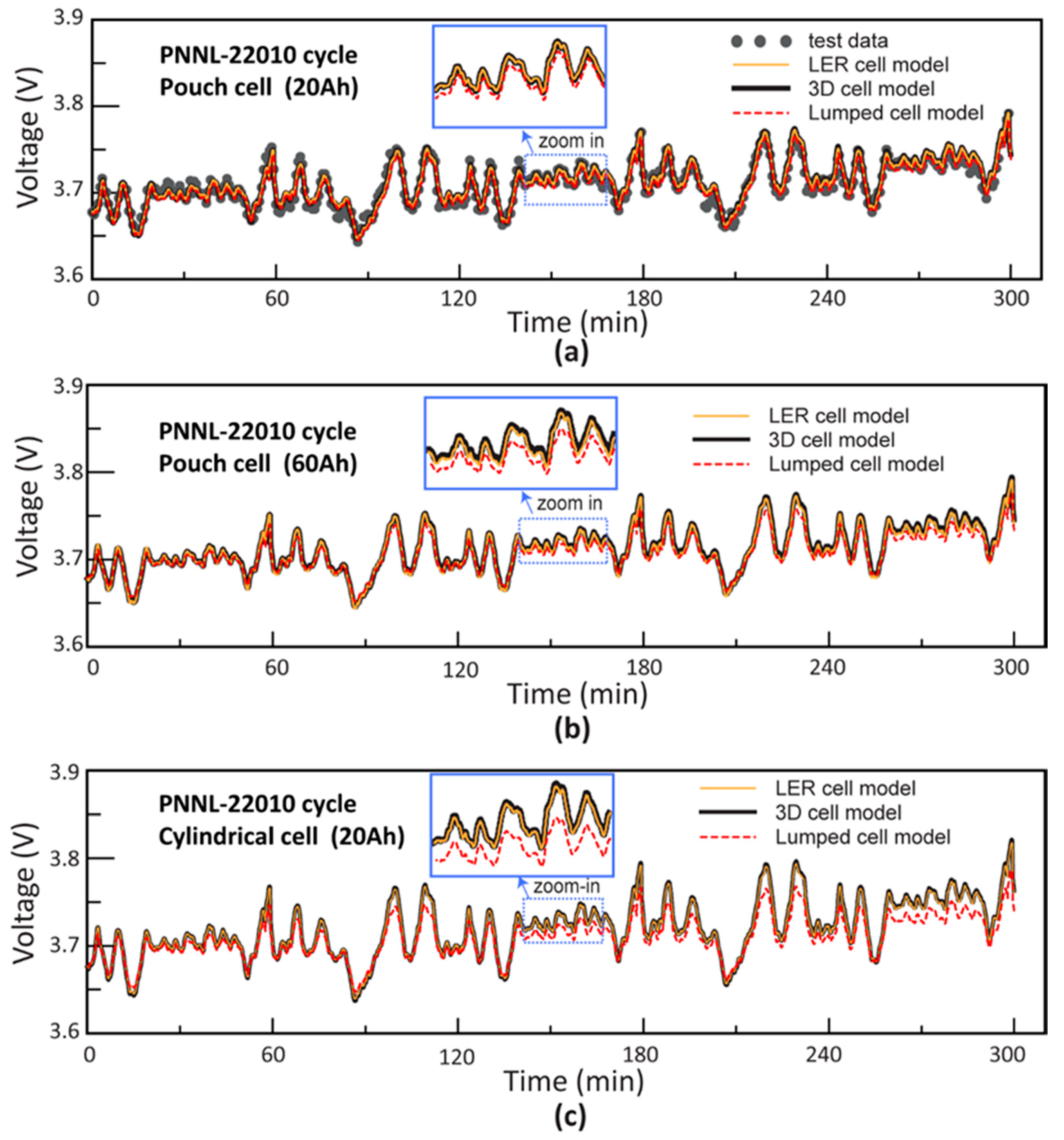
4.2. Power Profile Simulation
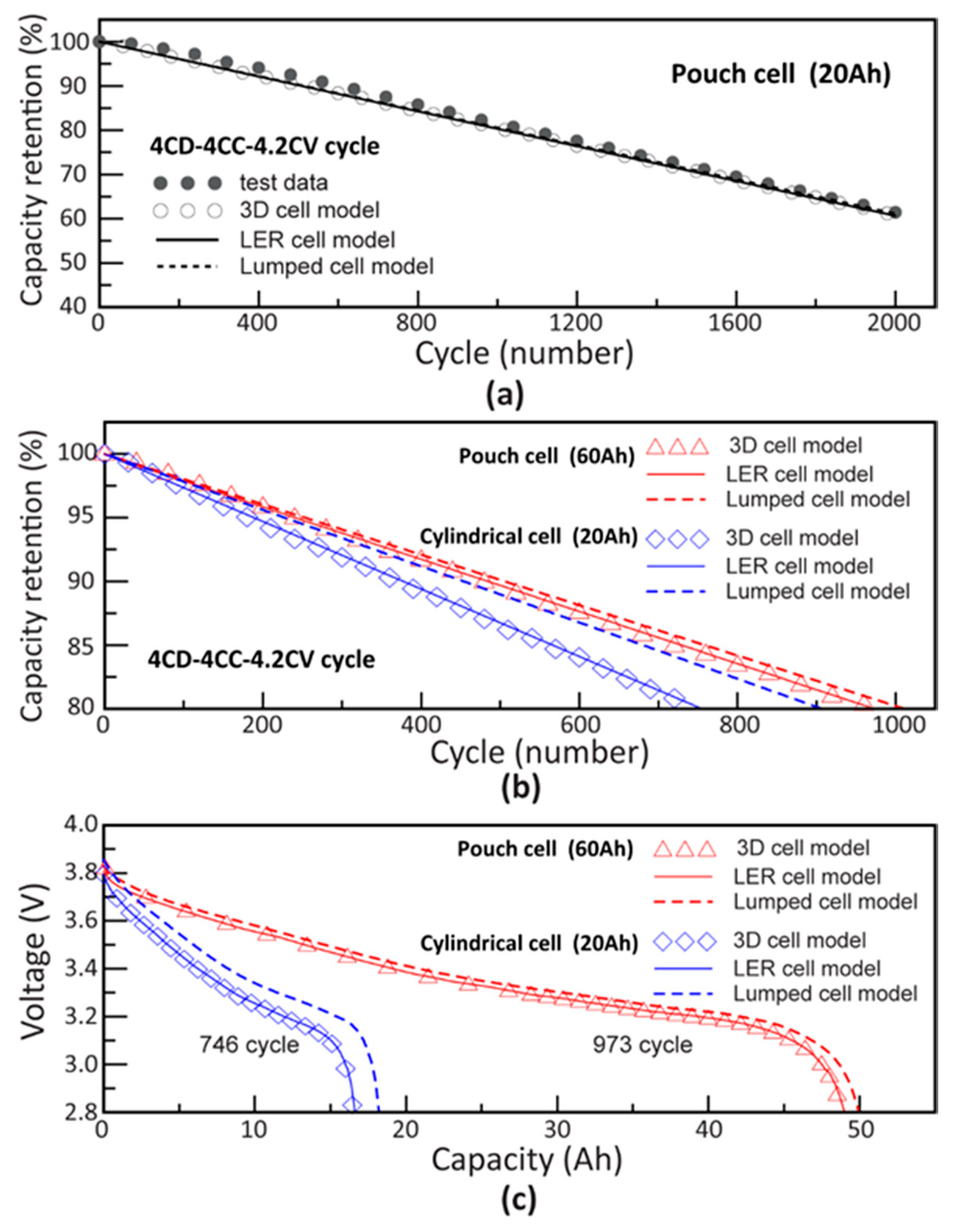
4.3. Cycle Life Simulation
4.4. Comparison of Calculation Times
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, L.J.; Peng, H.; Ning, Z.S.; Mu, Z.Q.; Sun, C.Y. Comparative Research on RC Equivalent Circuit Models for Lithium-Ion Batteries of Electric Vehicles. Appl. Sci. 2017, 7, 1002. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, J.L.; Yuan, S.F.; Yang, J.; Zhou, X. A novel method for identification of lithium-ion battery equivalent circuit model parameters considering electrochemical properties. J. Power Sources 2017, 345, 21–29. [Google Scholar] [CrossRef]
- Zhang, C.; Allafi, W.; Dinh, Q.; Ascencio, P.; Marco, J. Online estimation of battery equivalent circuit model parameters and state of charge using decoupled least squares technique. Energy 2018, 142, 678–688. [Google Scholar] [CrossRef]
- Saleem, K.; Mehran, K.; Ali, Z. Online reduced complexity parameter estimation technique for equivalent circuit model of lithium-ion battery. Electr. Power Syst. Res. 2020, 185, 106356. [Google Scholar] [CrossRef]
- Harris, S.J.; Harris, D.J.; Li, C. Failure statistics for commercial lithium ion batteries: A study of 24 pouch cells. J. Power Sources 2017, 342, 589–597. [Google Scholar] [CrossRef]
- Ma, Y.; Li, B.S.; Li, G.Y.; Zhang, J.X.; Chen, H. A Nonlinear Observer Approach of SOC Estimation Based on Hysteresis Model for Lithium-ion Battery. IEEE/CAA J. Autom. 2017, 4, 195–204. [Google Scholar] [CrossRef]
- Xiong, R.; Tian, J.P.; Mu, H.; Wang, C. A systematic model-based degradation behavior recognition and health monitoring method for lithium-ion batteries. Appl. Energy 2017, 207, 372–383. [Google Scholar] [CrossRef]
- Rodriguez, A.; Plett, G.L. Controls-oriented models of lithium-ion cells having blend electrodes. Part 2: Physics-based reduced-order models. J. Energy Storage 2017, 11, 219–236. [Google Scholar] [CrossRef]
- Lai, X.; Zheng, Y.J.; Sun, T. A comparative study of different equivalent circuit models for estimating state-of-charge of lithium-ion batteries. Electrochim. Acta 2018, 259, 566–577. [Google Scholar] [CrossRef]
- Deng, Z.W.; Deng, H.; Yang, L.; Cai, Y.S.; Zhao, X.W. Implementation of reduced-order physics-based model and multi parameters identification strategy for lithium-ion battery. Energy 2017, 138, 509–519. [Google Scholar] [CrossRef]
- Bonkile, M.P.; Ramadesigan, V. Power management control strategy using physics-based battery models in standalone PV-battery hybrid systems. J. Energy Storage 2019, 23, 258–268. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Simulation and Optimization of the Dual Lithium Ion Insertion Cell. J. Electrochem. Soc. 1994, 141, 1–10. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J.; Gozdz, A.S.; Schmutz, C.N.; Tarascon, J.M. Comparison of modeling predictions with experimental data from plastic lithium ion cells. J. Electrochem. Soc. 1996, 143, 1890–1903. [Google Scholar] [CrossRef]
- Kwon, K.H.; Shin, C.B.; Kang, T.H.; Kim, C.S. A two-dimensional modeling of a lithium-polymer battery. J. Power Sources 2006, 163, 151–157. [Google Scholar] [CrossRef]
- Kim, U.S.; Shin, C.B.; Kim, C.S. Modeling for the scale-up of a lithium-ion polymer battery. J. Power Sources 2009, 189, 841–846. [Google Scholar] [CrossRef]
- Kim, G.H.; Smith, K.; Lee, K.J.; Santhanagopalan, S.; Pesaran, A. Multi-Domain Modeling of Lithium-Ion Batteries Encompassing Multi-Physics in Varied Length Scales. J. Electrochem. Soc. 2011, 158, A955–A969. [Google Scholar] [CrossRef]
- Lee, K.J.; Smith, K.; Pesaran, A.; Kim, G.H. Three dimensional thermal-, electrical-, and electrochemical-coupled model for cylindrical wound large format lithium-ion batteries. J. Power Sources 2013, 241, 20–32. [Google Scholar] [CrossRef]
- Smith, K.; Wang, C.Y. Solid-state diffusion limitations on pulse operation of a lithium ion cell for hybrid electric vehicles. J. Power Sources 2006, 161, 628–639. [Google Scholar] [CrossRef]
- Cai, L.; White, R.E. Reduction of Model Order Based on Proper Orthogonal Decomposition for Lithium-Ion Battery Simulations. J. Electrochem. Soc. 2009, 156, A154–A161. [Google Scholar] [CrossRef]
- Guo, M.; White, R.E. A distributed thermal model for a Li-ion electrode plate pair. J. Power Sources 2013, 221, 334–344. [Google Scholar] [CrossRef]
- Rodriguez, A.; Plett, G.L.; Trimboli, M.S. Improved transfer functions modeling linearized lithium-ion battery-cell internal electrochemical variables. J. Energy Storage 2018, 20, 560–575. [Google Scholar] [CrossRef]
- Jin, X.; Liu, C. Physics-based control-oriented reduced-order degradation model for LiNiMnCoO2—Graphite cell. Electrochim. Acta 2019, 312, 188–201. [Google Scholar] [CrossRef]
- Li, Y.; Vilathgamuwa, M.; Farrell, T.; Choi, S.S.; Tran, N.T.; Teague, J. A physics-based distributed-parameter equivalent circuit model for lithium-ion batteries. Electrochim. Acta 2019, 299, 451–469. [Google Scholar] [CrossRef]
- Yin, Y.L.; Hu, Y.; Choe, S.Y.; Cho, H.; Joe, W.T. New fast charging method of lithium-ion batteries based on a reduced order electrochemical model considering side reaction. J. Power Sources 2019, 423, 367–379. [Google Scholar] [CrossRef]
- Yang, X.G.; Leng, Y.J.; Zhang, G.S.; Ge, S.H.; Wang, C.Y. Modeling of lithium plating induced aging of lithium-ion batteries: Transition from linear to nonlinear aging. J. Power Sources 2017, 360, 28–40. [Google Scholar] [CrossRef]
- Safari, M.; Morcrette, M.; Teyssot, A.; Delacourt, C. Multimodal Physics-Based Aging Model for Life Prediction of Li-Ion Batteries. J. Electrochem. Soc. 2009, 156, A145–A153. [Google Scholar] [CrossRef]
- Ramadass, P.; Haran, B.; Gomadam, P.M.; White, R.; Popov, B.N. Development of first principles capacity fade model for Li-ion cells. J. Electrochem. Soc. 2004, 151, A196–A203. [Google Scholar] [CrossRef]
- Ning, G.; White, R.E.; Popov, B.N. A generalized cycle life model of rechargeable Li-ion batteries. Electrochim. Acta 2006, 51, 2012–2022. [Google Scholar] [CrossRef]
- Kim, H.K.; Kim, C.J.; Kim, C.W.; Lee, K.J. Numerical analysis of accelerated degradation in large lithium-ion batteries. Comput. Chem. Eng. 2018, 112, 82–91. [Google Scholar] [CrossRef]
- Kim, H.K.; Choi, J.H.; Lee, K.J. A Numerical Study of the Effects of Cell Formats on the Cycle Life of Lithium Ion Batteries. J. Electrochem. Soc. 2019, 166, A1769–A1778. [Google Scholar] [CrossRef]
- Viswanathan, V.V.; Choi, D.; Wang, D.H.; Xu, W.; Towne, S.; Williford, R.E.; Zhang, J.G.; Liu, J.; Yang, Z.G. Effect of entropy change of lithium intercalation in cathodes and anodes on Li-ion battery thermal management. J. Power Sources 2010, 195, 3720–3729. [Google Scholar] [CrossRef]
- MeCleary, D.A.H.; Meyers, J.P.; Kim, B. Three-Dimensional Modeling of Electrochemical Performance and Heat Generation of Spirally and Prismatically Wound Lithium-Ion Batteries. J. Electrochem. Soc. 2013, 160, A1931–A1943. [Google Scholar] [CrossRef]
- Taheri, P.; Mansouri, A.; Yazdanpour, M.; Bahrami, M. Theoretical Analysis of Potential and Current Distributions in Planar Electrodes of Lithium-ion Batteries. Electrochim. Acta 2014, 133, 197–208. [Google Scholar] [CrossRef]
- Zhao, W.; Luo, G.; Wang, C.Y. Effect of tab design on large-format Li-ion cell performance. J. Power Sources 2014, 257, 70–79. [Google Scholar] [CrossRef]
- Conover, D.R.; Crawford, A.J.; Viswanathan, V.; Ferreira, S.R.; Schoenwald, D.A. Protocol for Uniformly Measuring and Expressing the Performance of Energy Storage Systems PNNL-22010 Rev. 1; Pacific Northwest National Laboratory: Richland, WA, USA, 2014. [Google Scholar]

| Governing Equations | Boundary Conditions | |
|---|---|---|
| 1D Spherical Particle Model | ||
| Li+ conservation in active material | , | |
| Charge transfer Kinetic (Butler–Volmer equation) | (2) where (negative electrode) and (positive electrode) | |
| Aging mechanism (SEI layer growth) | , ) (3) where , , , and | |
| 1D Porous Electrode Model | ||
| Li conservation in liquid phase | (4) | |
| Charge conservation in liquid phase | (5) where | , |
| Charge conservation in solid phase | (6) | , , |
| Particle Domain & Electrode Domain | Negative Electrode | Separator | Positive Electrode | |
|---|---|---|---|---|
| Particle radius, Rs (m) | 4 × 10−6 d | - | 4 × 10−6 d | |
| Diffusivity, Ds,a, Ds,c (m2/s) | 1.5 × 10−14 e | - | 2.0 × 10−14 e | |
| Reaction rate constant ka, kc (m/s) | 4.8 × 10−11 e | - | 5.5 × 10−11 e | |
| SEI layer molecular weight, (kg/mol) | 0.1 [27,28,29,30] | - | - | |
| SEI layer density, (kg/m3) | 2100 [27,28,29,30] | - | - | |
| Equilibrium potential of parasitic reaction, (V) | 0.4 [27,29,30] | - | - | |
| SEI layer conductivity, (S/m) | 3.8 × 10−6 e | - | - | |
| Initial concentration of EC, (mol/m3) | 4541 [30] | - | - | |
| Diffusivity of EC, (mol/m3) | 2.0 × 10−18 [30] | |||
| Reaction rate for SEI layer, k0,SEI (m/s) | 1.1 × 10−15 e | |||
| Initial SEI layer resistance () | 0.001 | - | - | |
| Electrode thickness, La, Ls, Lc (m) | 39 × 10−6 d | 20 × 10−6 d | 31 × 10−6 d | |
| Electrolyte diffusion coefficient, De (m2/s) | - | 3 × 10−10 e | - | |
| Conductivity, , (S/m) | 100 [16] | - | 10 [16] | |
| Porosity, | 0.397 d | 0.43 d | 0.404 d | |
| Volume fraction AB, | 0.044 d | - | 0.042 d | |
| Volume fraction PVDF, | 0.007 d | - | 0.064 d | |
| Initial salt concentration, ce, (mol/m3) | 1200 d | |||
| Transport number, | 0.363 [29,30] | |||
| Faraday’s constant, F, (C/mol) | 96,450 | |||
| Gas constant, R (J/mol·K) | 8.314 | |||
| Cell domain | Pouch, 20-Ah | Pouch, 60-Ah | Cylindrical, 20-Ah | |
| Dimension (mm) | 185 × 147 × 5.88 d | 278 × 195 × 8.85 d | 44(D) × 110(h) d | |
| Mass density of jelly roll (kg/m3) | 2580 d | |||
| Specific heat of jelly roll (J/kg∙K) | 975 d | |||
| Electric conductivity for Cu, (S/m) | 59.6 × 10 6 [16,17] | |||
| Electric conductivity for Al, (S/m) | 37.8 × 10 6 [16,17] | |||
| Thermal conductivity (W/m∙K) | x, y direction: 27 [16] z direction: 0.8 [16] | azimuthal direction, :27 [17] transversal direction, : 0.8 [17] | ||
| Convective heat transfer coefficient, (W/m2∙K) | 25 | |||
| Initial temperature, (°C) | 25 | |||
| Atmospheric temperature, (°C) | 25 | |||
| Number of Nodes | Pouch (20-Ah) | Pouch (60-Ah) | Cylindrical | |
| Lumped cell model | Particle domain | 15 | 15 | 15 |
| Electrode domain | 25 | 25 | 25 | |
| Cell domain | 1 | 1 | 1 | |
| 3D cell model | Particle domain | 15 | 15 | 15 |
| Electrode domain | 25 | 25 | 25 | |
| Cell domain | 3000 | 3000 | 15,000 | |
| Calculation Time (1 C discharge) | Pouch (20-Ah) | Pouch (60-Ah) | Cylindrical | |
| Lumped cell model | 1 CPU core | 6.6 s | 6.8 s | 6.6 s |
| 3D cell model | 1 CPU core | 1 h 53 min | 1 h 56 min | 7 h 20 min |
| 8 CPU core | 27 min | 28 min | 1 h 40 min | |
| Run Mode | Model | Pouch (20-Ah) | Pouch (60-Ah) | Cylindrical |
|---|---|---|---|---|
| Discharge (1CD) | 3D cell model | 27 min | 28 min | 1 h 40 min |
| LER cell model | 7.59 s | 7.86 s | 6.84 s | |
| PNNL cycle (300 min) | 3D cell model | 3 days | 3 days | 9 days |
| LER cell model | 4 m 30 s | 4 m 28 s | 4 m 12 s | |
| 4CD4CC42CV (~80%) | 3D cell model | 6 days | 7 days | 22 days |
| LER cell model | 35 min | 31 min | 24 min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.-K.; Lee, K.-J. Scale-Up of Physics-Based Models for Predicting Degradation of Large Lithium Ion Batteries. Sustainability 2020, 12, 8544. https://doi.org/10.3390/su12208544
Kim H-K, Lee K-J. Scale-Up of Physics-Based Models for Predicting Degradation of Large Lithium Ion Batteries. Sustainability. 2020; 12(20):8544. https://doi.org/10.3390/su12208544
Chicago/Turabian StyleKim, Hong-Keun, and Kyu-Jin Lee. 2020. "Scale-Up of Physics-Based Models for Predicting Degradation of Large Lithium Ion Batteries" Sustainability 12, no. 20: 8544. https://doi.org/10.3390/su12208544
APA StyleKim, H.-K., & Lee, K.-J. (2020). Scale-Up of Physics-Based Models for Predicting Degradation of Large Lithium Ion Batteries. Sustainability, 12(20), 8544. https://doi.org/10.3390/su12208544





