1. Introduction
Manufacturing industries are experiencing a transition of value creation patterns from the design and production of products to the design and the delivery of services based on products, to accommodate increasingly global competition and customer-centered business settings [
1]. As an overall solution that effectively integrates products and services [
2], product–service systems (PSS) [
3,
4,
5] play a vital role in accelerating this transition for manufacturers. By prolonging the service life of products and commoditizing the related services, PSS can change the revenue models and pricing capabilities for manufacturers [
6,
7]. This exemplifies a new source of competitive advantage and differentiation. Furthermore, compared to traditional business models, PSS has the potential to reduce environmental impact, thus receiving much attention as one strategic alternative for the sustainable development of firms [
8,
9,
10].
PSS can be divided into three types: (a) product-oriented PSS, (b) use-oriented PSS, and (c) result-oriented PSS [
5]. In product-oriented PSS, customers buy the product as usual; a service is also sold to customers additionally, which then will be operated on products or provided to customers [
11]. This means that the product is the principal purpose, so the service is rendered to help customers achieve a better user experience. This paper focuses extensively on product-oriented PSS.
Services help to attain higher margins, but performing the transition or maintaining the success of service strategy is still a challenge for companies [
12]. With the increase in service offers, higher costs or failures in achieving expected returns sometimes occur [
13,
14]. To overcome this glitch in the profit generation and commercial success, companies should target the role of PSS design [
15,
16]. Many studies have focused on PSS design to provide support, such as design frames [
17,
18,
19], design methods [
20], modularization approaches [
21,
22], configuration and evaluation methods [
23,
24,
25].
Product–service integration solutions provided to customers include product modules and service modules [
26]. There are usually many possible PSS solutions. A PSS configuration is the construction of technical systems by selecting and assembling preferable modules from a predefined product and service library according to customers’ needs under certain constraints [
27]. Thus, PSS configuration is an imperative part of PSS design. Studies on PSS configuration have mainly focused on the PSS configuration framework [
24,
28], customer perception in PSS configuration [
29], the extraction of PSS configuration rules [
30,
31,
32,
33], and PSS configuration optimization methods [
23,
34]. Most studies on PSS configuration, especially research on PSS configuration optimization, commonly deal with some predefined level of module granularity. Overall, the product module granularity is introduced to achieve flexible manufacturing systems for product functions realization. With regard to service module granularity, every service module is essentially a whole service flow, depending on the specific module’s granularity level. However, it presently lacks the PSS configuration on a finer granularity level, which can inspire the final configuration’s optimization.
Considering the balance between differentiated customization and mass production, inappropriate product module granularity will increase managerial difficulty and manufacturing cost [
35]. Services are generally under-designed in comparison to physical products [
36]. Also, service modules are not restricted to physical artefacts. Thus, service modules should be designed considering a finer granularity level, so they can integrate tangible and non-tangible artefacts. Recent studies on service modules in PSS have mainly focused on the identification and evaluation of customer requirements [
37,
38], modularization and related quantification [
39,
40], and the evaluation of internal and external performance (such as cost, customer satisfaction, service cycle time, availability, and reliability) [
11,
41]. Modularization can normalize the PSS configuration and improve its suitability. However, a service module in PSS is essentially a composition of service activities. It is coarse-grained to use a whole service flow as a service module unit in PSS configuration. Therefore, configuring a PSS in finer granularity by using service activity as the minimum configuration unit is proposed and developed in this paper.
There are various methods to optimize the composition of service activities, which can be embodied in the following three approaches [
42]:
(1) Service composition solver based on artificial intelligence planning, which can automatically generate service activities composition according to customer demands;
(2) The method based on semantics, studying the service matching and composability;
(3) The service workflow-based semiautomatic service composition method, which is the most widely used one.
In this context, Zhu et al. [
43] proposed an ontology-based service process model to support decision-making for maintenance, repair, and overhaul services in the aerospace industry. Cao et al. [
44] transformed the service process model into a process structure tree to consider service process structuration and service activities selection simultaneously. Wang et al. [
45] advocated a model of service activities composition based on stochastic Petri net. Hu et al. [
46] modeled the service process by logical Petri net to study the structural transformation of the service process.
The above-mentioned studies only focused on service activities selection. The impact of resource allocation on service activity has not been considered during the service activities selection. Service activities selection and resource allocation were consequently divided into two independent processes. In a practical situation, the performance of service activity operation will be altered based on different resource allocation instances. It is necessary to combine service activities selection and resource allocation into a whole process during the PSS configuration optimization. Furthermore, most of the previous studies highlighted multi-objective optimization of the overall solution, but high-importance service activities usually exert a greater impact on the solution, compared to low-importance services. Therefore, the importance degree of service activity is also taken into consideration in this paper, to improve the performance of service activities with higher importance.
Based on the above analysis, it was found that: (a) PSS configuration is an imperative part of PSS design; (b) existing PSS configuration solutions are obtained in the module granularity; and (c) the significant impact of service details on the performance of a PSS configuration solution has not been given sufficient attention in recent research studies. PSS configuration optimization is, therefore, studied from a fine-grained perspective in this paper. The optimization is performed by combining service activities selection and resource allocation. As a result, the PSS configuration solutions provided to the customer will be more refined and precise. In particular, the optimizing objectives, which present the performance of the solutions, will be calculated closer to the actual implementation.
The complex network is chosen as the framework for the PSS modeling because its structural properties enable the exploration of the interactions between products, resources, and service activities. The mathematical characteristics of complex networks are very useful for analyzing the characteristics of complex systems. However, it is difficult for a general complex network to effectively reveal the multilayered or multidimensional relationships in a complex system when the scale of the system increases substantially. Many approaches have been proposed to enrich the representation of networks. Hypernetworks [
47,
48,
49] are developed based on the definition of the hypergraphs to generalize the multidimensional relationships, in which multi-elements are connected rather than only two elements. Multilayer networks [
50] are applied to describe the complex structures of systems, which include different types of relationships between their components. Originally, multilayer networks were proposed to express different types of relationships between one single type of elements in different layers [
51,
52]. More recently, they have been used to model other systems, including those with different types of elements. Omodei et al. [
53] proposed a method based on the multilayer networks of citations and disciplines to assess the interdisciplinary importance of scholars, institutions, and countries. Additionally, Pasqual and Weck [
54] introduced a multilayer network model integrating three coupled layers (product layer, change layer, and social layer) to analyze and manage engineering change propagation. Leng and Jiang [
55] also offered a multilayer network model comprising processes, machines, and work in processes to assess dynamic scheduling in a radio frequency identification-driven discrete manufacturing system.
Based upon the comparison of the general complex network, hypernetwork, and multilayer network, it is obvious that a multilayer network can perfectly accommodate multiple heterogeneous elements and provide a better description of relationships between heterogeneous elements than a general complex network or hypernetwork. Therefore, a multilayer network, as a special type of complex network, is applied for the modeling of PSS in this paper.
The organization of this paper is as follows. In
Section 2, this paper’s research problem is described and the framework is then introduced. The PSS multilayer network model is constructed in
Section 3.
Section 4 establishes the mathematical model of PSS configuration. This section also delineates the improved optimization algorithms and their applications for obtaining the optimal solutions. Moreover, a case is studied in
Section 5 to discuss the feasibility and effectiveness of this method.
Section 6 highlights the benefits and the contributions to the sustainability of the proposed approach. Finally, conclusions are stated in
Section 7.
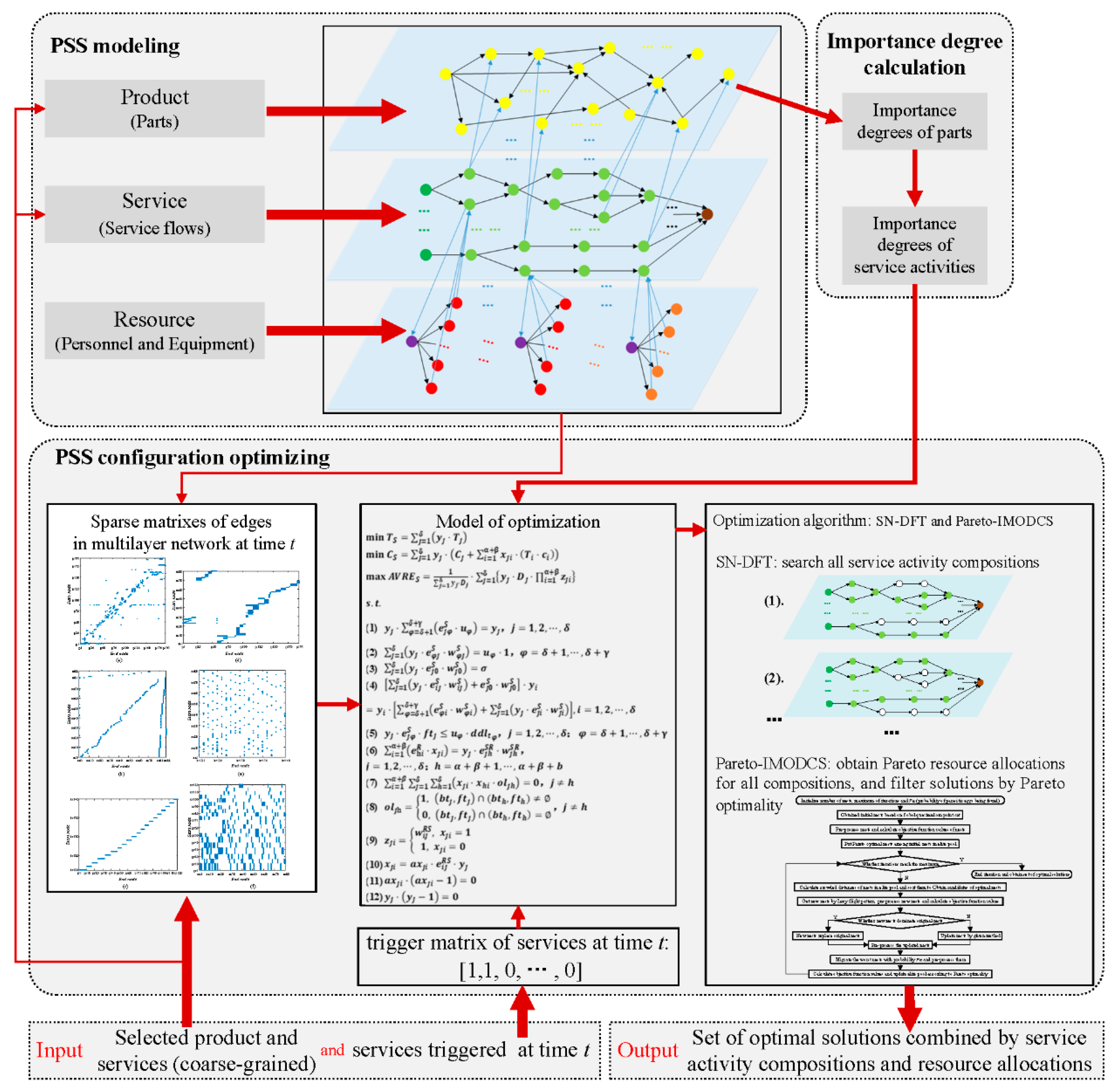
3. PSS Multilayer Network Model
The PSS multilayer network () is composed of the product layer (), service layer (), resource layer (), and set of inter-layer edges () which connect layers to each other. Therefore, there are three types of nodes and five kinds of edges considered in . Specifically, nodes in , nodes in , and nodes in are denoted as sets , , and , respectively; edges in , edges in , edges in , inter-layer edges between and , and inter-layer edges between and are denoted as sets , , , , and , respectively. The inter-layer edges between and are not considered in this model.
Then,
is described by Formula (1):
A product can be decomposed into parts according to required granularity. is formed by part nodes (p) connecting to each other by interrelationships between parts. consists of service flows, each of which is described by a service trigger node (ss), numbers of service activity nodes (sa), and a service end node (se) logically associated with each other. contains resources required by service activities, including personnel resources (pr) and equipment resources (er), as resource types are denoted as kr. contains , , and the weights on inter-layer edges. Detailed descriptions of , , , and are given in the following subsections.
3.1. Product Layer
A node
in
is described by Formula (2):
where
is the set of basic information, including information such as name, quality, and material.
is the set of accepted service records.
is the set of working statuses, including various data of physical status, material status, and environmental status. All statuses vary with time
t. For any
whose status data cannot be monitored,
.
There are four types of interactions among parts [
56]: spatial-type interaction, energy-type interaction, information-type interaction, and material-type interaction. These interactions could be extracted from the product design manually. If
provides spatial reference (adjacency or orientation) to
, then
. If
provides or transmits energy to
, then
. If
provides or transfers information to
, then
. If
determines or impacts the material selection of
, then
. If there are one or more interactions from
to
, then
, denotes the directed edge from
to
; otherwise,
. Obviously,
.
In order to describe the overall strength of the relationship between
and
, the weight on
is represented by the value
, following Formula (3):
where
,
,
, and
, respectively, represent the proportion of
,
,
, and
in the edge
.
is defined in [0,1]. If the four types of interactions are equal in importance, then
.
is consequently represented by Formula (4):
3.2. Service Layer
Services in a product lifecycle can be classified into two types: production services and product services. All services in are product services.
3.2.1. Service Trigger Node
A node
in
is as described by Formula (5):
where
is the set of parts whose working statuses are monitored by
.
is the set of triggering conditions of
,
is the triggering condition for working statuses
of
to trigger
.
denotes the status of
: if triggering conditions are satisfied, the status will be
, where
and
are, respectively, the start time and the deadline of the entire service set according to customer requirements; otherwise, the status will be
.
3.2.2. Service Activity Node
The function of service activity is to change the status of the service activity receiver [
57]. Service activity is operated by the specified resources and executed on the specified component. By decomposing the service flow at specified granularity, the corresponding set of service activities could be obtained. A service activity node
in
is as described by Formula (6):
where
is the set of service execution records of
.
and
are the theoretical executing time and fixed cost for operating
, which are extracted from historical data.
denotes the reliability of that
which can be completed in time
. It is represented by the ratio between the number of times that
has been completed in time
and the total number of times that
has been executed.
.
is set of service objects of
.
denotes the status of
:
is idle status,
denotes working status.
is the beginning time of
, ending time is defined as
.
3.2.3. Service End Node
A service end node is put in to distinguish whether the service flow is finished at the end of . An edge between and means that is the last service activity in the service flow.
3.2.4. Edges in Service Layer
Regarding and as the activities of “trigger service” and “end service”, respectively, then , , and are homogeneous. Edges between and , edges between and , and edges between and are all denoted by ; , . defined in the interval [0,1] denotes weight on . when . The description of an edge between two nodes considers the following cases:
Between and : if is the first one executed in the service flow triggered by , then , . can participate in different service flows triggered by , denoted as with , will not output any weight to ; between and ;
Between and : if is the last one in the service flow being executed, then ; for any and between and ;
Between and : if and are in same service flow and are executed in time sequence, then . Otherwise, .
There are three types of correlations among service activities [
58]: correlation of function similarity, correlation of function complementary, and no correlation. If two service activities have a correlation of function similarity, their function might be identical, inclusive, or partially similar. If two service activities have a correlation of function complementary, the composable situation might be accurate composition, inclusive composition, blocked composition, or crossed composition.
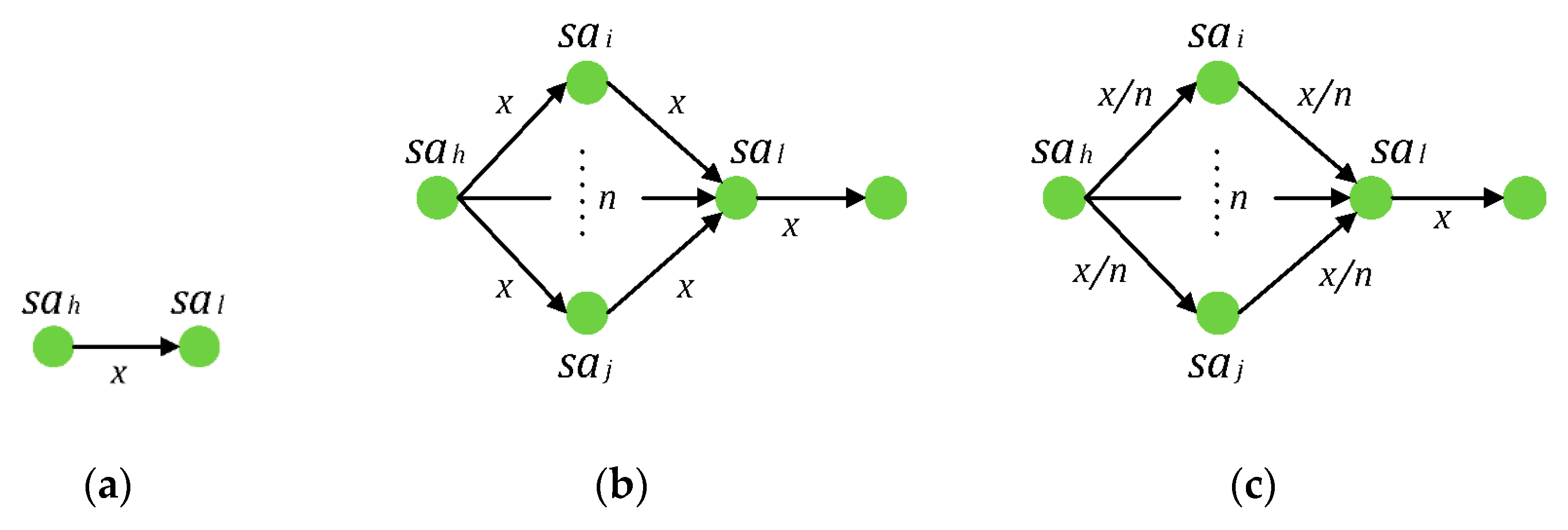
According to the above correlations, logical relationships among service activity nodes are divided into serial relationship, parallel relationship, and selective relationship. Two activities in a serial relationship are sequentially executed in chronological order. Two activities in a parallel relationship are executed at the same time, and only when they are fully completed will the execution of subsequent activities begin. In a selective relationship, there are multiple activities for selection: if only one of them is executed, then the execution of subsequent activities will begin.
The in-degree and out-degree of
in
are denoted as
and
which are described by Formulas (7) and (8):
Then, the description of the three types of logical relationships is expanded as follows:
If and are in a serial relationship, and , then , , ;
If n nodes () are in a selective relationship, and , then , , . In this case, and . If is selected, then , ;
If n nodes () are in a parallel relationship, and , then , , , and , . In this case, and .
Connections of these logical relationships are shown in
Figure 2. If
is replaced by a service trigger node, then
.
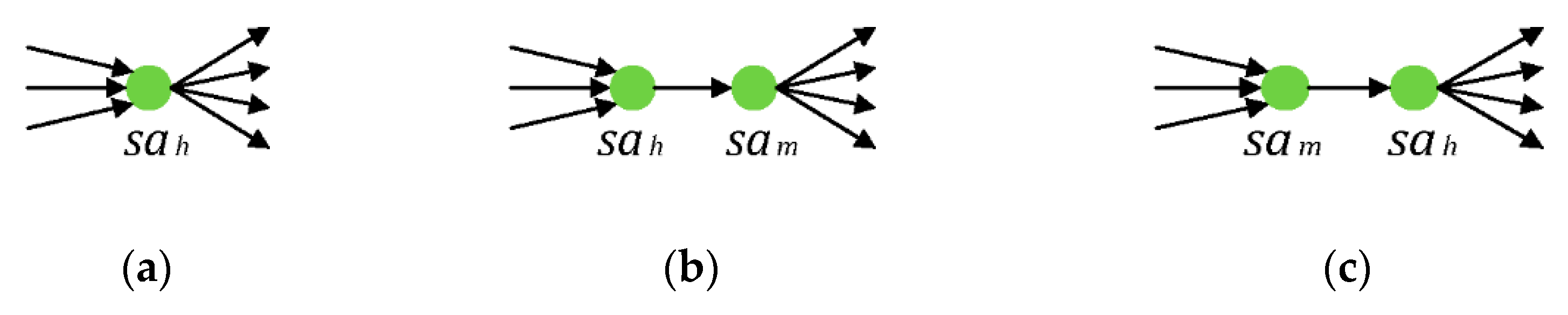
Then, the logical relationship between nodes in
can be distinguished by values of
and
. However, if
has multi inputs and multi outputs, as depicted in
Figure 3a, the logical relationship between
and other nodes will be uncertain. The virtual service activity node
is applied to prevent that. Then,
will become a node with a single input or single output, as shown in
Figure 3b,c. There is not any essential service content in a virtual service activity node, so
,
,
,
,
, and
does not require any resources.
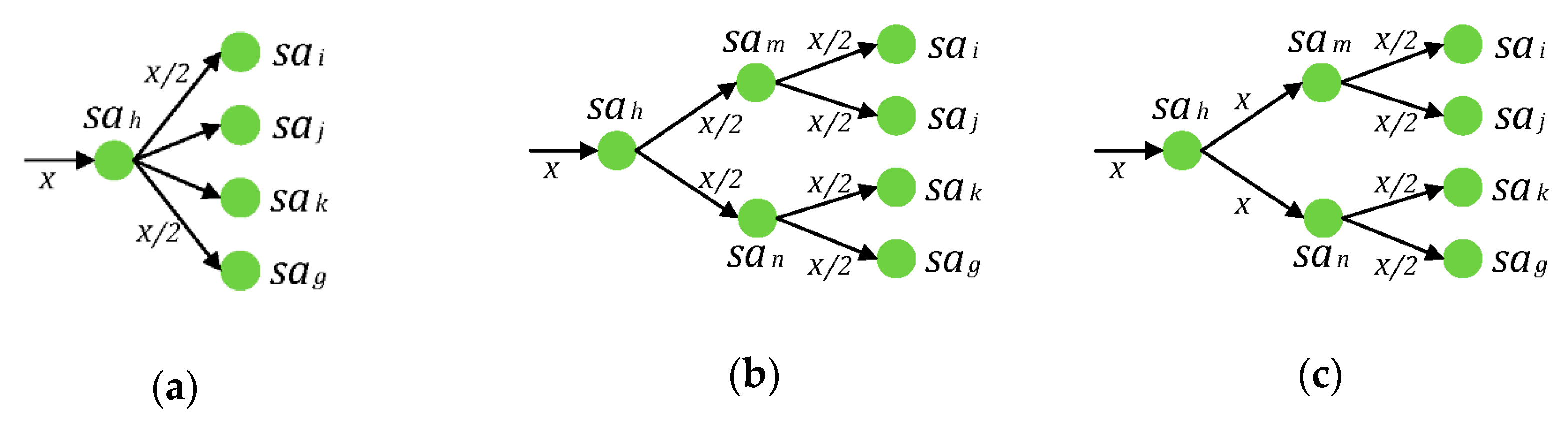
If
connects the other nodes, which are in selective relationships and parallel relationships, intricately, it will be impractical to distinguish different relationships by values of
and
. As shown in
Figure 4a, when
, relationships among
,
,
, and
cannot be distinguished directly. In order to solve this situation, there will be two situations to integrate in the virtual service activity nodes
and
, as follows:
means that
and
are in a selective relationship;
and
are in a selective relationship. Meanwhile,
(or
) and
(or
) are in a parallel relationship, as expressed in
Figure 4b.
,
means that
and
are in a parallel relationship;
and
are in a parallel relationship. Meanwhile, two parallel clusters are in a selective relationship, as indicated in
Figure 4c.
Assuming that the number of
and
in
are indicated, respectively, by
and
γ, and there is only one
, then the description of
is consequently shown by Formula (9):
3.3. Resource Layer
The node
or
in
is described by Formula (10):
where
is the set of records of services operated by
,
is the cost for
working in one unit of time,
denotes the status of
. If
, then
could accept a new assignment of the service activity; if
, it means
is in working status and will not accept any new assignments until the service activity
is working on is finished. If there are not any resource contents in
, then
,
,
.
If there is a subordinate relationship between and , which means that the resource type of is , then . This denotes that there is a directed edge from the father node to the child node . Otherwise, . For any , .
Assuming that quantities of
,
and
in
are indicated by
,
, and
, respectively, then the description of
is shown by Formula (11):
3.4. Inter-Layer Edges
The service content is determined by the working status of products, while service activities are executed on products by required resources. In the PSS multilayer network, some inter-layer edges exist between and , the rest exist between and .
3.4.1. Inter-Layer Edges Between and
For and , if , then , which denotes the directed inter-layer edge from to . This means that is one of the service objects of . Otherwise, . Meanwhile, only makes sense between and ; for or , .
Therefore, the set of inter-layer edges between
and
is as described by Formula (12):
3.4.2. Inter-Layer Edges Between and
Inter-layer edges between and include directed inter-layer edges from service nodes to resource nodes and directed inter-layer edges from resource nodes to service nodes. Their descriptions are depicted below:
The execution of service activities demands the resources be in corresponding specific kinds and quantities. If demands the resources whose type is , then , which denotes a directed inter-layer edge from to and the quantity demand is represented by integer weight . Otherwise, , . Meanwhile, only makes sense between and ; for other nodes, ;
If , , and , it means that is assignable to , then , which denotes a directed inter-layer edge from to . Otherwise, . Meanwhile, only makes sense between and ; for other nodes, . The reliability of being completed in time by is denoted by weight in [0,1].
Every has a different knowledge level and proficiency level about different . Assuming denotes the number of times that has been completed in the time by , denotes the total number of times that has participated in the execution of , then between and is represented by . Every has a constant function in a different . Assuming denotes the number of times that any has been completed in time by and denotes the total number of times that has participated in the execution of any , then between and is represented by .
The set of inter-layer edges between
and
, and the set of weights on these inter-layer edges are described by Formula (13):
Therefore,
is as given by Formula (14):
4. PSS Configuration Optimization
In most practical cases, many services are usually triggered at the same time. Consequently, the configuration optimization should be designed by considering multi-services. After any is triggered, service activities selection and resource allocation should be accomplished under given constraints to obtain the PSS configuration under constraint conditions.
Let us assume that the number of triggered
is
up to the point of time
. If
is triggered and is represented by
following Formula (15), then the situation of all
is represented by trigger matrix
with
:
As a result, service activities selection is regarded as a selection of the paths with multi as start points in . It is necessary to consider the executing time, cost, and reliability of in the selective relationship. The allocation of resources is viewed as resource allocation for multitasks (service activities), in which the cost and reliability of different are considered. Therefore, the services solution is optimized with the goal of executing time minimization, cost minimization, and reliability maximization.
4.1. Importance Degree of Service Activity
When a certain type of resource is required by several service activities simultaneously, then those resources with higher reliability should be allocated to more important service activities. Product parts are the objects of service activities; hence, the importance degree of product parts exerts a decisive influence on the importance degrees of service activities. Consequently, the importance degree of product parts is taken as the base of calculation for the importance degree of service activities, which provides a theoretical reference for the resource allocation.
Today, network-based importance measurement is thoroughly developed and widely applied. Various measure methods can be summarized as:
(1) Importance calculation methods based on neighbor relationships between nodes, such as degree centrality or semi-local centrality [
59];
(2) Path-based importance calculation methods, such as closeness centrality and betweenness centrality;
(3) Importance calculation methods based on eigenvectors, such as search algorithm LeaderRank [
60] and SRank [
61] based on algorithm PageRank [
62];
(4) Importance calculation methods based on node removal and contraction, in which the importance degree of nodes is measured by the variation in network attributes after node removal or contraction [
63].
4.1.1. Importance Degree of Product Parts
Importance calculation methods based on eigenvector are applied in this paper. In the concept of PageRank and LeaderRank, the importance of a page in a network is determined by the number and the quality of other pages pointing to it. However, the importance of
in
is ascertained by the number and quality of other nodes it points to. This makes PageRank and LeaderRank unsuitable for calculating the importance degree of product parts. Referring to the weighted LeaderRank [
64], PartRank is proposed to calculate the importance degree of product parts. Details are illustrated as follows.
A ground node
, which connects with every part node by a bidirectional edge, is introduced. Then
and
,
. Based on the concept of weighted LeaderRank, nodes with higher input intensity embody a higher probability of being visited by
. Inversely,
with a higher output intensity is more likely to visit
in
.
is consequently described by formula (16), where
is a free parameter,
is total number of nodes in
(excluding
).
is described as Formula (17):
The importance degrees are calculated iteratively until they reach a steady state. Assuming that calculation reaches a steady state at step
, then the importance degree of
will be allotted to every
. The importance degree of
is denoted as
, calculated as Formula (18),
where
is the input intensity of
in
.
4.1.2. Importance Degree of Service Activities
Knowing that the service object of
sa is
and if
is operated on
with a high importance degree, a designer should pay more attention to that
.
denotes the cross layer importance degree of
, which is related to the product parts on which
operates. The value of
is determined by
with the highest
in the set of service objects of
.
is consequently calculated by Formula (19):
After being normalized, the importance degree of is denoted as , where max is the maximum of all in . Therein, the virtual service activity node does not have any service object, so the importance degree of every virtual service activity node is consequently 0.
4.2. Mathematical Model
Define the binary variable
to indicate whether
is selected, and define the binary variable
to indicate whether to allocate
to
, by the Formulas (20) and (21), respectively:
The mathematical model of PSS configuration optimization is constructed by Formulas (A1)–(A15) in
Appendix A. The objective functions are given by Formulas (A1)–(A3) and constraints are given by the Formulas (A4)–(A15).
The objective function of executing time minimization is described by Formula (A1). The executing times of service activities are assumed to be fixed parameters, and they are not impacted by resource allocation. denotes the sum of executing times for all selected .
The objective function of cost minimization is described by Formula (A2). The executing cost of includes the fixed cost and the work costs of all resources allocated to , which are related to the executing times of . denotes the sum of executing costs of all selected .
The objective function of reliability maximization is described by Formula (A3). The executing reliability of
is determined by
of all
that are allocated to
. Therefore, a logic function
, which depends on
as the formula (A12) is defined. Then,
, denoting the executing reliability of
, is described as
. The target of reliability is always to maximize the executing reliability of the whole solution, which is related to the
of all selected
. However, if a certain type of resource is required by several service activities with overlapping service times, the allocation result of that type tends to make a
with a higher importance degree for reaching a higher
. Therefore,
is defined as the average executing reliability of all selected
, which is shown by Formula (22):
The of a with higher has a greater impact on the value of .
When and is assigned to , allocating to might be feasible. Therefore, is defined by the formula (A13). Here, means is allocated to successfully, means is not allocated to . Constraints for and are shown by Formulas (A14) and (A15). Constraints for the three objective functions are developed as indicated below:
All selected service activities must be part of the construction for the triggered service flows. They are represented by Formula (A4);
Every service flow starts with the triggered , and the out-degree of is 1. This is expressed by Formula (A5);
The number of triggered is . All triggered service flows end at . Consequently, the in-degree of is . This is shown by Formula (A6);
If all selected service activities constitute complete service flows, there will not be any selective relationship between selected and . As a result, the sum of weights on edges from triggered and selected to will equal to the sum of weights on edges from to and selected . This is shown by Formula (A7);
For every triggered , . Every triggered flow must be completed within the service time range requested by a customer, as illustrated in Formula (A8);
The resources allocated to the selected must satisfy the constraints as the resource type and the quantity demands of . This constraint is denoted by Formula (A9);
Every can only participate in a maximum of one service activity at the same time. For all service activities that is allocated to, their service time intervals cannot overlap. Defining oljh indicates whether there is any overlap between the service time intervals of and , as shown in Formula (A11). That constraint is described by Formula (A10).
4.3. Obtaining the Optimal Solutions
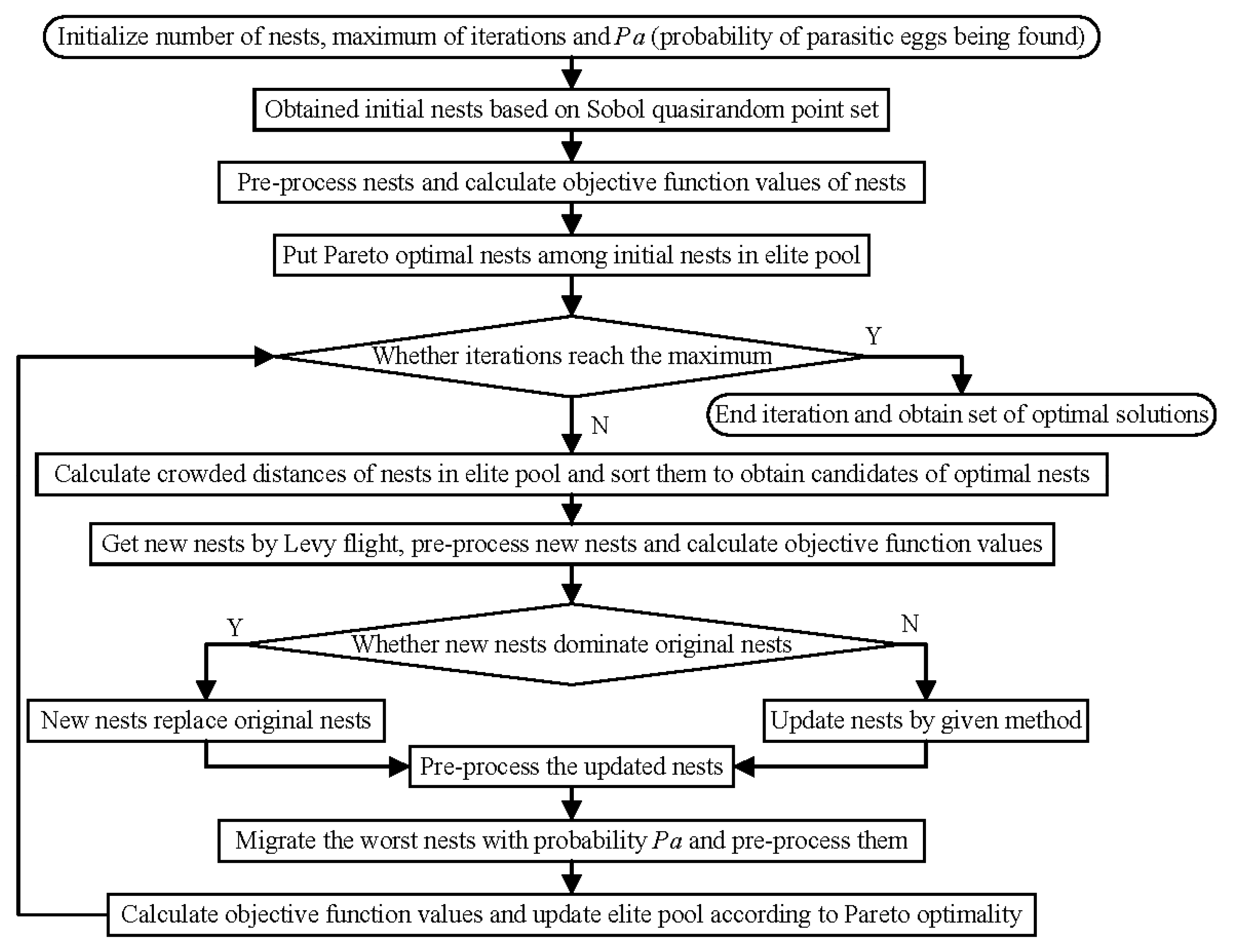
To obtain the optimal solutions by the trigger matrix and the proposed mathematical model, the solving procedures are as follows.
- Step 1:
Obtaining
as the service activities solution set for
, the number of solutions is denoted as
. If
, obtain
by Depth-First Traversal (DFT), wherein
is the set of all service activities selected in the
time traversal; if
,
is not activated, then
,
, wherein
.
is different from ordinary complex networks, and as a consequence, the traditional DFT is unsuitable for
. Depth-First Traversal based on service layer (SL-DFT) is designed and detailed in
Section 4.3.1.
- Step 2:
Solutions of service activities for each triggered are arranged by permutation and combination. Obtaining a solutions set of service activities as for system, , .
- Step 3:
Using the Pareto-improved multiple-objective discrete cuckoo search algorithm (Pareto-IMODCS) [
23] to obtain the set of optimal solutions of resource allocation for each
as
, the number of solutions is denoted as
. Pareto optimality and Pareto-IMODCS are detailed in
Section 4.3.2 and
Section 4.3.3, respectively.
- Step 4:
Merging all into one as , filter to obtain the set of non-dominated solutions as based on Pareto optimality. is the final set of optimal solutions.
4.3.1. Obtaining Solutions of Service Activities by SL-DFT
Obtaining by SL-DFT involves searching all paths from to in . Assuming the current visited node is :
If and , then add node into the path and continue searching from ;
If and , nodes satisfying are in a selective relationship, then select one of these to visit. Assuming that the selected node is , continue to search from until all paths from to are obtained, then backtrack to , selecting an unvisited node from nodes satisfying to visit. This new search forms a new path, so nodes visited in the search from can still be visited. Repeat this step until all nodes satisfying are visited;
If and , it means nodes satisfying are in a parallel relationship. Then, select one to visit and continue searching until the visited node satisfies and , which means is the confluence node of these parallel paths. Then, backtracking to , select an unvisited node from nodes satisfying to visit. Repeat this step until nodes satisfying are all visited. Add all nodes visited in this step into the path and continue to search from .
After all paths from to are obtained, if is a service trigger node, then end the search. Otherwise, backtrack to the node before . Based on the above search, service activity compositions obtained by SL-DFT satisfy the constraints as given by Formulas (A4)–(A7).
4.3.2. Pareto Optimality
In the optimizing process, the solution with smaller executing time, smaller executing cost, and greater executing reliability is considered better. However, objectives in one solution might conflict with each other in reality. Traditional linear weighting methods are unsuitable for solving such multi-objective optimization, which could be solved based on Pareto optimality [
65].
If and satisfy that , and , and at least one of these inequalities is a strict inequality, then dominates . If is not dominated by any , then is a non-dominated solution, which is the Pareto optimal solution.
4.3.3. Obtaining Optimal Solutions of Resource Allocation by Pareto-IMODCS
Let us assume that the number of in is regardless of , , and virtual service activity nodes. The types and quantities of resources that every demands can be determined based on the multilayer network model. Then, each possible resource allocation solution is represented by a cuckoo nest: the dimension of nest represents the th resource instance for the th resource type demand of the th in set ; various instances in each dimension are all represented by decimal integers. The subscript number of the service activity node corresponding to the th is denoted as . The subscript number of the resource type node corresponding to the th resource type is denoted as . and facilitate in decoding the nest into the corresponding resource allocation solutions, which satisfy the constraint defined by Formula (A9).
The original Pareto-IMODCS algorithm is detailed in reference [
23]. If multiple
in
demand same type of resources in the same time interval, the solution obtained by the original Pareto-IMODCS algorithm might allocate the same resource instance to multiple
simultaneously. This does not comply with the constraint described by Formula (A10). To avoid this, a “nest pre-processing” step is added to Pareto-IMODCS. The specific procedures of the improved Pareto-IMODCS algorithm to obtain Pareto optimal solutions for each
are shown in
Figure 5.
The procedure “nest pre-processing” is specified as: for any two dimensions as and , when and , it means that the same resource instance is allocated to multiple dimensions. If or , it denotes that service activities related to and are the same one or their working time intervals overlap, then and .
5. Case Study
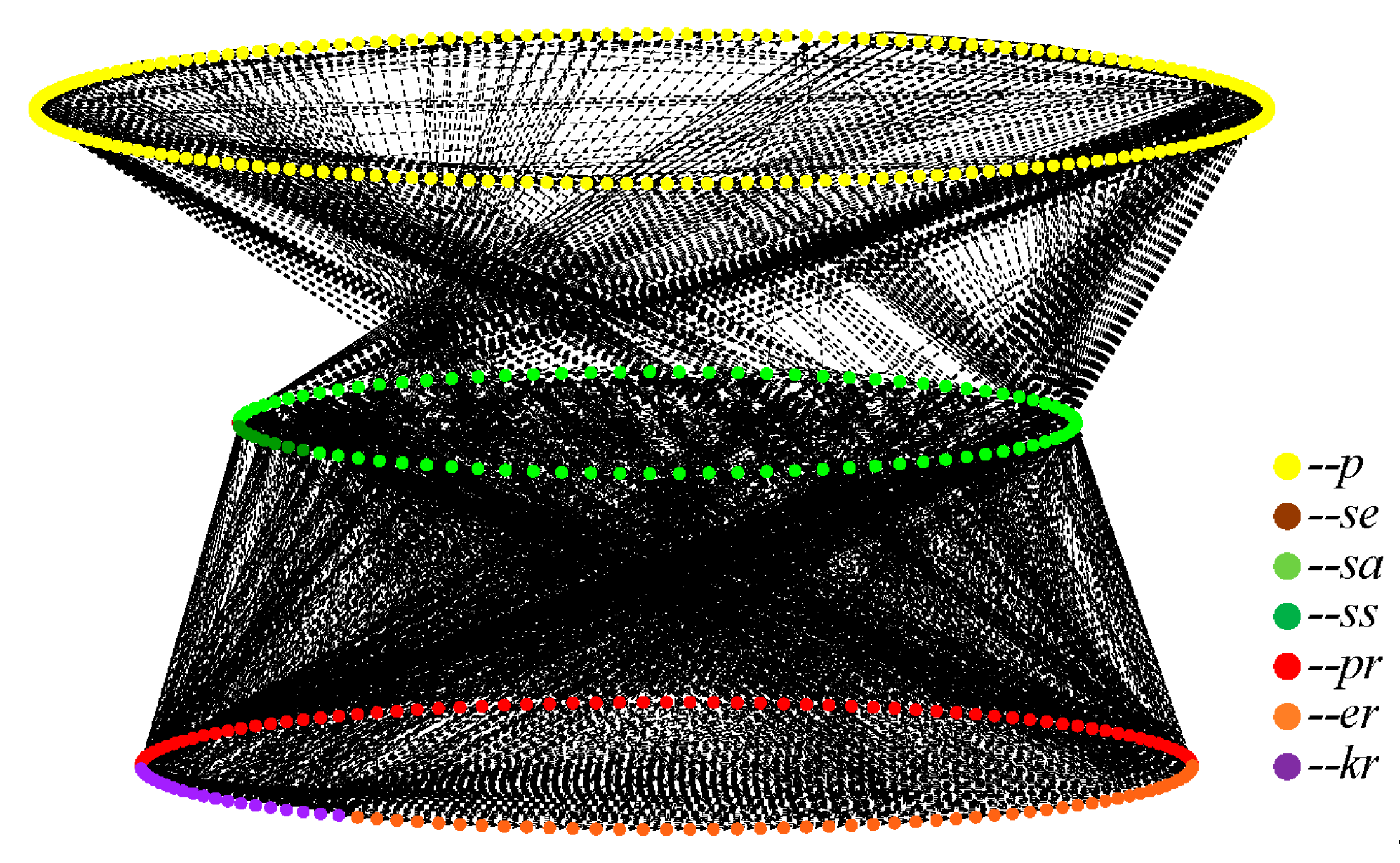
In this section, a case study for the PSS of an automobile enterprise is provided to validate the proposed multilayer network-based PSS model and the fine-grained PSS configuration optimization method. A product was delivered to a customer with a contract to implement eight selected services (running system maintenance, steering system maintenance, braking system repair, etc.). These services could be decomposed as service flows consisting of service activities. For example, running system maintenance was decomposed as the maintenance of axles, maintenance of suspensions, maintenance of shock absorbers, maintenance of wheels, and maintenance of frames. As indicated, the PSS of the automobile enterprise was modeled as a multilayer network, which included 193 product nodes, 89 service nodes (1 , 80 , and 8 ), and 140 resource nodes (70 , 50 , and 20 ).
When services are triggered, a set of PSS configuration solutions should be provided to the customer for making a final decision. The customer’s desired performances for the final solution were the minimal executing time and cost and maximal executing reliability. The designer had a PSS configuration optimization task at time
, which contained the configuration of services as running system maintenance (
) and steering system maintenance (
). The network status of the case at time
is modeled in
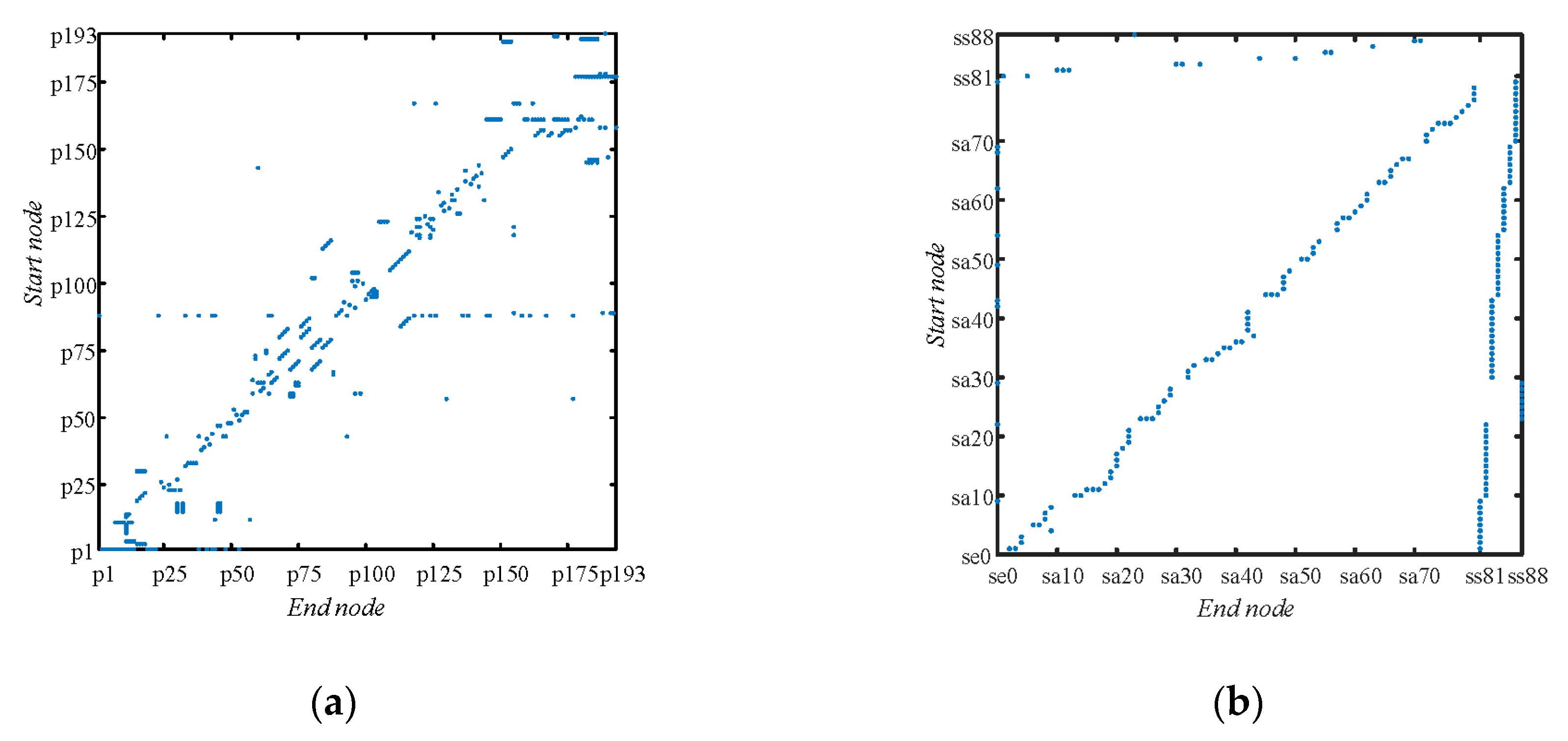
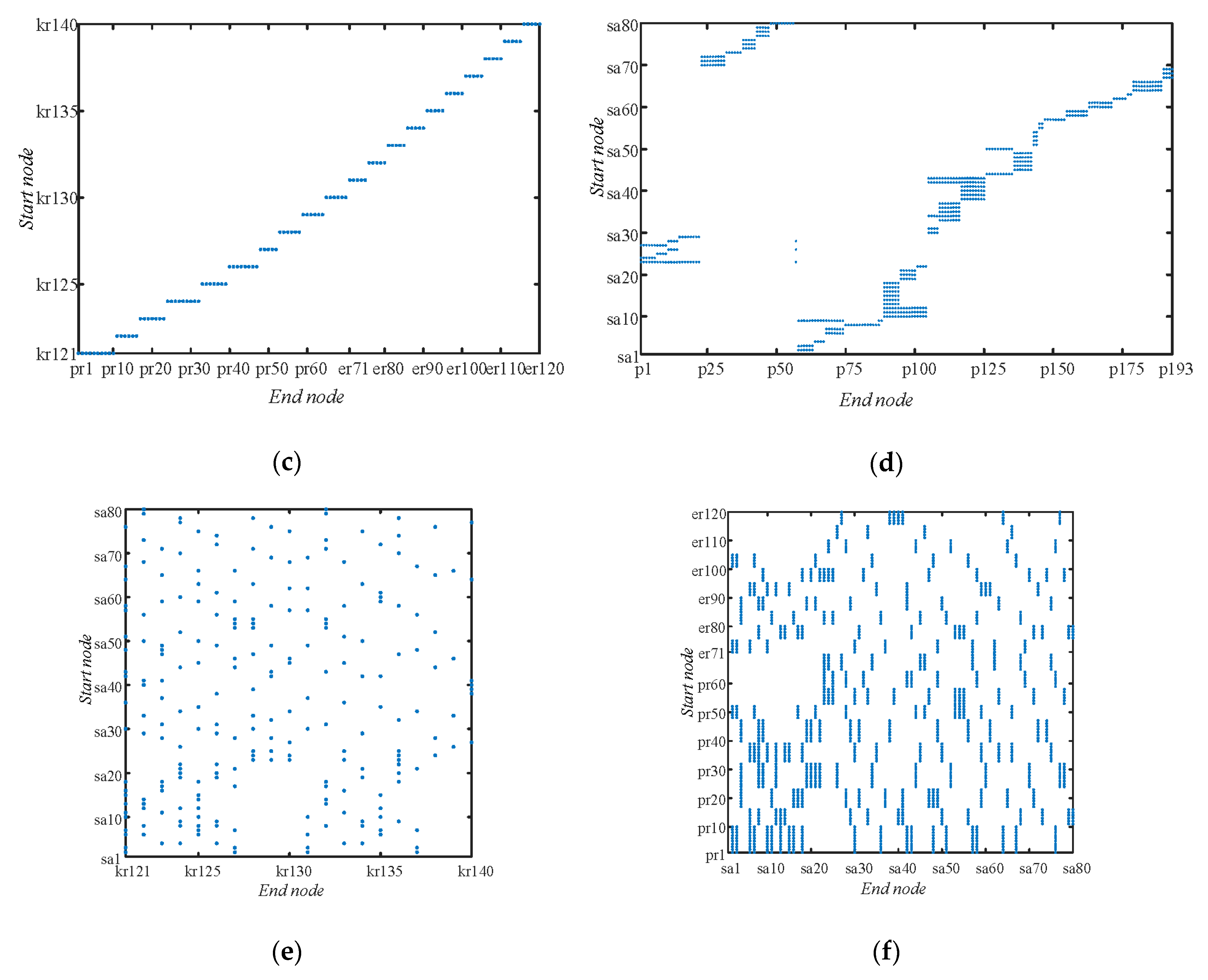
Figure 6, in which the sparse matrixes of edges denoting corresponding relationships among nodes in multilayer network are detailed in
Figure 7.
According to the PSS configuration optimization task, the trigger matrix at time
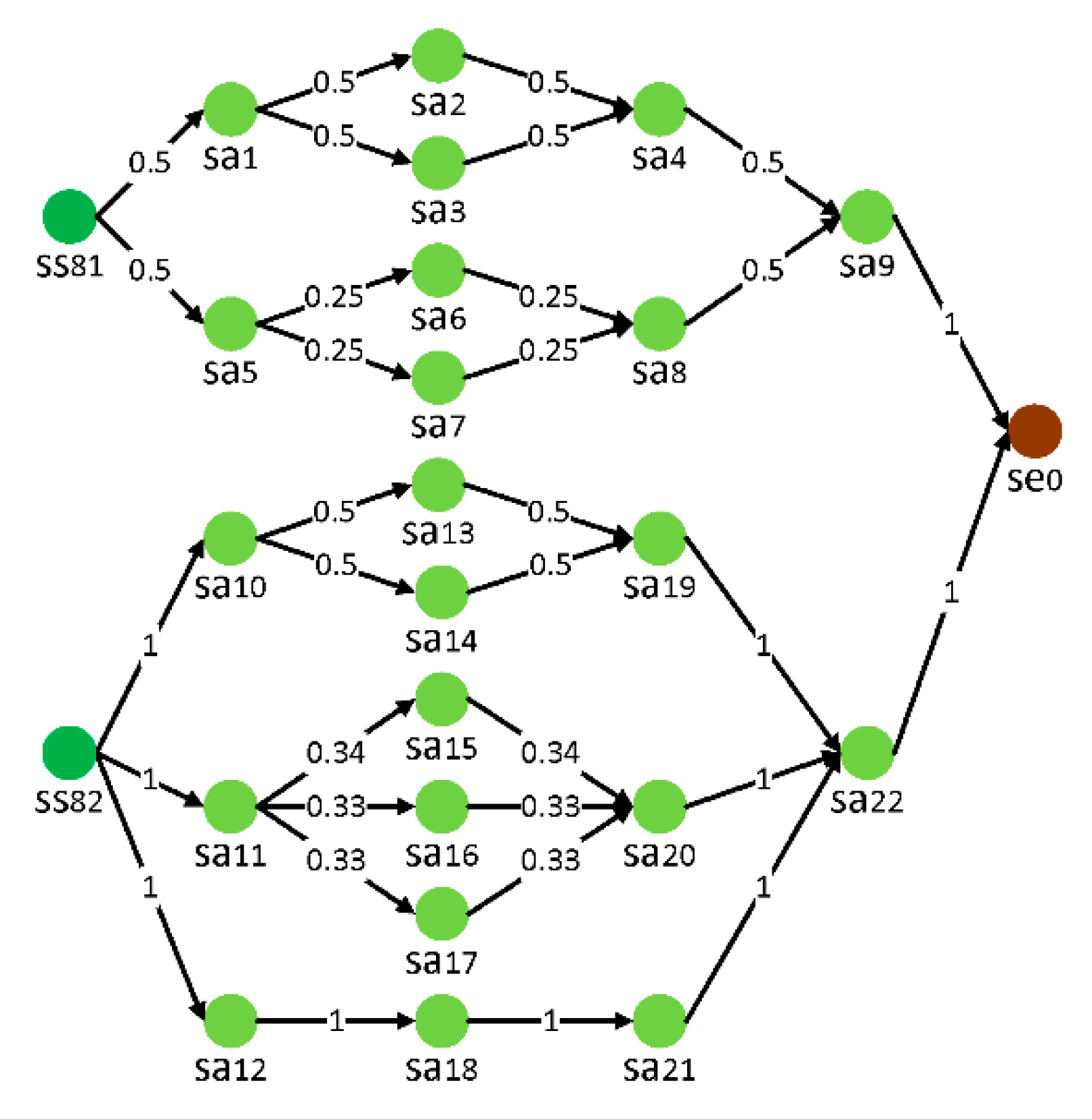
was [1 1 0 0 0 0 0 0]. Structures of triggered service flows in service layer are detailed in
Figure 8. The executing time, cost, and reliability of related
are detailed in
Table 1. It is evident that
and
were virtual service activity nodes. The cost for all
working in one unit of time is shown in
Figure 9.
In the above-mentioned network status and solution constraints, all paths from triggered
to
and all paths from triggered
to
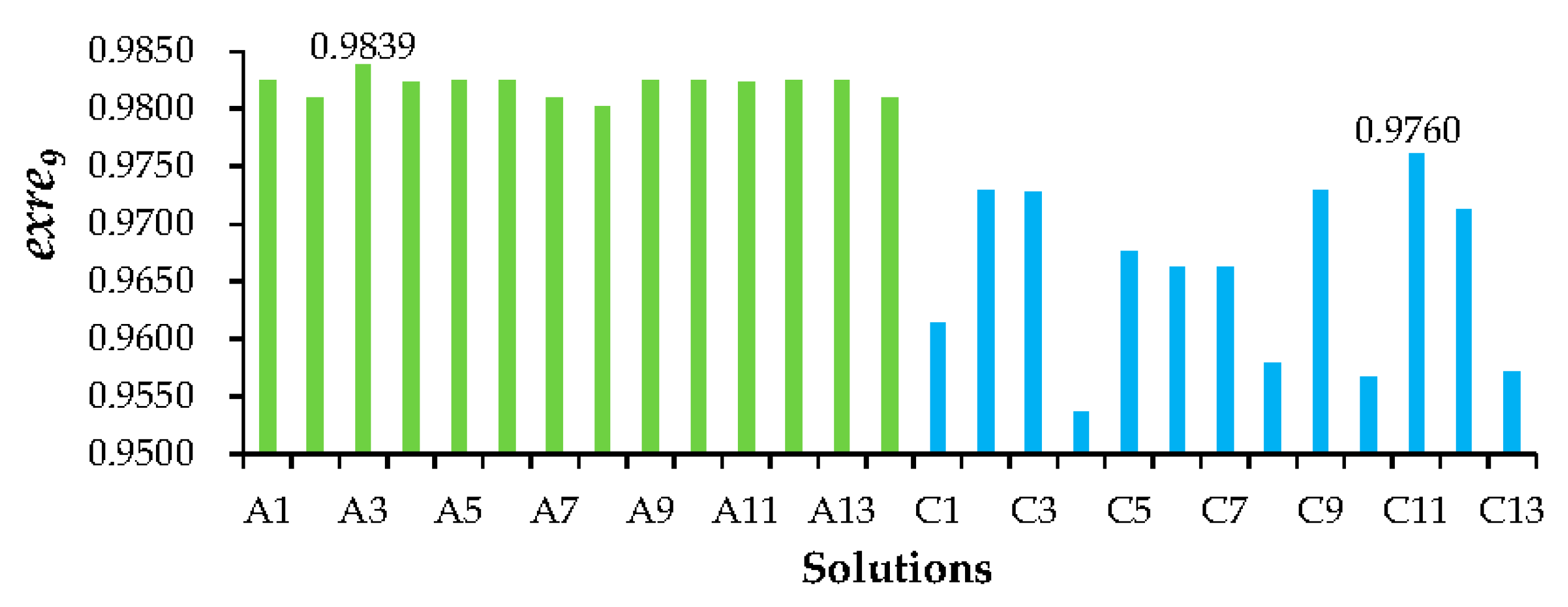
were searched by SL-DFT. Then, one from both sets of paths was selected to form service activity compositions. Pareto optimal solutions of resource allocation for every service activity composition were obtained by using the mentioned improved Pareto-IMODCS algorithm. Relevant parameters of the algorithm were as follows: the number of initial nests was 200, the probability of cuckoo eggs being found was 0.25, the maximum number of iterations for a nest was 3000, and the number of times of an iteration run was 10. Then, solutions of all compositions were filtered according to Pareto optimality. As a result, 14 non-dominated solutions were obtained, which were recorded as set A (
Table 2).
5.1. Comparison with Method For Selecting Service Activities Before Resource Allocation
To validate the effectiveness of combining service activities selection and resource allocation, the same case was solved with another method as a contrast. In summary, the details were as follows:
Firstly, all paths from triggered
to
were searched by SL-DFT and all service activity compositions were obtained. Next, all compositions were filtered by objective functions as executing time, cost, and reliability to obtain Pareto optimal service activity compositions. Then, Pareto optimal solutions of resource allocation for each composition were acquired using the improved Pareto-IMODCS with same parameters as last time. Finally, all solutions were filtered according to Pareto optimality. As a result, six non-dominated solutions were recorded as set B (
Table 3).
By analyzing solutions in
Table 2 and
Table 3, it can be found that set A and set B share four common solutions. Nevertheless, set A also contains other solutions in which service activity compositions are different from solutions in set B. The other two solutions in set B (solutions B5 and B6) are dominated by solution A3. Obviously, combining the service activities selection and resource allocation effectively enriches the diversity of the optimal solution set by retaining more non-dominated solutions. The last ones might have been hindered by using the method where service activities selection finished individually before resource allocation.
5.2. Comparison with the Method Using Different Objective Functions
By calculating the importance degrees of service activities related to triggered and , it was found that the importance degree of is significantly higher than other service activities. Reverting to the actual setting of the case, was frame maintenance in the running system maintenance. The frame is the base of the whole automobile assembly, which makes frame maintenance more important compared to other activities in the maintenance of the running system and the steering system.
To validate the maximization of , an objective function which improves the executing reliability of service activities with higher importance degrees, the same case was solved in another way, as follows.
The value 1 was given to the weights of all
in the objective function of executing reliability, regardless of the importance degrees of the service activities. The altered objective function of the executing reliability is shown in Formula (23), where
denotes the overall executing reliability of all selected activities. As a result, 13 Pareto optimal solutions were obtained, which were recorded as set C.
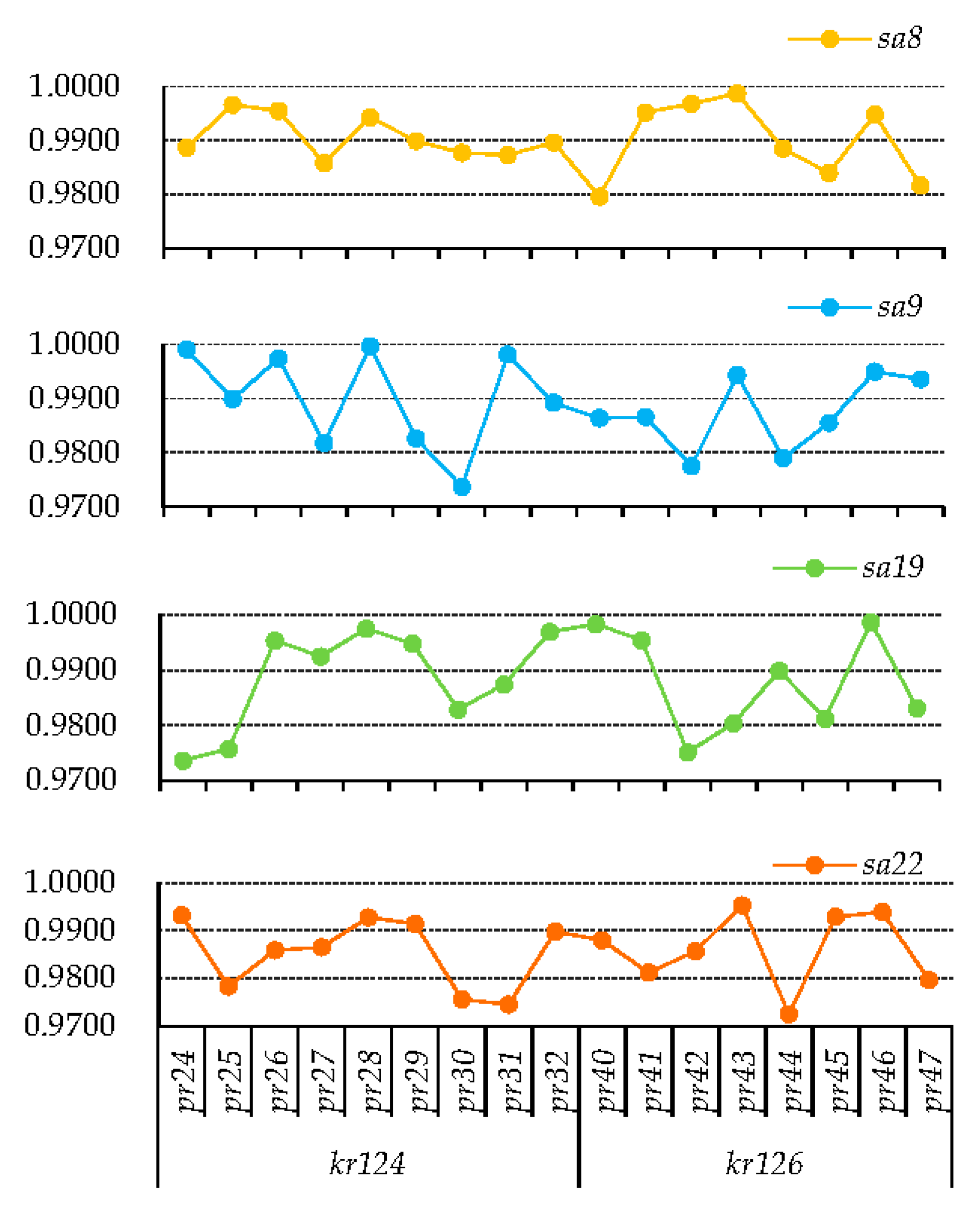
The executing reliabilities of
(
) in different solutions with set A and set C are shown in
Figure 10. The values of
in set A are all higher than those in set C. The values of
in solution A3 and C11 are the highest in set A and set C, respectively. Service activity compositions in solution A3 and C11 are the same. Comparing and analyzing these two solutions shows why maximizing
, as one of the objective functions, could facilitate more beneficial solutions, in which service activities with higher importance degrees have higher executing reliabilities.
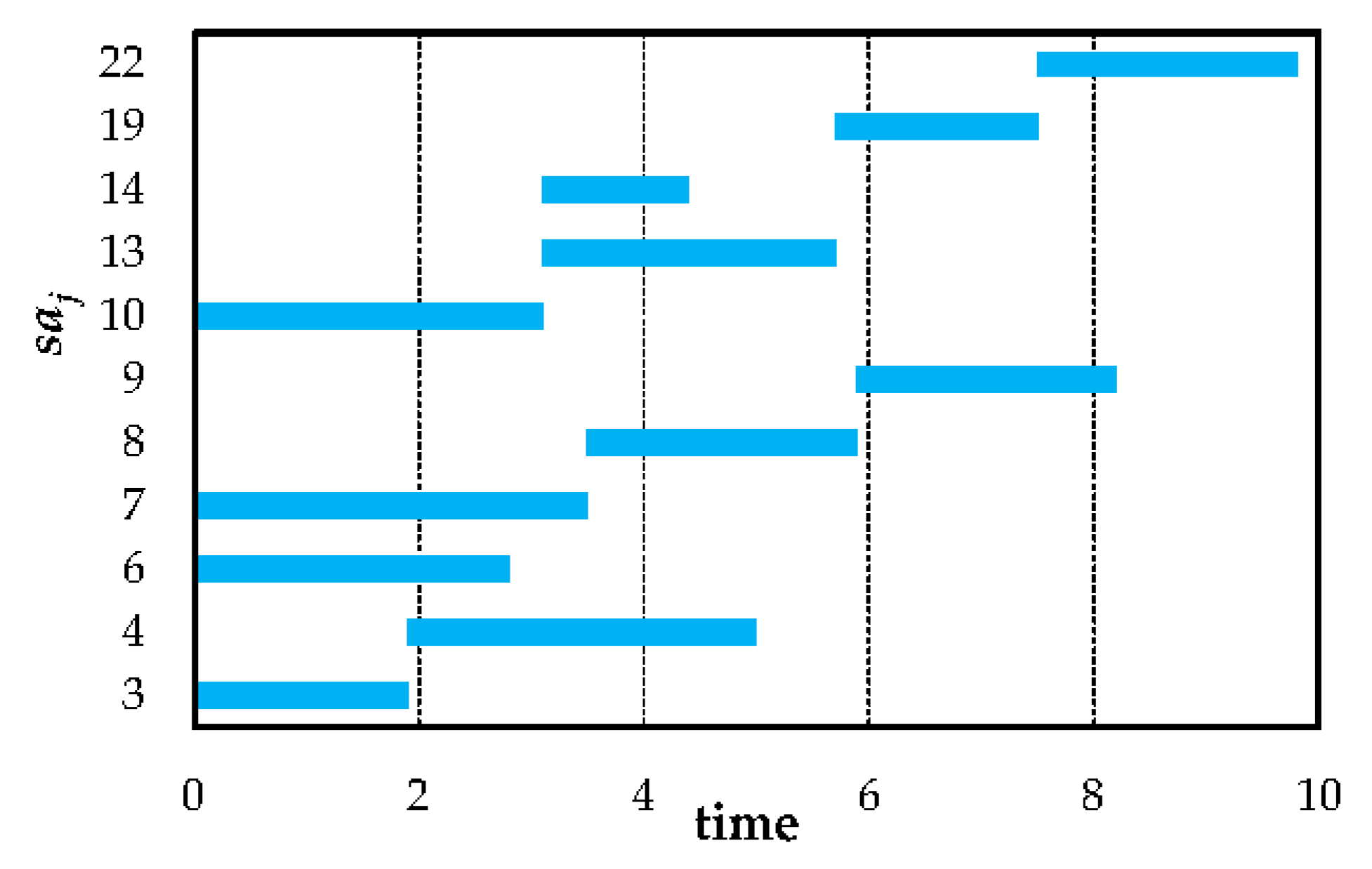
The Gantt chart of selected service activity nodes in solution A3 and C11 is depicted in
Figure 11. From the perspective of the service time interval,
overlaps with
and
,
overlaps with
,
overlaps with other nodes. Situations of service time interval overlap between service activities are intricate. Consequently, resource allocation of one activity might influence another one and indirectly impact other activities.
The types and quantities of resources demanded by
,
,
, and
are shown in
Table 4. The actual situation of resource allocation about the
related to
in solution A3 and C11 is illustrated in
Table 5.
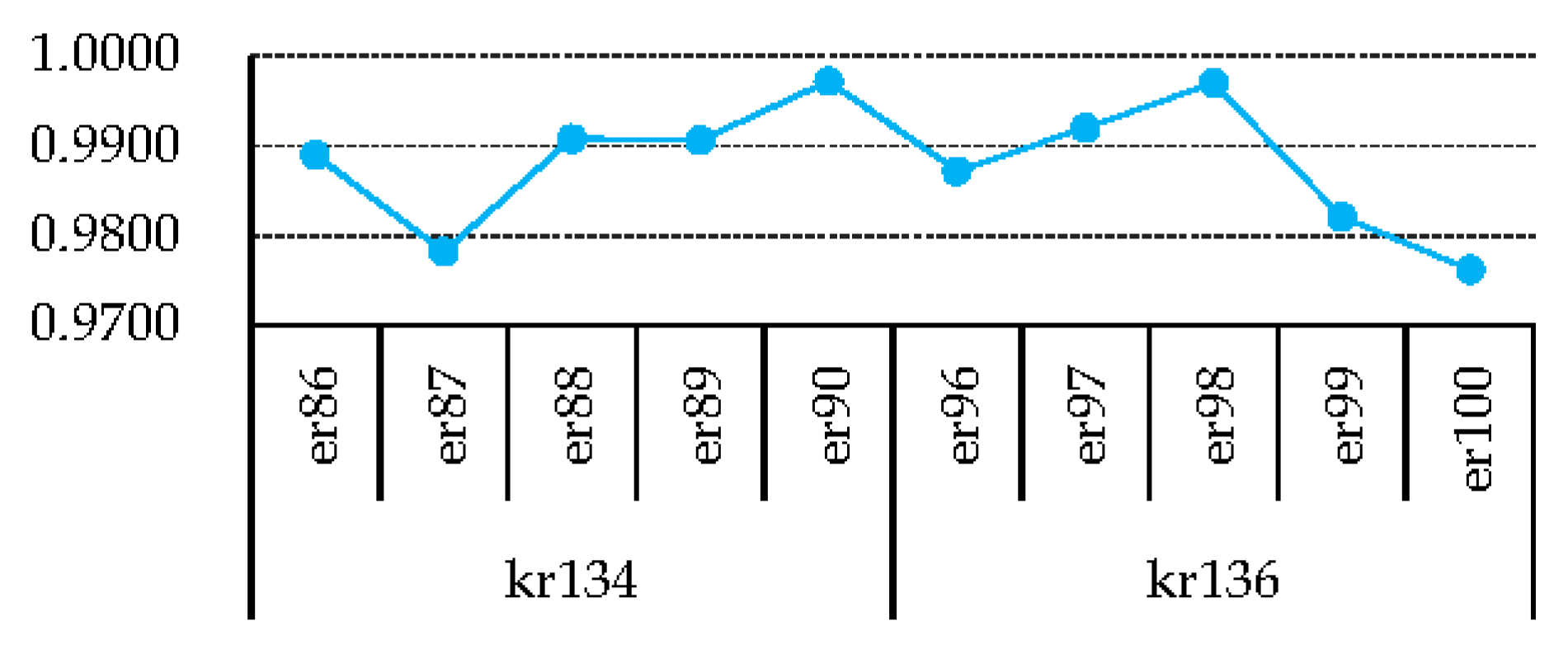
on the edges that connect
and
(all
and
that are related to
,
,
, and
) are detailed in
Figure 12 and
Figure 13.
The decision process in multi-objective optimization is complicated. In solution C11,
with the highest
is not allocated to
in the process of overall executing reliability maximization. In solution A3,
,
,
, and
are all allocated to
.
of these four resources is the highest among the same type of resources. In turn, the
in solution A3 is higher than solution C11. For the remaining three
, for whom the importance degrees are not conspicuously higher than each other, the resource allocation is not only based on
, but also on the cost (as shown in
Figure 9). By including the importance degree of
with the objective function of executing reliability as weight, it enables more important
to have higher executing reliabilities, by allocating
with the highest
to this
. If the importance degree of
is significantly higher, the impact on the overall executing reliability and executing cost will be tolerable.